An integrative clustering and modeling algorithm for dynamical gene expression data

Abstract

Motivation: The precise dynamics of gene expression is often crucial for proper response to stimuli. Time-course gene-expression profiles can provide insights about the dynamics of many cellular responses, but are often noisy and measured at arbitrary intervals, posing a major analysis challenge.

Results: We developed an algorithm that interleaves clustering time-course gene-expression data with estimation of dynamic models of their response by biologically meaningful parameters. In combining these two tasks we overcome obstacles posed in each one. Moreover, our approach provides an easy way to compare between responses to different stimuli at the dynamical level. We use our approach to analyze the dynamical transcriptional responses to inflammation and anti-viral stimuli in mice primary dendritic cells, and extract a concise representation of the different dynamical response types. We analyze the similarities and differences between the two stimuli and identify potential regulators of this complex transcriptional response.

Availability: The code to our method is freely available http://www.compbio.cs.huji.ac.il/DynaMiteC.

Contact: nir@cs.huji.ac.il

1 INTRODUCTION

Understanding a complex transcriptional response to stimuli is a key goal in biological research. Such a response involves a timely activation and repression of hundreds of genes, requiring a tight and accurate regulation. For example, the transcriptional response to inflammation in immune cells in mice is regulated by at least a dozen transcription factors, operating through different modes of activation, including fast responding factors (e.g. NFκB) and secondary response factors synthesized de novo during the response (e.g. Irf8), resulting in a wide range of dynamical transcriptional responses (Gilmore, 2006; Medzhitov and Horng, 2009). Thus, to fully understand the transcriptional response, a static analysis indicating which genes are induced at one given time point is not sufficient, and it is important to analyze the transcriptional dynamics of the induced genes.

A widely used approach to study transcription dynamics is by collecting time course measurements of gene-expression in predefined time points following a stimuli. A possible concern in analysis of such data is the inherent limitation of gene-expression measurements. These are exacerbated by the temporal aspects of the data—the chosen time points might not capture the interval in which a gene is up-regulated. As a result this data is often difficult to analyze, and the comparison between experiments carried over different time courses is non-trivial.

In the literature there are several approaches for analysis of time-course data. One approach is to cluster the data so that every cluster captures a group of genes with similar dynamical response. This can be done using traditional clustering algorithms, such as K-mean (Duda and Hart, 1973). However, the standard distance functions are not adequate to handle the given data which is sampled at various non-uniformly distributed time points. Several works addressed this specific task, Ernst et al. (2005) addressed this obstacle by assigning genes to a preselected set of potential profiles. However, the set of potential profiles are not selected from the data, and might contain profiles that do not represent true biological responses. An additional obstacle is that the clustering is done on the noisy and missing expression patterns of genes which might lead to false assignments to clusters. Thus, an unbiased clustering algorithm fitted for this type of data is needed.

An alternative approach is to consider a mathematical model of the response dynamics, and then fit it to measurements. This in effect, translates the discrete measurements to a continuous function from a biologically plausible family of functions. Moreover, the parameters of this class of functions can be biologically relevant and mark the important aspects of the dynamics e.g. point of induction). For example the impulse model proposed by Chechik and Koller (2009) (is designed to capture the typical impulse-like response to a stimulus, using a function with biologically meaningful parameters. A problem with models such as this one is that they have many parameters and can lead to overfitting over a typically small number of time points. In addition, the modeling is done per individual gene, thus clustering is still necessary to obtain a concise representation of the dynamical responses types.

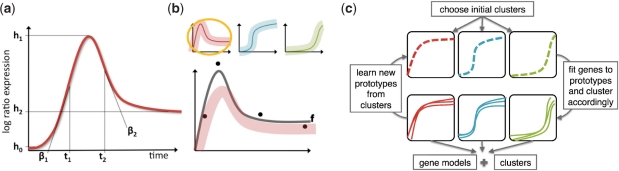
Here, we present DynaMiteC (Dynamic Modeling and Clustering), an integrative approach that simultaneously models time course gene-expression profiles with biologically meaningful parameters, and assigns them to clusters of different dynamical responses. Our approach is to model gene responses using an impulse model (Fig. 1a). Our premise is that many genes have a similar response. Thus, instead of estimating the profile of each gene separately, and thus risk overfitting, our method estimates the profile with a prior that prefers to match one out of a set of ‘prototype’ responses (Fig. 1b). We thus pose the parameter estimation task as jointly learning the prototypes and the parameters of individual genes. When learning these prototypes we, in fact, assign genes to clusters. These two problems are solved by iterating between them (Fig. 1c).

Fig. 1.

An integrative clustering-modeling algorithm. (A) The impulse model capturing a two-phase temporal response by a product of two sigmoids, with parameters: onset time (t₁), offset time (t₂), the original baseline height (h₀), peak response height (h₁), new baseline height (h₂), onset rate (β₁) and offset rate (β₂). (B) Fitting the model to the data with mixture priors on the parameters (bottom), which are distinct prototypes of responses (top). (C) A scheme describing our integrative clustering and modeling algorithm DynaMiteC: (i) Choosing initial clusters. (ii) Iterating between optimizing the fit to the genes and optimizing the prototypes. (iii) The resulting models per gene and clusters.

We used DynaMiteC to study the responses to two related stimuli in mice primary dendritic cells that simulate either inflammation (LPS stimulus) and anti-viral infection (polyIC stimulus). In their experiment, Amit et al. (2009) collected gene expression measurements of a dense time course following the stimulus. We show that our revised impulse model and algorithm result in a good fit for the induced genes and meaningful clusters. We reveal distinct types of dynamical response to stimulation, and compare between genes that have the same dynamical response under both conditions and other genes that change their response dynamics. In addition, we point out potential transcription factors that could regulate this complex transcriptional response.

2 MODELING WITH MIXTURE PRIORS AND CLUSTERING

Suppose we want to model time course data. A model is a family of functions f(t : θ) that for each choice of parameters θ (in a space of legal parameters Θ) determines how the expression behaves as a function of t (time). To simplify the discussion, we assume that f is differentiable with respect to {θ and that Θ is a convex set. We discuss an example of such a family of functions based on the impulse model explained below.

2.1 Mixture priors

We start by setting up the learning problem and examine how to integrate priors into the modeling procedure and their importance. Given a series of data points describing the behavior of a gene g, 𝒟_g=〈(t₁, x_1,g),…,(t_k,x_k,g)〉 (where x_i,g is the expression value of gene g at time point t_i) we define the loss (or error) of a set of parameters θ as the sum of square differences between the predictions and the observations:

We can also think of ℓ(θ:𝒟_g) as the negative of the log-likelihood of the parameters if we assume that the data has a Gaussian noise on top of the signal.

A natural way of parameter fitting is to find the parameters that minimize the loss (equivalently, maximize the likelihood):

The method for solving this optimization problem depends on the choice of f. However, in general we can use non-linear optimization methods, such as conjugate gradient descent, to find a solution (in the worst case, the solution will be only a local minima).

A major problem of using such a model in practice is the ratio between the number of observations and the number of free parameters. Since typical time-course experiments consists of few time points (5–10 points) (Ernst et al., 2005), fitting any non-trivial model is prone to overfitting.

There are multiple ways to avoid overfitting. An often used one is using a prior on the parameters, or similarly, a regularization penalty (such as L₂ or L₁ penalization) (Bishop, 1995; Gelman et al., 1995). A simple approach to integrate priors is to choose a set of parameters η that we take to be ‘prototypical’ and a distance function d_ω. Then, we can define the penalized loss over parameters as:

Where the first term is the fit error between the predictions and the observations, and the second term is the penalty for the function's parameters compared to the set of prototypical parameters, i.e. the prior (Fig. 1b). The relative contribution of each term to the overall loss can be set by the weight parameter ω, as well as the relative contribution of each parameter. We discuss how to choose ω in Section 3.

For this to match our intuition, we require that d_ω is non-negative and that d_ω(x,x)=0. For example, a natural term is a quadratic distance, where we essentially treat the parameters as though we have a Gaussian prior.

When we have such a prior, we can use maximum a posteriory estimation (MAP) to find the parameters that maximize the posterior:

The MAP estimate thus will balance between similarity of the parameters to the prior parameters η and the fit to the data. This tradeoff is governed by the weight parameter ω of the distance function d_ω. If the data supports parameter values that are far from these in η, the prior will force the parameters to be close to the prototype. Such regularization helps reduce the effect of noise on the estimation process and reduces overfitting.

While helping us to avoid overfitting, the prior, however, biases our estimates toward the parameters η. To deal with this problem, we assume that the responses can be divided into groups of genes with similar responses (Fig. 1b). In such a situation, we can assume that there are several distinct prototypical responses 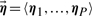, each corresponding to a range of responses with similar parameters. Such a prior is called a mixture prior (Gelman et al., 1995) or a hierarchical prior (Koller and Friedman, 2009), as it assumes that the prior involves first choosing which class the instance belongs to, and then choosing the appropriate parameters for that class.

In the mixture prior, given d_ω and a set of prototypes, we define the posterior loss as

And similarly define 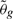as the parameters that minimize this loss:

This minimization problem can be solved by running P (the number of prototypes) minimization problems, one per prototype.

2.2 An integrative clustering-modeling algorithm

We motivated the use of a mixture prior by the assumption of several clusters of genes with similar responses, which we represent by distinct prototypes. When analyzing a dataset, we do not know these a priori, but rather need to estimate them from the data. This leads to a classical circular problem, which we solve using an iterative algorithm that alternates between improving the modeling of genes and improving the prior (prototypes).

To make the description of the algorithm clearer (Fig. 1c), we start with initial sets of genes with similar response. From these sets (clusters) we learn the prototypes. We fit each gene with a model using these prototypes as the mixture prior. During the fit we learn the model's parameters and the prototype that minimize the loss for each gene (see Section 2.1). Thus we can assign the genes to clusters according to their typical prototype.

We now explain this formally, starting with some definitions. We assume that the dataset consists of multiple sets (clusters). Each gene has an assignment to its typical prototype denoted p_g. A prototype assignment 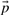is a vector of all assignments p_g for each gene. Given 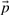, the loss of each gene is defined by its loss with respect to the p_g. The total loss of a set of prototypes and prototype assignment is the sum of the loss of individual genes.

We now can formulate our alternating procedure as step wise improvement of this objective.

• Cluster step: Given a set of prototypes 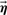, assign genes to prototypes and find their model parameters θ

  
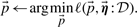
• Prototype step: Given assignment of genes to prototypes 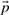(clusters), improve prototypes

  

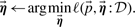
Since each step minimizes the global loss, alternating repeatedly between these steps will converge to a (potentially local) minima of the loss function.

We now elaborate on each step: Cluster step For each gene g we find the optimal parameters θ_g and typical prototype pg. The choice of pg is independent of the choice of prototype assignments to other genes. Thus, for each gene g, we perform:

This is done using gradient descent search for each value of p. Note that while optimizing p_g we also find the parameters θ_g that minimize .

Prototype step Here, we note that the choice of prototype parameters for each prototype is independent of the choice of other prototypes. Thus, we want to solve the optimization problem

Using simple but tedious algebraic manipulations, we can show that this is equivalent to performing the optimization

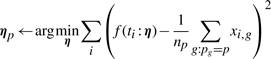where n_g is the number of genes with p_g, and x_i,g is the value at time t_i for the gene g. Stated differently, we choose the prototype η_p to fit the average expression of all genes assigned to prototype p. This again is a simple optimization in our model.

2.3 Relation to K-means

The procedure we described above is analogous to K-means (Duda and Hart, 1973). In fact, it is easy to show that K-means is a special case of this procedure. Suppose we define the parameter vector to be a vector of length k 〈μ₁,…,μ_k〉 and then define

Suppose we use this choice of ‘model’ family, and a quadratic distance function and the weight vector where 〈c₁,…, c_k〉 with c>0. Then, the procedure we describe above reduces to the standard K-means clustering procedure.

To see this, note that the prototype step reduces to finding the centriod of each cluster. Now consider the Cluster step. In this particular setting, we have

Using simple arithmetic, this reduces to

which is the K-means cluster selection step.

3 THE IMPULSE CLUSTERING APPROACH

We now apply this general framework for a relatively simple model of temporal gene expression based on the Impulse model (Chechik and Koller, 2009). This model is designed to capture a two-phase temporal response by describing an impulse function as a product of two sigmoids: The first describes the response onset (dealing with the stimulus), and the second describes the response offset (return to a new baseline) (Fig. 1a). The parameters of this model describe the time of the onset (t₁) and the time of the offset (t₂), three amplitude parameters: the height of the original baseline (h₀), peak response (h₁) and new baseline (h₂) and two slope parameters to models the rate of the onset and the offset (β₁, β₂, respectively).

Formally, given a parameter set θ=〈h₀,h₁,h₂,t₁,t₂,β₁,β₂〉 an impulse function has the form:

where

is a sigmoid that ranges between h_s and h_e with mid-point at time t_m and a slope of β·sign(h_e−h_s) at time t_m (the point of fastest change).

Our model differs from the original Impulse model of Chechik and Koller (2009) in several points: (i) We allow different onset and offset rates, as these rates are governed by different molecular processes: transcription and RNA degradation; (ii) Responses can have one or two phases. We require that two-phased responses are only of the following types: an increase in the expression level followed by a decrease, or a decrease followed by an increase.

We use this class of models in the generalized K-means procedure described above with the quadratic distance function.

In our implementation, we start the procedure with initial clusters obtained from the standard K-means procedure, using Pearson correlation coefficients as a distance measure.

To learn the number of clusters k and weight vector ω, we used a leave-one-out cross-validation procedure, which was repeated for every pair of potential k and ω. In more details, we apply the algorithm after excluding one randomly chosen time point for each gene (repeated five times). For each gene, we calculate the mean fit error for the missing time point (comparing the predicted value to the observed value), and the robustness of the assignment to clusters between the five repeats. We chose k and ω that minimized the mean fit error and maximized the robustness to cluster assignment.

4 EVALUATION ON SYNTHETHIC DATA

To better understand the properties of the Impulse clustering procedure, we started by examining its behavior on synthetic data where we know the underlying ‘truth’ and can change various properties of the data in a controlled manner.

Starting from cluster prototypes we generated data using two types of variation. First, the amount of variation within each cluster: how much the parameters of each gene deviate from the prototype it was generated from (using multiplicative Gaussian noise). Second, the noise in the data: how much the observed log-ratio expression value differs from the actual value for the gene (using additive Gaussian noise). From each prototype we created a set of 110–150 genes sampled across different time series (Fig. 2a), for each such gene both the model parameters and its cluster (according to the original prototype) are known. In this setting, we can test both our modeling method (prediction on new time points) and clustering method.

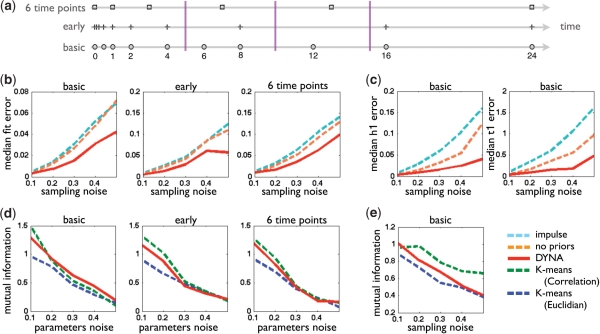
Fig. 2.

Evaluation on Synthetic Data. (A) Illustration of our three training datasets and our test set. Each horizontal line shows the time points in which the data was sampled, in each dataset. The purple vertical lines show the time points used as test data. (B) Median-squared fit error for test values across increasing sampling noise levels, as measured on the three different datasets: 10 time points dataset (basic), non-uniformly sampled dataset (early) and six time points dataset (six time points). Comparing DynaMiteC (DYNA) to our impulse model with no priors (no priors), and to the model of Chechik et al. (impulse). (C) As in (B), but showing the median squared error in the predicted parameters h₁ (left) and t₁ (right) compared to the true parameters, both on the basic dataset. (D) mutual information between the predicted and true clustering labels per gene. The datasets (from left to right): 10 time points dataset (basic), non-uniformly sampled dataset (early) and six time points dataset (six time points), all three with with increasing levels of parameter noise (variation in the clusters) and constant sampling noise. Compared methods are DynaMiteC (DYNA), K-means with Euclidean distance (Euclidian), and K-means with Pearson correlation (Correlation). (E) As in (D), but on the basic dataset with increasing levels of sampling noise and constant parameter noise.

We created three different training datasets, all initialized from three different dynamical prototypes learned on a real dataset [(Amit et al., 2009), Fig. 3a, Clusters 2–4]. We test each set with different levels of noise (ranging between standard deviation of 0.1 and 0.5), while we add constant noise in the parameters and increasing levels of noise to the data (and vice versa). The three sets are: (i) basic test set–time series data with 10 sampled time points along 24 h (as in the original study, Fig. 2a). (ii) Small sample size set: time series data with six time points along 24 h (Fig. 2a). (iii) Nonuniform sampling set: time series data with ten sampled time points along 24 h, denser in the early phase of the response (exponential series of time points from 0.125 to 24 h, Fig. 2a). In addition, for each of these datasets we created a test set composed of three time points that are not included in the learning datasets (Fig. 2a).

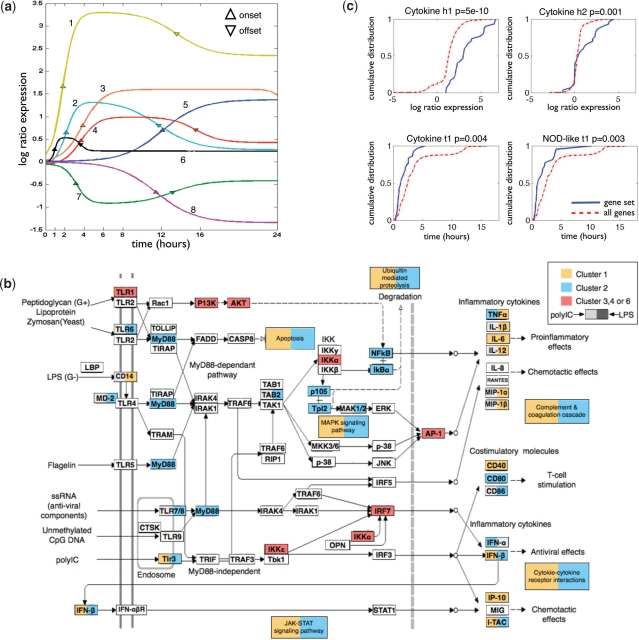
Fig. 3.

Dynamical modules of pathogen response. (A) Eight dynamical response prototype found in the pathogen response in mice Dendritic cells, by a combined analysis of time series data after LPS and polyIC stimuli. (B) The Toll-like receptor pathway [based on KEGG (Kanehisa and Goto, 2000; Kanehisa et al., 2006)], with genes colored according to their assigned cluster in polyIC (left side of the rectangle) and LPS (right side) stimuli. Comparing between Cluster 1 (yellow), Cluster 2 (blue) and Clusters 3, 4, or 6 (red). (C) Examples of parameters found to be specific for annotated genesets: The cytokine genes are specific for genes with high h₁, high h₂ and low t₁ parameters, while the NOD-like Receptor (NLR) pathway is specific for genes with low t₁ only. Showing the cumulative distribution of the relevant parameter across the functional set of genes (solid blue line), compared to all genes in the response (dashed red line). The title of each graph marks the Kolmogorov–Smirnov P-value for the differences between the two distributions, the name of the geneset, and the parameter tested.

To test how well we model the dynamics of genes, we run Impulse clustering on the different training datasets, and calculated the accuracy of fit of the modeling under the increasing levels of noise in the datasets. An unbiased measurement of fit is the median fit error across all genes at time points that were not included in the training set. Namely, the fit error is the difference between the generated expression value and the predicted value at those time points. As a straw-men we used the original impulse model of Chechik and Koller (2009) and our revised impulse model without using priors. As we expect, skewed sampling (non-uniform) and sparse sampling (six time points) increase the error of all methods (Fig. 2b). Moreover, the error increases with the level of noise on the data. However, estimates of our method are more robust to increasing levels of sampling noise in all three scenarios, and less sensitive to overfitting when the data is sparse or noisy (Fig. 2b).

Increasing the variability in the parameter space affects the Impulse clustering since it makes the clusters more diffused. The two straw-men are less sensitive to this change as they estimate parameters for each gene separately (Fig. 2c). Yet, on all three sets the Impulse clustering has smaller error levels compared to the two straw-men, showing that our method is robust to increasing levels of noise in the parameters space as well. On the dataset with fewer time points, Impulse clustering is more accurate than the impulse model of Chechik and Koller (2009); however, at a high variation level it is as good as our revised model with no priors. At this level of variation with relatively small amount of noise in the data, the prototypes are far from the actual parameters, thus the prior biases the estimates more than it helps avoid overfitting.

An alternative method to evaluate parameter fit, is to compare the estimated parameters to the true gene parameter. Again, we see that Impulse clustering performs better than the straw-men. For example, our peak height h₁ prediction is at least 6 times better, and onset time prediction t₁ is at least 4 times better then the straw-men (Fig. 2c).

In addition, we tested the clustering performance using the same three datasets, and calculated the accuracy of the clustering under increasing levels of noise. We measure the accuracy as the mutual information between the assigned clustering labels for each gene and the true labels. We compare our method to the standard K-means clustering (with the same number of clusters) using two alternative distance measures, the Pearson correlation coefficient and the Euclidean distance.

The results show that clustering using Impulse clustering are robust both to nonuniform sampling and to smaller number of samples, since the error in both sets is very similar to the error on the basic dataset. On all three datasets, the K-means algorithm with Pearson correlation coefficient is consistently less accurate. Impulse clustering has similar performance to the K-means algorithm with Euclidean distance, with advantage for the latter when the sampling noise is larger (Fig. 2d and Fig. 2e).

5 TRANSCRIPTIONAL RESPONSE TO PATHOGEN STIMULI

5.1 Dynamical modules of pathogen response in primary mice dendtritic cells

We applied our impulse clustering–modeling procedure to time-course gene expression data in primary mice Dendtritic cells stimulated by two different pathogen stimuli: lipopolysaccharide (LPS), a purified component from Gram-negative Escherichia coli; and polyinosine-polycytidylic acid (polyIC), a viral-like double-stranded RNA. The mRNA expression levels were measured at 0.5, 1, 2, 4, 6, 8, 12, 16 and 24 h after stimulation (Amit et al., 2009). Expression levels are represented as log (base 2) of the ratio to measurements at time 0. We selected 1293 genes that respond to one (or both) of the stimulations with at least 2-fold change compared to time 0.

To create a common set of prototypes for both stimulus, we applied our clustering algorithm to both datasets together (each gene was represented twice, once for each stimulus). This resulted in a set of eight prototypes (Table 1 and Fig. 3a). These types include: two different primary response dynamics, Cluster 1 and 2 (onset time of 2 h, offset time after 12.5 h), which differ mainly in their expression ratios, whereas Cluster 1 is highly expressed along the experiment (peak above 3-fold), Cluster 2 has lower peak expression and returns to the base expression values after a relatively short time. In addition, there are three different secondary response dynamics, where Clusters 3 and 4 are both induced (onset time after 3.7 h), and differ mainly in their offset time (15.5 h and more than 24 h, respectfully), while Cluster 7 is repressed with symmetrical dynamics to these of Cluster 3. We also find two symmetrical late response types (onset after more than 11.5 h), where Cluster 5 is induced and Cluster 8 repressed. Finally we find a low response dynamic, Cluster 6, describing stimuli specific genes (i.e. not responding at all to the other stimuli) or primary response genes with transient response.

Table 1.

The dynamical response prototype found in the pathogen response

Cluster	No of genes in cluster		Prototype parameters
	LPS	polyIC	h1	h2	t1	t2
1	88	41	3.31	2.34	1.80	13.58
2	437	173	1.35	0.26	2.13	11.70
3	147	260	1.59	0.42	3.83	25.20
4	145	336	0.99	0.42	3.66	15.54
5	125	100	1.37	0.86	12.11	28.05
6	226	188	0.53	0.24	0.94	3.16
7	84	124	−0.93	−0.42	3.16	13.15
8	37	50	−1.34	−0.84	11.44	32.22

Describing the number of genes in each cluster, and four parameters of each prototype: the time of the onset (t₁), the time of the offset (t₂), the height of peak response (h₁) and the hight of the new baseline (h₂).

Examining the genes in each of the dynamical response types we find each cluster to be enriched for specific annotations (Da Wei Huang and Lempicki, 2008; Dennis Jr et al., 2003) (P<0.01 after Bonferoni correction), indicating that the dynamical types represent functionally related sets of genes. Among these we find, for example, enrichment for immune response in various induced clusters under LPS and polyIC stimuli (but not for the down-regulated genes), purine nucleotide binding genes are enriched in the late down-regulated Cluster 3 after polyIC (P<4·10⁻⁵), and NADP oxidation reduction genes are enriched in the early down-regulated Cluster 2 genes after polyIC (P<7·10⁻⁴). Focusing on the primary response genes, we find in Cluster 1 (high response genes) enrichment for inflammation response (P<10⁻⁸) under LPS stimuli, and anti-virus response (P<10⁻⁴) under polyIC stimuli. Interestingly, the primary response genes in Cluster 2, are enriched for transcription regulatory genes under both stimulus, this response probably enables the cell to maintain the appropriate transcriptional response since these primary response genes are down-regulated faster than the genes in Cluster 1. Among the regulators in Cluster 2 are the master regulator NF-κB and its repressor IκBα.

The Toll-like signaling pathway, which is a signaling pathway for pathogen sensing in immune cells, is enriched under both LPS and polyIC stimulus in the two primary response clusters (1 and 2). However, zooming in on the genes in the pathway (Kanehisa and Goto, 2000; Kanehisa et al., 2006) (Fig. 3b) under LPS stimuli, we find an interesting division of genes according to these two dynamical types: the end effector genes in the pathways (inflammatory cytokines leading to pro-inflammatory and chemotactic effects) are mainly genes with high response levels (Cluster 1), such as the pro-inflammatory factor Il-6 and Tnfα. While along the signaling pathway we find mainly genes with fast offset and lower response level (Cluster 2), such as the adaptor protein MyD88, the MAPK signaling pathway, and the JAK-STAT signaling pathway. Moreover, under the polyIC stimuli this division of genes into two groups is less defined (Fig. 3b), however, while most genes along the signaling pathway belong to Cluster 2, the main polyIC receptor Tlr3 is reversely associated with Clsuster 1.

We next asked whether the dynamical clusters represent sets of coregulated genes and how is this regulation done. For this end, we focused on transcription factor mediated regulation, and applied the Allegro motif discovery algorithm (Halperin et al., 2009) on each set of genes, finding motifs enriched in the promoters of each set compared to the rest of the genome. For each set we found at least one significantly enriched motif (P<10⁻¹⁰), thus strengthening the biological relevance of the clusters and their coregulation. Several of the motifs are similar to motifs of known regulators (Matys et al., 2006) involved in the complex transcriptional response to LPS (Amit et al., 2009), which led us to suggest the following regulation scheme. Cluster 1 (primary response) is regulated by the factors NF-κB and STAT1/5/6, Cluster 2 (primary response) is regulated by the factor NFκB, Cluster 3 (early secondary response) is regulated by the factors NFκB and Irf1/2, and Cluster 5 (secondary response) is regulated by the factors STAT1/4. In the other clusters, we find motifs similar to motifs of known factors that were previously not indicated to be involved in these signaling pathways, and thus we have less evidence for their functionality, such as Egr1/2/3-like, Sp1-like and -PPAR-Rxrα-like motif regulating Cluster 7, and Gcnf-like motif regulating Cluster 8. Although this is a simplified regulatory scheme, it points out differences in the regulation programs of each clusters that can lead to the various dynamical response types we observe.

Since several clusters often share the same gene annotations, we wanted to test which parameters characterize the different genesets. For each of the genesets that contain at least 10 genes in our response (474 sets), we tested if it is characterized by a specific parameter (i.e. onset time, offset time, peak and steady state hight), using a Kolmogorov–Smirnov test comparing the distribution of a parameter in our gene set of interest compared to the rest of the genes in the response. We find that 15.2% of the sets are characterized by a specific range of parameters (P<0.005), where the most meaningful parameter was the peak of the response h₁ (for 11.4% of the sets), and to a smaller extent the onset time t₁ (3%), the offset time (2.3%) and finally the hight of the steady state (1.7%). For example, the cytokine genes Fig. 3c are characterized by an early onset time, and high peak and steady state levels, while the genes in the NOD-like receptor signaling pathway (detecting various pathogens and generating innate immune responses, Fig. 3c) are characterized by a fast onset time only.

5.2 Comparing two stimuli

An advantage of Impulse clustering is that it provides an easy way to compare between different transcriptional responses. We can apply our method simultaneously to different time series data, and test for each gene, not only in which of the responses is it involved, but also compare its dynamical expression profile across conditions. Note that since we model the expression of each gene by a continuous function, we can compare experiments measuring different time points. We compared between the response to LPS (inflammation) and polyIC (viral) stimuli using our method. In general, most of the genes respond to both stimuli, while only 148 genes are specifically anti-viral, and 110 are LPS specific. Among the shared genes, we can easily find genes that change their dynamical response between stimuli, by looking at genes classified to a certain cluster in LPS and a different cluster in polyIC (Fig. 4a). In general, 65% of the genes change their dynamical response between the two stimuli. We focused on sets of genes that change their dynamical response in a similar manner and characterized them by enrichments of gene annotations (hypergeometeric P-value with Bonferroni correction). Interestingly, the 286 genes that are classified as primary response genes (Clusters 1 or 2) in LPS and secondary response in polyIC (Clusters 3 or 4) are enriched for immune response genes (P<2×10⁻⁵), signaling cascade genes (P<6×10⁻⁴), and positive regulation of apoptosis (P<9×10⁻³). While the genes that maintain their cluster assignment in Cluster 1 are enriched for immune response (P<8×10⁻⁵) and anti-viral response (P<9×10⁻³), and these that remain in Cluster 2, are enriched for transcription regulation (P<6×10⁻⁴).

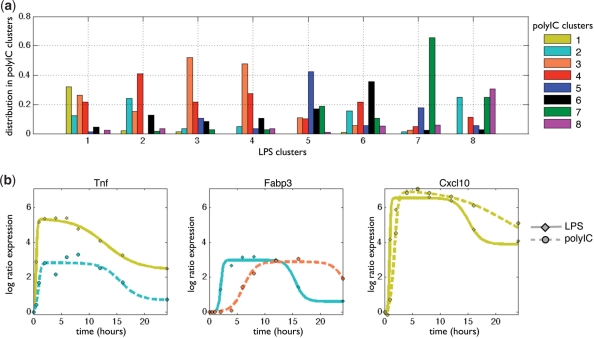
Fig. 4.

Comparing two stimuli. (A) Distribution of clusters reassignment in the polyIC response (PIC clusters) when compared to the cluster assignment in the LPS response. For each LPS cluster (X-axis), we see the distribution of genes (Y-axis) to polyIC clusters (colored bars). (B) Examples of the differences in dynamic response of a gene under LPS (straight line) and polyIC (dashed line) stimuli, and their assignment to clusters (color of the line). TNF (left) has lower response in polyIC (Cluster 2) compared to LPS (Cluster 1). FABP3 (middle) has a delayed response in polyIC (Cluster 3) compared to LPS (Cluster2). CXCL10 (right) has a very similar response to both stimuli (Cluster 1).

We can conduct a more detailed comparison by comparing a gene's model parameters between both stimuli. We compared each parameter across all genes, and found that the response to polyIC is lower and slower on average: 23% of the genes responding to polyIC have lower peak values compared to their response to the LPS stimuli (a difference of 1-fold at least), 20% have a delayed onset time (in at least 2 h, with mean delay of 4.8 h) and 50% have delayed offset time (in at least 2 h, with mean delay of 9.5 h). For example, the inflammation response regulator Tnf has a lower expression ratio in response to polyIC compared to LPS (Fig. 4b), the gene Fabp3 has a delayed response to polyIC (Fig. 4c), and the chemokine gene Cxcl10 has a similar dynamical response to both stimuli (Fig. 4d).

6 DISCUSSION

Time-series expression data are a valuable approach to study the dynamics of the transcriptional response to a stimuli. Here, we provide tools to address the challenge of analyzing such complex data. Our DynaMiteC method is an integrative approach where we use a simple two impulse model (Chechik and Koller, 2009) to describe the response dynamics, and at the same time cluster the data so that every cluster captures a group of genes with similar dynamics. By exploiting the fact that most responses contain groups of co-regulated genes with a similar behavior, we can estimate a set of prototypical responses in our function space, and use them as a meaningful prior when estimating the parameters for individual genes. As a consequence our method avoids overfitting and is more robust to measurement noise while still fitting each gene with specific parameters. In addition we cluster the genes into meaningful dynamical clusters, according to the typical prototype (prior) we learn for each gene. We validated our results first on synthetic data, demonstrating our robustness to noise, to a small number of samples, and to non-uniform sampling.

To demonstrate the properties of our method we applied DynaMiteC to a dataset describing the response to two related but distinct stimuli of immune cells. As we show the resulting clusters capture distinct parts of the immune response that represent separate biological functions and are regulated by different overlapping cis-regulatory motifs. Moreover, we show that the estimated model parameters are biologically meaningful and allow us to provide a finer description of the differences between the two stimuli.

Taken more broadly, we apply the general theme of parameter ‘sharing’ between genes to reduce overfitting when estimating the dynamics at the level of each gene. This theme can be realized in many different ways. We show a general approach that can be applied, while we are choosing to use a quadratic loss function on measurement noise. Such a loss function is the one most commonly used in analysis of gene expression data, and thus is a natural fit for this domain. We focused here on a specific parametric family of functions that provide a good tradeoff between simplicity and fit to typical observed responses, while enjoying the benefits of using a function with biologically meaningful parameters. However, the approach can be applied to any family of functions depending on the desired application.