Abstract
Motivation: Gene networks have been used widely in gene function prediction algorithms, many based on complex extensions of the ‘guilt by association’ principle. We sought to provide a unified explanation for the performance of gene function prediction algorithms in exploiting network structure and thereby simplify future analysis.
Results: We use co-expression networks to show that most exploited network structure simply reconstructs the original correlation matrices from which the co-expression network was obtained. We show the same principle works in predicting gene function in protein interaction networks and that these methods perform comparably to much more sophisticated gene function prediction algorithms.
Availability and implementation: Data and algorithm implementation are fully described and available at http://www.chibi.ubc.ca/extended. Programs are provided in Matlab m-code.
Contact: paul@chibi.ubc.ca
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Gene interactions can be used to infer functional relationships, a principle known as ‘guilt by association’ (GBA) (Oliver, 2000). Genes can be judged to be interacting based on direct evidence of protein (Cesareni et al., 2008; Guldener et al., 2006; von Mering et al., 2002; Xenarios et al., 2002) or genetic interaction (Pu et al., 2008; Tong et al., 2004; Typas et al., 2008), or by a similarity in behavior across a range of conditions such as expression profiles (Horan et al., 2008; Lee et al., 2004; Saito et al., 2008) or phylogenetic profiles (Pellegrini et al., 1999). The principle of GBA forms the basis for most gene function prediction algorithms, which typically use relational information (e.g. interactions) to predict new gene membership in gene function categories (Mostafavi et al., 2008; Pena-Castillo et al., 2008; Tsuda et al., 2005; Vazquez et al., 2003; Wolfe et al., 2005). Some of these algorithms operate directly by GBA (Mostafavi et al., 2008), while others infer function from more complex relational properties (Schietgat et al., 2010). In the simplest case, the function of a gene can be predicted by voting among its connected neighbors with known function (Schwikowski et al., 2000), perhaps with statistical control such as the Chi-square test (Hishigaki et al., 2001). For a given function, a gene's likelihood of possessing that function could be, for example, the fraction of its neighbors possessing that function. Simple nearest-neighbor voting (‘Basic GBA’ or BGBA) has been shown to predict gene function in a variety of biological networks, including protein interaction and gene co-expression (Pena-Castillo et al., 2008).
Our focus is on a natural extension of these methods, which is to incorporate the broader network structure—meaning indirect connections among genes–into predictions. A large variety of techniques have been proposed to extend GBA to indirect connections, including voting within a fixed radius, clustering into function classes, specialized support vector machine, prediction by path length, weighting indirect connections by local topology, network propagation, topological overlap as well as others (Chua et al., 2006; Ravasz et al., 2002; Weston et al., 2004; Yip and Horvath, 2007; Zhou et al., 2002). Most of these methods report improvement over GBA between direct connections, although where methods are compared they tend to perform comparably and only slightly better than direct GBA (Pena-Castillo et al., 2008).
Gene function prediction and network analysis methods typically employ networks that are sparse: only a subset of possible edges are retained, based on some implicit or explicit threshold. In co-expression analyses, this threshold may be a correlation P-value, but is often a simple threshold above a certain rank in order to attain a matrix sufficiently sparse to be computationally tractable. Even in protein–protein interaction networks (PPINs) the underlying data are typically some metric which must be thresholded (though there is also an earlier implicit threshold in terms of which proteins are even tested). Thresholding to determine confident interactions is particularly convenient for interaction networks which must aggregate the results of multiple studies. Also, this pre-filtered analysis leaves the networks performance open to the conventional interpretation of biological networks (in which specific network interactions have specific meaning). Of course, by applying a threshold for statistical confidence, information may be lost or disguised within the network. We will provide evidence that it is precisely this information which methods exploiting indirect connections reconstruct in their operation.
There is a larger variety of gene function prediction methods that use indirect connections implicitly, such as support vector machine approaches (Lanckriet et al., 2004) and Markov random fields (Deng et al., 2003), but there are broadly only two approaches to explicitly incorporating indirect connections into gene function prediction: label propagation (Mostafavi et al., 2008) and indirect connection weighting (Chua et al., 2006). In label propagation, a ‘seed list’ of genes with known function is propagated through the network along connections to determine other genes which are associated with the seed list and may, therefore, be candidates to be members of the function characterized by the seed list, according to GBA. In indirect connection weighting, indirect connections are calculated within a network and treated as equivalent to low-weight direct connections within the original network. These two methods are quite similar, but possess somewhat disjoint literatures. In both cases, numerous subtle modifications of the basic method exist, and these will reportedly increase gene function prediction performance.
In this article, we explore the mechanism whereby indirect connections improve gene function prediction performance. As a by-product, we are able to suggest a particularly efficient algorithm, but this is not our primary aim. We find, in general, it is exceptionally easy to improve gene function performance from the base implementation of GBA, but that different methods proposed for doing so act in essentially the same way, due to the insensitivity of the data. Based on our co-expression analysis, we also suggest that most methods simply reconstruct network information that was originally present as ‘weak’ connections and deliberately removed. We show this approach has broad applicability in a large-scale aggregated human PPIN, and in yeast and human data. Finally, based on this evidence, we discuss whether the conceptual convenience of discrete networks may not be the most informative approach to interpreting gene interactions.
2 METHODS
Evaluation of prediction performance: we used the area under curve for the receiver-operator characteristic (ROC) as our main measure of performance in prediction. An ROC of 0.5 represents classification at chance levels, while an ROC of 1.0 represents a perfect classification. In the gene function prediction literature, values >0.7 are considered good and values >0.9 are atypical. Additional measurements considered included positive predictive value (PPV), and area under the precision–recall curve (AUP).
Gene lists: we analyzed the list of human genes from the University of California, Santa Cruz GoldenPath database (Kent et al., 2002) ‘known gene’ table intersected with the microarray platforms used. Thus, we analyzed 18 724 of the 20 710 known human genes and 16 103 of the 18 592 known mouse genes. The 6200 yeast gene list was obtained from NCBI (NCBI, 2002).
Gene sets: human gene ontology (GO) annotations (Ashburner et al., 2000) consisted of 11 411 gene sets with 2193 sets having between 20 and 1000 genes within them; it was this subset used in analysis. By the same criterion, 1780 mouse gene sets and 1298 yeast gene sets from the gene ontology were assessed.
Gene function prediction algorithms: for GBA analysis, an implementation was written in Matlab (MathWorks Inc.) which ranked genes by a voting scheme within the training set (by ranked co-expression) relative to genes outside the training set. The sum of co-expression values between the training set and the candidate gene was divided by the sum of co-expression values between the genes outside the training set and the candidate gene to determine degree of candidacy. For precision–recall, genes without interactions in the protein interaciton network were given a negative weighting summing to the positive total for that gene. GeneMANIA was used without a negative training set across each training gene set (GO group) with 3-fold cross-validation to determine a ranked list scoring genes as to how well they belonged within the known gene set. The 8-fold and n-fold cross-validation was also performed on the GO categories to confirm that higher fold number did not alter results.
Extended GBA: networks were extended by self-multiplication to determine indirect links where, e.g. An gives the number of paths of length n connecting a given pair of genes from network A. Indirect links with one intermediary gene are labeled ‘level-2 connections’, with two intermediary genes as ‘level-3 connections’ and so on. Unless otherwise indicated, indirect links at a given level were weighted by setting the weighted sum of indirect links at that level equal to the sum of direct links. Also, unless otherwise indicated, indirect links beyond level-3 were not added to the network. Once the extended network was constructed, GBA was conducted as on the original network.
Gene networks: our human PPIN was obtained by aggregating data from Brown and Jurisica (2005), Ceol et al. (2010), Gilbert (2005), Lynn et al. (2008), Prasad et al. (2009), Razick et al. (2008) and contained 100 623 unique interactions. Our yeast PPIN was obtained by aggregating data from Breitkreutz et al. (2008), Cesareni et al. (2008), Costanzo et al. (2010), Guldener et al. (2006), Schwikowski et al. (2000), and Xenarios et al. (2002) and contained 72 481 unique interactions (strictly speaking this is not a pure ‘protein interaction’ network since one of the datasets is of genetic interactions, but for brevity we still call it a PPIN). Our co-expression matrices were constructed using publicly available microarray expression experiments obtained from the Gene Expression Omnibus (Edgar et al., 2002). Specifically, we used 100 GPL570 (Affymetrix U133 Plus 2.0) human experiments and 64 GPL1261 (Affymetrix 430 2.0) mouse experiments, each of which have over 20 samples. The list of experiments is available as Supplementary Material, along with the data and methods to construct the co-expression matrices used in our analyses. We used a threshold on the absolute value of the correlation between expression profiles of genes to determine co-expression. The full co-expression matrix is the sum of the individual co-expression matrices (we reserve the word matrix for the data which will be thresholded to create the network). In keeping with our previous work (Lee et al., 2004) and close to that used in GeneMANIA (Mostafavi et al., 2008), our default sparsity/threshold was 0.5%.
Prediction tasks: three types of prediction task were performed. The first prediction task used ‘indirect’ connections in thresholded (top 0.5%) co-expression networks to predict top ranks below the threshold in the co-expression correlations. Gene pairs were ranked by path length in the thresholded network and these lengths used as predictions to determine gene pairs which fell ‘just’ (next 0.5%) below the threshold in the network, giving an ROC of reconstruction. The second prediction task was to use the correlation ranks in the co-expression matrix to predict path lengths (outside the top 0.5% directly connected). Finally, gene function prediction was conducted in which cross-validation was performed using the gene sets to determine the algorithm's efficacy.
3 RESULTS
3.1 Indirect connections in co-expression networks are lower threshold direct connections
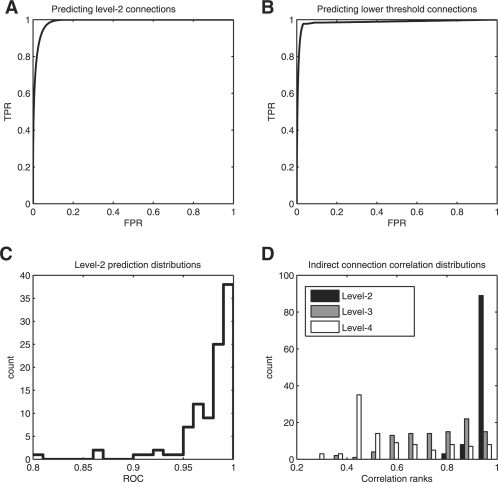
In 100 human co-expression matrices constructed using a conventional approach (Section 2), we examined the relationship between the original correlations and the distance between indirect connections. We find that level-2 connections in the sparsified network (indirect with one intermediary) are very strongly predicted by the original correlations. This means that level-2 connections are usually simply lower significance level-1 connections. For example, if level-2 connections were perfectly predicted by correlation, then weighting level-2 connections equivalently to level-1 connections would be identical to having simply chosen a lower significance threshold initially. In Figure 1A (the median performing network), we see that level-2 connections can be very strongly predicted by the original significance values with a median ROC of 0.986 and interquartile range (IQR) of 0.966–0.993. We note that our analysis ranks genes by the absolute value of correlation (or P-value), and will therefore include both positive and negative (correlation) links, so that the predicted connections are not simply similar expression values (which could be blocks of similar genes), but may include highly negatively correlated gene pairs. The performance across all networks of predicting level-2 connections is strikingly high (Fig. 1C), especially considering the original networks are potentially noisy.
Fig. 1.
Indirect connections are similar to lower significance connections. (A) Example of an ROC curve for predicting indirect connections in a sparse network from the original correlations (median-performing network). (B) Example of an ROC curve for predicting correlations of genes using indirect connections in a sparsified network (median-performing network). (C) The distribution of ROCs across 100 co-expression networks for predicting indirect connections from the original co-expression data shows generally high performance. (D) The distribution of the correlation between pairs of genes separated by a given path length across the (thresholded, sparse) 100 co-expression networks. Correlation values are the ranks (standardized to between 0 and 1) of the absolute value of the correlation between the pair of genes. Genes more closely connected have correlations nearer to the threshold.
The reverse is similarly true: it is possible to predict connections which ‘just missed’ the threshold by ranking gene pairs by their distance in the sparse network (Fig. 1B is the median performing network with an ROC of 0.985, IQR: 0.962–0.994). Likewise, given a thresholded network, the indirect connections are predictive of the (rank of the) correlations of the original matrix (giving median ranks of 0.96, 0.877 and 0.51 for connections of type level-2, 3 and 4, respectively. The level-2 connections are not only the most potentially significant, but also the most easily characterized by this method; the distribution of correlations is the narrowest.
The mouse co-expression data showed very similar properties, with an ROC of reconstructing the original giving a median value of 0.987 (IQR: 0.971–0.994). Similarly, the original connections were strongly predictive of secondary connections, with a median ROC of 0.991 (IQR: 0.976–0.995). The distribution of correlation ranks for the mouse data was also similar to the values for human data, with level-2, 3 and 4 connections taking values of 0.96, 0.83, and 0.57, respectively, in mouse data.
This property of ‘reconstructability’ is one shared by random data matrices generated from Gaussian noise (data not shown). This means that the ability to reconstruct a correlation matrix from a sparse version of that matrix is not necessarily indicative of any particularly interesting property with respect to biology. On the other hand, it is also possible to generate networks which are not easily reconstructed. While there is a lower bound guaranteed by the triangle inequality for correlations (r) between expression profiles A, B and C:
This bound was uniformly far too lax to allow correlations to be inferred in the real data (as the range of reconstructabilities in our data also suggests).
We next investigated whether the extension method's capacity to reconstruct the original matrix (measured by this reconstruction ROC) was related to the amount of functional information in the data (measured by GBA ROC). In general, the efficacy of using extended connections to reconstruct the original matrix (reconstruction ROC) is positively correlated with the performance of the network (GBA ROC) only where extension is not very effective. That is, when the ROC for guessing indirect connections is <0.95, the network reconstruction works better for networks with more ‘signal’ (higher BGBA functional performance), with a correlation of 0.62 between the two. Above a reconstruction ROC of 0.95, there is no strong pattern (r=0.12). This suggests that, up to a certain point, the better the network performance in function prediction, the better network reconstruction will work. However, a high ROC in extension is not a guarantee of functional information; correlation matrices constructed from random (uniform distribution) microarray values consistently perform best of all (ROC >0.99). Because of this, the correlation of the ROC of extended network's GBA with the ROC of reconstruction will generally be positive for poor network reconstructions (r=0.47 for reconstruction ROCs <0.95) and negative for very good network reconstructions (r=−0.66 for reconstruction ROC >0.95). In essence, extension never served as a bottleneck to obtaining functional information, although it also worked well at reconstructing non-functional information.
While neighbor-voting gene function prediction is most easily conceptualized as voting among links, it can equally well be applied to a weighted voting of neighbors (a natural weighting would be the absolute value of the correlation value itself). Unsurprisingly, sparsifying reduces the performance of neighbor voting (by 48% on average across all 100 networks). Adding back level-2 connections (and treating them as tied lower ranked correlations) improves performance (back to 70% on average) and adding back level-3 connections improves performance slightly beyond that (to 74% of the original on average). The improvement in performance from neighbor voting in the sparse case is expected, and is the essential premise behind both gene function prediction methods that weight indirect connections and those methods using rank propagation. In general, the same GO groups performed well before sparsification and after network reconstruction, averaged across the 100 networks (r >0.95).
3.2 Aggregation of co-expression networks
One important difference between PPINs and the co-expression networks characterized above is that the PPINs involve large-scale aggregation and have higher gene function prediction performance than any individual co-expression network (Pena-Castillo et al., 2008). Because we are using the availability of the underlying expression data in co-expression matrices to test properties which we will then apply more broadly (i.e. to PPINs), we consider the effect of aggregation in our co-expression data in some detail. Specifically, the individual co-expression matrices considered above do not provide high-prediction performance and may well be noisy (since the individual microarray experiments may consist of as few as 20 samples). It is therefore important to consider aggregated co-expression data in order to obtain a clearer signal for BGBA with the expectation that this will improve performance.
The 100 individual human gene co-expression networks have ROC performance across all GO groups ranging from 0.5 to 0.67, with a mean of 0.56 (Supplementary Fig. 1a). There was no readily identifiable characteristic predicting performance across this set of co-expression experiments (which were all large experiments conducted on the GPL570 array). Summing the co-expression networks (to produce an aggregate network) improved performance to an ROC of 0.71. As shown in Supplementary Figure 1b, calculating the ROC as matrices were added together to generate the aggregate produced an upward trending curve, leveling off at 20–30 experiments. The ordering of the experiments in the example shown was random and other randomly chosen orderings exhibited the same trend (resulting in the same final matrix). In fact, this trend is consistent enough to be predictable based on the ROC of the individual co-expression matrices. In Supplementary Figure 1c, the ROC of the individual experiment is plotted against its effect on the curve (change in ROC divided by number of experiments used at that point). The first 35 experiments exhibit a linear relationship (r2=0.85), indicating that the ROC of the individual experiment simply improves the aggregate performance by its own performance weighted by its contribution to the network (e.g. 1/20 if it is 1 of 20 networks included). After the initial 35 experiments where performance steadily improves, the predictability of the effect largely disappears (r2=0.22). These results suggest that ROC is an appropriate metric to evaluate network performance (since the performance of an aggregate is the sum of the individual performances, weighted by contribution, as they are successively added—up to a maximum). However, the results were not particularly dependent on the metric chosen, and in Supplementary Figure 2, we show that the ROC of GO groups in this matrix are well correlated with other conventional metrics (PPV and improvement in mean precision). We use the full 100 experiment co-expression matrix as our aggregate co-expression matrix. An alternative would have been to sparsify the individual matrices and then aggregate, a practice used in many existing network construction methods. Aggregation after sparsification results in relatively dense matrices (with links that were present in at least one of the input networks). In our case, this would have resulted in a matrix with only 71% zero values and very similar characteristics to the aggregate co-expression matrix; a mean ROC of 0.72, a correlation of GO group performances between the two matrices of 0.85 and node degree correlations between the two matrices of 0.55. Modifying the sparsification method (e.g. exact threshold, soft-threshold, rejecting versus retaining negative correlations) can alter the performance of individual datasets, but we found that the aggregate showed similar performance in all cases.
3.3 Weighting indirect connections
The original co-expression matrices we use are the ranks of the absolute value of the correlations. This is a convenient normalization step because it allows us to compare the results between matrices (and aggregate between matrices) when the distribution of correlation values are quite different (due to their differing number of samples). An explicit correction based on the expected correlation distribution (Fisher's transformation) would have resulted in a few large datasets dominating the results.
We treat the weighting of indirect connections as an attempt to reconstruct the information present in the original matrix. In the simplest case, we can treat all direct connections as tied at having the highest correlation and all level-2 connections as tied at having the next highest correlation, and all level-3 tied below that, and so on. Because the neighbor-voting calculation is simply a weighted sum, this can also be conceptualized as saying that the aggregate effect of all level-2 connections should not be greater than the aggregate effect of all level-1 connections, and so on. In fact, we find that even tied-level connections can be ranked to improve ROC, by ranking them by the proportion of their connectivity that occurs at their tie-level. This means that of two first-level connections, the higher ranked/correlation one will tend to be the one which has fewer second-level connections, but this effect is very minimal (effect on ROCs of extension and GBA of <0.01).
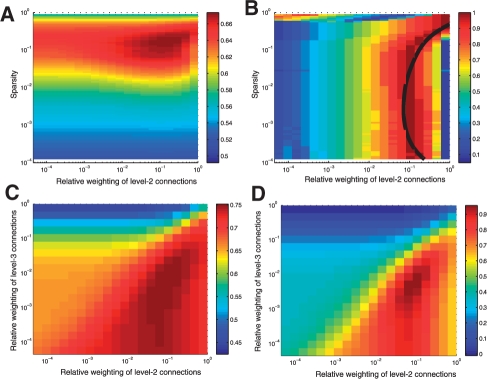
In Figure 2A, we show the ROC across all GO groups for a range of weightings of the second-level connections and over a range of sparsities. In each case, the sparsified co-expression network is purely binary, so a too high threshold and a too low threshold will both produce information free matrices (all zeros or all ones). The performance is strongly dependent on sparsity, but gives roughly equivalent performance across a wide range of weightings. By plotting the rank of each weighting's performance (Fig. 2b), for a given sparsity, we can see how the optimal relative weighting (for this co-expression matrix) changes as a function of sparsity. As suggested above, simply weighting second-level connections by the inverse of their relative prevalence closely matches the optimal performance, giving ROCs varying by <0.01 from the optimal, on average. Adding level-4 connections improves performance minimally.
Fig. 2.
Weighting indirect connections. (A) The performance of the aggregate co-expression network was assessed using a range of thresholds for the correlation data and a range of relative weightings on indirect connections. The ROC across all GO groups varies strongly with sparsity and weakly with relative weighting of the indirect connections. (B) The data from (A) are redrawn, with values at each sparsity replaced by ranks for that sparsity (ranks normalized to between 0 and 1). The black line is the weighting predicted by assuming that indirect connections are weighted, in aggregate, equivalently to direct connections. (C) The performance of the aggregate PPIN across possible weightings for level-2 and level-3 connections. As long as level-3 performance is below level-2, and level-2 below direct, performance is fairly stable. (D) The data from (C) are redrawn at a new (log) scale between 0 and 1, to accentuate variation.
We next considered a large PPIN (with over 100K connections). In this case sparsity is fixed, and there is no straightforward way to ascertain if our indirect weightings reconstruct original network values (since the original network is sparse). In Figure 2c, we see that the weighting of level-2 and level-3 does not strongly affect performance, so long as level-2 connections are weighted less than direct connections and level-3 connections are weighted less than level-2 connections. The insensitivity of performance to the exact weighting provides an explanation for the broad efficacy of gene function prediction methods founded (even if indirectly) in the weighting of indirect connections in seemingly complex ways. To better see if our simple principle of weighting—by relative prevalence—also applies in this quite different network, and to level-2 as well as level-3 connections, we rescaled the y-axis (on a log scale to between 0 and 1) to exaggerate variation in ROC. The principle of weighting the aggregate effect of all tied-level connections equivalently (e.g. weighting by the inverse of the number of connections), again predicts optimum performance, to <0.01 of the maximum ROC. However, there is a very broad range of weightings that will give roughly equivalent performance.
3.4 Performance as a gene function prediction method
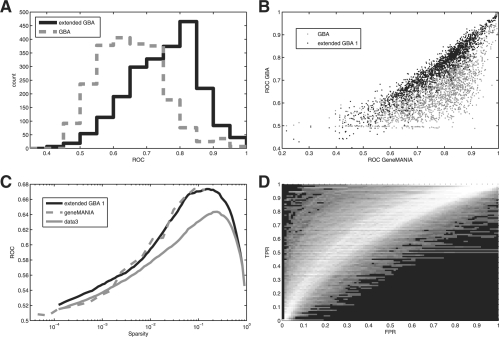
Our focus here has been on illustrating the role indirect connections play in generating network information. However, our crude method of weighting network connections can be implemented as a gene function prediction algorithm of its own, which we call extended GBA (EGBA). In fact, we treat our network reconstruction step (weighting of higher level connections) as a preprocessing step for our input matrix. In Figure 3A, we can see that this results in a dramatic improvement in performance across all GO groups in the PPIN over GBA on the original network.
Fig. 3.
Performance of the extended GBA network. (A) Extended GBA performs better than GBA across GO groups using the protein interaction network. (B) Extended GBA and GeneMANIA perform very similarly in each GO group using the protein interaction network, while GBA performs almost uniformly worse. (C) GeneMANIA and the extended GBA network perform very similarly across a range of thresholds for the aggregate co-expression network. (D) ROCs using the full co-expression matrix plotted on top of each other to create a surface.
We decided to use a state-of-the-art algorithm, GeneMANIA (Mostafavi et al., 2008), as an additional baseline for comparison; GeneMANIA is a network propagation algorithm that was the best performer in a comparison of algorithms (Pena-Castillo et al., 2008). Comparing the performance of GeneMANIA to basic GBA and extended GBA reveals that while GeneMANIA performs much better than BGBA, it performs very similarly to EGBA. GeneMANIA gives an average ROC of 0.77, while BGBA gives an ROC of 0.65. EGBA extended one step (to second-level connections) increases performance to 0.75, and extending it to level-3 connections increases it to 0.76. Using precision–recall produced very similar performances, with GeneMANIA giving a mean AUP across GO groups of 0.0975. In contrast, BGBA gave an AUP of 0.0760, extending to level-2 connections increased this to 0.083, and extending to level-3 connections increased this to 0.0981, above GeneMANIA. However, using ROC, even the fully reconstructed network (extending the number of steps till no additional connections are formed) still performs (ROC of 0.77) only very slightly below GeneMANIA. The fully extended PPIN has a substantially increased correlation with the aggregate co-expression matrix (r=0.178 versus r=0.036 for the sparse networks) across its values, and aggregating between the fully extended PPIN and the aggregate co-expression matrix improved performance slightly, to an ROC of 0.80. Using GBA was a minimum of 10 times faster regardless of sparsity or variation in implementation. For both algorithms, we excluded network construction steps (e.g. sparsification and extension) from our timing because these are relatively fast one time operations to be used repeatedly across at least thousands of prediction sets.
Basic GBA remains popular despite the existence of more sophisticated and better performing algorithms (Pena-Castillo et al., 2008). This is likely not just because it is simple to implement, but also because its mechanism of action can be directly understood. Why certain genes are ranked highly can be determined simply by examining their neighbors in the network. Extended GBA not only offers this same benefit but also incorporates the larger scale properties of the network (indirect connections). Using GeneMANIA on the extended networks provides similar performance, further suggesting that this is the mechanism whereby network propagation methods derive their power. The same principle applies over a range of sparsities (Fig. 3c), with GeneMANIA's performance tracking that of the extended network's GBA performance quite closely; variation is actually likely due to the necessity of using only a sampling of GO groups for GeneMANIA for calculations to be computationally feasible at low sparsities (the GO slim set was used at sparsities <1 in 102).
These results were confirmed using an aggregate yeast PPIN (>72K unique interactions). In this case, GBA gave an ROC of 0.738, which increased to 0.786 (with level-2 connections) and 0.791 (with level-3 connections) using extended GBA. This final ROC was virtually identical to that which we obtained using GeneMANIA (ROC of 0.791) with very similar performance across all GO groups (correlation of 0.94).
A more interesting case arose when we constructed a co-expression network from mouse 64 expression experiments. The aggregated matrix performed reasonably well at gene function prediction (mean ROC of 0.72). However, in contrast to the other networks we tested, sparsification dramatically reduced performance. The mouse co-expression network (0.5% sparsity) performed poorly in GBA (ROC of 0.56) with extended GBA performing only slightly better (0.57 for level-2 and 0.58 for level-3). It might be thought that in this case, a more sophisticated algorithm would perform better, but GeneMANIA again performed virtually identically to EGBA (with a mean ROC of 0.58). There is no reason to believe that information lost in sparsifying a matrix must be recoverable, and this may be such a case. Indeed, consistent with our earlier results (Fig. 3c) that less sparse networks perform better using GBA, using a threshold at 5% (instead of 0.5%) gave an ROC of 0.58 using GBA, and 0.62 and 0.63 with level-2 and 3 extended GBA. Using an alternative sparsification method, top-overlap (Agrawal, 2002; Chen et al., 2008; Faith et al., 2007; Mostafavi et al., 2008)—where connections must be top-ranked values for both of the connected genes—altered results significantly. In this case, GeneMANIA gave an ROC performance of 0.65, while BGBA gave an ROC of 0.58, extended to level-2 a mean ROC of 0.64, to level-3 a mean ROC of 0.66 and to 0.67 extended to level-4. Reconstruction ROCs were high in both cases (median >0.99)—although, again, this is not guaranteed to happen—so it is not immediately clear why the difference in sparsification method was crucial. It is commonplace in the literature to use either direct sparsification or ‘top-overlap’, without any particular justification. Crucially, from our perspective, ROCs for gene function prediction obtained by GeneMANIA, were closely tracked by those obtained simply by extending the network (and vice versa). And where one method failed (thresholded mouse aggregate data), both did, and the ROC of reconstruction remained high. Since performance in all co-expression cases fall below that obtained using GBA on the full matrix, for the purposes of this article, the point is likely moot.
4 DISCUSSION
Our main contribution in this article is to show that ‘indirect network connections’ participate in gene function inference in a surprisingly straightforward way, explaining the performance of a wide range of methods. In particular, we suggest that, at least for co-expression data, all network propagation methods are essentially just recovering information lost during sparsification.
4.1 Co-expression networks
In no case did a sparsified co-expression network perform better than the underlying co-expression matrix using simple GBA. Using networks for co-expression analysis has been an attractive proposition for a number of reasons, including sparsity, statistical confidence of individual connections, overlap with protein interaction and mathematical convenience. Many of these reasons remain valid. In particular, appropriate sparsification can provide insight into network structure that is difficult to obtain otherwise (Horvath and Dong, 2008; Zhang and Horvath, 2005). However, the results of this article suggest that gene function prediction studies using co-expression have been needlessly complicated. Rather than examining multiple methods, with varying details (including sparsification) that are difficult to exhaustively examine, we would suggest the gold standard analysis in this case is the simplest: GBA of the co-expression matrix. In addition, we have seen that having a sufficient quantity of data plays a critical role in obtaining usable functional information from co-expression studies. Analyses using single datasets gave very poor performance, which improved by aggregation to the point that performance is similar to that obtained with PPINs. Previous research has recognized the possibility that hard thresholding in co-expression may lead to less robust results (Zhang and Horvath, 2005). A soft-thresholding approach such as in weighted gene co-expression (Horvath and Dong, 2008) has been shown to work well in the analysis of functional modules within the network, combining both greater sparsity with similarity to the original correlation matrix (e.g. Yip and Horvath, 2007). Previous research has also suggested that using positive correlations alone may improve performance (e.g. Hibbs et al., 2007). Our own prior work has addressed systemic network biases due to multifunctional genes and their interaction with sparsification (Gillis and Pavlidis, 2011). Broadly speaking, an extended-GBA approach makes exhaustively examining these issues faster and easier (less subject to fine-tuning). If gene function prediction is always essentially just a variant of GBA, then exploring the effect of sparsification becomes much simpler, since the ‘control’ case is known.
4.2 PPINs
Most useful (for gene function prediction, meaning ‘large enough’) PPINs consist of aggregated ‘confident’ connections. The results from this article suggest an alternate avenue of investigation may be the aggregation of pre-thresholded data. In lieu of that, extended networks can be constructed for permanent use, and their additional connections investigated as potential ‘missing’ interactions. The five top interactions added by extension to our human PPIN were MKRN3 with MGRN1 and ZNRF1 with each of TRIM2, RNF114, RNF166 and RNF4. These relationships suggest caution in considering extended-interaction physical interactions; both MKRN3 and MGRN1 are ubiquitin ligases and therefore may be more usefully seen as level-2 interactions (interacting with the same eight ubiquitin conjugating enzymes, including tumor susceptibility gene 101), with shared functionality. Interestingly ZNRF1 is also a UL, and all four of its extended interactors are RING-finger domain proteins, a domain predominantly found in ubiquitin pathway genes including ubiquitin ligases. The improved similarity of the extended PPIN to the aggregate co-expression matrix suggests the extended PPIN is acting more like a co-expression network, where the metric represents similarity in behavior across a range of conditions, rather than strict interaction. Because extending the PPIN may be seen as including probabilistic (potentially condition-specific) interactions, the improved performance and similarity to co-expression suggests probabilistic interactions are important to consider in network data, a view supported by the lack of overlap among methods for determining protein interaction (von Mering et al., 2002). This question might be best answered by starting with weighted or even ‘unfiltered’ protein interaction data, a topic we leave for future work. While the improvement in function prediction when adding the PPIN to the co-expression data was slight, it was well above the apparent asymptote for aggregating expression data alone, reinforcing the idea that these different resources can be used together for improved performance (Pena-Castillo et al., 2008).
Supplementary Material
ACKNOWLEDGEMENTS
Sara Mostafavi and Quaid Morris generously provided the Matlab implementation of GeneMANIA. We thank Jennifer Gardy for assistance with InnateDB. We thank Kelsey Hamer for technical support.
Funding: National Institutes of Health Grant GM076990, salary awards to P.P. from the Michael Smith Foundation for Health Research and the Canadian Institutes for Health Research, and postdoctoral fellowships to J.G. from CIHR, MSFHR, and the MIND Foundation of British Columbia. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript.
Conflict of Interest: none declared.
REFERENCES
- Agrawal H. Extreme self-organization in networks constructed from gene expression data. Phys. Rev. Lett. 2002;89:268702. doi: 10.1103/PhysRevLett.89.268702. [DOI] [PubMed] [Google Scholar]
- Ashburner M., et al. Gene ontology: tool for the unification of biology. The Gene Ontology Consortium. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breitkreutz B.J., et al. The BioGRID Interaction Database: 2008 update. Nucleic Acids Res. 2008;36:D637–D640. doi: 10.1093/nar/gkm1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown K.R., Jurisica I. Online predicted human interaction database. Bioinformatics. 2005;21:2076–2082. doi: 10.1093/bioinformatics/bti273. [DOI] [PubMed] [Google Scholar]
- Ceol A., et al. MINT, the molecular interaction database: 2009 update. Nucleic Acids Res. 2010;38:D532–D539. doi: 10.1093/nar/gkp983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cesareni G., et al. Searching the MINT database for protein interaction information. Curr. Protoc. Bioinformatics. 2008;Chapter 8 doi: 10.1002/0471250953.bi0805s02. Unit 8 5. [DOI] [PubMed] [Google Scholar]
- Chen G., et al. Rank-based edge reconstruction for scale-free genetic regulatory networks. BMC Bioinformatics. 2008;9:75. doi: 10.1186/1471-2105-9-75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chua H.N., et al. Exploiting indirect neighbours and topological weight to predict protein function from protein-protein interactions. Bioinformatics. 2006;22:1623–1630. doi: 10.1093/bioinformatics/btl145. [DOI] [PubMed] [Google Scholar]
- Costanzo M., et al. The genetic landscape of a cell. Science. 2010;327:425–431. doi: 10.1126/science.1180823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deng M., et al. Prediction of protein function using protein-protein interaction data. J. Comput. Biol. 2003;10:947–960. doi: 10.1089/106652703322756168. [DOI] [PubMed] [Google Scholar]
- Edgar R., et al. Gene Expression Omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 2002;30:207–210. doi: 10.1093/nar/30.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faith J.J., et al. Large-scale mapping and validation of Escherichia coli transcriptional regulation from a compendium of expression profiles. PLoS Biol. 2007;5:e8. doi: 10.1371/journal.pbio.0050008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert D. Biomolecular interaction network database. Brief. Bioinform. 2005;6:194–198. doi: 10.1093/bib/6.2.194. [DOI] [PubMed] [Google Scholar]
- Gillis J., Pavlidis P. The impact of multifunctional genes on “guilt by association” analysis. PLoS One. 2011;6:e17258. doi: 10.1371/journal.pone.0017258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guldener U., et al. MPact: the MIPS protein interaction resource on yeast. Nucleic Acids Res. 2006;34:D436–D441. doi: 10.1093/nar/gkj003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hibbs M.A., et al. Exploring the functional landscape of gene expression: directed search of large microarray compendia. Bioinformatics. 2007;23:2692–2699. doi: 10.1093/bioinformatics/btm403. [DOI] [PubMed] [Google Scholar]
- Hishigaki H., et al. Assessment of prediction accuracy of protein function from protein–protein interaction data. Yeast. 2001;18:523–531. doi: 10.1002/yea.706. [DOI] [PubMed] [Google Scholar]
- Horan K., et al. Annotating genes of known and unknown function by large-scale coexpression analysis. Plant Physiol. 2008;147:41–57. doi: 10.1104/pp.108.117366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horvath S., Dong J. Geometric interpretation of gene coexpression network analysis. PLoS Comput. Biol. 2008;4:e1000117. doi: 10.1371/journal.pcbi.1000117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent W.J., et al. The human genome browser at UCSC. Genome Res. 2002;12:996–1006. doi: 10.1101/gr.229102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanckriet G.R., et al. Kernel-based data fusion and its application to protein function prediction in yeast. Pac. Symp. Biocomput. 2004:300–311. doi: 10.1142/9789812704856_0029. [DOI] [PubMed] [Google Scholar]
- Lee H.K., et al. Coexpression analysis of human genes across many microarray data sets. Genome Res. 2004;14:1085–1094. doi: 10.1101/gr.1910904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynn D.J., et al. InnateDB: facilitating systems-level analyses of the mammalian innate immune response. Mol. Syst. Biol. 2008;4:218. doi: 10.1038/msb.2008.55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S., et al. GeneMANIA: a real-time multiple association network integration algorithm for predicting gene function. Genome Biol. 2008;9(Suppl. 1):S4. doi: 10.1186/gb-2008-9-s1-s4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NCBI. The NCBI Handbook [Internet] Bethesda, MD: National Library of Medicine (US), National Center for Biotechnology Information; 2002. [Google Scholar]
- Oliver S. Guilt-by-association goes global. Nature. 2000;403:601–603. doi: 10.1038/35001165. [DOI] [PubMed] [Google Scholar]
- Pellegrini M., et al. Assigning protein functions by comparative genome analysis: protein phylogenetic profiles. Proc. Natl Acad. Sci. USA. 1999;96:4285–4288. doi: 10.1073/pnas.96.8.4285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pena-Castillo L., et al. A critical assessment of Mus musculus gene function prediction using integrated genomic evidence. Genome Biol. 2008;9(Suppl. 1):S2. doi: 10.1186/gb-2008-9-s1-s2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prasad T.S., et al. Human Protein Reference Database and Human Proteinpedia as discovery tools for systems biology. Methods Mol. Biol. 2009;577:67–79. doi: 10.1007/978-1-60761-232-2_6. [DOI] [PubMed] [Google Scholar]
- Pu S., et al. Local coherence in genetic interaction patterns reveals prevalent functional versatility. Bioinformatics. 2008;24:2376–2383. doi: 10.1093/bioinformatics/btn440. [DOI] [PubMed] [Google Scholar]
- Ravasz E., et al. Hierarchical organization of modularity in metabolic networks. Science. 2002;297:1551–1555. doi: 10.1126/science.1073374. [DOI] [PubMed] [Google Scholar]
- Razick S., et al. iRefIndex: a consolidated protein interaction database with provenance. BMC Bioinformatics. 2008;9:405. doi: 10.1186/1471-2105-9-405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saito K., et al. Decoding genes with coexpression networks and metabolomics – ‘majority report by precogs’. Trends Plant Sci. 2008;13:36–43. doi: 10.1016/j.tplants.2007.10.006. [DOI] [PubMed] [Google Scholar]
- Schietgat L., et al. Predicting gene function using hierarchical multi-label decision tree ensembles. BMC Bioinformatics. 2010;11:2. doi: 10.1186/1471-2105-11-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwikowski B., et al. A network of protein-protein interactions in yeast. Nat. Biotechnol. 2000;18:1257–1261. doi: 10.1038/82360. [DOI] [PubMed] [Google Scholar]
- Tong A.H., et al. Global mapping of the yeast genetic interaction network. Science. 2004;303:808–813. doi: 10.1126/science.1091317. [DOI] [PubMed] [Google Scholar]
- Tsuda K., et al. Fast protein classification with multiple networks. Bioinformatics. 2005;21(Suppl. 2):ii59–i65. doi: 10.1093/bioinformatics/bti1110. [DOI] [PubMed] [Google Scholar]
- Typas A., et al. High-throughput, quantitative analyses of genetic interactions in E. coli. Nat. Methods. 2008;5:781–787. doi: 10.1038/nmeth.1240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez A., et al. Global protein function prediction from protein-protein interaction networks. Nat. Biotechnol. 2003;21:697–700. doi: 10.1038/nbt825. [DOI] [PubMed] [Google Scholar]
- von Mering C., et al. Comparative assessment of large-scale data sets of protein-protein interactions. Nature. 2002;417:399–403. doi: 10.1038/nature750. [DOI] [PubMed] [Google Scholar]
- Weston J., et al. Protein ranking: from local to global structure in the protein similarity network. Proc. Natl Acad. Sci. USA. 2004;101:6559–6563. doi: 10.1073/pnas.0308067101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe C.J., et al. Systematic survey reveals general applicability of “guilt-by-association” within gene coexpression networks. BMC Bioinformatics. 2005;6:227. doi: 10.1186/1471-2105-6-227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xenarios I., et al. DIP, the Database of Interacting Proteins: a research tool for studying cellular networks of protein interactions. Nucleic Acids Res. 2002;30:303–305. doi: 10.1093/nar/30.1.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yip A.M., Horvath S. Gene network interconnectedness and the generalized topological overlap measure. BMC Bioinformatics. 2007;8:22. doi: 10.1186/1471-2105-8-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang B., Horvath S. A general framework for weighted gene co-expression network analysis. Stat. Appl. Genet. Mol. Biol. 2005;4 doi: 10.2202/1544-6115.1128. Article17. [DOI] [PubMed] [Google Scholar]
- Zhou X., et al. Transitive functional annotation by shortest-path analysis of gene expression data. Proc. Natl Acad. Sci. USA. 2002;99:12783–12788. doi: 10.1073/pnas.192159399. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.