A method for probing the mutational landscape of amyloid structure

Abstract

Motivation: Proteins of all kinds can self-assemble into highly ordered β-sheet aggregates known as amyloid fibrils, important both biologically and clinically. However, the specific molecular structure of a fibril can vary dramatically depending on sequence and environmental conditions, and mutations can drastically alter amyloid function and pathogenicity. Experimental structure determination has proven extremely difficult with only a handful of NMR-based models proposed, suggesting a need for computational methods.

Results: We present AmyloidMutants, a statistical mechanics approach for de novo prediction and analysis of wild-type and mutant amyloid structures. Based on the premise of protein mutational landscapes, AmyloidMutants energetically quantifies the effects of sequence mutation on fibril conformation and stability. Tested on non-mutant, full-length amyloid structures with known chemical shift data, AmyloidMutants offers roughly 2-fold improvement in prediction accuracy over existing tools. Moreover, AmyloidMutants is the only method to predict complete super-secondary structures, enabling accurate discrimination of topologically dissimilar amyloid conformations that correspond to the same sequence locations. Applied to mutant prediction, AmyloidMutants identifies a global conformational switch between Aβ and its highly-toxic ‘Iowa’ mutant in agreement with a recent experimental model based on partial chemical shift data. Predictions on mutant, yeast-toxic strains of HET-s suggest similar alternate folds. When applied to HET-s and a HET-s mutant with core asparagines replaced by glutamines (both highly amyloidogenic chemically similar residues abundant in many amyloids), AmyloidMutants surprisingly predicts a greatly reduced capacity of the glutamine mutant to form amyloid. We confirm this finding by conducting mutagenesis experiments.

Availability: Our tool is publically available on the web at http://amyloid.csail.mit.edu/.

Contact: lindquist_admin@wi.mit.edu; bab@csail.mit.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Under optimum conditions, proteins with diverse primary sequence exhibit the ability to self-assemble into structurally varied, but highly ordered β-sheet aggregates known as amyloid fibrils (Dobson, 2003). Those forming amyloid under normal physiological conditions can have profound effects on biological systems—deleterious and beneficial. On the one hand, amyloids play a role in diseases such as Alzheimer's, Parkinson's and Huntington's, as well as systemic amyloidosis. On the other, they serve vital functions in normal biology such as in human peptide hormone storage, biofilm formation and a mechanism of protein-only inheritance by yeast prions (Halfmann and Lindquist, 2010). However, the generic nature of the fold, the observation that most proteins do not form amyloid under normal conditions and the ability of many amyloids to adopt multiple amyloid structures from the same peptide sequence (structural strains) confounds standard sequence-specific models of protein folding (Ostapchenko et al., 2010). Moreover, sequences with only a small likelihood of forming amyloid can remain so given many mutations, or become abundantly amyloidogenic after only a single point change (Lie et al., 2004). Therefore, to better understand the sequence/structure relationship of amyloid fibrils, a meaningful predictive model is required that describes the relationship between a given sequence and its mutational neighborhood.

Countless experimental studies have been performed to probe the molecular mechanism of these enigmatic structures. However, most methods (developed primarily for globular proteins) are difficult to apply to amyloids due to their large size and insolubility. Techniques such as solid-state nuclear magnetic resonance (NMR) spectroscopy and hydrogen-deuterium exchange (H/D-exchange) have brought us the most information about fibril structure, but only through exhaustive work and complex experimental design (Luca et al., 2007; Lührs et al., 2005; Mukrasch et al., 2009; Vilar et al., 2007; Wasmer et al., 2008). The high cost of such studies has prevented the kinds of large-scale investigations that can reveal the underlying sequence/structure relationships in functional and pathogenic amyloid folds.

Seminal work has shown that computational prediction of sequence amyloidogenicity can help guide and speed investigations of amyloid structure (Alberti et al., 2009; Bryan et al., 2009; Fernandez-Escamilla et al., 2004; Tartaglia and Vendruscolo et al., 2008; Trovato et al., 2007). These advances enabled new possibilities for genome-wide studies, such as the discovery of 19 new functioning amyloid proteins in yeast (Alberti et al., 2009). More specialized tools (Maurer-Stroh et al., 2010; Thompson et al., 2006) have been further developed that detail the structure of one particular amyloid fibril conformation: ‘steric zippers’, a repeated, dry β-strand/β-strand packing consisting of a few amino acids (Sawaya et al., 2007). However, other more elaborate amyloid conformations such as β-solenoids (Wasmer et al., 2008) cannot be considered by these specialized methods. Unfortunately, while these techniques can generate high-resolution structural predictions, they can only predict structural detail for regions of ~6 to 10 residues at a time due to the assumption of a steric zipper conformation. While such short segments may act as hot spots for amyloid formation, a full-peptide structure prediction cannot be made, which encompasses the size of amyloid sequences found in nature. In the opposite vein, earlier tools are able to predict the amyloidogenicity of sequences of any length, and agnostic to a particular molecular conformation, but unfortunately their structural prediction accuracy can suffer, achieving at best ~40% sensitivity on per-residue β-sheet location assignment and can exhibit insensitivity to sequence mutation (Morel et al., 2006). Moreover, these tools do not predict complete super-secondary structures, and do not capture the finer details of β-sheet residue/residue interactions that allow one amyloid conformation to be distinguished from another.

In this article, we develop an algorithm, AmyloidMutants, which predicts amyloid fibril structural conformations, and the sequence mutations that stabilize, reconfigure and de-stabilize each fibril conformation. Like earlier tools, our approach handles full-length amyloid sequences, but greatly improves predictive accuracy by calculating Boltzmann-distributed energetics over only those β-strand arrangements likely to be found in amyloid fibrils. A statistical mechanical ensemble is constructed that scores a complete family of millions of conformational states and sequence polymorphisms (a ‘mutational landscape’). A comparison of these sequence/structure states allows for the prediction of likely conformations and the identification of sequence determinants of structural heterogeneity. The goal of our algorithm is thus to efficiently calculate all these possible states, and produce accurate, physically meaningful amyloid fibril predictions.

AmyloidMutants is sensitive enough to distinguish dramatic shifts from one amyloid conformation to another when as little as a single point mutation is made; at the same time, it provides highly accurate predictions of structure, strain conformations and mutant amyloidogenicity. Indeed, in agreement with experimental observations, our tool identifies separate, incompatible amyloid conformations that are preferentially induced by wild-type (WT) Aβ and the Aβ Iowa mutant (Tycko et al., 2009), as well as similarly distinct structures resulting from wild-type and yeast-toxic mutant strains of HET-s (Couthouis et al., 2009). AmyloidMutants also allows us to probe the amyloidogenic relationship between chemically similar residues such as Asn and Gln, which revealed a specific HET-s sequence sensitivity to Asn.

2 APPROACH

We present AmyloidMutants, a web-based tool for predicting the structural and mutational landscapes of amyloid fibrils using an ensemble algorithm. In an ensemble predictor, each peptide sequence is presumed to fold into a complete set of millions (or billions) of unique structural states, with a single energetic value calculated for each state according to its entire conformation (McCaskill, 1990). From this quantified set of all possible structures, clusters of low-energy states with similar conformations can be extracted as predictions of likely real-world structures, with relative probabilities of occurrence. A mutational ensemble predictor simply increases the dimensionality of this set by including sequence variation within each state. (Note, ‘ensemble’ predictors differ from consensus predictors; the latter produces a single prediction based on the consensus of multiple authors' algorithms.)

The definition of an amyloid fibril ‘state’ greatly impacts the accuracy of an ensemble predictor: including atomic details would result in an intractable computation, while high-level representations that work in 1D sequence space can miss important steric and energetic details. To capture critical 3D elements while retaining efficiency, we choose to model super-secondary structural information—each state contains a sequence and a unique set of residue/residue β-strand backbone interaction pairs. But even so, calculating the energy of all mathematically possible interactions would introduce an exponential number of states as a function of sequence length.

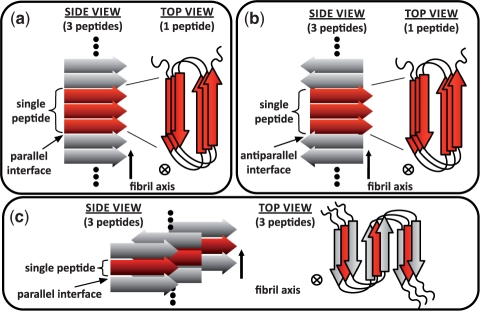
We introduce ‘schemas’ as an algorithmic construct to solve this by partitioning fibrillar from non-fibrillar conformations, enforcing steric consistency and enabling energetic calculations over all amyloid fibril sequence/structure states. For efficiency and usability purposes, putative amyloid fibril states are separated into three largely distinct topology families: schemas 𝒫, 𝒜 and 𝒮, which to our knowledge, together subsume the variation found in most published experimental and hypothetical amyloid fibril structure models (Fig. 1). These schemas also account for sequence variation through a simple user specification of the mutational possibilities that should be explored: e.g. ‘all Val can mutate to Ala, Leu, or Ile’. For example, schema 𝒫 and 𝒜 describes an abstract ‘β-solenoid” encompassing millions of structures with unique residue/residue interactions and varying numbers of β-strands, β-rungs, β-sheet width, coil location, residue orientation and residue packing neighbors (for example, HET-s 𝒜 predictions in Section 4 calculate the energy of ~4 billions states). Specific 2-, 3- and 4-sheet β-helix-like structures are accounted for by the introduction of ‘kinks’ (Fig. 2). Similarly, schema 𝒮 represents millions of possible full-length peptide ‘serpentine’ conformations, putatively containing multiple steric zipper interfaces.

Fig. 1.

Amyloid fibril schemas used for analysis. Amyloid fibril schemas, diagrammed from side and top perspectives. Red indicates a single fibril peptide flanked by two gray adjacent peptides along the fibril axis. (a) Schema 𝒫, a 2-sheet β-solenoid with unrestricted number of rungs per peptide and parallel intra- and interchain interactions. (b) Schema 𝒜, identical to 𝒫 except with antiparallel interchain interactions. (c) Schema 𝒮, a serpentine cross-β structure with unrestricted number of packed intrachain β-sheets. All β-strand hydrogen bonds formed interchain.

Fig. 2.

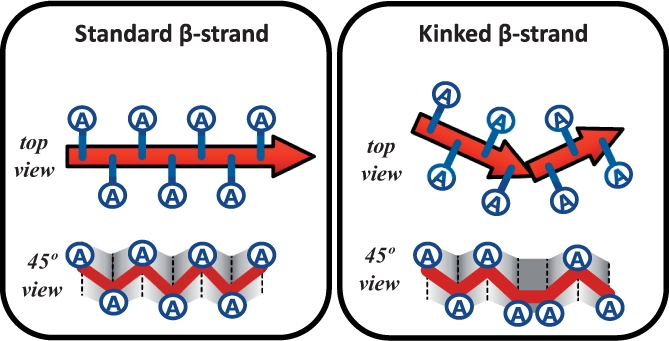
β-strand ‘kinks’ extend schemas in Figure 1 to allow AmyloidMutants to model sharp β-sheet turns like those found in β-solenoids. Kink represents a deviation in the standard β-sheet in/out residue sidechain orientation.

Conceptually, each schema ‘shape’ can be thought to resemble the ‘architecture’ level of CATH (Pearl et al., 2003) protein structure classification: for example, schema 𝒫 resembles the ‘2-solenoid’ and ‘3-solenoid’ classifications that make up 2 out of the 20 ‘mainly-beta’ architectures in all proteins in CATH. We note that schemas should not be confused with threading templates used in other protein and amyloid modeling tools (Thompson et al., 2006): threading tools fix a peptide backbone to a specific atomistic position and computationally score the effects of residue-specific side chains, whereas schemas cover a wide range of amyloid conformation and peptide backbone arrangements in 3D space. Further, AmyloidMutants does not predict kinetics of amyloid formation, but simply the set of possible conformations at steady-state encompassing arbitrary environment conditions. No restrictions are placed on the location or size of structural elements with the exception of individual β-strand lengths, which is fixed to a range of 6–12 residues for efficiency purposes, and can vary within a single structure (except when noted in Section 1 of Supplementary Material).

3 METHODS

3.1 Calculating amyloid ensembles

AmyloidMutants models the structural effects of sequence variation by conceptually scoring all possible amyloid fibril conformations that any sequence (and its mutants) can attain. Using a statistical mechanical approach, all structures are members of a canonical ensemble, with each state's energetic value assigned according to a Boltzmann distribution. Such an ensemble predictor differs fundamentally from existing techniques that perform an algorithmic search for an individual, lowest energy structure state. However, computing the score of all possible states in atomistic detail is considered computationally intractable (Istrail, 2000), so our approach uses a philosophy of domain restriction (via schemas) to efficiently predict accurate, physically meaningful amyloid structures at the level of super-secondary structure. The utility of such an approach has been demonstrated in RNA (McCaskill, 1990; Waldispühl et al., 2008b); however, protein structures are too complex to tractably apply their same methods.

At the core of our framework lies the ability to compute the Boltzmann partition function (𝒵) for given protein sequences. This thermodynamic normalization constant encodes the statistical variation of a system in equilibrium, and is used to identify the significance of structures within an ensemble. 𝒵 is defined by the sum: ∀s, 𝒵=∑_se^{−E_s/R T}, given temperature T, the physical constant R and a Boltzmann-distributed energy score E_s for every conformation s within the ensemble. AmyloidMutants extends the notion of a structural ensembles to analyze protein sequence/structure ensembles, redefining the partition function 𝒵 as: ∀ω, ∀s, 𝒵=∑_ω∑_se^{−E_s/R T}, given sequences ω and structures s. This encodes statistical variations in protein structure as well as sequence, distributed according to the energetic likelihood of that sequence's conformations. With this, one can identify energetically favorable sequence/structure assignments and quantitatively measure the energetic difference of between states.

AmyloidMutants is implemented using C++, with modular templates describing the recursively enumerable sequence and structure space. An analysis is performed on the sequence input to optimize the search across sequence/structure states, and a dynamic programming procedure is constructed that traverses and scores all possible states, tabulating these values. From this, 𝒵 can be calculated via a simple traversal.

3.2 Amyloid schema definition

Schemas are generative rules restricting the exponential set of peptide conformations to only those that form amyloid fibrils. These are defined in two parts, a recursive encoding of structure space and a protocol giving a list of all allowed sequence mutations. To model a theoretically endless fibril we employ a concept of symmetry, representing an amyloid as the conformation of single peptide combined with two sets of inter-peptide β-sheet interactions up and down the axis. We detail here specific characteristics used to define a schema, beyond the qualitative description in Figure 1.

Structure space is defined as putative geometric arrangement of β-sheets at the resolution of (i) intrapeptide hydrogen bonds along the fibril axis; (ii) β-sheet/β-sheet packing perpendicular to the axis (e.g. steric-zipper packings, etc.); and (iii) peptide/peptide symmetry describing interpeptide hydrogen bonds. Residue side chain orientations are also included in the model to indicate inward (hydrophobically packed) and outward (solvent exposed) states. Thus, a single structure can tell you whether a residue is in a β-sheet or coil, its orientation, which other residue(s) it forms a hydrogen bonding pair with and which topologically specific β-sheet its found in, indicating other β-sheets it may pack against. Finally, β-strand ‘kinks’ model two successive β-strand residues that have the same side-chain orientation (Fig. 2). Modeling kinks allows more precise energetic parameters when two sequentially adjacent β-strands form a sharp turn (as in many β-helices), since these junctions differ from coil-separated β-strands.

Sequence space is defined by a set of allowed mutations off a base sequence, per sequence position, per residue. For example, ‘position index 10 can either be Ala, Leu, or Val,’ input via programmable macros. This level of specification is required to avoid an exponential computation, as there are 20^N residue permutations in a sequence of length N. At runtime, an analysis is performed to determine the minimum dynamic programming table dimension required to fit each possible mutation. Presently, deletion and insertion mutations are not supported due to limitations of the energy models.

Although not used for results in this article, schemas can be further refined to incorporate specific point knowledge into the ensemble, enabling a more profitable, iterative back-and-forth between predictions and experimentation. These refinements include: (i) limiting β-strand or coil length; (ii) enabling or disabling β-sheet ‘kinks’; (iii) requiring a minimum/maximum total-fibril β-sheet concentration; (iv) enabling or disabling fibril twist; (v) permitting N- and C-terminal coil asymmetries; and (vi) allowing user-defined residue/residue hydrogen bond contacts to be fixed.

3.3 Energy model for amyloid-like interaction

AmyloidMutants uses a potential energy scoring function derived from observing the frequency of specific residue/residue interactions in (non-sequence-homologous) PDB (Berman et al., 2000) protein structures. Many protein and RNA modeling tools (Bradley et al., 2001; Trovato et al., 2007; Waldispühl et al., 2008a; Zuker and Stiegler, 1981) have successfully used such statistical potentials because of two main advantages: (i) residue/residue interactions (or base pairs in RNA) can efficiently capture the important, energetically stabilizing features of 3D structure without the need of molecular detail, and (ii) constructing an energetic scoring function from known PDB structures does not require a priori expert information, so as new structures are solved, typically accuracy increases. Note, such statistical potentials do not incorporate environmental conditions such as pH.

Traditional pairwise contact models calculate the frequency with which residues pair within a β-sheet (Bradley et al., 2001; Waldispühl et al., 2006). AmyloidMutants extends this by conditioning each probability by the local 3D environment, including amphipathicity and solvent accessibility, β-strand edge proximity, residue-stacking ladders, β-sheet edges and β-sheet twist [e.g. p(i|j,env)], discretizing higher resolution information important to amyloid structure. Accordingly, each residue position in every possible ensemble state has an associated environment that allows the search procedure to apply the correct energy. For example, residues/residue pairs facing toward the center of the β-solenoid in schemas 𝒫 and 𝒜 would be considered solvent inaccessible. These β-sheet potentials are combined and scaled with potentials for consecutive coil residues (p(i,j)), as well as an optional hydropathic packing score describing the propensity for β-sheet faces to pack against one another (Kyte and Doolittle, 1982). There is no explicit cost for the act of mutation, merely an energetic change due to a new sequence (Section 3 of Supplementary Material). The algorithm supports additional types of potentials, such as position-specific scoring matrices, stacked residue-pairs (Waldispühl et al., 2008a), and chemical propensities (Miyazawa and Jernigan, 1985), although these are not used here.

Formally, a fibril's energy is decomposed into independent substructure energy scores that recombine according to the schema topology. The energy of each state s is defined to be E_s=−RTlog(p_s)-RTlog(𝒵), and we make the assumption that E_s can be linearly decomposed into i parts such that E_s=∑_i−RTlog(p_si)−RTlog(𝒵) (Clote and Backofen, 2000). The probability p_sk thus represents the likelihood of observing a substructural state k, such as the propensity for two residues to pair within a β-sheet, and log(𝒵) serves as a statistical centering constant. Predicted states represent steady-state conditions and do not reflect folding kinetics.

3.4 Sampling and stochastic contact maps

The principal output of AmyloidMutants is a sampled set of unique sequence/structure states (a list of sequences and their corresponding conformations) that is statistically representative of the full ensemble. Prior work has demonstrated the higher predictive accuracy of ensemble sampling over minimum energy structures (Waldispühl et al., 2008a). To achieve this, a sampling procedure performs an energetically weighted stochastic backtrack over subsequence/substructure scores generated when computing 𝒵. Populations of similar structures are separated via PAM clustering, taking as input the number of clusters, and using a distance metric that optionally combines sequence, secondary structure, energy score, hydrogen bond registration, coil location and β-strand overlap. A mediod is selected to represent each cluster. User-definable distance metric changes allow for independent analysis of specific structural or sequential features.

Another form of output, the stochastic contact map, describes the Boltzmann-weighted likelihood p_i,j that any two residues i and j will form a β-sheet hydrogen bond, given all the conformations in the ensemble. To remove schema bias, the null hypothesis probability of any residue i and j forming a bond is subtracted from p_i,j (Section 3 of Supplementary Material). This allows AmyloidMutants to identify small β-strand interaction motifs within the ensemble that may be hard to discern from full conformation sampling. Furthermore, contact maps scores can be used to predict structural properties such as X-ray crystallography B-values (Waldispühl et al., 2008a).

4 RESULTS

4.1 Secondary and super-secondary structure prediction

Even in the absence of mutation predictions, AmyloidMutants offers the the highest structure prediction accuracy to date. We demonstrate this by comparing predictions against experimental data for five of the best studied WT amyloid proteins: Aβ (Lührs et al., 2005; Petkova et al., 2003) (39-42aa), HET-s (Wasmer et al., 2008) (73aa), amylin (Kajava et al., 2005; Luca et al., 2007) (37aa), α-synuclein (Heise et al., 2005; Vilar et al., 2007) (140aa) and tau (Mukrasch et al., 2009; von Bergan et al., 2000) (htau40, 441aa). This set covers pathogenic and functional amyloids found in nature for which there are a number of published structural experiments, including NMR secondary structure chemical shift and H/D exchange data. The ability to accurately predict the structure of such peptides could potentially help elucidate how native amyloid-related processes (such as biofilm formation) impact cellular function, and allow for targeted experimentation.

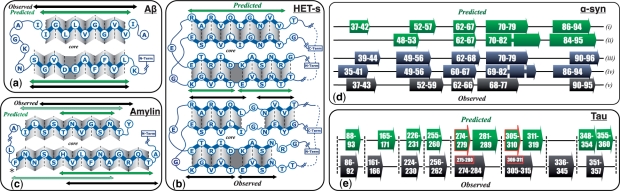
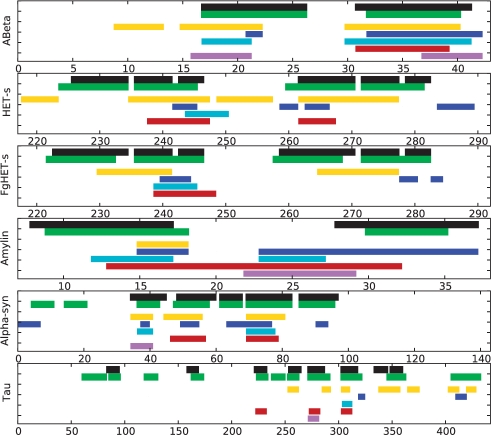
For these five proteins, AmyloidMutants correctly identifies experimentally observed β-sheet regions in 21 of 22 cases (Fig. 4, Table 1)—a per-residue secondary-structure classification sensitivity/specificity of 82%/95% and an average SOV score of 82 (Zelma et al., 1999). Using the same comparison, the best of the available full-length amyloid prediction tools (Bryan et al., 2009; Fernandez-Escamilla et al., 2004; Maurer-Stroh et al., 2010; Tartaglia and Vendruscolo et al., 2008; Trovato et al., 2007) produced a classification sensitivity/specificity of 42%/90% (Zyggregator) (Fig. 3). Per-residue β-sheet classification is used for this comparison since it can be inferred as a common output of all tools; however, AmyloidMutants can provide more rich predictions including super-secondary residue/residue interactions. Therefore, a detailed analysis of each protein's predictions is given to demonstrate these added benefits, along with a demonstration of how ensemble predictions can help identify alternate fibril conformations in agreement with published experimental data.

Fig. 4.

AmyloidMutants structure predictions match experimentally observed β-strand interactions of Aβ_1-42 (a), HET-s (b), amylin (c), α-synuclein (d) and tau (e). (a) Diagram depicts Aβ_1-42 β-strand in gray, residues in blue (with in/out orientation) and β-sheet/β-sheet packing as one β-strand above another, packed residues facing center. Predicted structure (green arrows) mirrors NMR structure (Lührs et al., 2005) (black arrows), including most packing orientations. Predicted kink occurs because schema does not account for known D23/K28 salt bridge. (b) Similar depiction of HET-s prediction (top, green arrows) compared with NMR model (Wasmer et al., 2008) (bottom, black arrows) shows near identical match, including residue orientations and kink location. (c) Top two amylin predictions (solid, striped green arrows) align well to NMR model (Luca et al., 2007) (black arrows). Predictions differ only by their inclusion of Phe23 (*) within β-sheet, a residue experimentally shown to form non-β-sheet interpeptide interactions not considered by schema. (d) Top two α-synuclein predictions (i,ii) agree very well with H/D exchange data (iii,iv) and NMR model (v) (Heise et al., 2005; Vilar et al., 2007). (e) Tau predictions identify 7/8 β-regions observed experimentally (Mukrasch et al., 2009). The highest AmyloidMutants scores (red boxes) specifically identify regions 274–279 and 305–310, positions believed crucial to fibril nucleation (von Bergan et al., 2000).

Table 1.

Summary of secondary-structure prediction results

	Aβ	HET-s	Amylin	α-syn	Tau
Sequence length	42	73	37	140	441
Correct β-regions	2 of 2	4 of 4	3 of 3	5 of 5	7 of 8
False-positive β-regions	0	0	0	2	2
Percent sensitive/specificity	100/100	95/95	70/91	81/95	68/95
SOV measure	100	90	97	62	62

Fig. 3.

AmyloidMutants per-residue β-strand assignments indicate amyloid core regions, comparable with existing per-residue amyloidogenicity predictors. AmyloidMutants predictions (green) outperform those tools available for testing when using their default settings and thresholds. BETASCAN (gold) (Bryan et al., 2009), ZYGGREGATOR (blue) (Tartaglia and Vendruscolo et al., 2008), TANGO (cyan) (Fernandez-Escamilla et al., 2004), PASTA (red) (Trovato et al., 2007) and Waltz (purple) (Maurer-Stroh et al., 2010), when compared against experimental structure models supported by NMR, H/D-exchange and mutational analysis (black) (Luca et al., 2007; Lührs et al., 2005; Mukrasch et al., 2009; Vilar et al., 2007; Wasmer et al., 2008, 2010). Note, the BETASCAN, ZYGGREGATOR, TANGO and PASTA tools most closely match our tool's ability to predict full-length per-residue amyloidogenicity, whereas Waltz aims to predict short hots pots that could specifically adopt a steric zipper.

AmyloidMutants was run on each sequence for all three schemas 𝒫, 𝒜 and 𝒮, with the schema that agreed best presented. An ensemble was calculated, and conformations were sampled and clustered, with the mediod structures reported (Section 1 of Supplementary Material). Although rough computational tests can be applied to evaluate the schema fitness (Section 3 of Supplementary Material), in a typical real-world scenario (and what has been applied thus far), an uncharacterized amyloid sequence is predicted using all schemas, and results are compared against the body of existing experimental data or used to guide further disambiguating experimentation.

Note, although atomic-resolution steric zipper structures have been solved for many short (~4 to 10aa) synthetic peptides (Maurer-Stroh et al., 2010; Sawaya et al., 2007), AmyloidMutants predictions on such short peptides are trivial. Schemas can predict the position and arrangement of steric zipper sites throughout a full-length peptide, but are not designed to distinguish side-chain rotamers (and are unrelated to steric zipper classes).

Amyloid Beta (Aβ): an ensemble analysis of Aβ is particularly poignant as it has many known isoforms (Aβ_1-40, Aβ_1-42, Aβ_1-40/D23N, Aβ_1-40/E22Q, etc.) and subsequences (Aβ_16-22, Aβ_11-25, etc.) that have been reported to form a diverse range of fibril structures, including strain polymorphisms within the same sequence (Petkova et al., 2005). Our tool predicts the experimentally observed structure of two possible Aβ conformations, recapitulating two distinct experimental models of the peptide based on NMR, H/D-exchange and mutational analysis (Lührs et al., 2005; Petkova et al., 2003). After clustering, the highest likelihood mediod structure nearly identically matches the latter of these two models (Lührs et al., 2005) (Fig. 4a), including β-strand positions, interior/exterior side chain orientation and the inter peptide parallel hydrogen bonding registration. This cluster accounts for 55% of the ensemble. Interestingly, the second highest likelihood mediod exhibits a clear shift in one of the β-strand regions and aligns very closely with the earlier NMR model (Petkova et al., 2003). This cluster is more heterogeneous, including many other structural arrangements, and accounts for 39% of the ensemble. Furthermore, recent experimental studies of Aβ conformational variation have shown that fibrils formed under quiescence and agitation differ, for instance, in the assignment of position 15 to β-strand (Petkova et al., 2005). The predicted clusters also make this rough distinction: the larger cluster does not contain a β-strand at position 15, while the smaller does. Moreover, brain-seeded fibrils have exhibited spatial proximity between residues F19/I31, whereas unseeded in vitro fibrils do not (Paravastu et al., 2009). AmyloidMutants also predicts such a divergence: in 16% of the ensemble, F19 and I31 are both oriented toward the center of the fibril, enabling proximal contact. Section 1 of Supplementary Material provides further detail.

HET-s: the 73 amino acid Podospora anserina HET-s prion is the most complex amyloid whose atomic-level 3D structure has been solved (Wasmer et al., 2008), forming a well-ordered β-helix with two rungs per chain and four β-sheets that are more appropriately modeled as two pairs of β-sheets separated by a kink in the standard ‘in/out’ residue orientation. AmyloidMutants strongly predicts two possible structures, the most likely of which forms a two-rung β-solenoid that almost exactly mirrors the NMR model, including hydrogen bond registration, side chain orientation and kink location (Fig. 4b, accounting for 68% of the ensemble). The lower likelihood conformation incorporates only a single rung, matching one of the rungs in the NMR structure. This strong predictive bias toward only two possible structures may relate to the observed conformational homogeneity of HET-s fibrils. Achieving such high accuracy on this difficult β-structural topology supports our tool's use for mutational analysis across broadly different fibril types. Furthermore, recent experimental studies have partially characterized a distant homologue to P.anserina HET-s found in Fusarium graminearum (Wasmer et al., 2010). Although FgHET-s exhibits only 38% sequence similarity, solid-state NMR and H/D-exchange data suggest an extremely similar β-solenoidal structure as in PaHET-s. Despite the large difference in sequence, predictions very well match the FgHET-s structural model, aligning β-strand location, hydrogen-bond registration, side-chain orientation and kink location (Supplemantary Fig. S1).

Amylin: AmyloidMutants predictions for human amylin indicate two viable conformations: a 2-sheet β-solenoid forms 80% of the ensemble and agrees closely with NMR and microscopy results (Luca et al., 2007) (Fig. 4c); and a much less likely three-sheet serpentine model that aligns almost perfectly with an older model of amylin structure (Kajava et al., 2005). Interestingly, the experimental model identifies an interprotofibril interaction between Phe23 and Tyr37—something beyond the scope of our schema. However, our β-solenoid predictions clearly separate into two distinct populations, one incorporating Phe23 into a β-sheet and one that does not. This highlights the importance of an ensemble analysis: the existence of high-likelihood alternate structures may draw attention to an overlooked structural interaction.

α-Synuclein: five β-sheet regions in α-synuclein have been identified through substantial experimental effort (Heise et al., 2005; Vilar et al., 2007). AmyloidMutants ensemble predictions agree extremely well with these results, aligning all five β-sheet regions, and identifying other important experimental observations such as a β-sheet break around residues 67–68 (Fig. 4d). One of the predicted clusters does produce a false positive, however, identifying amphipathic β-strands in the N-terminal region, a disordered segment thought to favor a lipid-binding amphipathic α-helical structure (Section 1 of Supplementary Material).

Tau(τ): NMR studies have shown this 441 amino acid long amyloid to form a mixture of up to eight transient β-sheet regions (Mukrasch et al., 2009), with two specific β-strands necessary for fibril assembly (von Bergan et al., 2000) (positions 306–311 and 275–280). Predicted β-sheets align very closely with these observed regions in seven of eight cases. Moreover, AmyloidMutants identifies the two hexapeptides experimentally observed necessary for assembly by predicting their β-strand interactions as having the strongest score (Section 1 of Supplementary Material). Four false positive regions are predicted to contain β-strands, although similar to α-synuclein, two overlap with observed α-helices which the schema does not incorporate and may contain sequences with high β-sheet propensity. Overall, the sensitivity and specificity of our predictions over such a long sequence considerably advance the state of the art (Fig. 3).

4.2 Prediction of a conformational switch in Aβ and HET-s mutants

AmyloidMutants is uniquely capable of identifying change in amyloid fibril conformation from one amyloid β-sheet topology to another. This distinction from tools that predict general amyloidogenicity is important as a structural change from one amyloid form to another can have a dramatic impact on oligomerization and nucleation rates (Kim and Hecht, 2008), disease infectivity (Tycko et al., 2009), and prion propagation (Alberti et al., 2009). We have used this ability to identify potential alternate, distinct amyloid fibril conformations that arise in the Aβ familial ‘Iowa’ mutation (Tycko et al., 2009) and yeast-toxic mutants of HET-s (Berthelot et al., 2009; Couthouis et al., 2009) (details and comment provided in Sections 2 and 3 of Supplementary Material). Described below are these AmyloidMutants results, highlighting consistencies with published experimental data.

Aβ Iowa mutant: recent studies (Tycko et al., 2009) suggest that Aβ_1-40/D23N may form an antiparallel β-strand fibril conformation that differs completely from known experimental models (Lührs et al., 2005; Petkova et al., 2003). This work suggests an antiparallel β-sheet around residues 16–22 (with unknown length), with an interβ-strand interface such that L17 bonds to A21 [designated ‘17+k↔21−k’ registry (Tycko et al., 2009)]. Similarly, a second antiparallel β-sheet likely exists around positions 30–36, with L34 and F19 in close contact. Interestingly, this specific Aβ₁₋₄₀ registry has only previously been seen in the peptide fragment Aβ₁₆₋₂₂, which lacks D23 (Tycko and Ishii, 2003), while the antiparallel forming fragment Aβ₁₁₋₂₅ shows inverted ‘17+k↔22−k’ and ‘17+k↔20−k’ registries (Petkova et al., 2004) (Table 2).

Table 2.

AmyloidMutants predictions reveal conformational switch between Aβ₁₋₄₀ and Aβ_1−40/D23N in agreement with published data

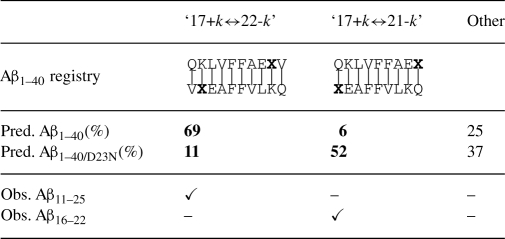Predictions show a significant change in the conformational landscapes of Aβ₁₋₄₀ and Aβ_1−40/D23N in agreement with published experimental evidence (Tycko et al., 2009) of an antiparallel, ‘17+k↔21-k’ registry β-sheet in Aβ_1−40/D23N (boldface). Sampled ensemble structures were classified into one of three categories of β-sheet registry, with the percent makeup of each provided. β-sheet registry is classified by residue/residue pairing, depicted with X highlighting position 23. Check marks indicate experimentally observed registrations in Aβ₁₁₋₂₅ (Petkova et al., 2004) and Aβ₁₆₋₂₂ (Tycko and Ishii, 2003).

To analyze this point mutant, we predicted ensembles for Aβ₁₋₄₀ and Aβ_1−40/D23N using schema 𝒜 (which allows antiparallel inter-peptide interactions). Detailed in Table 2, AmyloidMutants' Aβ_1−40/D23N predictions strongly preferred a ‘17+k↔21−k’ registry conformation, with predicted contacts between L34/F19, and very little variation within the ensemble. This arrangement agrees with observed Aβ₁₆₋₂₂ structures. Conversely, predictions for WT Aβ₁₋₄₀ are quite heterogeneous, although with the largest cluster of structures forming ‘17+k↔22−k’ registry, in agreement with observed Aβ₁₁₋₂₅ structure. More strikingly, the ‘17+k↔21−k’ registry conformation favored by Aβ_1–40/D23N appears to be strongly disfavored by Aβ₁₋₄₀ (and Aβ_{1−−40/D23N} appears to disfavor ‘17+k↔22−k’ registry). These predictions and the divergence in ensemble makeup between Aβ₁₋₄₀ and Aβ_1−40/D23N strongly supports the idea that the D23N mutation results in a singular energetically favorable conformational rearrangement from parallel β-sheets (in WT) to antiparallel β-sheets (in the D23N mutation). At the residue level, the adoption of this ‘17+k↔21−k’ conformation may be driven by both the alignment of oppositely charged K16 and E22 and the stacking arrangement of Q15 and N23 (Table 2).

HET-s yeast-toxic mutants: our technique is able to further predict putative conformational rearrangements between a set of HET-s mutants shown to exhibit toxicity in yeast. In recent studies (Berthelot et al., 2009; Couthouis et al., 2009), structural differences were found in a toxic HET-s mutant (named m8) and compared against four other non-toxic mutants (m3, m4, m9, m11) and WT. Notably, m8 exhibits a marked change from WT in secondary structure makeup, showing a shift of approximately half of the β-strand structure from parallel to antiparallel interactions.

AmyloidMutants can distinguish these phenotypically different mutants by inspecting predicted results using different schemas and comparing the relative structural heterogeneity of the ensembles. We premise that sequence mutants which significantly alter the predicted ensemble makeup (away from WT) are more likely to exhibit a different high-level conformational arrangement, and that high-likelihood conformations within an ensemble offer good predictive fits. Conversely, predictions that do not particularly favor any single conformation may suggest a poor fit. Table 3 reports ensemble predictions for the given six mutants, comparing schemas 𝒫 and 𝒜. Across all mutants, schema 𝒫 predict clusters of 2-rung and 1-rung structures, while schema 𝒜 predicts three clusters: two forms of 2-rung solenoids and one with 1-rung (Supplementary Fig. S11).

Table 3.

AmyloidMutants ensemble predictions of HET-s sequence variants reveal the yeast-toxic mutant m8 to be unique

Schema/class.	WT	m4	m8	m3	m9	m11
𝒫 2-rung (%)	75	95	72	13	49	55
𝒫 1-rung (%)	25	5	28	87	51	45
𝒜 2-rung-A (%)	45	42	81	44	56	50
𝒜 2-rung-B (%)	25	43	0	36	22	40
𝒜 1-rung (%)	30	15	19	20	22	10
Aggregation	Ring	Foci	Foci	diff.	diff.	diff.
Toxicity	–	Minor	Severe	–	–	–

Ensemble conformational landscape predictions of six HET-s variants produced two general structure classifications for schema 𝒫 and three general classifications for schema 𝒜 (rows, relative percent makeup given). While other mutants do not favor one particular schema 𝒜 structure, the yeast-toxic mutant m8 exhibits a strong energetic bias for 𝒜 2-rung-A. The differences in structure bias shown may suggest an increased likelihood that m8 adopts an antiparallel conformation (boldface). Observed phenotypic differences between mutants are summarized at the bottom (Couthouis et al., 2009).

The difference between schemas 𝒫 2-rung and 𝒜 2-rung correlates with the shift in secondary structure makeup observed — 𝒫 2-rung contains only parallel β-sheet structures while 𝒜 2-rung can contain an equal amount of parallel and antiparallel β-sheet structure. Under schema 𝒫, we see that WT, m4, and m8 form better 2-rung solenoids than a 1-rung solenoid, whereas with m3, m9, and m11, the opposite is true or no preference is apparent. This discrimination of mutants based on the structural landscape mirrors phenotypic variation seen by GFP-tagged aggregates (Couthouis et al., 2009) (independent of predictive accuracy). Under schema 𝒜, we see similarities between the structural distribution of WT, m4, m3, m9, and m11; however, the toxic m8 mutant appears to strongly prefer only one of the 2-rung conformations. Such a dramatic shift in the predicted ensemble could suggest that the m8 mutant is energetically inclined to form the structure in cluster 𝒜 2-rung-A.

4.3 Identification of preferential Asn amyloidogenicity over Gln in HET-s

Beyond its ability to discriminate amyloid fibril structure states, AmyloidMutants accurately models more coarse amyloidogenicity properties, allowing us to study a more fundamental question: the role chemically similar residues Asn and Gln play in fibril structure. Given the high propensity of Q/N-rich peptides to form amyloid (Chiti and Dobson, 2006), the amyloidogenic potential of Asn and Gln has often been considered equal—however, recent evidence suggests that N-rich proteins may have a slightly higher tendency to form amyloid (Alberti et al., 2009) [even though Gln mutations can improve stability (Gromiha et al., 1999)]. We study this question by considering the effect of four ladder-forming asparagine residues in P.anserina HET-s (positions 226, 243, 262 and 279) which are believed important for fibril stabilization (Wasmer et al., 2008), and whose regions are conserved in a F.graminearum homolog. AmyloidMutants sequence/structure landscapes were calculated permitting these four residues to mutate to Gln (‘HET-s/4N→Q’), and the likelihood and corresponding energetic weight of each sequence within the ensemble was compared. The WT HET-s sequence was much more energetically favorable than HET-s/4N→Q, comprising ~96% of the ensemble, suggesting a greatly reduced ability of HET-s/4N→Q to form fibrils, and a putatively higher amyloidogenic potential of Asn over Gln. Stochastic contact map predictions further illustrate this difference between sequences (Supplementary Fig. S9).

We tested these predictions experimentally, using purified recombinant WT and 4N→Q HET-s proteins (Section 4 of Supplementary Material). Denatured proteins were diluted into a physiological buffer and allowed to form amyloid. While the WT protein readily did so, as detected by the retention of detergent-insoluble aggregates on a non-binding membrane, the mutant protein was recalcitrant to amyloid formation (Fig. 5).

Fig. 5.

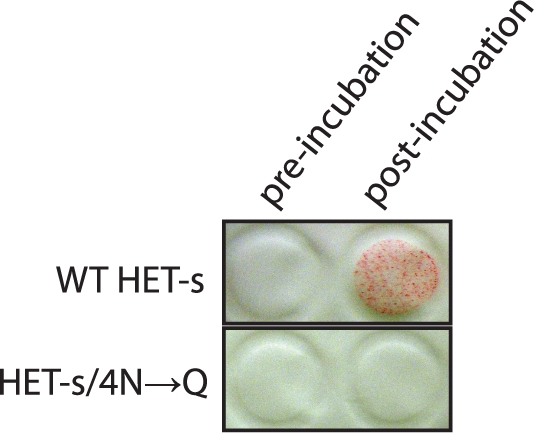
HET-s/4N→Q is defective for amyloid assembly. Purified proteins were filtered through a non-binding membrane either before or after incubation for 24 h in a physiological buffer. Protein aggregates that formed during the incubation are retained on the surface of the membrane, as visualized by Ponceau-S staining.

4.4 Mutational landscapes predict experimental amyloidogenicity

AmyloidMutants' ability to accurately predict amyloidogenicity is validated by comparing our results against a large number of experimentally characterized amyloid mutants. This includes an analysis of the 289-residue HET-s/HET-S natural homologs found in P.anserina, a combination of three Aβ scanning mutagenesis studies, and a set of 74 synthetic mutants of Aβ created by random mutagenesis. The amyloidogenicity of each mutation is predicted by computing a joint mutational landscape over WT and mutant sequences, and quantifying which sequence more readily forms amyloid according to its energetic weight within the ensemble. For example, if WT sequence/structure states occupy 90% of the ensemble, then any specified mutations are likely to result in a less amyloidogenic peptide (Supplementary Text Section 3).

HET-s/HET-S: In P.anserina, the HET-s allele forms an amyloid conformation in its prion form, while the HET-S allele does not, despite differing by only three residues in the amyloid-forming 72-residue C-terminus, and 13 overall (Coustou et al., 1999). Predicting the joint HET-s/HET-S mutational landscape, AmyloidMutants found that ~72% of the ensemble favored HET-s, indicating that it is more amyloidogenic than HET-S. Although N-terminal mutations can induce a prion state in HET-S (Coustou et al., 1999), our predictions suggests a sequence bias in HET-s permitting a more energetically favorable path for amyloid formation.

Aβ single-point proline mutagenesis: scanning mutagenesis studies have been performed on Aβ₄₀ to detect the sequence position effect of proline-, alanine- and cysteine-replacement on amyloid fibril formation, measured by WT/mutant ΔΔG (Shivaprasad et al., 2006; Williams et al., 2004, 2006). Although P, A and C-replacement ΔΔG values are difficult to interpret independently [due to experimental structural heterogeneity (Williams et al., 2006)], they support the broader conclusion that Aβ₄₀ positions 18–21, 25–26 and 32–33 are particularly sensitive to P-replacement (Williams et al., 2006). AmyloidMutants' predictions of the joint mutational landscape for individual proline replacements identified positions 16–25 and 31–35 as particularly disruptive in agreement with these studies. Supplementary Figure S12 plots this agreement along with similar predictions by TANGO and Zyggregator, although a direct one-to-one comparison between predictions and ΔΔG values would be inappropriate.

Aβ multiple-residue mutagenesis: AmyloidMutants predictions were also performed on a set of 74 Aβ mutants (Kim and Hecht, 2008, 2006; Wurth et al., 2002) whose relative aggregation levels were observed by GFP fluorescence relative to WT. AmyloidMutants accurately identifies which mutants form amyloid more (or less) readily than WT in 81% of sequences (60 of 74, Supplementary Fig. S8). AmyloidMutants' performance on such a large set further supports its general applicability.

5 DISCUSSION

AmyloidMutants provides the highest accuracy prediction to date of the full fibril structure of amyloid sequences, but its greater value is its unique ability to discover which mutations effect a change in amyloid structure(s), to predict what that structure is and to assign meaningful energetic weights comparing mutant conformations. This accuracy is due, in part, to the ability to model coarse, higher dimension spatial interactions, beyond simpler 1D sequence motifs. This is an important distinction from amyloidogenicity predictors that identify structurally homogeneous peptide sequences (Maurer-Stroh et al., 2010). While the latter can be helpful during an initial screen (searching for amyloid steric zippers in particular), AmyloidMutants can predict and provide insight into the full-length structure (Fig. 3) and residue/residue interactions of both β-solenoidal and serpentine steric zipper fibrils (Fig. 1), putatively identifying interactions critical to function or pathogenicity. Further, through the use of Boltzmann ensembles, our model of sequence/structure space is the only amyloid modeling tool that captures fibril structure variation and β-contact structural topology changes that may arise in in vivo.

The exploration of mutational landscapes is an important step in understanding differences between amyloid topologies, how mutational variants arise in the wild, and to elucidate evolutionary relationships between related amyloid proteins. This capability depends on AmyloidMutants' novel thermodynamic characterization of all points within a mutational landscape, and is necessary for the discovery of non-additive functional relationships between sequences and conformational epistasis (Ortlund et al., 2007). Further, we note that our tool provides additional features for experimentalists (not used in this article) that allows extra-sequential experimental data to be incorporated into the predictor (Supplementary Text Section 1)—as much or as little a priori knowledge as desired, enabling a new tactic for iterative tool re-use.

At face value, the ability of most proteins to form a characteristic cross-β-sheet amyloid structure in vitro (Dobson, 2003) seems at odds with the relatively small number of amyloid-forming proteins that have been identified in vivo, and the apparently high sequence dependence some amyloids show when compared against sequence homologs. Moreover, the existence of both beneficial functional amyloid sequences, and putatively pathogenic ‘misfolded’ amyloid proteins suggests a more complicated sequence/structure relationship than is found in standard protein folding models. The power to accurately predict amyloid structure from sequence, and to fully characterize the amyloidogenicity of an entire mutational landscape provides insight into this problem by identifying recurring sequence motifs, coarse 3D residue arrangements and putative mutational pathways linking the sequences of known amyloid structures. The immediate impact of this could improve our ability to identify amyloid structures from genomic data alone, to better understand familial mutations that intensify pathogenesis in diseases such as Alzheimer's, to predict the interaction strength of fibril regions that may be involved in nucleation and to enable targeted peptide design to alter fibril structure or inhibit fibril formation.

Funding: NIH grant (1R01GM081871 and GM25874, in part).

Conflict of Interest: none declared.