Longitudinal fMRI analysis: A review of methods

Abstract

Functional magnetic resonance imaging (fMRI) investigations of a longitudinal nature, where participants are scanned repeatedly over time and imaging data are obtained at more than one time-point, are essential to understanding functional changes and development in healthy and pathological brains. The main objective of this paper is to provide a brief summary of common longitudinal analysis approaches, develop an overview of fMRI by introducing how such data manifest, and explore the statistical challenges that arise at the intersection of these two techniques.

1. LONGITUDINAL DATA ANALYSIS

Longitudinal data frequently arise in biomedical and clinical settings, as well as many other areas of research. Such datasets consist of a collection of time series, one contributed from each of a number of subjects in a designed experiment or observational study [13]. The distinguishing feature of data collected longitudinally, then, is that each subject’s outcome/responses are observed or measured repeatedly, thereby allowing for the direct study of change over time or natural history. This setup is advantageous compared to cross-sectional studies (where, in contrast, subject responses are obtained at just one time-point). For example, a longitudinal study is more powerful for a fixed number of subjects, it allows each subject to serve as his/her own control, it permits the separation of aging effects from cohort effects, and it can provide information about individual change [32]. The fundamental objective of a longitudinal analysis is therefore to assess within-individual changes in the response and to explain systematic differences among individuals in their changes.

Despite these design advantages, investigations of a longitudinal nature can be methodologically challenging for a number of reasons. Most obviously, longitudinal studies are more expensive, time-consuming, and complicated to conduct. Further, the significant difference and difficulty of longitudinal data analysis (LDA) as compared to analysis of cross-sectional data is that while data from different subjects are assumed to be independent, data from the same subject tend to be correlated. Such dependency in the dataset invalidates an essential assumption of independence that underlies many standard statistical techniques and must be accounted for in the statistical methods used to analyze the data [17]. Failure to correctly specify the correlation among the repeated measures may result in incorrect estimates of the sampling variability and can lead to misleading scientific inference.

1.1 Approaches to LDA

Statisticians have approached the modeling of longitudinal data in a number of distinct ways. Three of the most commonly-used approaches, which differ in the way each accounts for within-subject association, are described in this section. The three classes of models arise from different specifications of (1) the joint distribution of the responses Y_i as well as (2) the source of correlation among the repeated measures of the same subject [17, 87]. Further, the three analytic approaches have slightly varying inference goals which reflect distinct questions of interest regarding longitudinal change in the response.

The first modeling technique explicitly models the heterogeneity between subjects (what Zeger et al. (1988) referred to as “subject-specific” modeling). An example of this technique is the mixed model, where there is an assumption that the subject-specific effects follow a parametric distribution. The second modeling technique does not explicitly account for the between-subject heterogeneity. It models the response as a function of the covariates (what Zeger et al. (1988) referred to as “population-averaged” modeling). The generalized estimating equations approach [46] is an example of a frequently-used method that generates estimates for these so-called marginal models. Finally, the third class of models for longitudinal data is the transitional or response-conditional approach. Such models treat both the explanatory variables and the prior responses as explicit predictors of the current outcome [81, 82]. It is useful to note that each of these three approaches has variations to handle datasets with continuous, binary, categorical, or count responses.

1.1.1 Population-averaged or marginal models

The main purpose of using population-averaged (or marginal) models in LDA is to make inference about population means. In such a setting, the model for the mean response at each time-point depends only on the covariates of interest and not on the unobserved random effects or previous responses [87]. The distinctive feature of marginal models is that the regression of the response on the explanatory variables is specified separately from the within-person correlation, guaranteeing that the assumptions regarding the within-subject association do not influence the interpretation of the marginal model’s estimated regression parameters [13]. This means that regression coefficients describe how the mean response in the population changes over time and how these changes relate to the covariates [17].

Typically, a population-averaged model for longitudinal data has a three component specification [13, 18] that can be viewed as an extension of the generalized linear model (GLM) [56] to longitudinal data. First, the marginal mean of each response, denoted by E(Y_ij|X_ij) = µ_ij, is assumed to depend on the covariates (or explanatory variables) via a known link function g(·) such that

$$g({\mu }_{ij})={\mathbf{X}}_{ij}^{\prime }\beta ,$$ (1)

where X denotes the design matrix of explanatory variables and β is a vector of fixed parameters (an example of a link function might be the logit link for binary responses where $\text{log}(\frac{{\mu }_{ij}}{1-{\mu }_{ij}})={\mathbf{X}}_{ij}^{\prime }\beta$ or a log link for count data where $\text{log}({\mu }_{ij})={\mathbf{X}}_{ij}^{\prime }\beta$). Second, the marginal variance of each Y_ij, given the covariates, is assumed to depend on the marginal mean according to

$$Var(Y_{ij}|{\mathbf{X}}_{ij})=\varphi \upsilon ({\mu }_{ij}),$$ (2)

where υ(µ_ij) is a known variance function and ϕ is a scale parameter that may need to be estimated. Lastly, the conditional, pairwise within-subject correlation among the vector of repeated responses, given the covariates, is assumed to be a function of the mean µ_ij and an additional set of association parameters α. It is this third part of the model specification that identifies the distinguishing dependence among the repeated observations by modeling within-subject association. Given this three-part formulation, it is noteworthy to mention that the marginal regression coefficients, β, have a similar interpretation to the coefficients from a cross-sectional analysis [13].

1.1.2 Subject-specific or GLMM models

The main idea behind subject-specific models is that there is a variability across individuals in the study population that is accounted for and estimated by a subset of regression parameters that are assumed to differ across individuals according to some fundamental distribution [13]. In contrast to marginal models, this alternative approach provides a source for the within-subject association by introducing random effects in the model equation for the mean response [18]. These random effects describe each subject’s trend across time and explain the correlation structure of the longitudinal data [32]. Conditional on the random effects, the assumption is that the repeated measurements for any given individual are independent observations. Subject-specific approaches are particularly useful when the objective is to make inference about individuals rather than just about the population average.

More specifically, such models are known as generalized linear mixed-effects models (GLMMs) and are characterized by the fact that the model for the mean response is conditional on both the observed covariates and the unobserved random effects. Typically, the generalized linear mixed model for longitudinal data has a two-part specification [18]. First, given a vector of random effects b_i, the responses Y_ij are assumed to be conditionally independent and to have an exponential family distribution with conditional mean depending upon both fixed effects (denoted by β) and random effects such that

$$g[E(Y_{ij}|{\mathbf{X}}_{ij},b_i)]={\mathbf{X}}_{ij}^{\prime }\beta +{\mathbf{Z}}_{ij}^{\prime }{b}_i$$ (3)

for some known link function g(·), where X is a matrix of fixed effects covariates and Z is a design matrix of random effects covariates. The conditional variance is assumed to be dependent on the conditional mean according to Var(Y_ij | X_ij, b_i) = ϕυ[E(Y_ij|X_ij, b_i)], where υ(·) is a known variance function and ϕ is a scale parameter that may need to be estimated. The second specification is that the random effects b_i have a multivariate normal distribution, with a zero mean and a covariance matrix G.

1.1.3 Conditional and transitional models

The third approach to handling longitudinal data focuses on modeling the mean and time dependence concurrently by conditioning a response on a subset of other responses [18]. Here, the conditional distribution of each outcome at any occasion is denoted as an explicit function of the previous outcomes and the covariates (for example see [88]). As presented in Fitzmaurice and Molenberghs (2008), the specification of a transitional model assumes that

$$g[E(Y_{ij}|{\mathbf{X}}_{ij},{\mathbf{H}}_{ij})]={\mathbf{X}}_{ij}^{\prime }\beta +{\displaystyle \sum {\alpha }_r{f}_r}({\mathbf{H}}_{ij}),$$ (4)

where H_ij = (Y_i1,…, Y_ij−1) denotes the history of the past responses at the j^th occasion and f_r(H_ij) represent some known functions of the history of the past responses. Thus, the characteristic feature of this modeling technique is that past outcomes are treated as additional explanatory variables [13]. Utilizing various link functions g(·) allows for transitional models (sometimes referred to as Markov models) to be applied to a range of situations and responses.

1.2 Concluding remarks regarding LDA

Longitudinal studies investigate change over time and the factors that influence change, producing complex datasets that pose interesting methodological challenges. Developments of regression models for longitudinal data have focused on extensions of the generalized linear model. Three main methods highlighted in this section include population-averaged (marginal) models, subject-specific (GLMM) models, and transitional (Markov) models. The choice between these analytic approaches should be based on the type of response variable measured as well as the target of inference and the scientific question at hand.

2. FUNCTIONAL MAGNETIC RESONANCE IMAGING & DATA ANALYSIS

During the past twenty years, a noninvasive neuroimaging technique used to study human brain function in vivo called functional magnetic resonance imaging (functional MRI or fMRI) has become an important part of current research in cognitive and clinical investigations as well as psychology and psychiatry. Ogawa et al. (1990) was the pioneer who first conducted an experiment that measured blood-oxygenation-level-dependent (BOLD) signal in the brain, establishing that fMRI could be used to measure brain function [63]. Since then, an ever-growing interest in this method has been shown by neuroscientists, physicists, statisticians, and psychologists who have worked to further develop fMRI research.

A primary use of fMRI is mapping brain function to brain structure as well as exploring physiological and pathological changes in functional activity of the brain. In an fMRI experiment, magnetic resonance images are obtained (based on the BOLD signal) while a subject engages in a passive, sensory, motor, or cognitive task designed to target specific brain functions. Researchers attempt to use these obtained images to detect how patterns of increased or decreased brain activity relate to task performance or disease group in order to understand and localize brain functions [14]. The brain regions with greater activation are presumed to be those related to the task or disease.

As the field grows and the methodology improves, so do the many computational and statistical problems that accompany the storage, processing, analysis, and interpretation of these very large and variable datasets. This section describes the scientific background related to the acquisition of fMRI data, fMRI experimental design and data preprocessing, current analysis techniques, as well as some data analysis problems unique to fMRI.

2.1 What does fMRI measure?

When the human brain activates in response to a particular task or stimulus, the rate of blood flow to brain regions involved in the task intensifies. The increased flow of blood occurs because the brain requires that glucose (a carbohydrate used by the brain as a source of energy) be delivered to relevant areas in the brain. As a consequence, metabolism of the neurons in the regions involved in the particular task is altered; the firing rate of these neurons increases and more oxygenated blood arrives in the pertinent brain areas. It is this increase of local oxygen levels in blood and the rise in metabolic demand of the neurons that is measured by the fMRI signal [55]. In other words, the fMRI signal relies on measuring blood oxygenation level, which changes based upon the metabolic demands of active neurons and is thought to indirectly reflect brain activity [42].

More specifically, the particular time-course of fMRI signal change (triggered by neuronal activity and variations to the ratio of oxygenated to deoxygenated blood) is described via something known as the hemodynamic response function (HRF), estimation of which is the focus of much statistical fMRI research. When a particular task or stimulus is presented to a subject, there is a delay of approximately two seconds prior to an observable change in signal as blood is delivered to the relevant area of the brain. A gradual increase in the response peaks at about six seconds following the stimulus. With no additional stimulation, the HRF steadily decays, returning to its original state. Friston and colleagues (1994) proposed that an estimated HRF can be used to obtain a predicted fMRI signal response for any arbitrary pattern of neural activity. In turn, these predicted signal responses could be utilized to consider hypotheses regarding the effect of task stimuli upon brain function [1, 23].

Magnetic resonance (MR) enters into this explanation because blood contains iron (hemoglobin), which is paramagnetic (a material which becomes a magnet in a magnetic field) [42]. Magnetic characteristics of the oxygenated versus deoxygenated blood are not the same; deoxygenated blood has a twenty percent greater magnetic susceptibility than oxygenated blood [67]. Because of the fact that hemoglobin in deoxygenated blood is strongly paramagnetic, it thus has the capacity to distort an MR field locally. A decrease in the local concentration of deoxyhemoglobin that occurs with the increase of oxygenated blood leads to a more uniform and stable magnetic field locally and the MR signal in a region of decreased deoxyhemoglobin concentration increases relative to its normal (neuronally resting) state. The local MR signal difference due to the changing magnetic properties of blood is called the BOLD effect and it is the major source of contrast in most functional MRI experiments [72]. See Figure 1 for a flowchart depicting the BOLD effect mechanism. The HRF is thought to locally reflect the fMRI BOLD signal change over time. This means that, as the concentration of oxygenated blood in the vicinity of the activated neuron changes (in response to a task stimulus), the measured MR signal via the BOLD effect detects these changes [64, 52]. An important point to consider here is that fMRI does not measure brain activity directly, but rather, through the mechanisms described above, measures the correlates of brain activity and, as a result, is an indirect indicator of brain function.

Figure 1.

BOLD signal mechanism.

2.2 Principles of MRI

To address the question of how functional MRI works, it is necessary to gain an understanding of the concept of magnetic resonance. The physical basis upon which fMRI rests is the Nuclear Magnetic Resonance (NMR) phenomenon. The physics theories underlying NMR were discovered in the 1920s and 1930s but it was not until the 1990s that fMRI techniques utilizing principles of NMR were developed for the study of human brain function [38]. An intuition behind this complex phenomenon and some definitions follow (detailed, technical descriptions regarding these theories can be found in Huettel et al. (2004), Jezzard et al. (2001), or Lazar (2008)).

2.2.1 Hydrogen atoms and net magnetization

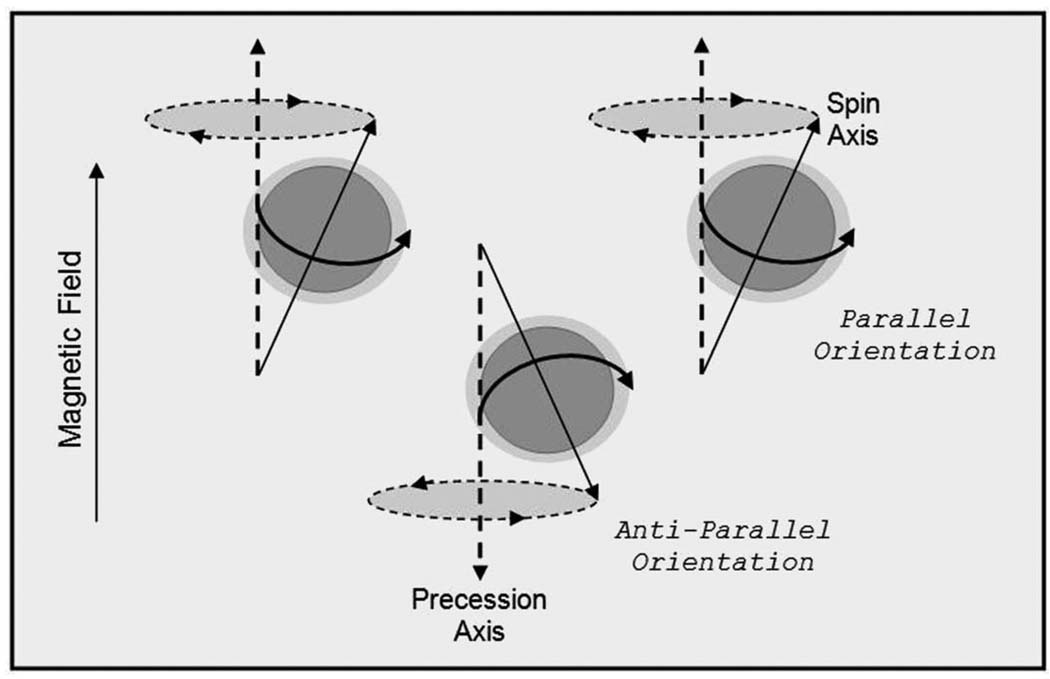
Hydrogen protons in the body are subatomic particles, which possess a characteristic property of spin. Under normal conditions, thermal energy causes these particles to spin, or precess, around a central axis in gyroscopic motion, much like a spinning top. When in their natural state, hydrogen nuclei are oriented randomly, so they spin in random directions. Because spins in random directions cancel each other out, the amount of net magnetization produced by these randomly precessing nuclei in their natural state is zero [42].

At the start of an MRI session, a subject undergoing a scan is placed horizontally into the bore of an MR scanner (a large magnet which generates a magnetic field that is typically 1.5 or 3 Tesla strong). When the subject is exposed to this magnetic field, hydrogen protons in the subject’s body (specifically, the ¹H isotope of hydrogen) precess on their axes at a rate or frequency proportional to the strength of the magnet. Placement in the magnetic field also causes these hydrogen nuclei to have a propensity to line up in the direction of that magnetic field (by convention, this is denoted the z-axis in a three-dimensional space), with approximately half of the protons going parallel (or with the magnet) and half going anti-parallel (or against the magnet), as pictured in Figure 2. There is a slight preference for their orientations in the direction of the main magnet to be parallel with the main field. The subject in the scanner becomes somewhat magnetized as a greater number of hydrogen protons align in the parallel direction [38, 42].

Figure 2.

Precessing protons; oriented in high energy (parallel) and low energy (anti-parallel) states.

However, because each proton precesses (like a spinning top coming to rest), this implies that each has a rotation phase at which it is precessing, known as the precessional path. Typically, the phases of the individual spins are random with respect to one another and this is no different when a subject is placed in the scanner magnet: the precessional paths of individual hydrogen nuclei is random (out of phase), meaning they have varying values in the conventionally denoted x and y dimensions. Consequently, the collection of spinning nuclei do not yield a detectable magnetic field or net magnetization [35]. Here, the hydrogen protons are out of phase with one other, although they are all spinning at a frequency that is proportional to the strength of the magnetic field [14].

It should be noted that many other atoms and nuclei with magnetic moments also have such an alignment. In practice, it is common to only study the hydrogen nuclei of water molecules because they are abundant in the tissues that are the target of magnetic resonance imaging.

2.2.2 Generating a detectable signal

In order for a detectable MR signal to be generated, the next step, then, is to introduce additional energy into the system. A radio frequency (RF) pulse of magnetic energy is applied, at the frequency of the spins of the hydrogen protons (what is denoted as the resonant frequency), causing all the hydrogen nuclei near the frequency of the applied RF pulse to absorb this energy and change orientation. By controlling the power and duration of the RF pulse, the hydrogen nuclei can be rotated or tipped to any desired angle relative to the main magnetic field. It is often the case that the parameters of the scanner are set a priori so that the protons are rotated ninety degrees (flip angle). Subsequent to the application of the RF pulse, the affected protons arrange in an identical direction and precess in phase in the new orientation. This causes the net magnetic field to flip away from its original orientation (when there was no extra energy in the system) and orient orthogonal to the axis of the original field. The result is a changing magnetic field that produces a detectable net magnetization [35, 42, 72]. So, when RF energy at the frequency of the spins is introduced into the system, the level of energy generates and temporarily increases the magnetic signal, but then returns it to equilibrium.

2.2.3 Relaxation time

The increased generated signal decays exponentially over time due to a number of processes. The hydrogen protons slowly give off absorbed energy, or begin to relax, when the RF pulse is turned off in order to return to their original state of equilibrium prior to the application of the pulse. The energy produced by the protons in the return to their initial state is at the resonant frequency. It is this selective emission of energy (or relaxation of spins) that produces the MR signal detected by the RF receiver coils in the MRI scanner, a signal which is proportional to the density of hydrogen protons in the tissue [14].

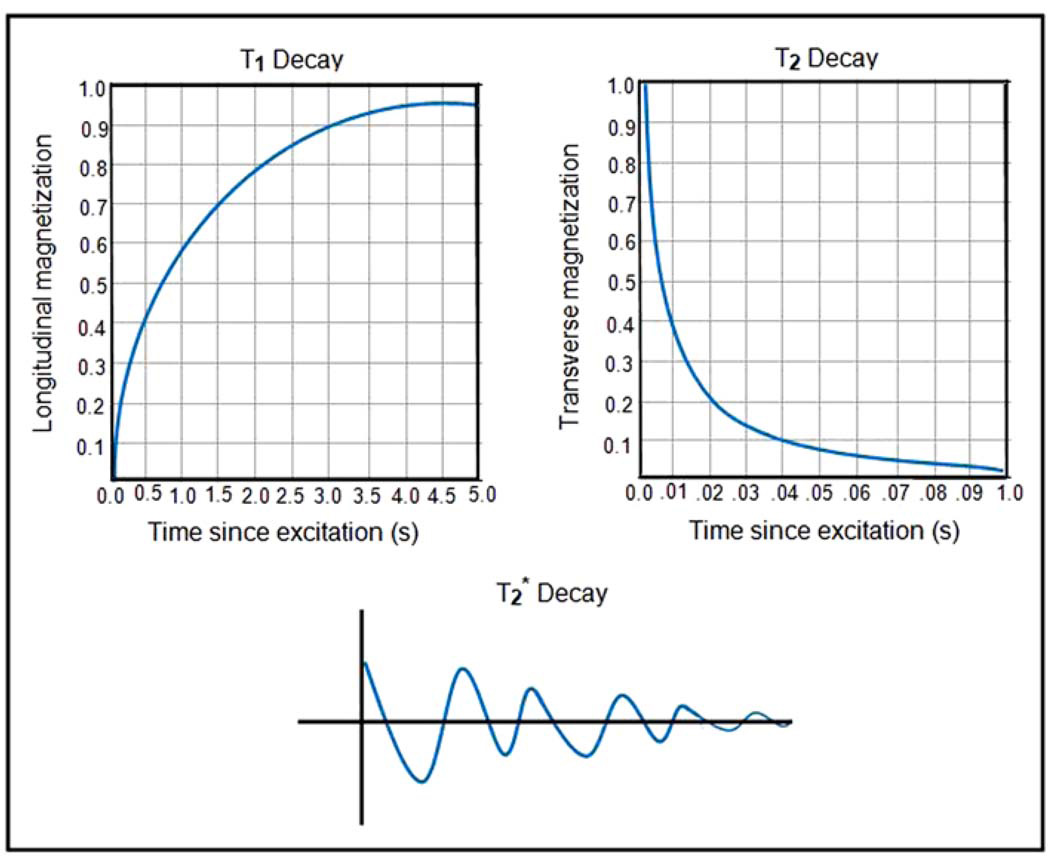
Three relaxation times (or contrast mechanisms) are relevant to MRI: T₁, T₂, and $T_2^{*}$ [42, 72] (the curves depicting the pattern of decay for each time constant are portrayed in Figure 3). If the natural, exponential decay of the signal is gauged freely (when the system is left free to decay at its own rate), the exponential time constant associated with that decay is conventionally called $T_2^{*}$, sometimes referred to as the “free induction decay” (FID) of the NMR signal. Such decay in the measured signal is affected by a number of different physical processes, one of which is the means by which the hydrogen protons release energy absorbed in order to return to their original orientation. This is called “longitudinal relaxation” and the time constant associated with this exponential process is denoted T₁. Additionally, “transverse relaxation” represents the time needed for the anti-parallel components of the magnetized field to return to their initial values and the time constant associated with this exponential process is called T₂. Thulborn et al. (1982) showed that the rate of T₂ relaxation of blood is linked (via an exponential relation) to the proportion of deoxygenated hemoglobin. This means that as the strength of the applied magnetic field increases, so does the BOLD effect and, further, it is possible to ascertain blood oxygenation levels from the MR signal via the relaxation time of the spins [79, 42].

Figure 3.

Time relaxation curves, corresponding to the T₁ (longitudinal decay), T₂ (transverse decay), and $T_2^{*}$ (free induction decay).

2.2.4 Acquiring magnetic resonance images

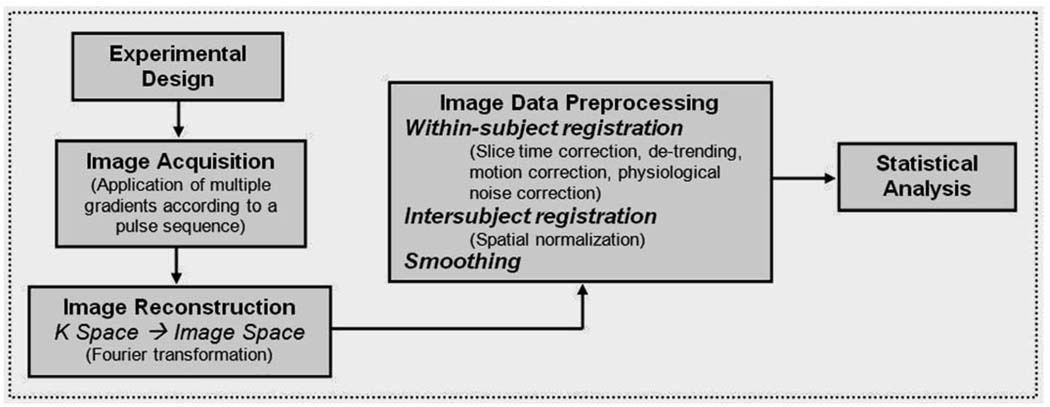
The above-described process of signal relaxation essentially yields a single number: $T_2^{*}$, the net NMR signal’s rate of decay. This relaxation time signal represents the indiscriminant effect of inducing an NMR signal from the entire area being influenced by the main magnet and the RF pulse that flips the orientation of the hydrogen protons. For “nuclear magnetic resonance” to become “magnetic resonance imaging,” spatial information must be recovered from this raw MRI signal. The process of image formation (one of the basic steps of fMRI data analysis shown in Figure 4) relies on the introduction of magnetic gradients that allow measurement of signal changes across space [35]. Non-uniform RF pulses referred to as gradients are purposefully applied using the gradient coil in order to construct images which reflect measurements of different NMR signals for different points in the three-dimensional volume. Such application alters the strength of the magnetic field so that each location in the brain has a distinctively identifiable resonant frequency [72]. Appropriate application of these gradients makes it possible to uniquely recognize and measure each location in space that is being imaged.

Figure 4.

Key steps of an fMRI analysis.

More specifically, gradient pulses are applied in each of three directions (denoted x, y, and z) in a two-step signal acquisition process. First, a gradient is applied in the z direction (parallel to the field of the magnet) which causes the magnetic field to differ in strength from the top of the brain to the bottom. Subsequently, a specific slice is selected within the total imaging volume (the gradient causes hydrogen nuclei in this slice to spin in a phase which matches the frequency of the RF pulse applied) and what is left after this slice selection is a two-dimensional encoding of that slice in the (x,y)-plane (which is perpendicular to the field of the magnet). As noted in Lazar et al. (2001), it is helpful to think of this slice as being partitioned into a matrix of rows and columns. Next, a phase-encoding gradient is applied to the magnetic field (in the y direction), which increases from the bottom row of the matrix to the top, making nuclei in different matrix rows spin in somewhat different phases (for example, atoms in the top row may spin faster than those in the next row, etc.). Applying a frequency-encoding gradient (in the x direction), which increases incrementally from the left column to the right of the slice matrix, leads nuclei in different columns to spin at different frequencies [14].

Thus, within a matrix defined by the selected slice, each element can be differentiated due to the fact that each has a different phase (defined by the y-axis coordinate) and frequency (defined by the x-axis coordinate). This means that the MR image can be thought of as a map of frequencies that depicts the spatial distribution of some property related to the spin of the protons. With the presence of gradients, each proton resonates at a unique frequency and emits its own $T_2^{*}–\text{weighted}$-weighted relaxation signal [35, 43, 42], a current which is collected in the scanner’s receiver coils.

2.2.5 Data conversion: From k-space to image-space

Raw MR signal data in their initial form are collected by the receiver coil during acquisition and stored in Fourier space, known as k-space in fMRI literature (see Jezzard et al. (2001) for details). After selecting one slice of the entire volume and encoding it for phase and frequency (as described in Section 2.2.4), this method of slice selection is duplicated so that data are collected and encoded for all of k-space (or the entire volume in the scanner), according to the size of the image being taken. For example, if the interest is in a 128 × 128 pixel image, then to fill k-space with data might be to take 128×128 = 16,384 samples. To obtain the samples, a particular blueprint for application of gradients and encoding process must be imposed that will be followed by the sampling path. The planning of the best sampling sequence (known as a pulse sequence) that generates data in k-space and resultant imaging method is a subject matter of research among physicists; one of the most common of such methods is echo-planar imaging (EPI) [43]. A pulse sequence denotes how a particular slice of the brain is chosen for imaging, how individual volume elements are encoded within each slice, and how the ensuing signals are preferentially selected to obtain information about the concentration of deoxygenated hemoglobin blood flow [72]. The EPI method forms a complete image from a single data sample (or a single shot), where gradients move through k-space using alternate left to right and right to left lines in a so-called boustrophedonic pattern.

Next, after data have been acquired by the MR scanner according to a particular type of pulse sequence, researchers begin data preprocessing with the reconstruction of the raw k-space data into images that actually look like brains. The data in k-space are the coefficients of the Fourier representations of the object being imaged and include information obtained from the relaxation of protons regarding the amplitude, frequency, and phase of the spinning nuclei [66]. The goal in data reconstruction is to extract information regarding the density of hydrogen nuclei at each location and create an image of the brain reflecting that density. The mathematical transformation used to change the frequency-space data (the measured MR signal) in k-space into an image in image-space reflecting the density of hydrogen protons is an inverse Fourier transformation and it provides a way to construct a spatially informative image from components in a spatial frequency domain [38]. This step of fMRI data analysis is shown in the flowchart depicted in Figure 4.

Combining the slices together forms a three-dimensional depiction of the brain, such that these data consist of “snapshots” of the working brain over time. More precisely, the transformed images in image-space are three-dimensional representations of brain volume, which are divided into measurable volume elements (known as voxels). The amplitude of the collected relaxation time MR signal at each voxel in each image is indicative of the average density of the hydrogen protons at that voxel [43]. Each voxel has a time series of image data associated with it, as depicted in Figure 5, denoting the activity level or activation in that area in the brain of the subject, as the experiment or task progresses.

Figure 5.

The same image slice is repeatedly obtained throughout the scanning session, generating a time series of activation images for each voxel. An active brain voxel shows a BOLD response.

2.2.6 Remarks regarding the science of fMRI

As concisely summarized in Savoy (2001), fMRI involves collecting data of brain activation by taking advantage of a series of connection in the brain: how neural activity (electrical and chemical events) is connected to changes in brain physiology and metabolism which in turn links to changes in the magnetic properties of substances (hydrogen nuclei) within the brain. By measuring the spin of the hydrogen nuclei based on adaptable (but very complex) application of numerous RF-pulses and multiple gradients, $T_2^{*}–\text{weighted}$-weighted images are created [72]. These images rely on the fact that deoxygenated hemoglobin in blood is paramagnetic, whereas oxygenated hemoglobin is not. The magnetic properties of deoxyhemoglobin cause rapid dephasing of hydrogen protons, meaning that the $T_2^{*}–\text{weighted}$-weighted signal is retained longer in a region when there is more oxygenated blood compared to when there is less oxygenated blood. Thus, an area with greater amounts of oxygenated blood will show a more intense signal on $T_2^{*}–\text{weighted}$ -weighted images comparatively to when there is less oxygenated blood in the area. This effect is referred to as the BOLD signal, introduced in the beginning of this section. The BOLD signal is collected in k-space, converted to image-space at each voxel for each time-point of the experiment.

A key point to take away here is that BOLD signal is an indirect indicator of brain activity, which have been shown by researchers to be intimately coupled [51]. The fMRI technique thus assumes that an area of the brain is comparatively more active when it has more oxygenated blood relative to another time-point. The crucial part of creating an image from which information can be extracted is contrast and in brain mapping, the main contrast used that causes a change in the MR signal from a given voxel comparatively to other voxels is the dissimilarity in relaxation times from voxel to voxel [72].

2.3 fMRI experimental design

2.3.1 Imaging parameters

In all imaging techniques, the quality of the collected data depends on the physics of the imaging modality [41]. fMRI is no exception and the primary required acquisition parameters that influence the resolution of data (both in space and in time) need to be predetermined preceding the beginning of the study. Acquisition parameters can have considerable influence on the image quality and analysis results. Often, these settings are chosen by a human operator and are determined by historical considerations, not necessarily by necessity. The choice of parameters can also be made with regards to considerations of image resolution and quality as well as the total time spent in the scanner by a subject (see Brown and Semelka (2004) for more details).

Parameters that concern the details of the data collection are called extrinsic parameters [10]. One such important setting is the imaging plane; images are most often collected in three different planes: axial (slices perpendicular to the longitudinal axis of the body), coronal (slices parallel to the front of the body), and sagittal (slices parallel to the midline of the body). Another extrinsic acquisition parameter is field of view (FOV), which designates the physical extent of the image, measured in mm², specifying the area of the brain from which the image was sampled. The size of the acquisition matrix determines how many voxels are acquired in each direction, meaning that it represents the size of the grid into which the plane of FOV is divided for each slice (it is often a square 64 × 64 or 128 × 128). Slice thickness denotes the thickness of each slice, measured in mm. The slice gap is the space between consecutive slices, measured in mm. The FOV, the size of the acquisition matrix, and the slice thickness determine the three dimensions of a voxel (the previously described volume element, which can be intuitively thought of as a volumetric pixel). Slices are acquired in an order that is determined by the excitation sequence (typically interleaved: all even or all odd) [42].

Parameters that affect the voxel’s signal (as opposed to affecting the data collection, described previously) are called intrinsic parameters [10]. Repetition time (TR) is the time, in msec, between successive applications of the RF pulses to a particular volume of tissue. As TR increases, there is more time for the RF energy to dissipate. Echo time denotes the time between the initial RF pulse and the maximum of the signal in k-space (restrictions in hardware make it difficult to obtain measurements directly subsequent to the application of the RF excitation pulse). The flip angle specifies the degree of rotation from the equilibrium axis following the RF pulse [42].

2.3.2 Design types

When subjects are placed inside the scanner to undergo an fMRI scan, they often participate in a task where they are asked to passively view a series of stimuli, pictures, or short film clips. Subjects may also be requested to respond via a hand-held device to those pictures or film clips. The two most basic types of task designs used in fMRI experiments differ with regard to how stimuli are presented to subjects during the task: they are block and event-related designs. Block designs [4] involve separating the experimental conditions into distinctive blocks so that each task condition of interest is presented continuously within this block for an extended period of time. Here, periods of rest (or fixation) alternate with periods of task. The idea is to ignore the temporal properties of the task by creating a continual state of hemodynamic change [36]. Data collected from such designs can be analyzed via a variety of statistical methods, which most commonly compare time-averaged activation across experimental conditions by averaging signals across many trials to create functional activation images. Block designs are most successful at identifying those voxels for which the level of activation is significantly different in the task conditions as compared to the control. However, these designs are not very effective at detecting and estimating the shape of the hemodynamic response [50].

In event-related designs, on the other hand, different stimuli are presented as individual events or trials in a random order (rather than in blocks of similar or identical stimuli), separated by an interstimulus interval (ISI). The hemodynamic response to each stimulus or event is measured. The assumption with this class of task designs is that brain activation of interest will occur for short and discrete intervals. Event-related designs are more effective at estimation of the hemodynamic response function and offer more adaptable analysis strategies, but may have reduced ability to detect activation [47].

2.4 Data preparation

2.4.1 Characteristics of fMRI data structure

A subject’s scan generates a substantial amount of fMRI data, the structure of which can be described as extremely noisy with an intrinsically complex spatio-temporal correlation structure. The data are essentially the MR signal as it progresses through the task at each voxel of the brain. Often hundreds of time-points long, the time-course consists of a series of three-dimensional images collected at each time-point. Further, the amount of data points (voxels) in space that comprise each of these collected images differs across experiments, but is usually in the thousands, depending on the predetermined acquisition parameters previously described [43].

Temporal correlation of the fMRI data arises because subjects perform tasks consisting of stimuli being presented continuously over time, meaning that the reaction to a stimulus at time t will clearly be affected by the stimulus at time t − 1. Spatial correlation comes about because all of the voxels in the brain come from an individual person’s brain and neighboring voxels will expectantly have similar behaviors [42]. The size and spatio-temporal complexity of the data presents numerous challenges to many conventional statistical procedures (particularly the full specification of a model).

2.4.2 Preparing data for analysis: Preprocessing

Data generated from fMRI are typically very noisy. As all measurements are susceptible to variation and error, so are fMRI data, and thus lend themselves to statistical analysis. Consequently, to prepare the data for an analysis, it is vital to eliminate as much of the irrelevant variability in order to parse out the BOLD signal. As discussed in Lazar (2008), there are three common sources of noise in fMRI analyses: thermal, system, and subject/task noise. Thermal noise is an inherent aspect of MR imaging and is indicative of the fluctuations in the strength of the MR signal throughout an imaging session. System noise reflects variations in the functioning of the MR hardware. Finally, subject/task-related noise is generated by the subject that participates in the scan and is most easily correctable [42]. An example of one of the most pervasive sources of subject-related noise is the problem of head motion because it can cause activation from one location in the brain to influence activation from adjacent regions of the brain, creating a blurring of a signal. Another example of a source of subject noise is when the MR signal is affected by a subject’s breathing and heartbeat, referred to as physiological noise [34]. Subject-based noise as opposed to machine-based (from the scanner) noise generated from fMRI data is regarded as the more important source of noise to correct. However, there is less consensus concerning how to correct or model these sources of noise in terms of the practical consequences for data analysis.

Two common ways to do away with or control noise inherent in collected fMRI data are to (1) prevent noise by controlling the scanning environment and (2) remove various sources of noise from the data signal with preprocessing methods [42]. Preprocessing includes a number of steps, all of which are intended to massage the data in a way that measures or removes unwanted variability so that it is in an appropriate form to be statistically analyzed (see Huettel et al. (2004) for more details).

The most widely-used preprocessing procedures include slice-time correction, detrending, motion-correction, physiological noise correction, smoothing, and registration. Slice-time correction corrects for the fact that slices of data are not all collected at once, but rather one at a time. A correction for this issue typically involves re-shifting the voxel time series on the image space data [74]. To correct for scanner drift, the preprocessing procedure known as detrending is done [77] one of a variety ways (e.g. using linear and polynomial models or using wavelets and splines). Further, estimating head motion and correcting the data for its effect (registration) prior to formal analysis is often an important step. Such preprocessing involves coregistering the images to a single reference volume and estimating the needed translations/rotations in various directions by minimizing the distance between the volume and the reference. Then, to correct for the head motion, the estimated translation and rotation parameters are used to shift the image to the reference (using one of a variety of interpolation methods). Several techniques can be undertaken to estimate and correct for physiological effects. Often, the physiological noise is estimated and monitored simultaneously as functional data are collected, the two are synchronized, and the effect is then removed from the phase and magnitude of the data [42].

2.4.2.1. Smoothing

Many researchers also include smoothing as part of the preprocessing step of fMRI data preparation, although not necessarily as a way to removing a particular type of noise but instead as a way to obscure residual anatomical differences [47]. The frequently-used way to smooth data is with a Gaussian filter, characterized by a measure called full-width-half-maximum (FWHM) of between of 5–10 mm. The arbitrary specification of smoothing extent in the initial smoothing step has been a source of contention in the neuroscience community. There are two main reasons often cited for smoothing [74]. For one, small amounts of smoothing improve the signal-to-noise ratio, since the effect of smoothing obscures the measured signal in neighboring voxels. Additionally, smoothing often makes the data more “normal,” thus potentially enhancing the validity of the data analysis. An important issue to highlight, however, is that smoothing can cause regions that are functionally different to combine with each other [19] and can consequently have a harmful effect on statistical analyses. In particular, smoothing methods can be very problematic near the edges of activated regions [76] because the brain is composed of spatial contiguous regions of activation rather than sharp edges defined by many fMRI studies.

2.4.2.2. Intersubject registration

It is necessary to note that nearly all fMRI studies use multiple subjects and that statistical analysis is often performed across data collected from multiple subjects. This practice introduces a number of practical problems which fMRI data analysis must address [47]. Considering each subject on an individual basis is relatively uncomplicated, but does not allow the researcher to draw meaningful conclusions comparing the behavior of the group of subjects. Thus, information from multiple subjects must be combined in order for higher-level statistical questions to be answered. The problem is that different subjects’ brains vary in shape, size, and the relative positions of the particular brain structures. Combining brain images from different individuals is only acceptable if the images are put on a comparable basis (or some form of a common space).

An overview of choices of various methods used to combine brains (spatial normalization) has been the topic of research [44]. One relatively simple example that allows for comparison of activity across brains of multiple subjects is to transform the representations of those brains so that they have the same overall size and are similarly oriented in space according to some atlas. To accomplish this, the brain images can be rigidly rotated and linearly scaled into a common space [72]. A frequently-used standard coordinate systems for comparing brains is the Talairach stereotactic coordinate. In an example of a Talairach transformation discussed by Savoy (1999), a rigid rotation and translation to a standardized orientation is carried out, and then independent linear scaling of the brain’s anterior, middle, and posterior parts of each hemisphere is completed [71]. A wide range of more powerful non-linear approaches have also been developed to facilitate data display and intersubject comparison.

2.5 Approaches to fMRI data analysis

As previously described, at each voxel for each subject, data are preprocessed, motion corrected, aligned to a standard brain atlas, and smoothed before statistical analysis begins. Needless to mention, there is no consensus in the literature about the ideal way to proceed or “the best method for fMRI analysis,” mainly due to the exceedingly complicated structure and size of a typical fMRI dataset. Once fMRI data are prepared for analysis, the choice of the method is fundamentally defined by the hypothesis of the researcher and a multitude of software packages are available to undertake these analyses.

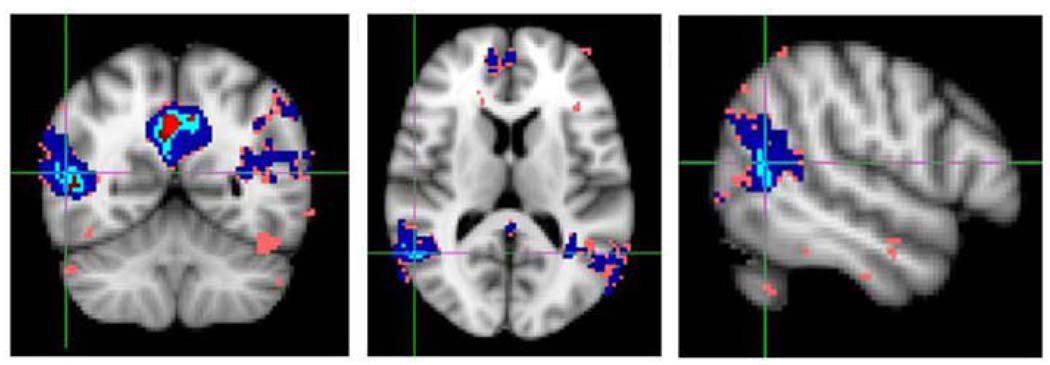
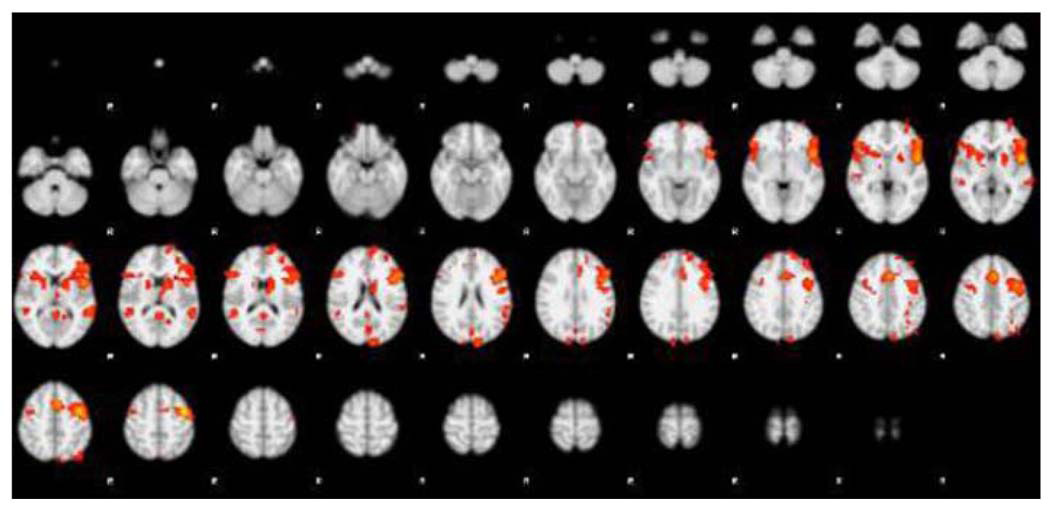
Most fMRI experiments aim to make an inference regarding a population as a whole, where the purpose is to determine whether the experimental task and stimuli has resulted in a measurable change in the MR signal, as well as to specify the location in the brain and when that change occurred. The recurrent goals of fMRI data analysis can be summed up as follow: determining which regions of the brain are activated by a certain task or stimuli (portrayed in Figure 6); localizing networks that correspond to particular brain functions; and making predictions about mental states [47]. These objectives relate to understanding how exposure to certain stimuli lead to changes in neuronal activity and all essentially come down to comparing images, or groups of images, in a statistically meaningful way by modeling the data to appropriately account for each subject’s differing responses [60].

Figure 6.

Activation analysis.

The analysis of fMRI data has been well described (see Lazar (2008), Lindquist (2008), and Bowman et al. (2007) for excellent overviews). Sections 2.5.1 through 2.5.4 broadly introduce some distinct analysis approaches currently being used.

2.5.1 Activation analysis: 2-stage general linear model

It is useful to think of a full fMRI analysis intended to localize brain activity in stages: first, a model is fit for each individual subject and then, at the second-stage, the individual analyses are combined for different subjects. Both stages rely on the concept of the general linear model (GLM) [56], and this two-stage formulation is one of the most common ways to analyze fMRI data [47]. In this straight-forward and effective analysis approach, researchers model fMRI response data as a linear combination of several different components of the signal and test whether activation in a particular brain region is related to any of the explanatory variables or task/stimuli presentations.

Recall that the linear model has the familiar form Y = Xβ + ε where Y is the response, X is the matrix of covariates, β is the vector of unknown coefficients corresponding to the covariates, and ε denotes the error (usually assumed to be normally distributed). In the fMRI context, let N represent the number of subjects (i = 1,…, N), let T denote the number of scans (t = 1,…, T), and let V indicate the number of voxels (υ = 1,…, V). As presented in Bowman et al. (2007), the first-stage linear model for the responses can be expressed as Y_it(υ) = X_iυ β_i(υ)+ ε_i(υ) [9]. Here, Y_i(υ) denotes a matrix of observed time-course BOLD fMRI response data of all the voxels, where one column corresponds to one voxel and one row corresponds to one time-point; X_iυ can be thought of as a design matrix reflecting the stimuli presented at a particular occasion; β_i(υ) indicates the subject-specific effects corresponding to the design matrix; and the random error vector ε_i(υ) represents characteristics of the measurement process that are unaccounted for by the statistical model, having either constant or nonconstant variance and nonzero covariance terms [42]. The design matrix incorporates covariates of interest, including factors that describe the experimental design, subject demographics, group membership, and other factors not of substantive focus (e.g. blood flow). The experimental stimuli of the design matrix in the most basic form usually consist of just zeros and ones, indicating the presence or absence of a stimulus [60, 9].

This basic first-stage linear model makes certain assumptions that are unrealistic and violated by fMRI data. As discussed in Lazar (2008), these strict assumptions are as follows. First of all, voxels are assumed to be independent, meaning the standard model makes no use of spatial information regarding the way that voxels are spatially distributed (which is problematic given the likelihood that adjacent voxels will have similar behavior). Similarly, there is an assumption that time-points are independent. Additionally, there is an assumption that the error variance at each time-point is the same and that the same model is appropriate for all voxels in the brain. As demonstrated by previous research, these assumptions are not valid (e.g. the residual error in fMRI is not independent and voxels exhibit excess variation) [42]. In many current analyses of fMRI data, modified assumptions accompany the model specification which allow for spatial and temporal correlation; the standard GLM model is adjusted to reflect such modifications. Much statistical research in fMRI has thus focused on ways to extend the simple GLM to loosen the unrealistic assumptions described above.

The second-stage analysis is used to relate subject-specific parameters β_i(υ) to population parameters β(υ) as follows: β_i(υ) = W_iυβ(υ) + ε_i(υ). Here, W_iυ is the second-level design matrix to test the mean response of subjects and β(υ) is a vector that contains group-level parameters that represent the effects related to various subpopulations. It should additionally be noted that researchers use contrasts to summarize evidence for a particular effect. Rarely is an investigator interested in all the elements of the β vector. Instead, the interest is typically focused on how one condition compares to another (e.g. is condition 1 different than condition 2?), meaning that contrasts must be defined in terms of the corresponding group-level parameters when formulating the model. Modeling a contrast at the population-level stage, rather than modeling the whole vector of subject-specific effects from the first-level analysis, is an expedient way to facilitate computations [9].

Standard methods for fitting this two-step model and estimating the β parameters involve iterative optimization algorithms such as restricted maximum likelihood, which can be statistically cumbersome and time-consuming. A more practical and efficient approach involves building summary statistics [60]. Various summary statistic methods utilizing mixed models and GEE approaches to account for both within-subject and between-subject variation have been developed using custom software (e.g. FSL, fMRIstat, SPM2) due to the massive size of fMRI datasets (see Mumford and Nichols (2006) for a succinct overview). It is now more common in fMRI analyses to treat certain within- and between-subject effects as random [25]. Consideration of the assumptions that underlie mixed-effects or GEE models allows researchers to generalize conclusions beyond the subjects in the conducted experiment to a greater population.

2.5.1.1. Inference in activation studies: Region-of-interest verses whole brain

Statistical inferences for activation studies typically focus on one of two levels: the voxel whole-brain level or a more general regional (region-of-interest) level [9]. Voxel-wise analyses allow a high degree of localization for identifying task-related alterations in neural processing by looking for significant effects in many different voxels, often encompassing the whole brain. This approach is preferred for a wide range of research hypotheses, where the basic question addressed is “Which brain region evokes a particular pattern of fMRI activity?” [35].

Region-of-interest (ROI) based methods, on the other hand, are spatially more coarse, but also likely more realistic, by evaluating statistical tests targeting a predetermined neuroanatomical structure or region (such as the amygdala) [9]. These methods are appropriate for more targeted hypotheses, where the main question of interest is “What pattern of activity occurs in a particular brain region?” [35]. Researchers establish the ROIs based upon a priori expectations about the likely involvement of different brain areas in a task (see Poldrack (2007) for review).

2.5.2 Extensions of the general linear model

Various techniques have loosened the stringent and unrealistic assumptions of the standard two-stage GLM model for activation studies described in Section 2.5.1. Such extensions may be more suitable for fMRI analyses because they address the dependence between observed brain activity responses across different voxels and time-points. One such approach is a temporal model that takes into account the correlation over time at each voxel and exploits the time series nature of voxel observations directly (see Lazar (2008) for summary). An example of an implementation of this method is an extension of the GLM so that the error term is a stochastic process; included in the variance term of the errors is a general matrix whose elements depend on the autocovariance function between two time-points [54]. An alternative solution was proposed by Worsley and Friston (1995) and involves allowing serial correlation in a regression setting by smoothing the time series [84]. For other examples, see [11, 49].

Other extensions focus on the spatial correlation problem intrinsic in fMRI data and are referred to as spatial models, which make an effort to account for the neurophysiologic associations that may exist between different brain areas [9]. A common technique that addresses the assumption of independent voxels applies Random Field Theory (RFT)-based methods to determine significantly activated voxels [83]. However, this technique nonetheless necessitates constraining assumptions and can alter the observed data by smoothing. A recently developed technique is the Multiscale Adaptive Regression Model (MARM) [89], which integrates adaptive smoothing methods with statistical modeling at each voxel for spatial and adaptive analysis. Much of the additional work is Bayesian in nature. An example of a type of Bayesian model is that of Hartvig and Jensen (2000), who consider the activation of clusters of voxels [31]. They formulate a model for activation in a cluster and use the spatial arrangement of voxels to calculate the posterior probability of a voxel being activated. For further examples, see [8, 73].

Additional techniques, although computationally and conceptually complicated, have considered modeling both space and time together in so-called spatio-temporal models. One method to do this is to apply clustering techniques to the time series data (either by clustering the raw time series [6] or by applying cluster techniques to a function of the time series [29]). Many implementations that cluster fMRI time-courses have been considered (e.g. [3, 16, 28]). Another example of spatio-temporal modeling of fMRI data is direct modeling, where both the spatial and temporal aspects of the data are modeled explicitly (e.g. [39, 57, 69]).

2.5.3 Multivariate analysis

Stepping away from extensions of the GLM model and hypothesis-driven analyses, alternative techniques common to fMRI are data-driven and aimed at finding or characterizing the multivariate nature of the data (see Lazar (2008) for summary). These methods include principle component analysis (PCA), independent component analysis (ICA), and canonical correlation analysis (CCA), all which take an investigative approach to data exploration and modeling in order to identify components in the data with interesting structure. The strength of such data-driven methods is that they can find components that cannot be modeled a priori; these methods are often used for the purpose of detecting unexpected components in the fMRI data, such as drifts and motion-related artifacts.

Principle components analysis (PCA) is one such multivariate statistical tool intended to find linear combinations of the original variables that parsimoniously describe the dependence structure of data [33]. An example PCA is partial least squares regression which seeks orthogonal components (called latent variables) by decomposing of both the neural responses Y and experimental covariates X simultaneously, such that these factors explain as much as possible of the covariance between X and Y [9]. For additional applications of PCA to fMRI, see [24, 78, 80]. Independent components analysis (ICA) seeks linear combinations of the collected data, assumed to be as far from normally distributed as possible, under the constraint that the components are uncorrelated [42]. As the most popular of the multivariate methods used in fMRI, ICAs have been performed in both the temporal and spatial domain and do not require any prior knowledge about the spatio-temporal structure underlying the measured brain activity. ICA identifies independently distributed spatial patterns that are associated with different time-courses. An example of results obtained from an ICA analysis are shown in Figure 7. For further reference, see [7, 12, 58]. Finally, canonical correlation analysis (CCA) is a way of quantifying the correlation between sets of variables. This method searches for components that have the most auto-correlation, under the constraint that they are mutually uncorrelated. The CCA method generates comparable conclusions as ICA but it is more robust and faster than conventional methods for ICA. For more examples, refer to [21, 61].

Figure 7.

Slices depicting a component identified by ICA.

2.5.4 Brain connectivity analysis

Another approach to analyzing fMRI datasets recently gaining popularity in the neuroimaging community is the technique of connectivity, which refers to networks that model or seek to explain relationships between brain regions. These analyses allow researchers to step away the specific hypotheses regarding “Which voxels are activated?” to the more broad question concerning how different areas of the brain interact to create thought and how these interactions depend on experimental conditions [42]. fMRI researchers generally distinguish between functional and effective connectivity [23]. Briefly, functional connectivity is defined as the undirected association between two or more fMRI time series. The simplest approach toward functional connectivity analyses compares correlations between regions of interest or between a “seed” region, and other voxels throughout the brain. Alternatively, effective connectivity refers to the directed influence of one brain region on others. In effective connectivity analysis, a cluster of regions with a hypothesized set of directional connections is specified a priori and tests are used to assess the statistical significance of individual connections [47]. Most effective connectivity methods depend on two models: a neuroanatomical model that describes the areas of interest and a model that describes how these areas are connected. Commonly-used methods include Structural Equation Modeling (SEM) [59] and Dynamic Causal Modeling (DCM) [22].

2.6 Concluding remarks regarding fMRI

fMRI is a very complicated imaging technique with respect to physics, measurement methods, physiological mechanisms, data analysis, and interpretation. Despite its complexities and shortcomings, fMRI is undoubtedly one of the best tools available for gaining insights into brain function. It allows for the formulation of motivating and testable hypotheses, even though the possibility of testing these hypotheses crucially depends on the experimental design, the type of statistical analysis, and insightful modeling. fMRI is an exceedingly rich data source with an abundant opportunity to answer many scientific questions.

3. LONGITUDINAL FMRI DATA ANALYSIS

The human brain is a constantly changing and developing organ. As such, studies that combine fMRI methodology and longitudinal design, in which subjects undergo a scan and are measured repeatedly over time, are essential in order to gain a better understanding of the true course of the neural changes and developments. While cross-sectional fMRI research is helpful for generating hypotheses for future investigations, these hypotheses need to be tested and confirmed by longitudinal research. Longitudinal studies of brain function and anatomy in normal and pathological brains aid in teaching researchers more accurately about the processes that impede and affect normal development as well as the progression of disease. Structural MR brain imaging studies of a longitudinal nature, which seek to investigate changes in regional brain volumes and tissue characteristics over time, have a longer history in imaging science than fMRI (e.g. [37]). But lifespan variations in brain structures and volumes coincide with development of cognitive and functional abilities. Thus, studying functional MRI changes over time can better inform researchers about the neural progression and development of certain brain functions and pathologies.

As alluded to, cross-sectional fMRI data, as opposed to longitudinal fMRI data, are not as sensitive to small magnitude changes in brain function and can misrepresent brain processes that occur within the individual [75]. The advantage of a longitudinal fMRI approach is that it provides the best possible power for identification of time-related changes because multiple within-subject observations are collected, as long as the variability between subjects is much greater than the variability between sessions for a particular subject. Hence, by using methodology that accounts for both within-subject along with between-subject information and that accurately characterizes longitudinal repeated measurements to study brain development, researchers can better characterize functional changes that occur in the human brain over time. Such studies are necessary to understand the developmental links of natural development and disease progression in terms of differential functional performance of specific brain regions, as well as the impact that different life occurrences can have on the developing brain. Appropriate modeling is important to consider because differences in longitudinal functional patterns between groups of subjects may be relevant to diagnosis, tracking of disease progression, and monitoring of potential disease-modifying treatments.

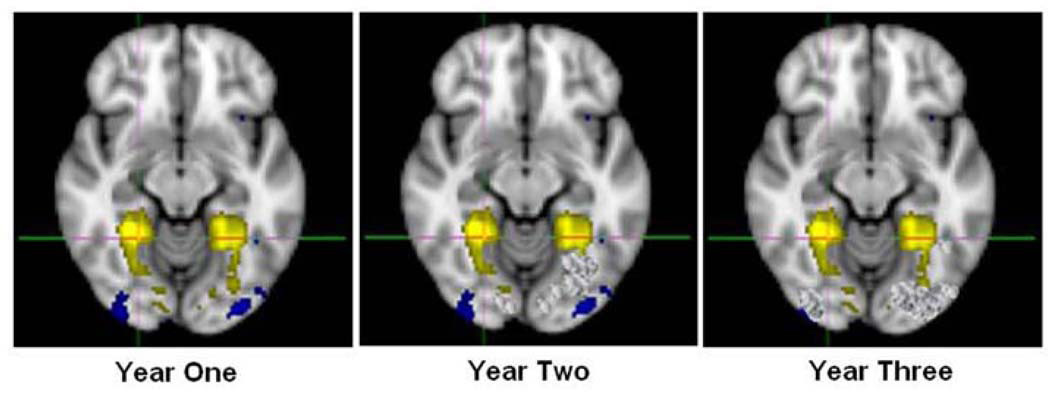
To better understand the neural development of brain structure and function, various longitudinal neuroimaging datasets have been collected and many studies are ongoing (e.g. NIH MRI study of normal brain function). An example of what such data might look like is illustrated in Figure 8. However, analysis of these data has been hindered by the lack of advanced statistical methods for analyzing such high-dimensional longitudinal data [45]. In most multi-subject fMRI studies, a subject is scanned only once and the activation magnitudes from each subject are submitted to a second-level statistical analysis. But longitudinal data analyses are complicated by the presence of both multiple sessions and multiple subjects. The following section outlines some of the methodological challenges that accompany the analysis of fMRI datasets of a longitudinal nature.

Figure 8.

Example of a fMRI activation analysis of a longitudinal nature.

3.1 Methodological challenges of longitudinal fMRI data

3.1.1 Multiple sources of correlation

As discussed in Section 1 of this paper, an unavoidable aspect of data collected longitudinally is that an individual subject’s repeated measurements are likely to be correlated over time. An outcome of brain activation at one scanning session is likely to predict and be related to the measurement of brain activation at the next scan. This means that responses collected at various scanning sessions for each individual are not necessarily independent, nor do they have equal variances. Further, another contributing factor to the correlation of the data in fMRI studies is that the distance between repeated measurements (or scanning sessions) will undoubtedly not be exactly equivalent, among or between subjects. The difference in distance between time-points has an effect on the correlation structure of the data because responses that are closer in time to one another are more likely to be related than those further apart. Additionally, because of differing schedules of subjects, the dataset may not be balanced between subjects (both in the distance between time-points and the number of scans obtained). As a result, the correlation structure between repeated measurements of different individuals is influenced [85].

These sources of correlation are in addition to the correlation that already exists and must be accounted for in cross-sectional fMRI data (discussed in Section 2). Recall that imaging datasets collected in a single session have an already complex spatio-temporal correlation structure. The high-dimensional structure of the fMRI data has an even higher-dimensional structure when the study design is longitudinal. Thus, analyzing such data requires a high level of statistical sophistication of the researcher as well as advanced modeling techniques that permit more general forms of correlation among repeated measures.

3.1.2 Irregularities between subjects

3.1.2.1. Different time-points

In considering the organization of a dataset, it is natural to group the repeated measurements of the same subject together. In such an organization, it becomes apparent that the number of responses may likely be different between subjects and that the time-points of subjects may not correspond at all if the subjects do not scan on the same day. In other words, it could be that each subject’s response vector corresponds to a different set of time-points or a different number of time-points. The statistical model employed, therefore, must handle these types of irregularity with flexibility.

3.1.2.2. Missing data

The likely presence of missing data poses an additional complication to longitudinal fMRI analysis. As stated above, different subjects may not necessarily match on the number of repeated measurements that exist in a dataset. Occurrences of missing data are not uncommon in an fMRI study; for instance, situations may arise where subject data must be thrown out due to excessive movement or scanner artifact. Data might also be missing at one of several measurement occasions due to missed appointments or due to attrition [32]. Statistical approaches to handle missing data in non-imaging longitudinal analyses are wide-ranging and include conducting analyses that are limited to only those subjects that completed the study or inputting the last available measurement to all subsequent missing measurement occasions. In fMRI longitudinal studies, the possible feature of missing data makes analysis far more complex than that of cross-sectional fMRI data.

3.1.3 Multiple responses at each time-point

Statistical analyses of fMRI data are multivariate in nature, meaning there are often many responses of interest at the same time (e.g. activation at multiple voxels and/or regions). Such experiments are unique in the sense that they allow the researcher to study the joint evolution of multiple neural outcomes over time. But compared to univariate analysis of longitudinal fMRI data, the analysis of multivariate longitudinal fMRI data is even more challenging because the variances of errors are likely to be different for different responses, the errors are likely to be correlated for the same region measured at different occasions, and the errors are also likely to be correlated among regions measured at the same time [5].

Current techniques to carry out statistical analysis of multivariate longitudinal data are as follows: analysis that creates a single summary measure from multiple outcomes (which can subsequently be analyzed using univariate longitudinal data methods); analysis without direct modeling of the correlation structure of the data; or analysis with explicit modeling of the correlation structure (meaning joint multivariate modeling of all outcomes) [5]. Most often, the multivariate nature of image data is ignored, either due to constraints on computational resources, or because limited data make the estimation of correlations unreliable [70]. Investigators may also prefer simpler statistical methods for the ease of communicating their results. Nevertheless, multivariate nature of data presents a statistical challenge to the analysis of longitudinal fMRI data that future research should seek to address.

3.1.4 Time effects on performance

fMRI experiments of a longitudinal design are susceptible to experiment or practice effects, due to the fact that subjects are scanned on multiple occasions performing the same task and may obtain knowledge or skill related to having taken part in the task before [68]. Performance and activation due to stimuli presented in the task are confounded with time because of a number of additional reasons as well. First of all, a subject may exhibit anxiety when first exposed to the scanner, an effect that is reduced with time, both in a single session and across multiple sessions. Such anxiety can appear as head motion (which can decrease signal-to-noise ratio) or increased attention to the task at hand (which can affect the measured activation response). Additionally, changes in scanner performance over time may also cause time effects. The purpose of most longitudinal investigations is to determine changes in brain activity over time, meaning that studies should focus on simple motor and cognitive tasks with an assumption of no trends in brain activity over time due to factors not associated with the hypothesized mechanisms of learning, recovery, or development. Employing the appropriate model that can separately measure the specific effects of time confounds may be beneficial [68].

3.1.5 Repeatability of fMRI studies

To date, a number of fMRI studies have investigated the repeatability of fMRI activation in neuroimaging studies and the consistency of activation for individual voxels. Some research indicates that the “test-retest reliability” of detected neural activity is quite low: a voxel that is active in one task session has about a fifty percent chance of activating in a later repetition of the same experiment [27, 53, 62]. Further, research has been inconclusive regarding the variability of activation volume between scans (meaning: the total number of voxels detected as active is, in some cases, inconsistent from scan to scan) [48]. Such research is a caution against relying too heavily on the outcome of a single scanning session, because effects may be distinctive to the day or time at which the imaging data are acquired. Uncertainty of reproducibility of fMRI results is an open question in imaging research as a field, although it seems that the fMRI tasks that may lead to habituation, difference in attention, as well as non-procedural learning should be avoided. This issue should be considered in the longitudinal design of fMRI studies and tasks should be chosen to avoid ceiling effects in behavioral performance.

3.2 Examples of longitudinal fMRI analysis approaches

Linear mixed-effects models

A common analysis template for longitudinal fMRI investigations conducted in the last ten years has been a linear mixed-effects model approach, often enacted in a univariate two-stage specification. The popularity of this method is due to the flexibility it offers in handling unbalanced repeated measurements with missing data [13]. At the first-level (the subject-level), a unique trajectory for each individual is defined (for each region or voxel being considered), meaning that activation measurements are condensed into summary statistics for each scan. At the second-stage (the population-level), individuals are considered as arising from a population of all such individuals, each with a unique intercept and slope, and a linear mixed-effects model is fit. With this modeling approach, it is reasonable to deduce that the within-individual variances are the fluctuations around the individual-specific trajectory, and the among-individual variances can be described as differences of parameters characterizing these trajectories. As one way to carry out this model using brain imaging data, statistical measures of brain activity responses serve as the dependent variable and one linear mixed-effect model is then fit for each ROI or voxel. Repeatability of fMRI can be directly addressed via certain parameters of this model (see [40, 65, 85] for examples of applications).

Generalized estimating equations

As discussed in Li et al. (2009), generalized estimating equations (GEE) is an alternative modeling approach to the mixed-effects model that produces consistent and robust regression estimates that may be appropriate for use in the analysis longitudinal imaging data (for an example of an fMRI application of this method, see [2]). Based on the observed imaging data, neu-roimaging measures are computed and denoted by the response vector for each voxel and time-point. The GEE approach can jointly model imaging responses with clinical and behavioral measures in a longitudinal study [45]. Because imaging measures from the same subject tend to be positively correlated, a working correlation matrix is specified. This flexible and free of distributional assumptions model gives consistent estimators and provides robust standard errors.

3.3 Future direction and motivating example

Both cross-sectional and longitudinal investigations in psychology, psychiatry, cognitive science, and neuropsychological studies aid in revealing time-associated changes in aspects of brain-related function. However, the neuroanatomical underpinnings of time-associated change remain underdeveloped, partially due to the lacking statistical methods needed to analyze complex, high-dimensional fMRI data. The unique properties of longitudinal fMRI data require more flexible and powerful models than those traditionally enacted. A goal for future research should be to develop statistical analysis approaches intended for longitudinal fMRI data that accommodate the challenges of repeatedly scanning subjects that perform cognitive tasks, as mentioned in the Section 3.1.

3.3.1 Motivating example

The development of fMRI technology has allowed researchers to better understand the mechanisms of brain structure and function relating to human behavior. As research expands, the next step is to investigate more statistically complex questions that depend on time frame. In this section, as a motivating example demonstrating the importance of developing statistical methodology for longitudinal imaging data, a research study conducted at the Early Brain Development Program at the University of North Carolina, Chapel Hill is considered. The ongoing purpose of this study is to learn more about the rapid and critical growth of brain development in the first years of life and to add insight to existing knowledge regarding causes of neurodevelopmental disorders. As one of the specific aims, investigators collected imaging data to investigate the longitudinal course and temporal development of the brain network engaged during passive mental states (referred to as the “default network”) by scanning pediatric subjects at repeated occasions.

Previous research has revealed a consistent pattern of anatomical representations of the default network [26], including the ventral/dorsal medial prefrontal cortex (MPFS), the posterior cingulate cortex (PCC), the inferior parietal lobule (IPL), the lateral temporal cortex (LTC), and hippocampus regions (HF). Research is lacking in investigations concerning when and how the default network formulates. Limited investigations regarding the pediatric default network seeking to address this question show the following: (1) sparse connection in 7–9 year-olds [15]; (2) no default network in preterm infants [20]; and (3) primitive/incomplete network in 2-week-olds, marked increase in number of brain regions exhibiting functional connectivity in 1-year-olds, and networks similar to the ones reported in adults in 2-year-olds (revealing both regions consistent with adults and regions not observed in adults) [26]. No previous analyses have considered data collected at repeated occasions from the same normally-developing, healthy pediatric subjects.

At baseline, the present study imaged 20 neonates (9 male), 24 1-year-olds (16 male), and 27 2-year-olds (17 male) during natural sleep or while resting quietly in the scanner without use of sedating medications (plus 15 healthy adult (11 male) controls). These subjects were imaged a total of three times over a two year period, making this data longitudinal in nature. The investigators now aim to determine how such data can inform knowledge regarding normal infant/early child brain development in this important afterbirth phase of life. Defining the functional organization of the human brain during this period is an important step in understanding the mechanisms of normal and pathological neurodevelopment. In particular, researchers hope to determine when and how the brain’s default network formulates.

Of note, cross-sectional analyses of this resting functional connectivity magnetic resonance imaging (rfcMRI) data previously required group independent component analysis (ICA) approaches [26]. More specifically, such ICA measure correlations over time in the BOLD signal’s low-frequency spontaneous fluctuations in order to detect networks with synchronous brain activity. To avoid the somewhat subjective nature of selecting components as the default network, researchers have previously relied on an automated template matching approach to explore the temporal and spatial evolution of the default network [30]. Statistical challenges of analyzing a longitudinal dataset of this resting state data, where participants return to scan on numerous occasions, mirror many of those previously presented in Section 3.1. An added challenge to analyzing data presented here is that the anatomical brain structure of neonates and infants is ever-growing. Taking this into account in a dataset that contains data collected at multiple time-points is a necessity.

3.4 Concluding remarks regarding longitudinal fMRI

The purpose of this paper was to give a broad overview of methods currently being used to analyze longitudinal data as well as to introduce fMRI data acquisition, study design, processing techniques, and analysis methodology. Further, this paper highlighted the need for longitudinal fMRI research, which has the potential to provide more accurate inferences regarding the developmental correlates of brain function in normal and pathological brains. In doing so, statistical challenges inherent in such data analyses were explored. A motivating example of a resting state fMRI dataset collected longitudinally was presented.

As fMRI designs expand and researchers seek to answer more complicated and sophisticated developmental questions, the need for novel statistical approaches will undoubtedly increase. Although previous investigations have analyzed fMRI data of a longitudinal nature, much work remains to develop methodology that better accounts for the complex correlation patterns in the data within and between scanning occasions. In particular, previous models have not been concerned with how to appropriately incorporate the spatial structure of neighboring voxels at each time-point and instead have primarily addressed temporal correlation across scanning sessions.

Extending methods developed for single session fMRI data that have attempted to account for the high-dimensional aspects of imaging datasets (such as spatial correlation) to further account for multiple time-points may be a helpful starting point for developing methods specific for the analysis of longitudinal datasets. As an example, a recently-developed method called Multiscale Adaptive Regression Modeling (MARM) proposed for spatial and adaptive analysis of neuroimaging data [89] seeks to analyze multivariate imaging data with complex spatial activation patterns. The method relies on building a sphere with a specified radius for each voxel and uses overlapping spheres to capture spatial dependence among different voxels. Further, this method uses adaptive weights for the voxels within each sphere to adaptively calculate parameter estimates and statistics. Such a method takes full advantage of the spatial structure of collected images and can be adapted to analyze more complex data structures that include a longitudinal time component. In particular, for repeated session fMRI data, MARM can be extended towards an application for generalized estimating equations [89]. This extension is just one example of how future modeling can address certain complexities of both fMRI design and longitudinal design in one model formulation.

Statistical analysis of a series of three-dimensional fMRI data of the same subject measured at multiple time-points is critical for neuroimaging research that focuses on development, aging, and evolution of pathology [86]. Development of statistical methods that can handle such data and account for its many complexities is open for research. The highly complex correlation structure, including the spatial correlation of data at each time-point as well as the temporal correlation of data across different time-points are just some of the topics that need to be addressed by future modeling. Methods should be flexible enough to permit statistical hypothesis testing, such as differences between patient and control populations.