Recent History Functional Linear Models for Sparse Longitudinal Data

Abstract

We consider the recent history functional linear models, relating a longitudinal response to a longitudinal predictor where the predictor process only in a sliding window into the recent past has an effect on the response value at the current time. We propose an estimation procedure for recent history functional linear models that is geared towards sparse longitudinal data, where the observation times across subjects are irregular and total number of measurements per subject is small. The proposed estimation procedure builds upon recent developments in literature for estimation of functional linear models with sparse data and utilizes connections between the recent history functional linear models and varying coefficient models. We establish uniform consistency of the proposed estimators, propose prediction of the response trajectories and derive their asymptotic distribution leading to asymptotic point-wise confidence bands. We include a real data application and simulation studies to demonstrate the efficacy of the proposed methodology.

1. Introduction

We address estimation in regression modeling of sparse longitudinal data. Sparse designs where the repeated measurements taken on each subject are irregular and the number of repetitions per subject is small, is encountered commonly in applications. An example is the longitudinal primary biliary liver cirrhosis data collected by the Mayo Clinic (see Appendix D of Fleming and Harrington, 1991). Due to missed visits the data is sparse and highly irregular where each patient visited the clinic at different times. We consider estimation in regression models where the sparse longitudinal predictor process only from the recent past has an effect on the sparse response trajectory.

Consider the commonly used functional linear model to relate a response trajectory to a predictor trajectory

$$Y(t)=\alpha (t)+{\int }_{{\mathrm{\Omega }}_t}X(s)\beta (s,t)ds+\epsilon (t),t\in [0,T],$$ (1)

first introduced by Ramsay and Dalzell (1991). For excellent reviews of functional data analysis, see Ramsay and Silverman (2002; 2005), Rice (2004) and Müller (2005). In (1), X(s) is the random predictor process, Y(t) is the random response process, and ε(t) is the mean zero error process with covariance function Γ_ε(t, t′), t, t′ ∈ [0, T]. When the predictor and response processes are observed over the same time interval, i.e. Ω_t = [0, T], the entire predictor trajectory is assumed to affect the current value of the response process at time t in the functional linear model. This assumption may not be feasible in many applications and variations of the functional linear model have been considered corresponding to different choices of the support Ω_t. A more suitable choice of Ω_t for predictions was proposed by Malfait and Ramsay (2003) for their recently proposed historical functional linear model, where only the past of the predictor process is involved in predicting the current response. Another special case which had wide applications over the past fifteen years is the varying coefficient model (Cleveland et al., 1992; Hastie and Tibshirani, 1993) with point-wise support where only the current value of the predictor process is assumed to have an effect on the current value of the response process.

An intermediate model considered in this paper between the functional linear model with global support and the varying coefficient model with point-wise support is the recent history functional linear model of Kim et al. (2009)

$$E\{Y(t)\mid X(s),s\in {\mathrm{\Omega }}_t\}=\alpha (t)+\sum _{k=1}^K{b}_k(t){\int }_{{\mathrm{\Omega }}_t}X(s){\phi }_k(s)ds,$$ (2)

where the two dimensional regression function β(s, t) of the functional linear model is approximated by the product form ${\sum }_{k=1}^K{b}_k(t){\phi }_k(s)$ of one dimensional functions. In (2), the predictor process from the recent past in a sliding window is assumed to affect the current response value, i.e. Ω_t = [t−δ₁, t−δ₂] for 0 < δ₂ < δ₁ < T. The two delay parameters help define the sliding window support where δ₂ denotes the delay for the predictor process to start affecting the response, and δ₁ is the delay beyond which the predictor process has no effect. Other regression models have also been proposed with a sliding window support such as the generalized varying coefficient model of Şentürk and Müller (2008) and the functional varying coefficient model of Şentürk and Müller (2010), where authors argue that the sliding support is useful in many applications where the response is affected by recent trends in the predictor process. Kim et al. (2009) consider the regression of river flow on rainfall as a motivating example where the river flow level would depend on the recent rainfall but not current rainfall or rainfall from distant past.

Kim et al. (2009) propose an estimation procedure for the recent history functional linear model for densely recorded functional data. In this paper, we propose a new estimation procedure for the recent history functional linear model specifically tailored for sparse longitudinal data. Sparsity is a real challenge in modeling longitudinal data, since nonparametric methods cannot feasibly explain a single trajectory for sparse designs. In addition, while standard semiparametric estimation approaches to longitudinal data have been studied extensively for irregular designs, they are not particularly designed to address sparsity issues and can yield inconsistent results for sparse noise contaminated longitudinal data.

Most recently there have been a number of proposals in the literature to broaden the reach of functional data analysis in general and functional linear models in specific, to include sparsely observed longitudinal data. Shi et al. (1996) proposed fixed and random effects which are linear combinations of B-splines, James et al. (2000) proposed an estimation method based on reduced rank mixed-effect model emphasizing the sparse data case among others. Yao et al. (2005a) proposed an estimation procedure for the functional linear model with Ω_t = [0, T], which is applicable to sparse longitudinal data based on functional principal component analysis. The main idea is that information across all the subjects can still be pooled effectively even for sparse data in the estimation of mean functions and covariance surfaces of the random processes, which are needed for functional principle components analysis.

The challenge of estimation based on sparse longitudinal data is intensified when one considers sliding window supports for the regression function such as the support [t − δ₁, t − δ₂] of the recent history functional linear model. That is even if the entire observed process is not very sparse, observations in the sliding window can easily get sparse fast as the window size decreases. We address this challenge by drawing connections between the proposed recent history functional linear model and the varying coefficient model and basing the estimation algorithm mainly on the estimation of auto-and cross-covariances following the proposals of Yao et al. (2005a). More specifically, note that for a set of K predetermined basis functions φ_k(s), the recent history functional linear model in (2) reduces to a multiple varying coefficient model with K induced predictors ∫_Ωt X(s)φ_k(s)ds. The unknown varying coefficient functions b_k(t) are then targeted based on a set of covariance representations which can be estimated efficiently based on sparse longitudinal data, pooling information across subjects.

The paper is organized as follows. In Section 2, we introduce the recent history functional linear model. The proposed estimation method is outlined and uniform consistency of the proposed estimators are established in Section 3. The prediction of the response trajectories is also proposed in Section 3 utilizing Gaussian assumptions, where asymptotic distributions are derived leading to point-wise asymptotic confidence bands. In Section 4, we discuss numerical issues in implementation along with the choice of model parameters. We study the finite sample properties of the proposed estimators through simulations given in Section 5. We apply the proposed method to a primary biliary liver cirrhosis longitudinal data in Section 6, to study the dynamic relationship between serum albumin concentration and prothrombin time. Concluding remarks are given in Section 7 and technical details are assembled in an Appendix.

2. Data and model

Taking a functional approach we view the observed longitudinal data as noise contaminated realizations of a random process that produces smooth trajectories. We will reflect sparsity in the following representation through random number of repeated measurements per each subject at random time points. Let (X_i, Y_i), i = 1, …, n, be the pairs of square integrable predictor and response trajectories, which are realizations of the smooth random processes (X, Y), defined on a finite and closed interval, 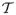= [0, T]. The smooth random processes have unknown smooth mean functions μ_X(t) = EX(t) and μ_Y(t) = EY(t), and auto-covariance functions G_X(s, t) = cov{X(s), X(t)} and G_Y(s, t) = cov{Y(s), Y(t)}. Throughout this paper, s and t refer to time indices defined on 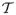. The observed trajectories of the i^th subject, X_ij = X(T_ij) + ε_ij, Y_ij = Y(T_ij) + e_ij, j = 1, …, N_i are noise contaminated realizations of the random processes X and Y measured at i.i.d. random time points, T_ij. Here, ε_ij and e_ij denote the additive i.i.d. zero mean finite variance measurement errors of the predictor and the response trajectories, respectively. The number of random time points per subject, N_i, are i.i.d. realizations of the random variable N where P(N > 1) > 0.

Under mild conditions, auto-covariance functions defined above have orthogonal expansions in terms of eigenfunctions ψ_m(·) and ϕ_p(·) with nonincreasing eigenvalues γ_m and η_p,

$$G_X(s,t)=\sum _{m=1}^{\infty }{\gamma }_m{\psi }_m(s){\psi }_m(t),G_Y(s,t)=\sum _{p=1}^{\infty }{\eta }_p{\varphi }_p(s){\psi }_p(t),\text{for}s,t\in [0,T].$$ (3)

Then, based on Karhunen-Loéve expansion (Ash and Gardner, 1975), the observations X_ij and Y_ij can be represented as

$$X_{ij}={\mu }_X(T_{ij})+\sum _{m=1}^{\infty }{\zeta }_{im}{\psi }_m(T_{ij})+{\epsilon }_{ij},Y_{ij}={\mu }_Y(T_{ij})+\sum _{p=1}^{\infty }{\xi }_{ip}{\varphi }_p(T_{ij})+e_{ij},$$ (4)

where ζ_im and ξ_ik denote the mean zero functional principal component scores with the second moments equal to the corresponding eigenvalues γ_m and η_p for ${\sum }_{m=1}^{\infty }{\gamma }_m<\infty$ and ${\sum }_{p=1}^{\infty }{\eta }_p<\infty$.

Let Δ_t denote the interval, [t − δ₁, t − δ₂], where 0 < δ₂ < δ₁ < T, t ∈ [δ₁, T], and let Δ denote the interval [0, δ₁ − δ₂]. Note that the first lag δ₁ is the time point beyond which the predictor function does not have an effect on the response function and the second lag δ₂ allows a delay for the predictor function to start having an effect on the response function. The recent history functional linear model where $\beta (s,t)={\sum }_{k=1}^K{b}_k(t){\phi }_k(s-t+{\delta }_1)$, can be given as

$$\begin{array}{l}E\{Y(t)\mid X(s),s\in {\mathrm{\Delta }}_t\}=\alpha (t)+\sum _{k=1}^K{b}_k(t){\int }_{{\mathrm{\Delta }}_t}X(s){\phi }_k(s-t+{\delta }_1)ds\\ =\alpha (t)+\sum _{k=1}^K{b}_k(t){\stackrel{\sim }{X}}_k(t),\end{array}$$ (5)

for K predetermined basis functions φ_k(t) defined on Δ. In (5) X̃_k(t) = ∫_Δt X(s)φ_k(s − t + δ₁)ds, k = 1, …, K, are the induced covariates and b_k(t), k = 1, …, K, are the unknown time varying coefficient functions of interest. Defining X̃(t) = [X̃₁(t), …, X̃_K(t)]^T and b(t) = [b₁(t), …, b_K(t)]^T, the model in (5) can be rewritten in vector form as E{Y(t)|X(s), s ∈ Δ_t} = α(t) + b^T(t)X̃(t).

In (5), K controls the resolution of the fit and should be chosen based on the data. Depending on the specific features of the regression function, various basis functions such as Fourier, truncated power, eigen and B-spline basis can be used in (5). Because of their fast computation and good properties, we will use B-spline basis in the following calculations. For more discussions on the B-spline basis, see Fan and Gijbels (1996) and Ramsay and Silverman (2005).

3. Estimation and asymptotic properties

3.1. Proposed estimation algorithm

In the proposed estimation procedure, we utilize connections of the proposed model to varying coefficient models. There are three main estimation methods for varying coefficient models proposed in the literature: local polynomial smoothing (Wu et al., 1998; Hoover et al., 1998; Fan and Zhang, 2000; 2008; Kauermann and Tut, 1999), polynomial spline (Huang et al., 2002; 2004; Huang and Shen, 2004) and smoothing spline (Hastie and Tib-shirani, 1993; Hoover et al., 1998; Chiang et al., 2001).

Note that the previously proposed methods cannot be directly employed here, since the induced covariates, X̃_k(t)’s in (5) cannot be estimated well for sparse designs due to the difficulty in numerically approximating the integral in their definition. In fact, the induced covariates may not be well approximated not only in sparse designs but also in longitudinal data in general, since the integration involved is over a narrow window into the past, where there may not be enough points. We propose to base the estimation on the covariance structure to address this difficulty, which will be shown to adjust for measurement error in predictors as well.

Let X̃_ik(t) denote observation of the k^th covariate in (5) for the i^th subject taken at time point t, i.e., X̃_ik(t) = ∫_Δt X_i(s)φ_k(s)ds, and X̃_i(t) = [X̃_i1(t), …, X̃_iK(t)]^T. The proposed estimation rests on the following equality that follows from (5)

$$\nu (t)b(t)=\theta (t),$$ (6)

where θ(t) is the K × 1 vector with the k^th element equal to cov{X̃_k(t), Y(t)}, ν(t) is the K × K matrix with the (k, ℓ)^th element equal to cov{X̃_k(t), X̃_ℓ(t)} and b(t) is the K × 1 vector of K varying coefficient functions. The elements ν_kℓ(t) and θ_k(t) can be given in terms of auto- and cross-covariance functions of the predictor and response processes as

$${\nu }_{k\ell }(t)=cov\{{\stackrel{\sim }{X}}_k(t),{\stackrel{\sim }{X}}_{\ell }(t)\}={\int }_{{\mathrm{\Delta }}_t}{\int }_{{\mathrm{\Delta }}_t}{G}_X(s_1,s_2){\phi }_k(s_1-t+{\delta }_1){\phi }_{\ell }(s_2-t+{\delta }_1){ds}_1{ds}_2$$ (7)

and

$${\theta }_k(t)=cov\{{\stackrel{\sim }{X}}_k(t),Y(t)\}={\int }_{{\mathrm{\Delta }}_t}{G}_{XY}(s,t){\phi }_k(s-t+{\delta }_1)ds,$$ (8)

where G_XY(s, t) = cov{X(s), Y(t)}. The estimation of the components given in (7) and (8) begins with estimation of the mean functions, μ_X(t) and μ_Y(t), via locally smoothing the aggregated data (T_ij, X_ij) and (T_ij, Y_ij), i = 1, …, n, j = 1, …, N_i. For the estimation of the auto- and cross-covariance functions, we apply two-dimensional local linear smoothing to the raw auto-and cross-covariances defined as G_X,i(T_ij, T_ij′) = {X_ij − μ̂_X(T_ij)}{X_ij′ − μ̂_X(T_ij′)}, G_XY,i(T_ij, T_ij′) = {X_ij− μ̂_X(T_ij)}{Y_ij′ − μ̂_Y(T_ij′)}, i = 1, …, n, j, j′ = 1, …, N_i, respectively. To obtain smooth estimates, the raw covariances are fed into a two dimensional local smoothing algorithm where special care needs to be taken in estimating the auto-covariance surface. Since the only terms in the raw auto-covaraince matrix that are perturbed by the additive measurement error on the predictors are along the diagonal, we remove the diagonal before the application of two dimensional smoothing, following (Yao et al., 2005a). Explicit forms of mean and covariance function estimators are given in Appendix C. The smoothing parameters used in the one and two dimensional smoothing procedures for the estimation of the mean functions and covariance surfaces respectively, can be chosen with respect to one-curve-leave-out cross-validation (Rice and Silverman, 1991). For computational efficiency we utilize generalized cross-validation (Liu and Müller, 2008) in simulation studies and data analysis. Plugging the covariance function estimators into equations (7) and (8), and performing numerical integrations, we can obtain the estimators of θ(t) and ν(t), μ̂(t) and ν̂(t), respectively. Then the estimator for varying coefficient vector, b(t), is defined as

$$\widehat{b}(t)={\widehat{\nu }}^{-1}(t)\widehat{\theta }(t),$$

leading to the final estimator $\widehat{\beta }(s,t)={\sum }_{k=1}^K{\widehat{b}}_k(t){\phi }_k(s)$ for the regression surface $\beta (s,t)={\sum }_{k=1}^K{b}_k(t){\phi }_k(s)$.

There are two major advantages of the proposed estimation procedure. The first advantage is that, since it depends on estimation of the mean functions and covariance surfaces which are estimated from the entire data, it enables us to surmount the sparsity of the design by pooling information. The second is that it naturally adjusts for measurement error in the predictor process by considering the covariance structure and removing the diagonal terms before smoothing. In addition note that we can get estimates of the covariance surfaces on a fine set of grid points through smoothing, which allows precise numerical integration approximations in the estimation of θ(t) and ν(t).

For a given number of components, K, uniform consistency of the proposed estimator is established by the below Theorem.

Theorem 1

Under Assumptions (A.1)–(A.5) given in Appendix A,

$$\underset{s,t\in {\mathrm{\Delta }}_t\times [{\delta }_1,T]}{sup}\mid \widehat{\beta }(s,t)-\beta (s,t)\mid =O_p\left\{\frac{1}{\sqrt{n}}\left(\frac{1}{h_X^2}+\frac{1}{h_1{h}_2}\right)\right\}.$$

Here, h_X is the bandwidth used in obtaining the smooth auto-covariance surface of the predictor process and, h₁ and h₂ are used in obtaining the cross-covariance surface between the response and predictor processes. The set of bandwidths depend on n and are all required to converge to 0 as n → ∞, for further details see Appendix A.

3.2. Prediction of response trajectories

We will establish the prediction of a new response trajectory, Y^*, based on the sparse predictor trajectory X^*. In what follows, let us define $P_m(t)={\int }_{{\mathrm{\Delta }}_t}\beta (s,t){\psi }_m(s)ds={\sum }_{k=1}^K{b}_k(t){\int }_{{\mathrm{\Delta }}_t}{\phi }_k(s){\psi }_m(s)ds$, where ψ_m(s) are the eigen-functions of the auto-covariance of the predictor process defined in (3). From the functional representation of the predictor trajectory given in (4), the predicted response trajectory can be given as

$$E\{Y^{\ast }(t)\mid X^{\ast }(s),s\in {\mathrm{\Delta }}_t\}={\mu }_Y(t)=\sum _{m=1}^{\infty }{\zeta }_m^{\ast }{P}_m(t),$$ (9)

where ${\zeta }_m^{\ast }={\int }_{\mathcal{T}}\{X^{\ast }(s)-{\mu }_X(s)\}{\psi }_m(s)ds$ is the m^th functional principal component score of the predictor function X^*. For estimation of (9), μ_Y(t) can be estimated from aggregated data as described above and estimators of the eigenfunctions, ψ_m(t), can be obtained from the eigen-decomposition of the estimated auto-covariance surface. Details on these estimation procedures are given in Appendix C. For estimation of ${\zeta }_m^{\ast }$ in sparse designs, we invoke Gaussian assumptions following Yao et al. (2005b).

Let us define the collection of N^* error contaminated observations from the predictor trajectory as ${X^{\prime }}^{\ast }={(X_1^{\ast },\dots ,X_{N^{\ast }}^{\ast })}^{\text{T}}$, where ${X^{\prime }}_{\ell }^{\ast }$ is the ℓ^th measurement observed at time point $T_{\ell }^{\ast }$. We assume that ( ${\zeta }_m^{\ast },{\epsilon }_{\ell }^{\ast }$), for ℓ = 1, …, N^*, are jointly Gaussian. Further define $X^{\ast }={\{X^{\ast }(T_1^{\ast }),\dots ,X^{\ast }(T_{N^{\ast }}^{\ast })\}}^{\text{T}},{\mu }_X^{\ast }={\{{\mu }_X^{\ast }(T_1^{\ast }),\dots ,{\mu }_X^{\ast }(T_{N^{\ast }}^{\ast })\}}^{\text{T}},{\psi }_m^{\ast }={\{{\psi }_m^{\ast }(T_1^{\ast }),\dots ,{\psi }_m^{\ast }(T_{N^{\ast }}^{\ast })\}}^{\text{T}}$ and $T^{\ast }={(T_1^{\ast },\dots ,T_{N^{\ast }}^{\ast })}^{\text{T}}$. Under the Gaussian assumption, the best linear predictor for ${\zeta }_m^{\ast }$ given X′^*, N^* and T^* is obtained by

$${\stackrel{\sim }{\zeta }}_m^{\ast }={\gamma }_m{\psi }_m^{\ast T}{\mathrm{\sum }}_{{X^{\prime }}^{\ast }}^{-1}({X^{\prime }}^{\ast }-{\mu }_X^{\ast }),$$ (10)

where ${\mathrm{\sum }}_{{X^{\prime }}^{\ast }}=cov({X^{\prime }}^{\ast }\mid N^{\ast },T^{\ast })=cov(X^{\ast }\mid N^{\ast },T^{\ast })+{\sigma }_{\epsilon }^2{I}_{N^{\ast }}$ with I_N^* denoting the N^* × N^* identity matrix and ${\sigma }_{\epsilon }^2=var(\epsilon )$ denoting the variance of the measurement error on the predictor process. Defining ${\widehat{\mu }}_X^{\ast }$ and ${\widehat{\psi }}_m^{\ast }$ to be the estimators of ${\widehat{\mu }}_X^{\ast }$ and ${\widehat{\psi }}_m^{\ast }$ respectively, the estimator of ${\stackrel{\sim }{\zeta }}_m^{\ast }$ can be given as

$${\widehat{\zeta }}_m^{\ast }={\widehat{\gamma }}_m{\widehat{\psi }}_m^{\ast T}{\widehat{\mathrm{\sum }}}_{{X^{\prime }}^{\ast }}^{-1}({X^{\prime }}^{\ast }-{\widehat{\mu }}_X^{\ast }),$$

where the (i, j)^th element of Σ̂_X′^* is defined as $\widehat{cov}\{X^{\ast }(T_i^{\ast }),X^{\ast }(T_j^{\ast })\}+{\widehat{\sigma }}_{\epsilon }^2{\delta }_{ij}$ where ${\widehat{\sigma }}_{\epsilon }^2$ is the estimator of the measurement error variance and δ_ij = 1 for i = j and δ_ij = 0 otherwise. Explicit form of ${\widehat{\sigma }}_{\epsilon }^2$ is deferred to Appendix C. Hence the predicted response trajectory is obtained by

$${\widehat{Y}}_M^{\ast }(t)={\widehat{\mu }}_Y(t)+\sum _{m=1}^M{\widehat{\zeta }}_m^{\ast }{\widehat{P}}_m(t),$$ (11)

where ${\widehat{P}}_m(t)={\int }_{{\mathrm{\Delta }}_t}\widehat{\beta }(s,t){\widehat{\psi }}_m(s)ds={\sum }_{k=1}^K{\widehat{b}}_k(t){\int }_{{\mathrm{\Delta }}_t}{\phi }_k(s){\widehat{\psi }}_m(s)ds$. The number M of eigenfunctions used in the decomposition of the predictor auto-covariance surface, given in (11) can be selected by leave-one-curve-out cross validation, generalized cross validation (GCV), or the Akiake information criterion (AIC). For more details on the selection of M, see Yao et al. (2005a). A consistency result of the predicted trajectory for the target trajectory ${\stackrel{\sim }{Y}}^{\ast }(t)={\mu }_Y(t)+{\sum }_{m=1}^{\infty }{\stackrel{\sim }{\zeta }}_m^{\ast }{P}_m(t)$ is established in Theorem 2.

Theorem 2

Under (A1)–(A5), (B1)–(B3) of Appendix A, given T^* and N^*, for all t ∈ [δ₁, T], the predicted trajectories satisfy

$$\underset{n\to \infty }{lim}{\widehat{Y}}_M^{\ast }(t)={\stackrel{\sim }{Y}}^{\ast }(t)in\mathit{probability}.$$

Note that, the number M of eigenfunctions used in the eigen-decomposistion of the predictor process is a function of n and tends to infinity as n → ∞.

3.3. Asymptotic confidence bands for the predicted response trajectories

In this section, we construct point-wise asymptotic confidence intervals for the predicted response trajectory, ${\widehat{Y}}_M^{\ast }(t)$. For M ≥ 1, let us define ${\zeta }^{\ast M}={({\zeta }_1^{\ast },\dots ,{\zeta }_M^{\ast })}^{\text{T}},{\stackrel{\sim }{\zeta }}^{\ast M}={({\stackrel{\sim }{\zeta }}_1^{\ast },\dots ,{\stackrel{\sim }{\zeta }}_M^{\ast })}^{\text{T}}$, where ${\stackrel{\sim }{\zeta }}_m^{\ast }$ is as defined in (10). Note that $cov({\zeta }_m^{\ast },{X^{\prime }}^{\ast })={\gamma }_m{\psi }_m^{\ast }$. Defining the M × N^* matrix $H=cov({\zeta }^{\ast M},{X^{\prime }}^{\ast }\mid T^{\ast },N^{\ast })={({\gamma }_1{\psi }_1^{\ast },\dots ,{\gamma }_M{\psi }_M^{\ast })}^{\text{T}}$, covariance matrix of ζ̃^*M can be given in terms of H as $cov({\stackrel{\sim }{\zeta }}^{\ast M}\mid T^{\ast },N^{\ast })=H{\mathrm{\sum }}_{{X^{\prime }}^{\ast }}^{-1}{H}^{\text{T}}$. Observing that $cov({\stackrel{\sim }{\zeta }}^{\ast M},{\zeta }^{\ast M}\mid T^{\ast },N^{\ast })=H{\mathrm{\sum }}_{{X^{\prime }}^{\ast }}^{-1}cov({X^{\prime }}^{\ast },{\zeta }^{\ast M})=H{\mathrm{\sum }}_{{X^{\prime }}^{\ast }}^{-1}{H}^{\text{T}}$, we have cov(ζ̃^*M − ζ^*M|T^*, N^*) = cov(ζ̃^*M|T^*, N^*) + cov(ζ^*M|T^*, N^*) − 2cov(ζ̃^*M, ζ^*M|T^*, N^*) = cov(ζ^*M|T^*, N^*) − cov(ζ̃^*M|T^*, N^*) ≡ Ω_M, where Ω_M = D − HΣ_X′^* H^T with D = diag{γ₁, …, γ_M}. Hence, under the Gaussian assumption, conditioning on T^* and N^*, ζ̃^*M − ζ^*M is distributed as N(0, Ω_M).

Let ${\widehat{\zeta }}^{\ast M}={({\widehat{\zeta }}_1^{\ast },\dots ,{\widehat{\zeta }}_M^{\ast })}^{\text{T}}$ and ${\widehat{\mathrm{\Omega }}}_M=\widehat{D}-\widehat{H}{\widehat{\mathrm{\sum }}}_{{X^{\prime }}^{\ast }}^{-1}{\widehat{H}}^{\text{T}}$, where D̂ = diag{γ̂₁, …, γ̂_M } and $\widehat{H}={({\widehat{\gamma }}_1{\widehat{\psi }}_1^{\ast },\dots ,{\widehat{\gamma }}_M{\widehat{\psi }}_M^{\ast })}^{\text{T}}$. Defining P̂(t) = {P̂₁(t), …, P̂_M(t)}^T, Theorem 3 gives the asymptotic distribution of the predicted response trajectory ${\widehat{Y}}_M^{\ast }(t)={\widehat{\mu }}_Y(t)+{\widehat{P}}^{\text{T}}(t){\widehat{\zeta }}^{\ast M}$.

Theorem 3

Under (A1)–(A5), (B1)–(B3), and (C1) of Appendix A, given N^* and T^*, for all t ∈ [δ₁, T ] and x ∈ ℝ,

$$\underset{n\to \infty }{lim}P\{\frac{{\widehat{Y}}_M^{\ast }(t)-E\{Y^{\ast }(t)\mid X^{\ast }(s)\in {\mathrm{\Delta }}_t\}}{\sqrt{{\widehat{\omega }}_M(t,t)}}\le x\}=\mathrm{\Phi }(x),$$ (12)

where ω_M(t, t) = P^T(t)Ω_M P(t), ω̂_M(t, t) = P̂^T(t)Ω̂_M P̂(t) and Φ denotes the Gaussian cdf.

From Theorem 3, it follows that ignoring the bias from the truncation in ${\widehat{Y}}_M^{\ast }$ at M eigen-components, the (1 − α)100(%) asymptotic pointwise confidence interval for E{Y^*(t)|X^*(s), s ∈ Δ_t} is

$${\widehat{Y}}_M^{\ast }(t)\pm \mathrm{\Phi }\left(1-\frac{\alpha }{2}\right)\sqrt{{\widehat{P}}_M^{\text{T}}(t){\widehat{\mathrm{\Omega }}}_M{\widehat{P}}_M(t)}.$$

4. Numerical issues in implementation and parameter selection

An important issue in the implementation of the proposed estimation algorithm is the inversion of the matrix ν̂(t) in equation (6). To obtain stable estimators for β, penalized solutions have been studied in literature (Cardot et al., 2003) minimizing the penalized least squares

$${\{\widehat{\nu }(t)b(t)-\widehat{\theta }(t)\}}^{\text{T}}\{\widehat{\nu }(t)b(t)-\widehat{\theta }(t)\}+\lambda b^{\text{T}}(t)Qb(t),$$

where Q is a K × K matrix that determines the type of penalty used. Here, λ is a tuning parameter that controls the amount of regularization and should be chosen from data balancing the stability and validity of the resulting estimator. The penalized estimator is then given by b̂_λ(t) = {ν̂(t) + λQ}⁻¹μ̂(t). A common choice of Q is the K × K identity matrix, which leads to the ridge solution, b̂_λ(t) = {ν̂(t) + λI}⁻¹μ̂(t). Another common choice of penalty used is on the degree of smoothness of the penalized solution where Q is chosen such that its (i, j)^th element is equal to ${\int }_{\mathrm{\Delta }}{\phi }_i^{(m)}(s){\phi }_j^{(m)}(s)ds$ with ${\phi }_k^{(m)}(t)$ denoting the m^th derivative of the k^th predetermined basis function. In the following applications, we use the ridge solution.

Hence, the proposed estimation procedure for the recent history functional linear model, includes three sets of parameters with different roles: K, λ, and (δ₁, δ₂). The number of predetermined basis functions used, K, controls the resolution of the fit; the tuning parameter, λ, controls the stability of the estimates; and the window, (δ₁, δ₂), determines the model used via controlling the predictor window affecting the response. An important observation in the current estimation set-up is that the proposed estimation procedure is not sensitive to the choice of K provided that there are enough number of basis functions used in the estimation, since the penalized solution employed via λ prevents over-fitting. Instead the choice of the tuning parameter λ is a more important choice controlling the stability of the estimates. This fact has been pointed out before in similar functional estimation problems, see Cardot et al. (2003) for further details. We run multiple simulation studies comparing the estimated regression surfaces obtained with different choices of K and λ to confirm this observation, where the results are summarized in Section 5.2. Based on the above argument, following Cardot et al. (2003), we fix K at a value that guarantees good precision and concentrate on the choice of λ and (δ₁, δ₂). For example, K is fixed at 10 in both the simulation studies and the data example that follow, to include 10 B-spline basis functions of order 4 with 6 interior equi-distance knots in the window Δ, which prove to provide good precision.

For the selection of λ and (δ₁, δ₂), consider the following two criteria. Define the normalized prediction error (NPE) as

$$\text{NPE}\{\lambda ;({\delta }_1,{\delta }_2)\}=\frac{1}{N}\sum _{i=1}^n\sum _{j=1}^{N_i^{\delta }}\frac{\mid {\widehat{Y}}_{ij}-Y_{ij}\mid }{\mid Y_{ij}\mid },$$

where Ŷ_ij is the predicted value for the j^th measurement on the i^th response trajectory obtained using λ and (δ₁, δ₂), $N_i^{\delta }$ is the number of observations from the i^th subject obtained in the interval, [δ₁, T ], and $N={\sum }_{i=1}^n{N}_i^{\delta }$. Note that NPE measures the relative absolute prediction error which will also be used in evaluating the finite sample performance of the proposed estimates in the simulations given in Section 5. We also define leave-one-curve-out cross validation squared prediction error as

$$CV\{({\delta }_1,{\delta }_2);\lambda \}=\sqrt{\frac{1}{N}\sum _{i=1}^n\sum _{j=1}^{N_i^{\delta }}{\{{\widehat{Y}}_{ij}^{(-i)}-Y_{ij}\}}^2},$$

where ${\widehat{Y}}_{ij}^{(-i)}$ is the fitted response function value of the i^th subject at time point T_ij obtained from the data excluding the i^th subject. Note that in both criteria, NPE and the cross validation score, the fitted response values are obtained via the prediction methods proposed in Section 3.2.

We propose to estimate λ and (δ₁, δ₂) in a hierarchical manner, where first λ is chosen for a set of (δ₁, δ₂) values using NPE and finally the set of (δ₁, δ₂) values are compared to yield the final choice of (δ₁, δ₂) with minimum cross validation score. This hierarchical approach has the advantage that the computationally faster NPE criterion is used within the inside loop of choosing λ and that the relatively more refined cross validation score is utilized for the selection of (δ₁, δ₂), which is similar to model selection in an outer loop. More specifically, the algorithm can be outlined as follows. Let Λ and D be the predetermined sets of λ and (δ₁, δ₂) values considered. For a fixed (δ₁, δ₂)₀ ∈ D, NPE values are calculated for all λ ∈ Λ. The λ that gives the smallest NPE value is selected as the optimal λ for the given (δ₁, δ₂)₀ and is thus used for calculating the cross validation score for (δ₁, δ₂)₀. Repeating the above steps for all (δ₁, δ₂) ∈ D, the optimal (δ₁, δ₂) is selected to be the one with the minimum cross validation score.

5. Simulation studies

In this section, we investigate the finite sample properties of the proposed estimators through two simulation studies. In the first simulation, we study efficiency of the NPE criterion for selecting the tuning parameter λ for a fixed (δ₁, δ₂) choice, along with the finite sample performance of the proposed estimator based on the selected λ from the algorithm. In the second simulation, we evaluate the performance of the cross validation method for choosing (δ₁, δ₂) with varying sample size. The following simulation results are reported based on 500 Monte Carlo runs. Bandwidths used in the smoothing of the mean and covariance functions are chosen by generalized cross-validation.

5.1. Data generation

For n subjects, the number of measurements made on the i^th predictor and response processes, N_i, are randomly selected from 3, 4, and 5. The design points, T_i1, …, T_iNi are randomly selected from the uniform distribution between 0 and 50. At a given time point t, the predictor function is evaluated around the mean function t + sin(t) using two principal components, ${\psi }_1(t)=-cos(\pi t/50)/\sqrt{5}$ and ${\psi }_2(t)=sin(\pi t/50)/\sqrt{5}$ for t ∈ [0, 50]. The corresponding two eigen component scores, ζ₁ and ζ₂, are independently sampled from the Gaussian distributions with mean 0 and the variances, ρ₁ = 4 and ρ₂ = 1, respectively. Hence, the predictor process at time t is generated via $X(t)=t+sin(t)+{\sum }_{m=1}^2{\zeta }_m{\psi }_m(t)$. In addition, i.i.d. measurement error, ε, simulated from the Gaussian distribution with mean 0 and variance ${\sigma }_{\epsilon }^2=0.025$, is added to the predictor observations in accordance with (4). The regression function is generated based on the same basis functions used for the predictor process via, $\beta (s,t)={\sum }_{i=1}^2{\sum }_{j=1}^2{c}_{ij}{\psi }_i(s){\psi }_j(t)$, s ∈ Δ_t, where c₁₁ = 2, c₁₂ = 2, c₂₁ = 1, and c₂₂ = 2. The true window combination, (δ₁, δ₂), is set at (20, 0). The error function, ε(t), is also generated using the same basis functions as the predictor process with eigen-component scores independently sampled from the Gaussian distributions with mean 0 and variance 0.025, 0.004, respectively. The response function, Y(t) is generated by the equation, ∫_Δt β(s, t)X(s)ds+ε(t) using the numerical integration procedure. To obtain a noisy version of the response function, we add i.i.d measurement error, e, generated from the Gaussian distribution with mean 0 and variance 0.025.

5.2. Simulation results

To evaluate the performance of the λ selection criterion, NPE, let us define relative square deviation (RSD) at time t as

$$\text{RSD}(t)=\frac{{\int }_{{\mathrm{\Delta }}_t}{\{\widehat{\beta }(s,t)-\beta (s,t)\}}^{2}ds}{{\int }_{{\mathrm{\Delta }}_t}\beta {(s,t)}^{2}ds}.$$

The RSD measures the relative size of the squared difference between the estimated and true regression functions at time t. The RSD integrated over the entire support, t ∈ [δ₁, T], will be called integrated RSD, denoted IRSD.

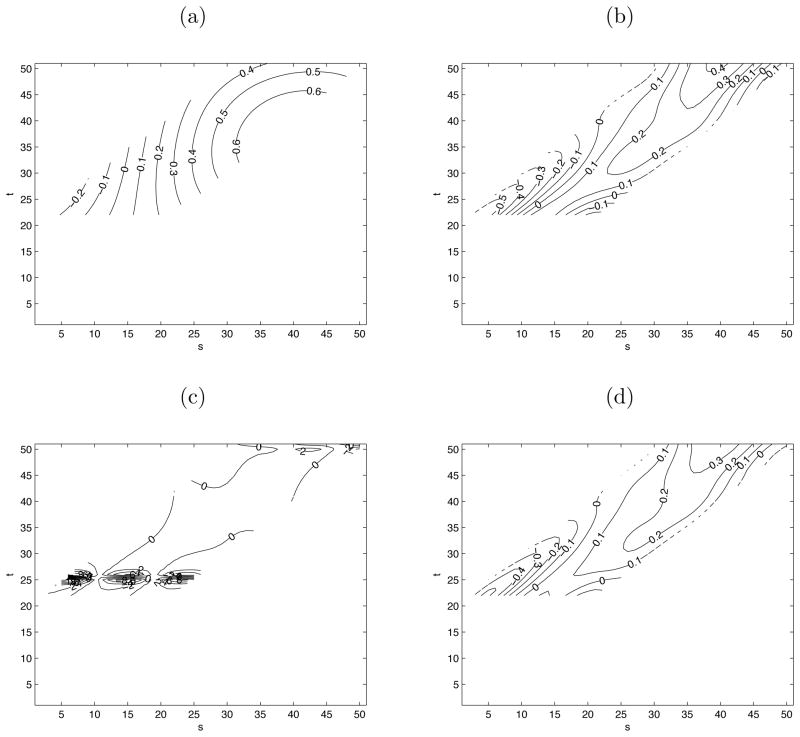
Before reporting on results from the two simulation set-ups, we present the true and estimated regression functions with different λ and K choices to demonstrate the relative importance of λ over K in the estimation procedure discussed in Section 4. The true and estimated regression functions are plotted in Figure 1 from three Monte-Carlo simulation runs at n = 200 with (K, λ) equal to (5, 7.4) (Figure 1b, for the NPE minimizer (λ = 7.4)), (5, 1) (Figure 1c) and (10, 7.4) (Figure 1d), respectively. While the difference between the estimators plotted in Figures 1b and 1d is small corresponding to doubling of the K choice, the estimator given in Figure 1c at the wrong λ value of 1 cannot recover the true regression function with IRSD= 298. This confirms that the choice of λ plays a more important role in the proposed estimation algorithm than the choice of K.

Figure 1.

(a) The true regression function defined on Δ = [0, 20]. The estimated regression function with (K, λ) equal to (5, 7.4) (plot b, estimated IRSD= 0.3632), (5, 1) (plot c, estimated IRSD= 298) and (10, 7.4) (plot d, estimated IRSD= 0.3274).

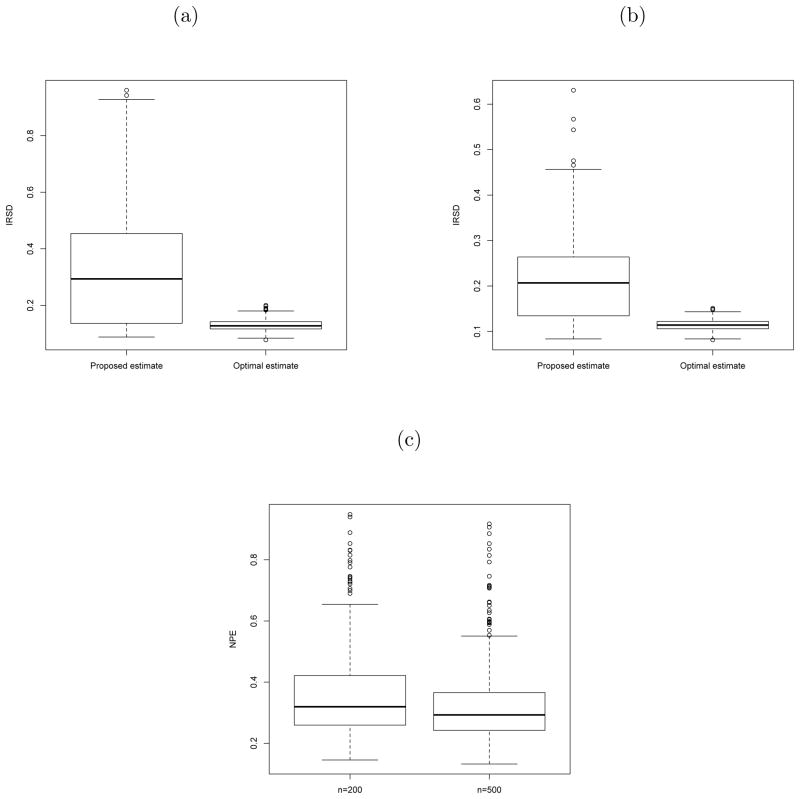
The estimated regression function β̂(s, t) with the tuning parameter λ equal to the minimizer of IRSD can be thought of as the “optimal estimate”, since information on the true regression function is utilized in the comparison. Hence, this estimate can only be obtained in a simulation setting where the true regression function is known. We compare this choice of λ with the minimizer of NPE, which is the only estimate that can be obtained from the data in reality. The performance of the two estimators are compared in Figure 2 in terms of IRSD, where boxplots of estimated IRSD values are given for the optimal and proposed estimates at n = 200 and 500 from 500 Monte-Carlo simulation runs. In the displayed boxplots, 22 and 12 outliers are removed for n = 200 and n = 500, respectively.

Figure 2.

Boxplots of the estimated IRSD values of the proposed and optimal estimators for n = 200 (a) and n = 500 (b). (c) Boxplot of NPE values of the proposed estimators for n = 200 and n = 500.

Figure 2 suggests that the estimator with the λ choice selected via NPE and the one with the optimal choice of λ, both improve with increasing sample size. For the proposed estimators with λ chosen by NPE, the median estimated IRSD is 0.2937 at n = 200 and is 0.20670 at n = 500, which implies that the estimated regression surface is close to the true one. We also give in Figure 2 the boxplots of NPE values of the proposed estimator with λ chosen by NPE. The median NPE value at n = 200 is 0.3196 and the median NPE drops to 0.2928 for n = 500.

The performance of leave-one-curve-out cross validation score for the selection of δ is studied through the second simulation. For the computational efficiency, we use 10 fold cross validation. The true value of (δ₁, δ₂), is set to be (20, 0), where 6 candidate (δ₁, δ₂) pairs are considered at (30, 0), (30, 5), (20, 0), (20, 5), and (10, 5). The correct (δ₁, δ₂) choice ratio out of 500 Monte Carlo runs are 0.8929 and 0.9214 for n = 200 and 500, respectively. There seems to be improvement with increasing sample size.

6. Data analysis

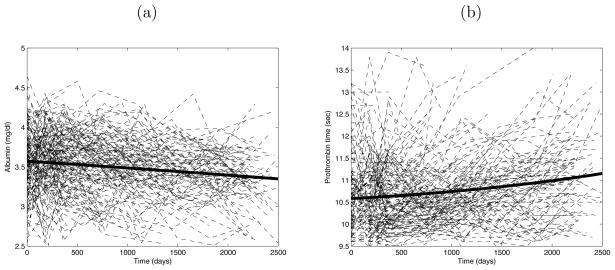
To demonstrate the proposed method, we include an application to the longitudinal primary biliary liver cirrhosis data collected between January 1974 and May 1984 by the Mayo Clinic. In the study design, patients were scheduled to visit the clinic at six months, one year and annually thereafter post diagnosis, where certain blood characteristics were recorded. However, due to missed visits, the data is sparse and highly irregular where each patient visited the clinic at different times. We explore the dynamic relationship between serum albumin level in mg/dl (predictor) and prothrombin time in seconds (response). Both variables are used as an indicator of the liver function, where a decrease in serum albumin levels and elevated prothrombin times are typically associated with malfunctioning of the liver (Murtaugh et al., 1994). We include 201 female patients in the analysis where predictor and response measurements before 2500 days are considered. The number of observations per subject ranges from 1 to 9, with a median of 5 measurements. Individual trajectories of the serum albumin level and prothrombin time overlaying their respective estimated mean functions are given in Figure 3. The generalized cross-validation choice of smoothing bandwidths used in estimation of the prothrombin time and serum albumin level mean functions are 1100 and 1250, respectively. Generalized cross-validation choice for smoothing bandwidths of auto- and cross-covariance surfaces are (400, 400) and (550, 550), respectively. The estimated mean functions indicate opposite patterns as expected, where there is a decreasing trend for the predictor process and an increasing trend for the response.

Figure 3.

(a) Individual predictor trajectories (dashed) overlaying the estimated cross-sectional mean of the predictor process (solid). (b) Individual response trajectories (dashed) overlaying the cross-sectional mean of the response process (solid).

We next fit the proposed recent history functional linear model to the data with K = 10 B-spline functions. Among the five candidate (δ₁, δ₂) choices considered, [1000, 0], [500, 0], [700, 200], [1000, 200], and [1000, 500], the minimizer of cross-validation error was [1000, 0], and the NPE choice of λ was 6502. To save on computational time, we report results from 10 fold cross validation.

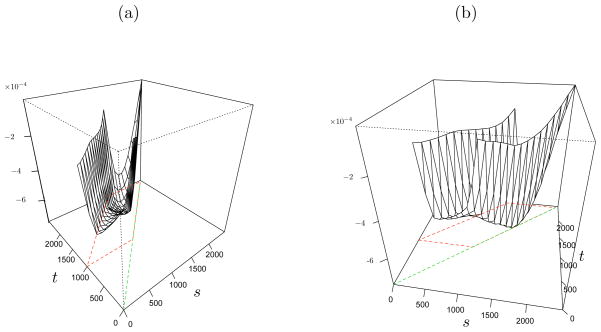
The estimated regression surface is displayed in Figure 4 viewed from two different angles. Most of the estimated regression surface is negative stressing the general opposing trends also observed in literature between serum albumin levels and prothrombin time. For a given time point, the albumin concentration has the strongest effect in magnitude on prothrombin time with a delay of about 500 days where the affect decays as the lag increases. Note also that the observed negative effect of the past albumin concentration levels on the current prothrombin time seems to get more pronounced towards the later stages of the study and hence the disease.

Figure 4.

The estimated regression surface defined on [t − 1000, t] × [1000, 2500] in the longitudinal primary biliary liver cirrhosis data obtained by λ = 6502 and K = 10.

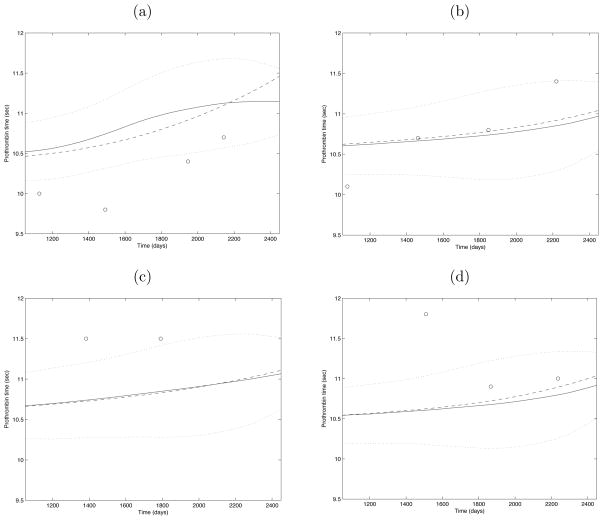
Predicted response trajectories for four randomly selected subjects obtained from the proposals of Section 3.2 and 3.3 and the corresponding 95% asymptotic confidence bands are given in Figure 5. We also include for comparison predicted trajectories obtained from the functional linear model proposed by Yao et al. (2005a). The predicted trajectories seem to be quite close to those from a functional linear model fit which uses the entire predictor trajectory including observations from future and distant past measurement times in the predictions as well. Hence, we conclude that the recent history functional linear model which models the effects of the predictor process from the recent past of 1000 days till the present time, provide a reasonable model for the data in terms of prediction. Given its ease in interpretation due to its restricted regression support when compared with the full functional linear model, the proposed model merges as a viable alternative for the analysis of the current data set.

Figure 5.

Predicted trajectories for 4 randomly selected subjects. In each plot, circles denote the original response observations, the solid line is the response trajectory predicted via the proposed method, the dashed line is the predicted trajectory using the functional linear fit of Yao et al. (2005a), and the dotted lines represent the 95% asymptotic confidence bands.

7. Discussion

We proposed an estimation algorithm for the recent history functional linear models which are useful in applications. The sliding window support of the recent history functional linear model strikes a useful balance between the global support of the functional linear models and the point wise support of the varying coefficient models. The assumption that only the predictor process from the recent past has an effect on the response rather than the future predictor values or only the current predictor value, is useful in many applications where changes in the response process can be explained using recent trends of the predictor process. In addition the product form assumed for the regression surface uses only one dimensional smooth functions considerably easing and speeding estimation.

Our proposal is geared towards sparse longitudinal data where the estimation procedure proposed also accommodates measurement error in variables. Sparsity and measurement error are both commonly encountered in longitudinal designs. We provide asymptotic properties of our estimators that enable the estimation of the predicted response trajectories and that lead to asymptotic confidence bands. Choice of model parameters is also addressed, where favorable properties of the proposed estimators are demonstrated in simulations and data applications.

Appendix A. Assumptions

We present the assumptions in three groups, assumptions (A) are needed for all three Theorems, assumptions (B) are needed for the consistency and asymptotic normality of the predicted response trajectories given in Theorems 2 and 3 respectively, and assumption (C1) is only used in Theorem 3.

The data (T_ij, X_ij) and (T_ij, Y_ij), i = 1, …, n, j = 1, …, N_i, are assumed to be the i.i.d. samples from the joint densities, g₁(t, x) and g₂(t, y). Assume also that the observation times T_ij are i.i.d. with marginal densities 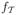(t). Let T₁ and T₂ be two different time points, and X₁ (respectively Y₁) and X₂ (respectively Y₂) be the repeated measurements of X (respectively Y) made on the same subject at times T₁ and T₂. The predictor (and response) measurements made on the same subject at different times are allowed to be dependent. Assume (T_ij, T_il, X_ij, X_il), 1 ≤ j ≠ l ≤ N_i, is identically distributed as (T₁, T₂, X₁, X₂) with joint density function g_XX(t₁, t₂, x₁, x₂) and analogously for (T_ij, T_il, Y_ij, Y_il) with identical joint density function g_{Y Y} (t₁, t₂, y₁, y₂). The following regularity conditions are assumed on 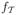(t), g₁(t, x), g₂(t, y), g_XX(t₁, t₂, x₁, x₂) and g_YY(t₁, t₂, y₁, y₂). Let p₁, p₂ be integers with 0 ≤ p₁ + p₂ ≤ 4.

• (A1)The derivative (d^p/dt^p) 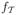(t) exists and is continuous on [0, T] with 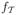(t) > 0 on [0, T], (d^p/dt^p)g₁(t, x) and (d^p/dt^p)g₂(t, y) exist and are continuous on [0, T] × ℝ, and {d^p/(dt^p₁dt^p₂)}g_XX(t₁, t₂, x₁, x₂) and {d^p/(dt^p₁dt^p₂)}g_YY(t₁, t₂, x₁, x₂) exist and are continuous on [0, T]²×ℝ² for p₁ + p₂ = p, 0 ≤ p₁, p₂ ≤ p.
• (A2)The number of measurements N_i made for the i^th subject is a random variable such that $N_i\stackrel{i.i.d}{\sim }N$, where N is a positive discrete random variable with P(N > 1) > 0. The observation times and measurements are assumed to be independent of the number of observations for any subset J_i ∈ {1,…, N_i} and for all i = 1, …, n, i.e. {T_ij, X_ij, Y_ij: j ∈ J_i} is independent of N_i.

Let K₁(·) and K₂(·, ·) be the nonnegative univariate and bivariate kernel functions for smoothing the mean functions μ_X and μ_Y, and auto-covariance surface, G_X, and cross-covariance surface, G_XY. Assume that K₁ and K₂ are densities with zero means and finite variances on a compact support.

• (A3)The Fourier transformations of K₁(u) and K₂(u, v), defined by κ₁(t) = ∫e^−iutK₁(u)du and κ₂(t, s) = ∫e^−(iut+ivs)K₂(u, v)dudv are required to absolutely integrable, i.e. ∫|κ₁(t)|dt < ∞ and ∫∫|κ₂(t, s)|dtds < ∞.

Let h_X and h_Y be the bandwidths used for estimating μ_X and μ_Y, respectively. Also let h_G be the bandwidth used for estimating G_X, and let (h₁, h₂) be bandwidths used in the estimation of G_XY.

• (A4)As n → ∞, the following are assumed about the bandwidths.
• (A4.1)h_X → 0, h_Y → 0, ${nh}_X^4\to \infty ,{nh}_Y^4\to \infty$, and ${nh}_X^6<\infty ,{nh}_Y^6<\infty$.
• (A4.2)h_G → 0, ${nh}_G^6\to \infty$, and ${nh}_G^8<\infty$.
• (A4.3)Without loss of generality, h₁/h₂ → 1, and ${nh}_1^6\to \infty ,{nh}_1^8<\infty$.
• (A5)Assume that the fourth moments of Y and X are finite.
• (B1)The number of eigenfunctions used in (11), M = M(n), is an integer valued sequence that depends on sample size n and satisfies the rate conditions given in assumption (B5) of Yao et al. (2005a).
• (B2)The number and locations of measurements for a given subject does not change as the sample size n → ∞.
• (B3)For all 1 ≤ i ≤ n, m ≥ 1 and 1 ≤ ℓ ≤ N_i, the functional principal component scores ζ_im and the measurement errors ε_iℓ in (4) are jointly Gaussian.
• (C1)There exists a continuous positive definite function ω(s, t) such that ω_M(s, t) → ω(s, t), as M → ∞.

Appendix B. Proofs

Proof of Theorem 1

Uniform consistency of Ĝ_X(s, t) is given in Theorem 1 of Yao et al. (2005b) and that of Ĝ_XY(s, t) is given in Lemma A.1 of Yao et al. (2005a). Consistency of ν̂_kl(t) and μ̂_k(t) for ν_kl and θ_k(t) follow from uniform consistency of Ĝ_X(s, t) and Ĝ_XY(s, t). This implies consistency of b̂(t) for b(t), and hence that of β̂(s, t).

Proof of Theorem 2

For fixed M, define ${\stackrel{\sim }{Y}}_M^{\ast }(t)={\mu }_Y(t)+{\sum }_{m=1}^M{\stackrel{\sim }{\zeta }}_m^{\ast }{P}_m(t)$, where ζ̂_m is as defined in (10) and P_m(t) = ∫_Δt β(s, t)ψ_m(s)ds. Then, it follows that

$$\mid {\widehat{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}^{\ast }(t)\mid \le \mid {\widehat{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}_M^{\ast }(t)\mid +\mid {\stackrel{\sim }{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}^{\ast }(t)\mid =Q_1+Q_2.$$

The convergence of Q₂ to 0 as n → ∞ follows from Lemma A.3 in Yao et al. (2005a). Note that, for Q₁,

$$Q_1=\mid {\widehat{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}_m^{\ast }(t)\mid \le \mid {\widehat{\mu }}_Y(t)-{\mu }_Y(t)\mid +\sum _{m=1}^M\mid {\widehat{\zeta }}_m^{\ast }{\widehat{P}}_m-{\widehat{\zeta }}_m^{\ast }{P}_m(t)\mid .$$

Uniform consistency of μ̂_Y(t) for μ_Y(t) follows from Theorem 1 in Yao et al. (2005b), and consistency of ${\widehat{\zeta }}_m^{\ast }$ for ${\stackrel{\sim }{\zeta }}_m^{\ast }$ follows from Theorem 3 in Yao et al. (2005b). From uniform consistency of β̂(s, t) established in Theorem 1 of Section 3.1 and that of ψ̂_k(t) shown in Yao et al. (2005a), uniform consistency of P̂_m(t) follows. Combining these results, we have

$$\underset{t\in [{\delta }_1,T]}{sup}\mid {\widehat{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}_M^{\ast }(t)\mid \stackrel{p}{\to }0\text{as}n\to \infty ,$$

and by Slutsky’s Theorem, Theorem 2 follows.

Proof of Theorem 3

Under the Gaussian assumption, for any fixed M ≥ 1, we have ${\stackrel{\sim }{\zeta }}_m^{\ast }-{\zeta }_m^{\ast }\sim \mathcal{N}(0,{\mathrm{\Omega }}_M)$. In proof of Theorem 2, it is shown that ${lim}_{n\to \infty }{sup}_{t\in \mathcal{T}}\mid {\widehat{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}_M^{\ast }(t)\mid \stackrel{p}{\to }0$. Observing that ${\widehat{Y}}_M^{\ast }(t)-Y_M^{\ast }(t)={\widehat{Y}}_M^{\ast }(t)-{\stackrel{\sim }{Y}}_M^{\ast }(t)+{\stackrel{\sim }{Y}}_M^{\ast }(t)-Y_M^{\ast }(t)$, we have $\{{\widehat{Y}}_M^{\ast }(t)-Y_M^{\ast }(t)\}\stackrel{\mathcal{D}}{\to }{Z}_m\stackrel{\mathcal{D}}{=}\mathcal{N}(0,{\omega }_M(t,t))$. Under assumption (C1), letting M → ∞ leads to $Z_M\stackrel{\mathcal{D}}{\to }Z\sim \mathcal{N}(0,\omega (t,t))$. From the Karhunen-Loéve Theorem, $\mid Y_M^{\ast }(t)-Y^{\ast }(t)\mid \stackrel{p}{\to }0$. Therefore, ${lim}_{M\to \infty }{lim}_{n\to \infty }\mid {\widehat{Y}}_M^{\ast }(t)-Y^{\ast }(t)\mid \stackrel{\mathcal{D}}{=}Z$. From the convergence of ψ̂(t), ${\widehat{\zeta }}_m^{\ast }$, γ̂_m and P̂_m for ψ(t), ${\zeta }_m^{\ast }$, γ_m and P̃_m, we can deduce ${\widehat{\omega }}_M(t,t)\stackrel{p}{\to }{\omega }_M(t,t)$ as n → ∞. Under the assumption (C1), it follows that lim_M→∞ lim_n→∞ ω̂_M(t, t) = ω(t, t) in probability. Applying Slutsky’s theorem, (12) follows.

Appendix C. Estimation procedures

In this section, we provide explicit forms for the local polynomial smoothing procedures used in estimating the mean functions and covariance surfaces. Eigendecompositions for the estimated covariance surfaces and explicit form of the measurement error variance estimator are also provided.

The estimator of mean function for the predictor process, μ̂_X(t), can be obtained by local linear regression via minimizing

$$\sum _{i=1}^n\sum _{j=1}^{N_i}{K}_1\left(\frac{T_{ij}-t}{h_X}\right){\{X_{ij}-{\eta }_0-{\eta }_1(t-T_{ij})\}}^2,$$

with respect to η₀, η₁, which leads to μ̂_X(t) = η̂₀. Estimation of μ_Y(t) follows similarly.

For estimation of the cross-covariance surface G_XY, the two dimensional local linear smoother is fitted to the raw covariances by minimizing

$$\sum _{i=1}^n\sum _{1\le j,\ell \le N_i}{K}_2\left(\frac{T_{ij}-s}{h_1},\frac{T_{i\ell }-t}{h_2}\right)[G_{XY,i}(T_{ij},T_{i\ell })-f\{\eta ,(s,t),(T_{ij},T_{i\ell })\}],$$ (C.1)

with respect to η = (η₀, η₁, η₂), yielding Ĝ_XY(s, t) = η̂₀. Estimation of the auto-covariance surface of the predictor process can be obtained similarly where the diagonal elements of the raw auto covariance matrix are not included in the smoothing as described in Section 3.1. Hence the second sum in (C.1) is taken over 1 ≤ j ≠ ℓ ≤ N_i, excluding the diagonal terms.

In order to obtain the estimator for the measurement error variance ${\sigma }_{\epsilon }^2$, we first estimate the diagonal elements of the auto-covariance surface G_X(t, t) excluding the diagonal raw covariances contaminated with error, by applying a local linear smoother along the diagonal and local quadratic smoother along the direction perpendicular to the diagonal. The resulting estimators of the diagonal elements are denoted by G̃_X(t). This estimator is then compared to a linear smoother fit only to the diagonal raw covariance terms {T_ij, G_X,i(T_ij, T_ij)}, estimating $G_X(t,t)+{\sigma }_{\epsilon }^2(t)$. This estimator is denoted by V̂(t). We estimate the error variance by these two estimators, yielding

$${\widehat{\sigma }}_{\epsilon }^2=\frac{2}{T}{\int }_{{\mathcal{T}}_1}\{\widehat{V}(t)-\stackrel{\sim }{G}(t)\}dt,$$

where 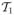= [T/4, 3T/4]. Here, the integration is taken over the middle half of in order to remove the boundary effect of the local polynomial smoother.

The eigenfunctions and eigenvalues of the estimated auto-covariance surface, Ĝ_X(s, t), for the predictor process are the solutions, ψ̂_k and γ̂_k, of the eigenequation given by

$${\int }_{[0,T]}{\widehat{G}}_X(s,t){\widehat{\psi }}_k(s)ds={\widehat{\gamma }}_k{\widehat{\psi }}_k(t),$$

where ${\int }_{[0,T]}{\widehat{\psi }}_k^2(t)dt=1$ and ∫_[0,T] ψ̂_m(t)ψ̂_k(t)dt = 0 for m ≠ k. For numerical solutions, discretization of the smoothed covariance function can be used following Rice and Silverman (1991).