MSCALE: A General Utility for Multiscale Modeling

Abstract

The combination of theoretical models of macromolecules that exist at different spatial and temporal scales has become increasingly important for addressing complex biochemical problems. This work describes the extension of concurrent multiscale approaches, introduces a general framework for carrying out calculations, and describes its implementation into the CHARMM macromolecular modeling package. This functionality, termed MSCALE, generalizes both the additive and subtractive multiscale scheme (e.g. QM/MM ONIOM-type), and extends its support to classical force fields, coarse grained modeling (e.g. ENM, GNM, etc.), and a mixture of them all. The MSCALE scheme is completely parallelized with each subsystem running as an independent, but connected calculation. One of the most attractive features of MSCALE is the relative ease of implementation using the standard MPI communication protocol. This allows external access to the framework and facilitates the combination of functionality previously isolated in separate programs. This new facility is fully integrated with free energy perturbation methods, Hessian based methods, and the use of periodicity and symmetry, which allows the calculation of accurate pressures. We demonstrate the utility of this new technique with four examples; (1) subtractive QM/MM and QM/QM calculations; (2) multi-force field alchemical free energy perturbation; (3) integration with the SANDER module of AMBER and the TINKER package to gain access to potentials not available in CHARMM; and (4) mixed resolution (i.e. coarse grain / all-atom) normal mode analysis. The potential of this new tool is clearly established and in conclusion an interesting mathematical problem is highlighted and future improvements are proposed.

1 Introduction

Although computational methodologies have improved vastly over the last 10 years, it has become blatantly obvious that the most commonly employed techniques are not ideal for solving the challenging problems that exist at the interface of biology, chemistry, physics, and medicine. Many of the most important events surrounding biomedical processes take place on different time and length scales. For example, electronic excitations typically occur on the femto to picosecond time scale whereas aggregation, folding, and diffusion events can range in time from microseconds to hours.¹ This corresponds to approximately 10 orders of magnitude in the spatial regime and 15 orders of magnitude in the temporal regime.

In the past these multiple (time and length) scales have by and large been treated independently. The most notable exception is the coupling of quantum and classical (i.e. molecular mechanical) mechanics in a hybrid QM/MM treatment. This scheme, which was first devised by Warshel and Levitt² with subsequent work by Singh and Kollman,³ and Field, Bash, and Karplus,⁴ involves division of the system of interest into three regions. The first region is treated with quantum mechanics, while the larger second region is described with molecular mechanics. The third region is the smallest and describes the boundary between the QM and the MM sections. Inspired by the success of this methodology, Morokuma and co-workers introduced a general approach to coupling different levels of theory; dubbed the ONIOM method. ⁵

The term multiscale modeling typically describes the use of disparate methods to solve problems that span methodological, temporal, or spatial scales. For example, hybrid QM/MM schemes utilize two different methodological scales. It is generally accepted that there are two main approaches used in multiscale modeling: sequential and concurrent.^6,7 The sequential multiscale treatment employs more accurate models that are then used to parameterize coarser ones. Coarse-grained (CG) molecular dynamics (MD) simulations is one area where the idea of sequential multiscale modeling has been particularly useful. In general, coarse-graining seeks to accurately represent a system with a reduced number of degrees of freedom. Examples of this include treating an atomistic amino acid residue as a single or series of beads (e.g. BLN model) or representing an alpha carbon as an elastic or Gaussian network (e.g. ENM, GNM).^8–24 In these cases the, sequential, force-matching approaches can significantly improve results as they typically use classical atomistic simulations to derive coarse-grain parameters that ideally reproduce the desired properties of the parent system.^25–27 The other main approach is concurrent multiscale modeling which is exemplified by the hybrid QM/MM scheme; instead of using one model to improve another, both models are executed simultaneously on different parts of the system. Further, concurrent modeling can be subdivided into additive and subtractive approaches with the contrasting ways used to couple QM and MM methodologies perfectly highlighting the two subcategories.

The original QM/MM scheme from Warshel and Levitt is an additive concurrent approach where the interactions that couple the QM region to the MM region are comprised of a hybrid Hamiltonian (including polarization effects from the MM regions) that are \added” to the total energy of the system.

$${\widehat{H}}_{\text{eff}}={\widehat{H}}_{\text{QM}}+{\widehat{H}}_{\text{MM}}+{\widehat{H}}_{\text{QM}/\text{MM}}$$ (1)

where Ĥ_QM is the pure QM Hamiltonian, Ĥ_MM is the classical Hamiltonian and Ĥ_QM/MM is the hybrid QM/MM Hamiltonian. In contrast, Morokuma and co-workers developed a subtractive approach where the interaction between the QM and MM systems is described only at the MM level of theory:

$$E^{\mathit{ONIOM}}=E_{\mathit{real}}^{MM}+E_{\mathit{model}}^{QM}-E_{\mathit{model}}^{MM}$$ (2)

where the final E^ONIOM is the final extrapolated energy and is meant to approximate the full system treated at the QM level of theory. The first term on the right hand side describes the “real” system which is comprised of all the atoms (treated at the lowest level of theory, MM). The second term on the right hand side is the energy of the model system (i.e. the region treated at the highest level of theory, QM); while the final term repeats the model system calculation, however, only treated at the low level. This final term is needed to prevent double counting of the model system. Note the fundamental difference between the additive and subtractive methodologies here; the final term in equation 1 describes the interactions between the QM and MM regions directly, however, in equation 2 this interaction is completely encompassed as part of the first term ( $E_{\mathit{real}}^{MM}$). The subtractive scheme is sometime referred to as \mechanical embedding.” It should be noted that this incarnation of the ONIOM scheme does not accommodate direct polarization of the model region by the remaining portion of the system, however, improvements to this scheme have been developed to overcome this weakness.²⁸

In general, it is believed that the additive approach is more robust and accurate, however, that is predicated on deriving and implementing the hybrid coupling term which can in practice be rather difficult. ^29,30 Therefore, the subtractive approach has the attractive features of being both conceptually easy to understand and implement. Additionally, further development has been carried out to extend the subtractive QM/MM approach with ideas from the additive scheme (i.e. electronic embedding).²⁸

Although QM/MM is clearly the most widely utilized multiscale method, the modeling community continues to clamor for more general approaches. A recent review correctly highlights this point: “very few packages implement the CG and coarser models, and even fewer integrate more levels in a fully multiscale software. An effort in this direction would be very useful and promote the use of multiscale approaches.”⁶

In the following sections we describe such a general framework, called MSCALE. We briefly review the conceptual basis of our current multiscale approach and describe the implementation of this scheme within CHARMM.³¹ Periodic systems and symmetry are fully supported within this framework. The results section highlights four representative examples that showcase a range of the functionality supported by MSCALE. The first example will highlight the use of MSCALE as a general subtractive, either QM/MM or QM/QM, engine. The second example will demonstrate the ability to combine multiple classical force fields into a single calculation and interface into the alchemical free energy perturbation module of CHARMM. A third case will describe the implementation of AMBER’s SANDER module and the TINKER software suite as “servers” to CHARMM’s MSCAle command. This functionality allows CHARMM users a general way to access features exclusive to AMBER or TINKER (e.g. implicit water models, polarizable force fields) and can easily be extended to support new developments in both programs. The final example will showcase the ability to perform a mixed model normal mode analysis (NMA) by combining both atomistic and CG treatments.

2 Computational Details

The current work describes the extension of concurrent multiscale approaches and introduces a general framework called MSCALE to access this functionality, which has been fully implemented in CHARMM via the MSCAle command. Throughout this paper, MSCALE will be used to refer to the general framework while MSCAle refers to the specific CHARMM command. This multiscale approach makes the coupling of both additive and subtractive schemes possible within a single framework, and allows for both types of methods to be used in a single calculation.

To actually perform an MSCALE calculation, the MSCAle command is invoked by the user, followed by one or more SUBSystem commands to define the different structural regions of the calculation. An executable must be given along with an input file, output file path, weighting coefficient of the subsystem, other optional parameters, and an atom selection (i.e. atomic coordinates) as arguments to the SUBSystem command. The executable may be any MSCALE-compatible program (although not all features are supported on codes other than CHARMM). Examples of optional arguments to SUBSystem are the CRYStal keyword to specify that periodic image data should be transmitted and the NPROC argument, which specifies how many processors the subsystem should use in a parallel / parallel calculation. Example input scripts are given in the supporting information.

Once all subsystems are defined, the user can perform calculations as usual. The calculation is executed in a parallel client/server fashion (Figure 1), with basic communication being handled by version 2 of the standard message passing interface (i.e. MPI-2).³² The “client” acts as the controlling process with “server” calculations being spawned based on the SUBSystem commands entered by the user; one server is launched for each defined subsystem using the executable, atom selection, and other parameters specified by the user. This spawning is done through the MPI Comm spawn MPI-2 routine. The client stores the MPI intercommunicator needed to transfer data to and from the newly spawned server. Whenever the energy, gradient, or Hessian is required, the client sends each server the coordinates it needs and, if necessary, other data such as unit cell dimensions for a periodic system via an MPI broadcast on that server’s intercommunicator. It then waits to receive the energy, gradient, and optional hessian elements (the virial is also transmitted for periodic systems) from each server, scales them by the specified subsystem coefficient, and adds them to those terms calculated by the client. If it is not desired to include the terms calculated on the client in the final energy, CHARMM’s SKIPe or BLOCk commands can be used to discard them.

Figure 1.

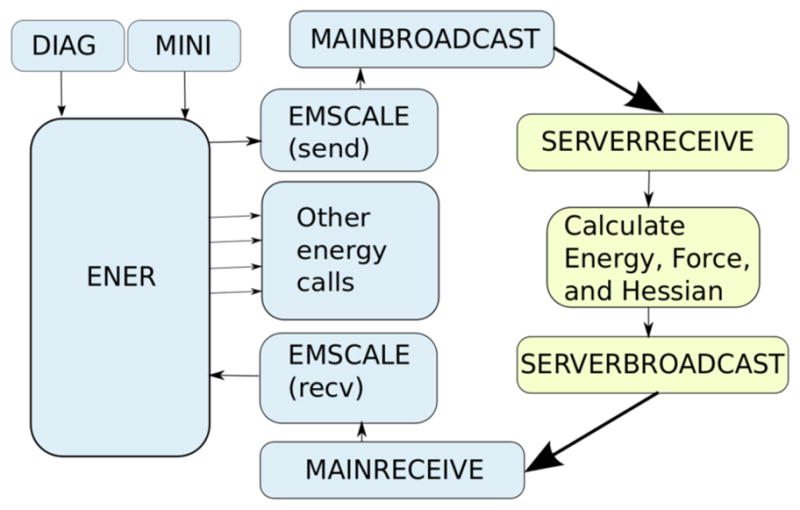
Illustration of the subroutine calling sequence of the MSCALE facility; showing the information flow of a typical energy (ENER), minimization (MINI), or normal mode analysis (DIAG) calculation. The broadcast and receive routines handle both coordinate and energy/gradient communication. Routines in blue are executed on the main processor (client) while those in yellow take place on the subsystems (servers). Thin black lines represent information being passed between subroutines where the thick black lines represent MPI calls and the sharing of information between the controlling client process and the server process, which acts only as an energy, force, or Hessian engine. The EMSCALE subroutine is called twice from CHARMM’s main energy routine, once at the beginning to send the data to the servers and again at the end to receive the energy, force, etc. terms from them. Therefore, the servers and clients are performing calculations in parallel. Further details of how MSCALE is implemented is given in the supporting information.

Currently, only CHARMM³¹ is supported as the client with the server calculations being able to employ either CHARMM, TINKER,^33,34 or the SANDER module of AMBER³⁵ as servers directly through MPI calls. Periodic systems are not fully supported for non-CHARMM servers, but this functionality will be added in the future. There is an additional set of quantum chemical programs that are supported as servers. These packages are interfaced through external wrappers that handle MPI communication. At this time the following QM packages are supported this way: NWChem,³⁶ Molpro,³⁷ PSI3,³⁸ and Gaussian 03/09.³⁹ It should be noted that all of CHARMM’s “built-in” QM packages (e.g. Q-Chem,⁴⁰ GAMESS-US,⁴¹ GAMESS-UK,⁴² SCC-DFTB,⁴³ MNDO,⁴⁴ QUANTUM⁴ and SQUANTUM,⁴⁵ etc.) are supported directly via MPI. Using this functionality both additive and subtractive methodologies can be combined in a single calculation.

In a mixed scale calculation, coarse grained centers can be handled by either co-locating them with a center from the all-atom model (e.g. a C₃) or by connecting them through constraints or restraints. For example, CHARMM’s LONEpair facility can be employed to constrain a single CG center to be located at the center of mass of a group of atoms.³¹ Using one of these two options we have defined a general procedure for mixing models of different resolution.

In this manner, MSCALE supports multiple independent, but connected, calculations. The user is free to define an unlimited number of subsystems (i.e. layers) and assign arbitrary coefficients to combine them. The individual calculations are run as separate processes, usually on different computers (e.g. on a Beowulf style cluster).⁴⁶ For example, the typical subtractive QM/MM approach, (i.e. executed as an ONIOM-type calculation) would have a coefficient matrix as such:

$$\begin{array}{ccc}& \mathit{Real}& \mathit{Model}\\ MM& 1& -1\\ QM& 0& 1\end{array}$$

with the final energy expression being that of equation 2. Using the MSCALE utility this general approach can be extended to arbitrary levels of theory (i.e. QM, MM, coarse-grain, etc.) and arbitrary numbers of subsystems. An example of four layer subsystem matrix:

$$\begin{array}{ccccc}& \mathit{Full}& \mathit{Big}& \mathit{Medium}& \mathit{Small}\\ \$& 1& -1& 0& 0\\ \$\$& 0& 1& -1& 0\\ \$\$\$& 0& 0& 1& -1\\ \$\$\$\$& 0& 0& 0& 1\end{array}$$

where the left side of the matrix represents the cost of level of theory (increasing from top to bottom) and the top represents the size of the system (increasing from right to left). This matrix yields the following MSCALE energy:

$$E^{\mathit{MSCALe}}=E_{\$}^{\mathit{Full}}+(E_{\$\$}^{\mathit{Big}}-E_{\$}^{\mathit{Big}})+(E_{\$\$\$}^{\mathit{Medium}}-E_{\$\$}^{\mathit{Medium}})+(E_{\$\$\$\$}^{\mathit{Small}}-E_{\$\$\$}^{\mathit{Small}})$$ (3)

Using this equation one can easily derive the force and Hessian expressions with the proper link-atom projections.^47,48 More complex multiscale systems can be set up that involve a combination of additive and subtractive schemes. This can be done easily, without any need for reprogramming, and there is effectively no limit to the number of different subsystems.

The coefficients on the subsystems are not just used for ONIOM type calculations; they may also change dynamically based on the λ values used in CHARMM’s alchemical free energy PERTurbation procedure.³¹ This method calculates the free energy difference (ΔG) between two molecular systems. To do so, an initital system (the λ = 0 state) is defined, and then some change (e.g. changing the protonation state of a titratable amino acid) is made to define a second state (the λ = 1 state). A molecular dynamics simulation is then run during which λ is gradually moved from 0 to 1. The free energy difference between these two end states may then be estimated by Thermodynamic Integration⁴⁹ (Thermodynamic Perturbation is also supported). With MSCAle, subsystems may be given a weighting of λ or 1–λ, which allows the contribution of these subsystems to the total energy to change over the course of the simulation. When energy terms are scaled by λ or 1–λ, derivatives of the energy and forces with respect to λ are computed and applied appropriately. This allows MSCALE to be fully compatible with other free energy methods in CHARMM. Compatibility of MSCAle and PERT is important because until now the PERT facility has been limited in functionality and in many cases the direct implementation of new methods in PERT was both conceptually and technically challenging. Now, using MSCAle individual CHARMM (or other programs as described above) processes can be spawned that are not dependent on the limited PERT module. One example of this is the use of additive QM/MM; it was not until recently that PERT supported an ab initio QM program.⁵⁰ However, with MSCAle all currently supported quantum packages in CHARMM will have access to free energy perturbation. Another example is that, until this development, the only alchemical changes that could be studied with PERT are those that could be represented by a structural change (e.g. changing the type or connectivity of an atom or group of atoms). Because each subsystem is entirely independent under MSCALE, non-structure based changes (e.g. changing force field parameters or even the entire force field) can be made. This is demonstrated below with an example of estimating the change of ΔG of solvation in moving a system from the CHARMM22 force field ⁵¹ to the AMBER99SB force field.⁵²

Initially, one thinks about mixing atomistic models and CG models, but this facility will allow the mixing of multiple CG models as well. An example of this would be the combination of a 1 site elastic network model (ENM) with a 1 or multi-site beaded CG model. An interesting application of this could be to study protein-protein interactions where the beaded model can better describe local interactions while the ENM ensures proper protein structure. Additionally, two atomistic models can be combined just as easily. For example, there is great need in the biomedical engineering community to be able to model protein-surface interactions with a consistent approach;^53–56 this facility allows for using a proper materials based potential while combining that with state-of-the-art biological force fields like CHARMM, AMBER, OPLS, etc.

The MSCALE framework and its implementation in CHARMM fully support periodic systems, as mentioned above. The accurate single-sum pressure calculation is used.^31,57 This single sum method can be used in CHARMM without MSCALE support, since image atom positions are explicitly treated and used when computing the internal virial. This avoids objections to this methodology that have been raised in previous work.⁵⁸ Within CHARMM’s MSCAle implementation, there is support for constant pressure and temperature simulations even when the “servers” do not support virial calculations.

As alluded to above, MSCALE currently supports analytic and finite difference energies, forces, and Hessians. ¹ Therefore, minimization, dynamics, and normal mode analysis are all possible within this framework. In the following section several examples of this functionality will be presented. It should be stressed that the goal of this effort is to provide an extensive and flexible tool for multiscale modeling, as opposed to a single tool with a dominant focus on performance. The use of multiple processes allows for simple parallelization that can enhance performance, but communicating selected coordinates and associates energies, forces, and optionally Hessian terms on every step does entail a performance cost. CHARMM’s MSCAle implementation does allow subsystems to be run on multiple processors if the server program has been parallelized.

3 Results and Discussion

3.1 Subtractive QM/MM and QM/QM

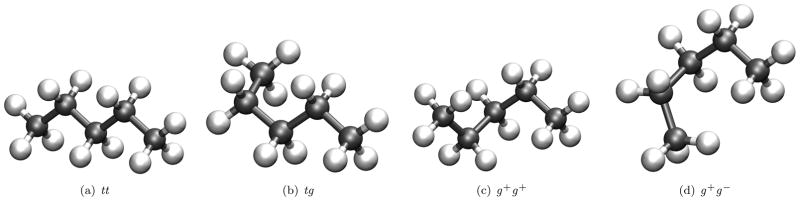
Subtractive MSCALE calculations of pentane in its trans-trans (tt), trans-gauche (tg), gauche plus-gauche plus (g⁺g⁺), and gauche plus-gauche minus (g⁺g⁻) conformations (Figure 2) were performed. All QM/MM and QM/QM calculations utilized the Q-Chem/CHARMM⁵⁰ or SCC-DFTB/CHARMM⁴³ interfaces. All “high-level” QM results were obtained at the MP2/cc-pVDZ level of theory except for the full-QM results for which MP2/cc-pVTZ was used. The CHARMM force field was used for MM and the semi-empirical SCC-DFTB method employed as the “low-level” QM in QM/QM calculations. The MP2/cc-pVDZ level was chosen as to be comparable to previously published work.⁵⁹ All subtractive calculations were repeated four times with 1, 2, 3, and 4 methyl groups included as part of the QM region (Figure 2). The single link atom (SLA) boundary scheme coupled with the LONEpair facility, to ensure co-linearity of the link atom, was used for all additive QM/MM calculations. Results were obtained by performing 50 steps of steepest descent minimization followed by adopted-basis Newton Rhapson (ABNR) minimization until reaching a root mean squared gradient (GRMS) tolerance of 0.001 kcal/mol·Å² except for the full QM case, which was minimized in Q-Chem to a gradient tolerance of at least 1.5×10⁻⁵ hartree/bohr using the MP2/cc-pVDZ level of theory. Full QM, additive QM/MM, subtractive QM/MM, and subtractive QM/QM energy differences of all conformations are reported in table 1. In all cases the tt conformation was the global minimum with the tg, g⁺g⁺, and g⁺g⁻ energy differences progressively increasing.

Figure 2.

Conformations of pentane.

Table 1.

Energy differences in kcal/mol between the optimized trans-trans conformation (TT) and the trans-gauche (TG), positive gauss-positive gauche (G+G+), and positive-gauche-negative gauche (G+G−) conformations of pentane. The leftmost column (N) indicates the number of groups represented at the MP2/cc-pVDZ level of theory. QM/QM refers to mixed MP2/cc-pVDZ - SCC-DFTB calculations

N	TG	G+G+	G+G-
Additive QM/MM
1 (CH4)	0.62	1.07	2.79
2 (CH3CH3)	0.28	0.82	2.59
3 (CH3CH2CH3)	0.48	0.61	2.73
4 (CH3CH2CH2CH3)	0.68	0.96	2.95
Subtractive QM/MM
1 (CH4)	0.60	1.13	2.83
2 (CH3CH3)	0.56	1.10	2.78
3 (CH3CH2CH3)	0.55	1.05	2.97
4 (CH3CH2CH2CH3)	0.68	1.22	3.04
Subtractive QM/QM
1 (CH4)	0.47	0.92	2.32
2 (CH3CH3)	0.43	0.89	2.26
3 (CH3CH2CH3)	0.53	0.95	2.36
4 (CH3CH2CH2CH3)	0.68	1.14	2.66
Full QM	0.56	0.80	2.81
Full SCC-DFTB	0.47	0.92	2.32
Full MM	0.60	1.13	2.82

One area of interest that can be addressed from these results centers around the recent hypothesis of adjacent gauche stabilization.⁵⁹ Klauda et al. found that adding a single gauche state to an alkane resulted in a 0.54 – 0.62 kcal/mol penalty. Further, they reported adding a second gauche state of the same sign required 0.22 – 0.37 kcal/mol of energy while adding one of opposite sign cost 2.49 – 2.85 kcal/mol. Examining the ΔEs from table 1 reveals several trends.

Beginning with the tt-tg conformational change it is clear from all results that treating only the terminal methyl group classically overestimates the ΔE (~ 0.68 kcal/mol). This is in part due to the neglect of long range dispersive interactions between the terminal methyl groups which occurs in all three models. Specifically, this is a result of the energy differences of the MP2 subsystem (CH₃-CH₂-CH₂-CH₃), 0.67 kcal/mol and 0.65 kcal/mol for the subtractive QM/MM and QM/QM, respectively. The additive QM/MM case mirrors this since the electrostatics on the terminal methyl group are excluded (vide infra).

The subtractive results, going from 2 → 4 methyl groups, converge relatively smoothly towards the results of the low level of theory (i.e. MM and SCC-DFTB, respectively). However, there is significant variation in the additive QM/MM results. This is easily explained as an artifact of the single link atom (SLA) approach coupled with excluding group electrostatics (EXGR) which is a standard scheme for preventing over polarization in QM/MM calculations. Although this clearly leads to underestimation of energy differences, it is fairly consistent throughout all conformations. Further, Das et al. showed this effect can be mitigated easily by using more advanced link atom approaches (e.g. Delocalized Gaussian MM charges).⁶⁰

Next, examining the tt-g⁺g⁺ ΔEs leads again to clear trends. For example, the subtractive QM/MM calculations fail to reproduce the adjacent gauche penalty (0.22 – 0.37 kcal/mol). This results from a combination of both the neglect of dispersive effects and overestimation by the underlying force field, table 2. Due to the correct handling of dispersion at the MP2 level of theory and explicit polarization, it is clear why additive QM/MM does a better job of reproducing this subtle effect. The other subtle effect at play here is the adjacent gauche destabilization which results in an ~ 2.81 kcal/mol ΔE between tt and g⁺g⁻. Again, additive QM/MM handles this interaction relatively well as does subtractive QM/MM; largely due to parameterization of the CHARMM force field, ΔE(tt- g⁺g⁻) = 2.82 kcal/mol. However, the problem with incorrect treatment of dispersion pops up again; SCC-DFTB ΔE(tt- g⁺g⁻) underestimates this by nearly 0.5 kcal/mol.

Table 2.

Conformational energy differences between the tg and g⁺g⁺ states. These highlight the effect of level of theory on adjacent gauche stabilization

Level of Theory	ΔE
MP2/cc-pVDZ	0.24
SCC-DFTB	0.45
CHARMM	0.53

Overall, the results indicate that the additive and subtractive QM/MM and QM/QM methods both do a reasonable job of reproducing the energy surface for alkane molecules at a substantially lower computational cost. However, specific choices of model systems and levels of theory can lead to incorrect descriptions of subtle effects. Use of the subtractive method with MSCALE allowed for combined quantum mechanical and semi-empirical calculations, which are not possible with previously-existing methods in CHARMM.

3.2 Free-energy perturbation

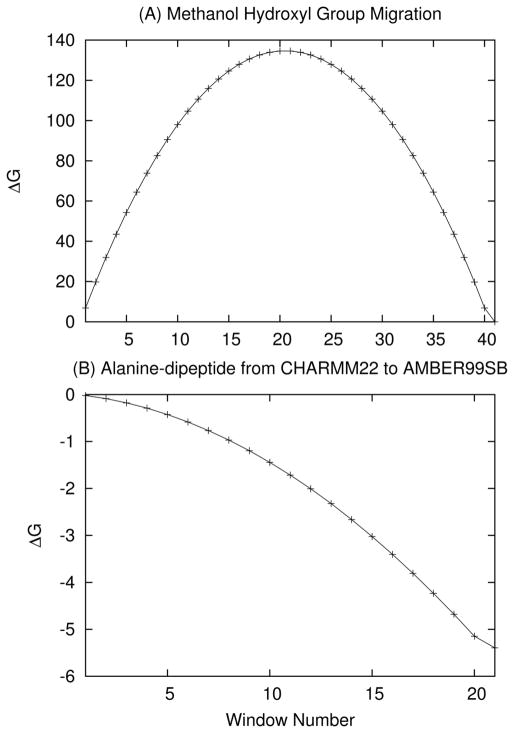
The PERT module in CHARMM is a single topology based potential implemented to calculate alchemical and/or conformational free energies. CHARMM’s MSCAle implementation has been integrated with this module and vastly expands the features compatible with PERT. All MSCAle+PERT simulations were run without SHAKE constraints unless otherwise noted, but the use of SHAKE with MSCAle is supported. Basic PERT functionality was tested with MSCAle using two simple systems. The first examined migration of the hydroxyl group (−OH) of methanol (CH₃OH) using the CHARMM22 force field.⁵¹ For the PERT run, 16.4 nanoseconds (ns) of vacuum MD was carried out using a 1 fs time step. The alchemical process was divided into 41 windows, each running 400 picosceconds (ps) with the first 200 ps being used for equilibration and final 200 used for collecting statistics. Lambda (λ) was increased by 0.025 at each window; this yielded a net free energy change (ΔG) of effectively zero, as would be expected. The ΔG as a function of PERT window is shown in Figure 3(A).

Figure 3.

ΔG as a function of window for (A) the OH move of methanol and (B) the alanine dipeptide moving from the CHARMM22 to AMBER99SB force fields. In both cases the free energy curve is smooth, representing a gradual shift from one force field or structure to another.

The second simple test was reversing the chirality of a single alanine molecule (R → S). For this simulation, 82 ns of Langevin dynamics (LD) was run with a collision frquenct of 2 ps⁻¹; again utilizing 41 windows (Δλ = 0.025) with 2 ns of dynamics per window (1 ns for equilibration and 1 ns for data collection). Once again, the total free energy change was effectively zero as would be expected. For validation the calculation was repeated with two different random seeds and all simulations yielded ΔG values within a few hundredths of a kcal/mol from 0.

To extend this functionality to a more novel application, we examined the alchemical free energy of an alanine dipeptide moving from the CHARMM22 to AMBER (AMBER99SB) force field (as implemented in CHARMM).^31,51,52 This was carried out in both vacuum and in solvent using AMBER’s version of the TIP3P water model. A consistent water model was used for both force fields to prevent solvent free energy changes from dominating the total ΔG. For both force fields, non-bonded interactions were calculated in full applying no cutoffs.

To validate the methodology, the vacuum structure was minimized to the C7 equatorial conformation and a free energy perturbation calculation, changing the CHARMM22 to the AMBER99SB force field, was carried out. For the dynamics, LD was run at 0K for 168 ns with a Langevin collision frequency of 1 ps⁻¹. The simulation consisted of 21 windows running 8 ns each with only the last 7 ns being used for data collection. Cut-offs were disabled by setting the nonbonded cut-off to 996 Å. Under these conditions, the measured ΔG_{CHARMM→AMBER} was −6.15 kcal/mol, which is effectively identical to the difference in potential energy between the CHARMM and AMBER99SB force fields for this conformation, as would be expected with 0K dynamics where entropic effects are nonexistent.

The vacuum structure was also run under the same PERT set-up with LD at 300K and a collision frequency of 1 ps⁻¹. In this case ΔG_{CHARMM→AMBER} yielded was −5.39 kcal/mol (ΔG as a function of window for this run is shown in Figure 3(B)). At 300K, the structure samples multiple wells therefore a harmonic limit free energy is not expected to perfectly reproduce the dynamics. However, the harmonic limit ΔG_{CHARMM→AMBER} was determined from normal mode analysis to be −5.44 kcal/mol for C7 equatorial conformation, −5.50 kcal/mol for the C7 axial conformation, and −5.10 kcal/mol for the C5 conformation. These are consistent with the ΔG obtained from the PERT simulation.

To explore the effects of solvent, the vacuum minimized C7 equatorial conformation was placed in a pre-equilibrated water sphere with a radius of 15 Å (periodic boundary conditions were not used). Langevin dynamics was run at 300 K for 2.1 ns with a collision frequency of 0.5 ps⁻¹ using the same windowing scheme as in the vacuum case but with each window containing only 100 ps of dynamics, of which the last 75 ps are used for collecting statistics. As in the case of the gas-phase systems, no cutoffs were applied. SHAKe was applied to the TIP3P waters only. Under these conditions, ΔG_{CHARMM→AMBER} was calculated to be −6.48 kcal/mol.

The differences between current results and those reported by Boresch and coworkers⁶¹ can be explained by the fact we used CHARMM’s AMBER99SB implementation instead of PARM94. Additionally, our solvated simulations were performed without periodic boundary conditions and with no cutoffs; finally, our results are computed with thermodynamic integration as opposed to the Bennett Acceptance Ratio.⁶² The total change of free energy caused by solvation ( $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{CHARMM}\to \text{AMBER}}^{\text{solvation}}$) under these conditions is −1.09 kcal/mol at 300K. Much of the difference between this result and the previous one is likely explained by changes between the AMBER94 and AMBER99SB force fields and the fact that the boundary conditions for the solvated system were different, as the previous work notes that they were able to obtain Themodynamic Integration results consistent with those found with the Bennett Acceptance Ratio. Finally, the previous work notes that the choice of cut-off radius has a substantial effect on the calculated ΔG, and therefore applying a cut-off to this system is likely to yield a somewhat different $\mathrm{\Delta }\mathrm{\Delta }{G}_{\text{CHARMM}\to \text{AMBER}}^{\text{solvation}}$.

3.3 Integration with AMBER and TINKER

Through the MSCAle implementation in CHARMM, the SANDER module in AMBER³⁵ can be called to perform energy and analytic gradient calculations. Such an implementation enables external use of the AMBER energy function, AMBER force fields, and implicit solvation models while the controlling dynamics and/or analysis is carried out in CHARMM. Likewise, an interface was developed to the TINKER suite of programs,^63,64 allowing access to the polarizable AMOEBA force field.^33,34 Clearly the ability to interface with already-developed simulation codes will save countless hours of reimplementation and valdiation of methods that are being ported from package to package.

3.3.1 AMBER implementation

In order to implement the MSCALE communication paradigm in the SANDER module of AMBER, a new command line option (-server) was added to tell SANDER that instead of running an energy minimization or molecular dynamics simulation, it should call a special routine that handles MSCALE communication. This routine waits for an MPI message from the master processor (the client) containing the coordinates of the subsystem it has been assigned to calculate. SANDER then calculates the energy and forces as normal using these coordinates and passes these back to the main processor (which is assumed to be running CHARMM). Essentially, the server-side routines (denoted by yellow boxes in Figure 1) were added to SANDER, with necessary changes (e.g. calling SANDER’s energy routine instead of CHARMM’s) being made. In addition to these changes to SANDER, a few small modiffications needed to be made to CHARMM’s MSCAle implementation. A new option (AMBEr) was added to the SUBSystem command alerting CHARMM that the executable being called is AMBER’s SANDER program and that the -server flag should be used as an argument to the specified executable.

To test the implementation, alanine dipeptide simulations were run in standard AMBER and the CHARMM-MSCALE-AMBER combination. In both cases the AMBER99SB force field ⁵² and Generalized Born (GB^OBC) implicit solvent model⁶⁵ were used. Langevin dynamics with a 1 fs step and collsion frequency of 1 ps⁻¹ was used to include solvent friction and temperature control. All bonds involving hydrogen atoms were constrained using the SHAKE ^66,67 algorithm. Simulations were started from a linear conformation and run for 500 ns.

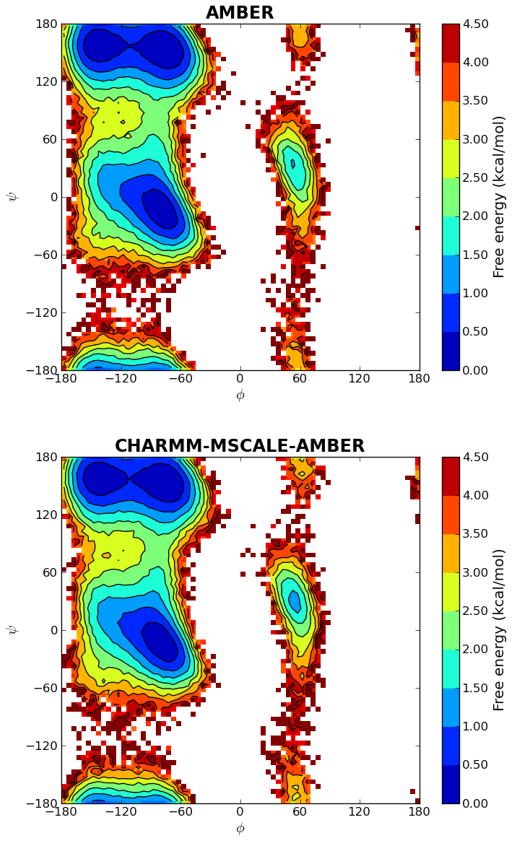
Analysis was performed on snapshots taken at 1 ps intervals. The first 10 ns (10000 snapshots) were discarded during analysis for equilibration. 2D-histograms of the dihedral angles were calculated with a bin size of 5°×5° and free energies were plotted using the populations of each bin by setting the most populated bin at 0 kcal/mol (Figure 4) using the matplotlib module in Python version 2.6. As seen from Figure 4, almost identical free energy profiles and barriers were obtained for all relevant conformations (α, β, P^II and α_L). The minimum for the α_L region has the same free energy for both methods, but the MSCALE plot seems to be slightly broader. This is most likely a sampling issue since the α_L region is visited less frequently than the other dominant conformations.

Figure 4.

Ramachandran free energy landscapes of alanine dipeptide with standard AMBER and CHARMM-MSCALE-AMBER simulations. Both free energy proffiles are very similar. Slight differences are expected even though same force field and solvent method are used since the molecular dynamics runs were performed with different packages with their own implementations of Langevin Dynamics.

3.3.2 TINKER implementation

For the TINKER implementation of the MSCALE communication routines, a new program called mslave was written and linked against the main TINKER library. The only purpose of this program was to manage the communication between the “client” program and TINKER running as a “server”. The functionality is similar to that enabled by the -server option to SANDER that is mentioned above, but because TINKER is implemented as a collection of programs rather than a monolithic binary, it is desirable to have a dedicated program to handle communication. The mslave program uses MPI to receive the coordinates from the client and calls the main TINKER energy and gradient routines and, if desired by the user, the appropriate routines to compute the Hessian. The energy, forces, and (if specified) Hessian are then returned to the client.

As a test case, the alanine dipeptide was again used. Six local minima, as defined by the AMOEBA force field, were located using the SEARCH program in TINKER. These conformations included the C7 equatorial, C7 axial, and C5 conformations used for the PERT test case above (although the AMOEBA minima were at slightly different positions than those found for the CHARMM22 force field). Additionally, three more local minima, denoted B2, aP, and aL, were found. The energies of these structures were evaluated using both TINKER directly and TINKER called from CHARMM through the MSCAle command to ensure equivalent results. Using TINKER through MSCALE, the Hessians were then calculated and ΔG was determined in the harmonic limit. The values of the φ and Ψ angles for the results are reported in table 3. The six TINKER local minima were also each minimized using the CHARMM22 force field with default non-bonded cut-offs; energies and free energies of the resulting CHARMM22 local minima are also reported in table 3.

Table 3.

Initial conformations (obtained using TINKER’s SEARCH program) and final (i.e. minimized) energy differences of the alanine dipeptide. Raw energies and free energies are listed in parentheses. The AMOEBA energies were calculated using the original starting conformations, whose φ and Ψ angles are given. A minimization was performed with the CHARMM22 force field from each starting conformation. The resulting minimized structure was used to calculate the CHARMM22 (C22) energy and free energy. All energies and free energies are in kcal/mol

Conformation	φ	Ψ	ΔE (AMOEBA)	ΔG (AMOEBA)	ΔE (C22)	ΔG (C22)
C7eq	−83.1	76.4	0.00 (−26.97)	0.00 (24.95)	0.00 (−14.10)	0.00 (37.92)
C7ax	72.1	−53.0	2.47 (−24.50)	2.40 (27.35)	2.08 (−12.02)	2.39 (40.31)
C5	−155.1	−162.6	1.20 (−25.77)	0.24 (25.19)	1.13 (−12.97)	0.35 (38.27)
B2	−116.8	10.8	2.78 (−24.19)	1.64 (26.59)	0.00 (−14.10)	0.00 (37.92)
aP	66.1	30.2	4.41 (−22.56)	4.27 (29.22)	2.08 (−12.02)	2.39 (40.31)
aL	−168.2	−35.2	5.54 (−21.43)	5.55 (30.50)	1.13 (−12.97)	0.35 (38.27)

The energies and free energies shown in table 3 clearly illustrate the difference between the CHARMM22 and AMOEBA force fields. Of particular interest was the fact that the B2, aP, and aL minima from AMOEBA were not near any local minima under the CHARMM22 force field. When minimized using CHARMM22, these conformation fell back to the C7eq, C7ax, and C5 conformations respectively. It is not surprising that the AMOEBA force field presents a rougher energy surface with more local minima, since it is a polarizable force field that is more complex than CHARMM22.

3.4 Multiscale Normal Mode Analysis

In addition to supporting the multiscale evaluation of energies and forces, the MSCALE facility also fully supports analytic and finite difference Hessian calculations (i.e. normal mode analysis). In the same way that energies and forces are returned from the server process to the controlling client process, Hessian matrix elements are also passed back and mapped to their full system counterparts. In this way both fully atomistic and mixed model normal mode analyses can be performed. Of particular interest is the ability to combine coarse grained models with all-atom representations, such that the most interesting part of a macromolecular system (e.g. a binding domain) can be represented as all-atom while the larger scaffolding is modeled at a more tractable level. The resulting reduced-dimension Hessian matrix is advantageous as computer memory is limited. However, such a multiscale model is only useful if it can accurately describe both global (i.e. “low” frequency) and local (i.e. “high” frequency) motion at their respective resolutions.

3.4.1 Analyzing normal modes with SHAPEs

The Elastic Network Model (ENM) has proven able to qualitatively capture low frequency, large scale vibrational motion of protein systems.^68,69 It is therefore desirable to use MSCALE to describe the bulk of a system using coarse-grain methods (i.e. ENM) while important areas are treated atomistically.^23,48,70 However, direct comparison between the normal modes of different representations of a structure are problematic because the Hessians and normal mode vectors are different dimensions. Thus, it is not particularly easy to validate this method.

In order to overcome this difficulty, an analysis method was developed that is independent of the length of the mode vectors. This scheme makes use of the shape descriptor facility in CHARMM. Shape descriptors provide a convenient way to calculate the cartesian moments of a given structure. For example, the three first order moments are the mass-weighted averages of the x, y, and z coordinates (the coordinates can be weighted in many ways, but for this work mass weighting was used exclusively). These values provide the center of mass of the system. Likewise, the six second order moments are < x² > – < x >², < y² > – < y >², < z² > – < z >², < xy > – < x >< y >, < xz > – < x >< z >, and < yz > – < y >< z >, which are the moments of inertia of the system.

For this analysis, coarse grained centers were treated as homogeneous spheres of a given radius. Changing the radius of any atom will only affect moments which contain solely even-order terms because the spatial extent of the spheres will increase or decrease by the same amount in the positive and negative directions. Therefore, the changes in the odd order terms will cancel each other out. For this work, a sphere radius of 4 Å was employed as this value best reproduced the spatial extents of the all-atom systems. This is intuitive because in the ENM, beads are centered at C_α positions, and adjacent alpha carbons are generally slightly less than 4 Å away. It is therefore reasonable that 4 Å spheres were found to most closely represent the actual spatial extent of the all-atom system, including side chains.

For each of the modes being analyzed, the derivatives of the shape moments were calculated via finite differences. Large derivatives for low order shape moments indicate large scale global deformation of the system. For example, bending a helical structure aligned parallel to the z-axis in the x direction will result in a significant < xz² > moment change. To make a finite difference estimation, the starting structure was deformed by 0.01 Å along the mode vector and the shape moments were generated for both the original and deformed structure up to the third order. The difference between the original and deformed moment provides an idea of how much the shape moments change for a very small change along the normal mode. The first order moments (and their differences) will be 0 if there is no net translation in the modes being studied.

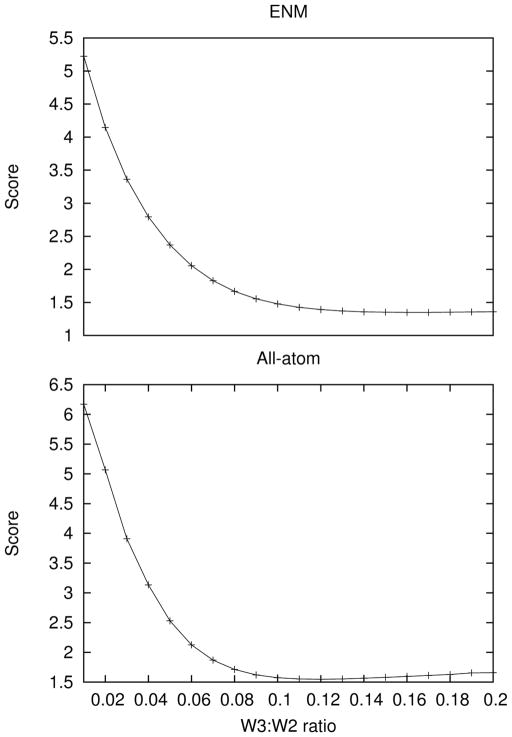
In order to determine ideal weighting of the third order moments relative to the second order ones, the all-atom and ENM modes were generated for a test system, which consisted of a 31 residue α-helix that is described in more detail below. For each of these two representations, the dot products of the shape differences of the five lowest non-rotational/translational modes were calculated. This means that the moments of all-atom mode 1 were treated as a vector, normalized, and dotted against the moments of modes 2 through 5. This was done for each of the five “shape difference vectors” corresponding to the motion of the modes, producing a symmetric 5×5 matrix. Since the shape differences do not form a mutually orthogonal basis set as the normal modes themselves do, the off-diagonal elements will not all be 0 (all diagonal elements will be 1).

A scoring function can be developed by taking the sum of squares of the off-diagonal upper triangle elements of the matrix. In the ideal case this scoring function would yield 0, indicating that the shape differences perfectly describe orthogonal motion of the structure. The value of this scoring function was calculated for various possible weightings of the third order shape moments. The plot for a portion of this parameter space showing the minima for the all-atom and ENM cases is shown in Figure 5. The optimal parameter for this test system is that the third order moments should be weighted by 0.135 relative to the the second order moments (the scoring function was optimal in the all-atom case when the weight was 0.12 and in the ENM case when it was 0.15, so the average of these two values was chosen).

Figure 5.

The sum of squares of the off diagonal upper triangular elements of the 5×5 matrix obtained by dotting the normalized shape difference vectors against one another for the ENM and all-atom cases (see section 3.4.1 for details) as a function of the weighting between the third and second order moments. Since off-diagonal elements are expected to be minimal, the optimal weighting was determined to be 0.12 in each case, but slightly higher for the ENM than the all-atom model.

3.4.2 Results

Normal mode analysis was performed on a 31 residue α-helix taken from the Leucine zipper (PDB code 1GCL).⁷¹ This structure was minimized and all-atom and ENM normal modes were generated. A force constant of 60 kcal=mol Ų was used for adjacent centers and a force constant of 6 kcal=mol Ų was used for all other pairs of centers within a 10 Å cutoff. These values were chosen so that the lowest modes yielded similar vibrational frequencies to those in the all-atom structure. Next, three multiscale models of the structure were generated with: one model having residues 29–31 represented at the all-atom level (multiscale structure I), the next with residues 18–31 so treated (multiscale structure II), and the final one with residues 4–31 treated atomistically (multiscale structure III). The force constants for the ENM parts of these models were the same as those used to generate the pure ENM modes. The five lowest non-rotational/translational modes of each of the five mode sets (the all-atom, ENM, and three multiscale mode sets) were then generated and evaluated using the method described above. Shape derivatives for each of the 25 modes being studied were estimated via finite differences. The dot products of the shape derivatives for each of the lowest five modes of the three multiscale mode sets were then take against the shape derivatives of the five lowest modes of both the all-atom and ENM mode sets. These are given in table 4.

Table 4.

Dot products of the normalized vectors built from the shape moments of the five lowest non-rotational/translational modes of the given representations of a 31 residue λ -helix

All-atom vs. ENM
	1	2	3	4	5
1	−0.797	0.583	−0.739	−0.217	−0.538
2	−0.689	−0.642	0.179	0.045	−0.232
3	0.027	0.720	−0.464	0.649	0.491
4	−0.417	−0.379	0.012	−0.747	−0.731
5	−0.300	−0.209	0.290	0.876	0.230
All-atom vs. All-atom 4–31
	1	2	3	4	5
1	0.217	−0.970	0.230	−0.375	−0.156
2	−0.900	−0.112	−0.774	−0.709	0.022
3	0.208	−0.402	0.725	0.725	0.515
4	−0.058	−0.106	−0.506	−0.890	−0.573
5	−0.590	−0.098	−0.242	−0.069	0.918
All-atom vs. All-atom 18–31
	1	2	3	4	5
1	−0.235	−0.937	0.849	0.216	−0.211
2	0.851	−0.394	−0.035	−0.556	−0.131
3	−0.614	−0.066	0.352	0.799	0.629
4	0.458	−0.402	0.124	−0.651	−0.714
5	0.454	−0.199	−0.323	0.438	0.844
All-atom vs. All-atom 29–31
	1	2	3	4	5
1	−0.730	0.667	−0.715	−0.301	−0.731
2	−0.765	−0.567	0.318	0.046	−0.222
3	0.118	0.701	−0.614	0.619	−0.052
4	−0.470	−0.319	0.178	−0.763	−0.297
5	−0.299	−0.167	0.212	0.857	−0.060
ENM vs. All-atom 4–31
	1	2	3	4	5
1	0.407	0.784	0.295	0.675	−0.009
2	0.731	−0.651	0.878	0.500	0.004
3	−0.424	0.769	−0.657	−0.121	0.285
4	−0.375	0.009	0.089	0.411	0.938
5	−0.110	0.420	0.296	0.692	0.468
ENM vs. All-atom 18–31
	1	2	3	4	5
1	−0.351	0.928	−0.557	0.096	0.125
2	−0.900	−0.320	0.706	0.695	0.115
3	0.589	0.529	−0.958	−0.283	0.230
4	0.088	0.088	−0.314	0.643	0.962
5	−0.180	0.603	−0.295	0.259	0.526
ENM vs. All-atom 29–31
	1	2	3	4	5
1	0.993	−0.156	0.314	0.089	0.679
2	0.070	0.993	−0.875	−0.023	−0.296
3	0.323	−0.785	0.973	0.274	0.443
4	0.052	0.033	0.074	0.996	0.110
5	0.509	−0.045	0.073	0.568	0.820

The results indicate that multiscale modes qualitatively reproduce the same types of deformations as the all-atom and ENM modes. When visualizing the motion of the structure as it is deformed along each mode, the five low frequency modes represent either a bending or twisting movement of the helix. The modes which yield bending and twisting movements are not the same for each mode set, however, and this can be observed from the results. For example, looking at the comparison between the shape derivatives of the ENM structure and multiscale structure II, the highest overlaps are reversed between modes one and two. Taking such re-ordering of modes into account, the shape derivatives for the multiscale structure where more residues are simulated at the all-atom level appear to overlap better with the shape derivatives for the all-atom structure; likewise, the shape derivatives for the structure where the fewest residues are simulated atomistically seem to overlap better with the ENM shape derivatives. The shape derivatives for multiscale structure II, which is split roughly half and half between all-atom and coarse-grained representation, represent a middle ground.

In order to characterize these overlaps in a quantitative manner, a new scoring method was developed. For each row of the matrices given in table 4, a score was generated by summing the squares of all of the elements except for the highest element in each row. This implicitly assumes that this element should be on the diagonal if there was no mode reordering. This method therefore yields the sum of squares of what would be the off-diagonal elements in this case. The results of the scoring function are given in table 5. As expected, the shape derivatives of multiscale structure I have the best score function when compared to the ENM shape derivatives. Likewise, the shape derivatives of multiscale structure III score best against the all-atom shape derivatives. Interestingly, multiscale structure II is the worst scorer against the all-atom structure, but scores in the middle against the ENM structure, as expected. This indicates that the low frequency modes of this structure are much closer to those of the ENM structure than they are to the all-atom motions. As is to be expected, the scoring function is the worst when the ENM shape derivatives are compared to the all-atom ones. Furthermore, this method will not take into account motion that does not change the spatial extents of the molecule (e.g. a pure twisting motion of the helix that does not incorporate any bending).

Table 5.

Score function of off diagonal elements for each of the three multiscale models compared to the all-atom and ENM shapes. The score of the all-atom versus ENM shape derivatives is 3.722

	All-Atom	ENM
All-atom 29–31	3.440	3.053
All-atom 18–31	3.602	3.305
All-atom 4–31	3.394	3.436

4 Conclusions

This work introduces a general concurrent multiscale modeling framework and describes its implementation into CHARMM and several other classical and quantum mechanical packages. This approach, dubbed MSCALE, generalizes the ideas underlying both additive and subtractive multiscale schemes. Using a completely generalized implementation, this functionality allows coupling of multiple, independent but connected calculations with each being a separate single or group of processes. This allows for arbitrary combinations of additive and subtractive schemes of any level of complexity. General symmetry and triclinicity is supported allowing periodic systems with contant pressure and temperature; an example will be given in future work. One of the most attractive features of the MSCALE framework is the relative ease of implementation, since MSCALE is based on the standard MPI communication protocol. This allows easy external access to the MSCALE framework, making the method widely available to the computational community. As multiscale modeling has increasingly become integral to biophysical simulations, the need for generalized and open software has likewise gained importance; MSCALE was created to fill this void and bring together functionality previously isolated in separate programs.

We report four examples that demonstrate the efficacy of the MSCALE approach and implementation. Perhaps the most straightforward use of such a tool is to perform subtractive QM/MM and QM/QM calculations (i.e. ONIOM-type). Although this is an easy way to apply multiscale modeling techniques, it is clear the limit of accuracy is at the low level of theory and thus care must be taken to choose computational methods appropriately. Secondly, we detail the implementation of MSCAle with CHARMM’s free energy perturbation module (PERT) and showcase the application of this with multiple force fields (CHARMM and AMBER99SB). Using this feature, vacuum and solvation free energies of the alanine dipeptide were computed. These were previously calculated for an earlier version of the AMBER force field in a previous study,⁶¹ however, MSCALE’s functionality allowed the calculation to be performed in a more straightforward manner, using existing CHARMM functionality. Thirdly, porting of the MSCALE communication paradigm was demonstrated by connecting AMBER’s SANDER module to CHARMM and using the implicit GB^OBC solvation model (only implemented in SANDER) with the CHARMM potential. Furthermore, an implementation of MSCALE for the TINKER program was developed, allowing CHARMM access to the AMOEBA force field through this interface. Finally, multiscale normal mode analysis (NMA) was carried out combining ENM and classical all-atom methodologies. This is interesting as the algorithms needed to perform atomistic NMA have not kept pace with computational hardware. Although various techniques have been developed for simplifying the Hessian calculation of large system, they generally require either numerical estimation or fixing or integrating out part of the system’s motion. Therefore, combining unrestrained coarse grain and all-atom methods and achieving near atomistic quality results is highly desirable; this has been accomplished and demonstrated within the current framework.

Although this work significantly improves the tools available to the computational community, there is still a wide variety of possibilities for future work. Ongoing is an effort to integrate MSCALE with CHARMM’s distributed replica methods (REPD), which will allow this facility to be used with chain-of-states or string methods within CHARMM,^72–74 or to facilitate the use of the MSCAle command with replica exchange. To give another example, there is much work that needs to be done to characterize the relationships between normal mode vectors produced by different multiscale models. As mentioned above, many analysis techniques do not deal with different ly sized mode vectors, making these difficult to compare directly. Similar issues arise for different types of calculations. Further consideration of the inherent trade-offs involved in multiscale modeling is therefore an important area of future study.