A model of cellular dosimetry for macroscopic tumors in radiopharmaceutical therapy

Abstract

Purpose: In the radiopharmaceutical therapy approach to the fight against cancer, in particular when it comes to translating laboratory results to the clinical setting, modeling has served as an invaluable tool for guidance and for understanding the processes operating at the cellular level and how these relate to macroscopic observables. Tumor control probability (TCP) is the dosimetric end point quantity of choice which relates to experimental and clinical data: it requires knowledge of individual cellular absorbed doses since it depends on the assessment of the treatment’s ability to kill each and every cell. Macroscopic tumors, seen in both clinical and experimental studies, contain too many cells to be modeled individually in Monte Carlo simulation; yet, in particular for low ratios of decays to cells, a cell-based model that does not smooth away statistical considerations associated with low activity is a necessity. The authors present here an adaptation of the simple sphere-based model from which cellular level dosimetry for macroscopic tumors and their end point quantities, such as TCP, may be extrapolated more reliably.

Methods: Ten homogenous spheres representing tumors of different sizes were constructed in GEANT4. The radionuclide ¹³¹I was randomly allowed to decay for each model size and for seven different ratios of number of decays to number of cells, N_r: 1000, 500, 200, 100, 50, 20, and 10 decays per cell. The deposited energy was collected in radial bins and divided by the bin mass to obtain the average bin absorbed dose. To simulate a cellular model, the number of cells present in each bin was calculated and an absorbed dose attributed to each cell equal to the bin average absorbed dose with a randomly determined adjustment based on a Gaussian probability distribution with a width equal to the statistical uncertainty consistent with the ratio of decays to cells, i.e., equal to ^N_r-1∕2. From dose volume histograms the surviving fraction of cells, equivalent uniform dose (EUD), and TCP for the different scenarios were calculated. Comparably sized spherical models containing individual spherical cells (15 μm diameter) in hexagonal lattices were constructed, and Monte Carlo simulations were executed for all the same previous scenarios. The dosimetric quantities were calculated and compared to the adjusted simple sphere model results. The model was then applied to the Bortezomib-induced enzyme-targeted radiotherapy (BETR) strategy of targeting Epstein-Barr virus (EBV)-expressing cancers.

Results: The TCP values were comparable to within 2% between the adjusted simple sphere and full cellular models. Additionally, models were generated for a nonuniform distribution of activity, and results were compared between the adjusted spherical and cellular models with similar comparability. The TCP values from the experimental macroscopic tumor results were consistent with the experimental observations for BETR-treated 1 g EBV-expressing lymphoma tumors in mice.

Conclusions: The adjusted spherical model presented here provides more accurate TCP values than simple spheres, on par with full cellular Monte Carlo simulations while maintaining the simplicity of the simple sphere model. This model provides a basis for complementing and understanding laboratory and clinical results pertaining to radiopharmaceutical therapy.

INTRODUCTION

Targeting of radiopharmaceuticals to specific tissues provides an important tool for the therapy of malignancy. Often tumor targeting strategies seem to work at the macroscopic level, but it is unclear whether the tumor is completely killed—macroscopic dosimetric quantities such as average tumor absorbed dose values are not sufficient to explain the fate of each and every individual tumor cell. A dosimetric quantity does exist, which translates the fate of the individual tumor cells into an assessment of a macroscopic tumor’s treatment outcome, namely, the tumor control probability (TCP), but this quantity requires knowledge of the absorbed doses at the level of the individual cells. As yet, imaging and other quantitative methodologies are unable to provide absorbed dose assessments of all individual cells in a growing tumor, hence the recourse to modeling and Monte Carlo simulation to complement measurements. However, running Monte Carlo simulation and cell-level dosimetry for macroscopic tumors is a logistical challenge. We present a model that enables the calculation of cellular-based dosimetric end point quantities, such as TCP, surviving fraction of cells, and the equivalent uniform dose (EUD) from simple macroscopic simulations (spheres) by the simple adjunct of a random statistical fluctuation per cell in the local absorbed dose. We compare this model to a range of similar-sized complete cellular Monte Carlo simulations for validation and apply the model to results obtained in mice treated for lymphoma using the Bortezomib-induced enzyme-targeted radiotherapy (BETR) strategy and the ¹³¹I radionuclide.

Modeling

Modeling of tumor absorbed dose and TCP and theoretical dependencies based on tumor size, uptake distribution and radionuclide have been studied extensively,^{1, 2, 3, 4, 5, 6, 7, 8, 9} though less frequently with any direct link to experimental data.^{10, 11, 12} The 10¹¹–10¹⁴ decays in 10⁸–10¹¹ cells necessary for a fully cellular simulation are beyond the time frame for a reasonable Monte Carlo simulation and would strain the file storage abilities of any cluster. The traditional remedy consists of using point kernels obtained from Monte Carlo distributions, convoluted with activity distribution and using fast Fourier transforms to collect the energy in the volumes of interest.^{1, 9, 13} However, this method relies on a statistically significant number of decays and a statistically significant ratio of number of decays to number of active cells in order that the radial distribution of the Monte Carlo-derived point kernel be reasonably valid isotropically and on an individual cell basis. Since the basis of comparison to experimental data is often TCP, which is most affected by the shape of the cell absorbed dose distribution rather than the average cell absorbed dose, especially by the outliers on the lower end of the distribution,^{2, 3} a method that does not take statistical averages is preferred.

Import

By introducing a randomly generated cell-by-cell statistical fluctuation around a binned average absorbed dose value based on the ratio of number of events (decays) to number of cells, a model is created which overcomes this issue and provides results much more in keeping with the individual cell-based model while maintaining the simplicity and convenience of the simple sphere model, thus providing a valuable asset in the assessment and development of new radiopharmaceutical therapy strategies.

METHODS

Approach

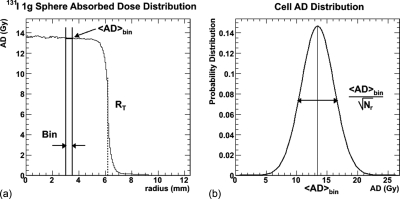
We present a spherical tumor model that enables the calculation of cellular-based dosimetric end point quantities, such as TCP and EUD. By assigning a number of cells to each radial bin in the sphere and assuming that the distribution of cell absorbed doses is Gaussian and centered on the bin absorbed dose average, randomly determined specific absorbed doses are assigned to each cell according to the Gaussian assumption and the dosimetric quantities are calculated. Figure 1 illustrates this concept. These adjusted spherical models are then compared to explicitly cellular models to validate the technique.

Figure 1.

Illustration of the adjusted spherical model method. (a) Binned absorbed dose as a function of tumor radial position for ¹³¹I in a 1 g tumor (of radius R_T). The thick horizontal line shows the average absorbed dose in a particular bin, delimited by the vertical lines (bin size is larger than typical for illustrative purposes). (b) The individual cell absorbed dose distribution, for the chosen bin, centered on the average absorbed dose value. The cell absorbed doses are determined from a Gaussian probability distribution, with a width determined by the number of events per cell. The contribution of this methodology is that, in the assessment of TCP for the cells in the spherical shell identified in (b), the single mean value that would be used for the tumor cell population is replaced by the Gaussian absorbed dose distribution shown in (b). Since TCP is impacted most by the population of cells receiving lower absorbed doses, this replacement is essential in properly determining the TCP of each shell and therefore of the tumor, especially at low tumor activity concentrations.

Monte Carlo

GEANT4 is a general-purpose Monte Carlo program developed in the context of simulating high energy physics experiments.¹⁴ It is seeing increased use in other fields, including medical physics, for which the specific GATE interface has been developed. Its use has been validated in the field of medical physics for ¹³¹I (Refs. ^{15, 16}) by comparison with other often-used Monte Carlo codes [electron gamma shower (egs), mcnp].

GEANT4 allows the simulation of a comprehensive set of physics effects, such as hadronic, electromagnetic, and optical processes. Electromagnetic interactions down to energies smaller than 1 keV may be simulated, and the output can be stored in ordered sets of chosen parameters, known as “n-tuples,” for further analysis. Comparisons between monoenergetic photon and electron energy deposition in GEANT and MCNP has been carried out extensively.^{17, 18}GEANT4 modeling has been implemented in radioprotection studies¹⁹ and in clinical cases of radioimmunotherapy²⁰ as a supplement to measurable data.

As an additional assessment, a direct comparison between S-values calculated for a range of unit density spheres was made between geant4 (Ref. ¹⁶) and 3D-RD,^{21, 22, 23} a personalized dosimetry package based on the EGS Monte Carlo. The comparison was also made to OLINDA/EXM,²⁴ a commercially available software based on the MIRD methodology²⁵ (see also the updated formalism²⁶), which converts time-integrated activity into absorbed dose by using pre-established S-values calculated using the MCNP Monte Carlo and the Cristy–Eckermann phantoms.²⁷ For tumors, OLINDA/EXM offers a range of unit density sphere models that were used as the basis for comparison.

Spherical model

Ten different sizes of simple spheres with uniform distributions of ¹³¹I with a density and composition of water were simulated and 10 × 10⁶ events were run for each simulation, enough to provide stable values for the different bin-averaged absorbed doses. The choices for the different sphere (tumor) radii, R_T, were made based on the choice of the number of cells, N_c, in the equivalent fully cellular models; the different values of N_c and R_T are listed in Table TABLE I.. The spheres were centered in 10 cm of water in all directions to allow for backscatter.

Table 1.

Tumor radius R_T (in units of cell radii and micrometers), total number of cells, N_c, and tumor mass, M_T, for each model size.

Nomenclature	Nc	RT (cells)	RT (μm)	MT (μg)
1k	984	11	82.5	1.74
2k	2036	14	105	3.60
5k	5066	19	142.5	8.95
10k	10,235	24	180	18.1
20k	19,979	30	225	35.3
50k	51,046	41	307.5	90.2
100k	98,252	51	382.5	174
200k	203,346	65	487.5	359
500k	504,526	88	660	892
1M	1,012,668	111	832.5	1790

Adaptation

The following steps relate the conversion of the simple spheres into an approximation of a cellular model, i.e., the adapted spherical model:

• 1.
  The total number of cells, N_c, must be estimated; often, a simple ratio of volumes suffices:

  $$N_c\cong \frac{V_T}{V_c}=f_{\mathit{occ}}\frac{4∕3\pi R_T^3}{4∕3\pi R_c^3},$$ (1)

  where f_occ is the fraction of occupancy for a hexagonal lattice of cells (0.74), R_T and R_c are the radii of the tumor and cell, respectively.
• 2.
  the ratio, N_r, of the number of decays to the number of total cells in the tumor is established:

  $$N_r=\frac{N_e}{N_c},$$ (2)

  where N_e is the total number of events (or nuclear transformations) obtained, e.g., by taking the integral of the activity in the tumor. For the comparisons with the cellular models, a range of values for N_r was chosen: N_r = 10, 20, 50, 100, 200, 500, and 1000, obtained by a single simulation of 1000 events per cell and considering only the appropriate fraction of decays for each N_r.
• 3.
  For each radial bin, i, the number of cells per radial bin, N_ci, of the homogenous spheres are calculated:

  $$N_{\mathit{ci}}=\frac{4∕3\pi (R_i^3-R_{i+1}^3)}{4∕3\pi R_T^3}{N}_c.$$ (3)
• 4.
  The absorbed dose for the radial bin, D_i, is calculated and scaled to the number of events, N_e, in the tumor, giving the average cell absorbed dose within each radial bin, i:

  $$D_i=\frac{E_i}{4∕3\pi (R_i^3-R_{i+1}^3)}·\frac{N_e}{N_{\mathit{MC}}},$$ (4)

  where E_i is the energy deposited in the radial bin and N_MC is the number of Monte Carlo events used for the simple sphere (in this case, 10 × 10⁶).
• 5.
  For each cell, j, within the bin, an absorbed dose value, D_j, is randomly determined from a Gaussian probability distribution centered on the simple sphere bin average and with a width equal to the statistical uncertainty associated with a numeric value equal to the event-to-number of cell ratio, N_r (see Fig. 1):

  $$D_j=D_i(1+\mathit{Rnd}\left(\frac{1}{\sqrt{N_r}}\right)).$$ (5)

From the individual absorbed dose values, the dosimetric quantities of surviving cells, TCP and EUD were calculated (see below).

Cellular model

Using geant4, spherical tumor models of spherical cells (of radius R_c = 7.5 μm) arranged in a hexagonal lattice (74% occupied volume vs 52% for a cubic lattice) were constructed; only those cells positioned at a radius of less than the tumor radius, R_T, were considered part of the tumor. For each model, 1000 atoms of ¹³¹I per cell were placed in the cells and allowed to decay. The event information including the event number was stored, allowing for the assembly of data for differing numbers of events to cells ratios, specifically, as with the adjusted spherical models, the energy deposition was tallied in each tumor cell after seven different ¹³¹I decays-to-total number of cells ratios: N_r = 10, 20, 50, 100, 200, 500, and 1000. The cells and the interstitial spaces were filled with water, and the matrix was surrounded by water out to 10 cm to allow for backscatter. The results were divided by the cell mass to obtain absorbed dose values for all scenarios.

Activity distribution

The localization of each decay was determined randomly (each cell having an equal probability); consequently, the distribution of the number of decays for each active cell is also based on a Gaussian probability distribution centered on the average number of decays per cell, with a width equal to the statistical uncertainty from a number equal to the ratio of number of decays per active cell (^N_r-1∕2). The position of the decay within each cell is determined randomly such that the distribution of activity within each cell is uniform.

Dose cell histograms

The energy deposited in each cell was collected and the absorbed dose to each cell in the Monte Carlo calculated after 1000 events per number of cells by dividing by the cell mass. The absorbed doses for different number of decays to number of cells ratios were also tabulated (N_r = 1000, 500, 200, 100, 50, 20, and 10).

Dosimetric quantities

The cellular absorbed dose values from both models were used to calculate the number of surviving cells. According to the linear-quadratic model,²⁸ the surviving fraction (SF) of cells receiving an absorbed dose, D, is

$$\mathit{SF}=e^{-\alpha D-\beta D^2},$$ (6)

where α and β are the linear-quadratic radiosensitivity parameters, specific to a particular tissue or disease type. Here, for comparative purposes, the values were set to those for lymphoma: 0.451 Gy⁻¹ and 0.051 Gy⁻², respectively.²⁹ These values are relatively large for tumor radiobiological parameters and reflect a probability of at least partial clinical response for absorbed doses as low as 2 Gy. Most tumor cells are more radioresistant and would have correspondingly smaller α and β parameters, although an α/β ratio on the order of 10 is typical of tumors as opposed to normal tissue cells with α/β ratios of 1–2 Gy.

From basic statistical principles, the surviving fraction of a large population of cells is equal to the survival probability (SP) of an individual cell. For a population of cells receiving different cell absorbed doses, D_i, the surviving fraction becomes

$$\mathit{SF}=\frac{{\sum }_{i=1}^{N_c}S{P}_i}{N_c},$$ (7)

where N_c is the total number of cells. The EUD is defined as the single uniform absorbed dose that could be delivered to a cell population to obtain the same surviving fraction as from the nonuniform absorbed dose distribution:³⁰

$$e^{-\alpha \mathit{EUD}-\beta \mathit{EU}{D}^2}=\frac{{\sum }_{i=1}^{N_c}{e}^{-\alpha D_i-\beta D_i^2}}{N_c}.$$ (8)

Solving for EUD and discarding the extraneous (negative) solution in the quadratic formula gives:

$$\mathit{EUD}=\frac{1}{2\beta }(-\alpha +\sqrt{{\alpha }^2-4\beta ·\mathit{ln}({\sum }_{i=1}^{N_c}{e}^{-\alpha D_i-\beta D_i^2}∕N_c)}).$$ (9)

The TCP is calculated with the formula:

$$TCP={\displaystyle \prod _{i=1}^{N_c}(1-S{P}_i)},$$ (10)

that is, the TCP is the probability that all of the tumor cells are killed.

Model comparison

The surviving fraction, EUD and TCP results from the adapted simple sphere model are compared to the hexagonal cellular model Monte Carlo results for all scenarios. For these studies, Eq. 1 in the simple spherical model is bypassed as the number of events and cells are already known from the hexagonal lattice model.

As an additional test, to approximate comparisons for models with a greater number of total events without running the full simulations, the α and β values were varied in the surviving fraction, EUD and TCP calculations of the largest model (1M cells). Since EUD and TCP are greatly affected by the lowest outliers in the absorbed dose distribution,^{2, 3} and all follow from Eq. 6, a simple method of approximating an x-fold increase in absorbed dose is to multiply α by the desired size difference and β by the square of that same difference, thus artificially providing a greater range of absorbed dose variability than that provided by the Monte Carlo simulations.

Nonuniform activity—Exponential penetration

As a second step, a nonuniform distribution of activity was chosen, one that might reflect a more realistic biologically driven distribution, namely: an activity, A(r), with exponentially decreasing concentration as a function of penetration from the surface with a nonactive (necrotic) core. This distribution is represented by the following formula:

$$\begin{array}{c}\left\{\begin{array}{c}A(r)\propto e^{(r-R_T)∕\theta },r>R_I\\ A(r)=0,r\le R_I\end{array}\right\}\end{array},$$ (11)

where R_T is the tumor radius, θ is the penetration parameter, and R_I is the radius of the necrotic core. This activity distribution was applied to both models, and the results were also compared.

Experimental application

Finally, the simple sphere model was applied to an experimental scenario for 1 g lymphoma tumors in mice treated with [¹³¹I]2′-fluoro-2′-deoxy-β-D-5-iodouracilarabinofuranoside ([¹³¹I]FIAU) using the BETR treatment strategy,^{31, 32} and the results were compared to the experimental data.³¹

The BETR treatment strategy has been described in previous publications; briefly, it is founded on the well established herpes simplex virus-thymidine kinase/[*I]FIAU (HSV-TK/FIAU) system,^{33, 34, 35, 36} which has been used as a reporter system for gene therapy studies and has been approved for therapeutic clinical trials using [¹³¹I]FIAU.

Epstein-Barr virus (EBV)-associated cancers harbor a viral TK gene obviating the need for tumor cell transfection with HSV-TK. The viral TK is not expressed unless lytic cycle viral gene expression is activated. Bortezomib, an FDA approved proteasome inhibitor used in therapy for multiple myeloma and mantle cell lymphoma, is effective at activating expression of the viral TK, thereby enabling selective targeting of virally infected cancers with [¹³¹I]FIAU.^{31, 32}

The ratio of the number of decays in the tumor for 37 MBq (1 mCi) of administered activity to the number of total cells in a 1 g tumor was established. The total number of ¹³¹I decays was approximated by

$$N_e={\int }_0^{\infty }A(t)\mathit{dt}\cong \frac{{A_0}_{(\mathit{tumor})}}{{\lambda }_{\mathit{eff}}}=\frac{A_0·f_{\mathit{tu}}·m·T_{\mathit{eff}}}{\ln (2)},$$ (12)

where A₀ is the initial injected activity, f_tu is the fraction of tumor uptake in units of percentage of ID per gram, measured to be 2%, m is the tumor mass (1 g), and T_eff is the effective half-life of ¹³¹I in the tumor, considered to be the physical half-life of ¹³¹I (8.02 days) modulated by the biological half-life taken to be 30 days, for an effective half-life of 6.33 days.

RESULTS

Monte Carlo comparison

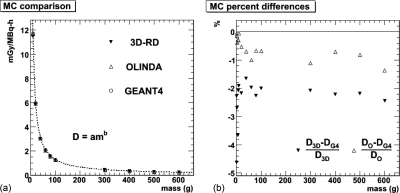
The results for the direct comparison between geant4, 3D-RD, and OLINDA/EXM, for ¹³¹I-filled homogenous spheres ranging in size from 1 to 600 g are shown in Fig. 2. Each sphere was simulated with 1 × 10⁶ events for each Monte Carlo type. The difference between GEANT4 and OLINDA/EXM was (0.59% ± 0.38%) averaged over all spheres [Fig. 2b]; the difference between GEANT4 and 3D-RD was (2.42% ± 0.74%). Note that for the small mass values, the voxelization of 3D-RD contributes to the observed differences.

Figure 2.

(a) S-values obtained from three different sources for 1 × 10⁶ events: geant4 (empty circle), olinda (empty triangle), and 3D-RD EGS (triangle) for ¹³¹I-filled homogenous spheres ranging in size from 1 to 600 g. The dotted line is a power law fit (D = am^b) to the olinda data. (b) The difference (in percentage) between the olinda/exm and geant4 results (empty circle) as well as the difference between the 3D-RD and geant4 results (empty triangle).

Dose cell histogram comparison

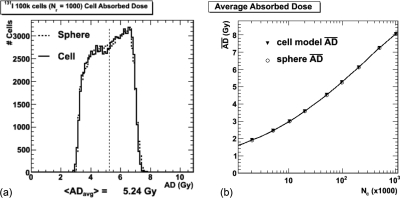
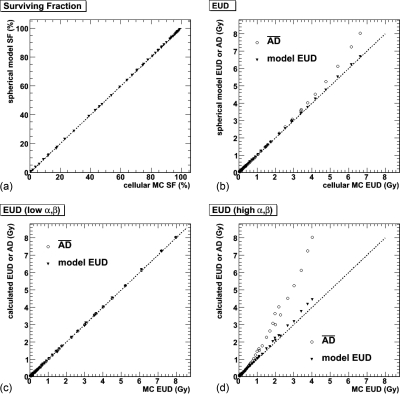
The dose cell histograms from both models for the 1000 events-to-number-of-cells ratio (N_r) scenario for the 100k cell number is shown in Fig. 3a. A selected set of average and root-mean-square (rms) absorbed dose values from the histograms are given in Table TABLE II.. The average absorbed doses from the hexagonal lattice cellular model and the simple spheres are compared in Fig. 3b.

Figure 3.

Global absorbed dose (AD) results. (a) The cell absorbed dose histograms for the 1000 decays-per-cell ratio (N_r) and 100k cell scenario. (b) Comparison of the average absorbed dose from the MC-simulated hexagonal lattice models with the simple spheres.

Table 2.

Monte Carlo results from a selected group of scenarios.

Nc	Events per cell (Nr)	AD avg (Gy)	AD rms (Gy)	SF (%)	EUD (Gy)	Gauss Avg (%)	Gauss rms (%)	R2
10k	10	0.03	0.01	98.7	0.03	−0.26	31.2	0.977
10k	100	0.30	0.07	87.0	0.30	−0.04	10.6	0.993
10k	1000	3.00	0.62	17.9	2.88	−0.04	3.75	0.995
20k	10	0.04	0.01	98.6	0.03	−0.05	30.8	0.981
20k	100	0.36	0.08	84.8	0.35	−0.03	10.6	0.995
20k	1000	3.57	0.75	12.1	3.38	0.02	3.78	0.996
50k	10	0.05	0.02	97.9	0.05	0.29	30.8	0.986
50k	100	0.45	0.10	80.8	0.45	0.06	10.6	0.996
50k	1000	4.51	0.95	6.2	4.18	0.12	3.76	0.996
100k	10	0.05	0.02	97.7	0.05	0.14	31.4	0.990
100k	100	0.52	0.12	77.9	0.52	0.04	10.6	0.996
100k	1000	5.24	1.12	3.71	4.75	0.01	3.79	0.997
200k	10	0.06	0.02	97.2	0.06	0.06	30.7	0.989
200k	100	0.61	0.14	74.5	0.61	0.07	10.8	0.997
200k	1000	6.12	1.32	1.98	5.40	0.04	3.83	0.997
500k	10	0.07	0.03	96.8	0.07	0.03	33.2	0.991
500k	100	0.72	0.17	70.4	0.72	0.09	11.2	0.997
500k	1000	7.24	1.58	0.91	6.14	0.07	4.41	0.998
1M	10	0.08	0.03	96.4	0.08	0.04	34.8	0.991
1M	100	0.81	0.19	67.5	0.80	0.07	11.6	0.997
1M	1000	8.03	1.75	0.52	6.65	−0.21	3.97	0.998

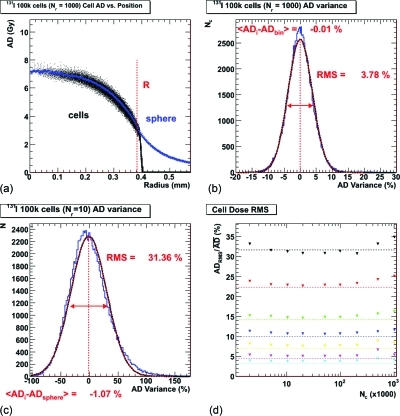
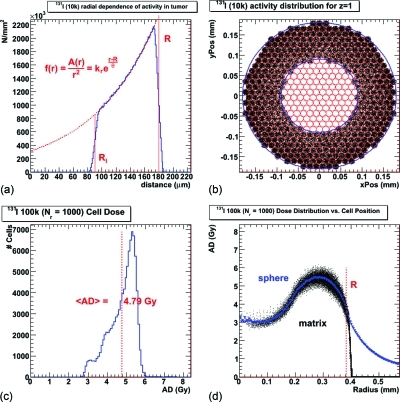
Figure 4a shows the same distributions as in Fig. 3a as a function of radial position of the cell in the tumor. Additionally, the scaled absorbed dose values as a function of radius for the same-sized homogenous spheres are shown on the same plot.

Figure 4.

(a) The cell absorbed dose (AD) as a function of radial position in the tumor for the same scenario as (Fig. 3a) (black dots) and the same-sized simple sphere radially binned absorbed dose values (blue triangles). The black dots tail off significantly outside the tumor, as the algorithms perform incomplete absorbed dose calculations for cells between radii of R_T and R_T + R_c. (b) The same cell absorbed dose distribution with respect to the simple sphere’s radial binned average (blue histogram) and the Gaussian fit (red dotted line). (c) A similar cell absorbed dose distribution for a different scenario: 100k cells but with a 10 decays-per-cell ratio (N_r). (d) The rms values of the Gaussian fits obtained for the seven different events-to-cells ratios (N_r) as a function of model cell number: 10 (black), 20 (red), 50 (green), 100 (blue), 200 (yellow), 500 (pink), and 1000 (light blue). The dotted lines show the statistical uncertainty value for the ratio values.

Figures 4b, 4c show the results of the difference between the individual cell absorbed doses from the cellular model and the radial bin absorbed doses from the spherical model; for [Fig. 4b] the same data is illustrated as shown in Figs. 3a, 4a, and in [Fig. 4c] the 100k cell and ratio of decays-to-cells, N_r, equal to 10 scenario is shown. The distributions appear to be Gaussian to first order and fits with a Gaussian function are made to the data. The width of the Gaussian fits (the rms values) for all scenarios are shown in Fig. 4d as a function of tumor size, each different color representing a different ratio of events to cells (N_r). The width of the Gaussian fits decrease as a function of tumor size quite quickly to gravitate to a value that depends on the ratio of events to cells, N_r, and is remarkably close to the width that would be expected from a strictly statistical standpoint. These values equal to ^N_r-1∕2 are represented by the colored dotted lines. This particular figure illustrates well the motivation and justification for the adjusted spherical model. Results from a selected range of scenarios, including average absorbed dose, surviving fraction, and absorbed dose rms as well as the R² values for the Gaussian fits are given in Table TABLE II., where it can be seen that the fits to the lower N_r values are slightly worse than those fit to the higher N_r values.

Dosimetric quantity comparison

The surviving fraction and EUD comparisons between the two models are illustrated in Figs. 5a, 5b. Additionally, the average absorbed dose is plotted in the EUD graph for comparative purposes. Figures 5c, 5d show the same results for α (and β) values multiplied by a factor of 0.1 (0.01) and 10 (100), respectively.

Figure 5.

Comparison of calculated dosimetric values from simple homogenous spheres and Monte Carlo (MC) results. (a) The model-calculated SF compared to the individual cell Monte Carlo surviving fraction. The dotted line represents equivalence. (b) A similar comparison for the EUD, where the round circles show the average absorbed dose, that is, the simple sphere values before statistical adjustment. (c) and (d) The same EUD comparisons for different α and β values: for (c), α = 0.0451 Gy⁻¹ and β = 0.0051 Gy⁻²; for (d), α = 4.51 Gy⁻¹ and β = 5.1 Gy⁻².

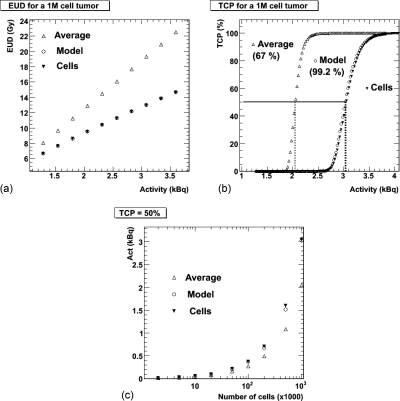
Since the point of comparison with experimental data is the TCP and the experimental input is the amount of administered activity, Figs. 6a, 6b show the EUD and TCP, respectively, as a function of activity in the tumor for the 1M simulation. These results are obtained by converting the number of events per Monte Carlo simulation into cumulated activity and, by assuming an effective half-life of 6.33 days based on experimental considerations, converting to activity. The cell absorbed dose results are then scaled incrementally as a function of increasing tumor activity, again assuming the 2% tumor uptake obtained in the BETR experiments. The basis for the comparison of model TCP to cellular TCP is made for the amount of activity necessary to obtain a TCP of 50%. These results are given in Table TABLE III. and are illustrated in Fig. 6c. Figures 6b, 6c illustrate the consequence and importance of the addition of the statistical cell-by-cell absorbed dose fluctuation to the simple spherical model: the adjusted spherical model activity values predicted to achieve tumor control are within a few percents of the full cellular model Monte Carlo values, while the average bin absorbed dose-based results predict only two thirds of the activity necessary to achieve tumor control.

Figure 6.

(a) and (b) Dosimetric results as a function of activity in the tumor for the largest (1M) model. The tumor activity corresponds to 2% of the injected activity in the present study (Ref. ³¹). (a) EUD and (b) TCP. The combined TCP = 50% results from all models are illustrated in (c).

Table 3.

Administered activity required to achieve 50% TCP for the homogenous activity model and for the exponential decay [Eq. (11)] model, denoted by (exp).

Nc	Model TCP activity (Bq)	Avg. AD TCP activity (Bq)	Cellular TCP activity (Bq)
1k	8.25	6.73	8.19
2k	14.9	12.0	14.9
5k	31.7	24.8	31.4
10k	54.5	42.8	55.8
20k	98.5	74.0	97.4
50k	207	157	213
100k	374	272	373
200k	677	495	703
500k	1.52 kBq	1.09 kBq	1.60 kBq
1M	3.03 kBq	2.05 kBq	3.05 kBq
10k (exp)	53.7	47.0	54.0
100k (exp)	389	298	389

Exponential penetration activity distribution

An identical methodology was implemented for the cell (and simple sphere) activity distribution based on a biological model of exponential penetration from the surface with a necrotic core [Eq. 11]. Figure 7 illustrates results pertinent to this activity distribution. The distribution of activity within the tumor is shown in Fig. 7a; a cross-section of activity distribution for a specific layer of the hexagonal lattice is shown in Fig. 7b for the 10k cell scenario. The dose cell histogram for the 100k scenario is shown in Fig. 7c, and the radial dependence of the cell absorbed dose compared to the binned simple sphere absorbed dose is given in Fig. 7d. Table TABLE IV. shows all the dosimetric results for the exponential penetration simulations, except for the TCP results which are in Table TABLE III..

Figure 7.

The exponential penetration model given by Eq. (11). (a) The tumor radial activity in the simple sphere where the dotted red line shows the fit to the equation. (b) A layer of the cellular hexagonal lattice with activity in the individual cells represented by the dots. The red lines show the outlines of the individual cells. The outer blue line shows the limit of the tumor, while the inner blue line shows the limit of the activity penetration. (c) The cellular absorbed dose distribution, which is shown as a function of tumor radius and compared to the simple sphere radial absorbed dose in (d), similar to Fig. 4a for the homogenous model. The minor inconsistencies in the low radial bin average absorbed dose values (blue triangles) are due to the low statistics in those bins.

Table 4.

Monte Carlo results from a selected group of scenarios for the exponentially penetrating activity model.

Nc	Ratio (Nr)	AD avg (Gy)	AD rms (Gy)	SF (%)	EUD (Gy)	Gauss avg (%)	Gauss rms (%)	R2
10k	10	0.03	0.01	98.77	0.03	0.16	31.60	0.970
10k	20	0.05	0.01	97.55	0.05	−0.04	23.49	0.976
10k	50	0.14	0.03	93.93	0.14	0.01	15.40	0.987
10k	100	0.27	0.04	88.07	0.27	−0.01	11.15	0.992
10k	200	0.55	0.08	76.97	0.55	0.09	8.10	0.994
10k	500	1.37	0.18	49.17	1.36	0.22	5.39	0.998
10k	1000	2.74	0.34	20.33	2.71	0.19	4.10	0.999
100k	10	0.05	0.02	97.86	0.05	−0.09	31.04	0.978
100k	20	0.10	0.03	95.73	0.10	−0.06	23.29	0.992
100k	50	0.24	0.05	89.52	0.24	−0.10	15.33	0.997
100k	100	0.48	0.08	79.69	0.48	−0.08	11.08	0.999
100k	200	0.96	0.15	62.09	0.95	−0.01	8.03	0.999
100k	500	2.39	0.35	25.98	2.36	−0.08	5.38	0.999
100k	1000	4.79	0.69	4.35	4.58	−0.01	4.12	0.999

Experimental test case

By substituting the experimental values into Eqs. 1, 12, the number of cells and decays in the experimental case can be established and the ratio between the two numbers used to test the model. f_occ = 0.74 is the fraction of occupancy for a hexagonal lattice, R_T = 0.62 cm and R_c = 7.5 μm are the radii of the tumor and cell, respectively. The total number of cells in a 1 g solid tumor is then ∼4.18 × 10⁸ cells.

For the total number of ¹³¹I decays, T_1/2 is the effective half-life of ¹³¹I in the tumor, estimated to be 6.33 days, based on a physical half-life of 8.02 days and an assumed biological clearance rate of 30 days. The total number of decays was ∼4.38 × 10¹¹ per unit (37 MBq) of activity, for a ratio of decays to cells (N_r) of 1050.

Using the model described above, the absorbed dose, surviving fraction, and TCP values for a 1 g lymphoma tumor treated with 37, 63, and 111 MBq of ¹³¹I-FIAU are calculated; the results are given in Table TABLE V.. These compare favorably with the published results, which show initial shrinkage followed by a period of renewed growth for the 37 MBq treatment, shrinkage followed by a nonzero stable tumor size for 63 MBq of injected activity, and complete tumor control when treated with 111 MBq. No toxicities in the mice were observed, also consistent with dosimetric calculations performed for the normal organs from biodistribution data (results not shown).

Table 5.

Modeled dosimetric results for a 1 g lymphoma model using the experimental parameters and activities (Ref. ³¹).

Activity (MBq)	AD (Gy)	SF (%)	EUD (Gy)	TCP (%)
37	11.8	9.98e-4	11.2	0
63	20.1	3.14e-9	17.8	98.7
111	35.4	6.64e-24	29.6	100

DISCUSSION

The TCP as an important dosimetric end point criterion, arguably the most important criterion, has been extensively discussed,^{2, 7, 13, 37, 38, 39, 40} mostly theoretically, including more recently by Bouchat et al.⁴¹ who introduce the concept of SCP or shell control probability as a radial dependent TCP. Traditionally, Monte Carlo models are made based on S-values decomposed into self-dose and cross-dose terms.^{4, 6, 9, 11, 12, 13, 42} However, as previously mentioned, the relatively low (10–1000) number of events per cell (N_r), typical of therapeutic regimens, would reduce the value of such average-value approaches in determining TCP since each individual cell’s absorbed dose can significantly impact the dosimetric results and a substantial amount of fluctuation in the individual cell absorbed doses can be expected. Spaic et al.³ did indeed use the Monte Carlo “FOTELP” in a model with individual tumor cells and varying parameters (density, active cells) and calculated DVHs but with a maximum of 1000 cells. The model proposed here, by adding a statistical fluctuation, provides a more realistic distribution of cellular absorbed doses and therefore of TCP, while maintaining the advantage of shorter simulations, since it is only necessary to simulate a number of events which provides stable average absorbed dose per bin values in the simple spheres. The comparisons with the explicitly cellular models validate this approach.

Statistical considerations in modeling

The disadvantage of lower statistics is that even simulation, assuming perfect representation, is not strictly speaking accurate: it merely represents a possible decay scenario given the distribution of radioactive material. There is no certainty that energy will be deposited in a given cell no matter the odds. The rather large number of simulations helps to overcome one aspect of this problem; by examining tendencies as a function of parameters over a range of simulations [see Fig. 4c], the weight of individual Monte Carlo results that may not be very representative (especially for the smaller-size models) are diminished, while at the same time contributing to the maintenance of the intrinsic uncertainty.

Monte Carlo accuracy

While the accuracy of geant4 Monte Carlo absorbed dose estimations for small distances (cellular level) is questionable, it is a problem which is inherent to all Monte Carlo codes and to first order, there is a little variation between the different commonly used options (geant4, EGSnrc, and mcnp4),¹⁶ as illustrated in Fig. 2.

Absorbed dose distributions

Figure 4a clearly shows that the distributions of cell absorbed doses follow the same pattern as for the homogenous spheres, with an added width of distribution around the radial average [Fig. 4b], consistent with the model prediction [Fig. 1b]. Although the initial absorbed dose distributions [Fig. 3a] are not Gaussian, the variation from the radial homogenous sphere average fit well with Gaussians, to a great degree, as evidenced by the R² values in Tables 2, TABLE IV.. Moreover, the width of these Gaussians relates closely to the expected width from statistical considerations of a population with an event per cell ratio equal to N_r, i.e., equal to ^N_r-1∕2, except for the simulations with very small total number of cells [Fig. 4c]. This statistical fluctuation is the same as found in the distribution of activity per cell. This was verified by plotting the number of events per cell in a histogram per scenario and fitting to a Gaussian (data not shown); the fits to the activity were indistinguishable from the histograms themselves and the values of the fit widths differed from the theoretical (statistical) value by less than 1%. However, no correlation was found between an excess (or deficiency) of activity in a given cell and an excess (or deficiency) of absorbed dose proportionate to the radial norm. This is possible because of the long range nature of the decaying particle. Clearly, for a localized decay, such as from ¹²⁵I, the fluctuations would remain, but the correlation between the number of decaying particles and absorbed dose per cell would be very strong. The Gaussian shape of the activity distribution could, in theory, be improved upon, since Neti and Howell¹⁰ have shown that a lognormal distribution of radioactivity in cells using spheroids and ²¹⁰Po is more representative. However, the fact that no correlation of excess or deficiency between activity and absorbed dose exists indicates that the effect should be negligible, at least for longer ranged particles.

Dosimetric end point comparison

The EUD and surviving fraction values calculated from the simple sphere model are in excellent agreement with the Monte Carlo derived values (Figs. 56). While a small discrepancy begins to appear between model and simulation EUD for large values, the results shown in Figs. 5c, 5d indicate that this is not because of the growing size of the models, but rather because of an increasing absorbed dose to α (and β) ratio. As expected, the dosimetric quantities are most affected by the lower end of the absorbed dose distributions, in particular, once those distributions move beyond the 1/α [and (1/β)^1/2] values. For lower α and β values [Fig. 5c], the discrepancies disappear. For larger α (and β) values, they increase. Quantitatively, this difference grows to an order of magnitude for a surviving fraction of 1 in 10¹⁰. This means, for example, a difference between a 100% chance of having a single cell survive in a 100 g tumor (∼10¹¹ cells) and only a 10% chance of having a cell survive in the same tumor. There is a caveat to the indications that these results hold true for larger sizes. As the tumor grows in size, the contribution from long-range particles (photons) will increase. The contribution of this component to the cell-by-cell absorbed dose variability is unclear, and it could potentially have a smoothing effect, which would reduce the width of the absorbed dose distributions. Although the variation in α and β values in Figs. 5c, 5d are an artifice to replace the simulation of larger models, they can also be informative for cellular constructs with those specific α and β values. While it is unlikely that there exists tumors cells or even normal tissue with the higher values of α and β (extremely radiosensitive), Fig. 5c represents the results for a more radioresistant tumor cell line. This is not to imply that more highly resistant strains are more accurately represented by this model; rather that, as stated above, the absorbed doses delivered here are well below the values required for tumor control.

The adjusted spherical models’ TCP values are comparable with the cellular model TCP values, validating the adjusted spherical model. The results in Fig. 6 show a difference of 0.8% in administered activity for a same TCP result for the largest (1M cell) model. The average for all models is 1.2% ± 0.67%, very reasonable values, and clearly below typical experimental uncertainties, as well as a considerable improvement over the nonadjusted values, which significantly underestimate the activity needed for tumor control at larger tumor sizes (the “average” values in Fig. 6; for a 1 g tumor the average value would only be 77% of the model value).

Exponential penetration model

More realistic models that include some activity penetration and the subsequent decomposition of contributing dosimetric quantities in radial bins have been studied by, among others, Lechner et al.,⁴⁰ using mcnp, and Bouchat et al.,⁴¹ who introduced the concept of SCP or shell control probability as a radial dependent TCP. However, here too, average absorbed dose values are used as the basis for calculating the dosimetric quantities. The adjusted spherical model presented here works equally well for the given example of nonhomogenous activity distribution (Tables 3, TABLE IV.); this is in fact, indicative of independence with respect to any parameter dependence of the distribution of activity, such as the radius. A reasonable assumption would be that any macroscopically measured activity, including clinical cases measured with SPECT or PET, may be modeled dosimetrically at the cellular level by the adjunction of the cellular statistical fluctuation.

Application to experimental data

Concerning the TCP results corresponding to the invivo results (0% for 37 MBq and 100% for 111 MBq), it must be noted that the TCP definition employed here is quite strict and that potentially tumor shrinkage and even control is possible with less stringent conditions. Nevertheless, to first order, these values confirm the experimentally observed results. One caveat is that the modeling has been done with a 10 cm surrounding volume of water, which is relevant for backscatter in humans but not so for mice. However, a simple 1 g tumor simulation run with only 0.5 cm of surrounding water showed less than a 0.01% difference in total energy deposited as compared to the simple 1 g tumor with the 10 cm water buffer. The average of the absolute values of the radial bin differences (for 100 bins) between the two simulations was less than 0.3%, including the low statistic low radius bins. Moreover, the dosimetric quantities calculated from this sphere showed the same degree of comparison with the fully cellular model (data not shown) as the 10 cm buffered data.

Future work

The model exposed here could be tested on other radionuclides, although intuitively, the results should be similar for any radionuclide with decays having a range greater than several cell widths. As mentioned in the Sec. 1, the most successful models depend on the symbiotic relationship between the model and data provided directly from experiment, generally obtained by imaging; the more complete the information from imaging, the more accurate the modeling results will be. Though we have exposed here a general model, it has shown sufficient versatility (the exponential penetration results) to be adaptable to any supplementary constraints or parameters imposed by experiment. A specific consideration not exposed here is that not all cells may be active, i.e., within a macroscopically homogenous activity, at the cellular level, only a small percentage of cells may be actively taking up the radionuclide; this is particularly an issue in a treatment strategy such as BETR, where the uptake depends on activation of a specific cellular mechanism.

CONCLUSIONS

The adjusted spherical modeling results compare very favorably to the cellular simulations. The model presented here is an improvement from simple spheres for full cellular level Monte Carlo simulations, in particular for calculating TCP. The next step in developing this model will be to study the effect on EUD and TCP of having only a certain percentage of cells actively take up the radionuclide.