Modeling MR Signal Change Induced by Oxygen Effect in Neural Tissue Preparations of Various Geometries

Abstract

Tissue preparation has recently been utilized for detection of neuronal activation in multiple non-BOLD based functional MRI studies to eliminate vascular contamination. However, undesired signal change could still occur in such systems due to the concentration change of dissolved O₂ upon tissue activation. To estimate the impact of such effects, the O₂ concentration distribution and the consequent susceptibility field in tissue-solution systems were simulated with various tissue geometries and experimental parameters. Our results indicate that substantial signal change between the resting and activated states could potentially be induced by the O₂ effect in highly oxygenated solutions, and thus caution should be taken in interpreting any signal change observed in such experiments.

INTRODUCTION

There has been great interest in developing non-BOLD functional imaging methods for better detection of neural activity. Two promising areas of endeavor have been the neuronal current MRI (ncMRI) and the diffusion-weighted functional MRI (dfMRI). Although several encouraging results have been reported (1–4), controversy remains whether the observed signal changes were from a true neuronal origin or due to residual BOLD effect. To eliminate vascular contamination, bloodless animal models have been adopted to verify the feasibility of ncMRI (5–8) and dfMRI (9,10).

Though devoid of hemoglobin, these experiments may yet suffer from artifacts caused by paramagnetic O₂ molecules. To estimate the magnitude of oxygen effect in animal tissue experiments, Luo et al. (11) performed theoretical calculations of the MR signal change caused by the O₂ concentration ([O₂]) change by modeling tissue slices as infinitely large, one-side-diffusible planes. Recently, neural tissues with more complicated geometries, such as frog (10) and earthworm (8) nerve cords and turtle brains (7), have been used in ncMRI and dfMRI studies. The present work extends Luo et al.’s analysis (11) to address O₂ effect in these tissue geometries. For simplicity, we used an infinitely long cylinder to model isolated nerve bundles, and a sphere to model whole animal brains. In addition, we re-examined the planer tissue slice model and considered situations where O₂ diffusion from the two opposing surfaces could interfere with each other.

METHODS

1, Effect of dissolved oxygen on magnetic resonance property of tissue/solution

Dissolved oxygen increases the transverse relaxation rate R₂ of tissue/solution through a direct dipole interaction between the unpaired electrons of O₂ molecules and tissue/solution protons. The change in R₂ is proportional to [O₂] (12,13):

$$\mathrm{\Delta }{R}_2=r_2[{\mathrm{O}}_2],$$ [1]

where r₂ can be calculated using the Solomon-Bloembergen-Morgan relation (13):

$$r_2=B_1[\frac{13{\tau }_c}{1+{({\omega }_s{\tau }_c)}^2}+7{\tau }_c]+B_2[\frac{{\tau }_e}{1+{({\omega }_s{\tau }_e)}^2}+7{\tau }_e],$$ [2]

where τ_c = 2.3×10⁻¹³ s, τ_e = 1.7×10⁻¹¹ s, B₁ = 2.0×10¹³ M⁻¹s⁻², B₂ = 3.2×10¹³ M⁻¹s⁻², and ω_s = γ_sB₀ is the electronic Larmor frequency. γ_s = 2.8×10¹⁰ s⁻¹T⁻¹. Moreover, dissolved oxygen could increase the magnetic susceptibility (χ_O2) of the medium and this effect is also proportional to [O₂] (14):

$${\chi }_{O2}\approx f_{\chi }[{\mathrm{O}}_2],$$ [3]

where f_χ = 4.0×10⁻⁸ mM⁻¹. Consequently, variation of [O₂] within an imaging voxel would lead to signal attenuation with a gradient echo sequence.

2, Oxygen distribution in tissue-solution system

We consider the scenario where a tissue preparation is immersed in solution in which [O₂] is maintained at a known level ([O₂]_sol). The distribution of [O₂] in tissue is then determined by the following factors: the diffusion coefficients of O₂ in tissue (D_t = 1.54×10⁻⁵ cm²/s) and in solution (D_s = 2.48×10⁻⁵ cm²/s) (15,16), the O₂ consumption rate in the tissue (V̇_O2) and [O₂]_sol.

Oxygen can only penetrate into the tissue by a limited depth (d_max). Beyond that point, cells are considered to be dead and V̇_O2 is zero. d_max is of the order of a few hundred microns depending on [O₂]_sol and V̇_O2. [O₂]_sol can be calculated using Henry’s law (17)

$${[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}=k·P·F_{O2},$$ [4]

where k = 1.34×10⁻³ mM/mmHg is the solubility coefficient of O₂ in saline, P is the barometric pressure, and F_O2 is the O₂ fraction. In all the previous tissue preparation experiments, the oxygen tension was either at the atmospheric level (F_O2 = 21%) (5,6,8–10) or at a nearly pure level (F_O2 = 95%) (6,7). V̇_O2 has been shown to be independent of [O₂] in cat brain tissue (15). A wide range of V̇_O2 values have been reported in mammalian brain tissues (15,16,18), and we used a typical value of 3.38×10⁻² mlO₂·cm⁻³min⁻¹ (16). The percentage increase of V̇_O2 upon tissue activation (δV̇_O2 ≡ (V̇_O2,activated − V̇_O2,rest)/V̇_O2,rest) depends on the type and strength of stimulation, and may be up to 100% under optimal electrical stimulation (19). In this study, we used 10% and 50% for δV̇_O2 to represent physiological stimulation and electrical stimulation, respectively.

The mass transfer of O₂ molecules from saline into tissue mainly occurs in a thin layer of saline adjacent to the tissue surface. The actual mass transfer in this transition layer is mediated by not only diffusion but also macroscopic motions such as convection (20), and requires complicated modeling to describe. To simplify analysis, a film model (20) was adopted to calculate [O₂] distribution, which assumes the existence of an unstirred layer adjacent to the tissue surface. The mass transfer in this layer is considered to be caused solely by diffusion, whereas out of this layer [O₂] is maintained at the bulk solution level ([O₂]_sol) by diffusion and macroscopic mechanisms. The thickness of the unstirred layer d_UL is determined by [O₂]_sol, V̇_O2 and tissue geometry, and was estimated to be 64 µm using data given by Ganfield et al. (15).

With the above assumptions, [O₂] distribution in tissue/solution can then be obtained from the diffusion equation D · ∇²[O₂] = V̇_O2 with proper boundary conditions. We used a 1-mm-diameter infinitely long cylinder to model nerve bundles such as frog sciatic nerves used in (10) and earthworm nerve cords used in (8), and a 1-cm-diameter sphere to represent structures such as intact turtle brains used in (7). Luo et al. (11) has previously modeled tissue slices with a one-side-diffusible plane. This approach is adequate for thick slice, but for thin slice (less than ~500 µm) such as in (9) diffusion from the two opposing surfaces can influence each other, leading to a different [O₂] profile. We simulated this situation with a 0.4-mm-thick infinitely large slab. The analytic solutions to the diffusion equation for these three tissue geometries are given in Appendix.

3, O₂ induced susceptibility field and MR signal change

The oxygen induced susceptibility would produce a magnetization distribution M in both tissue and saline. Under first-order approximation (21), M can be given by

$$\mathit{M}=\chi {\mathit{H}}_0,$$ [5]

where H₀ is the external field without the presence of M, and χ can be obtained from Eq. [3] combined with the knowledge of [O₂] profile given in Appendix. The total field would be the sum of H₀ and the susceptibility field produced by M:

$$\mathit{H}={\mathit{H}}_0+{\mathit{H}}_s.$$ [6]

One convenient way to calculate H_s from the distribution of M is to use the concept of the “magnetic charge” defined by

$${\rho }_m=-\nabla ·\mathit{M}.$$ [7]

And H_s can be derived from a scalar potential function Φ_s:

$${\mathit{H}}_s=-\nabla {\mathrm{\Phi }}_s,$$ [8]

where Φ_s can be found by solving Poisson’s equation

$${\nabla }^2{\mathrm{\Phi }}_s={\rho }_m.$$ [9]

Once equipped with the knowledge of H_s, one can calculate the off-resonance field ΔB:

$$\mathrm{\Delta }\mathit{B}\equiv \mathit{B}-{\mathit{B}}_0={\mu }_0(1+\chi )({\mathit{H}}_0+{\mathit{H}}_s)-{\mu }_0{\mathit{H}}_0\approx {\mu }_0{\mathit{H}}_s+\chi {\mathit{B}}_0,$$ [10]

where B and B₀ are the magnetic flux density with and without the presence of M. The MR signal from a pixel is then given by

$$S\propto {\displaystyle {\int }_{\mathit{\text{pixel}}}\text{exp}[-\mathrm{\Delta }{R}_2(\mathit{r})·\text{TE}]·\text{exp}[-i\gamma \mathrm{\Delta }{B}_z(\mathit{r})·\text{TE}]·d\mathit{r}}$$ [11]

where TE is the echo time, γ = 42.6 MHz/T is the gyromagnetic ratio and ΔB_z is the component of ΔB along the B₀ direction. To estimate the greatest potential signal change, we allowed both the imaging pixel size and position to vary, with the constraint that the pixel should be entirely located within the tissue to avoid any partial volume effect. A range of pixel sizes from 0.5×0.5 mm² up to 1.0×1.0 mm² was used in our simulation, which covered most of the previous tissue preparation studies (6,7,9,10). A pixel was used instead of a voxel because for the three geometries we considered, the magnetic field is uniform in at least one direction.

RESULTS

Fig. 1 shows [O₂] profiles for the three tissue geometries, as were obtained from Eqs. [A1], [A3] and [A5]. Oxygen can penetrate into the tissue by a maximum depth of about 100 µm and 300 µm for F_O2 = 21% and F_O2 = 95% respectively. [O₂] in tissue is slightly lower in the activated state than in the resting state.

FIG. 1.

[O₂] profile obtained with a film model for tissue at resting state (solid line) and activated state (dashed-dot line) for F_O2 = 21% and F_O2 = 95%. δV̇_O2 was assumed to be 50%. The tissues are modeled by (a) a D = 1 mm, infinitely long cylinder, (b) a D = 1 cm sphere and (c) a 0.4 mm thick plane with diffusion from two opposing surfaces. The vertical lines indicate the location of the tissue-solution interfaces. Note for the last case (c), only F_O2 = 95% would lead to interference of diffusion patterns from the two opposing surfaces, while F_O2 = 21% leads to the same diffusion profile as that of a one-side-diffusible planer tissue, which is discussed in (11). In (c) [O₂] is zero for r < 4.5 mm.

The susceptibility field caused by O₂ depends on the direction of B₀. When B₀ is parallel with a planer tissue or with the axis of a cylindrical tissue, ρ_m as determined by Eq. [7] is zero, and hence H_s would also vanish. From Eqs. [3] and [10], we have the simple result that

$$\mathrm{\Delta }\mathit{B}=f_{\chi }[{\mathrm{O}}_2]{\mathit{B}}_0$$ [12]

If B₀ is perpendicular to a planar tissue, by symmetry the total B would also be perpendicular to the plane. Then, from ∇ · B = 0 we can conclude that B = B₀ everywhere. Therefore, in this particular case B is not perturbed by [O₂] variation at all.

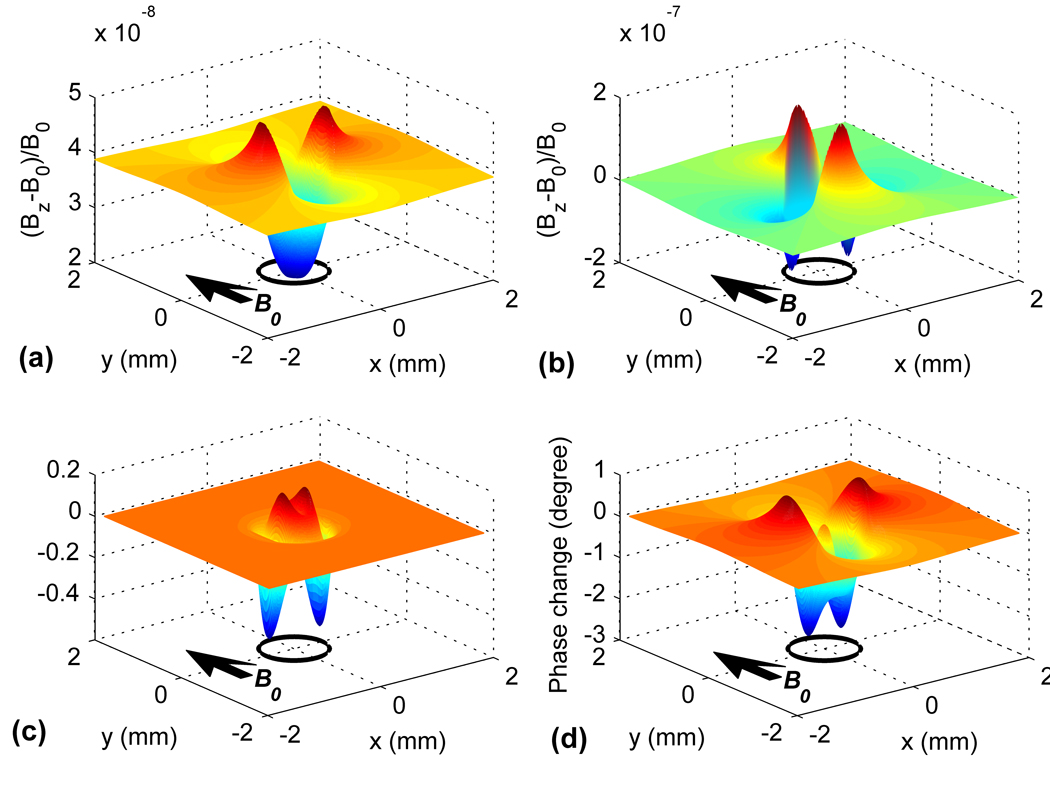
On the other hand, if B₀ is perpendicular to a cylindrical tissue or is applied to a spherical tissue, then ΔB is more complicated and we only show an example for the cylindrical tissue in Fig. 2 (a). It can be observed that the susceptibility field is on the order of 10⁻⁸ B₀. B_z is uniform and at its lowest value well inside the cylinder, where [O₂] is zero. It increases rapidly in the vicinity of the tissue-solution interface, and finally reaches a constant level in the bulk of the solution, which is determined by f_χ [O₂]_sol B₀. Also shown in comparison (Fig. 2 (b)) is the susceptibility field caused by deoxyhemoglobin (dHB) in a cylindrical vessel (22). Both the fields due to O₂ effect and due to dHB exhibit a dipole pattern outside the cylinder, the magnitude of which depends only on the concentration difference of O₂/dHB, not on the diameter of the cylinder. Inside the cylinder the field due to dHB is uniform because of uniform distribution of dHB in the blood vessel, while the field due to O₂ effect changes rapidly because of non-uniform [O₂] distribution in the tissue.

FIG. 2.

(a): The susceptibility field induced by O₂ effect for a D = 1 mm cylindrically shaped tissue immersed in oxygenated saline (F_O2 = 95%). (b): The susceptibility field induced caused by deoxyhemoglobin for a D = 1 mm cylindrical blood vessel. (c) and (d): The MR signal change in magnitude and phase due to O₂ effect as functions of the position of the imaging pixel for the D = 1 mm cylindrical tissue. Simulation was performed with the following parameters: B₀ = 9.4 T, TE = 20 ms, pixel size = 0.2×0.2 mm². B₀ is perpendicular to the cylinder axis in (a)–(d). The circles indicate the location of the cylinder and the arrows indicate the direction of B₀.

To estimate the maximum MR signal change inducible by the oxygen effect, maps of signal magnitude and phase changes were generated as a function of the position of the imaging pixel. Examples of such maps are shown in Fig. 2 (c) and (d) for the D = 1 mm cylinder. It can be seen that the signal magnitude and phase may both increase and decrease upon tissue activation, depending on the pixel position. However if the pixel is to be restricted within the tissue, only a negative phase change is possible. The maximum signal change occurs where the susceptibility field changes most steeply.

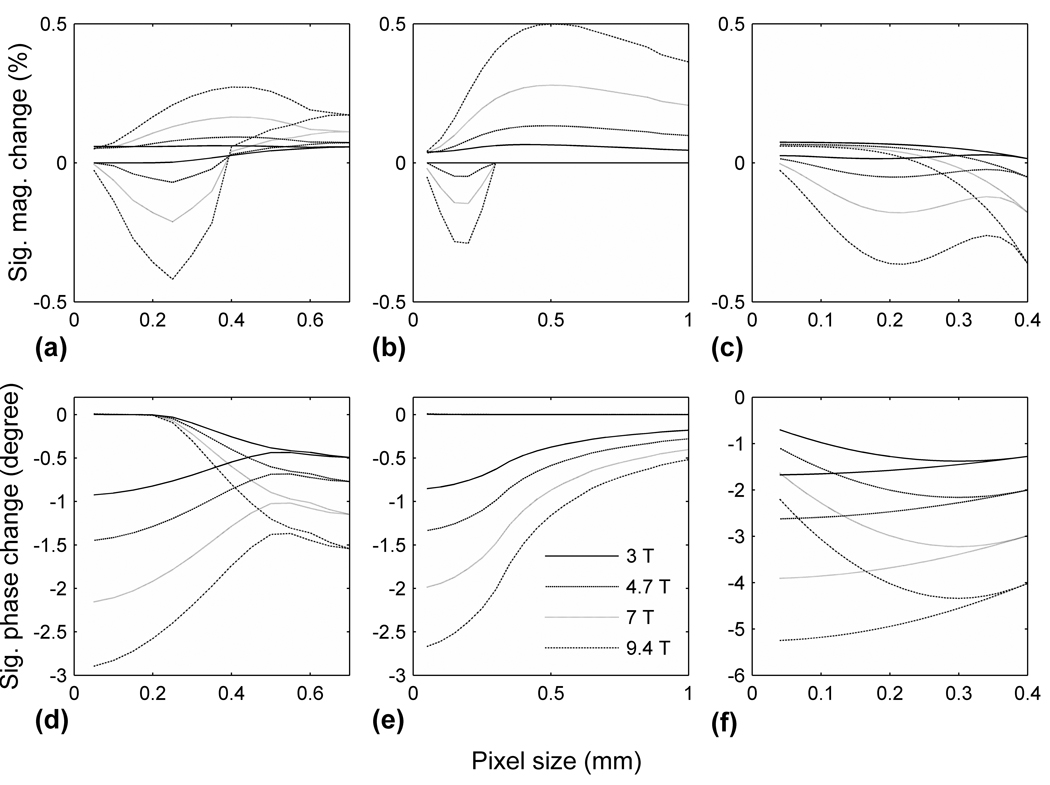
Fig. 3 shows the range of signal changes as a function of pixel dimension and B₀. A magnitude increase may occur at all pixel sizes, and reaches its maximum when the pixel is slightly larger than d_max and is placed adjacent to the tissue surface. But a magnitude decrease can only occur when the pixel is located within the oxygen penetration layer, that is, the pixel size must be smaller than d_max. The signal phase can, however, only decrease upon tissue stimulation, because reduced [O₂] leads to a lower χ and hence lower B. Table 1 summarizes the range of potential signal changes obtainable with all combinations of pixel size and position.

FIG. 3.

Range of MR signal change as a function of imaging pixel size and B₀ field strength. (a) – (c): signal magnitude change for a D = 1 mm, infinitely long cylinder, a D = 1 cm sphere and a 0.4 mm thick planer slice with two-sided diffusion. (d) – (f): signal phase change for the same structures. There are two curves at each field strength, corresponding to the upper and lower limits of signal change. In (a), (c), (d) and (f), the maximum pixel size was reached when the pixel span the entire tissue and has only one possible position; the curves converge to one point on the right end of the horizontal axis for the same reason. In (b), the four lower curves overlap for pixel size > 0.3 mm; in (e) the four upper curves overlap.

Table 1.

Range of MR signal change in magnitude and phase induced by the O₂ effect between the activated and the resting states for different tissue geometries. (The actual signal change depends on the position and size of the imaging voxel.) For planer tissues, B₀ was chosen to be either perpendicular to (⊥) or parallel with (//) the tissue surface. For cylindrical tissues, B₀ was chosen to be either perpendicular to (⊥) or parallel with (//) the axis of the cylinder.

Geometry	FO2	B0 direction	δV̇ = 10%		δV̇ = 50%
			Mag. (%)	Phase (°)	Mag. (%)	Phase (°)
Cylinder	95%	⊥	[−0.42, 0.27]	[−2.9, 0]	[−1.47, 1.22]	[−11.8, 0]
		//	[−0.50, 0.58]	[−4.1, 0]	[−1.70, 2.5]	[−16.1, 0]
	21%	⊥	[0, 0.021]	[−0.55, 0]	[0, 0.085]	[−2.3, 0]
		//	[0, 0.027]	[−0.62, 0]	[0, 0.11]	[−2.5, 0]
Plane, 1-side-diffusible	95%	⊥	[0, 0.03]	<10−13	[0, 0.13]	<10−13
		//	[−0.23, 0.50]	[−2.6, 0]	[−0.89, 2.1]	[−11.0, 0]
	21%	⊥	[0, 0.006]	<10−13	[0, 0.025]	<10−13
		//	[0, 0.023]	[−0.53, 0]	[0, 0.095]	[−2.2, 0]
Plane, 2-side-diffusible	95%	⊥	[0.029,0.060]	<10−13	[0.23, 0.28]	<10−13
		//	[−0.36, 0.06]	[−5.2, −2.5]	[−2.2, 0.30]	[−26.2, −12.6]
Sphere	95%		[−0.29, 0.50]	[−2.7, 0]	[−1.16, 2.11]	[−11.2, 0]
	21%		[0, 0.024]	[−0.54, 0]	[0, 0.10]	[−2.3, 0]

DISCUSSIONS AND CONCLUSIONS

Our results indicate that substantial MR signal changes could be induced by the O₂ effect in highly oxygenated saline, while at low oxygen tension such effect is much reduced (Table 1). Fig. 4 shows the influence of F_O2 and δV̇_O2 on signal change. The maximum signal change increases about linearly with δV̇_O2. It increases with F_O2 too, but relatively slowly at low F_O2 and more rapidly at high F_O2.

FIG. 4.

The effect of O₂ fraction in gas (F_O2) and O₂ consumption rate increase upon activation (δV̇_O2) on the maximum signal change (including both increase and decrease) in magnitude (a) and phase (b) for a D = 1 mm cylindrically shaped tissue.

Figs. 3 and 4 also show the effect of B₀ on signal change. The maximum magnitude and phase changes are roughly proportional to $B_0^2$ and B₀ respectively. This can be explained by considering a simplified case with field variation in only one direction, where we would have

$$\text{Magnitude Change}\propto \text{sinc}(\gamma \mathrm{\Delta }B·\text{TE})\approx 1-{(\gamma \mathrm{\Delta }B·\text{TE})}^2,\text{and Phase Change}\propto \gamma \overline{B}·\text{TE},$$

where ΔB and B̅ are the span and the mean of the susceptibility field in a pixel. It could also be expected from these two equations that increasing TE would have a similar effect to increasing B₀.

Between the two effects of dissolved O₂, the induced susceptibility field has much greater impact on MR signal than the R₂ relaxation rate change. The latter effect contributes to less than 0.3% magnitude change and negligible phase change (Table 1). The susceptibility field depends strongly on the direction of B₀. It is greatest when B₀ is parallel with the tissue-solution interface, and vanishes when the two are perpendicular (see, e.g., Fig. 2 (c–d)). Therefore, a simple way to eliminate any undesired O₂ effect is to position tissue slices perpendicular to B₀. Alternatively, a spin echo sequence can also serve to eliminate the susceptibility effect. However, almost all ncMRI experiments require a gradient echo based sequence because of its sensitivity towards the susceptibility field induced by neuronal firing. And for dfMRI experiments, even with a spin echo based sequence, the susceptibility field can still couple with the diffusion-weighting gradients and alter the b-value.

The [O₂] profiles in Fig. 1 for the D = 1 mm cylinder and D = 1 cm sphere are both very similar to those obtained with an one-side-diffusible planar tissue model (11), despite the quite different tissue geometries and dimensions. This is because the radii of the cylinder and sphere are much larger than the depth of O₂ penetration into the tissue (100 – 300 µm), and thus lateral diffusion is only minor. So in practice, it would be safe to estimate the size of O₂ effect using a simple plane model, provided that the radius of curvature of the tissue in question is larger than a few hundred microns.

It is worth pointing out that in simulation we did not include the effect of proton diffusion in calculating the MR signal S (Eq. 11). Proton diffusion in the presence of a susceptibility field will in principle cause additional attenuation of S. However, our analysis (data not shown) reveals that such effect would alter the present results by a factor less than 10⁻⁷, and hence is negligible.

In a previous ncMRI study using snail ganglia (5) at 3.0 T and atmospheric O₂ tension, a signal magnitude drop by 2.97% upon electrical stimulation was reported with a voxel size of 2×2×2 mm³. Given that voxel size exceeded d_max, it is expected that O₂ effect could only cause a positive signal magnitude change (see Results). Thus the reported signal change could be attributed to sources other than O₂ effect. In another study on earthworm axon current at 9.4 T (8), a phase drop within ~1.5 ms after electric stimulation followed by a quick recovery within ~1 ms was observed from free induction decay signal. Since O₂ molecules can only diffuse across a mean distance of ~1.2 µm in 1 ms, which is much shorter than d_max, it is unlikely that such quick recovery could have been due to O₂ effect. In a previous study (7) using intact turtle brain under visual stimulation with F_O2 = 95%, no statistically significant signal change was detected with a magnitude/phase threshold of 0.1%/0.1°. Based on our calculation for a spherical tissue, we estimate that δV̇_O2 under such stimulation should be less than 1%. It is also interesting to consider the O₂ effect in in vivo experiments. In a previous study (23) using rat cortex and electrical stimulation, tissue oxygen partial pressure (baseline = 38.4 mmHg) was found to decrease by 10% during stimulation, followed by a poststimulation increase by up to 35%. We estimated that such oxygen level change could lead to a signal magnitude change by ~0.005%, much smaller than typical BOLD effect. The phase change was estimated to be 2°.

Other than O₂ effect, hemoproteins from non-blood sources might be another cause of MR signal change in bloodless tissue preparations. For example, cytochrome c in mitochondrion contains an iron center that may be in either a ferrous or ferric state, leading to variable magnetic susceptibilities. If the fraction of ferricytochrome changes upon tissue activation, MR signal change could potentially occur. More detailed analysis of potential effect of hemoproteins on functional MRI is underway in our laboratory.

In summary, we simulated [O₂] distribution and its effect on MR signal in tissue-solution systems for different tissue geometries, and discussed the effects of various experimental parameters. We conclude that the O₂ effect could cause substantial MR signal change with highly oxygenated saline, mainly through an induced susceptibility field. It is most severe where the tissue-solution interface is parallel with B₀ and with a gradient echo sequence. The O₂ effect is restricted in a thin tissue layer up to 300 µm thick from the tissue-solution interface, depending on F_O2. Therefore, interpretation of any signal change observed in this region should be made with caution.

APPENDIX

The [O₂] profile in a tissue-solution system is a function of D_t, D_s, V̇_O2 and the tissue geometry, and can be found by solving the diffusion equation D · ∇²[O₂] = V̇_O2. For an infinitely long cylinder with a radius of R, the result is

$$[{\mathrm{O}}_2](r)=\{\begin{array}{cc}0\hfill & (r\le r_0)\hfill \\ \frac{{\dot{V}}_{O2}}{4D_t}\{r^2-r_0^2[1-\text{ln}(\frac{r}{r_0})]\}\hfill & (r_0<r\le R)\hfill \\ {[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}-\frac{{\dot{V}}_{O2}}{2D_s}·(R^2-r_0^2)·\text{ln}(\frac{R+d_{\mathit{\text{UL}}}}{r})\hfill & (R<r\le R+d_F)\hfill \\ {[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}\hfill & (r>R+d_F)\hfill \end{array},$$ [A1]

where [O₂](r) is O₂ concentration at a distance r from the cylindrical axis, r₀ is the radius at which [O₂](r) falls to zero, and d_UL is the thickness of the unstirred layer, which is discussed in Methods. r₀ could be found using the condition of continuity of [O₂] at r = R:

$$\frac{{\dot{V}}_{O2}}{4D_t}\{R^2-r_0^2[1-\text{ln}(\frac{R}{r_0})]\}={[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}-\frac{{\dot{V}}_{O2}}{2D_s}·(R^2-r_0^2)·\text{ln}(\frac{R+d_F}{R}).$$ [A2]

In our simulation Eq. [A2] was solved numerically to obtain r₀.

For a spherical tissue with radius of R, the [O₂] profile is

$$[{\mathrm{O}}_2](r)=\{\begin{array}{cc}0\hfill & (r\le r_0)\hfill \\ \frac{{\dot{V}}_{O2}}{6D_t}·\frac{1}{r}(r+2r_0){(r-r_0)}^2\hfill & (r_0<r\le R)\hfill \\ {[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}-\frac{{\dot{V}}_{O2}}{3D_s}·(R^3-r_0^3)(\frac{1}{r}-\frac{1}{R+d_{\mathit{\text{UL}}}})\hfill & (R<r\le R+d_F)\hfill \\ {[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}\hfill & (r>R+d_F)\hfill \end{array},$$ [A3]

where the symbols have the same meanings as above. And r₀ is again to be found from the continuity condition at r = R:

$$\frac{{\dot{V}}_{O2}}{6D_t}·\frac{1}{R}(R+2r_0){(R-r_0)}^2={[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}-\frac{{\dot{V}}_{O2}}{3D_s}·(R^3-r_0^3)(\frac{1}{R}-\frac{1}{R+d_F}).$$ [A4]

For a two-side-diffusible planar tissue slice, the [O₂] profile is given by:

$$[{\mathrm{O}}_2](x)=\{\begin{array}{cc}\frac{{\dot{V}}_{O2}}{6D_t}·{\mathrm{x}}^2+{\mathrm{C}}_0\hfill & (r\le r_0)\hfill \\ \frac{({[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}-{[{\mathrm{O}}_2]}_i)}{d_{\mathit{\text{UL}}}}·\left|x-d_i\right|+{[{\mathrm{O}}_2]}_i\hfill & (r_0<r\le R)\hfill \\ {[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}\hfill & (r>R+d_F)\hfill \end{array},$$ [A5]

where [O₂](x) is the O₂ concentration at a distance x from the mid-plane of the tissue slice, d_t is the distance to the tissue-solution interface (half of the slice thickness). [O₂]_i and [O₂]₀ are the O₂ concentration at the interface and at the mid-plane, respectively, and are given by ${[{\mathrm{O}}_2]}_i={[{\mathrm{O}}_2]}_{\mathit{\text{sol}}}-{\dot{V}}_{\mathrm{O}2}{d}_i{d}_F/D_s\text{ and }{[{\mathrm{O}}_2]}_0={[{\mathrm{O}}_2]}_i-{\dot{V}}_{\mathrm{O}2}{d}_i^2/(2D_t)$.