Sparse Logistic Regression for Diagnosis of Liver Fibrosis in Rat by Using SCAD-Penalized Likelihood

Abstract

The objective of the present study is to find out the quantitative relationship between progression of liver fibrosis and the levels of certain serum markers using mathematic model. We provide the sparse logistic regression by using smoothly clipped absolute deviation (SCAD) penalized function to diagnose the liver fibrosis in rats. Not only does it give a sparse solution with high accuracy, it also provides the users with the precise probabilities of classification with the class information. In the simulative case and the experiment case, the proposed method is comparable to the stepwise linear discriminant analysis (SLDA) and the sparse logistic regression with least absolute shrinkage and selection operator (LASSO) penalty, by using receiver operating characteristic (ROC) with bayesian bootstrap estimating area under the curve (AUC) diagnostic sensitivity for selected variable. Results show that the new approach provides a good correlation between the serum marker levels and the liver fibrosis induced by thioacetamide (TAA) in rats. Meanwhile, this approach might also be used in predicting the development of liver cirrhosis.

1. Introduction

Chronic hepatitis, characterized by hepatic fibrosis, is recognized as a health problem with a worldwide prevalence, and it may gradually progress toward cirrhosis and hepatocellular carcinoma which may induce death. Successful and early treatment of chronic hepatitis can prevent development of cirrhosis and hepatocellular carcinoma. There are two major symptoms of chronic hepatitis: necroinflammatory activity and fibrosis. Liver fibrosis is the best sign for predicting the development of liver cirrhosis [1]. Since there is no correlation between aminotransferase activities and fibrosis, aminotransferase activities cannot be used for the diagnosis of fibrosis. Considering that liver fibrosis is reversible in the early stage, accurate and early diagnosis of liver fibrosis is required for better prognosis of chronic hepatitis.

Liver biopsy has to date been the gold standard for the grading of hepatic inflammation and the staging of hepatic fibrosis and has been used as the reference standard method in evaluations of plasma markers of liver diseases [2]. However, it is an expensive, invasive procedure with a considerable risk of complications (particularly bleeding) and a small chance (<1 : 1000) of death [3]. And liver biopsy sample is only 1 : 50000th of the mass of the liver and therefore causing the risk of false negative. Even with sample of adequate sized biopsies, cirrhosis may still be missed in 15–30% of liver biopsies [4]. Due to the limitations of biopsy including the small but significant mortality rates, sampling error, inter- and intraobserver variation in pathology reporting, and provision of a static picture of liver architecture in a dynamic disease process, it is still necessary to look for alternative approaches. Moreover, to evaluate drug efficacy, it is essential to establish appropriate animal models of liver fibrosis. Since establishing an animal model is time-consuming, usually lasting 8 to 12 weeks, histopathologic examination may lead to the consumption of animals, and the testing small proportion cannot reflect the condition of whole population. All these would increase the cost and decrease the efficiency and reliability of the research. In order to build appropriate animal models for liver fibrosis, also it is necessary to develop a reliable and accurate method to diagnose liver fibrosis quickly.

The search of a noninvasive method to assess liver fibrosis has encouraged the development of various approaches. Transient elastography for the noninvasive measurement of liver stiffness was developed [5–7]. Currently, it is notable that monitoring serum markers of liver fibrosis could offer an attractive alternative to liver biopsy, as it allows dynamic calibration of fibrosis efficaciously. Liver fibrosis is characterized by an overall increase of the extracellular matrix, mainly produced by hepatic stellate cells (HSCs) [8, 9], which undergo a phenotypic switch induced within the inflammation process by numerous cells and cytokines. A number of potential serum markers of fibrosis and cirrhosis have been used in the diagnosis of a variety of chronic liver diseases.

Therefore, monitoring a variety of plasma markers, especially collagen-related biomarkers such as aminoterminal peptide of procollagen III (PIIINP), is a novel approach for liver fibrosis diagnosis. In general, there are many plasma markers identified but some of them still have not been determined yet. So constructing a sparse classification for the progression of liver fibrosis based on detected plasma markers has attracted much attention. A novel method is linear discriminant analysis with stepwise variable selection. Guyon et al. [10] proposed a recursive feature elimination technique with support vector machine to analyze gene expression data. Rocke and Nguyen [11] raised dimension reduction of microarray-based classification. Li et al. [12] introduced two bayesian approaches with technique of automatic relevance determination for the same problem. Debashis and Arul [13] suggested that linear discriminant function by optimal scoring with LASSO was an alternative approach. Sparse Fisher's linear discriminant analysis, suggested by Qiao et al. [14], was also an excellent method.

The aim of this study, therefore, is to develop classification rules based on the consideration of measures of diagnostic accuracy. In particular, we are interested in finding liver fibrosis that can discriminate between two populations. Our solution was to combine the problems of variable selection and classification. We suggested an approach for classification using the smoothly clipped absolute deviation penalty (SCAD) [15] approach with logistic regression [16]. We compared it with the stepwise linear discriminant analysis (SLDA) and sparse logistic regression (SLR) with least absolute shrinkage and selection operator (LASSO-)penalized function [17, 18]. At last, we analyzed the sensitivity of these methods using the receiver operating characteristic (ROC). Considering the small sample size, we fit the ROC curve and compute the area under the curve (AUC) using Bayesian bootstrap [19, 20].

2. Materials and Method

2.1. Animals

Twenty-eight Sprague-Dawley (SD) rats were provided from SLAC Laboratory Animal Co.ltd (Shanghai, China, SCXK: 2007-0005). The rats were maintained under specific-pathogen-free conditions, with a constant temperature ranging between 25 and 27°C, and a constant humidity ranging between 45 and 50% at animal laboratory of China Pharmaceutical University. Animal care was in accordance with the guidelines of the animal laboratory of China Pharmaceutical University.

2.2. Induction Of Liver Fibrosis

The modeling method is in accord with Imanishi et al. [21] and Kuriyama et al. [22]. The rats were randomly divided into 4 subgroups: (I) model group (8 weeks, n = 8), (II) model group (12 weeks, n = 8), (III) normal control group (8 weeks, n = 6), and (IV) normal control group (12 weeks, n = 6). All rats were observed at 8th week and 12th week after TAA treatment. Rats in the model subgroup were injected intraperitoneally (i.p) with TAA 3 consecutive days per week and lasted for 8 weeks at a dose of 6% TAA 200 mg/kg as an initial dose. The doses after the first time were modified according to weekly weight and AST changes in response to TAA during the induction. Rats in normal control groups were treated with saline. After the final administration in the 8th and 12th weeks, blood samples were collected and serum was separated by centrifugation at 4°C and kept at −20°C for further analysis. Then all rats were sacrificed under anesthesia. The livers were washed with cold saline, and a part of the right hepatic lobular was removed and stored in liquid nitrogen for content detection of hydroxyproline. The remaining part of the right hepatic lobular was made into slices for pathological diagnosis. Several serum markers and liver function indices studied in clinical research were measured at the 8th and 12th weeks, respectively. There are many serum markers reported as the liver function indices. After consideration, we ultimately chose hyaluronan (HA), serum laminin (LN), collagen Type I (Col I), IV collagen (IVC), procollagen III (PC-III), aspartate aminotransferase (AST), albumin (Alb), hydroxyproline (Hyp), total protein (TP), and total bilirubin (T.Bil) [7, 23] in this study. The liver tissue slices were observed and diagnosed by HE, Masson-trichrome staining, and transmission electron microscope. Then the relationship between the serum index and the occurrence of liver fibrosis was analyzed by statistics model.

2.3. Statistics Model and Solution

2.3.1. Statistics Model.

Let {(x₁, y₁), (x₂, y₂),…, (x_n, y_n)}be input-output pairs of a given data set, where x_i in R^p is variable levels of plasma markers and y_i in {0,1} is the type of liver fibrosis occurs or not identified in liver biopsy. Here, n is the number of liver biopsy and p is the number of plasma markers. For binary logistic regression, we can write it as

$${\pi }_i\left(x\right)=p_r(y_i=1\hspace{0.17em}\mid \hspace{0.17em}{x}_i)=\frac{\exp \hspace{0.17em}\left\{g\left(x_i^T\beta \right)\right\}}{1+\exp \hspace{0.17em}\left\{g\left(x_i^T\beta \right)\right\}},$$ (1)

where g(x_i^Tβ) = x_i^Tβ,   i = 1,2,…, n. Then, the log-likelihood function of this binary logistic regression is

$$l\left(\beta \right)={\displaystyle \sum }[y_i\log \hspace{0.17em}{\pi }_i+\left(1-y_i\right)\log \hspace{0.17em}\left(1-{\pi }_i\right)].$$ (2)

Further, the SCAD-penalized maximum likelihood function is

$$l\left(\beta \right)+n{\displaystyle \sum }_{j=1}^p{p}_{{\lambda }_j}\left(\left|{\beta }_j\right|\right),$$ (3)

where

$$p_{{\lambda }_j}^{\prime }\left(\theta \right)=\lambda \{I\mathrm{\hspace{0.17em}\hspace{0.17em}}\left(\theta \le \lambda \right)+\frac{{\left(a\lambda -\theta \right)}_{+}}{\left(a-1\right)\lambda }I\mathrm{\hspace{0.17em}\hspace{0.17em}}\left(\theta >\lambda \right)\}$$ (4)

for some a > 2 and θ > 0.

In general, p_λjmay be different coefficients. Here, we make λ = λ_j. In other words, the same penalty function is applied to each component of β [24]. Generally, λ can be selected by GCV. Another alternative penalized function is the least absolute shrinkage and selection operator [17]. They suggested the penalized function could be selected with p_λj = λ_j | β_j|. The algorithm can be carried with least angle regression [25]. Making λ = λ_j, the penalized maximum likelihood with LASSO is

$$n^{-1}l\left(\beta \right)+\lambda {\displaystyle \sum }_{j=1}^p\left|{\beta }_j\right|.$$ (5)

Once the regression coefficient β is estimated, the classifier is constructed as follows. Let c(i | j) be the cost of classifying an observation to the i class when the true class is j. Then, a new tissue sample with plasma markers x is classified into class c(x), where c(x) becomes

$$c\left(x\right)=\arg \hspace{0.17em}\min \hspace{0.17em}{\displaystyle \sum }c\left(i\hspace{0.17em}\mid \hspace{0.17em}j\right)p_r\left(y=j\hspace{0.17em}\mid \hspace{0.17em}x\right).$$ (6)

In practice, c(i | j) are equal which is most frequent. So minimum c(x) is equal to arg max_j p_r(y = j | x).

2.3.2. Solution

In this study, we principally discuss the SCAD penalized. It can be locally approximated by a quadratic function as follows:

$${\left[p_{\lambda }\left(\left|{\beta }_j\right|\right)\right]}^{\prime }=p_{\lambda }^{\prime }\left(\left|{\beta }_j\right|\right)\left({\beta }_j\right)\approx \frac{p_{\lambda }^{\prime }\left(\left|{\beta }_{j0}\right|\right)}{\left|{\beta }_{j0}\right|}{\beta }_j\left(1\right).$$ (7)

In other words,

$$p_{\lambda }\left(\left|{\beta }_j\right|\right)\approx p_{\lambda }\left(\left|{\beta }_{j0}\right|\right)+\frac{1}{2}{p}_{\lambda }^{\prime }\left(\left|{\beta }_{j0}\right|\right)\left({\beta }_j^2-{\beta }_{j0}^2\right).$$ (8)

Then, the penalized log-likelihood can be locally approximated by

$$\begin{array}{cc}\hfill & l\left({\beta }_0\right)+\nabla l{\left({\beta }_0\right)}^T\left(\beta -{\beta }_0\right)+\frac{1}{2}{\left(\beta -{\beta }_0\right)}^T{\nabla }^{2}l\left({\beta }_0\right)\left(\beta -{\beta }_0\right)\hfill \\ \hfill & \hspace{1em}\hspace{1em}+\frac{1}{2}n{\beta }^T{\displaystyle \sum }_{\lambda }\left({\beta }_0\right)\beta ,\hfill \end{array}$$ (9)

where

$$\begin{array}{cc}\hfill & \nabla l\left({\beta }_0\right)=\frac{\partial l\left({\beta }_0\right)}{\partial \beta },\hspace{1em}\hspace{1em}{\nabla }^{2}l\left({\beta }_0\right)=\frac{{\partial }^{2}l\left({\beta }_0\right)}{\partial \beta \partial {\beta }^T},\hfill \\ \hfill & {\displaystyle \sum }_{\lambda }^{}\left({\beta }_0\right)=\mathrm{diag}\hspace{0.17em}\{\frac{p_{\lambda }^{\prime }\left|{\beta }_{10}\right|}{\left|{\beta }_{10}\right|},\dots ,\frac{p_{\lambda }^{\prime }\left|{\beta }_{p0}\right|}{\left|{\beta }_{p0}\right|}\}.\hfill \end{array}$$ (10)

We then estimate β  as follows:

$${\beta }_1={\beta }_0-{\left\{{\nabla }^{2}l\left({\beta }_0\right)+n{\displaystyle \sum }_{\lambda }\left({\beta }_0\right)\right\}}^{-1}\left\{\nabla l\left({\beta }_0\right)+n{\displaystyle \sum }_{\lambda }\left({\beta }_0\right)\right\},$$ (11)

where

$$\begin{array}{cc}\hfill & \nabla l\left({\beta }_0\right)=\frac{\partial l\left({\beta }_0\right)}{\partial \beta }=X^{\prime }\left(Y-{\displaystyle \prod }\right),\hfill \\ \hfill & {\nabla }^{2}l\left({\beta }_0\right)=\frac{{\partial }^{2}l\left({\beta }_0\right)}{\partial \beta \partial {\beta }^T}=X\prime VX,\hfill \end{array}$$ (12)

Y = (y₁, y₂,…,y_n)′, ∏ = (π₁, π₂,…, π_n), V = diag (π_i · (1 − π_i)), and X is an index matrix. Given the good initial value β₀, the penalized maximum likelihood can be as efficient as the fully iterative procedure.

2.3.3. Simulation Studies

In this subsection, we numerically compare the proposed approach of variable selection and classification methods with SLDA and LASSO methods.

We simulate 1000 datasets when n = 20, 40, 60, 100 respectively, from the model Y ~ Bernoulli{π(x^Tβ)}, where π(u) = exp (u)/(1 + exp (u)) and β = (3,1.5,0, 0,2, 0,0, 0). The previous six components of x come from a standard normal distribution. The correlation between x_i and x_j is ρ^|i−j| with ρ = 0.5. The last two components of x are independently and identically distributed as a Bernoulli distribution with probability of success 0.5. All covariates are standardized. This model was used in Tibshirani et al. [17]. The classification standard is based on the probability arg max  p_r(y = j | x).

Define

$$\begin{array}{cc}\hfill & \text{MedTrue}=\text{median}\left\{1-\frac{{\rm Y}\left|Y_{\text{Predict}}-Y_{\text{Oracle}}\right|}{n}\right\},\hfill \\ \hfill & \text{MeanTrue}=\text{mean}\left\{1-\frac{{\rm Y}\left|Y_{\text{Predict}}-Y_{\text{Oracle}}\right|}{n}\right\}.\hfill \end{array}$$ (13)

The true classification ratio is computed via 1000 Monte Carlo simulations. The summary of simulation results is depicted in Table 1.

Table 1.

True classification ratio simulations results.

n	SLDA		SLR-LASSO		SLR-SCAD
	MedTrue	MeanTrue	MedTrue	MeanTrue	MedTrue	MeanTrue
20	0.95	0.9335	0.9	0.8559	0.9	0.8974
40	0.95	0.9558	0.925	0.9285	0.925	0.9254
60	0.9667	0.9657	0.9667	0.9546	0.95	0.9488
100	0.98	0.9728	0.98	0.9729	0.98	0.9687

SLDA: stepwise linear discriminant analysis.

SLR-LASSO: sparse logistics regression-least absolute shrinkage and selection operator.

SLR-SCAD: sparse logistics regression-smoothly clipped absolute deviation penalty.

Table 1 shows that the true classification ratio associates with the sample size n. With the increase of the sample size n, the true classification ratio tends to one. Another important key point: three methods are all working well for large sample size n.

3. Result

3.1. Histopathology of Liver Fibrosis

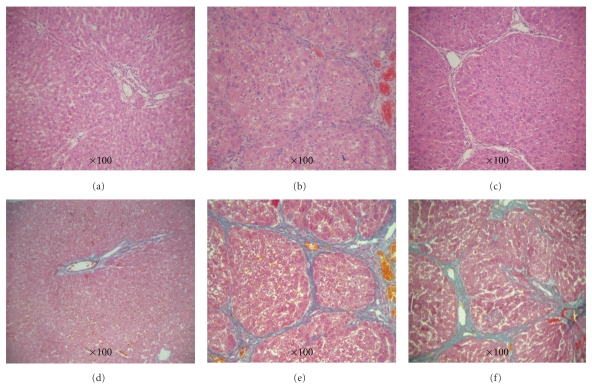
Typical liver fibrosis was induced after 8 weeks of TAA treatment, with the hepatofibrosis pathological characteristics of fibroblast extending around from central venous or portal area, forming the obvious fiber separator without the formation of false lobules. From the light microscope, it could be seen that pathological slice of normal animals had clear lobule, there was no edema or denatured fat in liver cells, and Sinus hepaticus had no expansion and congestion (Figures 1(a) and 1(d)). The pathological slice of model animals had obvious fibroplasias extending from the central venous or portal area to surrounding area, which formed the clear fibrous septa. The liver cells had mild steatosis with lipid droplet and vacuoles accompanied by mild bile duct hyperplasia (Figures 1(b), 1(c), 1(e), and 1(f)).

Figure 1.

Progression of TAA-induced liver fibrosis in SD rats was assessed by HE and Masson-Trichrome staining at different time points of treatment. (a–c) HE staining, (a) Nomal, (b) 8 w Model, and (c) 12 w Model, (d–f) Masson-trichrome staining, (d) Nomal, (e) 8 w Mode, and (f) 12 w Mode.

3.2. Serum Markers Analysis

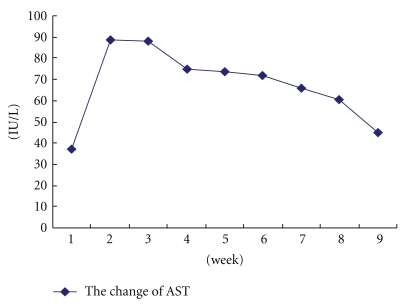
According to Table 3, there was a major difference between the normal group and control group in several serum markers and liver function indices such as HA,LN, IVC, and I Collogen. During the 1st–4th weeks, AST activity reached the peak and there is no significant difference (P > .05) in the 5th to 8th weeks (Table 2). In Figure 2, it is shown that after peak value AST activity gradually decreased and returned to normal during the 12th week. As a matter of fact the level of AST in human goes up obviously during acute hepatitis, and it correlate with the severity of the disease. Then the activity of AST decreases during the course of liver fibrosis [26]. AST activity of control group was significantly higher than the normal group and decreased slightly in the 12th week without TAA for four weeks which agrees with the literature [27]. At last typical liver fibrosis was induced after 8 weeks of TAA.

Table 3.

The content of determined parameters in the serum during TAA induction (x ± s).

Group	(A/T)	( AST)	(Hyp)	(IVC)	( LN )	(PC-III)
	(%)	(IU/L)	(ng/mL)	(ng/mL)	(ng/mL)	(ng/mL)
Normal	46.53 ± 12.13	36.80 ± 6.94	137.14 ± 12.98	18.14 ± 3.08	10.28 ± 7.49	7.44 ± 4.38
Model	40.45 ± 11.40	54.09 ± 13.26	193.96 ± 14.29**	21.60 ± 4.07**	17.78 ± 6.68**	10.88 ± 3.25**
Group	(Col I)	(HA)	(T.Bil)	(A/G)	(Alb)	(TP)
	(ng/mL)	(ng/mL)	(ng/mL)	(%)	(mg/mL)	(mg/mL)
Normal	31.48 ± 5.27	5.26 ± 5.49	5.55 ± 1.19	83.99 ± 14.45	37.27 ± 11.56	79.62 ± 8.64
Model	48.10 ± 14.68**	16.86 ± 8.6**	4.91 ± 1.75	73.52 ± 11.92	32.09 ± 9.62	79.28 ± 7.69

**P < .05, compared to the normal group.

Table 2.

The level of AST in liver tissue during induction (x ± s).

Group	Week	AST (IU/L)
Normal	8 w	37.33 ± 6.94
	12 w	36.27 ± 6.21
Model	8 w	67.37 ± 8.83**
	12 w	40.8 ± 7.26

**P < .05, compared to the normal group.

Figure 2.

The change of AST during induction.

3.3. Application

We applied the proposed sparse logistic regression with SCAD, LASSO, and SLDA to the classification of liver fibrosis. The dataset consisted of 26 observations. The binary response variable Y is 1 for those rats who have liver fibrosis and 0 otherwise. All the twelve covariates are considered. All covariates' meanings were listed in Table 4.

Table 4.

List of covariates for plasma markers.

Covariates	Plasma markers
Y	Diagnosis the degree liver fibrosis by using the pathological diagnosis
x1	Albumin ratio of total protein (A/T)
x2	Aspartate aminotransferase (AST)
x3	Hydroxyproline (Hyp)
x4	IV collagen (IVC)
x5	Serum laminin (LN )
x6	III collagen (PC-III)
x7	I collagen (Col I)
x8	Hyaluronan (HA)
x9	Total Bilirubin (T.Bil)
x10	Albumin ratio of the globulin (A/G)
x11	Albumin (Alb)
x12	Total protein (TP)

Carrying out the procedure, including the SLDA, SLR-SCAD, SLR-LASSO, then the outcome about the selected variable and the classification true rates were obtained, respectively, according to Tables 5 and 6.

Table 5.

List of variable selection results.

SLDA	SLR-LASSO	SLR-SCAD
Hydroxyproline	Hydroxyproline	Hydroxyproline
I collagen	LN	LN
Hyaluronan	IV	—
—	Hyaluronan	—

Table 6.

List of classification true rates.

	SLDA	SLR-LASSO	SLR-SCAD
Classification true rates (%)	96.15	92.31	96.15

3.4. Test Significance

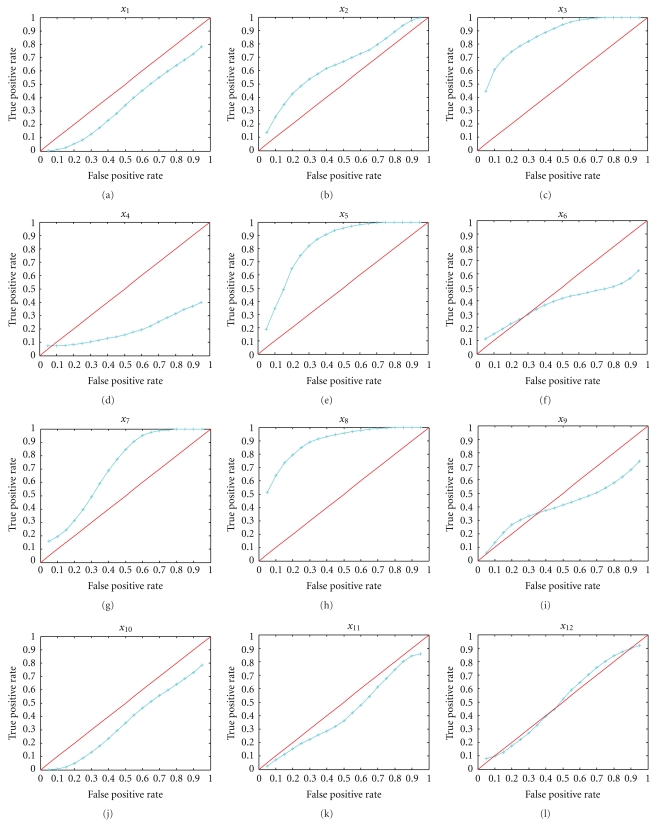
The receiver operating characteristic (ROC) curve is an excellent method to test the significance of selected variables. The ROC curve is a plot of the true positive fraction (TPF) as a function the false positive fraction (FPF), or sensitivity versus one minus specificity, and is obtained by varying the threshold criterion distinguishing between a positive and negative diagnosis. For example, the diagnostic variables X ~ F are for the population without liver fibrosis and Y ~ G are for those with liver fibrosis, where F and G are the distribution functions. Some features such as the invariance property and interpretation of the area under the curve (AUC) as p_r(Y > X) make the ROC analysis extremely popular in diagnostics research. Generally, the selected variables are sensitive for the classification if the AUC > 0.7. However, estimation of AUC for the ROC curve is very difficult, especially for the small sample size. Here, we use the Bayesian bootstrap (BB) estimation of AUC, proposed by Kuriyama et al. [22], to test the variables in SLDA, LASSO, and SCAD. The AUC calculation results are shown in Table 7, displaying the sensitivity for classification variable Y. Figure 3 described these covariates' ROC curves.

Table 7.

ROC curve analysis.

	x1	x2	x3	x4	x5	x6
AUC	0.3134	0.5869	0.7989	0.1685	0.7632	0.3450
	x7	x8	x9	x10	x11	x12
AUC	0.6510	0.8173	0.3729	0.3169	0.3733	0.4569

Figure 3.

BB estimates of ROC curves for diagnostic covariates for markers.

The ROC of x₃, x₅, and x₈ are more than 0.7, and they represent the hydroxyproline, LN, and hyaluronan, respectively.

As shown in Table 7 and Figure 3, we come to a conclusion that some covariates may be very important for diagnosis of the occurrence of liver fibrosis, such as hydroxyproline, LN, hyaluronan, as the AUCs for these covariates are more than 0.7.

Fortunately, these covariates are all selected by the three statistical models. Though SLR-SCAD chose only two covariates, it gets higher diagnostic accuracy, equaling to SLDA, better than SLR-LASSO, as shown in Tables 5 and 6. It elucidates that by using SLR-SCAD we could obtain high diagnostic accuracy with fewer serum indices so as to save the experiment cost. Meanwhile, the SLDA and SLAR-LASSO also display well. But their high diagnosis accuracy needs more variables to be selected.

4. Discussion and Conclusion

It has been thought that the research on liver fibrosis is entering a new era of the whole wound and heal reaction [28]. The ideal animal model, which is a reliable and reproducible on hepatic fibrosis, should have the basic pathological characteristics with the same phase change on pathology as human liver fibrosis. However, there are some defects on detection methods in the process of establishing animal model. Considering the limitation of traditional test method in modeling, we propose an alternative approach to construct the quantification between fibrotic condition and serum indices. Since accurate diagnosis of liver fibrosis remains a difficult and crucial problem in both the animal models and patients, an ongoing challenge is to identify new prognostic markers that are directly related to liver fibrosis and that can more accurately predict the likelihood of gaining liver fibrosis. Here we introduce a new approach to the jointing problems of simultaneous classification and variable selection utilizing the sparse logistics regression with SCAD-penalized function. The proposed method is applied in our study to analysis the data of plasma makers for diagnosis of the liver fibrosis in rat model and to determine the occurrence of cirrhosis.

In this study, the pathological section results were used to determine whether the reliable animal model with liver fibrosis induced by the dose individualization of TAA was established successfully. Despite, there is, difference between liver biopsy of human in clinic and pathological section of dead animal, they are both expensive, invasive and have a chance of death, especially the inevitable death of animals. It is because that the pathological slice from the whole rat's liver could supply the highest accuracy that the results can be as the standard to verify the outcome of statistical model. There is no doubt that sacrificing animal life attributes to significant mortality rates and disobeys the morality and ethics. Our proposed method by using serum indices may indeed greatly decrease the consumption of a lot of animals when used in hepatic drug screening.

Monitoring a variety of plasma markers, especially the levels of collagen-related markers, is becoming a novel approach of liver fibrosis diagnosis with simple procedure and high sensitivity and accuracy. According to Table 1, the novel SLR-SCAD method performs as well as other well-known methods such as SLDA and SLR-LASSO in statistical classification and variable selection. They all perform well for the fixed sample size. The SLR-SCAD achieved higher classification ratio by the two selected variables, hydroxyproline and LN, which are reasonable by the verification of ROC curve. The two variables also have significant sense in clinic. If SLDA and SLR-LASSO want to obtain higher classification, they need to test more serum indices. In addition, it is mentioned that the SLDA method has its own drawback especially when the variables have collinearity [26, 29]. Compared with the SLDA and SLR-LASSO methods, SLR-SCAD is quite befitting for penalized regressions.

It will be a very useful approach to determine the occurrence of liver fibrosis in animals based on statistic models with fairly high diagnosis accuracy and without loss of animals. The occurrence of liver fibrosis can be effectively estimated in rats by using our proposed SLR-SCAD method with the right serum indices. In summary, we propose a new method by combining the analysis of serum index of fibrosis and statistic model which represent a reliable diagnostic and prognostic approach of liver disease. It could be beneficial to extend this study to other fields where classification and many variables exist.