Migration of connective tissue-derived cells is mediated by ultra-low concentration gradient fields of EGF

Abstract

The directed migration of cells towards chemical stimuli incorporates simultaneous changes in both the concentration of a chemotactic agent and its concentration gradient, each of which may influence cell migratory response. In this study, we utilized a microfluidic system to examine the interactions between Epidermal Growth Factor (EGF) concentration and EGF gradient in stimulating the chemotaxis of connective-tissue derived fibroblast cells. Cells seeded within microfluidic devices were exposed to concentration gradients established by EGF concentrations that matched or exceeded those required for maximum chemotactic responses seen in transfilter migration assays. The migration of individual cells within the device was measured optically after steady-state gradients had been experimentally established. Results illustrate that motility was maximal at EGF concentration gradients between .01- and 0.1-ng/(mL.mm) for all concentrations used. In contrast, the numbers of motile cells continually increased with increasing gradient steepness for all concentrations examined. Microfluidics-based experiments exposed cells to minute changes in EGF concentration and gradient that were in line with the acute EGFR phosphorylation measured. Correlation of experimental data with established mathematical models illustrated that the fibroblasts studied exhibit an unreported chemosensitivity to minute changes in EGF concentration, similar to that reported for highly motile cells, such as macrophages. Our results demonstrate that shallow chemotactic gradients, while previously unexplored, are necessary to induce the rate of directed cellular migration and the number of motile cells in the connective tissue-derived cells examined.

INTRODUCTION

Chemotaxis is the directed movement of cells in response to chemical attractant stimuli (reviewed in [1, 2].) Chemotactic phenomena bear critical roles in numerous biological processes, including morphogenesis, tissue repair, and response to infection [3–5]. Mechanisms of cellular motility within three-dimensional matrixes [6, 7] and upon two-dimensional substrates are well-established, as are the structures of receptors activated by chemotactic stimuli [8–11] and their consequent intracellular signaling pathways [1, 12, 13]. Yet, much less is known about the complex mechanisms by which cells sense the directionality and strength of a chemotactic stimulus, in large part because the stimulus needed to initiate cell movement requires simultaneous changes in attractant concentration and concentration gradient [8, 14–16]. While traditional benchtop technologies such as Boyden and Dunn chambers, scrape and agarose assays have contributed significantly to indentifying cytokine concentrations that generate directed cell movement (reviewed in [7, 17]), these systems cannot be used to measure mechanistic parameters like motility, polarization, directionality or the sensitivities of individual cells to concentration gradients and thresholds [8, 10, 15, 18, 19]. Widespread usage of microfluidic devices in biological engineering has circumvented many of these limitations. Numerous microdevice-based studies have analyzed cell motility within precisely-controlled microenvironments [20], leading to experimental demonstrations that: i) Chemotaxis is activated by the so-called specific gradient [21] defined as the change in chemical concentration gradient across the length of a cell, and, ii),Gradient sensitivities differ with cell type [4, 16, 22]

The ability to exert precise environmental control makes microdevices ideally suited to study the relative contributions of attractant concentration and specific gradient to cellular chemotaxis. However, many microfluidics-based experiments have studied chemotaxis in the presence of significant bulk flow, using micro-valves and -actuators, external pumps and power supplies to vary the concentration, flow, perfusion, and/or streaming of chemotactic agents [20, 23, 24]. As established works have illustrated that significant bulk flow can itself influence cell behavior and migratory responses [25, 26], such systems may be useful to study cells that routinely experience fluid flow under physiological conditions (e.g. circulating cells), but less so for examining the chemotaxis of cells not normally exposed to high levels of fluid flow (e.g. connective tissue fibroblasts).

Chemotaxis of cells derived from soft connective tissues has received growing interest, in large part because of the community's efforts to enhance the notoriously slow rates of repair and regeneration in these tissues [27, 28]. In particular, many tissue engineering studies have begun to focus upon the microenvironment experienced by these cells as a strategy for developing more effective soft tissue biomaterials that can be used for surgical dressings and sutures (reviewed in [29]). The cellular microenvironment of soft tissue injury is expected to house concentration gradients of chemotropic growth factors that are very shallow (i.e. exhibit small changes in concentration over long distances) as a consequence of the large cell-to-cell distances within the collagenous extracellular matrix of these tissues. While cellular microenvironments of low specific gradient fields have been incompletely-studied in the literature, our group has recently developed a microfabricated system, called the bridged µLane [30], that enables study of cell chemotactic responses within microenvironments of ultra-low attractant concentration and gradient. In this system, buoyancy-driven forces initiate minute convective velocities that assist molecular diffusion of chemotropic factors over long distances. The bridged µLane enables sequential optical monitoring of individual cell movement within predictable microenvironments that create precise spatial and temporal profiles of attractant concentration and gradient. We previously analyzed the molecular transport within the system by solving the constitutive relations of convective-diffusive flux exactly, as well as experimentally validated these results using microbeads and fluorescent dyes [30]. In the present study, we utilized the device to investigate the changes in motility of ligament-derived fibroblast cells in response to changes in concentration and specific gradient of epidermal growth factor (EGF), a known chemoattractant for these cells. Experiments utilized minute specific gradients of 10⁻¹⁶M to 10⁻¹²M of EGF per micron length of cell to examine the migratory responses of over 100 individual cells under different attractant profiles. Our results indicate that while the attractant concentration is significant to initiate cellular motility, the specific gradient substantially influences: i) The ability of cells to orient themselves in the attractant gradient; ii) The numbers of cells that respond to the stimulus, and iii) The directed cell speed. In addition, correlation of experimental data with established mathematical models of migration illustrated that soft tissue fibroblasts exhibit surprising intrinsic chemosensitivity to small changes in EGF concentration comparable to that of highly motile cells, such as leukocytes and macrophages [31]. These results suggest that expanded study of the chemotactic abilities of soft-tissue derived cells within low specific gradient fields may provide a distinctive strategy for the development of more effective soft tissue biomaterials.

MATHEMATICAL MODELING

The motility of a cell population can be described in terms of a cell flux model from probabilistic arguments of cell movement. Such a cell flux model defined migration as having significant contributions from random movement, chemokinesis, and chemotaxis [22, 32–34].

$$\left(\frac{\partial c}{\partial t}\right)=-\left(\frac{\partial J_c}{\partial x}\right)$$ (1)

$$J_c=-\mu (a)\frac{\partial c}{\partial x}+[-\frac{1}{2}\frac{d\mu (a)}{\mathit{\text{da}}}-\chi (a)]\frac{\partial a}{\partial x}c$$ (2)

Where c is cell density (cells/area) J_c is cell flux, t is migration time, and x is migration distance. The parameter μ represents the random motility coefficient (defined as a persistent random walk), a the attractant concentration, and χ is the chemotaxis coefficient, defined as the ability of cells to bias their direction, i.e. orient themselves, in a gradient of attractant concentration.

Established work from Farrell et al later illustrated that the response of a given cell population can be mathematically modeled as an average of its individual cell responses [32]. The chemotactic movement of single cells can be then modeled in terms of the cell speed, S, root-mean-square center-of-mass location, <x²(t)>, and persistence time, P, the average time in which a cell moves in given direction before significant changes in directionality. The model also defines chemotactic index, CI, a measure of the directedness of a cell’s path towards an attractant source. The index approaches zero for pure random motion, and approaches 1 for perfectly directed motion as defined below:

$$<x^2(t)>=2s^{2}P(t-P(1-e^{-t/P})$$ (3)

$$\mathit{\text{CI}}=\left(\frac{X}{L}\right){[1-(\mathit{\text{Pt}})(1-e^{-t/P})]}^{-1}$$ (4)

where L is total path length of a motile cell, X is its straight line path, t is time, and P is a cells persistence time.

Chemotaxis is is a receptor-mediated phenomenon that depends not only on local attractant concentration and gradient, but also upon the number of bound receptors and the intrinsic cellular processes regulating receptor expression and receptor down regulation in the presence of the attractant ligand. The number of bound receptors on a given cell is a function of attractant concentration, as described by:

$$N_b=N_T(a)\left[\frac{a}{K_D+a}\right]$$ (5)

Where N_T is the total number of receptors in the presence of attractant concentration, a, and K_D is the dissociation constant, i.e. the attractant concentration at which the probability that the receptor will be bound is 1/2 [35, 36]. The chemotactic index, CI, can then be correlated to the population intrinsic chemotactic sensitivity of cells to an attractant.

$$\mathit{\text{CI}}=\frac{\left[{\chi }_0\right(\frac{{\mathit{\text{dN}}}_b}{\mathit{\text{da}}}\left)\right(\frac{\partial a}{\partial x}\left)\right]}{[1+{\chi }_0(\frac{{\mathit{\text{dN}}}_b}{\mathit{\text{da}}}\left)\right(\frac{\partial a}{\partial x}\left)\right]}$$ (6)

Where χ₀ is termed the intrinsic chemotactic sensitivity, N_b is the number of bound receptors and a is the attractant concentration.

Using this well-established model of migration, researchers have been able to correlate cell speed with the fraction of a cell population oriented along an attractant gradient [33] and with the number of bound receptors in a cell specific gradient [8], and to indentify physiological sensitivity of particular cell types to known attractants [32]. In this work, we interpret our experimental data in terms of this model, and also use it to provide a mathematical basis for describing the motility of soft tissue-derived fibroblasts to specific gradients of EGF.

METHODS AND MATERIALS

Cell culture

Fibroblasts were harvested from bovine medial collateral ligament (MCL) explants received from the laboratory of Dr. Peter Torzilli (Hospital for Special Surgery New York, NY) as described previously [25, 37]. Cells were washed and cultured in Eagle’s Medium (EMEM) supplemented with 10% fetal bovine serum (FBS) 2% L-Glutamine and 1% (v/v) antibiotic-antimycotic solution (Mediatech Inc., VA) at 37°C in a 5% CO₂ humidified incubator. Cells were subcultured when cultures became ~ 90% confluent using a five-minute treatment with 0.05% trypsin-0.53mM EDTA (Mediatech Inc., VA) at 37°C followed by centrifugation. All cells were used for experiments prior to the 5th passage.

Transwell assays

Transwells for 24-well plates (Becton Dickinson and Company, Franklin Lakes, NJ) were coated with 50 µl of 1-mg/mL collagen (BD Biosciences, Bedford, MA) in 0.1% acetic acid (EMD Chemicals Inc., Gibbstown, NJ) and allowed to dry overnight at room temperature. Fibroblast suspensions (350 µl; 5×10⁴ cells/mL) were pipetted into each insert, which were then placed in wells containing EGF (MW: 6 kDa, Molecular Probes, Eugene, OR; 0 to 100 ng/mL final concentration) in 700 µl of EMEM with 10% FBS. After incubating at 37° C for 20 hours, inserts were removed from the plate and stained following manufacturer specifications. Fibroblasts on the underside of each insert were counted using a Nikon microscope and Relative Chemotaxis Factor (RCF), defined as the ratio between the number of cells that migrated in the presence and absence of EGF was determined for each concentration. Four wells were counted for each treatment group in the experiment, and the experiment was repeated 4 times.

Cell proliferation assays

Fibroblasts were suspended at 5×10⁴ cells/mL in complete medium containing 10% FBS and EGF (0-ng/mL to 400-ng/mL), and 100 µL portions were added to 96 well culture plates. The cells were cultured for 96 hours, after which cell numbers were assayed using a Cell Titer 96 assay kit (Promega Corp, Madison, WI) following the manufacturer’s instructions. A 2-hour incubation with dye was used. Absorbance at 470 nm was measured using a Synergy HT plate reader (BioTek Instruments Inc., Winooski, VT). Eight wells per treatment group were assayed at each time point, and the experiment was repeated 4 times.

In-cell western blotting

This technique has been used to detect growth factor receptor phosphorylation. Fibroblasts were cultured in 48-well plates (Corning Inc., Corning, NY) for 3 days until they reached confluence with a density of 10⁶ cells/well. Cells were then fed with serum-free EMEM for 4 hours and treated with EGF (0 ng/mL – 400 ng/mL). After 1 hour, cells were fixed with 3.7% paraformaldehyde (Sigma-Aldrich Inc., St. Louis, MO), permeabilized with 0.1% Triton X-100 (Sigma-Aldrich Inc., St. Louis, MO), washed with 0.1% Tween-20 (Acros Organics, Morris Plains, NJ), treated with blocking buffer (Li-Cor, Inc., Lincoln, NE) at room temperature (25°C) and incubated with rabbit polyclonal anti-EGFR primary antibody (Abcam Inc, Cambridge, MA, part #: ab2430) and mouse monoclonal anti-phosphorylated EGFR primary antibody (Biodesign International, Saco, ME, part #: K67902M) at 4°C for overnight (~14 hours). The cells were then washed and incubated with goat-anti-rabbit secondary antibody (Li-Cor, Inc., Lincoln, NE, part #: 926-32211) and goat-anti-mouse secondary antibody (Li-Cor, Inc., Lincoln, NE, part #: 926-32220) at room temperature for 1 hour. Subsequently, an infrared imaging system, Odyssey (Li-Cor, Inc., Lincoln, NE), was used to record the infrared intensity from EGFR and the phosphorylated EGFR within the cells.

Microfabrication of the bridged µLane system

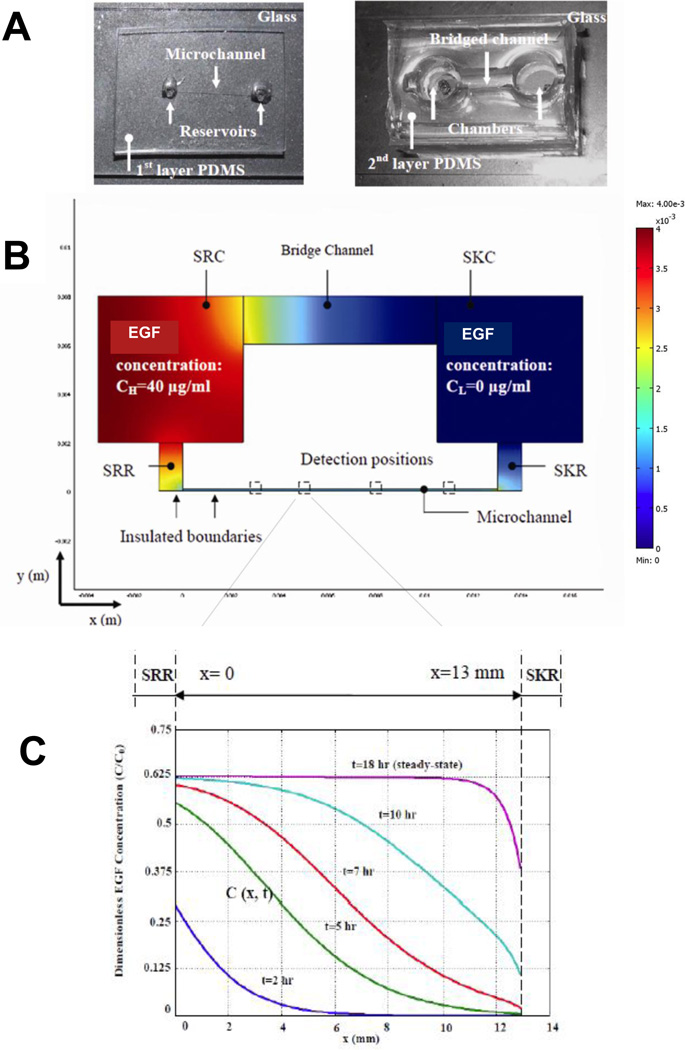
The bridged µLane system was designed to generate chemical concentration gradients within a transparent system that facilitates observation of cell responses to stimuli. The fabrication and operation of the system has been described previously [30]. In brief, it consists of two layers of poly-dimethylsiloxane (PDMS) with a closed microchannel (95-µm-hydraulic diameter; 1.2-cm-length), a source reservoir (SRR; 3µL-volume) and a sink reservoir (SKR; 3µL-volume) on the bottom layer, as well as a source chamber (9-mL volume), a sink chamber (9-mL volume) and an open, hemispherical bridge channel (2-mm-depth; 9-mm-length) on the top layer (Figure 1A). The bridged µLane system was fabricated using contact photolithography, elastomeric molding of PDMS, and bonding of PDMS to glass and PDMS to PDMS. The SRC and SKC chambers are vertically and fluidically connected with the SRR and SKR reservoirs, respectively, in the bottom layer, and the bridge channel connects the SRC and SKC chambers in order to balance their solution volumes. The complete bridged µLane system is thus composed of an open bridge channel that connects the SRC and SKC chambers, as well as a closed microchannel that connects the SRR and SKR reservoirs.

Figure 1.

Characterization of the bridged µLane system as adapted from [30]. (A) The two-layer PDMS system consists of a microchannel, two reservoirs, two vertically-fluidic chambers, and a larger so-called bridge channel. Images of the two layer system are shown. EGF solutions at concentration of C₀ are manually inserted into the source chamber (SRC) and allowed to transport toward the sink reservoir (SKR) through the 12-mm-long microchannel. (B) Schematic of EGF transport within the microchannel as mathematically modeled via FEMLab. (C) The change in dimensionless EGF concentration, defined as C(x,t)/C₀, as a function of time and axial position within the microchannel is graphically illustrated at 2, 5, 7, 10 and 18 hours.

The overall system works by using the large volume chambers and bridge channel on the 2^nd to generate concentration gradients within the smaller volume microchannel on the first layer. Solution is manually loaded until it has filled the SRR reservoir, microchannel, SKR reservoir, SKC chamber, and bridge channel. Sample is then loaded into the SRC chamber until the sample makes dropwise contact with solution within the bridge channel to initiate system operation (Figure 1B). The volume of each chamber (170 µl) is designed to be much larger than the volume within each reservoir (9µL) and µLane (0.1µL), in order to facilitate manual loading via conventional pipette or syringe to initiate gradual transport into the microchannel with minimal channel entrance effects. Movement of solute (e.g. EGF) from the source to sink chambers generates concentration gradients within the closed microchannel on the bottom layer.

As reported in ref. 30 the µLane system is loaded with a reagent of interest, in this case EGF, via the Source Chamber (SRC). The hydrostatic pressure head generated by loading within the SRC is described below:

$$-\nabla P+\rho \mathit{\text{gh}}=0$$ (7)

Where P is pressure, ρ is reagent density, g is gravity and h is height. Using the manufacturer- provided values of reagent densities, our previous work was able to show that the loading of Dextran (ρ=1.440 g/mL) within PBS (ρ=1.020 g/mL) into the µLane system generated a pressure difference of ~10⁻²N/m². This is equivalent to 10⁻⁷ atmospheres or 0.01 mmH₂O. At first glance one might question whether such a miniscule pressure difference could generate a physiologically relevant flow in the µchannel. However, such tiny pressure differences have previously been shown to drive many microfluidic systems [20]. The velocities in the microchannel are indeed very small, as it requires approximately 10 hrs for the flow entering at the source reservoir, SRR, to exit at the sink reservoir, SKR. In marked contrast, the characteristic diffusion time, t= L²/D (where D = 2×10⁻⁶ cm²/s for EGF), is approximately 10 days, and far longer than the convection time. The µchannel flow is, thus, convection dominated despite the miniscule driving force.

Using the well-known Poiseuille relation for laminar flow in an equivalent circular cylinder, one can easily estimate the average bulk velocity within the microchannel driven by the miniscule hydrostatic pressure difference between the source and sink reservoirs of the microchannel with the relation below:

$$Q=\nu \pi R^2=\frac{\pi R^4\mathrm{\Delta }P}{8\mu L}$$ (8)

Where Q is volumetric flow rate, v is average bulk velocity, R is radius, P is pressure, μ is viscosity, and L is length. This average bulk velocity is predicted to be 0.17um/s, with a centerline velocity of twice this value. Actual experimental measurement of 0.1um-diameter beads within the microchannel over 4 hours resulted in an average bulk velocity of 0.37+/−0.11 um/s. Note that the radial distribution of particles along the parabolic velocity profile could not be measured, but it is known that very small inertial effects cause an axial drift, known as the Segre-Silberberg effect, and this could partially account for the difference between predicted and measured values in addition to the fact that the channel is not circular and there is sedimentation. Further, the flow of beads was experimentally measured to become steady, i.e. exhibit minimal difference in velocity over time, after several minutes and was seen to remain steady for several hours afterwards. The reason that the velocity remains nearly constant is that the height of the SRC (1mm) is an order of magnitude larger than the height of the SRR (0.47 mm) and although the EGF concentration is changing within the SRR, it remains virtually unchanged in the SRC over the duration of the experiment. With a bulk velocity of v=0.37 µm/s, it takes ~10 hours for fluid to traverse the µchannel. As the entire volume of the channel is 0.12µl, only 0.9% of the fluid in the SRR actually moves into the µchannel during this 10-hour period and the convective velocity in the SRR and SRC are negligible

The addition of convection within the microchannel with a miniscule bulk velocity adds several benefits to the system. First, the convective flow dramatically reduces the time required to achieve a steady-state concentration profile within the microchannel. Whereas diffusion of EGF alone along the 13-mm-length channel would require 10 days to reach steady-state, convective diffusion across this entire length requires only 18 hours. Second, such ultra-low bulk velocities enable the SRC and SKC to act as volumetric reservoirs that sustain the microchannel flow for several days. As per the measured bulk velocity of 0.37um/s (~13mm per hour), 10 hours are required for the microchannel volume to be displaced into the SKC, meaning the steady-state profile of the microchannel flow is maintained for well over 100 hours before the SKC concentration is appreciably affected. Note that even after 100 hours only 1.2µL will have passed between the SRC and the SKC, whereas their volumes are more than 100 times this.

EGF Concentration Profiles

We previously determined the time course of gradient formation by dextran in this system and used the same mathematical analysis to model and experimentally measure the transport of EGF. Two-dimensional numerical simulations of the bridged µLane system were performed in order to model the transport within entire the microsystem, i.e. the microchannel, both the SRR and SKR reservoirs in the 1^st layer PDMS, the bridge channel, and both the SRC and SKC chambers in the 2^nd layer PDMS. The mass transport within the entire microsystem was modeled using the constitutive relations of continuity, convective-diffusion, momentum equation and hydrostatics. These coupled equations were solved using finite element methods (FEMLab Version 3.4, Comsol Inc., Burlington, MA). A fine mesh of 1504 elements was used, which confined the distance between nodes to approximately 8 µm and computational time of less than 3 minutes. Note that simulation results remained approximately unchanged (<1%) when finer meshes were used.

A subtle but significant engineering design in our µLane system is the relevance of the driving force, i.e. the reagent perturbation in the SRC. As seen in Figure 1C, the concentration of EGF in the SRR, i.e. the inlet to the microchannel directly below the SRC, increases over time. This occurs because the pressure head generated by reagent loading in the SRC drives the transport of the reagent into the microchannel. As shown in the figure, the initial normalized EGF concentration at time t=2hrs is approximately C/C₀=0.26, and rises to a maximum of C/C₀=0.625 after approximately t=10hrs. This reflects reagent diffusive transport from the SRC to the SRR, and into the microchannel entrance, a distance of < 1 mm. Similarly only diffusion is considered in the SKR, SKC and across the bridge. In marked contrast, transport in the µchannel is dominated by convection with diffusion having a minimal effect, basically a blurring of an advancing convective front. This coupling is modeled via finite element of interconnected continuity, momentum, hydrostatics, and convective diffusion relations. The volumes of the SRR and SKR are so much smaller than those of the SRC and SKC (9ul to 140ul), that the SRC and SKC effectively act as infinite reservoirs, and as such their concentrations do not change. This is of great importance because if transport within the microchannel had been dominated by diffusion, the quasi-steady state would be a linear gradient between the slowly changing inlet and outlet concentrations within the SRR and SKR. Evidence that they do not illustrates the interconnected analysis of the µLane system, which includes the perturbation loading with the SRC, the SRR, microchannel, SKR, and bridge channel.

The initial concentrations of EGF in the SRC chamber were set to the values used in experiments, i.e. 40-ng/mL, 80-ng/mL, or 400-ng/mL, while EGF concentration within the SKC chamber was initially set to 0-ng/mL. Experimental measurement of EGF transport within the channel over time generated a diffusivity value of 2.0×10 ⁻⁶ cm ² /s, which is well within the range of published EGF diffusivities shown in Table 1 [38–41] Our device-measured EGF diffusivity of 2.0×10 ⁻⁶ cm ² /s was then used to generate mathematically precise EGF concentration profiles within the bridged µLane as a function of time and position shown in Figure 1C. As seen, the data illustrate that a steady-state EGF concentration distribution is established after approximately 18 hours. After steady-state is reached, the concentrations of EGF near the source (SRR) and sink (SKR) reservoirs at the ends of the microchannel are approximately 63% and 38%, respectively, of the initial EGF concentration pipetted into the source chamber (SRC), i.e. 40-ng/mL, 80-ng/mL, or 400-ng/mL. More detailed analysis reveals that the time courses and shape of concentration gradient profiles within the microchannel are virtually identical for all starting concentrations of EGF.

Table 1.

Published EGF diffusivities measured using different experimental and computational methods. EGF diffusivity measured within the in vivo rat cortex was reported to be 0.50–0.53×10⁻⁶ cm²/s, while the in vitro measure of EGF diffusivity using dilute agarose gel yielded 1.2–1.7×10⁻⁶ cm²/s. The computation of EGF diffusivity using the Stokes-Einstein Equation was also reported in the literature with a value of 2.1–2.3×10⁻⁶ cm²/s. The EGF diffusivity used in the present simulation was chosen to be 2.0×10⁻⁶ cm²/s, i.e. the average of published EGF diffusivities in free solution.

Experiment	EGF Diffusivity (10−6 cm2/s)	Reference
In vivo (rat cortex)	0.50–0.53	39,40
In vitro (dilute agarose)	1.2–1.7	38,40
Computational models	2.1–2.3	41,42
Simulation	2.0	Present study

Cell and EGF loading

Bridged µLane systems were coated overnight with 10- µg/mL fibronectin (Sigma-Aldrich Co., St. Louis, MO) in PBS before cells were inserted. After coating, fibroblast suspensions (3 × 10⁵/mL) were injected into the microchannel from the SRC chamber using a 1-mL syringe. The SRC chamber, the SKC chamber and the bridged channel were then filled with complete media and the systems were incubated overnight (~14 hours) to allow cells to adhere and visibly spread prior to initiation of the experiments.

To begin experiments, medium was first removed from the chambers and then carefully aspirated from the microchannel to avoid cell detachment. In experiments where uniform EGF concentrations were applied, complete medium containing 0, 40-ng/mL, 80-ng/mL or 400-ng/mL EGF was injected into the microchannel using a syringe and then into the SRCand the SKC chambers and the bridge channel. For experiments where EGF gradients were applied, growth medium was aspirated from the entire system, and fresh growth medium containing no EGF was added to the microchannel, the SKC chamber and the bridge channel. Next, EGF solution at the desired concentration was added to the SRC chamber until it came into contact with the medium present in the bridge channel. After filling, the systems were placed in a micro-incubator (Warner Instruments LLC, Hamden, CT) mounted on a motorized stage of an inverted microscope (Nikon TE2000). The temperature in the micro-incubator was maintained at 37°C. Experiments of this study utilized 7 different bridged µLane systems and repeated experiments at least five times per channel for data analysis.

Microscopy and cell images

An inverted microscope (Nikon TE2000) with a 20X microscope objective (Nikon Plant 20X, Morrell Instrument Company Inc., Melville, NY) was used to image cells that adhered in the culture plates and the µlane systems via a cooled CCD camera (CoolSNAP EZ, Photometrics, Tucson, AZ) with Nikon software (Nikon Instrument Element 2.30 with 6D module, Morrell Instrument Company Inc., Melville, NY). All images were in dimensions of 0.38-mm-length by 0.46-mm-width, and displayed the specific cell positions within the culture plates and the microchannels. A shutter (HF204, Prior Scientific Inc., Rockland, MA) mounted in the Nikon TE2000 was used to control the exposure time. Approximately 50 individual cells were imaged for the analysis of each experimental condition tested.

Statistical analysis

One-way and two-way analysis of variance (ANOVA) was performed using Origin (version 7.5) to test for significant differences between groups. Tukey comparison was utilized to identify significant interaction between growth factor concentration and gradient. Significance level was set to p< 0.001.

RESULTS

We chose EGF concentrations for chemotaxis studies in the bridged µLane system based on the ability of fibroblasts to respond in well-established assays. In classical chemotaxis assays based on transfilter migration, concentrations of EGF between 0.1-ng/mL and 100-ng/mL led to significant increases in cell migration over controls, with maximal stimulation (approximately 3.5-fold) seen at 40-ng/mL EGF (Figure 2A). Acute receptor activation, as assessed by levels of phosphorylated EGF receptor via in-cell western blotting, indicated maximum stimulation over a broad range of EGF concentrations between 1-ng/mL and 400-ng/mL, with nearly 90% of that level achieved by 0.1-ng/mL (Figure 2B). The mitogenic response to EGF exhibited a maximum similar to that seen for transfilter chemotaxis, with the greatest increases in cell numbers seen at 40-ng/mL and 80-ng/mL EGF. However, in contrast to the chemotaxis assay, solutions of 0.1-ng/mL and 1.0-ng/mL EGF did not lead to detectable increases in cell numbers over control (Figure 2C). Based on these results, we chose concentrations of EGF for this study that included and exceeded the maximum levels of chemotactic and mitogenic stimulation in fibroblasts: 40-ng/mL, 80-ng/mL and 400-ng/mL.

Figure 2.

EGF dosage-dependent effects on fibroblast migration, EGF receptor phosphorylation, and proliferation. (A) Migration response of cells to varying EGF concentration (0.1-ng/mL to 100-ng/mL) in terms of the Relative Chemotaxis Factor (RCF), defined as the ratio of motile cells in the presence of EGF to the number of cells in control experiments (n=16). Note that the RCF of control experiments were normalized to a value of 1. (B) The percentage of phosphorylated EGF receptor, pEGFR, to the total EGF receptor in response to varying EGF concentration (0.1-ng/mL to 400-ng/mL). The number of samples tested is displayed in parentheses. (C) Cell proliferation measured after 72-hour exposure to different EGF concentrations (0.1-ng/mL to 400-ng/mL) (n=3).

Effects of uniform EGF concentrations and EGF gradients on cell migration

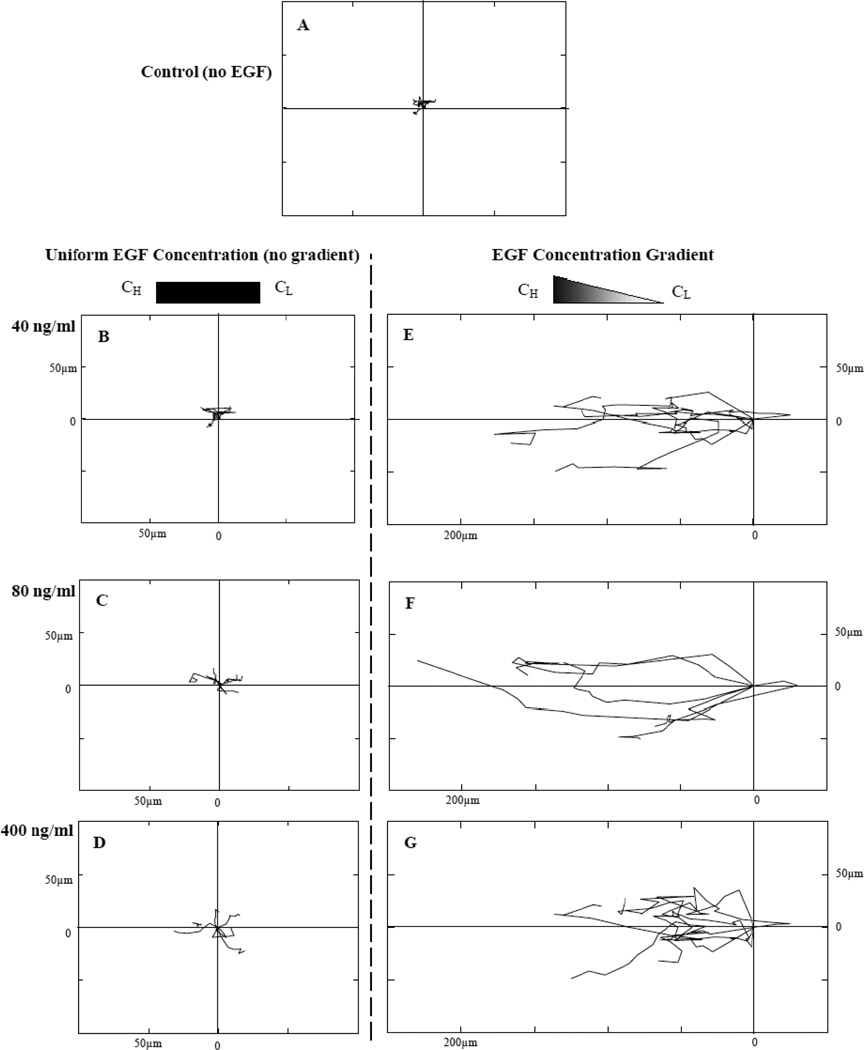
Fibroblasts exposed to uniform EGF solutions of 40-ng/mL, 80-ng/mL and 400-ng/mL concentration within the bridged µLane system exhibited dose-dependent increases in cell speed, as shown by the trajectories of representative cells in the Wind-Rose plots in Figure 3. However, these cells were exposed to zero gradients (i.e. uniform concentration) and migrated without preferred direction. In the absence of EGF, the maximum displacement averaged 6.1±3.4 µm from the cell centroid, and the cell speed was experimentally observed to be 2.4±2.1 µm/hr (Table 2). With increasing uniform EGF concentration (Figure 3B–3D), cells progressively increased their displacements to 20.8±5.1 µm and their speeds to 6.2±2.7 µm/hr, also without demonstrating directional migration. In contrast, Wind-Rose plots of individual cell movements in the presence of EGF concentration gradients illustrated additional increases in both displacement and preferential movement in the direction of higher EGF concentration (Figure 3E–3F). In all cases, increases in cell displacement and directed speed within EGF gradients were significantly higher than those observed for the same EGF concentrations applied uniformly. These experimentally-derived values were maximal at 237.8±76.8 µm and 25.4±3.4 µm/hr, respectively, at 80-ng/mL EGF, and declined to 174.3±53.2µm and 7.4±2.9 µm/hr at 400-ng/mL EGF (Table 2). All comparisons in these experiments were statistically significant as two way and one way ANOVA analysis yielded values of p<10⁻⁴.

Figure 3.

Wind-Rose plots of cell trajectory in response to EGF stimulation within the microchannel. Six representative cell paths are illustrated in each plot for different experimental conditions at 15 hours post steady-state: (A) control (no EGF applied), (B) uniform EGF concentration (no EGF gradient generated) of 40-ng/mL, (C) uniform EGF concentration of 80-ng/mL, (D) uniform EGF concentration of 400-ng/mL, (E) EGF concentration gradients generated by using 40-ng/mL (D) EGF concentration gradients generated by using 80-ng/mL, and (F) EGF concentration gradients generated by using 400-ng/mL as initial stimulus. Distance between hatch marks on both axes in each plot is 50 µm. Note that the induced cell migration is seen from right to left.

Table 2.

Maximum cell displacement and speed measured in response to uniform EGF concentrations (no gradient) and EGF concentration gradients, generated by 40-ng/mL, 80-ng/mL and 400-ng/mL 15 hours post steady-state. Note that data illustrate values accumulated from all gradients. Values are experimentally measured and shown with mean and standard deviation. The total number of cells per experiment is shown in parenthesis.

Uniform Concentration (ng/mL)	Maximum Displacement (µm)	Speed (µm/hr)
0 (n=49)	6.1 +/− 3.4	2.4 +/− 2.1
40 (n=44)	10.5 +/− 4.4	4.4 +/− 1.1
80 (n=52)	13.3 +/− 4.2	5.4 +/− 2.4
400 (n=40)	20.8 +/− 5.1	6.2 +/− 2.7

Gradient- Concentration (ng/mL)	Maximum Displacement (µm)	Directed Speed (µm/hr)
0 (n=49)	6.1 +/− 3.4	2.4 +/− 2.1
40 (n=62)	218.5 +/− 80.6	22.4 +/− 2.1
80 (n=60)	237.8 +/− 76.8	21.4 +/− 3.4
400 (n=64)	174.3 +/− 53.2	7.4 +/− 2.9

Experimental measurements of individually-tracked fibroblasts within the microsystem were then used with mathematical models to generate values of persistence time, P, and chemotactic index, CI. A consistent persistence time of approximately 2 minutes (114 +/−6s) was determined via Equation 3 for cells exposed to uniform EGF concentrations (i.e. no gradients). Similarly, values of CI were determined via Equation 4 to be CI=0.12+/−0.02 using uniform concentrations of EGF attractant.

Cell motility in response to EGF gradients

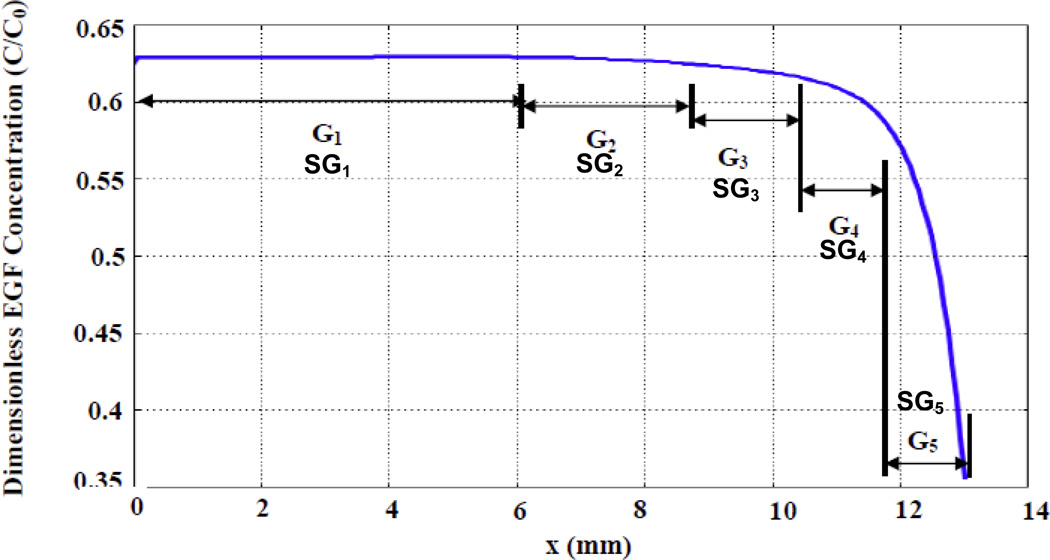
In the bridged µLane system, the concentration of EGF within the microchannel varied in an analytically-defined manner (as per Equation 6), and became constant once steady-state was achieved. As a result, it was possible to establish values of both EGF concentration and gradient across each cell examined, based on its location within the system microchannel. (Note that gradient, G, is defined as a difference in concentration (ng/nL) over channel length (mm)). For each concentration of EGF used (i.e. 40-ng/mL, 80-ng/mL, or 400-ng/mL), five ranges of concentration gradient, G₁–G₅, were identified along sequential locations in the microchannel: 0<G₁<10⁻³ ng/(mL.mm), 10⁻³<G₂<10⁻² ng/(mL.mm), 10⁻²<G₃<10⁻¹ ng/(mL.mm), 10⁻¹<G₄<10⁰ ng/(mL.mm), and 10⁰<G₅<10¹ ng/(mL.mm), as shown in Figure 4. The lowest gradient, G₁, was located near the SRR reservoir and occupied the largest segment (approximately 6-mm-length) of the microchannel, while the highest gradient G₅ was located near the SKR reservoir and occupied the shortest segment of approximately 1 mm. Gradients G₁, G₂ and G₃ displayed approximately linear profiles, while G₄ and G₅ were highly non-linear. Finally, values of specific gradient, SG, i.e. gradients across individual cell lengths, ranged from 10⁻⁵ ng/mL (SG₁) to 10⁻² ng/mL (SG₅) within the microsystem, corresponding to G₁–G₅ gradient fields, as also shown in Figure 4.

Figure 4.

Graph of steady-state EGF concentration gradients and specific gradients distributed along the microchannel. EGF gradients were categorized into 5 ranges: 0<G₁<10⁻³ ng/(mL.mm), 10⁻³<G₂<10⁻² ng/(mL.mm), 10⁻²<G₃<10⁻¹ ng/(mL.mm), 10⁻¹<G₄<10⁰ ng/(mL.mm), and 10⁰<G₅<10¹ ng/(mL.mm). These gradients were sequentially, but unevenly, distributed along different positions of the microchannel length as shown. In addition, values of specific gradient, SG₁–SG₅, i.e. gradients along the cell length, are also shown. Specific gradients were similarly categorized into 5 ranges: 0<SG₁<10⁻⁶ ng/mL, 10⁻⁶<SG₂<10⁻⁵ ng/mL, 10⁻⁵<SG₃<10⁻⁴ ng/mL, 10⁻⁴<SG₄<10⁻³ ng/mL, and 10⁻³<SG₅<10⁻² ng/mL.

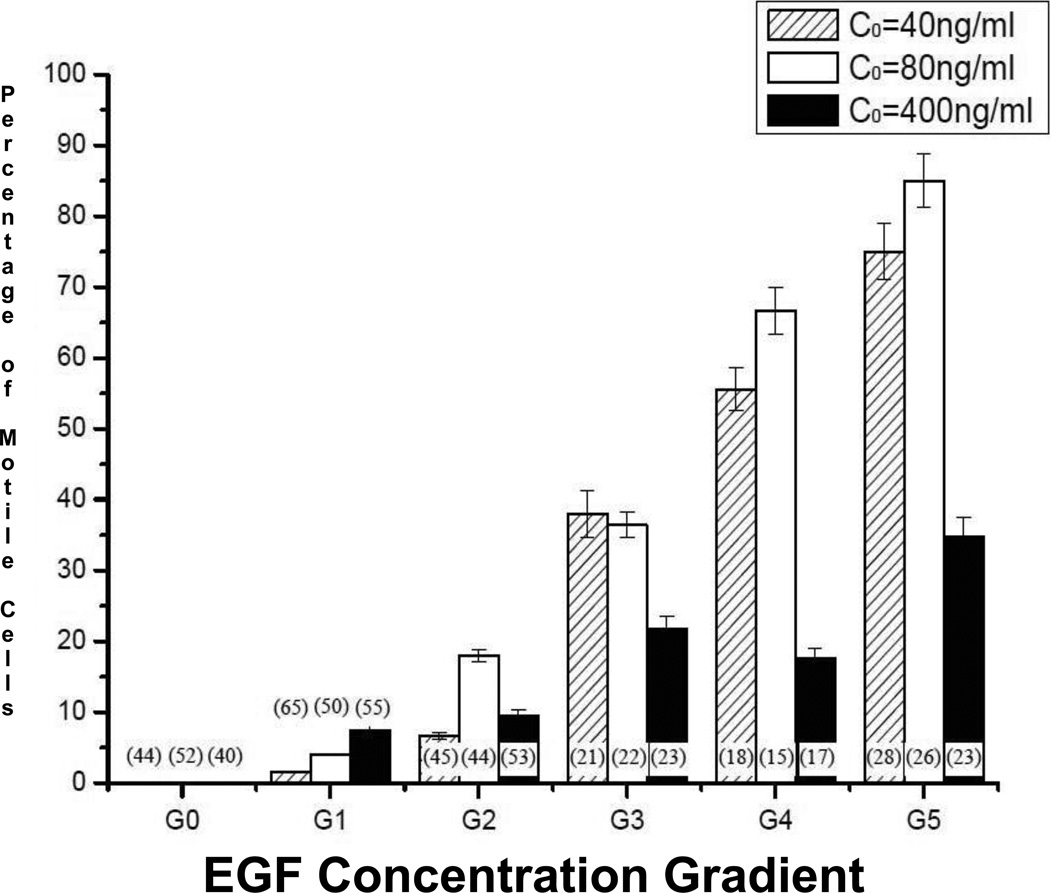
The number of motile fibroblasts whose cell centroids migrated more than 80 µm during the experiment increased when exposed to gradients of increasing steepness (G₁ to G₅) established by 40-ng/mL, 80-ng/mL, and 400-ng/mL EGF (Figure 5), For gradients established by both 40-ng/mL and 80-ng/mL EGF, 75–85% of all cells examined were motile in the steepest gradient range, G₅. EGF at 400-ng/mL led to markedly lower and more variable increases, although the greatest percentage of motile cells (35%) was also seen at the steepest G₅ gradient. In addition, fibroblast motility increased 5 to 6-fold over levels seen when EGF at the same concentrations was applied uniformly, i.e. no gradient, G₀.

Figure 5.

Percentage of motile cells observed in response to imposed EGF gradients G₀ through G₅ 15 hours post-steady-state: G₀=0, 0<G₁<10⁻³ ng/mL per mm, 10⁻³<G₂<10⁻² ng/mL per mm, 10⁻²<G₃<10⁻¹ ng/mL per mm, 10⁻¹<G₄<10⁰ ng/mL per mm, and 10⁰<G₅<10¹ ng/mL per mm of the microchannel. The percentage was defined as the ratio of the number of cells whose centroids migrated more than 80 µm to the total number of cells in the microchannel. The total number of cells is displayed in parentheses.

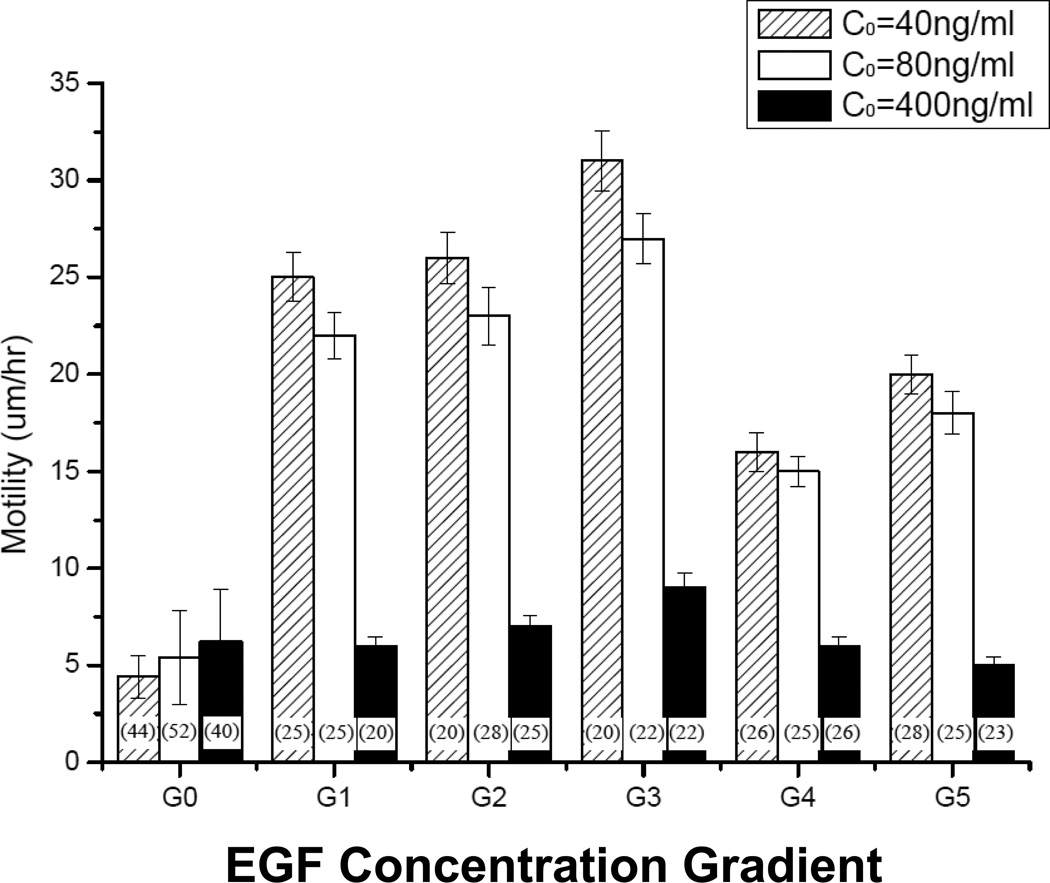
Similar experiments measured directed cell speed, or motility, when exposed to different gradient fields. As seen in Figure 6. The shallow gradient ranges G₁–G₃ produced the greatest motility, while steeper gradients G₄ and G₅ were less stimulatory. In contrast, gradients established using 400-ng/mL EGF failed to stimulate fibroblast motility, and the steepest gradients (G₄, G₅) inhibited motility in comparison to uniform EGF concentrations (G₀). The majority of differences among groups were highly significant by ANOVA (p<10⁻⁴). However, while differences between motility data in gradients generated by 40-ng/mL and 80-ng/mL EGF were consistent, they were not statistically significant (0.05<p<0.08).

Figure 6.

Cell motility measured as a function of EGF concentration gradients G₀ through G₅ 15 hours post-steady-state: G₀=0, 0<G₁<10⁻³ ng/mL per mm, 10⁻³<G₂<10⁻² ng/mL per mm, 10⁻²<G₃<10⁻¹ ng/mL per mm, 10⁻¹<G₄<10⁰ ng/mL per mm, and 10⁰<G₅<10¹ ng/mL per mm of the microchannel. Cell motility was defined as the directed distance traveled by each cell divided by time. The number of cells per experiment is shown in parentheses.

Chemotactic sensitivity of Fibroblasts

Experimental data was used in conjunction with mathematical modeling to determine the value of chemotactic sensitivity, χ₀, of ligament fibroblasts studied. Reference values for the dissociation constant, K_D, and total EGFR population per cell, N_T, were K_D=2.5nM and N_T=118576 [42, 43], respectively. First, the number of bound receptors in the presence of an attractant concentration, N_B, was determined via Equation 5 to be on the order of 10⁴ EGFR for all attractant concentrations used. The change in the number of bound receptors in the presence of a given attractant concentration, dNb/da was then determined to be 10⁴ receptors per nM of EGF. Next, values of CI shown in Table 2 were used to determine the cell intrinsic chemotactic sensitivity via Equation 7. Using these equations, a value of χ₀ on the order of 10⁻⁶ cm/Receptor was derived. This parameter indicates that ligament fibroblasts exhibited an average spacing of 100nm between receptors on the cell surface.

DISCUSSION

This study utilized our microfluidic system to measure the migratory responses of ligament-derived fibroblasts to a range of concentration gradients generated by using different concentrations of the attractant, EGF. Specific gradients across individual cells were generated via the bridged µLane system, a device that uses buoyancy-driven differences between the attractant and cell media solution to create distinct concentration gradients along different channel lengths. The spatial and temporal patterns of chemoattractant generated using this system were rigorously analyzed in previous work from our laboratory by solving the convective-diffusion flux between the system reservoirs and channels exactly and by verifying these mathematical predictions experimentally using fluorescent dyes and microbeads. Using the attractant EGF, the bridged µLane was able to generate multiple concentration gradient fields, G₁–G₅, that spanned 5 orders of magnitude within one experimental setting, 10⁻³ng/mL to 10¹ng/mL per millimeter of channel. The spatial distribution of attractant within the microsystem generated a wide range of gradients along the 12-mm-long channel length. Here, gradient fields G₁–G₃ were generated via small changes in absolute concentration of attractant, and were therefore shallow and approximately linear, while gradient fields G₄–G₅ were created via much greater changes in attractant concentration, and where thus steeper and highly non-linear. Further, the parallelization enabled by microfluidic technology facilitated the experimental tracking of 25–50 distinct cells for each microenvironment-generated gradient field.

Initial experiments using functional assays illustrated comparable dosage-dependencies for fibroblast proliferation and transfilter migration, but a very different response in acute receptor phosphorylation. The fibroblasts examined exhibited an extreme sensitivity to small changes in EGF concentration, as levels of total phosphorylated EGF receptor, pEGFR, appear to plateau after a minute 1-ng/mL concentration of EGF. While these disparities may arise from complexities of downstream EGF responses, we note that they may also reflect an insensitivity of the conventional assays used. Hence, we employed the bridged µLane system to conduct migration experiments able to detect measureable cell responses to the minute changes in EGF concentration and gradient that were in line with those concentrations seen to produce acute pEGFR activation.

Using our microsystem, the next set of data illustrated a marked increase in chemokinesis when cells were exposed to increased attractant concentration. Representative cell paths in Figure 3 illustrate random cell directionality with increased distance when cells are exposed to higher concentrations of EGF attractant. Furthermore, using established mathematical models, experimental data of cell distance and cell speed were used to determine the parameters of chemotactic index, CI, and persistence time, P, of the soft tissue-derived fibroblasts studied. The values of CI in Table 2 illustrate that the average CI was higher for cells exposed to EGF gradients than those of cells exposed to uniform concentrations of attractant, as expected. Second, the persistence time, P, was mathematically predicted to be much lower for cells within gradient fields than for cells exposed to uniform concentration environments. However, we note that calculated values were obtained from experimental data collected only at 60 minute intervals, which likely influenced the P values as fibroblasts persistence times are known to be on the order of minutes. Nonetheless, lower P values indicate the cells exhibit a large number of directional changes during migration, which is typically associated with cells that are very motile by nature [32]. Correspondingly, the loser persistence time is consistent with the minute level of pEGFR activation seen in Figure 2C, and reinforces the suggestion that these fibroblasts have a high sensitivity to extremely small changes in local EGF attractant concentration.

The next set of results illustrated that the number of motile cells within the bridged µLane system increased when exposed to increasing EGF gradient independent of initial attractant concentration. This behavior was seen over a wide range of EGF concentrations at steady-state. Based on the gradient fields created within the µLane system, G₁–G₃ were established using concentrations greater than the dissociation constant, K_D, while G₄ and G₅ were created using concentrations approximate to, or slightly lower than, K_D (Figure 1C: 0.63<C/C_o <0.38). Thus, cells in G₅ predictably exhibited the largest number of motile cells while cells in G₁ exhibited the lowest number, as concentrations greater than K_D are known to interfere with cell ability to sense gradient fields. One unexpected finding is that the data illustrate a increase in the number of motile cells with increasing gradient. While the reasons behind this seemingly linear pattern remain unclear, we postulate that increased specific gradient, SG or the gradient across individual cells, may create a correspondingly steep distribution of bound EGF receptors across cells, thereby activating chemotactic signaling mechanisms more readily. The effect of SG was thus further examined in subsequent motility measurements.

Our last set of results point to a difference in the average, single-cell directed speed with increased gradient. Cells exposed to low G₁–G₃ gradient fields exhibited higher motility than cells in the higher G₄–G₅ fields. Further, the motility of cells exposed to G₁–G₃ fields were comparable, and statistically larger than the motility of single cells exposed to G₄–G₅ gradients. We believe this can be explained by the intrinsic chemotactic sensitivity of the soft tissue fibroblasts used, as well as the specific gradient they experience. The data of pEGFR activation illustrates that the number of bound EGFR receptors reaches a plateau at very low concentrations, between control levels within media (<0.001-ng/mL) and 0.1-ng/mL. Using mathematical models to predict χ₀, we used our experimental data to predict that fibroblast sensitivity to EGF is on par with very highly motile cells such as macrophages and leukocytes, χ₀ ~ 10⁻⁶ cm/Receptor [32]. This is surprising, as soft tissue fibroblasts have not been reported to exhibit such chemotactic phenotypes. Yet our data suggest that fibroblasts can detect changes in microenvironments generated as part of the G₁ field, whose minimum difference in absolute value of concentration is 0.001-ng/mL (i.e. C/C₀~0.63 in Figure 1C), but not between changes in the microenvironment generated as part of G₅, whose minimum difference in absolute value of concentration is 0.1-ng/mL (i.e. C/C₀~0.37 in Figure 1C). A closer look at specific gradient provides additional insight. The value of SG₅ that accompanies the G₅ field corresponds to a 0.1-ng/mL concentration across individual cells, the value where bound pEGFR reaches a plateau in the acute phosphorylation data of Figure 2B. At this concentration, receptor down regulation, and/or other cell process, begin and detract from chemotactic signaling, leading to decreases in cell motility. By contrast, SG values in gradient fields G₁ through G₄ are orders of magnitude lower at 10⁻⁶ ng/mL to 10⁻³ng/mL, suggesting little effect of receptor down regulation. As established work suggests cell sensitivity to a particular cytokine is linearly proportional to attractant concentration at low dosages [22], it appears that levels as low as 0.001ng/mL may stimulate pEGFR activity in these cells. Thus, our data implies that differences in SG can actively affect cell motility even at such minute concentrations.

In summary, the results of this study illustrate that the chemotaxis of fibroblasts is highly sensitive to minute changes in EGF, exhibiting intrinsic chemotactic sensitivities comparable to that of highly motile cells, such as macrophages. The chemotactic response was principally determined by the magnitude of the EGF specific gradient, although elevated EGF concentrations did independently influence cellular migration at the highest dosage tested. The ability to specify patterns of chemotactic gradient and concentration with the bridged µLane system illustrates the device's particular utility for investigations of chemotactic mechanisms. Future studies utilizing such a microsystem in tandem with fluorescent markers of EGFR effectors will greatly aid in the development of more effective soft tissue biomaterials that rely upon the development of precise specific gradient fields to direct fibroblast chemotaxis.

Abbreviations

EGF

Epidermal Growth Factor