A point process model for auditory neurons considering both their intrinsic dynamics and the spectro-temporal properties of an extrinsic signal

Abstract

We propose a point process model of spiking activity from auditory neurons. The model takes account of the neuron’s intrinsic dynamics as well as the spectro-temporal properties of an input stimulus. A discrete Volterra expansion is used to derive the form of the conditional intensity function. The Volterra expansion models the neuron’s baseline spike rate, its intrinsic dynamics - spiking history - and the stimulus effect which in this case is the analog of the spectro-temporal receptive field (STRF). We performed the model fitting efficiently in a generalized linear model framework using ridge regression to address properly this ill-posed maximum likelihood estimation problem. The model provides an excellent fit to spiking activity from 55 auditory nerve neurons. The STRF-like representation estimated jointly with the neuron’s intrinsic dynamics may offer more accurate characterizations of neural activity in the auditory system than current ones based solely on the STRF.

I. Introduction

Understanding the factors that are responsible for inducing neurons to spike is an important, active topic of investigation in neuroscience. One approach is to fit statistical models containing the most salient factors to neural spiking activity and use the fitted model to evaluate the relative importance of the factors. Two key factors or covariates to consider in standard neurophysiology experiments are the intrinsic dynamics of the neuron such as the absolute and relative refractory periods, bursting and network dynamics whereas the primary extrinsic factor is the external stimulus applied in the experiment. In an auditory experiment the stimulus is typically a specific sound pattern.

The intrinsic dynamics modeled typically in terms of the neuron’s past spiking history has been established as an important descriptor of spiking propensity in a number of neural systems [1]–[5]. Analyses of auditory neurons have focused on constructing a spectro-temporal receptive field (STRF) by estimating a linear relation between a spectro-temporal representation of the auditory stimulus and the rate function of the neuron [6]. The coefficients of the linear model comprise the STRF. To date no statistical model has characterized the spiking propensity of auditory neurons by representing simultaneously the intrinsic dynamics and the complete spectro-temporal representation of the auditory stimulus. Given the point process nature of neural spiking activity, a principled approach to constructing the model would be to relate the covariates to the spiking propensity of the neuron in terms of the conditional intensity (rate) function (CIF) because a point process is completely described by its CIF.

We present a point process model for auditory neural spiking activity that considers both the neuron’s intrinsic dynamics and the spectro-temporal properties of the auditory stimulus. We formulate the log of the conditional intensity function in terms of a discrete-time Volterra series expansion of the neuron’s spiking history and the spectro-temporal decomposition of the auditory stimulus. The Volterra expansion contains a parameter representing the baseline spike rate, a set describing the intrinsic dynamics and a second set characterizing the stimulus effect, the analog of the STRF. Using the generalized linear model (GLM) in a ridge regression framework to address properly the ill-posed inverse nature of this maximum likelihood estimation problem we illustrate our approach by fitting the model to the spiking activity of 55 auditory nerve neurons in an anesthetized cat in response to an auditory stimulus.

This paper comprises the following sections: the proposed statistical model is derived in Section II; the model estimation is presented in Section III; results, including goodness of fit of the model and model parameter analyses, are presented in Section IV and Section V concludes the work.

II. The statistical model

Given an observation interval (0, T] and spike times 0 < u₁, u₂, …,< u_N(T) < T. The CIF of the spike train is defined by [1]

$$\underset{\mathrm{\Delta }\to 0}{lim}\frac{Pr\{[N(t+\mathrm{\Delta })-N(t)]=1\mid H_t\}}{\mathrm{\Delta }}=\lambda (t\mid H_t)$$ (1)

where N(t) is the number of spikes in the interval (0, t] for t ∈ (0, T] and H_t is the relevant history of the covariates at t. It follows that for Δ small

$$Pr(\text{spike}\text{in}(t,t+\mathrm{\Delta }]\mid H_t)\approx \lambda (t\mid H_t)\mathrm{\Delta }.$$ (2)

The CIF is for a point process a history-dependent generalization of the rate function of a Poisson process. To obtain a discrete formulation of the CIF we choose K sufficiently large so that each subinterval Δ = K⁻¹T contains at most one spike. We index the subintervals k = 1, …, K and define n_k to be 1 if there is a spike in the subinterval ((k−1)Δ, kΔ] and 0 if there is no spike. For our analysis we choose K so that Δ is 1 millisecond, consistent with the absolute refractory period of a neuron.

Let s_k,j be the value of a spectro-temporal representation of the sound stimulus with frequency band j at time kΔ for j = 1, …, J. Define the relevant history of the sound stimulus for predicting the current spiking propensity as H_k,j = {s_k,j, …, s_k−L,j}, assuming a dependence that goes back L time periods. Similarly, define the relevant spiking history for predicting the current spiking propensity as H_k,J+1 = {n_k−1, …, n_k−P}, assuming a dependence that goes back P time periods. Let H_k = {H_k,1, …, H_k,J+1}. If we assume that there is a functional F which describes the relation between H_k and the CIF λ(kΔ|H_k) then we can expand the log of the CIF in a discrete Volterra series as [7]

$$\begin{array}{l}log(\lambda (k\mathrm{\Delta }\mid H_k,\mathit{\beta }))=F(H_k,\mathit{\beta })\\ ={\beta }_0+\sum _{j=1}^J\sum _{l=0}^{L-1}{\beta }_{l,j}{s}_{k-l,j}+\sum _{p=1}^P{\beta }_{p,J+1}{n}_{k-p}+\text{higher}\text{terms}\end{array}$$ (3)

where β = {β₀, β_0,1, …, β_L−1,J, β_1,J+1, …, β_P,J+1} is the (JL + P + 1) × 1 vector of Volterra kernels. We interpret the Volterra series expansion as the sum of the outputs of J + 1 linear filters having Volterra kernels as the impulse responses. The kernels β_l,j are the analogs of the STRFs used to characterize auditory neurons. The kernel β_p,J+1 models the effect of the spiking history and β₀ governs the mean spiking rate. Exponentiating both sides of (3) yields the CIF

$$\lambda (k\mathrm{\Delta }\mid H_k,\beta )=exp\left\{{\beta }_0+\sum _{j=1}^J\sum _{l=0}^{L-1}{\beta }_{l,j}{s}_{k-l,j}+\sum _{p=1}^P{\beta }_{p,J+1}{n}_{k-p}\right\}$$ (4)

where we have neglected the higher order terms.

Constructing the Volterra series expansion in terms of the log of the discrete CIF ensures that the CIF is non-negative and that the relation between the spiking activity and the sound stimulus and the spiking history can be modeled using a generalized linear model (GLM) with either a binomial or a Poisson link function [3]. Models with a similar structure as the one derived in (4) have been considered previously for other neural systems [1]–[5]. None of these analyses was motivated by a Volterra series expansion nor has this model been used in an analysis of auditory spiking activity in which the intrinsic dynamics and the STRF were simultaneously estimated.

III. Model estimation

We can rewrite (3) in a more compact form as

$$log(\mathbf{\lambda })=\mathbf{X}\mathit{\beta }$$ (5)

where X is the RK × (JL + P + 1) matrix of covariates, R has been added to take account of the number of trial and the logarithm function is applied element-wise. It follows that the log likelihood function for estimating β is [1]–[4]

$$\mathbb{L}(\mathit{\beta })=\sum _{k=1}^K\sum _{r=1}^R{n}_{k,r}log({\lambda }_k\mid \mathit{\beta })-\sum _{k=1}^K\sum _{r=1}^R({\lambda }_k\mid \mathit{\beta })\mathrm{\Delta }$$ (6)

where the inner sum is over trials. An advantage of (5) is that it shows that (6) is equivalent to a GLM with a Poisson log likelihood function. We can therefore use the GLM framework to estimate β.

It is well known that the Fisher scoring algorithm for GLM parameter estimation with canonical link functions can be solved by iteratively reweighted least-squares (IRLS) [8]. In the IRLS algorithm, the maximum likelihood estimate of β is computed iteratively by solving successive weighted least squares (WLS) subproblems. The WLS subproblems are solved using a conjugate gradient algorithm that greatly reduces the computational time. Our problem has an additional feature that must be considered. The design matrix X includes 1 ms delayed version of the input spectro-temporal representations. As a consequence, many of the columns of X are highly correlated, especially when the auditory stimulus is presented across a large number of trials. This suggests that the estimation of β is an ill-posed inverse problem which can be solved by regularization. We can estimate β using the truncated regularized iteratively reweighted least squares (TR-IRLS) algorithm for GLM parameter estimation [8]. The TR-IRLS is a variant of the IRLS algorithm in which a ridge parameter can be included in each WLS subproblem to provide a quadratic regularization.

Introducing the regularization term τ the estimate of β at iteration i + 1 of the TR-IRLS is computed as

$${\widehat{\mathit{\beta }}}_{i+1}={({\mathbf{X}}^T{\mathbf{W}}_i\mathbf{X}+\tau \mathbf{I})}^{-1}{\mathbf{X}}^T{\mathbf{W}}_i{\mathbf{z}}_i$$ (7)

where W_i is an RK × RK diagonal weight matrix whose diagonal elements are λ_i, the vector of CIF estimates at iteration i, ${\mathbf{z}}_i=\mathbf{X}{\widehat{\mathit{\beta }}}_i+{\mathbf{W}}_i^{-1}(\mathbf{n}-{\mathbf{\lambda }}_i)$ is the so-called adjusted dependent covariate [8] and n is the column vector of all of the n_k,r spiking activity across all trials and across all times in the experiment.

IV. Results

We applied the proposed statistical model to neural spiking activity recorded in the auditory nerves of anesthetized cats following the presentation of the input sentence “Wood is best for making toys and blocks” spoken by a male voice and sampled at 10 kHz [9]. The dataset was composed of the spike train responses of 55 distinct neurons each recorded across R = 20 trials. The spectro-temporal representation of the input speech was obtained through a modified version of an auditory spectrogram [10] which applied a gammatone filterbank to the input speech signal. The bandwidths of the filters were modified according to [11] to represent adequately the processing performed by the cat’s cochlea. To obtain comparable frequency bins, each was normalized by its Euclidean norm over the entire time domain. We used P = 40, L = 10 and J = 25, where the center frequencies ranged from 20 Hz to 4.4 kHz, and τ = 0.1 was the regularization parameter in the TR-IRLS algorithm.

A. Model Goodness of fit

To evaluate the model goodness-of-fit, we used the time rescaling theorem with rescaled times computed from the estimated CIF [3]. If the latter is a good approximation to the true CIF of the point process, then the rescaled times will be independent and uniformly distributed on the interval [0, 1). We used Kolmogorov-Smirnov (KS) plots to assess the uniformity of the rescaled times and the autocorrelation function (ACF) of transformed rescaled times to assess their independence [3], [12].

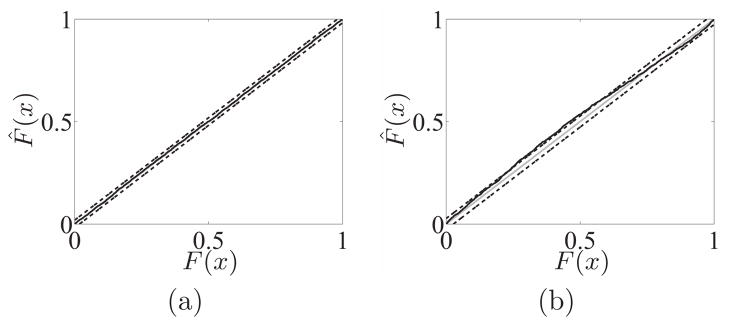
Fig. 1 shows the KS plots of the best and worst fits in which the upper and lower 95% confidence bounds are indicated by dashed lines. If the model is accurate, the KS plot should show an empirical distribution F̂(x) versus the fitted cumulative distribution F(x) that lies along the 45° line. As shown in Fig. 1a, the curve for the best fit is indistinguishable from the 45° line indicating a close model fit. Even for the worst case (Fig. 1b), the fitting is also quite good, with the KS plot being always within or extremely close to the confidence bounds.

Fig. 1.

KS plots (black lines) of (a) the best and (b) worst fits from a set of 55 auditory nerve recordings. Dashed lines indicate the 95% confidence bound.

To evaluate the fitting in the entire dataset, we used the normalized KS statistic which is defined as:

$$\widehat{D}=sup\left|\frac{\widehat{F}(x)-F(x)}{\widehat{B}}\right|$$ (8)

where B̂ is the width of 95% confidence bound. A value of D̂ < 1 thus indicates that the entire KS plot is within the 95% confidence bound. Table I shows the number of occurrences of normalized KS statistics values determined using 4-fold cross-validation. Forty-four of the 55 (80%) D̂ values were less than 1 which supports the excellent fit of the models. Most of the D̂ values that were greater than 1 were less than 1.05, suggesting that these models as well were in close agreement with the data.

TABLE I.

Occurences of normalized KS statistic values D̂ for the complete 55 auditory nerve dataset obtained using 4-fold cross validation.

D̂ values	0 − 0.5	0.5 − 1	1 − 1.5	1.5 − 2	> 2
number of occurences	1	43	10	1	0

The ACF of the transformed rescaled times were also evaluated to assess their independence. It was observed (results not shown here) that the rescaled times were highly independent with 92.5% of the ACF values in the entire auditory nerve dataset (n = 55) being inside their respective confidence bounds for lags up to 100 ms. The findings from the KS and ACF analyses suggest that the estimated CIFs provide excellent approximations to the true CIFs.

B. Model parameter analyses

We present the estimated values of the model parameters, i.e. the Volterra kernels β₀, β_p,J+1 and β_l,j obtained using the 20 trials for each neuron recording.

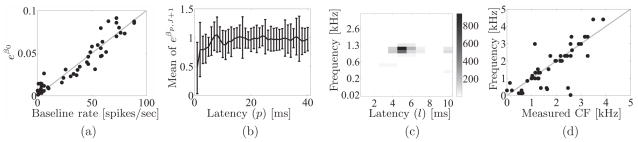
Figure 2a shows a scatter plot of the estimated baseline parameter exp(β₀) versus the baseline firing rate measured in [9]. As can be observed, there is a strong correlation between exp(β₀) and the measured baseline firing rate (Pearson correlation coefficient ρ = 0.92).

Fig. 2.

CIF parameter values. (a) Scatter plot of exp(β_o) vs. the measured baseline firing rate with Pearson correlation coefficient ρ = 0.92. (b) Mean of e^β_p,J+1, with 95% confidence interval, versus a latency p up to P = 40 ms (c) Example of exponentiated β_l,j values displayed according to the center frequency of the corresponding gammatone filter j and latency l (CF = 1024 Hz) with J = 25 and L = 10 ms. (d) Scatter plot of the center frequency of the filter corresponding to the β_l,j with the highest value versus the measured characteristic frequency of the corresponding neuron; ρ = 0.82.

The mean values of the exponentiated history parameters β_p,J+1 with the error bars of the 95% confidence interval is plotted in Fig. 2b. This plot shows that these parameters accurately capture the refractory behavior of the neurons because the mean value of exp(β_p,J+1) is appreciably less than 1.

The values of the exponentiated stimulus parameters β_l,j for a neuron with a characteristic frequency of 1024 Hz are shown in Fig. 2c. This representation resembles closely that of an STRF. It has a well defined preferred spectro-temporal region that is fairly restricted for auditory nerve recordings. Moreover, the center frequency of the filter with the highest parameter value (1140 Hz) corresponds to the measured characteristic frequency (1024 Hz). We plot in Fig. 2d the center frequency l of the filter corresponding to the spectro-temporal parameter β_l,j with the highest value as a function of the measured characteristic frequency for the entire dataset. There is a high correlation between the two (ρ = 0.82) indicating a good description of the CF by the model.¹

V. Conclusion

We presented a point process model of neural spiking activity in the auditory system that takes account of both the neuron’s intrinsic dynamics and the spectro-temporal properties of an input sound stimulus. We derived the associated CIF using a discrete Volterra expansion formulated in terms of the spiking history and the spectro-temporal components. This CIF model makes it possible to assess the relative importance of the neuron’s intrinsic dynamic (spiking history) and the STRF (spectro-temporal components). We fit the model to actual auditory nerve spiking activity by regularized maximum likelihood estimation. The models gave accurate descriptions of neural spiking activity in terms of KS goodness-of-fit analyses. This model, which considers both the neuron’s intrinsic dynamics and the STRF, may offer a way of obtaining more accurate characterizations of activity in other parts of the auditory system.