Motor nucleus activity fails to predict extraocular muscle forces in ocular convergence

Abstract

For a given eye position, firing rates of abducens neurons (ABNs) generally (Mays et al. 1984), and lateral rectus (LR) motoneurons (MNs) in particular (Gamlin et al. 1989a), are higher in converged gaze than when convergence is relaxed, whereas LR and medial rectus (MR) muscle forces are slightly lower (Miller et al. 2002). Here, we confirm this finding for ABNs, report a similarly paradoxical finding for neurons in the MR subdivision of the oculomotor nucleus (MRNs), and, for the first time, simultaneously confirm the opposing sides of these paradoxes by recording physiological LR and MR forces. Four trained rhesus monkeys with binocular eye coils and custom muscle force transducers on the horizontal recti of one eye fixated near and far targets, making conjugate saccades and symmetric and asymmetric vergence movements of 16–27°. Consistent with earlier findings, we found in 44 ABNs that the slope of the rate-position relationship for symmetric vergence (k_V) was lower than that for conjugate movement (k_C) at distance, i.e., mean k_V/k_C = 0.50, which implies stronger LR innervation in convergence. We also found in 39 MRNs that mean k_V/k_C = 1.53, implying stronger MR innervation in convergence as well. Despite there being stronger innervation in convergence at a given eye position, we found both LR and MR muscle forces to be slightly lower in convergence, −0.40 and −0.20 g, respectively. We conclude that the relationship of ensemble MN activity to total oculorotary muscle force is different in converged gaze than when convergence is relaxed. We conjecture that LRMNs with k_V < k_C and MRMNs with k_V > k_C innervate muscle fibers that are weak, have mechanical coupling that attenuates their effective oculorotary force, or serve some nonoculorotary, regulatory function.

mays and porter (1984) found that the mean slope of the abducens neuron (ABN) rate-position relationship for symmetric vergence (k_V) was lower than that for conjugate eye movement (k_C) at distance, i.e., k_V/k_C = 0.62. Consequently, the decrease in the mean firing rate of ABNs in convergence would be smaller than in conjugate movement to the same adducted eye position, so that a lateral rectus (LR) muscle would be innervated more strongly when its eye assumed a given adducted position in convergence than in conjugate gaze with vergence relaxed. Gamlin et al. (1989a) showed, by comparing abducens interneurons (AINs) identified by antidromic medial longitudinal fasciculus (MLF) stimulation to undistinguished ABNs, that LR motoneurons (MNs) themselves were significantly less sensitive for vergence than for conjugate movement, i.e., k_V/k_C = 0.58.

The finding that LRMNs fire at higher rates in convergence implies, under the venerable assumption of an oculomotor final common path (Robinson 1968, 1975), that LR muscle forces are higher in converged gaze than in unconverged gaze for a given position of the eye in the head (Miller et al. 2002). Furthermore, if those higher LR abducting forces were balanced by higher medial rectus (MR) adducting forces, the result would be horizontal rectus cocontraction and, consequently, retraction of the globe in the orbit. An alternative to MR cocontraction might be for cyclovertical eye muscles to provide adducting forces to balance the predicted excess LR forces, although biomechanical analysis has shown this to be unlikely (Miller et al. 2002). In any case, the prediction of higher LR forces in convergence seemed an inescapable consequence of well-replicated brain stem recording studies. Some electromyographic (EMG) studies in humans have indeed suggested cocontraction in convergence (Tamler et al. 1958), although most have not (Blodi et al. 1957; Breinin 1957).

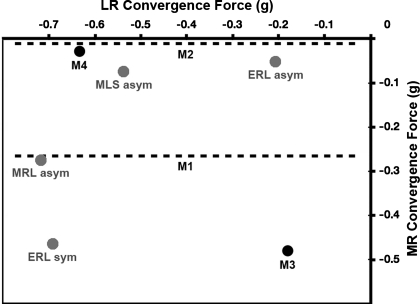
Miller et al. (2002) developed a unique, chronically implantable muscle force transducer (MFT) and used it to measure physiological oculorotary LR and MR forces in converged (mean: 22°) and unconverged gaze. Surprisingly, no convergence-related force increases were found at gaze positions comparable with those used in the brain stem recording studies, and forces at given eye positions in converged gaze were actually slightly lower than in unconverged gaze, −0.52 g for LR and −0.24 g for MR, averaged across the various asymmetric and symmetric movement conditions (see Fig. 7 for component data) (Miller et al. 2002).

Fig. 7.

LR and MR convergence force. Mean values of convergence force (the increase in force associated with convergence at a given eye position) are shown for the LR (abscissa) and MR (ordinate). In all cases, convergence force was found to be negative (P < 0.0001, binomial test, n = 14), meaning that convergence was associated with decreased LR and MR muscle forces. Data for the present study are shown as solid circles where both LR and MR data were available and as dashed lines where only MR data were available. Data from Miller (2002) are shown as shaded circles. Monkeys M1, M2, M3, and M4 are the four animals in the present study; monkeys ERL, MLS, and MRL are the three animals from the study of Miller (2002), in connection with which “asym” refers to asymmetric vergence trials with the MFT-instrumented eye aligned and “sym” refers to symmetric vergence trials at different horizontal gaze angles, from which near and far fixations with equal positions of the MFT-instrumented eye were extracted and compared.

Subsequently, applying methods developed by Miller et al. (1989, 1993), Demer et al. (2003) used MRI to study human asymmetric convergence of magnitudes similar to those used in Miller et al.'s muscle force studies. If convergence was associated with increased horizontal rectus muscle forces, Demer et al. would have found thickening of the horizontal rectus muscles, posterior movement of their maximum cross-sections, movement of the muscle paths toward the orbital axis, and retraction of the globe of the aligned eye (Miller 1989). To the contrary, and consistent with the findings of Miller (2002), Demer et al.'s scans showed none of these contraction-related changes. Demer et al. even reported a hint of globe protrusion in convergence, consistent with the small decreases in LR and MR forces Miller measured in convergence.

Findings as unexpected as these, which confound fundamental assumptions about the relationship between innervation and muscle force, demand exceptionally strong empirical confirmation. The brain stem recording results reviewed above, particularly those for ABNs, are consistent across several laboratories and seem secure. The corresponding muscle force measurements, however, are from only three animals in one laboratory, and although they are supported by results from an independent laboratory using an entirely different (human MRI) methodology, they certainly require replication. Most importantly, the two sides of this missing force paradox–motor nucleus recordings on one side and muscle force measurements on the other–were until now measured in different animals, in different laboratories, and never simultaneously, in the same preparation.

Here, we complete the demonstration of the missing force paradox with results from four animals that confirm and extend the brain stem recording findings of Mays and Porter (1984) and Gamlin et al. (1989a) and, simultaneously, the muscle force findings of Miller et al. (2002).

Some of this work has been presented at a scientific meeting (Miller et al. 2008).

METHODS

Muscle Force Measurement

LR and MR forces were measured with MFTs of our design, earlier versions of which have been described elsewhere (Miller et al. 2002; Miller et al. 1992). A MFT measures total oculorotary force, delivered by the muscle at its insertion into the globe, summed across the width of the muscle. It measures neither isometric nor isotonic force but physiological force, the force determined by the relationship between innervation and stretch that obtains as the eye rotates normally in an alert, behaving subject.

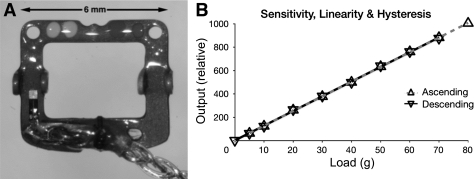
The current MFT/M-2.11 version is fabricated on a 0.25-mm-thick half-hard stainless steel frame, which has been photochemically machined and electropolished. Four “ears” are bent upward to form bearings for a pin that is inserted during implantation to direct the muscle through and attach it to the transducer. The end of the frame distal to the leads, which has no strain gauges (SGs) or wiring, is bent down 20° so the device better conforms to the globe and maintains its three lines of contact with the muscle even if the device wraps around the globe in eccentric gaze. The overall width of a MFT is 6.0 mm, with a 4.0-mm-wide aperture for the muscle. The overall length is 5.5 mm, with a 3.0-mm-long aperture. The maximum height of the device (at the ears) is 1.1 mm. In passing through a MFT, deflected by its raised pin, the attached muscle is stretched 0.6 mm. Transducer-grade, U-shaped, semiconductor SGs were chosen for their small size and high gauge factor (sensitivity to strain). One SG is bonded to a beam on the top of the frame and another to the opposite beam on the bottom. The two function differentially, with muscle tension compressing the top gauge and stretching the bottom gauge. Wired as arms of a Wheatstone bridge, this arrangement achieves high output, temperature compensation, and sums forces across the width of the muscle. MFTs are fabricated in two orientations: “left” (shown in Fig. 1) for the implantation on the left LR and right MR and “right” (mirror image) for the right LR and left MR, with the intent being that lead wires course superiorly in the orbit as they depart the device.

Fig. 1.

Muscle force transducer (MFT). A: finished device (“left” orientation). A stainless steel frame carries two semiconductor strain gauges (SGs; one visible near the bottom left and the other on the underside of the opposite beam, near the bottom right) wired as the arms of a Wheatstone bridge. The device is encapsulated in epoxy resin and Parylene-C and is attached by pushing a pin (not shown) through holes in the four upward-bent bearing tabs and under the muscle and held in the desired orientation (see Fig. 2) with nonabsorbable sutures passed through the muscle margins and the holes visible in the top left and right corners. B: typical MFT calibration. Bench calibration with ascending and descending weights showed the devices to be linear (r² > 0.999) and without measurable hysteresis. The device sensitivity is overwhelmingly determined by the stiffness of the steel frame, so individual MFTs differed little, and the tissue that grows around implanted devices is unlikely to affect sensitivity.

The formed and polished frame is sandblasted, and insulating epoxy coatings are applied. Wiring terminals are shaped to be as small as possible to minimize surfaces over which electrical leaks might develop, tinned, and grooved to help position the fragile gold SG lead wires. Matched semiconductor SGs (Entran ESU-025-500-4, www.meas-spec.com) and prepared terminals are bonded to the frame. Unlike film SGs, silicon SGs shatter if clamped, so it is critical to apply enough epoxy to form a complete bond but not so much as to float the gauge above the frame, which would result in compliant coupling. The assembly is air dried and baked to cure. The gold SG leads are soldered into their terminal grooves, the near sides of top and bottom SGs are joined via their terminals with copper magnet wire passing through an oblong hole in the frame, and proximal ends of the FEP-insulated lead wires (Cooner AS-631, www.coonerwire.com) are conditioned with adhesion promoter, stripped of insulation, and tinned. Two lead wires are soldered to the bottom terminals and passed up alongside the copper interconnect wire to join a lead wire soldered to the terminal on the free end of the top SG, and the three lead wires are braided. To lengthen paths of potential leakage, the wiring is designed so that points of electrical attachment are as far as possible from where lead wires emerge from the device's protective coatings to depart the frame. A silicone rubber strain-relief sleeve is slipped up the lead wires, onto the frame, and tied to the frame with Prolene suture. The strain-relief assembly and surface wiring are fixed in place, the SGs and their gold lead wires are mechanically protected, and sharp protrusions are buried to prevent the overlaid Parylene from being selectively abraded, with a clear epoxy encapsulant that has low uncured viscosity, allowing it to wick into gaps, and that cures to a tough, flexible solid, so it can be applied as needed without affecting device sensitivity. The terminals, SGs, and wiring are given several coats, and the strain-relief sleeve is filled, sealing the FEP-coated lead wires against the silicone rubber (Fig. 1A). The lead wires are masked, the devices are etched with cold plasma, and Parylene-C is vapor deposited to a thickness of 20 μm to provide a biocompatible surface and a moisture barrier to protect the SGs, on-board wiring, and frame itself.

We recorded the resistance of each SG at several stages of fabrication. To test the integrity of encapsulation, we suspended each completed MFT in warm saline for several weeks, testing for leaks between grouped lead wires and bath with an ohmmeter able to measure >500 MΩ. If a leak was found, we localized it by immersing the MFT, connected to the negative terminal, in a saline bath, connected to the positive terminal of a variable source able to produce several hundred volts, thereby causing H₂ bubbles to appear where the bath contacted electrically live surfaces. Repair was sometimes possible, although the technique has been more useful in refining design and fabrication.

Each MFT was calibrated by attaching it to a SG amplifier with 2-V excitation, inserting a pin through its bearings, threading a length of 1/8-in.-wide Mylar tape through it as far the muscle would go, and hanging weights of 5–80 g from the end of the tape. All functioning devices had similar sensitivities, no measurable hysteresis, and were almost perfectly linear (Fig. 1B). A successfully implanted MFT is stable for several months or longer.

Animal Preparation

Four rhesus macaque (Macaca mulatta) were used in this study. One experiment was run at the Smith-Kettlewell Eye Research Institute (monkey M1), and three experiments were run at the University of Alabama (Birmingham, AL) (monkey M2, M3, and M4). All experiments were approved by the Institutional Animal Care and Use Committees of both institutions and followed the National Institutes of Health Guide for the Care and Use of Laboratory Animals (National Research Council, 1996). Surgery was performed under aseptic conditions, with general anesthesia induced with ketamine and maintained with isoflurane gas, supervised by veterinary specialists. Analgesics and antibiotics were administered postsurgically under the supervision of attending veterinarians.

Scleral search coils (Robinson 1963) were implanted in both eyes of each monkey using the method of Judge (1980) except that we sutured the coil to the sclera with 7-0 Dacron or 6-0 Vicryl on a spatula needle to prevent slip. After monkeys had been trained to fixate on targets and perform vergence eye movements for a juice reward, we performed a second surgery to implant MFTs on the LR and MR of one eye.

MFT implantation does not require disinserting the muscle or disturbing the connective tissues deeper than ∼10 mm behind the insertion. The devices are small and protrude little from the muscles that they are attached to. MFT frames, conforming to the shape of the globe, as described above, are unlikely to become unloaded when the muscle wraps around the globe in contralateral gaze. It is possible to imagine the surrounding tissues exerting changing pressures on a MFT or restricting eye rotation, but we have shown that any such forces are insufficient to produce detectable binocular misalignment within a ±20° field with the eyes visually dissociated (that is, when binocular motor fusion could not mask a mechanical imbalance) and that effects on saccade dynamics are modest (10% decrease in peak saccadic velocity) (Miller et al. 2002). The two beams to which SGs are bonded are each 1-mm-wide × 0.25-mm-thick half-hard stainless steel, which is much stiffer than the connective tissue that grows to envelop the implanted device, so that device sensitivity is unlikely to be measurably affected by scarring. Nevertheless, the least contestable measurements are comparisons made in close temporal contiguity between oculomotor states for which the MFT-instrumented eye is in the same position, this being one of the methodological advantages of studying forces in the aligned eye in asymmetric vergence. We have shown that such studies give comparable results to studies of symmetric vergence, in which forces are compared with the instrumented eye in different positions and effects of eye rotation are removed by calculation (Miller et al. 2002).

We implanted MFTs on the LR and MR. Under general anesthesia, with the monkey's body in the supine position, we shaved and scrubbed the region surrounding the eye, crushed and cut the outer canthal skin to improve LR exposure, and spread the lids with a speculum or traction sutures. We disinserted the conjunctiva at the limbus in quadrants containing the muscles to be implanted and placed traction sutures in cut conjunctival edges to aid in visualizing muscles. We cleared each muscle of attachments by blunt dissection to ∼10 mm posterior to its insertion and placed it on a special tendon lifter. With the MFT of the appropriate configuration held in special forceps, we passed the tendon lifter up through the MFT's aperture and, while holding the MFT down against the globe, pulled the muscle gently upward and pushed a fitted pin through the proximal bearings, under the muscle, and through the distal bearings. With the MFT positioned a few millimeters behind the insertion and oriented squarely on the muscle, we passed a 6-0 Prolene suture on a round, noncutting needle through each tie-down hole and secured it to the underlying muscle margin; MFTs must be stabilized until they are enveloped with connective tissue or they will rotate on the muscle, delivering a signal reduced by the cosine of the angle of rotation. We positioned the lead wire in the orbit, allowing enough slack for a full range of eye rotation, and routed it to the scalp, following the method used for eye coil wires (Fig. 2).

Fig. 2.

MFT installation on the monkey lateral rectus (LR). The muscle is shown attached to the MFT with a pin passing under the muscle. Sutures are shown through the tie down holes and the muscle's margins. Implantation does not require disinserting the muscle or disturbing deep orbital tissues.

Because SG signals are small resistance changes, electrical connections must be scrupulously maintained. The braided MFT lead wires were passed uninterrupted into a special plastic Connector Can, where they were soldered to easily cleaned gold plated pins, onto which SG amplifier connections were made for data collection.

MFT signals were read with a SG amplifier (model 2120B or model 2311, Vishay) using 2.0-V bridge excitation, which was sufficient to produce a strong output signal without instabilities related to ohmic heating. A previous study (Miller et al. 2002) has shown that MFT gains are stable from implantation to excision unless moisture intrusion has caused the device to fail. Thus (with the caveats noted above), we assumed that gains measured before implantation were valid during implantation. Baseline or zero values, however, are not stable, so it is necessary to establish the MFT output corresponding to zero force. This is done during data analysis by finding minimum force signals, when the eye is turned toward the MFT (the muscle is unstretched) and is beginning a saccade in the opposite direction (the muscle is inhibited) (see Fig. 9 in Miller and Robins 1992).

Once the animal learned to perform conjugate and vergent refixation, a second surgery was performed to implant recording chambers over 15-mm-diameter holes trephined on each side of the skull, positioned stereotaxically above the midbrain at a 15–25° angle to the sagittal plane.

Brain Stem Recording

We used a hydraulic microdrive (models 650 or 670, David Kopf Instruments, www.kopfinstruments.com) to advance a Parylene-insulated tungsten microelectrode mounted in a 26-gauge cannula through a 21-gauge hypodermic needle puncturing the dura. Unit activity was sharply filtered above 5 kHz, and spikes were detected with a window discriminator and recorded digitally to the nearest 0.1 ms. A recording electrode (impedance: 0.3–0.6 MΩ) was lowered to either ABNs or neurons in the MR subdivision of the oculomotor nucleus (MRNs). The criteria for identifying ABNs and MRNs have previously been described (Gamlin et al. 1989a; Gamlin et al. 1992). We are confident all measured neurons fell within classically defined motor nuclei. Only a small percentage of our MRNs were likely to have been oculomotor internuclear neurons (Clendaniel et al. 1994; Langer et al. 1986). In the case of ABNs, a significant fraction of the population is expected to have been AINs, although LRMNs and AINs have similar conjugate and vergence sensitivities (Gamlin et al. 1989a; Sylvestre and Cullen, 2002; see, however, King and Zhou 2000).

Other Instrumentation

At the beginning of each recording session, horizontal and vertical eye position gains of each eye were calibrated by having the animal monocularly fixate a horizontal and vertical range of targets. A near LED target was positioned to elicit symmetric and asymmetric vergence movements of 12–28°. Eye positions and muscle forces were sampled at 1 kHz, spike profiles were sampled at 30 kHz, and all data were stored on disk for later analysis.

For monkey M1 (run at the Smith-Kettlewell Eye Research Institute), LED visual targets at 100-cm distance were controlled, binocular eye position was monitored and recorded, juice reward was dispensed, and neuronal firing was recorded with a PXI-based LabOS data-acquisition and control system (www.eidactics.com). For monkey M2 (run at the University of Alabama at Birmingham), the visual display was a dual-channel optical stimulator with a field of view of ±18° (Gamlin et al. 2000; Zhang et al. 1998). To elicit saccades and smooth pursuit eye movements, monkeys M3 and M4 (run at the University of Alabama at Birmingham) viewed a 90 × 70° rear-projection display at 95 cm (8500 Electrohome Marquee). To elicit symmetric and asymmetric vergence eye movements, a pen plotter under computer control was used to move the LED visual target in depth and horizontally.

Data Collection and Analysis

Stored data were analyzed on Linux and OSX computers using custom interactive software.

Single-unit analysis.

We measured firing rates and eye positions for conjugate fixation with vergence relaxed and for symmetric and asymmetric vergence, with the latter being movements for which the MFT-instrumented eye was in approximately the same position before and after. Eye position and neuron activity were displayed, and periods of steady fixation were manually delineated with a cursor. Averages of horizontal and vertical positions of left and right eyes as well as average firing rates were computed for successive 100-ms samples over this period. Cells recorded from both sides of the brain are reported with reference to the on direction of the population. Thus, positive slopes correspond to increasing firing rates in the on direction, and threshold (T) values increase in the on direction (note that this sign convention differs from that of previous studies from our laboratories). Two scatter plots were generated for each cell, and correlation coefficients and linear regression parameters were calculated. For eye positions with vergence relaxed and held constant, we plotted the firing rate as a function of conjugate gaze. This yielded the position sensitivity of the cell for k_C. Extrapolating to zero firing rate yielded T for the cell. For various symmetric vergence angles, with conjugate gaze held constant, we measured the position sensitivity of the cell for k_V. We used a t-test (P < 0.001, two tailed) to determine if k_C and k_V were significantly different from zero.

For some MRNs (see Table 2), this analysis could not be completed, and the expected change in the firing rate for asymmetric convergence was calculated from measured k_V and k_C values, assuming linear summation of equal-angle vergence and conjugate commands to the aligned eye (e.g., Gamlin et al. 1989). For MRNs in which k_V was not measured, it was calculated similarly from the measured change in the firing rate during asymmetric convergence and the measured k_C value (e.g., Gamlin et al. 1989).

Table 2.

Medial rectus neurons

Cell	kV, spikes/s per deg	kC, spikes/s per deg	kV/kC	T, °	FR-F, spikes	FR-AC, spikes
1	0.3‡	2.4*	0.1†	−55.0	131.0	101.0
2	0.3‡	2.2*	0.1†	−51.0	114.0	87.0
3	0.3‡	3.1*	0.1†	−45.0	142.0	103.0
4	0.5‡	2.9*	0.2†	−49.0	145.0	112.0
5	1.1*‡	3.0*	0.4†	−43.0	127.0	101.0
6	1.5*	2.4*	0.6	−28.0	69.0	63.6§
7	1.7*‡	3.3*	0.5†	−40.0	127.0	104.0
8	1.8*‡	2.9*	0.6†	−47.0	130.0	115.0
9	2.0*‡	3.5*	0.6†	−38.0	136.0	115.0
10	2.1*	4.9*	0.4†	−25.0	136.0	115.0
11	2.1*‡	3.7*	0.6†	−39.0	145.0	123.0
12	2.2*	3.6*	0.6†	−38.0	141.0	155.0
13	2.5*	3.3*	0.8†	−40.0	143.0	137.0
14	3.0*	4.3*	0.7†	−26.0	119.0	119.0
15	3.0*	2.9*	1.0	−26.0	75.4	76.0§
16	3.0*	4.5*	0.7†	−25.0	107.0	84.0
17	3.1*	4.5*	0.7†	−18.0	81.0	72.6§
18	4.1*	2.9*	1.4	−32.0	90.0	102.0
19	4.8*	1.5*	3.2†	−2.0	17.0	42.0
20	4.9*	4.2*	1.2	−3.0	12.6	16.8§
21	5.0*‡	4.2*	1.2	−21.0	87.0	98.0
22	5.1*	4.6*	1.1	−7.0	32.2	35.2§
23	5.4*	6.7*	0.8	4.0	−26.8	−34.6§
24	5.7*	7.9*	0.7†	−10.0	87.0	84.0
25	5.9*	5.0*	1.2	−13.0	65.0	70.4§
26	5.9*	5.6*	1.1	−7.0	39.2	41.0§
27	6.2*	4.0*	1.6†	−17.0	68.0	81.2§
28	6.4*	5.7*	1.1	−5.0	35.0	51.0
29	6.5*	3.5*	1.9†	−17.0	59.5	77.5§
30	7.5*	5.6*	1.3†	−9.0	62.0	97.0
31	7.8*	5.4*	1.4†	−7.0	46.0	86.0
32	8.9*	5.2*	1.7†	−8.0	50.0	102.0
33	9.5*	1.5*	6.3†	−10.0	17.0	97.0§
34	9.5*	7.0*	1.4†	−2.0	13.0	47.0
35	10.6*	3.0*	3.5†	−15.0	44.0	112.0
36	13.9*	9.3*	1.5†	14.0	30.0	86.0
37	18.6*	13.6*	1.4†	20.0	40.0	100.0
38	19.0*	1.8*	10.6†	−27.0	48.6	151.8§
39	20.0*	3.7*	5.4†	15.0	55.0	153.0§
Mean	5.68	4.34	1.53	−20.3	77.9	89.2

^*Slope significantly different from 0 (P < 0.001);

^†k_V/k_C significantly different from 1 (P < 0.001);

^‡k_V estimated;

^§FR-AC estimated.

MFT analysis.

Convergence force, the muscle force in converged gaze minus that with convergence relaxed, with the position of the MFT-instrumented eye constant, was measured for the LR and MR by comparing MFT records before and after the asymmetrical convergence eye movements described above. By subtracting forces measured only a few seconds apart we avoided any effects of slow drift in MFT signals.

RESULTS

ABNs

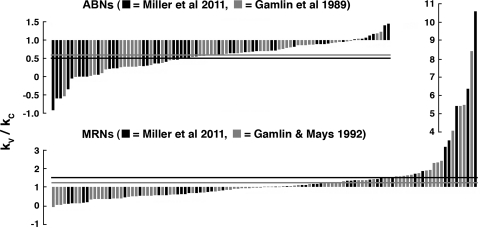
Forty-four ABNs were recorded on the left and right sides during conjugate gaze shifts and vergence movements of 16–27°. The rate-position sensitivity for k_C ranged from 10.8 to 2.2 spikes/s per deg. k_V ranged from 8.4 to −3.2 spikes/s per deg, with 10 neurons having no significant vergence sensitivity or increasing firing in convergence. The mean k_V/k_C was 0.50 (see Table 1 and Fig. 8).

Table 1.

Abducens neurons

Cell	kV, spikes/s per deg	kC, spikes/s per deg	kV/kC	T, °	FR-F, spikes	FR-AC, spikes
1	−3.2*	3.5*	−0.9†	−31.0	107.0	170.0
2	−1.5*	2.5*	−0.6†	−35.0	86.0	112.0
3	−1.3*	2.2*	−0.6†	−11.0	25.0	53.0
4	−1.0	2.9*	−0.3†	−19.0	56.0	78.0
5	−0.2	3.8*	−0.1†	−16.0	55.0	110.0
6	0.0	3.1*	0.0†	−24.0	75.0	95.0
7	0.0	6.0*	0.0†	−8.0	45.0	97.0
8	0.0	4.1*	0.0†	−8.0	36.0	63.0
9	0.2	3.9*	0.1†	−33.0	130.0	157.0
10	0.5	2.2*	0.2†	−58.0	130.0	137.0
11	0.5*	2.4*	0.2†	−46.0	109.0	123.0
12	1.1*	3.8*	0.3†	−24.0	82.0	105.0
13	1.4*	6.2*	0.2†	−12.0	75.0	115.0
14	1.5*	3.7*	0.4†	−29.0	107.0	126.0
15	1.5*	4.2*	0.4†	−27.0	113.0	138.0
16	1.5*	3.1*	0.5	−1.0	10.0	28.0
17	1.8*	3.5*	0.5†	−24.0	84.0	102.0
18	2.1*	4.5*	0.5†	−35.0	158.0	185.0
19	2.2*	6.3*	0.4†	−16.0	92.0	105.0
20	2.6*	5.7*	0.5†	−24.0	118.0	131.0
21	2.7*	4.2*	0.6†	−28.0	114.0	126.0
22	2.7*	4.2*	0.6†	−36.0	152.0	148.0
23	2.7*	3.9*	0.7	−20.0	76.0	87.0
24	2.8*	9.4*	0.3†	−2.0	15.0	83.0
25	3.3*	4.6*	0.7†	−31.0	142.0	153.0
26	3.4*	4.8*	0.7†	−35.0	168.0	165.0
27	3.6*	6.1*	0.6†	−30.0	180.0	190.0
28	3.7*	4.2*	0.9	−36.0	133.0	159.0
29	3.7*	5.4*	0.7†	−32.0	171.0	199.0
30	3.8*	4.7*	0.8	−34.0	157.0	170.0
31	3.9*	7.6*	0.5†	−20.0	150.0	163.0
32	4.6*	6.9*	0.7†	−15.0	102.0	112.0
33	4.8*	5.4*	0.9	−38.0	203.0	209.0
34	5.2*	4.9*	1.1	−18.0	86.0	90.0
35	5.6*	5.9*	0.9	−24.0	128.0	132.0
36	6.0*	4.3*	1.4†	−34.0	142.0	132.0
37	6.0*	10.8*	0.6†	−2.0	38.0	72.0
38	6.2*	6.9*	0.9	−14.0	93.0	90.0
39	6.3*	6.1*	1.0	−28.0	170.0	171.0
40	6.5*	4.5*	1.4†	−32.0	141.0	124.0
41	6.6*	5.9*	1.1†	−26.0	153.0	154.0
42	6.6*	7.4*	0.9†	−14.0	107.0	111.0
43	6.6*	6.5*	1.0	−20.0	132.0	118.0
44	8.4*	7.2*	1.2	−25.0	180.0	181.0
Mean	2.88	4.99	0.50	−24.4	109.7	126.6

k_V and k_C, rate-position linear regression slopes for vergence and conjugate eye movement, respectively; T, threshold, with on-direction positive; FR-F, firing rate in far viewing; FR-AC, firing rate in near viewing with asymmetric convergence.

^*Slope significantly different from 0 (P < 0.001);

^†k_V/k_C significantly different from 1 (P < 0.001).

Fig. 8.

Distribution of k_V/k_C for ABNs and MRNs. Values of k_V/k_C are plotted as bars, in order of signed magnitude, along with comparable data from earlier studies. Solid and shaded horizontal lines show mean values of k_V/k_C for the present and earlier studies, respectively. ABNs with k_V/k_C < 1 and MRNs with k_V/k_C > 1 are “paradoxical” in the sense discussed in the text. It can be seen that the vast majority of ABNs have k_V/k_C < 1, whereas only about half of MRNs have k_V/k_C > 1, but, for some, k_V/k_C >> 1.

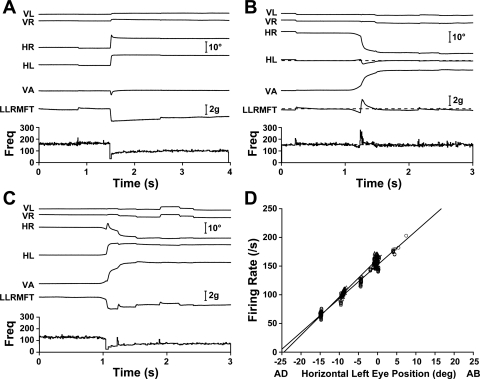
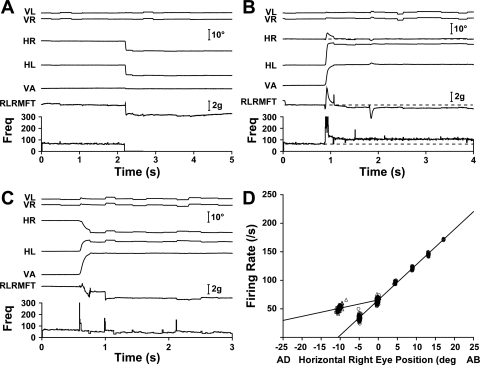
A left ABN with roughly equal conjugate and vergence sensitivities (k_V ∼ k_C) is shown in Fig. 3. Figure 3A shows a 10° rightward saccade, with little vertical component. The saccade was slightly rounded in the left eye, likely related to implantation surgery, and slightly overshot in the right eye, likely the result of subsequent motor adaptation. ABN activity and left LR muscle force dropped sharply just before the saccade, with a small or absent inhibitory pulse and slide phases characteristic of antagonists. After completion of the saccade, the left eye was adducted 10°, left LR muscle force was decreased, and left ABN activity was decreased, as expected. Figure 3B shows a 20° asymmetric convergence movement in which, apart from the familiar counterproductive saccade (Enright 1992), the MFT-instrumented left eye maintains its orbital position. The oculomotor system exhibited little hysteresis (Goldstein and Robinson 1986), so there is likely to be no effect of such transient movements on subsequent steady-state muscle forces and firing rates. To wit, this counterproductive saccade was associated with a transient force increase, so any residue would increase subsequent forces, whereas the record showed slightly decreased steady-state force, relative to before the eye movement. A neuron such as this, with k_V ∼ k_C, would be expected to show little change in activity when only contralateral eye position changes, as here, and steady-state left ABN activity was indeed unchanged from before to after the movement. Figure 3C shows a 20° symmetric convergence eye movement in which the left eye adducts 10°, as in the saccadic eye movement shown in Fig. 3A. Decreases in steady-state left ABN activity were comparable for the two movements, although decreases in left LR muscle force were smaller with convergence. The similarity of ABN activity in vergence and saccadic movements is reflected in the rate-position slopes for this neuron: k_V = 6.6 spikes/s per deg and k_C = 5.9 spikes/s per deg (Fig. 3D).

Fig. 3.

Abducens neurons (ABNs) with symmetric vergence (k_V) approximately equal to conjugate eye movement (k_C). The left ABN is cell 41 in Table 1. A: 10° rightward saccade with a small upward component and small transient divergence. Left LR force and left ABN firing both decreased, as expected. B: 20° asymmetric convergence in which the left MFT-instrumented eye returned to its preconvergence orbital position. After movement-related transients, left LR force settled at a value slightly lower than before the movement, whereas firing rate was unchanged. C: 20° symmetric convergence, in which both the firing rate and muscle force decreased, and which contributed a data point to the cluster around −10°, as shown in D. D: firing rate-eye position relationships are given by lines fitted to vergence (▵; k_V = 6.6 spikes/s per deg) and conjugate (○; k_C = 5.9 spikes/s per deg) eye movement data, respectively. VL, vertical left eye position; VR, vertical right eye position; HR, horizontal right eye position; HL, horizontal left eye position; VA, vergence angle; LLRMFT, left LR muscle force; Freq, neuron firing frequency.

A right ABN with vergence sensitivity significantly lower than conjugate sensitivity (k_V < k_C) is shown in Fig. 4. Figure 4A shows a normal leftward saccade from the straight-ahead position, after which the right eye is adducted 10° and both right LR force and right ABN activity have decreased, as expected. Figure 4B shows a 20° asymmetric convergence movement in which, as shown in Fig. 3B, the ipsilateral eye maintains its steady-state position. Despite there being no change in right eye position, right LR muscle force decreased by 0.3 g. Furthermore, unlike for the k_V ∼ k_C ABN shown in Fig. 3B, right ABN activity paradoxically increased markedly. Figure 4C shows a 20° symmetric convergence eye movement in which steady-state right eye adduction was similar to that in the saccadic movement shown in Fig. 4A, but, in contrast to the ABN shown in Fig. 3, the activity of this ABN did not decrease as much for convergence as for the equivalent saccadic eye movement.

Fig. 4.

ABNs with k_V < k_C. The right ABN is cell 13 in Table 1. A: 10° leftward saccade showing the expected decrease in right LR force. There was no evidence of impaired movement mechanics. B: 20° asymmetric convergence in which the right MFT-instrumented eye quickly returned to its preconvergence orbital position. Although the firing rate substantially increased from before to after the movement, muscle force clearly decreased. C: 20° symmetric convergence contributing a point to the cluster at −10° in D. D: the linear firing rate-eye position relationship for vergence (▵; k_V = 1.4 spikes/s per deg) was less steep than that for conjugate movement (○; k_C = 6.2 spikes/s per deg).

In symmetric convergence, LR muscle force, of course, decreases with adduction (e.g., Fig. 4C), but the decrease tends to be slightly smaller than in an equivalent conjugate movement. Negative convergence force is most apparent with asymmetric convergence, in an eye that does not change position (e.g., Fig. 4B), but as we have shown elsewhere (Miller et al. 2002), symmetric convergence is also associated with negative convergence force, although it is not apparent by inspection.

The difference in steady-state activity of this ABN for vergence and saccadic eye movements is summarized by its rate-position relationships: k_V = 1.4 spikes/s per deg and k_C = 6.2 spikes/s per deg (Fig. 4D), with k_V/k_C being at the low end of the range for our sample of ABNs. Few ABNs have k_V > k_C (see Fig. 8).

MRNs

Thirty-nine MRNs were recorded on the left and right sides during conjugate gaze shifts and vergence movements of 16–27°. The rate-position sensitivity for k_C ranged from 13.6 to 1.5 spikes/s per deg. k_V ranged from 20.0 to 0.3 spikes/s per deg, with four neurons having no significant vergence sensitivity. The mean k_V/k_C was 1.53 (see Table 2 and Fig. 8).

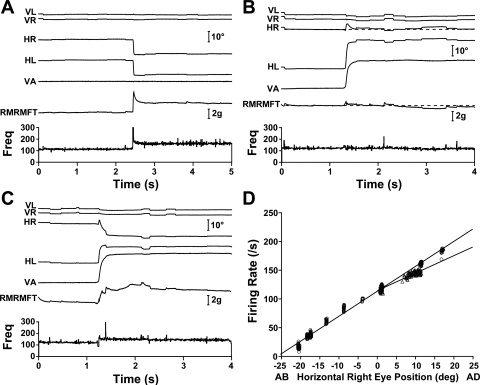
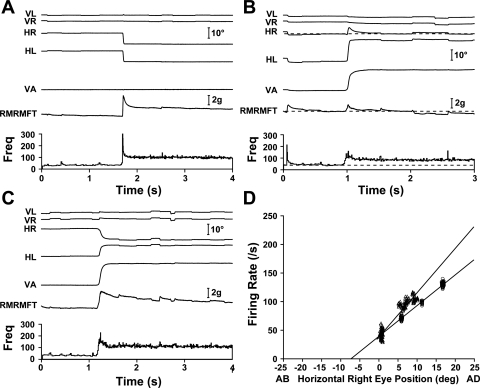
A right MRN with vergence sensitivity approximately equal to conjugate sensitivity (k_V ∼ k_C) is shown in Fig. 5. Figure 5A shows a 10° leftward saccade for which both right MRN activity and right MR force exhibit the strong pulse-slide patterns expected in agonists and steady-state firing rate and muscle force increase, as expected. Figure 5B shows a 20° asymmetric convergence movement in which the MFT-instrumented right eye maintains its steady-state orbital position, with no change in MRN activity. Steady-state right MR force appeared unchanged, and as shown in Fig. 7, mean convergence force, although always less than zero, was sometimes very close to zero, particularly for the MR. Figure 5C shows a 20° symmetric convergence movement in which steady-state right eye adduction is the same as in the saccadic movement shown in Fig. 5A. Steady-state changes in right MRN activity and right MR muscle force were also comparable to those shown in Fig. 5A. The similarity of MRN activity in vergence and saccadic movements is reflected in this neuron's rate-position relationships: k_V = 3.0 spikes/s per deg and k_C = 4.3 spikes/s per deg (Fig. 5D).

Fig. 5.

Medial rectus (MR) neurons (MRNs) with k_V ∼ k_C. The right MRN is cell 14 in Table 2. A: 10° leftward saccade showing the classic agonist pulse-slide-step pattern in both firing rate and right MR muscle force. Movement dynamics were crisp. B: 20° asymmetric convergence in which the MFT-instrumented right eye approximately maintained its position and the firing rate was unchanged by the saccade. C: 20° symmetric convergence. D: firing rate-eye position relationships for vergence (▵; k_V = 3.0 spikes/s per deg) and conjugate movements (○; k_C = 4.3 spikes/s per deg). RMRMFT, right MR muscle force; Freq, firing frequency.

A right MRN with vergence sensitivity higher than conjugate sensitivity (k_V > k_C) is shown in Fig. 6. Figure 6A shows a leftward 10° saccade. Both right MRN activity and right MR force showed the strong pulse-slide pattern of an agonist and the expected steady-state increases in firing rate and muscle force. Figure 6B shows a 20° asymmetric convergence eye movement in which, very much like the MRN shown in Fig. 5B, the MFT-instrumented right eye maintained its steady-state orbital position. Here, however, unchanged eye position and little changed muscle force were accompanied, paradoxically, by a large increase in MRN activity.

Fig. 6.

MRNs with k_V > k_C. The right MRN is cell 31 in Table 2. A: 10° leftward saccade showing the classic agonist pulse-slide-step pattern in both firing rate and right MR muscle force. B: 20° asymmetric convergence in which the MFT-instrumented right eye maintained its position and showed a large increase in firing rate but no increase in muscle force. C: 20° symmetric convergence. D: the firing rate-eye position sensitivity for vergence (▵; k_V = 7.8 spikes/s per deg) was higher than that for conjugate movements (○; k_C = 5.4 spikes/s per deg).

Figure 6C shows a 20° symmetric convergence eye movement in which steady-state right eye adduction is the same as in the saccadic movement shown in Fig. 6A. The right MR muscle force reflected the 10° adducting movement of the right eye and settled at a value similar to that shown in Fig. 6A. However, in contrast to the MRN shown in Fig. 5, the activity of this MRN increased more than for the equivalent saccade.

The difference in steady-state activity of this MRN for vergence and saccadic eye movements is summarized by its rate-position relationships: k_V = 7.8 spikes/s per deg and k_C = 5.4 spikes/s per deg (Fig. 6D).

Convergence Force

Convergence force, the increase in force at a given eye position related to convergence, is shown in Fig. 7. With vergence movements between 16 and 27°, we found that LR convergence force was −0.40 g and MR convergence force was −0.20 g, on average. Also shown are the similar results of Miller (2002), who found LR convergence force of −0.52 g and MR convergence force of −0.24 g, on average. As shown for all seven monkeys (4 monkeys in the present study and 3 monkeys in the earlier study), in both LR and MR, in both asymmetric and symmetric vergence paradigms, and in two different laboratories (monkeys M1, ERL, MLS, and MRL at the Smith-Kettlewell Eye Research Institute and monkeys M2, M3, and M4 at the University of Alabama), that mean convergence force was always in the “third quadrant” and that both LR muscle force and MR muscle force always decreased in convergence (P < 0.0001, binomial test, n = 14). Our finding that mean convergence forces are reliably less than zero should not, however, obscure the main point, which is that there are no increases in convergence forces, despite large increases in LR and MR innervations.

DISCUSSION

Motor Nucleus Activity

We studied conjugate and vergence eye movements and found that for ABNs, presumably a mixture of LRMNs and AINs, mean vergence sensitivity was half of conjugate sensitivity, k_V/k_C = 0.50. In comparable studies, Mays and Porter (1984) measured k_V/k_C = 0.62 and Gamlin et al. (1989a) measured k_V/k_C = 0.58, with the latter study showing specifically that sensitivities of undistinguished ABNs were not different from those of AINs identified by antidromic activation and also not different from the sensitivities of LRMNs. We also found for MRNs that mean vergence sensitivity was higher than conjugate sensitivity, k_V/k_C = 1.53. In a comparable study, Gamlin et al. (1989a) measured k_V/k_C = 1.22. The great majority of these MRNs were, no doubt, MRMNs (Clendaniel et al. 1994; Langer et al. 1986).

Several laboratories have focused instead on “disjunctive” eye movements, mainly movements of the ipsilateral or contralateral eye alone. Zhou and King (1998) recorded directly from VIth nerve rootlets and found that most LRMNs had binocular sensitivities with a preference for the ipsilateral eye. Neurons with k_V = k_C would, in disjunctive terms, be sensitive to only the ipsilateral eye, neurons with k_V = 0 would be equally sensitive to both eyes, and neurons with k_V < k_C would be sensitive to both eyes but more sensitive to the ipsilateral eye. Thus, the results of Zhou and King (1998) are consistent with the present results, those of Mays and Porter (1984), and those of Gamlin et al. (1989a). Sylvestre and Cullen (2002) studied ABNs, indirectly distinguishing LRMNs from AINs by their distributions in a plot of pursuit velocity sensitivity against threshold (Fuchs et al. 1988). They reported that many neurons were binocularly responsive with ipsilateral bias, apparently consistent with k_V < k_C. Similarly, Van Horn and Cullen (2009) found a few cells that might correspond to our k_V > k_C MRNs. Unfortunately, no clear comparisons with these two studies are possible because they classified neurons by velocity criteria, whereas the present study and the other studies with which we have compared ours measured fixation behavior. As Van Horn and Cullen (2009) caution, “mean position sensitivity estimated during fixation was significantly larger than that estimated during conjugate saccades.”

Gamlin et al. (1989a) found that values of k_V and k_C measured for undistinguished ABNs could be taken to separately describe LRMNs and AINs. Sylvestre and Cullen (2002), using a dynamic methodology, also found no significant differences in the sensitivities of LRMNs and AINs. King and Zhou (2000), in contrast, found that k_V/k_C tended to be higher for LRMNs than for AINs, and, although this finding is unique, it must be given weight because one cannot assert a null hypothesis. Overall, we think it reasonable to conclude that any mean differences in the sensitivities of LRMNs and AINs are small and that our findings, those of Gamlin (1989a), and those of Mays and Porter (1984) at least approximate the sensitivities of LRMNs.

Muscle Forces

There is, then, strong evidence that ensemble LR innervation for a given position of the eye in the orbit is stronger in convergence, and one might therefore think that the LR of an eye in convergent adduction would fail to relax as much as, and therefore be under greater tension than, the LR of an eye in the same position achieved by conjugate adduction with vergence relaxed. There is similarly strong evidence that MR innervation is higher for a given eye position during convergence, similarly suggesting that the MR of an eye in convergent adduction would be under greater tension than in the same position under conjugate adduction. Furthermore, these two inferences about horizontal rectus forces support one another, because if LR and MR forces were not balanced, the eye would not be in mechanical equilibrium, and it has been shown that the cyclovertical eye muscles cannot produce sufficient horizontal forces to make up a significant LR-MR discrepancy (Miller et al. 2002). One might expect both LR and MR convergence forces to be greater than zero. Against these expectations, which follow directly from the motor nucleus recording studies reviewed above, in combination with the assumption of an oculomotor final common path, we found that convergence forces were always less than zero and that muscle forces were slightly lower in convergence, the difference averaging −0.40 g for the LR and −0.20 g for the MR. In comparable studies of muscle force alone, Miller et al. (2002) found LR convergence force to be −0.52 g and MR convergence force to be −0.24 g.

We see two principal ways, not mutually exclusive, in which the missing force paradox might be resolved. For brevity, we will refer to ABNs with k_V < k_C and MRNs with k_V > k_C as “paradoxical neurons,” with the understanding that it is only in the total, ensemble innervation that a paradox actually occurs and that there would be no paradox, for example, if these neurons were balanced by neurons with complementary sensitivities.

Sampling Bias

It seems likely that methods commonly used to isolate oculomotor system neurons for study undersample or miss significant populations (Barmack 1977; Büttner-Ennever et al. 1998; Lemon 1984). In the present study, we isolated cells from which we could record burst-tonic activity during saccades in the population's on direction and would have overlooked cells with other characteristics. It is possible that unsampled neurons had k_V-to-k_C ratios distributed differently than ours, but as an explanation of the missing force paradox this makes the implausible supposition that we had undersampled opposite types of neurons in the two nuclei: LRMNs with k_V > k_C and MRMNs with k_V < k_C.

Still, common selection methods would miss any cells with little burst response or conjugate sensitivity, and, to get a more complete picture, future studies would do well to sample both more widely and more precisely, perhaps using antidromic activation or spike-triggered EMG recordings to identify neurons of interest.

Motor Unit Specialization

The second sort of resolution would depend on motor unit specialization such that paradoxical MNs were preferentially associated with muscle fibers that were weak, whose serial or parallel mechanical coupling attenuated their effective oculorotary force, or that served a regulatory function rather than an oculorotary function.

At least six fiber types have been morphologically distinguished in extraocular muscle (EOM), and these fall into two groups: singly innervated twitch fibers (SIFs) and multiply innervated nontwitch fibers (MIFs), with the latter being unique to EOMs (Porter et al. 1995). Büttner-Ennever et al. (2001) used tract tracers to identify outer MNs around the periphery of classical oculomotor, trochlear, and abducens nuclei, separate from SIF MNs, as the source of innervation to global layer MIFs (MIFs in the morphologically distinct layer facing the globe). Wasicky et al. (2004) used an anterograde tracer to identify premotor inputs to oculomotor neurons in and surrounding the classical oculomotor nucleus, and Ugolini et al. (2006) used a retrograde transneuronal tracer to determine the premotor connectivity of abducens MNs innervating global MIFs. These studies provide evidence that nontwitch motor units differentially receive input suitable to controlling slow eye movements such as vergence, tonic muscle activity as in gaze holding, and regulatory functions as in the putative feedback system involving palisade afferents found at the insertional ends of global MIFs (Büttner-Ennever et al. 2002). They establish for the oculomotor system the important principle of functional specialization by motor unit or muscle fiber type and raise the possibility that MNs outside the classical nuclei are active in vergence (perhaps they have properties complementary to those of our paradoxical neurons).

Less is known about neurons innervating orbital layer fibers (fibers in the EOM layer facing the orbital wall). Orbital fibers do not insert in the globe but rather in the midorbital connective tissues that function as EOM pulleys, which control effective muscle pulling directions (Miller 1989, 2007; Oh et al. 2001; Demer et al. 2000). If paradoxical MNs were found to innervate orbital fibers, it might explain why their activity does not correlate with oculorotary force. We know of no anatomic or functional data that bear on this issue.

EOM fibers are sometimes imagined to extend, independent, uninterrupted, and homogeneous, from their muscle's origin in the bony orbit to their insertion in either the sclera or pulley, although the mechanics are certainly more complex. Goldberg (1997) showed in squirrel monkey EOM that 1/3-width myectomy reduced whole muscle twitch tension by only 5%, implying substantial lateral mechanical coupling among fibers. It is common for long mammalian skeletal muscles to be composed of fibers that terminate midbelly with collagenous bridges or myomyonal junctions to neighboring fibers (Young et al. 2000), and Oh et al. (2001) showed in human and monkey EOMs that the number of fibers in both global and orbital layers varied by a factor of two or more over the length of the muscle belly (excluding, that is, the tapering original and insertional ends). McLoon et al. (1999) found that the rabbit EOM showed extensive variation of myosin heavy chain isoforms, within and between fibers, along both the muscle's length and across lamina. There are, then, mechanical and molecular mechanisms through which the oculorotary effectiveness of motor units might vary, and if there were a relationship between MN properties and motor unit effectiveness, it might be such as would account for the missing force paradox.

The distribution of paradoxical neurons is different in the abducens and oculomotor nuclei, and this difference appears in both present and previous studies (Fig. 8). In the abducens nucleus, the great majority of neurons have k_V/k_C < 1, whereas in the oculomotor nucleus, about half are on either side of 1, and mean k_V/k_C > 1 is due to a relatively small number of neurons with k_V/k_C >> 1. Perhaps the lone finding that k_V was not significantly different from k_C for MRNs (Mays et al. 1984) was due to the relatively rare neurons with k_V > k_C being missed.

The small number of ABNs with k_V/k_C < 0 from the present study can be seen to have k_V < 0 in Table 1, and the one from Gamlin et al. (1989; see Table 3) similarly has k_V with a sign opposite to that of the population mean. Such neurons may be driven by contralateral MR interneurons (see, e.g., Mays 2004).

An implication of the skewed distribution of k_V/k_C for MRNs is that if only the small number of MRMNs with k_V/k_C >> 1 preferentially innervated fibers that, for one reason or another, contributed little to oculorotary muscle force or contributed nonadditively, the paradox could be resolved for that muscle. In contrast, the vast majority of ABNs are paradoxical (k_V/k_C < 1), making it unlikely that preferential innervation could more than ameliorate the paradox for the LR. However, if, as King and Zhou (2000) suggest, k_V/k_C were closer to 1 for LRMNs than for AINs, this would be another ameliorating factor.

Loss of the final common path assumption means that we must now look inside what had long been assumed to be a simple, homogeneous output channel. It seems clear that doing so will require verified MN recordings in conjunction with measurements of oculorotary forces of individual motor units. Such measurements would make it possible, for instance, to characterize the relationship of k_V/k_C to effective motor unit strength, thereby testing the hypothesis that paradoxical MNs tend to drive weak, poorly coupled, or regulatory muscle fibers. Particularly in the abducens, it should be straightforward to record MNs with a range of k_V-to-k_C ratios (see Fig. 8). We elsewhere describe a technique for spike-triggered averaging of MFT signals, which provides a way to measure oculorotary twitch forces related to individual, isolated MNs, i.e., to study individual motor units in alert, behaving animals (Gamlin et al. 2007a, 2007b).

GRANTS

This work was supported by National Eye Institute Grants EY-015314 (to J. M. Miller) and P30-EY-03039 (to the University of Alabama, Birmingham, AL).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).