The impact of seasonal and year-round transmission regimes on the evolution of influenza A virus

Abstract

Punctuated antigenic change is believed to be a key element in the evolution of influenza A; clusters of antigenically similar strains predominate worldwide for several years until an antigenically distant mutant emerges and instigates a selective sweep. It is thought that a region of East–Southeast Asia with year-round transmission acts as a source of antigenic diversity for influenza A and seasonal epidemics in temperate regions make little contribution to antigenic evolution. We use a mathematical model to examine how different transmission regimes affect the evolutionary dynamics of influenza over the lifespan of an antigenic cluster. Our model indicates that, in non-seasonal regions, mutants that cause significant outbreaks appear before the peak of the wild-type epidemic. A relatively large proportion of these mutants spread globally. In seasonal regions, mutants that cause significant local outbreaks appear each year before the seasonal peak of the wild-type epidemic, but only a small proportion spread globally. The potential for global spread is strongly influenced by the intensity of non-seasonal circulation and coupling between non-seasonal and seasonal regions. Results are similar if mutations are neutral, or confer a weak to moderate antigenic advantage. However, there is a threshold antigenic advantage, depending on the non-seasonal transmission intensity, beyond which mutants can escape herd immunity in the non-seasonal region and there is a global explosion in diversity. We conclude that non-seasonal transmission regions are fundamental to the generation and maintenance of influenza diversity owing to their epidemiology. More extensive sampling of viral diversity in such regions could facilitate earlier identification of antigenically novel strains and extend the critical window for vaccine development.

1. Introduction

Influenza A viruses are responsible for regular epidemics, and occasional pandemics, throughout the world [1]. From 1968 until the recent emergence of a new pandemic influenza A (H1N1) virus, the majority of infections have been caused by the H3N2 subtype [1–3]. Rapid but low-fidelity replication facilitates genetic diversification in the viral population. Mutations affecting the virus surface proteins may result in less efficient recognition by protective antibodies and necessitate regular updates of the influenza vaccine [4–6]. Genetic changes accumulate continuously in the influenza genome. Antigenic change, however, appears to take the form of punctuated jumps interspersed with small-scale drift [7–9]; clusters of antigenically similar strains persist for several years until an antigenically distant strain emerges to found a replacement cluster. Modelling studies suggest that the punctuated aspect of the evolutionary pattern can be explained by broad short-term cross-immunity [10,11] or antigenic landscapes composed of ‘neutral’ networks [12]. In the latter case, following the founding of a new antigenic cluster, antigenically neutral or nearly neutral drift mutations accumulate, exploring the sequence space until an antigenically distant mutant emerges to seed a new cluster that replaces the existing one.

In temperate regions, influenza incidence is seasonal. There is a pronounced epidemic peak in winter and infections are rarely observed in summer [13,14]. Influenza incidence is less variable in tropical and subtropical regions and, over the course of a whole year, the total number of infections is believed to be similar in all regions [15]. Phylogenetic analysis has suggested that temperate epidemics are probably reseeded every year from an external source [2,16,17] and revealed little evidence for positive selection over the course of temperate region influenza seasons [17]. Early phylogenetic studies suggested that many new antigenic variants of influenza emerge in China and neighbouring countries [18,19]. A more recent study suggested that seasonal influenza epidemics are started each year by viruses imported from a region of East–Southeast Asia, and implied that the majority of antigenic evolution occurs in this region [20]. This area includes countries with tropical and subtropical climates; local oscillations in incidence are relatively small and poorly synchronized, resulting in year-round transmission on a regional scale.

Here, we use a mathematical model to examine how seasonal and non-seasonal transmission regimes, and their global interplay, influence the evolution of influenza over the 3–5 year periods between large punctuated antigenic jumps, which we do not model. A mutant with a large antigenic advantage relative to circulating strains will experience a relatively large susceptible population. As such, the system is not at equilibrium and epidemic infection dynamics are expected even if the underlying transmission rate is seasonally invariant. Within this transient epidemiological context, we focus on the impact of antigenically neutral and nearly neutral mutations but, where pertinent, also explore the implications of more significant antigenic changes. We start with simple intuitive models, and gradually build up layers of insight to arrive at a fuller understanding of the various mechanisms at work, and how they fit together in more complex models.

2. Mathematical model

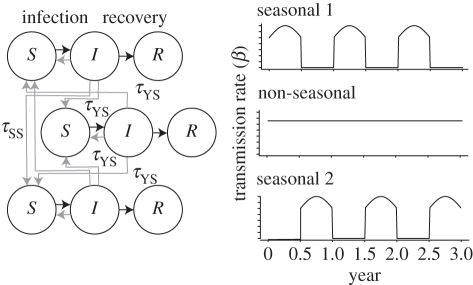
Our model is based on a conventional extension of the standard SIR framework to multiple co-circulating strains with immune cross-reaction [7,10–12,21–32]. The global population is divided into three distinct regions (figure 1), each of population size N. Two regions are characterized by transmission and non-transmission seasons that each last six months and do not overlap. The underlying probability of transmission intensity β is zero in the non-transmission season and positive in the transmission season, changing sinusoidally with a maximum of (1 + δ)β at the midpoint of the season. In the third region, transmission is constant year round. In each region, individuals make transmissible contact with other individuals in the same region at rate β, and with individuals in other regions at rate τ_ZWβ, where τ_ZW is much less than 1. The seasonal transmission regions are directly coupled to each other by τ_SS, and coupled with the non-seasonal transmission region by τ_YS. Infected individuals recover at rate γ. Natural mortality occurs at rate μ, and an equal birth rate ensures the population size remains constant.

Figure 1.

Schematic model diagram. The global population is divided into three regions. Transmission is seasonal in two regions, year round in the third. Each population consists of susceptible (S), infected (I) and recovered (R) individuals. Black lines indicate the flow between these states. Grey lines indicate transmission interaction.

The interaction of multiple strains is modelled using a history-based approach. Hosts are classified according to the virus strains with which they are currently infected, and those with which they have been previously infected. Virus strains are defined by a 50-element binary genotype. Forty elements are phenotypically neutral, 10 determine antigenic similarity. Immunity reduces susceptibility. Hosts who have recovered from an infection acquire permanent complete immunity to the infecting strain and partial immunity to other strains. There is no temporary immunity. The antigenic Hamming distance between two strains h is the number of antigenic bitstring locations at which they are different. Cross-immunity g is linearly related to the Hamming distance g(h) = min{σh, 1}, where 0 < σ < 1 is the antigenic advantage associated with a single point mutation. Nearly neutral mutations are represented by values of σ close to 0. If a host has experienced more than one previous infection, the immune response is determined by the previous strain most closely related to the challenging strain.

The start point of our time frame is the emergence of a mutant, termed the wild-type, that is antigenically distant from previously circulating strains. We approximate this circumstance with the assumption that the entire population is susceptible. Consequently, the epidemiological dynamics are transient in all regions. In the non-seasonal transmission region, there is a single wild-type epidemic lasting several years (electronic supplementary material, figure S1). In the seasonal transmission regions, there are sequences of epidemics over several years. The epidemics end because of stochastic fade out when the susceptible population is sufficiently depleted. Generally, the time until fade-out is longer if the transmission intensities are lower. The model is iterated as a discrete population, continuous-time Markov process using the Gillespie algorithm [33]. Full details can be found in the electronic supplementary material.

3. Results

(a). Decoupled regions, wild-type and up to one mutant

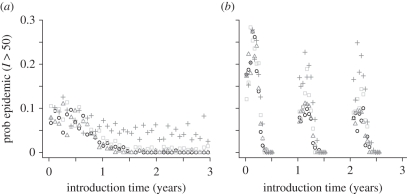
Here we consider individual, decoupled, regions to assess the effects of seasonal and non-seasonal transmission on epidemic potential. Classically, the epidemic potential of a pathogen is expressed by the basic reproductive number R₀, the number of secondary infections resulting from a single infected individual in an otherwise naive population. If transmission is non-seasonal, R₀ = βN/(γ + μ) [34,35]. If transmission is seasonal, the expected number of secondary infections depends on the time at which the infected individual is introduced, and is termed the effective reproductive number R_e(t) = β(t)N/(γ + μ). For basic models, branching process arguments give expressions for the probability that a single infected individual causes a significant outbreak [36–38]. In order to compute corresponding probabilities using our model, we define an ‘epidemic’ to be at least 50 simultaneous infections. When transmission is non-seasonal, the time of the initial infection does not affect the probability of an epidemic. When transmission is seasonal, even though R_e(t) > 1 and each infection is expected to lead to more than one secondary infection throughout the transmission season, infections introduced in the latter half of the season rarely lead to significant outbreaks (electronic supplementary material, figure S2). Immediately after introduction, the number of infections increases slowly. A declining transmission rate exacerbates this effect and the end of the season curtails transmission before the epidemic gains momentum.

As the wild-type strain circulates, immunity accumulates in the host population. The epidemic potential of a second, mutant, strain depends on the size of the immune classes in the population and their susceptibility to re-infection. Mutant epidemics, defined as at least 50 simultaneous infections, will usually manifest as outbreaks within the wild-type epidemic. As the wild-type epidemic progresses, the probability that a single neutral or nearly neutral mutant strain will cause an epidemic decreases (figure 2). If transmission is non-seasonal, this decrease becomes rapid as the wild-type epidemic approaches its peak. If transmission is seasonal, the decrease is less pronounced because wild-type epidemics are curtailed by the end of each season, before the susceptible population is exhausted, and immunity accumulates more slowly. Furthermore, the mid-season peak in the transmission rate may allow an infected individual to infect several others, even when there is extensive immunity in the population. Mutants in seasonal regions are most likely to be successful if they are introduced around the second month of the transmission period. The success rate of earlier mutants is reduced by the low transmission rate. Later mutants are compromised by the low transmission rate, accumulating host immunity and the brevity of the remaining transmission season. Relatively large antigenic advantages—for our parameter set, re-infection probabilities of up to 0.6—have only a weak impact on the probability that a mutant will be successful. However, when the re-infection probability exceeds around 0.6, mutant epidemic probabilities increase rapidly and become almost independent of the wild-type dynamics (electronic supplementary material, figure S2).

Figure 2.

Probabilities, as a function of introduction time, that a significant outbreak (at least 50 simultaneous infections) results from the introduction of one individual infected with a mutant strain into a population experiencing a wild-type epidemic. (a) Non-seasonal transmission; (b) seasonal transmission. Circles, black: mutant strain has no antigenic advantage (σ = 0); triangles, mid-grey: mutant can re-infect individuals immune to wild-type with probability σ = 0.1; squares, pale grey: σ = 0.3; plus symbols: σ = 0.7. Each set of points is based on 10 000 independent trials with random introduction times. Initially all hosts susceptible except for 10 individuals with wild-type infections. Parameter values as in electronic supplementary material, table S1.

(b). Coupled regions, wild-type and one mutant

Here we assess the effects of coupling on mutant epidemics, persistence and global spread using the model with two seasonal transmission regions and one non-seasonal transmission region. We consider a wild-type, introduced at time t = 0, and a single mutant strain with a probability σ of re-infecting individuals immune to the wild-type. Coupling affects the wild-type epidemic behaviour in all regions. Stronger direct coupling between the seasonal regions increases the magnitude of the seasonal epidemics (electronic supplementary material, figure S3). Stronger coupling between the seasonal and non-seasonal regions increases the magnitude of epidemics in all regions (electronic supplementary material, figure S4). The mutant strain is introduced into this epidemiological context at a random time. We define a mutant epidemic in a region to be at least 50 simultaneous infections.

A nearly neutral mutant introduced to the seasonal region is more likely to cause an epidemic in that region than in other regions (figure 3a). If it does escape from the seasonal region, it usually becomes established in all regions, which we term cosmopolitan. Mutants are only likely to spread to other regions if they are introduced in the first year of the wild-type epidemic (figure 3b–d), near the start of the transmission season (electronic supplementary material, figure S5). In the second year, the probability that a mutant becomes established locally is 20–40% lower than the first year, and the probability that it spreads elsewhere is 80–90% lower. Stronger coupling between seasonal and non-seasonal transmission regions increases the probability that the seasonal region mutant becomes cosmopolitan. A nearly neutral mutant introduced to the non-seasonal region has a lower probability of becoming established locally than a mutant in the seasonal region. However, a large proportion of locally successful mutants become cosmopolitan (figure 3e). Mutants are most likely to spread to other regions if they are introduced some time during the first year of the wild-type epidemic (figure 3f–h and electronic supplementary material, figure S5). In the second year, the probability that a mutant becomes established locally is 60% lower, and the probability that it spreads elsewhere is 95% lower. Stronger coupling between the seasonal and non-seasonal transmission regions has little impact unless close to zero, in which case it increases the probability that non-seasonal mutants become cosmopolitan.

Figure 3.

Probabilities, as a function of coupling between seasonal and non-seasonal regions, that a significant outbreak results from the introduction of one individual infected with a mutant strain into a population experiencing a wild-type epidemic. (a–d) Mutant introduced in seasonal region 1. (e–h) Mutant introduced in non-seasonal region. (a,e) Total probability over all introduction times in the first four years of the wild-type epidemic. (b,f) Probability if the mutant strain is introduced in year 1. (c,d,g,h) Probability if the mutant is introduced in year 2 or 3, expressed as the percentage change relative to year 1. Circles, probability of mutant epidemic in seasonal region 1; triangles, non-seasonal region; plus symbols, seasonal region 2; crosses, all regions. Each point is the result of 10 000 independent trials. Initially, all hosts susceptible except for 10 individuals with wild-type infections in seasonal region 1. Parameter values as in electronic supplementary material, table S1, except σ = 0.1. No mutation.

Regardless of the region into which the mutant is introduced, the direct coupling between seasonal regions has little impact (electronic supplementary material, figure S6). Results are similar if the mutant is neutral, has a small or intermediate antigenic advantage (electronic supplementary material, figures S5–S9). However, the overall probability that a non-seasonal mutant becomes cosmopolitan begins to increase rapidly when the re-infection probability exceeds approximately 0.5 (electronic supplementary material, figure S10). This increase is driven by mutants introduced in the second and third years having a much higher chance of becoming established.

(c). Coupled regions, multiple spontaneous mutants

Here we extend the coupled model to allow mutant strains to emerge spontaneously. Initially, the wild-type strain is introduced and an epidemic commences. Each element of the dominant viral genotype associated with each infected individual has a small probability of switching as long as that individual is infected. Each difference in the antigenically relevant section of the genotypes confers a re-infection probability of σ, up to a maximum of 1.

When the antigenic advantage of each mutation is nil (σ = 0), weak (σ = 0.1) or intermediate (σ = 0.3), mutants are more likely to be successful, i.e. cause significant outbreaks, in the region where they originate than elsewhere (figure 4a,b and electronic supplementary material, figure S11). In the seasonal region, the majority of all mutants appear in the first year of the wild-type epidemic, when the number of wild-type infections is highest. Most of these mutants appear in the second half of the transmission season. Nevertheless, a large proportion of all mutants that cause significant outbreaks appear in the first half of the transmission season (electronic supplementary material, figures S16 and S17). In the non-seasonal region, the majority of all mutants appear almost 2 years into the wild-type epidemic, again when the number of wild-type infections is highest, but the majority of successful mutants appear six months before this.

Figure 4.

Probabilities that mutant strains emerging spontaneously from existing strains cause epidemics: (a,b) depending on the strength of coupling between seasonal and non-seasonal regions when each difference between antigenic genotype sections translates into a re-infection probability of σ = 0.1; (c,d) depending on the re-infection probability (σ) conferred by each difference between antigenic genotype sections when the coupling between seasonal and non-seasonal regions is τ_YS = 0.0005. (a,c) Mutant strains emerging in seasonal region 1. (b,d) Mutant strains emerging in the non-seasonal region. All panels show the probability that the mutant causes at least 50 simultaneous infections in seasonal region 1 (circles), non-seasonal region (triangles) and seasonal region 2 (plus symbols). Each point is the result of 100 independent trials. Initially, all hosts susceptible except for 10 individuals with wild-type infections in seasonal region 1. Parameter values as in electronic supplementary material, table S1.

In general, mutants arising in the non-seasonal region are more likely to spread globally than mutants arising in seasonal regions. Stronger coupling between non-seasonal and seasonal regions increases the probability that mutants will spread globally, weakly for seasonal mutants, more strongly for non-seasonal mutants (figure 4a,b). If coupling is stronger, the majority of successful non-seasonal mutants still appear before the majority of all mutants, although everything happens earlier.

Stronger coupling causes the majority of all non-seasonal mutants to appear earlier, but still after the majority of successful mutants. A larger proportion of seasonal mutants appear in the second year, but again after most of the successful mutants in that year (electronic supplementary material, figure S17). Stronger coupling between seasonal regions has little impact (electronic supplementary material, figures S12 and S17). The amplitude of the transmission rate fluctuations determines, to some extent, whether or not seasonal epidemics occur at all. Consequently, low-amplitude fluctuations can severely limit the epidemic potential or wild-type and mutant strains alike. Away from this region, however, the amplitude of seasonal fluctuations has little clear impact on the epidemic potential of mutant strains (electronic supplementary material, figures S13 and S17).

If mutation is neutral or weakly advantageous, higher non-seasonal transmission intensity leads to weak increases in the probabilities that seasonal or non-seasonal mutants will be successful in the non-seasonal region (electronic supplementary material, figures S14 and S18). If mutation has an intermediate advantage, the probability of a significant outbreak increases rapidly when non-seasonal transmission intensity exceeds a certain threshold, in this case R₀ = 1.3, and there is an explosion in diversity. Similarly, if R₀ is fixed, greater antigenic advantages conferred by each mutation have little impact until the re-infection probability reaches a certain threshold, in this case around 0.5 (figure 4c,d). Then, the probability that non-seasonal mutants cause significant outbreaks locally, and in seasonal regions, begins to increase rapidly until, at σ = 0.7, there is an explosion in diversity. Weak to intermediate antigenic advantages have little impact on the phase lag between the appearance of the majority of successful mutants and the majority of all mutants (electronic supplementary material, figure S18). A large antigenic advantage, however, leads the majority of successful non-seasonal mutants to appear in phase with the majority of all mutants.

Viral diversity, expressed transiently in terms of the number of extant genotypes, and cumulatively in terms of the total number of genotypes appearing over several years, is generally similar if the antigenic advantage of mutation is nil, weak or intermediate. Transient diversity is proportional to the number of infected individuals (electronic supplementary material, figure S19). Cumulative diversity depends mainly on transmission intensity, again an indicator for the number of infected individuals, and most mutants arise directly from the wild-type (electronic supplementary material, figure S20). However, when the re-infection probability associated with each mutation exceeds a certain threshold, which depends on the intensity of non-seasonal transmission, diversity begins to increase rapidly in the non-seasonal region. If the re-infection probability increases further, there is an explosion in diversity.

4. Discussion

We have used a mathematical model to investigate how seasonal and non-seasonal transmission paradigms influence the evolution of influenza A between the relatively large, punctuated, antigenic jumps. A study based on a deterministic model of a single epidemic with non-seasonal transmission found that longer epidemics facilitate greater antigenic drift, and that the majority of this drift occurs before the epidemic peaks [24]. In the context of a spatially structured host population with multiple coupled transmission paradigms and viral evolution in a high-dimensional antigenic space, we have shown that the epidemiology of regions with non-seasonal transmission makes them central to viral evolution, while the role of seasonal regions is limited by their epidemiology. In particular:

• — in non-seasonal regions, mutant strains with the highest chance of causing significant local outbreaks emerge before the wild-type epidemic peaks—earlier than the majority of mutants. A large proportion of these mutants become cosmopolitan. After the epidemic peak, the effective reproductive number of mutants is low, even if they have a moderate antigenic advantage, and they do not benefit from the epidemic momentum enjoyed by the wild-type;

• — in seasonal regions, the mutant strains with the highest chance of causing significant local outbreaks, throughout the global wild-type epidemic, emerge in the first half of the transmission season—earlier than the majority of mutants. However, these mutants are unlikely to spread globally unless they emerge at the start of the first season of the wild-type epidemic. The seasonal fluctuation in transmission intensity introduces a strong founder effect and allows mutants to temporarily escape the effects of herd immunity. However, mutants must appear early for an outbreak to build momentum before the transmission season ends;

• — the extent of migration between non-seasonal and seasonal transmission regions strongly influences whether mutant strains become cosmopolitan, wherever they first arise. Throughout the transmission periods, there is continuous potential migration between non-seasonal and seasonal regions. Strains arising in seasonal regions can persist by migrating to non-seasonal regions. Strains circulating year round have multiple opportunities to migrate to seasonal regions at the beginning of a transmission period when it is easier to found an epidemic;

• — direct migration between out-of-phase seasonal transmission regions has little impact on the global spread of mutant strains. The overlap is brief, the epidemic in the donor region is winding down and colonization of the destination region is difficult because the transmission rate is low at the beginning of the season. The accumulation of host immunity accentuates this effect as it effectively shortens the transmission seasons, reducing the overlap; and

• — the probability that mutants cause significant outbreaks is similar if all mutations are antigenically neutral, or some mutations confer a weak to moderate antigenic advantage. However, after the antigenic advantage conferred by mutation exceeds a certain threshold, there is a rapid increase in the probability of significant outbreaks in the non-seasonal region and an explosion in the global viral diversity. This threshold depends on the intensity of non-seasonal transmission. In the non-seasonal region, most mutants appear around the epidemic peak, but by this time there is extensive immunity in the population. Therefore, the epidemic potential of the majority of mutants only increases significantly when their antigenic advantage allows them to escape herd immunity at, and beyond, this point of the wild-type epidemic.

Our insights are based on numerical solutions of stochastic, discrete population, continuous-time models. In order to maintain computational efficiency, we used relatively small population sizes and a coarse spatial structure with clearly defined seasonal and non-seasonal transmission paradigms. We expect larger, more structured populations to lead to non-seasonal epidemics that build more gradually and last longer as immunity accumulates more slowly. This change of intensity may make it easier for multiple strains to co-circulate. Allowing low-level transmission throughout seasonal ‘non-transmission’ periods may enhance the persistence of mutants in these regions. Additional regions with less clearly defined transmission paradigms may lead to increased migration between the well-defined seasonal and non-seasonal transmission regions. Weak localized seasonality in subregions of ‘non-seasonal’ regions may introduce some disruptive noise into the pattern of circulation and evolution. Assessing the impact of these factors is an important area for future research. The results presented here provide a baseline for comparison. Given that our results are consistent across a range of model complexities, we do not, however, expect them to be substantially modified by any of these additional factors.

Our analysis indicates that one key characteristic of a source region is consistency of transmission. Factors often considered to enhance the regularity and duration of transmission include large host populations and a regional population structure composed of well-connected but semi-autonomous patches [39–41]. A second key characteristic of a source region is strong connectivity to seasonal regions. A pronounced founder effect means that a strain introduced at the start of the seasonal transmission period is likely to dominate for the whole winter. Even antigenically advantaged mutants must be introduced in the first half the of the transmission period if they are to cause a significant outbreak. Regions with year-round transmission and strong global connectivity are much more likely to supply these founders. Genetic surveillance has suggested that most seasonal epidemics are started by viral seeds from East–Southeast Asia [2,18–20]. Asynchronous subregional epidemic patterns, high population density and widespread exchange with temperate region populations suggest that epidemiological conditions in this region are ideal for a source of antigenic novelty. As more epidemiological data become available from the tropics and subtropics, it should be possible to identify further potential source regions.

Our analysis also indicates that antigenically novel mutants that rise to global predominance are likely to appear in a region with a stable transmission pattern, from lineages established some time before the peak of the epidemic associated with the currently predominant antigenic cluster. Extensive sampling of viral genetic diversity in regions identified as likely evolutionary sources will be required to identify such strains. Real-time phylogenetic monitoring, in combination with analysis of antigenic and epidemiological data, may then aid the earlier detection of novel antigenic variants. Improving our understanding of the epidemiology of influenza throughout tropical and subtropical regions, and integrating this information with evolutionary analysis, is thus essential to improve predictions of the antigenic cluster transitions that are critical for vaccine efficacy.