Whole brain diffeomorphic metric mapping via integration of sulcal and gyral curves, cortical surfaces, and images

Abstract

This paper introduces a novel large deformation diffeomorphic metric mapping algorithm for whole brain registration where sulcal and gyral curves, cortical surfaces, and intensity images are simultaneously carried from one subject to another through a flow of diffeomorphisms. To the best of our knowledge, this is the first time that the diffeomorphic metric from one brain to another is derived in a shape space of intensity images and point sets (such as curves and surfaces) in a unified manner. We describe the Euler–Lagrange equation associated with this algorithm with respect to momentum, a linear transformation of the velocity vector field of the diffeomorphic flow. The numerical implementation for solving this variational problem, which involves large-scale kernel convolution in an irregular grid, is made feasible by introducing a class of computationally friendly kernels. We apply this algorithm to align magnetic resonance brain data. Our whole brain mapping results show that our algorithm outperforms the image-based LDDMM algorithm in terms of the mapping accuracy of gyral/sulcal curves, sulcal regions, and cortical and subcortical segmentation. Moreover, our algorithm provides better whole brain alignment than combined volumetric and surface registration (Postelnicu et al., 2009) and hierarchical attribute matching mechanism for elastic registration (HAMMER) (Shen and Davatzikos, 2002) in terms of cortical and subcortical volume segmentation.

Introduction

Whole brain mapping has been widely used in neuroimaging research for multiple purposes, including structural segmentation, voxel-based and tensor-based morphometry, group analysis on functional magnetic resonance imaging (MRI) and positron emission tomography (PET) (e.g., Miller and Qiu, 2009). Due to the complexity of the human brain anatomy, it is challenging to accurately warp one brain to the other (van Essen et al., 1998).

There has been great emphasis on developing volume-based nonlinear registration approaches for whole brain mapping (e.g., Beg et al., 2005; Ashburner, 2007; Vercauteren et al., 2009; Collins and Evans, 1997; Christensen et al., 1997; Davatzikos, 1997; Fischl et al., 2004). Such approaches seek a deformation field that is driven by intensity information, and hence, provide accurate mappings in subcortical and ventricular regions where intensity contrast is clear and structural shapes are relatively simple. However, these approaches fail to accurately align the cortical region since the convoluted cortical sheet cannot be well characterized based on image intensity alone. There is an additional need to consider the geometric property of the cortex as functionally distinct regions are close to each other in a volume space but geometrically distant in terms of distance measured along the cortex. Such a geometric property of the cortex has been well preserved in a cortical surface model (van Essen et al., 1998; van Essen, 2004; Fischl et al., 1999a; Clouchoux et al., 2005; Lyttelton et al., 2007). As tools are available for the automated construction of gyral/sulcal curves and cortical surfaces (e.g., Mangin et al., 2004; Dale et al., 1999), registration approaches for aligning the cortical surfaces across individuals have been recently developed based on sulcal/gyral curves, the geometry of the cortical surface, and the spherical representation of the cortical surface (Qiu and Miller, 2007; van Essen, 2005; Glaunès et al., 2008; Fischl et al., 1999b; Thompson et al., 1996; Vaillant et al., 2007; Zhong and Qiu, 2010). These registration approaches have shown superior performance in the alignment of highly complex cortical folding pattern over volume-based registration approaches, and thus resulted in increased statistical power for averaging of functional data in the cortical region across subjects. This is presumably due to their accurate alignment of functionally homologous regions across subjects (Anticevic et al., 2008). This accuracy stems from the direct use of the geometric representation of the cortex that well characterizes the folding pattern and functional properties of the cortex and is generally unavailable in the volume-based registration. However, unlike volume-based registration approaches, surface-based mapping approaches suffer from the inability of providing the deformation field across the entire brain, such as the white matter, subcortical, and ventricular regions.

As mentioned previously, volume-based registration fails to align cortical regions partly because the initialization using volume-based affine transformation cannot bring the cortical regions close enough to facilitate nonlinear intensity-based alignment. Therefore, to alleviate this problem, a number of iterative approaches have been proposed to first align the cortical regions using landmarks, gyral/sulcal curves, or cortical surfaces (Collins et al., 1998; Johnson and Christensen, 2002; Hellier and Barillot, 2000; Cachier et al., 2001; Joshi et al., 2007; Postelnicu et al., 2009; Joshi et al., 2009) before registering the whole brain using image volumes. Recent works by Postelnicu et al. (Postelnicu et al., 2009) and Joshi et al. (Joshi et al., 2007) have employed the spherical cortical surface mapping implemented in FreeSurfer (Postelnicu et al., 2009) or the harmonic cortical surface mapping constrained by gyral/sulcal curves (Joshi et al., 2007) to first seek the deformation field on the cortical boundary and then extend it to the 3D volume for further brain volume registration. These two approaches have shown tremendous improvement in mapping accuracy when compared to the advanced volume-based approach, hierarchical attribute matching mechanism for image registration (HAMMER) (Shen and Davatzikos, 2002), where geometric features of the cortex have been intrinsically incorporated. However, HAMMER simultaneously aligns the cortical and subcortical regions by integrating geometric features of the cortex and image intensity into one optimization procedure. This avoids the cortical misalignment while the volume registration is applied without constraints on the cortical geometric information in the iterative approaches given in Postelnicu et al. (2009) and Joshi et al. (2007). Furthermore, HAMMER does not need to extend the deformation field on the cortical surface to the 3D volume as it is in recent work by Postelnicu et al. (2009) and Joshi et al. (2007), which does not provide useful initial alignment to the subcortical and ventricular regions.

Taking into consideration the advantages of HAMMER (Shen and Davatzikos, 2002) and the iterative approaches (Postelnicu et al., 2009; Joshi et al., 2007), we introduce a novel large deformation diffeomorphic metric mapping for whole brain registration. Unlike previous LDDMM whole brain approaches based on the image intensity (LDDMM-image) (Beg et al., 2005), the proposed approach provides a one-to-one, differentiable, and invertible deformation field that simultaneously aligns gyral/sulcal curves, cortical surface, and intensity image volume from one subject to the other. For the first time, a diffeomorphic metric from one brain anatomy to another is derived in a shape space of images and point sets (such as curves and surfaces) in a unified manner. For sake of simplicity, we call this new algorithm as 6D-LDDMM from the differential geometry point of view where curves, surfaces, and volumes are respectively considered as one-, two-, and three-dimensional manifolds and simultaneously integrated in our new LDDMM. We associate 6D-LDDMM with a variational problem whose Euler–Lagrange equation is characterized using momentum, a linear transformation of the velocity vector field of the diffeomorphic flow. We numerically solve this problem by introducing a class of computationally friendly kernels to make it feasible to compute large-scale kernel convolution in an irregular grid involved during the optimization process. Finally, the 6D-LDDMM accuracy is quantified in terms of gyral/sulcal curve anatomical variation, sulcal region alignment, as well as structural segmentation in both cortical and subcortical regions when compared to that of LDDMM-image (Beg et al., 2005), HAMMER (Shen and Davatzikos, 2002), and combined volumetric and surface registration approaches (Postelnicu et al., 2009).

Methods

Overview: 6-dimensional diffeomorphic metric mapping

The geometry and photometric information of the brain can be characterized using gyral or sulcal (gyral/sulcal) curves, cortical surfaces, and intensity image volumes. In the differential geometry point of view, a curve can be locally seen as a one-dimensional manifold in the sense that the local region of every point on the curve is equivalent to a line which can be uniquely defined by this point and the tangent vector at this location; a surface can be locally seen as a two-dimensional manifold such that the neighborhood of every point on the surface is equivalent to a two-dimensional plane in a Euclidean space; a volume is seen as a three-dimensional manifold whose local region can be characterized as a function of three variables defined in a Euclidean space. We thus call this unified brain representation as 6-dimensional manifold and denote it as O = {γⁱ, i = 1, 2,…, n_γ; Sⁱ, i=1, 2,⋯, n_S; Iⁱ, i=1, 2,⋯^··, n_I}, where n_γ, n_S, n_I represent the number of curves, surfaces, and images, respectively. We propose a diffeomorphic metric mapping under the setting of LDDMM, denoted as 6D-LDDMM, that seeks a flow of diffeomorphisms to simultaneously align the 6D brain representation from one to another. Assume two brains: one as template, O_temp, and the other as target, O_targ. 6D-LDDMM can be solved through a variational problem in the form of

$$J(\mathrm{\varphi })=\underset{\mathrm{\varphi }}{\mathit{\text{inf}}}\mathrm{\rho }{(O_{\text{temp}},O_{\text{targ}})}^2+{\displaystyle \sum _{i=1}^{n_I}}{\mathrm{\lambda }}_{I^i}{E}_{I^i}(\mathrm{\varphi }·I_{\text{temp}}^i,I_{\text{targ}}^i)+{\displaystyle \sum _{i=1}^{n_{\mathrm{\gamma }}}}{\mathrm{\lambda }}_{{\mathrm{\gamma }}^i}{E}_{{\mathrm{\gamma }}^i}(\mathrm{\varphi }·{\mathrm{\gamma }}_{\text{temp}}^i,{\mathrm{\gamma }}_{\text{targ}}^i)+{\displaystyle \sum _{i=1}^{n_S}}{\mathrm{\lambda }}_{S^i}{E}_{S^i}(\mathrm{\varphi }·S_{\text{temp}}^i,S_{\text{targ}}^i),$$ (1)

where ρ determines the metric distance of the geodesic connecting O_temp and O_targ in a shape space. The E terms quantify the dissimilarity between the two objects based on the geometry of curves and surfaces as well as image intensity, respectively. ϕ denotes the diffeomorphic group action on objects. λ_Iⁱ, λ_γⁱ, and λ_Sⁱ are weights associated with images, curves, and surfaces, respectively.

We discuss how to define each term in Eq. (1) in the following sections. We first describe the metric distance in a general form before discussing its specific expressions associated with images, curves, and surfaces, respectively. In particular, we interpret the metric distance as a length of a geodesic diffeomorphic flow connecting one shape to the other through momenta that are directly viewed from physics as a product of a mass of the object and the velocity of the geodesic flow. We interpret the object mass through a kernel, which is discussed below. We then define E_Iⁱ, E_γⁱ, and E_Sⁱ based on the intensity of the image, the geometry of curves and surfaces, respectively.

Diffeomorphic metric for curves, surfaces, and images

In the setting of LDDMM (Miller et al., 2002), the brain is modeled by assuming that its anatomy can be generated from one to another via flows of diffeomorphisms, solutions of ordinary differential equations ϕ̇_t=υ_t(ϕ_t), t∈[0,1], starting from the identity map ϕ_t=id. They are therefore characterized by time-dependent velocity vector fields υ_t, t∈[0, 1]. We define a metric distance between a target O_targ and a template O_temp as the minimal length of curves ϕ_t · O_temp, t ∈ [0,1], in a shape space such that, at time t=1, ϕ₁·O_temp is as similar as possible to O_targ. The latter notation represents the group action of ϕ₁ on O_temp. For instance, in the image case, for which O_temp=I_temp (x), x ∈ Ω⊂ℛ³, it is ${\varphi }_1·I_{\text{temp}}=I_{\text{temp}}\circ {\varphi }_1^{-1}=I_{\text{temp}}({\varphi }_1^{-1}(x))$ . Lengths of such curves are computed as the integrated norm ‖υ_t‖_V of the vector field generating the transformation, where υ_t∈V, a reproducing kernel Hilbert space, with kernel k_V and norm ‖·‖_V. To ensure solutions are diffeomorphisms, V must be a space of smooth vector fields (Dupuis et al., 1998). Using the duality isometry in Hilbert spaces, one can equivalently express the lengths in terms of m_t, interpreted as momentum, and defined as follows. For each u ∈ V, ${\langle m_t,u\circ {\varphi }_t\rangle }_2={\langle k_V^{-1}{v}_t,u\rangle }_2$ where we let 〈m, u〉₂ denote the L² inner product between m and u, but also, with a slight abuse, the result of the natural pairing between m and υ in cases where m is singular (e.g., a measure). This identity is classically written as ${\varphi }_t^{*}{m}_t=k_{\mathrm{v}}^{-1}{\upsilon }_t$ , where ${\varphi }_t^{*}$ is referred to as the pullback operation on a vector measure, m_t. Using the identity ${\Vert {\upsilon }_t\Vert }_V^2={\langle k_V^{-1}{\upsilon }_t,{\upsilon }_t\rangle }_2$ and the standard fact that energy-minimizing curves coincide with constant-speed length-minimizing curves, one can express the geodesic distance, ρ, as

$$\mathrm{\rho }{(O_{\text{temp}},O_{\text{targ}})}^2=\underset{m_t}{\mathit{\text{inf}}}{\displaystyle {\int }_0^1}{\langle m_t,{\upsilon }_t\circ {\mathrm{\varphi }}_t\rangle }_2\text{dt}$$ (2)

The minimum is computed over all m_t such that ${\dot{\mathrm{\varphi }}}_t={\upsilon }_t({\mathrm{\varphi }}_t),{\upsilon }_t=k_V({\varphi }_t^{*}{m}_t)$ , ϕ₀=id, and ϕ₁·O_temp=O_targ. Note that since we are dealing with vector fields in ℝ³, k_V (x, y) is a matrix kernel operator in order to get a proper definition. We now discuss the expression of the metric distance in Eq. (2) for images, curves, and surfaces, respectively.

Image case

Assume I_temp(·) and I_targ(·) are functions defined over Ω⊂ℛ³. The momentum, m_t, takes the form m_t=α(t, ·)⊗dx, such that 〈m_t, u〉₂=∫α(t, x)·u(ϕ_t(x))dx, where u(x)∈V. We refer to α(t, x) as momentum vector at location x ∈Ω and time t. dx is volume measure. Eq. (2) can then be simplified as

$$\mathrm{\rho }{(I_{\text{temp}},I_{\text{targ}})}^2=\underset{\mathrm{\alpha }}{\mathit{\text{inf}}}{\displaystyle {\int }_0^1}{\displaystyle {\int }_{\mathrm{\Omega }}}{\displaystyle {\int }_{\mathrm{\Omega }}}[k_V({\mathrm{\varphi }}_t(x),{\mathrm{\varphi }}_t(y))\mathrm{\alpha }(t,x)]·\mathrm{\alpha }(t,y)\mathrm{d}x\mathrm{d}y\mathrm{d}t$$ (3)

$$\begin{array}{cc}\text{subject to}{\dot{\mathrm{\varphi }}}_t(x)\hfill & ={\displaystyle {\int }_{\mathrm{\Omega }}}{k}_{\mathrm{V}}({\mathrm{\varphi }}_t(y),{\mathrm{\varphi }}_t(x))\mathrm{\alpha }(t,y)\mathrm{d}y,\hfill \\ \hfill {\varphi }_0& =\text{id and}{\varphi }_1·I_{\text{temp}}=I_{\text{targ}.}\hfill \end{array}$$

Curves and surfaces

Assume $O_{\mathrm{\text{temp}}}=\mathrm{x}={(x_i)}_{i=1}^n\text{ and }{O}_{\mathrm{\text{targ}}}=\mathrm{y}={(y_i)}_{i=1}^m$ are the point sets, where O_temp and O_targ can be curves or surfaces. The momentum, m_t, becomes singular and is defined as a sum of Dirac measures on O_temp

$$m_t={\displaystyle \sum _{i=1}^n}\mathrm{\alpha }(t,x_i)\otimes {\mathrm{\delta }}_{{\mathrm{\varphi }}_t(x_i)},$$ (4)

such that for any u∈V, ${\langle m_t,u\rangle }_2={\displaystyle {\sum }_{i=1}^n{\langle \mathrm{\alpha }(t,x_i),u({\mathrm{\varphi }}_t(x_i))\rangle }_2}$ , where α(t, x_i) is the momentum vector of the ith point at time t. Thus, Eq. (2) can be simplified as

$$\mathrm{\rho }{(O_{\text{temp}},O_{\text{targ}})}^2=\underset{\mathrm{\alpha }}{\mathit{\text{inf}}}{\displaystyle {\int }_0^1}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left[k_V\right({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t\left(x_j\right))\mathrm{\alpha }(t,x_i)]·\mathrm{\alpha }(t,x_j)\mathrm{d}t$$ (5)

subject to ${\dot{\mathrm{\varphi }}}_t(x)={\displaystyle {\sum }_{j=1}^n{k}_V}\left({\mathrm{\varphi }}_t\left(x_j\right),{\mathrm{\varphi }}_t(x)\right)\mathrm{\alpha }\left(t,x_j\right)$ , ϕ₀=id and ϕ₁ ·O_temp=O_targ.

Based on the knowledge described in Eqs. (3, 5), we now define the metric distance in a unified manner when O_temp and O_targ contain images, curves, and surfaces. We first introduce measure $\mu =\mathrm{d}x+{\displaystyle {\sum }_{i=1}^n{\mathrm{\delta }}_{x_i}}$ , which is the sum of Lebesgue's measure and Dirac measure. The momentum in this 6D-LDDMM problem (Eq. (1)) takes the form of ${\langle m_t,u\rangle }_2={\displaystyle {\int }_{\mathrm{\Omega }}(\alpha (t,x)·u({\varphi }_t(x)))\mathrm{d}x+{\displaystyle {\sum }_{i=1}^n\alpha (t,x_i)·u({\varphi }_t(x_i))}}$ .

We assume u=υ_t ∘ ϕ_t. Over all α(t): ${\dot{\mathrm{\varphi }}}_t={\mathrm{\upsilon }}_t\circ {\mathrm{\varphi }}_t=k_V\left({\mathrm{\varphi }}_t^{*}{m}_t\right)\circ {\mathrm{\varphi }}_t,{\mathrm{\varphi }}_0=\text{id}$ , the diffeomorphic metric in Eq. (2) can be written as

$$\mathrm{\rho }{(O_{\text{temp}},O_{\text{targ}})}^2=\underset{\mathrm{\alpha }}{\mathit{\text{inf}}}{\displaystyle {\int }_0^1}\langle \mathrm{\alpha }(t,x)\otimes (\mathrm{d}x+{\displaystyle \sum _{i=1}^n}{\mathrm{\delta }}_{x_i}),k_V\mathrm{\alpha }(t,x)\otimes (\mathrm{d}x+{\displaystyle \sum _{i=1}^n}{\mathrm{\delta }}_{x_i})\rangle \text{dt}=\underset{\mathrm{\alpha }}{\text{inf}}{\displaystyle {\int }_0^1}{\displaystyle {\int }_{\mathrm{\Omega }}}{\displaystyle {\int }_{\mathrm{\Omega }}}[k_V({\mathrm{\varphi }}_t(x),{\mathrm{\varphi }}_t(y))\mathrm{\alpha }(t,x)]·\mathrm{\alpha }(t,y)\mathrm{d}x\mathrm{d}y\mathrm{d}t+2{\displaystyle {\int }_0^1}{\displaystyle {\int }_{\mathrm{\Omega }}}{\displaystyle \sum _{i=1}^n}[k_V({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t(x))\mathrm{\alpha }(t,x_i)]·\mathrm{\alpha }(t,x)\mathrm{d}x\mathrm{d}t+{\displaystyle {\int }_0^1}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left[k_V\right({\mathrm{\varphi }}_t\left(x_j\right),{\mathrm{\varphi }}_t(x_i)\left)\mathrm{\alpha }\right(t,x_j\left)\right]·\mathrm{\alpha }(t,x_i)\mathrm{d}t.$$ (6)

E_I, E_γ, and E_S

Since E_I, E_γ, and E_S have been previously defined in the LDDMM image (Beg et al., 2005), curve (Qiu and Miller, 2007; Glaunès et al., 2008), and surface (Vaillant et al., 2007; Vaillant and Glaunès, 2005) mapping algorithms, we briefly review their definitions for the completion of the paper.

In Eq. (1), $E_{I^i}({\varphi }_1·I_{\text{temp}}^i,I_{\text{targ}}^i)$ quantifies the similarity between the deformed template image, ${\varphi }_1·I_{\text{temp}}^i$ , and the target image, $I_{\text{targ}}^i$ , based on the intensity value.

Thus, the matching functional E_Iⁱ is defined as

$$E_{I^i}({\mathrm{\varphi }}_1·I_{\text{temp}}^i,I_{\text{targ}}^i)={\Vert I_{\text{temp}}^i\circ {\mathrm{\varphi }}_1^{-1}-I_{\text{targ}}^1\Vert }_2^2.$$ (7)

It is well known that both curves and surfaces are geometric objects. Previous studies (Vaillant and Glaunès, 2005; Vaillant et al., 2007; Glaunès et al., 2008) have associated the geometry of curves and surfaces with vector-valued measures, μ_x=Σ_iw_i⊗δ_xi, such that 〈μ_x, u〉₂=Σ_i〈w_i, u(x_i)〉₂ for all vector fields, u, in a re-producing kernel Hilbert space, W. w_i is the tangent vector at x_i for the curve case, while w_i is the normal vector at x_i for the surface case. The action of ϕ₁ on the discrete measure μ_x is given by

$${\mathrm{\varphi }}_1·{\mathrm{\mu }}_x={\displaystyle {\sum }_i}{w}_i\otimes {\mathrm{\delta }}_{{\mathrm{\varphi }}_1(x_i)}.$$

We use a kernel norm to compare ϕ₁·μ_x and μ_y. Let k_W be a kernel and μ_x be a measure. We define

$${\Vert {\mathrm{\mu }}_x\Vert }_{\mathit{\text{kw}}}^2\dot{=}{\displaystyle \sum _i}{\displaystyle \sum _j}{w}_i·w_j{k}_w(x_i,y_j).$$

The W in the notation comes from the fact that k_W can be interpreted as the reproducing kernel of a vector space (W) of smooth vector-valued functions and ‖·‖_kw is then the dual norm (Qiu and Miller, 2007; Glaunès et al., 2004; Vaillant and Glaunès, 2005; Glaunès et al., 2008). We will let

$$E({\mathrm{\varphi }}_1·\mathrm{x},\mathrm{y})={\Vert {\mathrm{\varphi }}_1·{\mathrm{\mu }}_{\mathrm{x}}-{\mathrm{\mu }}_{\mathrm{y}}\Vert }_{k_w}^2.$$ (8)

With ${\mu }_{\mathrm{x}}={\displaystyle {\sum }_{i=1}^n{w}_i}\otimes {\mathrm{\delta }}_{x_i}\text{ and }{\mathrm{\mu }}_y={\displaystyle {\sum }_{j=1}^m{\tilde{w}}_j}\otimes {\mathrm{\delta }}_{y_j}$ , this is equal to

$$E({\mathrm{\varphi }}_1·\mathrm{x},\mathrm{y})={\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}{w}_i·w_j{k}_w({\mathrm{\varphi }}_1(x_i),{\mathrm{\varphi }}_1(x_j\left)\right)-2{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^m}{w}_i\times {\tilde{w}}_j{k}_w({\mathrm{\varphi }}_1(x_i),y_j)+{\displaystyle \sum _{i=1}^m}{\displaystyle \sum _{j=1}^m}{\tilde{w}}_i·{\tilde{w}}_j{k}_w(y_i,y_j)$$ (9)

We now briefly describe how this representation is implemented with curves and surfaces in the discrete setting (details about the continuous case in Glaunès et al. (2008); Vaillant and Glaunès (2005)). For the sake of simplicity, here we only discuss one pair of curves, γ_temp and γ_targ, and one pair of surfaces, S_temp and S_targ.

When each curve is represented by a sequence of points, still denoted as ${\gamma }_{\text{temp}}=x={(x_i)}_{i=1}^n\text{ and }{\gamma }_{\text{targ}}=y={(y_j)}_{j=1}^m$ , we use the representation of Glaunès et al. (2008) and Qiu and Miller (2007)

$${\mathrm{\mu }}_{\mathrm{x}}={\displaystyle \sum _{j=1}^{n-1}}{w}_{c_j}\otimes {\mathrm{\delta }}_{c_j}$$

with c_j=(x_j+1+x_j)/2 and w_j=x_j+1−x_j, and similarly for y. This representation in terms of vector-valued measure is sensitive to both the location and the first order local geometry of the curve.

Now, let S_temp and S_targ be triangulated meshes with vertices $x={(x_i)}_{i=1}^n\text{ and }y={(y_j)}_{j=1}^m$ , respectively. Then, we let (Vaillant and Glaunès, 2005; Vaillant et al., 2007)

$${\mathrm{\mu }}_{\mathrm{x}}={\displaystyle \sum _{f\in {ℱ}_{\mathrm{x}}}}{w}_{c_f}\otimes {\mathrm{\delta }}_{c_f},$$

where ℱ_x is the set of faces in the triangulation, and, for a positively ordered face $f=(x_{f1},x_{f2},x_{f3}),w_{c_f}=\frac{1}{2}(x_{f1}-x_{f2})\times (x_{f3}-x_{f1})\text{ and }{c}_f=\frac{1}{3}(x_{f1}+x_{f2}+x_{f3})$ ; μ_y is defined similarly. The representation makes a direct use of the geometry of the point set as a triangulated surface. Note that the definitions of μ_x in the curve and surface cases come from discretizations of mathematical objects called currents, as described in Vaillant and Glaunès (2005).

Euler–Lagrange equation for 6D-LDDMM

We now rewrite the variational problem in Eq. (1) by combining the metric distance defined in Eq. (6) and the dissimilarity metrics of images, curves, and surfaces given in Eqs. (7, 9). This variational problem optimizes a time-dependent momentum vector based on the geometry of curves and surfaces as well as image intensity in the form of

$$J({\mathrm{\alpha }}_t)=\underset{\mathrm{\alpha }}{\mathit{\text{inf}}}{\displaystyle {\int }_0^1}{\displaystyle {\int }_{\mathrm{\Omega }}}{\displaystyle {\int }_{\mathrm{\Omega }}}[k_V({\mathrm{\varphi }}_t(x),{\mathrm{\varphi }}_t(y))\mathrm{\alpha }(t,x)]·\mathrm{\alpha }(t,y)\mathrm{d}x\mathrm{d}y\mathrm{d}t+2{\displaystyle {\int }_0^1}{\displaystyle {\int }_{\mathrm{\Omega }}}{\displaystyle \sum _{i=1}^n}[k_V({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t(x))\mathrm{\alpha }(t,x_i)]·\mathrm{\alpha }(t,x)\mathrm{d}x\mathrm{d}t+{\displaystyle {\int }_0^1}{\displaystyle \sum _{i=1}^n}{\displaystyle \sum _{j=1}^n}\left[k_V\right({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t\left(x_j\right))\mathrm{\alpha }(t,x_i)]·\mathrm{\alpha }(t,x_j)\mathrm{d}t+{\displaystyle \sum _{i=1}^{n_I}}{\mathrm{\lambda }}_{I^i}{E}_{I^i}({\mathrm{\varphi }}_1)+{\displaystyle \sum _{i=1}^{n_{\mathrm{\gamma }}}}{\mathrm{\lambda }}_{{\mathrm{\gamma }}^i}{E}_{{\mathrm{\gamma }}^i}({\mathrm{\varphi }}_1)+{\displaystyle \sum _{i=1}^{n_S}}{\mathrm{\lambda }}_{S^i}{E}_{S^i}({\mathrm{\varphi }}_1),$$ (10)

where E_Iⁱ, E_γⁱ and E_Sⁱ are defined in Eqs. (7) and (9), respectively. Its Euler–Lagrange optimality conditions imply

$$\frac{\mathrm{d}\mathrm{\alpha }(t,x)}{\mathrm{d}t}=-{\displaystyle {\int }_{\mathrm{\Omega }}}\mathrm{\alpha }(t,x)·\mathrm{\alpha }(t,y){\mathrm{\nabla }}_1{k}_V({\mathrm{\varphi }}_t(x),{\mathrm{\varphi }}_t(y))\mathrm{d}y,$$ (11)

where ∇₁ denotes taking derivative of k_V with respect to its first variable. This is completed by boundary conditions

$$\mathrm{\alpha }(1,x)=-\{{\displaystyle \sum _{i=1}^{n_I}}{\mathrm{\lambda }}_{I^i}{\nabla }_{{\mathrm{\varphi }}_1}{E}_{I^i}+{\displaystyle \sum _{i=1}^{n_{\mathrm{\gamma }}}}{\mathrm{\lambda }}_{{\mathrm{\gamma }}^i}{\nabla }_{{\mathrm{\varphi }}_1}{E}_{{\mathrm{\gamma }}^i}+{\displaystyle \sum _{i=1}^{n_S}}{\mathrm{\lambda }}_{S^i}{\nabla }_{{\mathrm{\varphi }}_1}{E}_{S^i}\},$$

where ∇_ϕ1E_Ii, ∇_ϕ1E_γⁱ and ∇_ϕ1E_sⁱ are the derivatives of E_Iⁱ, E_γⁱ and E_sⁱ with respect to ϕ₁. ∇_ϕ1E_γⁱ was discussed in Beg et al. (2005), ∇_ϕ1E_γⁱ in Glaunès et al. (2008), and ∇_ϕ1E_Sⁱ in Vaillant and Glaunès (2005). The proof of Eq. (11) is similar to the one given in Glaunès et al. (2008) for curve matching.

Numerical implementation

The numerical implementation of 6D-LDDMM is not as straight-forward as that of the LDDMM-image mapping algorithm (Beg et al., 2005). In LDDMM-image mapping, images were represented by discrete regular grids such that the convolution with kernels involved in the metric distance calculation can be computed using Fast Fourier Transform (FFT). However, 6D-LDDMM integrates images discretized on regular grids, curves and surfaces discretized on irregular grids. FFT cannot be directly applied for the convolution computation. In this section, we provide a simple way to make it feasible to numerically solve the 6D-LDDMM problem. In addition, we give the numerical scheme of solving 6D-LDDMM with respect to momentum, which was not given in the LDDMM-image algorithm (Beg et al., 2005).

In discretization, we first represent the ambient space, Ω⊂ℛ³, using a finite number of points, $\Omega \cong \{{(x_i^I)}_{i=1}^N\}{\cup }_{i=1}^{n_{\gamma }}\{{(x_j^{{\gamma }^i})}_{j=1}^{N_{\gamma i}^x}\}{\cup }_{i=1}^{n_S}\{{(x_j^{S^i})}_{j=1}^{N_{\mathit{\text{Si}}}^x}\}$ for the template coordinates and $\Omega \cong \{{(x_i^I)}_{i=1}^N\}{\cup }_{i=1}^{n_{\gamma }}\{{(y_j^{{\gamma }^i})}_{j=1}^{N_{\gamma i}^y}\}{\cup }_{i=1}^{n_S}\{{(y_j^{S^i})}_{j=1}^{N_{\mathit{\text{Si}}}^y}\}$ for the target coordinates. Here, ${(x_i^I)}_{i=1}^N$ is a regular grid on images $I_{\text{temp}}^i(x)\text{ and }{I}_{\text{targ}}^i(x),i=1,2\dots ,n_I;{\cup }_{i=1}^{n_{\gamma }}\{{(x_j^{{\gamma }^i})}_{j=1}^{N_{\gamma i}^x}\}\text{ and }{\cup }_{i=1}^{n_y}\{{{(y_j^{{\gamma }^i})}_{j=1}^{N_{\gamma i}}}^y\}$ are the curve sets with respective tangent vectors w_xj^γi of the template and ${\tilde{w}}_{y_j}^{{\gamma }^i}$ of the target, where $N_{{\gamma }^i}^x\text{ and }{N}_{{\gamma }^i}^y$ denote the number of points in the curve γ_i of the template and target respectively. Similarly, ${\cup }_{i=1}^{n_s}\{{(x_j^{S^i})}_{j=1}^{N_{\mathit{\text{Si}}}^x}\}\text{ and }{\cup }_{i=1}^{n_s}\{{(y_j^{S^i})}_{j=1}^{N_{\mathit{\text{Si}}}^y}\}$ are the surface sets with respective normal vectors $w_{x_j}^{S^i}$ of the template and ${\tilde{w}}_{y_j}^{S^i}$ of the target, where $N_{S^i}^x\text{ and }{N}_{S^i}^y$ denote the number of point in the surface Sⁱ of the template and target respectively.

Thus, the discrete form of J is given by:

$$J({\mathrm{\alpha }}_t)=\underset{\mathrm{\alpha }(t):{\dot{\mathrm{\varphi }}}_t=k_V\mathrm{\alpha }(t,{\mathrm{\varphi }}_t),{\mathrm{\varphi }}_0=\text{id}}{\text{inf}}{\displaystyle {\int }_0^1}{\displaystyle \sum _{x_i\in \mathrm{\Omega }}}{\displaystyle \sum _{x_j\in \mathrm{\Omega }}}\mathrm{\alpha }(t,x_i)·k_V({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t(x_j\left)\right)\mathrm{\alpha }(t,x_j)\text{dt}+{\displaystyle \sum _{i=1}^{n_I}}{\mathrm{\lambda }}_{I^i}{\displaystyle \sum _{j=1}^N}{\left(I_{\text{temp}}^i\right({\mathrm{\varphi }}_1^{-1}\left(x_j^I\right))-I_{\text{targ}}^i(x_j^I\left)\right)}^2+{\displaystyle \sum _{i=1}^{n_{\mathrm{\gamma }}}}{\mathrm{\lambda }}_{{\mathrm{\gamma }}^i}{\Vert {\mathrm{\varphi }}_1·{\mathrm{\mu }}_{{\mathrm{\gamma }}_{\text{temp}}^i}-{\mathrm{\mu }}_{{\mathrm{\gamma }}_{\text{targ}}^i}\Vert }_{k_w^{\mathrm{\gamma }}}^2+{\displaystyle \sum _{i=1}^{n_S}}{\mathrm{\lambda }}_{S^i}{\Vert {\mathrm{\varphi }}_1·{\mathrm{\mu }}_{S_{\text{temp}}^i}-{\mathrm{\mu }}_{S_{\text{targ}}^i}\Vert }_{k_w^S}^2$$ (12)

where $k_W^{\gamma }\text{ and }{k}_W^S$ are kernels associated with curves and surfaces, respectively.

The gradient descent method is used to perform the minimization of J in Eq. (12) with respect to the momentum α(t, x_i) with the initialized values described below. During each iteration, J and its gradient are updated in the following steps:

1. Use the forward Euler method to compute the trajectory based on the flow equation:

   $$\frac{\mathrm{d}{\mathrm{\varphi }}_t(x_j)}{\mathrm{d}t}={\displaystyle \sum _{x_j\in \mathrm{\Omega }}}{k}_V({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t(x_j\left)\right)\mathrm{\alpha }(t,x_j).$$ (13)

2. Compute ∇_ϕ1 E_Iⁱ, i=1,…n_I (Beg et al., 2005), ∇_ϕ1 E_γⁱ, i=1,…n_γ (Glaunès et al., 2008) and ∇_ϕ1 E_Sⁱ, i=1,…, n_S (Vaillant and Glaunès, 2005).

3. Solve η(t, x_i) using backward Euler integration of the ODE equation,

   $$\frac{\mathrm{d}\mathrm{\eta }(t,x_i)}{\mathrm{d}t}={\displaystyle {\sum }_{x_j\in \mathrm{\Omega }}}{\mathrm{\nabla }}_1{k}_V({\mathrm{\varphi }}_t(x_i),{\mathrm{\varphi }}_t(x_j\left)\right)\mathrm{\alpha }(t,x_j)(\mathrm{\alpha }(t,x_i)+\mathrm{\eta }(t,x_i))+{\displaystyle {\sum }_{x_j\in \mathrm{\Omega }}}{\mathrm{\nabla }}_2{k}_V\left({\mathrm{\varphi }}_t\right(x_j),{\mathrm{\varphi }}_t(x_i))\mathrm{\alpha }(t,x_i)\left(\mathrm{\alpha }\right(t,x_j)+\mathrm{\eta }(t,x_j\left)\right),$$ (14)

   given $\eta (1,x_i)={\displaystyle {\sum }_{i=1}^{n_I}{\lambda }_{I^i}{\nabla }_{{\mathrm{\varphi }}_1(x_i)}{E}_{I^i}+}{\displaystyle {\sum }_{i=1}^{n_{\gamma }}{\lambda }_{{\gamma }^i}{\nabla }_{{\varphi }_1(x_i)}{E}_{{\gamma }^i}+}{\displaystyle {\sum }_{i=1}^{n_S}{\lambda }_{S^i}}{\nabla }_{{\mathrm{\varphi }}_1(x_i)}{E}_{S^i}$

4. Compute the gradient ∇J(t, x_i)=2α(t, x_i)+η(t, x_i).

5. Evaluate J when α(t, x_i)=α^old (t, x_i)−λ(∇J (t, x_i)).

When N + Np is large, where $N_p={\displaystyle {\sum }_{i=1}^{n_{\gamma }}{N}_{{\gamma }^i}^x+}{\displaystyle {\sum }_{i=1}^{n_S}{N}_{S^i}^x}$ , the convolution with kernel k involved in ρ(O_temp, O_targ), E_Sⁱ and their derivatives is intensive (in the order of O((N + N_p)²). We adopt the work in Arrate (2010); Durrleman (2010) where only surfaces were discussed and had defined a numerical kernel that allows one to use a Fast Fourier Transform (FFT). Assume that the ambient space is discretized into a regular grid with N points. The kernel, k, is defined as

$$k(x,y)={\displaystyle {\sum }_{h=1}^{h=N}}{\displaystyle {\sum }_{l=1}^{l=N}}{u}_h(x)\mathrm{\Gamma }(x_h,x_l)u_l(y)$$

where $\mathrm{\Gamma }(x_h,x_l)=\mathit{\text{exp}}\left(-\frac{{\Vert x_h-x_l\Vert }^2}{{\sigma }^2}\right)$ and u_l and u_h are trilinear basis functions for extrapolation and interpolation, respectively. Convolution with k decomposes as

$${\displaystyle \sum _{j=1}^{j=N+N_p}}k(z_i,z_j)f\left(z_j\right)=\stackrel{3}{\overbrace{{\displaystyle \sum _{h=1}^{h=N}}{u}_h(z_i)\underset{2}{\underbrace{{\displaystyle \sum _{l=1}^{l=N}}\mathrm{\Gamma }(x_h,x_l)\underset{1}{\underbrace{{\displaystyle \sum _{j=1}^{j=N+N_p}}{u}_l\left(z_j\right)f\left(z_j\right)}}}}}}$$ (15)

for i=1,2,…,N + N_p. Three steps are involved in the implementation of Eq. (15):

1. Extrapolation of the momentum to the regular grid;

2. Convolution of the momentum with Gaussian kernel using FFT;

3. Interpolation of the data back to the points in Ω.

This reduced the computation cost to c(N + N_p) + N log N, where c is constant and dependent on the extrapolation and interpolation functions. This numerical kernel convolution scheme is applied to compute E_Sⁱ and Eqs. (13) and (14).

Whole brain mapping procedure

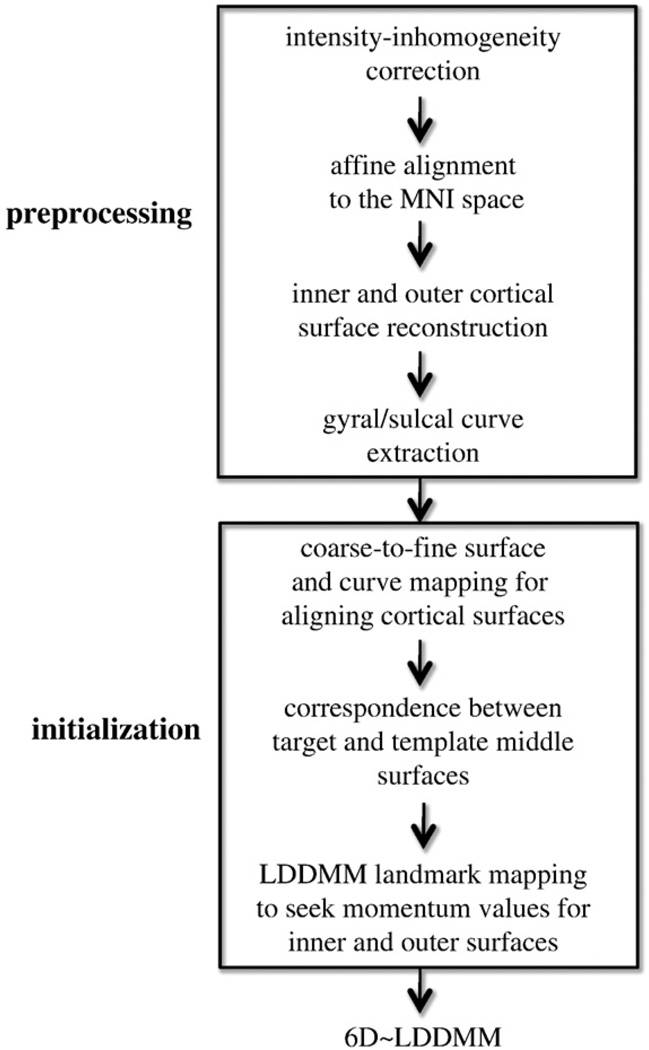
Fig. 1 shows the procedure for the whole brain mapping using 6D-LDDMM given T1-weighted MR images, including the image preprocessing, mapping initialization, and 6D-LDDMM. In the preprocessing, the intensity-inhomogeneity corrected T1-weighted MR images (Sled et al., 1998) were first aligned to the Montreal Neurological Institute (MNI) space using the affine transformation when maximizing the cross-correlation of the subjects' images with the MNI atlas (Jenkinson and Smith, 2001). FreeSurfer (Dale et al., 1999) is then applied to reconstruct the cortical surfaces at the boundary of the white matter and gray matter (termed as inner surface) and at the boundary of the gray matter and CSF (termed as outer surface) of each hemisphere. The outer surface is constructed by propagating the inner surface to the boundary of gray matter and CSF via a flow with the force based on the image labeling and gradient such that the topologies of the outer and inner surfaces are preserved (Dale et al., 1999). Thus, the middle surface of each hemisphere can be generated by averaging the inner and outer surfaces and is used as the geometric surface representation of the cortex. Fourteen sulcal and twelve gyral curves (Table 1) are semi-automatically delineated from the middle surface of each hemisphere using dynamic programming (Ratnanather et al., 2003). These curves are chosen because they are consistently present and easily identifiable on the cortex. The anatomical definitions of these curves are described in Zhong et al. (2010) and Zhong and Qiu (2010) and online (http://www.bioeng.nus.edu.sg/cfa/mapping/curveprotocol.html). Briefly, the initial starting and ending points of each curve are manually defined on the middle surface and the gyral (or sulcal) curve between them is automatically generated using dynamic programming by maximizing (or minimizing) the curvature information along the curve (Ratnanather et al., 2003).

Fig. 1.

Schematic diagram of the whole brain mapping procedure using the 6D-LDDMM approach.

Table 1.

Sulcal and gyral curves and their abbreviations.

Curve ID	Abbreviation	Name
1	CeS	Central sulcus
2	SF	Sylvian fissure
3	CoS	Collateral sulcus
4	CC	Superior callosal sulcus
5	CaS	Calcarine sulcus
6	POS	Parieto-occipital sulcus
7	SFS	Superior frontal sulcus
8	IFS	Inferior frontal sulcus
9	PoCeS	Postcentral sulcus
10	IPS	Intraparietal sulcus
11	aSTS	Anterior segment of the superior temporal sulcus
12	PreCeS	Precentral sulcus
13	ITS	Inferior temporal sulcus
14	OS	Olfactory sulcus
15	SFG	Superior frontal gyrus
16	PreCeG	Precentral gyrus
17	PoCeG	Postcentral gyrus
18	IPG	Intraparietal gyrus
19	PoPreCu	Posterior border of precuneus
20	ParaCeG	Paracentral gyrus
21	LOG	Lateral occipital gyrus
22	ACG	Anterior border of cuneus gyrus
23	CG	Cuneus gyrus
24	LG	Lingual gyrus
25	STG	Superior temporal gyrus
26	MTG	Middle temporal gyrus

To reduce the complexity of the 6D-LDDMMwhole brain mapping, especially in the cortical region, we identify the initial value of the momentum in the 6D-LDDMM alignment process through coarse-to-fine multi-manifold LDDMM (MM-LDDMM) cortical surface mappings when the sulcal and gyral curves as well as the middle surface are considered as mapping objects (Zhong and Qiu, 2010; Zhong et al., 2010), and LDDMM landmark mapping (Vaillant et al., 2004). In this coarse-to-fine scheme, the middle surface is first smoothed by changing the location of each vertex toward the barycenter of its neighbors (average of the coordinates of its neighbor vertices) to reduce noise features and geometric variation of the cortical shape (Toro and Burnod, 2003). This is the solution of a variational problem that minimizes the surface curvature with respect to the locations of the surface vertices. This smoothed surface is then registered with its sulcal and gyral curves to those of the target using MM-LDDMM described in Zhong and Qiu (2010) and Zhong et al. (2010). We further seek the paired correspondence points between the target surface and the template surface deformed by MM-LDDMM using the shortest distance criteria. Such information is then used in the LDDMM-landmark mapping to find the time-dependent momentum that drives the template inner and outer surfaces to those of the target. This time-dependent momentum is considered as initial values of the optimization process in 6D-LDDMM, where the inner and outer cortical surfaces (both hemispheres), fifty-two curves (twenty-six curve per hemisphere), and T1-weighted intensity image are considered as the mapping objects. The intialization process and 6D-LDDMM each takes 15 h on average.

Results

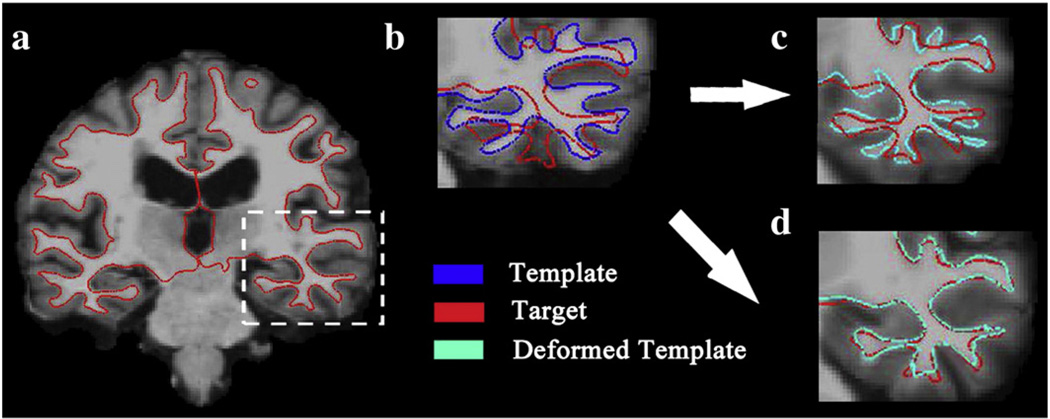
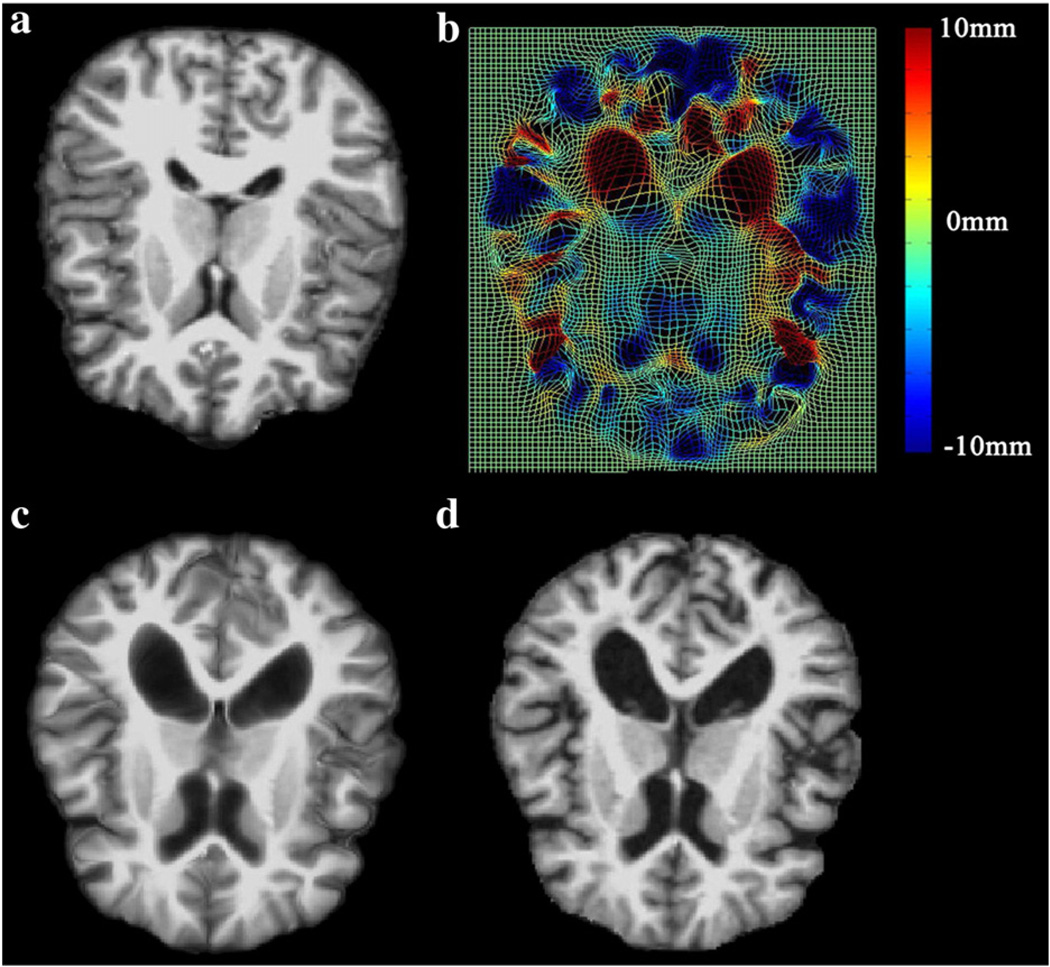
Fig. 2 shows the mapping results of 6D-LDDMM when the momenta were initialized as zero (panel (c)) or assigned the initial values obtained using the procedure in Whole brain mapping procedure section. This demonstrates the importance of the initialization procedure in 6D-LDDMM. As a mapping example, Fig. 3 illustrates the deformation field and deformed template image obtained using 6D-LDDMM. These two figures indicate that the large deformation in the cortical and subcortical regions from the template brain to the target brain can be well characterized by 6D-LDDMM. To evaluate the accuracy of the 6D-LDDMM whole brain mapping, two experiments were designed. In the first experiment, we chose 40 subjects aged 20 years and above. We compared the mapping accuracy of 6D-LDDMM with that of traditional image-based whole brain mapping approaches, including affine (Jenkinson and Smith, 2001) and LDDMM-image (Beg et al., 2005) in terms of gyral/sulcal curve variation, sulcal regional alignment, and volume segmentation. In the second experiment, we compared 6D-LDDMM with HAMMER (Shen and Davatzikos, 2002) and combined volumetric and surface mapping (CVS) (Postelnicu et al., 2009) in terms of the brain segmentation accuracy using a public dataset.

Fig. 2.

Panel (a) shows the coronal slice of the target image with the inner surface contour in red. Panel (b) shows the template image (corresponding to the region in the white box of panel (a)) with its inner surface in blue and the target inner surface in red. Panels (c, d) illustrate the mapping results of 6D-LDDMM when the momentum was initialized as zero (panel (c)) and assigned the value obtained from the procedure given in Fig. 1 (panel (d)). The deformed template inner surface is colored in cyan on panels (c, d).

Fig. 3.

A mapping example of 6D-LDDMM. Panels (a, d) show the template and target images, respectively. Panel (b) shows the deformation field generated by 6D-LDDMM. The deformation in the in-paper dimension is color coded. Panel (c) shows the deformed template image.

Comparisons of affine, LDDMM-image and 6D-LDDMM

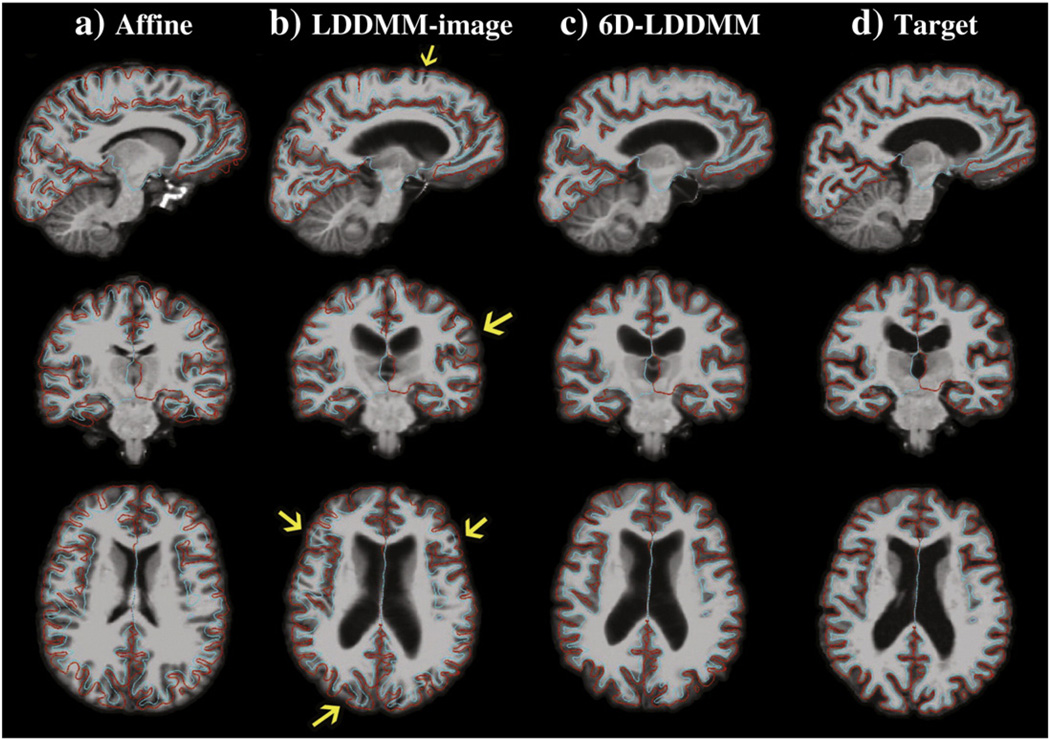
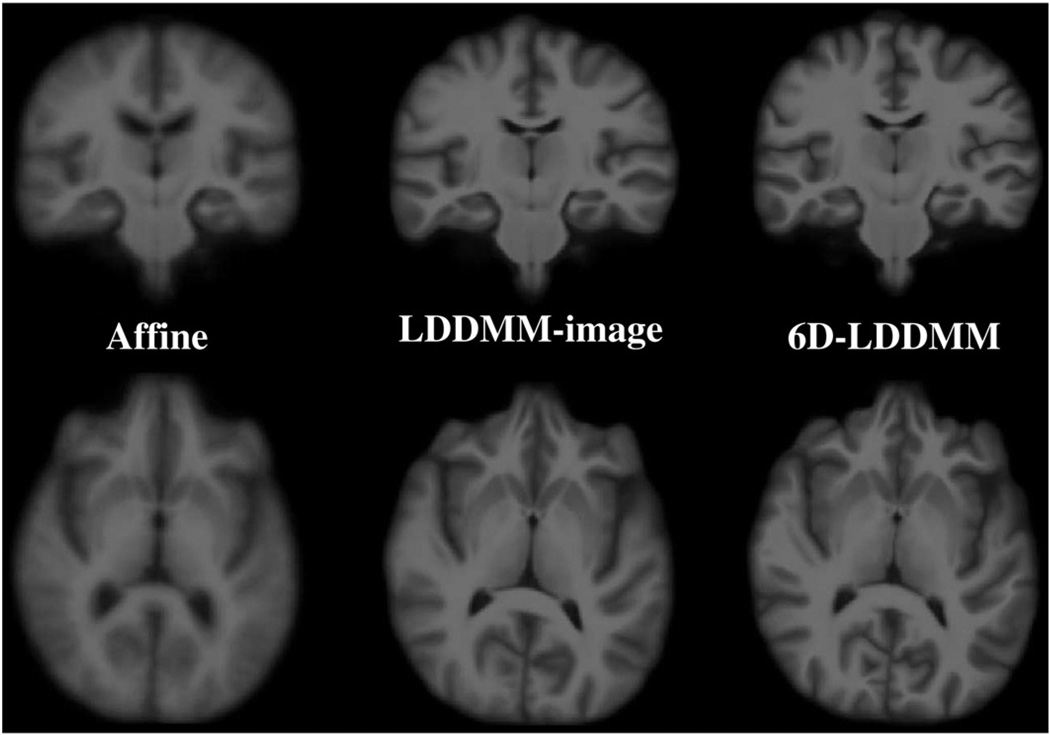
In the first experiment, 40 subjects comprising of ten young adults (5 males and 5 females, age: 23.4±2.55 years), ten middle-aged adults (5 males and 5 females, age: 49.3±1.89 years), ten elderly (5 males and 5 females, age: 73.9±2.02 years), and ten patients with Alzheimer's disease (5 males and 5 females, age: 76.4±2.55 years) were randomly selected from the Open Access Series of Imaging Studies (OASIS) (Marcus et al., 2007). The template was constructed using an MRI scan collected from a healthy subject (female, age: 54 years) otherwise not included in the study. Following the procedure described in Whole brain mapping procedure section, the whole brain images of the 40 subjects were aligned to the template image. We empirically determined λ_γi=1, i=1,…,52, λ_Sⁱ=10, i=1, …,4, and λ_I=0 for the initialization stage and λ_γi=1, i=1,…,52, λ_Sⁱ=100, i=1,…,4, and λ_I=10⁶ for the 6D-LDDMM whole brain mapping. The parameters were determined in the way that λ_IE_I≈λ_γiE_γi≈λ_SⁱE_Sⁱ. Additionally, all 40 images were also aligned to the template image using the LDDMM-image approach when λ_γⁱ=λ_Sⁱ were set to zero. Fig. 4 shows an example of the mapping results using the affine, LDDMM-image, and 6D-LDDMM approaches. Additionally, we show the average images over all subjects through the affine, LDDMM-image, and 6D-LDDMM transformations in Fig. 5. Visually, 6D-LDDMM provided the best alignment in both cortical and ventricular regions among the three algorithms and thus generated clearer average images. We quantitatively evaluated the accuracy of each approach in terms of the alignment accuracy of gyral/sulcal curves, sulcal regions, and volume segmentation.

Fig. 4.

An example of affine, LDDMM-image, 6D-LDDMM whole brain mapping. From left to right columns, panels respectively show the template image after the affine, LDDMM-image, 6D-LDDMM registration, and the target image. Rows from top to bottom show the brain image in the sagittal, coronal, and axial views, respectively. The target inner (cyan) and outer (red) surfaces are superimposed with the image on each panel. Yellow arrows point the location where the cortical regions of the deformed template are misaligned with the target cortical surfaces.

Fig. 5.

Columns show average images over all subjects through the affine, LDDMM-image, 6D-LDDMM transformations, respectively. The top and bottom rows illustrate the average images in the coronal and axial views, respectively.

Gyral and sulcal curves

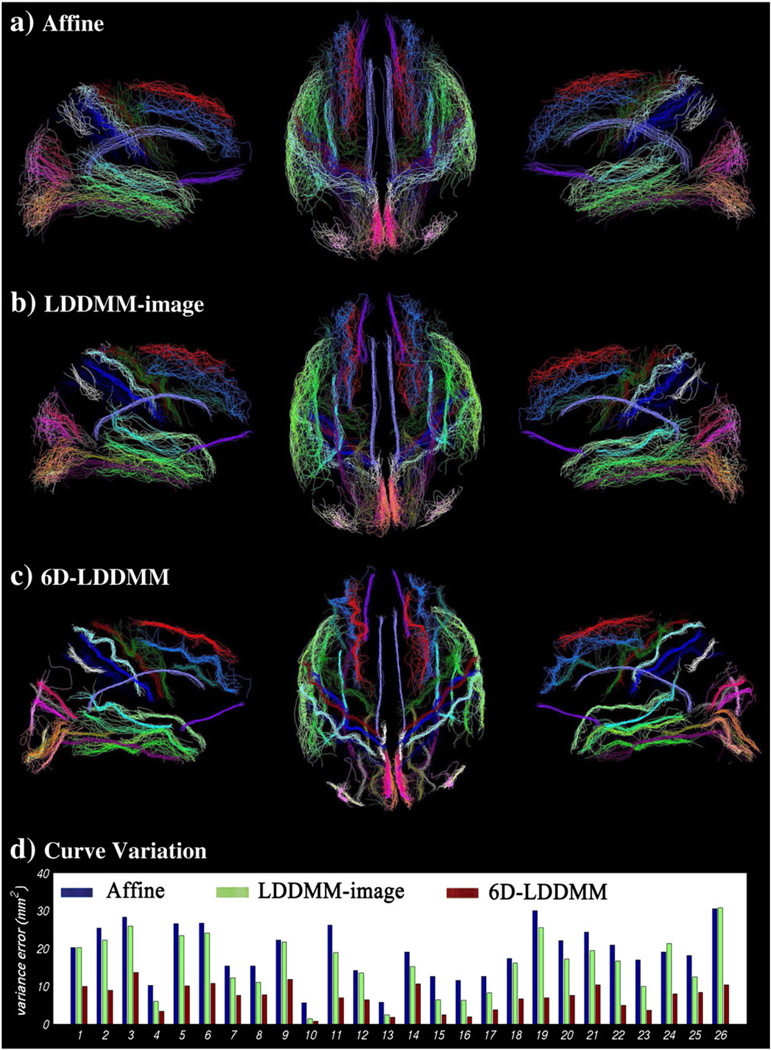
Fig. 6(a–c) illustrates the gyral/sulcal curve alignment after affine, LDDMM-image, and 6D-LDDMM registration. To evaluate the anatomical variation of a specific sulcal/gyral curve among subjects, which cannot be characterized through brain registration, we calculated a curve variation error (Pantazisa et al., 2010; Zhong et al., 2010) as

$$\text{Var}=\frac{1}{2J(J-1)}{\displaystyle \sum _{i=1}^J}{\displaystyle \sum _{j=1}^J}{\left[d\right({\mathrm{\gamma }}^i,{\mathrm{\gamma }}^j\left)\right]}^2$$

where J=40 is the number of subjects in the study. d(γⁱ, γ^j) is the Hausdorff distance between curves i and j, computed as

$$d({\mathrm{\gamma }}^i,{\mathrm{\gamma }}^j)=0.5\frac{1}{N_1}{\displaystyle \sum _{x\in {\mathrm{\gamma }}^i}}{\text{min}}_{y\in {\mathrm{\gamma }}^j}|x-y|+0.5\frac{1}{N_2}{\displaystyle \sum _{y\in {\mathrm{\gamma }}^j}}{\text{min}}_{x\in {\mathrm{\gamma }}^i}|x-y|$$

where N1 and N2 are the number of points on γⁱ and γ^j, respectively (Dubuisson and Jain, 1994). |x−y| denotes the Euclidean distance between points x and y. Lower value of the curve variation error indicates better alignment of this curve across all subjects. Fig. 6(d) shows the curve variation errors after the affine, LDDMM-image, and 6D-LDDMM registration, suggesting that 6D-LDDMM showed the best alignment for all twenty-six gyral/sulcal curves when compared with affine and LDDMM-image. We noted that since our approach uses explicitly labeled gyri and sulci, we can expect better performance than either affine or LDDMM-image in terms of alignment of these features. Overall, the variation errors averaged across the twenty-six curves are 19.13 mm² for affine, 15.73 mm² for LDDMM-image, and 7.14 mm² for 6D-LDDMM. Student's t-test revealed statistically significantly lower curve variations given by 6D-LDDMM than by affine and LDDMM-image (p<0.0001).

Fig. 6.

Rows (a–c) show gyral/sulcal curves of the 40 subjects after the affine, LDDMM-image, 6D-LDDMM whole brain mapping, respectively. Panels from left to right in rows (a–c) respectively illustrate the left twenty-six gyral/sulcal curves in the medial view, the fifty-two bilateral gyral/sulcal curves in the superior view, and the right twenty-six gyral/sulcal curves in the medial view. Row (d) shows the curve variation errors of each curve after the affine (blue), LDDMM-image (green), and 6D-LDDMM (red) registration. The index of the curves is listed in Table 1.

Sulcal regions

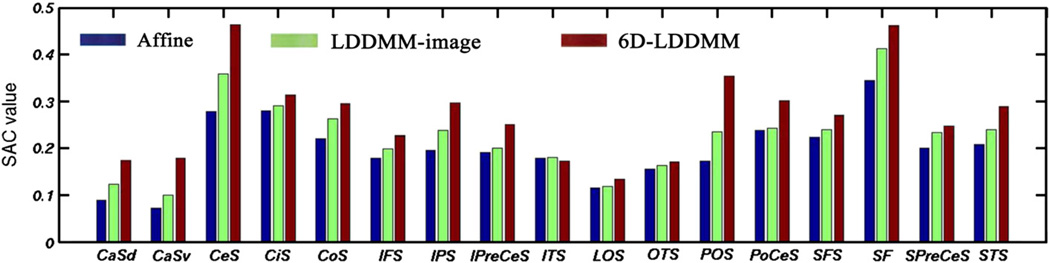
To evaluate the mapping accuracy in the cortical region, independent of the features used in 6D-LDDMM, seventeen sulcal regions (Table 2) were manually delineated from each hemispherical inner surface based on the protocol given in Zhong et al. (2010) and available at http://www.bioeng.nus.edu.sg/cfa/mapping/sulcalprotocol.html. The intra-reliability of the manual delineation was above 0.9 for individual sulcal regions (Zhong et al., 2010). These sulcal regions (Fig. 7(a–c)) were chosen because they are distributed broadly over the cortical surface and have been used for quantifying cortical mapping accuracy in previous studies (Zhong et al., 2010; Essen, 2005). We computed surface alignment consistency (SAC) (Essen, 2005) as

$$\text{SAC}=\frac{1}{N_v}{\displaystyle \sum _{i=1}^J}\frac{i-1}{J-1}{n}_i$$

where J=40 is the number of subjects involved in the study. N_v is the total number of vertices that contains the vertices corresponding to this sulcal region of all subjects on the template surface. A consistency probability, $p(x)=\frac{i-1}{J-1}$ , denotes the proportion of subjects who agree that vertex, x, belongs to this sulcal region. SAC is defined as an average of p(x) over N_v vertices. For a short notation, we assemble all vertices with $p(x)=\frac{i-1}{J-1}$ as n_i. SAC is ranged from 0 to 1, i.e., the higher the value, the better the sulcal alignment. Fig. 7 shows SAC of each individual sulcal region for affine (blue), LDDMM-image (green), and 6D-LDDMM (red). The mean and standard deviation of SAC over seventeen sulcal regions were 0.19 (0.07), 0.22 (0.08) and 0.27 (0.08) for affine, LDDMM-image and 6D-LDDMM, respectively. Student's t-test revealed that the mean SAC value obtained from 6D-LDDMM was significantly higher than that from LDDMM-image (p<0.05).

Table 2.

Sulcal regions and their abbreviations.

Sulcal region ID	Abbreviation	Name
1	CaSd	Dorsal bank of calcarine sulcus
2	CaSv	Ventral bank of calcarine sulcus
3	CeS	Central sulcus
4	CiS	Cingulate sulcus
5	CoS	Collateral sulcus
6	IFS	Inferior frontal sulcus
7	IPS	Intraparietal sulcus
8	IPreCeS	Inferior precentral sulcus
9	ITS	Inferior temporal sulcus
10	LOS	Lateral occipital sulcus
11	OTS	Occipital temporal sulcus
12	POS	Parietal occipital sulcus
13	PoCeS	Postcentral sulcus
14	SFS	Superior frontal sulcus
15	SF	Sylvian fissure
16	SPreCeS	Superior precentral sulcus
17	STS	Superior temporal sulcus

Fig. 7.

Figure shows surface alignment consistency (SAC) for each sulcal region listed in Table 2 after affine (blue), LDDMM-image (green), and 6D-LDDMM (red) registration.

Volume segmentation

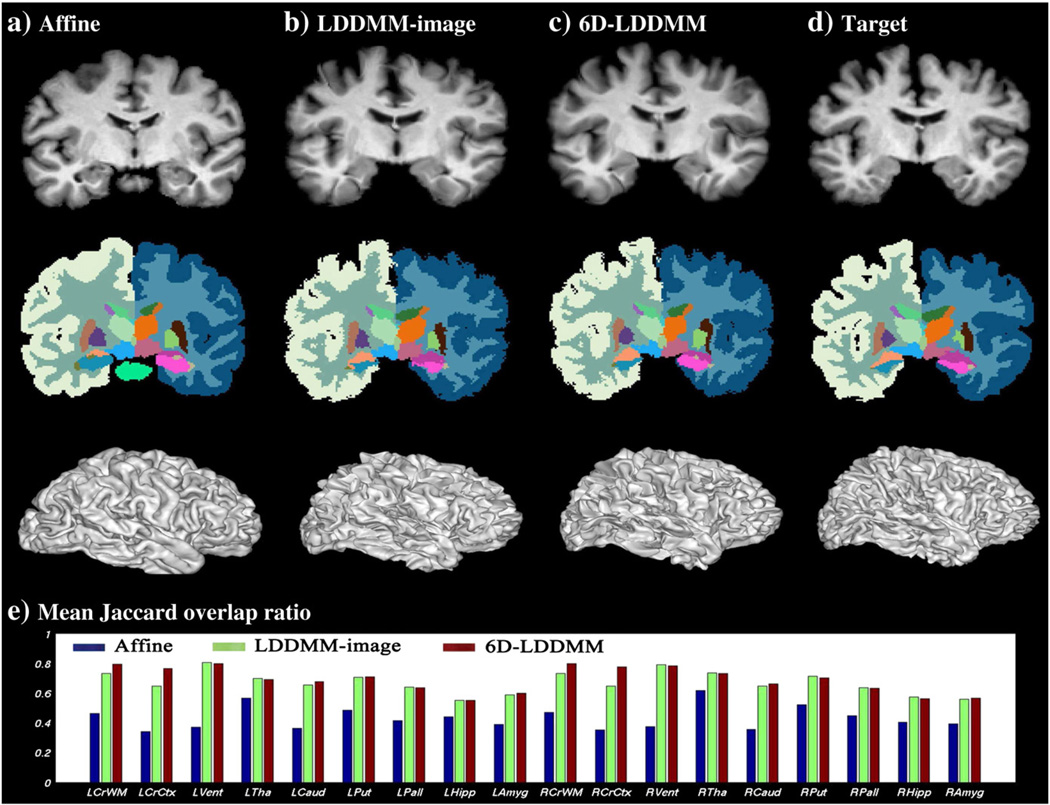
To evaluate the performance of 6D-LDDMM in terms of cortical and subcortical segmentation, we manually labeled the 41 brain image volumes into the cortical gray matter, white matter, lateral ventricles, and six subcortical structures (thalamus, caudate, putamen, pallidum, hippocampus, and amygdala). Fig. 8(a–d) shows an example of the template brain labels after applying affine, LDDMM-image, 6D-LDDMM registration compared to that of the target brain. To quantify the alignment accuracy in each structure, we computed Jaccard overlap ratio that describes the overlap between the labels of registered images (A and B) as $\frac{A\cap B}{A\cup B}$ . Its value ranges from zero for disjoint sets to unity for identical sets. The mean and standard deviation of Jaccard overlap ratio computed across all subjects are listed in Table 3 and shown in Fig. 8(e). Both LDDMM-image and 6D-LDDMM achieved higher accuracy compared to the affine approach. When we compared 6D-LDDMM with LDDMM-image, two-sample t-test revealed that the Jaccard overlap ratios of white matter and cortex in both hemispheres obtained from 6D-LDDMM were significantly higher than those from LDDMM-image (p<0.0001), while those of ventricle and main subcortical structures showed no significant difference between two methods.

Fig. 8.

Panels (a–c) illustrate an example of the template segmentation after affine (first column), LDDMM-image (second column), and 6D-LDDMM (third column) registration when compared with that of the target image (panel (d)). The top row shows the template image after the affine, LDDMM-image, and 6D-LDDMM registration as well as the target image from left to right, respectively, while the middle and bottom rows show the corresponding labeled images and deformed inner surfaces, respectively. Panel (e) illustrates the mean Jaccard overlap ratio of each segmented structure for affine (blue), LDDMM-image (green), and 6D-LDDMM (red).

Table 3.

Mean and standard deviation of Jaccard overlap ratio computed across subjects for comparisons of affine, LDDMM-image, and 6D-LDDMM. Bold typesetting indicates that Jaccard overlap ratio for 6D-LDDMM is statistically significantly higher than that of affine and LDDMM-image (p<0.0001).

	Affine	LDDMM-image	6D-LDDMM
Left-white matter	0.4638 (0.04)	0.7325 (0.02)	0.7948 (0.02)
Left-cortex	0.3414 (0.02)	0.6490 (0.03)	0.7659 (0.02)
Left-lateral ventricles	0.3691 (0.13)	0.8048 (0.05)	0.7983 (0.05)
Left-thalamus	0.5660 (0.13)	0.6982 (0.06)	0.6915 (0.06)
Left-caudate	0.3645 (0.20)	0.6539 (0.06)	0.6789 (0.05)
Left-putamen	0.4870 (0.10)	0.7073 (0.04)	0.7104 (0.05)
Left-pallidum	0.4161 (0.12)	0.6409 (0.06)	0.6372 (0.08)
Left-hippocampus	0.4401 (0.10)	0.5509 (0.11)	0.5516 (0.10)
Left-amygdala	0.3908 (0.10)	0.5886 (0.07)	0.5982 (0.08)
Right-white matter	0.4701 (0.03)	0.7331 (0.02)	0.7985 (0.01)
Right-cortex	0.3541 (0.02)	0.6471 (0.03)	0.7753 (0.02)
Right-lateral ventricles	0.3744 (0.12)	0.7898 (0.05)	0.7854 (0.06)
Right-thalamus	0.6177 (0.10)	0.7351 (0.04)	0.7331 (0.04)
Right-caudate	0.3553 (0.19)	0.6474 (0.06)	0.6638 (0.06)
Right-putamen	0.5226 (0.09)	0.7130 (0.03)	0.7032 (0.04)
Right-pallidum	0.4477 (0.12)	0.6352 (0.07)	0.6314 (0.08)
Right-hippocampus	0.4028 (0.10)	0.5730 (0.11)	0.5614 (0.11)
Right-amygdala	0.3929 (0.09)	0.5583 (0.09)	0.5647 (0.08)

Comparisons of 6D-LDDMM, CVS, and HAMMER

In the second experiment, we compared the 6D-LDDMM whole brain mapping with those of combined volumetric and surface registration (CVS) (Postelnicu et al., 2009) and HAMMER (Shen and Davatzikos, 2002) in terms of segmentation accuracy in the cortical and subcortical regions. CVS and HAMMER were chosen for the comparison because they provide the state-of-art mapping accuracy among the most widely used and best performing algorithms for whole brain registration. To do so, we obtained eight labeled brain T1-weighted images from the Internet Brain Segmentation Repository (IBSR) database at the Center for Morphometric Analysis at Massachusetts General Hospital. Each brain dataset consists of a T1-weighted image and its manual segmentation of individual structures, including the bilateral white matter, cortical gray matter, lateral ventricles, thalamus, caudate, putamen, pallidum, hippocampus, and amygdala. We repeated the same mapping analysis as described in Whole brain mapping procedure section for this dataset. Table 4 lists the mean and standard deviation of Jaccard overlap ratio computed across all subjects.

Table 4.

Mean and standard deviation of Jaccard overlap ratio computed across subjects for comparisons of HAMMER, CVS, and 6D-LDDMM. Bold typesetting indicates that Jaccard overlap ratio for 6D-LDDMM is statistically significantly higher than that of HAMMER and CVS (p<0.0001).

	HAMMER	CVS	6D-LDDMM
Left-white matter	0.5722 (0.04)	0.6860 (0.02)	0.7579 (0.01)
Left-cortex	0.5544 (0.05)	0.7701 (0.01)	0.7661 (0.02)
Left-lateral ventricles	0.6533 (0.06)	0.6792 (0.02)	0.7891 (0.03)
Left-thalamus	0.6328 (0.07)	0.5976 (0.03)	0.7310 (0.03)
Left-caudate	0.5566 (0.04)	0.5331 (0.03)	0.6840 (0.04)
Left-putamen	0.5114 (0.05)	0.4648 (0.04)	0.7000 (0.03)
Left-pallidum	0.4091 (0.06)	0.2245 (0.07)	0.6162 (0.06)
Left-hippocampus	0.4866 (0.05)	0.4282 (0.02)	0.5732 (0.03)
Left-amygdala	0.4716 (0.05)	0.4113 (0.02)	0.5175 (0.11)
Right-white matter	0.5731 (0.03)	0.6937 (0.01)	0.7557 (0.02)
Right-cortex	0.5444 (0.05)	0.7620 (0.01)	0.7584 (0.02)
Right-lateral ventricles	0.6530 (0.06)	0.6648 (0.02)	0.7753 (0.04)
Right-thalamus	0.6438 (0.07)	0.6036 (0.02)	0.7468 (0.03)
Right-caudate	0.5436 (0.04)	0.5327 (0.02)	0.6514 (0.05)
Right-putamen	0.5269 (0.04)	0.4976 (0.04)	0.7230 (0.03)
Right-pallidum	0.4095 (0.06)	0.2437 (0.07)	0.5902 (0.05)
Right-hippocampus	0.4847 (0.05)	0.4630 (0.02)	0.5675 (0.03)
Right-amygdala	0.4395 (0.05)	0.4171 (0.02)	0.5418 (0.10)

Note that the Jaccard overlap ratio for HAMMER and CVS were directly taken from Postelnicu et al. (2009), which we believe is a fair comparison for two reasons. First, the same image dataset, including raw T1-weighted images and their manual labels, was used in the three mapping algorithms. Second, the results of CVS and HAMMER were provided by the researchers who knew them best. Student's t-test revealed that the mapping accuracy of 6D-LDDMMis significantly higher than that of HAMMER and CVS (p<0.0001) for all the tested structures except the bilateral cortical gray matter. The performance of 6D-LDDMM for the cortical gray matter is still significantly higher than that of HAMMER (p<0.0001) but equivalent to that of CVS (left: p=0.92; right: p=0.90).

Conclusion

We present the 6-dimensional diffeomophic metric mapping algorithm that integrates multiple brain anatomical manifolds, including gyral/sulcal curves, cortical surfaces, and intensity image volumes, into a unified framework for whole brain registration. It seeks an optimal diffeomorphic transformation to simultaneously carry these anatomical manifolds from one subject native space to another. We further design the initialization procedure to facilitate the 6D-LDDMM optimization so that large deformation in both cortical and subcortical regions can be found.

Even though a variety of LDDMM algorithms have been developed for aligning intensity images (Beg et al., 2005) or point sets (e.g., landmarks, curves, and surfaces) (Qiu and Miller, 2007; Glaunès et al., 2004; Vaillant and Glaunès, 2005; Glaunès et al., 2008; Zhong and Qiu, 2010), for the first time, the diffeomorphic metric in the shape space of both intensity image volumes and point sets of curves and surfaces is derived in a unified manner. There are several differences between the 6D-LDDMM and LDDMM-image algorithms for whole brain registration. First, 6D-LDDMM seeks the deformation simultaneously driven by gyral/sulcal curves, cortical surfaces, and image intensity, while LDDMM-image seeks the deformation only based on image intensity (Beg et al., 2005). Second, we derive the variational problem for simultaneously mapping 6-dimensional brain manifolds with respect to the time-dependent momentum, while the variational problem associated with LDDMM-image is defined with respect to the time-dependent velocity field. Since 6D-LDDMM incorporates images and point sets (curves and surfaces) that are not on the image regular grid, it is difficult to directly adopt the numerical implementation of LDDMM-image, such as large scale kernel convolution in a regular grid using FFT (Arrate, 2010; Durrleman, 2010). We thus introduce a class of computationally friendly kernels that facilities the kernel convolution in an irregular grid using FFT. This numerical scheme described in the paper can also be applied to large-scale point set LDDMM registration, such as the one in Zhong and Qiu (2010). Compared to LDDMM-image, 6D-LDDMM significantly improves alignment in gyral/sulcal curves, sulcal regions, as well as cortical volume segmentation but produces equivalent mapping accuracy in the subcortical and ventricular regions. Since the first experiment in this study used the same dataset and evaluation measures as those in multi-manifold LDDMM (MM-LDDMM) for cortical surface registration (Zhong et al., 2010), we can also demonstrate that incorporating additional image manifold in 6D-LDDMM does not influence the mapping accuracy of cortical surfaces (see Figs. 6 and 7 in this paper and Figs. 5 and 6 in Zhong et al. (2010)).

We use the IBSR dataset with manually segmented labels to quantify the mapping accuracy of 6D-LDDMMagainst two other well-known registration methods, CVS and HAMMER (Postelnicu et al., 2009; Shen and Davatzikos, 2002). In general, our registration framework outperforms these two methods in terms of cortical and subcortical segmentation accuracy. This is due to several methodological differences among the three mapping algorithms. CVS is an iterative approach that first aligns the cortical surfaces using spherical mapping (Fischl et al., 1999a) and then registers the image volume using the image matching (Fischl et al., 2004). The volume registration without constraints of the cortical geometry may further modify the good alignment of the cortical surface that is achieved in the first step. Conversely, HAMMER warps the whole brain using attributes that explicitly describe image intensity and implicitly incorporate cortical geometry via intensity distribution functions of neighborhood voxels. It gives one consistent deformation map for both cortical and subcortical regions as 6D-LDDMM does. Relatively poor performance of HAMMER against the other two may be due to this implicit representation of the cortical feature. This is also an advantage of HAMMER over 6D-LDDMM and CVS since it does not require cortical surface or gyral/sulcal curves reconstruction.

In conclusion, 6D-LDDMM is a robust whole brain mapping approach. It is a unified framework that allows simultaneous integration of multiple brain anatomical manifolds for whole brain mapping. Future work on incorporating the information of the white matter tracts into 6D-LDDMM will provide a nice brain mapping tool for aligning both detailed gray and white matter structures.