Effective Sample Size: Quick Estimation of the Effect of Related Samples in Genetic Case-Control Association Analyses

Summary

Affected relatives are essential for pedigree linkage analysis, however, they cause a violation of the independent sample assumption in case-control association studies. To avoid the correlation between samples, a common practice is to take only one affected sample per pedigree in association analysis. Although several methods exist in handling correlated samples, they are still not widely used in part because these are not easily implemented, or because they are not widely known. We advocate the effective sample size method as a simple and accessible approach for case-control association analysis with correlated samples. This method modifies the chi-square test statistic, p-value, and 95% confidence interval of the odds-ratio by replacing the apparent number of allele or genotype counts with the effective ones in the standard formula, without the need for specialized computer programs. We present a simple formula for calculating effective sample size for many types of relative pairs and relative sets. For allele frequency estimation, the effective sample size method captures the variance inflation exactly. For genotype frequency, simulations showed that effective sample size provides a satisfactory approximation. A gene which is previously identified as a type 1 diabetes susceptibility locus, the interferon-induced helicase gene (IFIH1), is shown to be significantly associated with rheumatoid arthritis when the effective sample size method is applied. This significant association is not established if only one affected sib per pedigree were used in the association analysis. Relationship between the effective sample size method and other methods – the generalized estimation equation, variance of eigenvalues for correlation matrices, and genomic controls – are discussed.

Introduction

One of the major obstacles in statistical analysis of genetic association studies in a case-control setting (Lewis, 2002; Balding, 2006; Li, 2008) is the violation of the independence assumption. Dependence between samples, such as members from the same family, invalidates a basic assumption in many statistical tests, thus potentially making the p-value estimation unreliable.

As dependence has been an important theme in statistics for many years, there is large amount of literature in genetics as well as in statistics to tackle the problem. For example, the maximum likelihood or Bayes estimation of allele frequencies in relatives (Boehnke 1991; Thomas and Camp, 2006; Coram and Tang, 2007); the use of principal components or eigenvectors to identify clusters of samples (Price et al., 2006; Patterson et al., 2006), or the reduction of effective number of markers in a linkage disequilibrium block (Cheverud, 2001; Nyholt, 2004); sample weighting to suppress contributions from correlated samples (Broman, 2001; Browning et al., 2005), etc.

The transition from genetic linkage analyses to association studies (Risch and Merikangas, 1996; Li et al., 2005) presents a situation when affected sibs or affected pedigree members are often used as case samples in a case-control association study (Bourgain, 2005; Epstein et al., 2005; Moore et al., 2005; Biedermann et al., 2006; Klei and Roeder, 2007; Köhler et al., 2007; Yoo et al., 2007; Visscher et al., 2008; Knight et al., 2009). Since the correlation structure between sibs or relatives is given, it is not necessary to use techniques such as the generalized estimating equation as has been carried out in (Silverberg et al., 2003). Instead, variance of correlated samples can be calculated (Slager and Schaid, 2001) and its effect on the test statistic can be determined. The method discussed in (Slager and Schaid, 2001) is however only applied to the Armitage trend test.

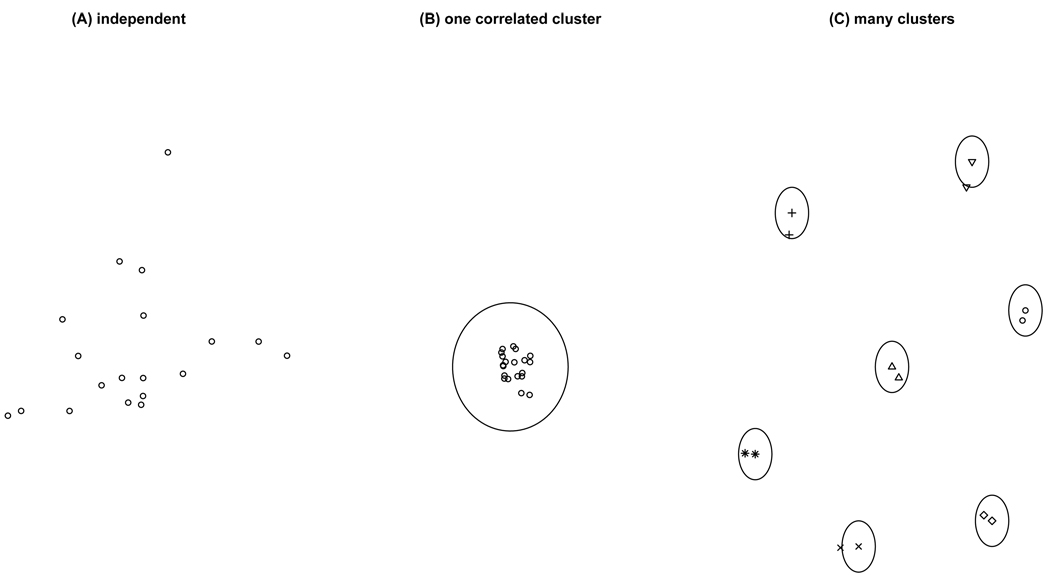
To avoid confusion, Fig.1 illustrates the situation to be addressed in this paper. Fig.1(A) is the standard situation where samples are independent. Fig.1(B) shows the situation where all samples are correlated with one another. This is however not the situation we will address. Fig.1(C) consists of correlated clusters, whereas there is no correlation between clusters themselves. Fig.1(C) is the situation when relatives of the same family are used for association analysis.

Figure 1.

Illustration of three situations concerning sample correlations: (A) samples are independent; (B) all samples are correlated with each other to form one cluster; (C) samples within a cluster are correlated, whereas there is no correlation between clusters. This is called “cluster-correlated data” in (Williams, 2000).

Fig.1(B) leads to a smaller variance compared to independent situation Fig.1(A) with the same number of samples. Since larger sample size leads to smaller variance, it is as if the “effective sample size” is increased in Fig.1(B). The trend in Fig.1(C) is the opposite: the “effective sample size” is actually reduced. Take an extreme example of monozygotic twins: since monozygotic twins have identical genotypes, a pair of twins provide the same genetic information as one twin, and the two points within a circle in Fig.1(C) is equivalent to one point. In other words, the effective sample size is only half of the apparent sample size. These concepts have already been understood in the study of clustered/clumped data and are associated with phrases like “variance inflation” and “overdispersion”.

In this paper, we advocate the use of “effective sample size” (ESS) as a simple method to capture the effect of sample correlation and variance inflation. The term effective sample size has appeared in the literature before (Kish, 1965; Thiébaux and Zwiers, 1994; Rosner and Milton, 1988; Rao and Scott, 1992; Madden and Hughes, 1999) but has not become a commonly used tool in genetic analysis. We define effective sample size N_E as the equivalent number of independent samples that leads to the same variance of an intensive quantity, i.e., a quantity that does not change with the sample size.

For example, if the sample proportion of heads in a coin tossing is estimated to be p, its variance is p(1−p)/N where N is the number of coin tosses; if the observed variance is larger than what is expected from this equation, and can be fitted by the formula p(1−p)/N_E, then N_E is the effective sample size. Note that this definition of N_E is very similar to the “variance effective size” used in population genetics, but different from, and should not be confused with, the “inbreeding effective population size” (N_e) also used in population genetics (Wright, 1938).

In genetic case-control studies, the association signal originates from the allele or genotype frequency difference in the diseased and the normal group. The estimation of allele or genotype frequency is very much like the estimation of heads proportion in the tossing coin example given above. We will show that for allele frequency, effective sample size captures the effect of sample correlation exactly. Even for situations where the effective sample size does not provide an exact solution, for example, in estimating genotype frequencies, an averaged parameter usually leads to good approximation. Because the calculation of test statistics X², p-value, and power all directly involve sample size, replacing the apparent sample size with the effective sample size is a quick and convenient solution to the problem of correlated samples without the need to use a custom program.

As there are many publications on the effect of sample correlation on association analysis, and on using pedigrees in association studies, related questions that are not addressed here include: (1) combining linkage and association signals (Göring and Terwilliger, 2000; Li et al., 2005); (2) family-based associations such as transmission disequilibrium test (TDT) and its extensions (Nagelkerke et al., 2004; Allen-Brady et al., 2005; Gray et al., 2009); (3) association using multiple family members with novel test statistics instead of the standard chi-square test (Risch and Teng, 1998; Teng and Risch, 1999; Li et al., 2000); (4) association with unknown (“cryptic”) correlations (Voight and Pritchard, 2005; Astle and Blading, 2009; Rakovski and Stram, 2009; Thornton and McPeek, 2010; Sillanpää, 2011) where the relativeness between samples is detected instead of given (Weir et al., 2006; Choi et al., 2009). This paper is about a simple and accessible method to incorporate sample correlations in genetic case-control studies within the standard chi-square test framework.

Mathematical Details

Effective sample size for sibpairs

For simplicity, let’s first consider N_sib sibpairs. For the quantity of interest x_i (i = 1, 2,⋯2N_sib, the 2N_sib × 2N_sib correlation matrix for x_i is:

$$R=\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill r\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill r\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill r\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill r\hfill & \hfill 1\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \end{array}\right)$$ (1)

Each 2-by-2 sub-matrix in Eq.(1) represents a sibpair with off-diagonal element r being the correlation coefficient Cor(x_i, x_i+1) between two sibs i and i + 1. The variance of the extensive variable X = ∑_i x_i is then equal to the weighted sum:

$${\mathit{\text{Var}}}_X={\displaystyle \sum _{\mathit{\text{ij}}}}{\sigma }_i{\sigma }_j{R}_{\mathit{\text{ij}}}$$

where σ_i and σ_j is the standard deviation of x for person i and j, and the variance of the intensive quantity x = ∑_i x_i/(2N_sib) is

$${\mathit{\text{Var}}}_x={\displaystyle \sum _{\mathit{\text{ij}}}}{\sigma }_i{\sigma }_j{R}_{\mathit{\text{ij}}}/{(2N_{\text{sib}})}^2$$

Since here we are dealing with sibpairs of the same affection status, σ_i = σ_j = σ, which simplifies the variance for the correlation matrix in Eq.(1):

$${\mathit{\text{Var}}}_X=N_{\text{sib}}\cdot {\sigma }^2\cdot 2(1+r)\mathit{\text{\hspace{1em}and\hspace{1em}}}{\mathit{\text{Var}}}_x=\frac{{\sigma }^2(1+r)}{2N_{\text{sib}}}$$

The equivalent number independent samples that lead to the same variance for x can be derived by equating σ² · 2(1 + r)/(2N_sib) = σ²/N_E, or, the ESS for sibpairs is:

$$N_E=\frac{2N_{\text{sib}}}{1+r}.$$ (2)

The effective sample size reduction α is defined as the ratio between the ESS and the apparent sample size, and for sibpairs, it is equal to:

$$\alpha \equiv \frac{N_E}{2N_{\text{sib}}}=\frac{1}{1+r}.$$ (3)

Effective sample size for larger sibships

For N_tri pedigrees each with three siblings, the 3N_tri × 3N_tri correlation matrix can be written as:

$$R=\left(\begin{array}{ccccccc}\hfill 1\hfill & \hfill r\hfill & \hfill r\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill r\hfill & \hfill 1\hfill & \hfill r\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill r\hfill & \hfill r\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill r\hfill & \hfill r\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill r\hfill & \hfill 1\hfill & \hfill r\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill r\hfill & \hfill r\hfill & \hfill 1\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \end{array}\right)$$ (4)

and the variance of x, ESS, and sample size reduction are:

$${\mathit{\text{Var}}}_x=\frac{{\sigma }^2(1+2r)}{3N_{\text{tri}}},N_E=\frac{3N_{\text{tri}}}{1+2r}\mathit{\text{\hspace{1em}and\hspace{1em}}}\alpha =\frac{1}{1+2r}.$$ (5)

More generally, for sibship of k sibs, the sample size reduction is

$$\alpha =\frac{1}{1+(k-1)r}.$$ (6)

Effective sample size for a mixture of relatives

For pedigrees with a specific mixture of relatives, for example, two sibs and one uncle, the correlation matrix consists of identical sub-blocks:

$$R=\left(\begin{array}{ccccccc}\hfill 1\hfill & \hfill r_1\hfill & \hfill r_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill r_1\hfill & \hfill 1\hfill & \hfill r_2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill r_2\hfill & \hfill r_2\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill r_1\hfill & \hfill r_2\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill r_1\hfill & \hfill 1\hfill & \hfill r_2\hfill & \hfill .\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill r_2\hfill & \hfill r_2\hfill & \hfill 1\hfill & \hfill .\hfill \\ \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill & \hfill .\hfill \end{array}\right)$$

where r₁ is the correlation coefficient between two sibs, and r₂ is that between a sib and the uncle. It can be shown that the sample size reduction is

$$\alpha =\frac{3}{3+2r_1+4r_2}=\frac{1}{1+2\overline{r}}$$ (7)

where the averaged correlation r̄ = (1/3)r₁ + (2/3)r₂ is defined in such a way that we can assume all relatives were similar and any two relatives have a correlation coefficient of r̄. The similar derivation can be generalized to any combination of relatives.

Correlation coefficient of two relatives’ allele counts

The correlation coefficient between allele count x (x=2,1,0 for marker genotype AA, AB, BB, with probability of p², 2pq, q²) of two sibs is:

$$r\equiv \frac{\mathit{\text{Cov}}[x_{\text{sib}1},x_{\text{sib}2}]}{\sqrt{\mathit{\text{Var}}[x_{\text{sib}1}]}\sqrt{\mathit{\text{Var}}[x_{\text{sib}2}]}}=\frac{E[x_{\text{sib}1},x_{\text{sib}2}]-E{[x]}^2}{\mathit{\text{Var}}[x]}.$$

The mean and variance of the number of alleles is E[x] = 2p, Var[x] = 2pq, and the joint probability E[x_sib1, x_sib2] can be calculated by the Li-Sacks conditional probability given the identity-by-descent (IBD) status (Li and Sacks, 1954; Li 1998; Li and Reich 2000; Dai and Weeks, 2006). The three Li-Sacks matrices (the so called ITO matrices) are the probability of the second relative to have one of the genotypes given the genotype of the first relative, and given the IBD status between the two relatives:

$$\begin{array}{ccc}\hfill \text{IBD}=2& \hfill \text{IBD}=1\hfill & \text{IBD}=0\hfill \\ \hfill I=\left(\begin{array}{ccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right),\hfill & \hfill T=\left(\begin{array}{ccc}\hfill p\hfill & \hfill q\hfill & \hfill 0\hfill \\ \hfill p/2\hfill & \hfill 1/2\hfill & \hfill q/2\hfill \\ \hfill 0\hfill & \hfill p\hfill & \hfill q\hfill \end{array}\right),\hfill & \hfill O=\left(\begin{array}{ccc}\hfill p^2\hfill & \hfill 2\mathit{\text{pq}}\hfill & \hfill q^2\hfill \\ \hfill p^2\hfill & \hfill 2\mathit{\text{pq}}\hfill & \hfill q^2\hfill \\ \hfill p^2\hfill & \hfill 2\mathit{\text{pq}}\hfill & \hfill q^2\hfill \end{array}\right).\hfill \end{array}$$

By using the ITO matrices, we have (π_k is the probability of k copies of IBD alleles between two relatives):

$$\begin{array}{cc}E[x_{\text{rel}1},x_{\text{rel}2}]\hfill & ={\displaystyle \sum _{i,j=0}^2}i\cdot j\cdot P(x_{\text{rel}1}=i,x_{\text{rel}2}=j)={\displaystyle \sum _{i,j=0}^2}\mathit{\text{ij}}{\displaystyle \sum _{k=0}^2}P(x_{\text{rel}2}=j|i,k){\pi }_{k}P(x_{\text{rel}1}=i)\hfill \\ \hfill & ={\pi }_{0}4p^2+{\pi }_1(4p^2+\mathit{\text{pq}})+{\pi }_2(4p^2+2\mathit{\text{pq}})=4p^2+\mathit{\text{pq}}({\pi }_1+2{\pi }_2).\hfill \end{array}$$

Inserting it back to the correlation coefficient formula, we have:

$$r=\frac{4p^2+\mathit{\text{pq}}({\pi }_1+2{\pi }_2)-4p^2}{2\mathit{\text{pq}}}=\frac{{\pi }_1}{2}+{\pi }_2$$

The probability that a randomly selected allele from one relative is IBD with a randomly selected allele from another relative, called kinship coefficient Φ, is equal to Φ = π₂(1/2) + π₁(1/4) (Malécot, 1948; Lange 1997). The correlation coefficient r is twice the value of kinship coefficient: r = 2Φ. The same relationship was derived more tediously in, e.g., (Broman, 2001) without using the ITO matrices.

Correlation coefficient of two relatives’ genotype indicator variable

Genotype indicator variable x is 1 for a particular genotype of interest, and 0 for other genotypes. For example, x=1,0,0 for AA, AB, BB is the indicator variable for the homozygous genotype AA. Using the same ITO matrices, the joint probability for AA-indicator variable x between two relatives is

$$\begin{array}{cc}E[x_{\text{rel}1},x_{\text{rel}2}]\hfill & =P(x_{\text{rel}1}=1,x_{\text{rel}2}=1)={\displaystyle \sum _{k=0}^2}P(x_{\text{rel}2}=1|1,k){\pi }_{k}P(x_{\text{rel}1}=1)\hfill \\ \hfill & =p^2({\pi }_2+{\pi }_{1}p+{\pi }_0{p}^2)\hfill \end{array}$$

and correlation coefficient is:

$$r_{\text{AA}-\text{indicator}}=\frac{p^2({\pi }_2+{\pi }_{1}p+{\pi }_0{p}^2)-{(p^2)}^2}{p^2(1-p^2)}=\frac{{\pi }_2+{\pi }_{1}p+({\pi }_0-1)p^2}{1-p^2}$$ (8)

Similarly, for AB and BB indicator variable,

$$\begin{array}{cc}{r}_{\text{AB}-\text{indicator}}=\hfill & \frac{{\pi }_2+{\pi }_1/2+({\pi }_0-1)2\mathit{\text{pq}}}{1-2\mathit{\text{pq}}}\hfill \\ r_{\text{BB}-\text{indicator}}=\hfill & \frac{{\pi }_2+{\pi }_{1}q+({\pi }_0-1)q^2}{1-q^2}\hfill \end{array}$$ (9)

Correcting X² test statistic and 95% confidence interval of odds-ratio by the effective sample size

Single-marker case-control association analysis can be carried out with chi-square test, odds-ratio (OR), and confidence interval of OR. Typically, the control samples are randomly collected from a normal population with no need for correcting correlated samples, whereas case samples might be collected during the linkage analysis stage, thus are correlated. For allele-based analysis (Sasieni, 1997), denote the allele counts in case group as N_A,case, N_B,case and those in control group as N_A,con, N_B,con, the Pearson’s chi-square test statistic can be recalculated by replacing N_A,case, N_B,case with αN_A,case and αN_B,case:

$$X_e^2=\frac{\alpha {(N_{\mathrm{A},\text{case}}{N}_{\mathrm{B},\text{con}}-N_{\mathrm{B},\text{case}}{N}_{\mathrm{A},\text{con}})}^2(\alpha N_{\mathrm{A},\text{case}}+\alpha N_{\mathrm{B},\text{case}}+N_{\mathrm{A},\text{con}}+N_{\mathrm{B},\text{con}})}{(N_{\mathrm{A},\text{case}}+N_{\mathrm{B},\text{case}})(N_{\mathrm{A},\text{con}}+N_{\mathrm{B},\text{con}})(\alpha N_{\mathrm{A},\text{case}}+N_{\mathrm{A},\text{con}})(\alpha N_{\mathrm{B},\text{case}}+N_{\mathrm{B},\text{con}})}.$$ (10)

The modified test statistic $X_e^2$ can then be used to determined the p-value.

For OR θ̂ = N_A,caseN_B,con/(N_A,conN_B,case), the uncorrected 95% confidence interval (CI) is estimated by the Woolf’s formula: [l, u] = [e^{log θ̂−1.96σ̂(log θ̂)}, e^{log θ̂+1.96σ̂(log θ̂)}], with σ̂(log θ̂) = (1/N_A,case + 1/N_B,case + 1/N_A,con + 1/N_B,con)^0.5. This can be corrected in a similar way by replacing N_A,case,N_B,case with αN_A,case and αN_B,case:

$${\widehat{\sigma }}_e(\text{log}\widehat{\theta })={\left(\frac{1}{\alpha N_{\mathrm{A},\text{case}}}+\frac{1}{\alpha N_{\mathrm{B},\text{case}}}+\frac{1}{N_{\mathrm{A},\text{con}}}+\frac{1}{N_{\mathrm{B},\text{con}}}\right)}^{1/2}.$$ (11)

It can be shown that $\alpha <X_e^2/X^2<1$ and σ̂_e/σ̂ > 1, when α < 1. In other words, when the effective sample size is smaller than the apparent sample size, the test statistic is smaller (leading to larger p-values), and the 95% CI of OR is wider.

Results

Diminishing return in adding more relatives from the same pedigree in an association study

The kinship coefficients and sample size reduction with respect to allele frequency estimation of common relative pairs are listed in Table 1, and those for sibships with 1,2, … siblings are listed in Table 2. For more complicated relationships or pedigrees with loop, one can consult (Maruyama and Yasuda, 1970; Lange 1997). Several rules-of-thumb can be stated: two siblings contribute 1.333 samples, uncle-nephew pair contributes 1.6 samples, three siblings are equivalent to 1.5 samples, etc. If the relationship between two pedigree members is distant, the correlation is close to zero and they can be treated as two independent samples (e.g., second cousins contribute 1.94 samples). For larger sibship, there is a diminishing return in adding extra sibs: adding the second, the third, the fourth, and the fifth sibs only adds 0.333, 0.167, 0.1, 0.067 samples. Even in the limit of infinite number of sibs, the effective sample size can not be larger than 2, as the extra sibs merely resample the finite pool of four parental alleles.

Table 1.

For several common relative pairs, these quantities are listed: π₂, π₁, π₀: probabilities of 2,1,0 copies of allele that are identity-by-descent (IBD); Φ: kinship coefficient; r: correlation coefficient between the number of allele A (or B) counts; α: sample size reduction; N_E: effective number of samples in the relative pair.

pair relationship	π2	π1	π0	Φ	r	α	NE
parent-child	0	1	0	1/4	1/2	2/3	4/3 ≈ 1.333
sibs	1/4	1/2	1/4	1/4	1/2	2/3	4/3 ≈ 1.333
half-sibs	0	1/2	1/2	1/8	1/4	4/5	8/5 = 1.6
uncle/aunt-nephew/niece	0	1/2	1/2	1/8	1/4	4/5	8/5 =1.6
first cousins	0	1/4	3/4	1/16	1/8	8/9	16/9 ≈ 1.778
second cousins	0	1/16	15/16	1/64	1/32	32/33	64/33 ≈ 1.939

Table 2.

The sample size reduction α and effective sample size N_E of sibships with 2, 3, 4, 5, and k sibs.

size of sibship	α	NE
2	2/3	4/3 ≈ 1.333
3	1/2	3/2=1.5
4	2/5	8/3=1.6
5	1/3	5/3 ≈ 1.667
k	2/(k+1)	2k/(k + 1) ≈ 2(1 − 1/k)

These results show that while one should include as many samples as possible, whether correlated or not, in an association study, it does not seem necessary to include too many relatives from the same pedigree. While distant relatives are essentially independent samples, for close relatives such as siblings, two persons are perhaps a good compromise between the desire to add more samples and the diminishing return due to correlations.

When a mixture of relatives from the same pedigree is included, one can use the averaged correlation coefficient discussed in the Method section. For example, with two siblings and one aunt/uncle, the averaged correlation coefficient r̄ = (1/3)0.5 + (2/3)0.25 = 1/3. The ESS for the two-sib-one-uncle is 1.8, larger than the value of 1.6 for three siblings.

Improving p-value by using all samples

For the PTPN22 data in Table 4, if one affected sib per sibpair is selected for association as in (Begovich et al., 2004), X² = 31.42 leads to p-value of 2.1 ×10⁻⁸ (with Fisher’s exact test, the p-value is 5.6 ×10⁻⁸), and 95%CI of OR is (1.55–2.50). We know this is an underuse of the samples as the second sibs in sibpairs were discarded. Using all sibs in sibpairs without correction leads to the incorrect result of X² =53.26, p-value of 2.9 ×10⁻¹³, and 95% CI of OR of (1.73–2.62). The overall ratio of effective sample size and the apparent sample size is: α = (86 + 377 × 2 × 2/3)/(86 + 377 × 2) ≈ 0.70. Using the Eq.(10) and Eq.(11), the modified X² = 45.73 leads to p-value of 1.36 ×10⁻¹¹, and modified 95% CI of OR (1.70–2.66). Compared to the one-sib-per-pair dataset, even though the conclusion on statistical significance is unchanged, the p-value is 1500 times smaller.

Table 4.

Genotype counts of a SNP in PTPN22 in human chromosome 1 in case (rheumatoid arthritis) and control group. The first line summaries the genotype counts of all case samples, including 86 singletons (uncorrelated samples) and 377 sibpairs. The second line is a subset of the case group with one affected sib per pedigree (sibpair) randomly chosen. The third line is for the control group.

	TT	TC	CC	N	Nallele=2N
case (86 singletons and 377 sibpairs)	21	241	578	840	1680
case (86 singletons and 377 sibs)	10	126	327	463	926
control	9	143	774	926	1852

The ratio of two chi-squares, one for all samples with ESS correction and another without, is calculated to be $X_e^2/X^2=45.73/53.26=0.86$. This ratio can also be approximately estimated from ESS. Since X² and $X_e^2$ can be written in the form: X² = (p̂_A,case − p̂_A,control)²/[(1/N_case + 1/N_control)·p̄·q̄], $X_e^2\approx {({\widehat{p}}_{\mathrm{A},\text{case}}-{\widehat{p}}_{\mathrm{A},\text{control}})}^2/[(1/(\alpha N_{\text{case}})+1/N_{\text{control}})·\overline{p}·\overline{q}]$ (in an approximation, the pooled allele frequency estimation for A and B is not greatly affected by the change of sample size), $X_e^2/X^2\approx (1/0.7\times 1680)+1/1852)/(1/1680+1/1852)=0.82$.

For the IFIH1 gene in Table 5, we applied the effective sample size method both globally or pedigree-type-specifically. Using Eqs.(2,5,6,7), and by a conservative use of relatives in assuming all relatives to be sibships, we have the averaged effective number of allele counts: 2(67+512·2/(1+0.5)+64·3/(1+2×0.5)+8·4/(1+3×0.5)+5/(1+4×0.5)+8/(1+7×0.5) ≈ 1724, or, the average sample reduction of α = 861.9111/1328 ≈ 0.649. The ESS-based method leads to a p-value of 0.0023 in chi-square test, improved upon the p-value of 0.0179 when only one case per family is used (second line in Table 5). At the significance level of 0.01, adding correlated samples in this dataset makes an insignificant result significant.

Table 5.

Genotype counts of a SNP in IFIH1 gene in human chromosome 2 in case (rheumatoid arthritis) and control group. Those of all case samples, of independent case samples, and of control samples, are listed in lines 1,2, and 3.

	CC	TC	TT	N	Nallele=2N
case (all)	169	624	535	1328	2656
case (1 sample per ped)	87	308	258	653	1306
control	247	603	494	1344	2688

The SNP minor allele frequency (MAF) for the control population in the IFIH1 gene was reported to be 40.4% in the initial round, and 38.7% in the follow-up round (Smyth et al., 2006); that in the type 1 diabetes population was 35.3% in the first round, and 34.0% in the second round, each with thousands of samples. The control MAF in Table 5 is 40.8%, consistent with the value in (Smyth et al., 2006). However, the MAF for the rheumatoid arthritis samples in Table 5 is 36.2%, larger than the MAF for the type 1 diabetes samples. The weaker association signal in rheumatoid arthritis study as compared to diabetes study implies a larger sample size requirement for its detection, and as a result, ESS method proves to be important in incorporating extra sibling samples to increase the sample size.

One can also apply the ESS method to each pedigree-type specifically. We count the T and C alleles in pedigrees with only affected sibpairs, then reduce the count by the factor 1/(1 + 0.5) = 2/3. Similarly, the allele counts in pedigrees with three affected sibs are reduced by the factor of 1/(1 + 2 × 0.5) = 1/2, etc. The pedigree-type-specific allele count reduction leads to p-value of 0.00467. We can partially explain why this p-value is not as good as the one derived by the global sample size reduction: the association signal is largely due to an enrichment of the major allele T in the case group; however, the largest pedigree with 8 affected members with 13 counts of the T allele leads to an effective contribution in the “local method” of 3.3 counts, as versus the 9.7 counts in the “global method”.

A single effective sample size does not capture all variance inflations in genotype frequency estimations, but it provides a good approximation

With the correlation coefficient for genotype indicator variable in Eq.(8,9), we can derive the sample size reduction α and variance inflation 1/α for genotype frequencies obtained from relative pairs, sibships, and cluster of relatives: α_G = 1/(1 + r_G), 1/(1 + (k − 1)r_G), and 1/(1+(k − 1)r̄_G) respectively, where r_G (G=(AA,AB, BB) is the genotype-specific correlation coefficient. Compared to the variance inflation for allele frequency estimation, the number of ESSs for genotype frequencies is 3 instead of 1, as r_AA, r_AB, r_BB are not equal to each other. Furthermore, these correlation coefficients depend on p, q.

We illustrate these properties by the example of sibpairs. Using Eq.(8,9,3), the genotype-specific sample size reductions are:

$$\begin{array}{cc}{\alpha }_{\text{AA},\text{sibpair}}\hfill & =\frac{1}{1+(1+3p)/(4+4p)}\hfill \\ {\alpha }_{\text{AB},\text{sibpair}}\hfill & =\frac{1}{1+(1-3\mathit{\text{pq}})/(2-4\mathit{\text{pq}})}\hfill \\ {\alpha }_{\text{BB},\text{sibpair}}\hfill & =\frac{1}{1+(1+3q)/(4+4q)}.\hfill \end{array}$$ (12)

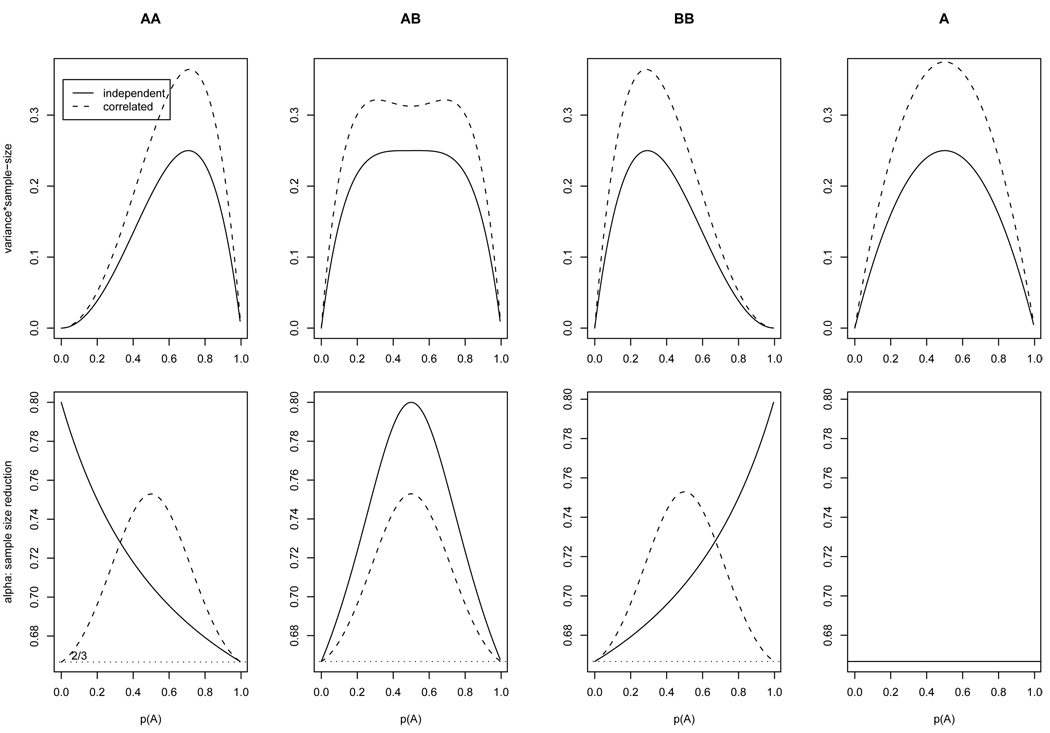
Figure 2 shows α_G,sibpair’s of the three genotypes as a function of p; also shown are the genotype frequency variance (multiplied by the sample size). Variances of genotype frequencies calculated from independent samples are shown in solid lines as a comparison. It can be seen from Figure 2 that the variance inflation of allele frequency is distinct from those of genotype frequencies in that its α is a constant value 2/3 independent of p. It illustrates that one should not expect a single parameter to correct the variance inflation in correlated samples for all circumstances.

Figure 2.

(Upper row) expected variance of genotypes AA, AB, BB and allele A (multiplied by the sample size) as a function of the allele frequency p(A). The solid line indicates the result from independent samples, and dashed line from sibpairs. (Lower row) effective genotype count reduction α₁, α₂, α₃ for sibpair data as a function of p(A) (Eq.(12)). For allele count, the sample size reduction is a constant number of 2/3. The grey line is the α_a(p), the weighted average of α₁, α₂, α₃. The α=0.7096 line is the average of α_a(p) over p’s.

The genotype-specific sample size reductions in Eq.(12) can be applied in the following way: (1) the allele frequency p is estimated from the data; (2) three α_Gs are calculated by Eq.(12); (3) each genotype count is discounted by the genotype-specific α_G, then these modified genotype counts can be used for further genotype-based association. Notice that α_G’s in Eq.(12) are confined to the range (2/3, 4/5). One can also obtain an averaged ESS by averaging over three genotypes: α_avg,sibpair(p) = p²α₁ + 2pqα₂ + q²α₃, and α_avg,sibpair (p is estimated from the data first) can be used to discount all three genotype counts by the same factor. In yet another approach, α_avg,sibpair can be averaged over p: $\overline{\alpha }\equiv {\displaystyle {\int }_0^1{\alpha }_a(p)\mathit{\text{dp}}}$. This leads to ᾱ = 0.7096. One can use ᾱ to discount all three genotype counts without the need to estimate p first. Note that this sample size reduction is less severe than that to account for variance inflation in allele frequency estimation, α = 0.6667.

Effective sample size method performs well in simulation and in comparing the score test

Using the simulated data described in the Methods and Material section, we have checked the validity of the effective sample size method. We first compare the test errors in using the uncorrected chi-square test statistic X² and the ESS-corrected $X_e^2$, for the allele-based test. Table 3 shows the type I error under the null distribution in chi-square test using the naive X² and ESS-corrected $X_e^2$. Note that for the null distribution, different disease model has no effect on the allele/genotype frequencies, and we simply consider the R/A/D models in Table 3 as three independent runs. It is clear that $X_e^2$ leads to the more correct type I errors, practically identical to the nominal significance, whereas the naive X² clearly leads to larger type I errors.

Table 3.

Empirical type I errors for the allele-based association test at the nominal significance level of 0.01 and 0.05, either by using the naive (uncorrected) X² or the $X_e^2$ modified by the effective sample size. The allele frequencies in case and control group are the same, even though different simulation runs are labeled as recessive (R), additive (A) and dominant (D).

		α = 0.01		α = 0.05
p	model	using X2	using $X_e^2$	using X2	using $X_e^2$
0.1	R	0.022	0.011	0.082	0.054
	A	0.022	0.011	0.083	0.051
	D	0.019	0.009	0.078	0.051
0.3	R	0.022	0.011	0.073	0.048
	A	0.020	0.009	0.078	0.049
	D	0.022	0.010	0.082	0.052
0.5	R	0.022	0.011	0.082	0.053
	A	0.020	0.009	0.078	0.050
	D	0.022	0.010	0.082	0.053

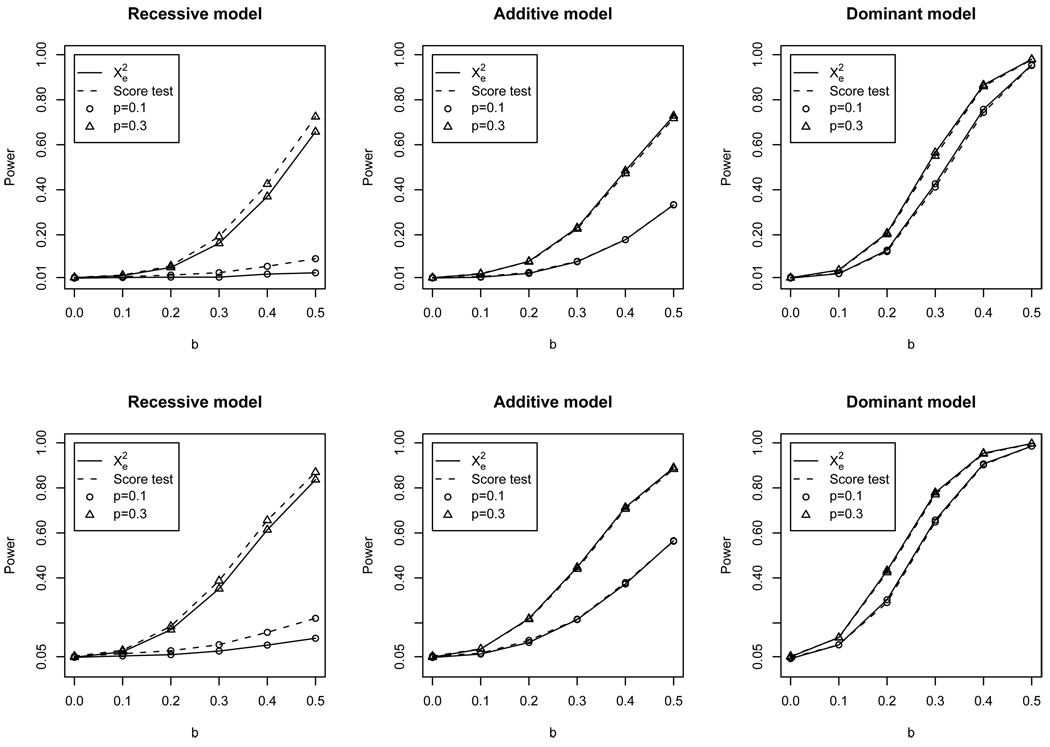
The locally most powerful test among all tests with the correct type I errors is the score test (Cox and Hinkley, 1974) which sets a standard other tests can be compared to. For allele-based analysis, ESS-corrected $X_e^2$ is identical to the score test, sharing the same power. For genotype-based test (i.e. chi-square test on 2-by-3 genotype count table), chi-square test using ESS-corrected $X_e^2$ is not identical to the score test. Here we adopt the simplest ESS correction for genotype data: multiplying the genotype counts by a constant reduction value ᾱ = 0.7096. The power curve in Figure 3 shows that the difference between the ESS-corrected $X_e^2$ test and score test is negligible for dominant or additive disease models. The difference for recessive models is non-zero, but nevertheless small.

Figure 3.

Empirical power curve for the genotype-based test of three different models (recessive, additive, dominant) at the nominal significance level of 0.01 (upper row) and 0.05 (lower row). The x-axis is the log-odds ratio parameter b in the disease model Eq.(14). Two power curves are shown: using effective sample size corrected $X_e^2$ (solid line), and by the score test (dashed line).

Discussion

Cheverud’s formula for the number of independent variables

Based on the idea that the overall amount of correlation among several variables can be measured by the variance of the eigenvalues derived from their correlation matrix, Cheverud proposed a formula to calculate the effective number of variables (Cheverud, 2001):

$$N_E=N\left(1-(N-1)\frac{\mathit{\text{Var}}[\lambda ]}{N^2}\right)$$ (13)

where N is the number of variables, and λ = (λ₁, λ₂,…λ_N) are the eigenvalues of the N × N correlation matrix for these N variables. Eq.(13) has been applied to QTL mapping in the inbreeding system and to human association analysis to determine the number of independent markers in a linkage disequilibrium block (Cheverud, 2001; Nyholt, 2004). Although this formula has not been used to determine the number of independent samples, it can be interesting to compare Eq.(13) with the ESS formula derived in this paper.

We consider the large sibship situation where the correlation matrix is characterized by Eq.(4). It can be shown that each submatrix (the 3 × 3 block in Eq.(4)) contributes an eigenvalue equal to 1 + (3 − 1)r = 1 + 2r, and two eigenvalues equal to 1 − r. The variance of the eigenvalues for Eq.(4) is then equal to 2r²(N/(N −1)). Inserting it to Eq.(13), we have the Cheverud’s effective number of variables: N − 2r². Compared to the ESS of N/(1 + 2r) determined by Eq.(5), Cheverud’s formula leads to a larger effective number of degrees of freedom, and less reduction, in particular in the large N limit.

We believe that our effective sample size formula makes better sense: in the three-sib sibship case, because each sibship is independent of another, the number of independent samples is at least N/3. Note that the ESS formula involves an operation of rescaling the original sample size N, instead of subtracting a correction term. In order for Cheverud’s formula to have a similar effect, the variance of eigenvalues has to increase with the sample size N. This can be true only if there is a collective correlation for all variables, or if there is haplotype block-block correlation. If the variables (samples) can be split into independent blocks, the effective degrees of freedom (sample size) should always be a rescaled version of the original one. Interestingly, for a model discussed in (Salyakina et al., 2005) where the correlation coefficient within a block is 1 and those between blocks are small non-negative values, the effective number of variables is indeed a rescaled value of the original number of variables.

The variance inflation factor in the genomic control method

The genomic control method in association studies was proposed in (Devlin and Roeder, 1999; Bacanu et al., 2000; Devlin et al., 2001) to correct population stratification and “cryptic relatedness” between samples. Despite quantitative differences in the mechanism for correlation, population stratification and family clusters could have similar consequences, and this similarity is exploited in a unified framework for association studies of quantitative traits (Yu et al., 2006). In the genomic control method, neutral markers are used to estimate the variance inflation factor λ, and λ is used to divide the chi-square statistic: $X_{\text{gc}}^2=X^2/\lambda$ for a modified test statistic. This can be compared to our formula for an ESS-corrected chi-square test statistic in Eq.(10), $X_e^2\approx \alpha X^2$ (if the allele counts N_A,con,N_B,con in control group are not too small). In this approximation, $X_e^2\approx X_{\text{gc}}^2$ if α = 1/λ.

Whether genomic control can correctly capture the population substructures is still under debate (Devlin et al., 2004), with reports of either under- or over-correcting the correlation depending on the number of markers used (Marchini et al., 2004; Köhler and Bickeböller, 2006), and its performance perhaps also depends on whether the markers used to estimate λ are ancestral-informative or not. For whole genome association studies with a large number of markers, it is recommended to use a Bayesian version of the genomic control (Devlin et al., 2004). In our situation, we are correcting the known relatedness between samples, and there is no issue of under- and over-correcting the test statistic.

One key debate on genomic control is whether $X_{\text{gc}}^2$ follows a central or non-central chi-square distribution (Gorroochurn et al., 2006). For a truly admixed population with a positive Wright’s F_ST value, the variance of the allele frequency is Var_p = p(1 − p)(F_ST − F_ST /N + 1/(2N)) (the inbreeding coefficient is assumed to be zero) (Weir, 1996), which is inflated by a factor (F_ST−F_ST /N+1/(2N)). This admixture-induced variance inflation cannot be accounted for by a simple sample size reduction, because even of the infinite sample limit the residual variance is still nonzero. At the infinite sample size limit, the variance inflation factor is equal to F_ST, which is why F_ST is also called the standardized measure of variance, or Wahlund’s variance (Cavalli-Sforza and Bodmer, 1971). The only way to reconcile the variance inflation and sample size reduction here is to set α = 1/(1+2(N−1)F_ST), i.e., the sample size reduction itself depends on sample size. All these issues in correcting admixed subpopulations are not problematic for our relative samples because we assume the allele frequency does not change from pedigree to pedigree.

Comparison to the generalized estimation equation approach

The method of generalized estimation equation (GEE), similar to ESS method, has a goal of utilizing correlated samples in an analysis (Liang and Zeger, 1986; Hanley et al., 2003). However, one major difference between GEE and ESS is that GEE relies on data to estimate the within-cluster correlation among samples, whereas ESS calculates the correlation by the information given. Typically in GEE, only a single correlation coefficient r is estimated for all clusters, which can be unreliable if clusters of different natures are included in the data. For example, if the dataset contains both sibpairs and cousin-pairs, the r for samples within sibpairs should be larger than that for cousin-pairs. Another difference is that GEE corrects not only variance, but also mean as well, whereas ESS only modifies variance. Similar to an argument made in (Devlin et al., 2004), we believe that sample correlation mainly affects the variance, and has less effect on bias.

We use the IFIH1 genotype data in Table 5 to illustrate differences between GEE and ESS. Using the corstr=“exchangeable” option in the gee subroutine in R statistical package (VJ Carey, T Lumley, and B Ripley, “The gee package”, version 4.13–12, Feb 2007), the averaged within-family correlation coefficient for the allele count variable was estimated as r =0.4349. This r value is slightly smaller than that for sibpairs (r =0.5), but close, reflecting the fact that this dataset is dominated by sibpairs. In the Results section, we have shown that using r = 0.5, the sample size reduction for the dataset in Table 5 is equal to 0.649. If we use the within-group correlation coefficient r =0.4349 estimated by GEE, the sample size reduction is 0.678. The GEE and ESS results are more or less the same, though GEE does not seem to correct the correlation enough. A similar observation that GEE tends to underestimate variance for smaller sample sizes was made in (Trégouët et al., 1997).

The estimation equation is essentially a procedure to determine weights of samples. When samples are correlated, their weights are lower than 1. It was shown in Hanley et al., (2003) that the weight for sibpairs w that minimizes the variance is exactly equal to the Eq.(3) used in this paper. We expect that in general, the weight of related samples determined by minimizing the variance will be equal to the sample size reduction α if the weight for independent individuals is set to 1.

In conclusion, among alternative approaches in handling correlated samples in genetic association studies, such as likelihood-based approach (Bourgain et al., 2003), sample weighting (Browning et al., 2005), and estimation equation (Trégouët et al., 1997), effective sample size is perhaps the most accessible method: easier to use, and with no need to have new computer software. Since the reason that correlated samples are often avoided in practice is not because solutions do not exist, but because the existing methods are relatively hard to use, we believe the ESS method discussed here will help medical geneticists to routinely use pedigree data in association studies.

Methods and Materials

Data sets

A missense SNP rs2476601 in the protein tyrosine phosphatase non-receptor type 22 gene on chromosome 1 (PTPN22) was shown to be associated with the autoimmune disease rheumatoid arthritis (Begovich et al., 2004; Lee et al., 2005). The rheumatoid arthritis samples were collected by the North American Rheumatoid Arthritis Consortium (NARAC) for genetic linkage analysis (Jawaheer et al., 2001, 2003), and all pedigrees contain two or more affected siblings. In the original report (Begovich et al., 2004), one sib per affected sibpair is randomly selected from 377 affected sibpairs for the association analysis (plus 86 singletons). This procedure cuts the number of case samples almost by half. An association analysis of all affected sibs with a correction of the correlation between sibs was not carried out. We reproduce this dataset in Table 4 (corresponds to the “replication study” in Table 1 of (Begovich et al., 2004)).

Another dataset used here is the genotype of a non-synonymous SNP in IFIH1 gene on chromosome 2, also collected by NARAC. IFIH1 gene has recently been shown to be associated with type 1 diabetes (Smyth et al., 2006), but its association status with rheumatoid arthritis is unknown. This dataset consists of 1344 independent control samples and 1328 case samples distributed in 653 pedigrees – including 67 singletons, 512 affected relative-pairs (the majority are affected sibpairs), 64 affected triples (most are sibship with 3 affected sibs), 8 affected quadruples, and two pedigrees with 5 and 8 affecteds. The three genotype counts of this SNP are listed in Table 5.

Simulations

Simple simulated datasets were created for checking the effective sample size method as applied to sibpair data. For each replicate, genotypes of 500 “case” samples consisting of 250 sibpairs and 500 “control” samples were simulated. The genotype in control group was sampled from the genotype distribution of P_control(G) = (p², 2pq, q²) for genotypes AA, AB, BB. Those in the case group is sampled by the model:

$$P_{\text{case}}(G)\propto \frac{e^{a+b·f(G)}}{1+e^{a+b·f(G)}}{P}_{\text{control}}(G)$$ (14)

where f(G) represents the disease models, a is the baseline log-odds, and b is the log-odds ratio. The dominant model (D) is equivalent to f(G)=(1,1,0) for genotype AA, AB, BB; recessive model (R) corresponds to f(G)=(1,0,0); and additive model (A) corresponds to f(G) = (1, 0.5, 0). For the null distribution to be used to check the type I error, b = 0, i.e, genotype has no effect on the disease status, and P_case = P_control. For the alternative distribution to be used to check the power, a is chosen at −4 and b is chosen between 0 and 0.5.