The Onset of Collective Behavior in Social Amoebae

Abstract

In the social amoebae Dictyostelium discoideum, periodic synthesis and release of extracellular cyclic AMP (cAMP) guides cell aggregation and commitment to form fruiting bodies. It is unclear whether these oscillations represent an intrinsic property of individual cells or if they only exist as a population-level phenomenon. Here we show by live-cell imaging of intact cell populations that pulses originate from a discrete location despite constant exchange of cells to and from the region. In a perfusion chamber, both isolated single cells and cell populations switch from quiescence to rhythmic activity depending on the level of extracellular cAMP. A quantitative analysis shows that stochastic pulsing of individual cells below the threshold concentration of extracellular cAMP plays a critical role in the onset of collective behavior.

Populations of microorganisms often undergo transitions to coordinated activities depending on nutrient availability and presence of other microbes in the environment. In a process termed quorum sensing (1) small signaling molecules are synthesized and secreted into extracellular space. When the level of the molecules reaches a threshold, the cell population undergoes a transition to a state that collectively can cope with the new environment. Studies on chemical oscillators (2), glycolytic oscillations in yeast (3) and a synthetic gene circuit in bacteria (4) have demonstrated that synchronized oscillations may rely on a similar quorum-sensing type transition. Unlike in cases where synchronized oscillations appear by entrainment of phase and frequencies of autonomously oscillating elements (e.g. fireflies (5), circadian rhythms (6), somite segmentation (7), Josephson junction arrays (8), chemical reactions (9), etc (10)), the quorum-sensing type transition is accompanied by a spontaneous change from quiescence to oscillations at the population level. The transition, referred to as “dynamical quorum sensing”, encodes cell density-information in the frequency of the oscillations (2, 3), because the small molecule threshold may be reached more quickly at higher cell densities. Although the scheme can provide a robust means for a single cell to change its state qualitatively depending on the cell density, exposing the basis of the oscillatory transition in cell populations has remained a challenge (11, 12) because of difficulties in analyzing the dynamics of individual cells and the population simultaneously. Moreover, how microorganisms use cellular oscillatory mechanisms to implement complex life-cycle strategies at the population scale remains unexplored.

Chemoattractant signaling in the social amoebae Dictyostelium discoideum is one of the best-known examples of cell-cell signaling that mediates cooperation in microorganisms (13). When stimulated with extracellular cAMP, cells respond by synthesizing and secreting more cAMP which results in non-dissipating waves of cAMP (14, 15) that guides aggregation of individual amoeboid cells. Most of our understanding of the cAMP oscillations in Dictyostelium is based on population-level optical-density observations (15–17) or isotope dilution assays of cAMP on fixed samples (14, 18–20). Since such measurements hide possible cell-cell heterogeneities, it is unknown whether the initiation of the periodic behavior is due to synchronization of cells that can autonomously oscillate regardless of interactions with other cells, or whether it is a “dynamical quorum sensing”-type phenomenon (3) –i.e. individual cells remain non-oscillatory unless the entire population becomes oscillatory.

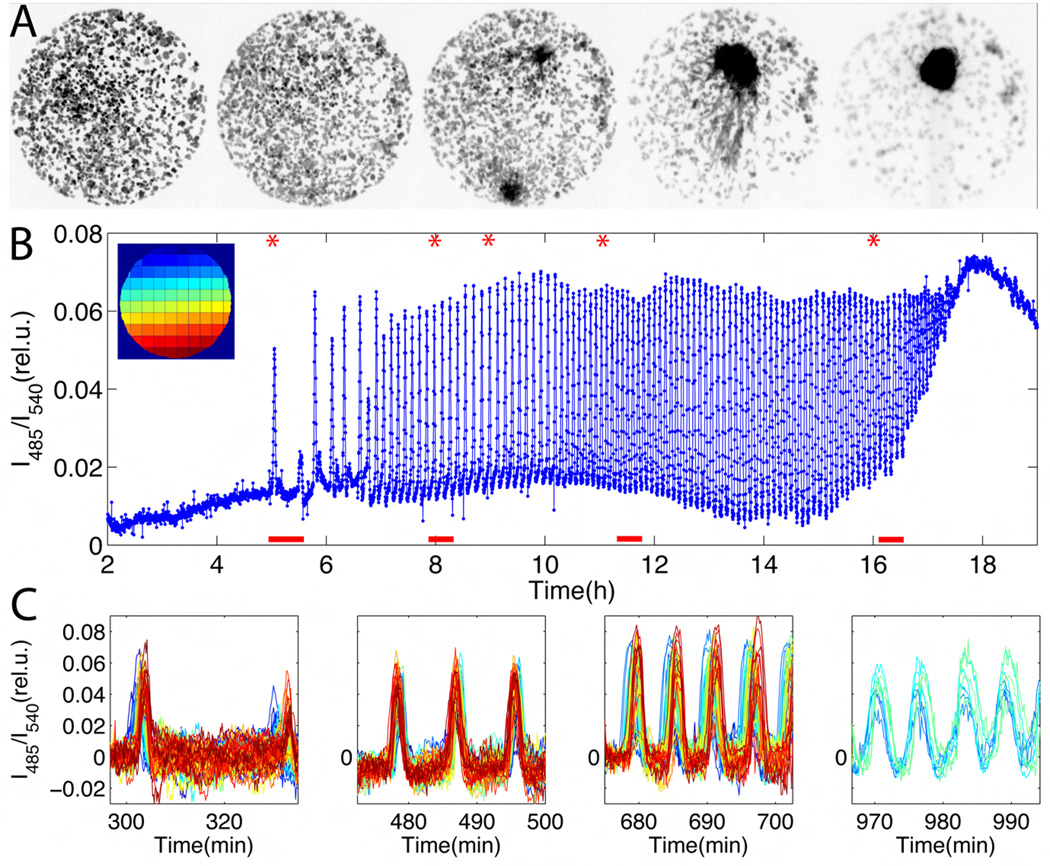
To elucidate the onset of the cAMP oscillations, we employed a FRET-based sensor (21) to directly monitor cytosolic cAMP in live Dictyostelium cells (Supporting Online Materials (SOM); fig. S3). Inhibiting synthesis of cAMP inhibited oscillations, confirming that changes in FRET efficiency reflect changes in cytosolic cAMP levels (fig. S1). A representative time-course of development is shown in Fig. 1A and Fig. 1B (SOM; Mov. S1). Cells began to fire synchronously 5 hours after nutrient deprivation with pulses occurring sporadically every 15 to 30 min (Fig. 1B; 5–7h). Over the next two hours, the period of firing shortened to 8 min and thereafter to 6 min when cells began to aggregate. The entire population participates in the firing from the very first pulse (Fig. 1C, left most panel). Differences in the phase of the oscillations depending on the regions indicate that pulses propagated in space as waves (fig. S7). Different spatial locations competed for wave initiation (Fig. 1C, second panel from the left). However, a single region eventually dominated and determined the aggregation center (Fig. 1A, middle panel). Tracking of individual cells revealed a continuous exchange of cells to and from the signaling centers. Together, these observations suggest that the oscillations do not originate from autonomous activities of specialized cells, but rather that they are likely to result from inhomogeneous fluctuations in the level of extracellular signaling molecules that favor pulse generation.

Fig. 1.

Live-cell imaging of cAMP signaling during early development of Dictyostelium discoideum cells. (A) Approximately 180 cells are confined to a 420 µm diameter area on hydrophobic agar (SOM). Snapshots are taken at times indicated by the red asterisks in (B). Dark area in right-most snapshot corresponds to final aggregation site of the population. (B) Time course of changes in FRET efficiency, averaged over all cells (time indicates hours after starvation). The fluorescent intensities of the CFP-channel divided by that of the YFP-channel are plotted on y-axis. The upper left inset is a colored schematic for the sub-regions analyzed in (C). (C) Close-ups of the time-series for each sub-region, containing 0–5 cells. Red bars indicate time windows in (B), chronologically ordered from left to right. Colors correspond to the colors of the spatial regions displayed in the inset in (B). Small differences in the rising phase of the pulses for individual regions correspond to cAMP waves that are propagating in space (see also fig. S7).

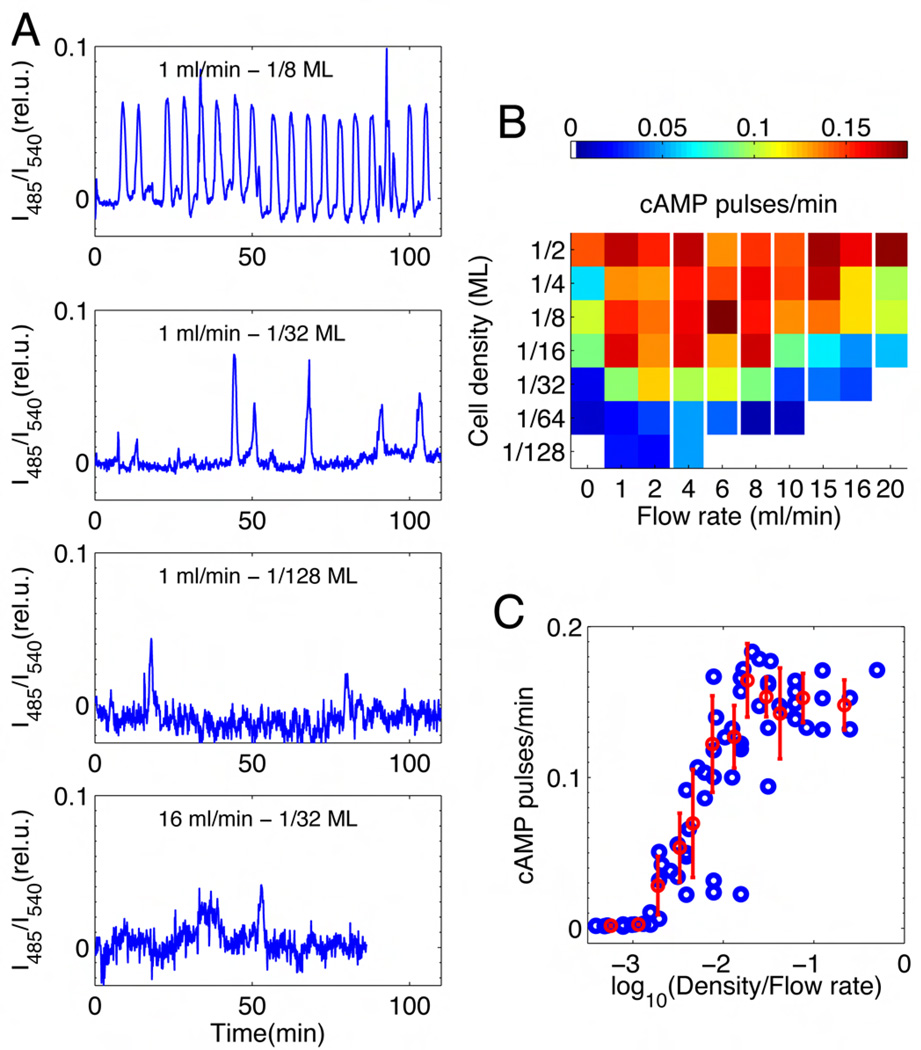
To probe the extracellular conditions necessary to initiate periodic pulses, cells were placed in a perfusion chamber that provides rapid mixing and exchange of extracellular buffer to ensure a uniform and controlled environment. Pulsing rates were systematically measured for a wide range of cell densities and dilution rates. Representative data are shown in Fig. 2A. At sufficiently high densities (~10³ cells/mm²) and under moderate flow speed (~1 ml/min), cells periodically fire approximately once every 6 min on average (Fig. 2A, top panel), which is typically observed in an intact population near a monolayer density (14, 16, 17) (Fig. 1B). With decreasing cell density the occurrence of synchronized pulses becomes sporadic and finally cease (Fig. 2A). The dependence of the firing rate on cell density and dilution rate is presented as a phase diagram (Fig. 2B). The frequency of pulsing at flow rates above 1 ml/min is proportional to a single parameter ρ/k – the ratio of cell density ρ to flow rate k (Fig. 2C). The pulsing-rate is close to zero when ρ/k is small. As ρ/k is increased, the frequency increases

Fig. 2.

Synchronized population-level oscillations of cytosolic cAMP. Cells are placed in a perfusion chamber (volume ~ 0.25 ml) 4–6 hour after starvation. (A) Population averaged behavior at cell densities of 1/8 MonoLayer (ML; 1ML unit is 6,600 cells/mm²), 1/32 ML and 1/64 ML (top to bottom panel respectively) under buffer at a fixed flow rate of 1 ml/min. The lowest panel is at 1/32 ML and 16 ml/min. (B) A phase diagram summarizes 148 experiments at various densities and flow rates. The mean firing rate (min⁻¹) is represented in color. Red regions display the highest firing rates (period of ~6 minutes). Sporadic firing occurs in the blue regions (see also fig. S5). White regions correspond to regimes of no spontaneous firing; white vertical lines indicate non-linear breaks in the x-axis. (C) Firing rate as a function of the ratio between cell density and flow rate (ρ/k) (blue circles). Mean and standard error indicated in red are computed from equi-populated bins. 4 points around a value of −2 on the x-axis are treated as outliers as they are sampled at very low k (flow rates < 1ml/min) where the effect of extracellular PDE is non-negligible (29).

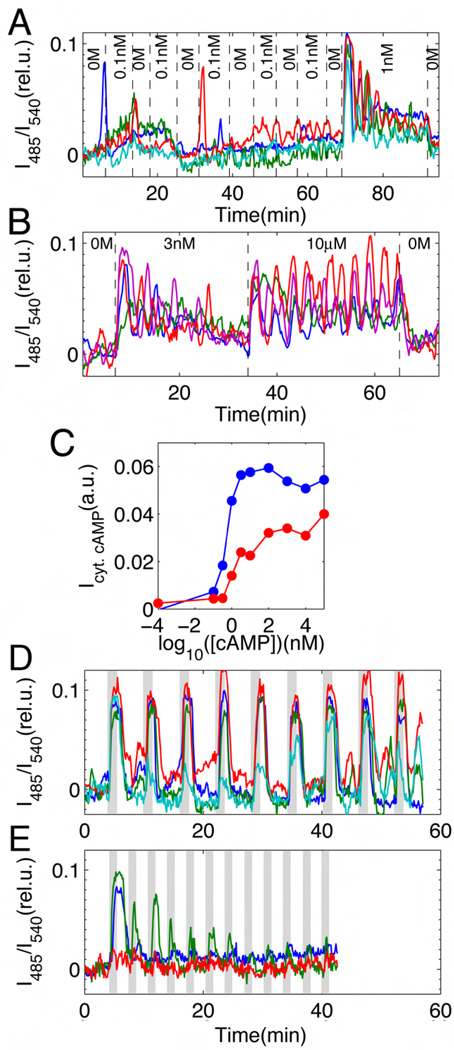
To understand the origin of this dynamical transition, we quantified the response of single isolated cells to continuous application of exogenous cAMP (Figs. 3A and 3B). In the absence of extracellular cAMP, cytosolic cAMP levels remain steady with some fluctuations (fig. S4). At sub-nanomolar stimulation, cells pulse randomly (Fig. 3A). Upon application of nanomolar-levels of cAMP, cells display excitatory behavior (1 nM in Fig. 3A and 3nM in Fig. 3B) – a sharp transient rise that reaches a peak after ~30 sec followed by smaller peaks that gradually attenuate. Damping of the response becomes less marked at micromolar-levels of cAMP (Fig. 3B; 10µM). The oscillatory responses persist at 2.5 to 8 min periods, which vary from cell to cell. The peaks appear even at 100 µM cAMP (fig. S9) well above the saturation dose of the cAMP receptors (22), suggesting that cytosolic oscillations can occur without periodic changes in the level of extracellular cAMP. Note, however, that this persistent oscillatory behavior depends strictly on the presence of extracellular cAMP, since when the stimulus is removed, cytosolic cAMP returns to its pre-stimulus level within 30–60 sec (Fig. 3A at 90 min; Fig. 3B at 65 min). From fluorometeric measurements, we estimate that the basal and the peak levels of cytosolic cAMP concentrations correspond on average to ~400nM and ~10µM, respectively (fig. S3). Fig. 3C summarizes the cytosolic cAMP responses in the form of an input/output relationship (see also fig. S9). The input corresponds to the applied cAMP levels and the output to the integrated response over two time intervals: 1. 3 min corresponding to the initial peak of the response (Fig. 3C; blue curve), and 2. 30 min (red curve). The 3-minute interval exhibits a half-maximal output at 0.5±0.1 nM cAMP, suggesting that a cell can be excited by a very low number of cAMP molecules. For the longer interval, the half-maximal concentration becomes 1.7±0.2 nM due to damping of the response.

Fig. 3.

The cAMP-induced cytosolic cAMP signaling response of isolated individual cells in a perfusion chamber. (A) Representative time courses of sub-threshold response (4 cells are represented by different colors). The concentration of extracellular cAMP was changed at time points indicated by dashed lines (0M, perfusion with buffer only, no cAMP). (B) Damped and persistent oscillations of cytosolic cAMP when perfused with 3 nM and 10 µM exogenous cAMP, respectively (colors indicate 4 individual cells). (C) Single-cell input/output relationship of time- and cell-averaged responses to applied cAMP ranging from 100 pM to 100 µM (blue and red lines correspond to 3 and 30 min averages). The relative cAMP output of an isolated cell for a given input stimulus over a time period T is evaluated here by computing the time-integral of I₄₈₅/I₅₄₀ given by $I_{\mathit{\text{cyt}}.\mathit{\text{cAMP}}}(T)=\frac{1}{T}{\displaystyle {\int }_0^T{\mathrm{I}}_{485}(t)/{\mathrm{I}}_{540}(t)\mathrm{d}t}$, where the stimulus is applied at t = 0 (see text, SOM and fig. S9). (D, E) Individual cells responding to repetitive stimuli at 6 min (D) and 3 min (E) intervals (see fig. S8 for 4 min and 15 min intervals). Shaded regions stimulus ON (10 nM cAMP perfusion for 1 min); white regions stimulus OFF (buffer perfusion only, no cAMP). Cells are set well below the transition point shown in Fig. 2C (separation >1mm; flow rate >4 ml/min).

The results in Figures 2 and 3 indicate that accumulation of extracellular cAMP ([cAMP]_ext) in the population is essential for excitatory and oscillatory cell responses. At low ρ/k, if cells secrete cAMP on average at a constant rate r, then [cAMP]_ext changes according to

$$\frac{\mathrm{d}{[\text{cAMP}]}_{\text{ext}}}{\mathrm{d}t}=\rho r-\frac{k}{V_{\mathrm{T}}}{[\text{cAMP}]}_{\text{ext}}$$ (Eq. 1),

which states that variations in cell density ρ alter the effective synthesis rate of extracellular cAMP, while the rate of dilution k divided by the chamber volume V_T determines how fast extracellular cAMP is removed. Assuming that the system is at steady state in this regime, [cAMP]_ext must be proportional to the parameter ρ/k (eq. S4), and hence Eq. 1 assumes a constant cell secretion rate for cAMP. Isolated cells exposed to extracellular cAMP levels below the threshold concentration of ~500 pM (Fig. 3C), however, display non-negligible excitable dynamics that appear to be stochastic (Fig. 3A and fig. S4). This observation matches well with the sporadic pulses observed experimentally at the population-level (fig. S5), when ρ/k is near the transition point (i.e. ρ/k ~10⁻³ in Fig. 2C). Incorporating first order secretion (23) into Eq. 1 allowed us to compute the effective synthesis rate per monolayer cell density to be r = 5.2 (nM/min) by (eqs. S3 and S8), implying that near the transition point cells should only be able to accumulate extracellular cAMP of less than ~10 pM (eq. S7). Such low concentrations, however, are more than an order of magnitude below the responsive range of a single cell (Fig. 3C) indicating a limitation of the static picture provided by Eq. 1.

At high ρ/k, the firing rate reaches a plateau (~ 1/6 min⁻¹ in Fig. 2C) which cannot be deduced from the observed cell responses to persistent stimuli (Fig. 3C) alone. When isolated cells are given repetitive stimulation of 10 nM cAMP at 6-minute intervals, cells responded in pace with the stimuli (Fig. 3D). However, at shorter intervals the response gradually diminished (see Fig. 3E and fig. S8A), and at longer intervals random bursts appeared spontaneously (fig. S8B). Thus an individual Dictyostelium cell behaves as a resonance filter that selects a stimulus at 6-minute-intervals. In other words, extracellular cAMP needs to be removed for a certain time period in order for cells to respond to further stimuli. Such a time scale is a single-cell level property. The requirement of cAMP removal is consistent with population experiments that we performed in the absence of flow (<1ml/min; Fig. 2B). They clearly demonstrate that synchronized oscillations require removal of extracellular cAMP by extracellular phosphodiesterase (PDE, the enzyme that degrades extracellular cAMP) (figs. S2 and S10A). Together with the observed cytosolic oscillations in cells under prolonged stimulation (Fig. 3B), these observations indicate that besides the time it takes for the extracellular cAMP to return to its original pre-pulse level (a global process mediated by extracellular PDE), there exist additional local mechanisms that monitor time intracellularly before individual cells fully recover their state of excitability.

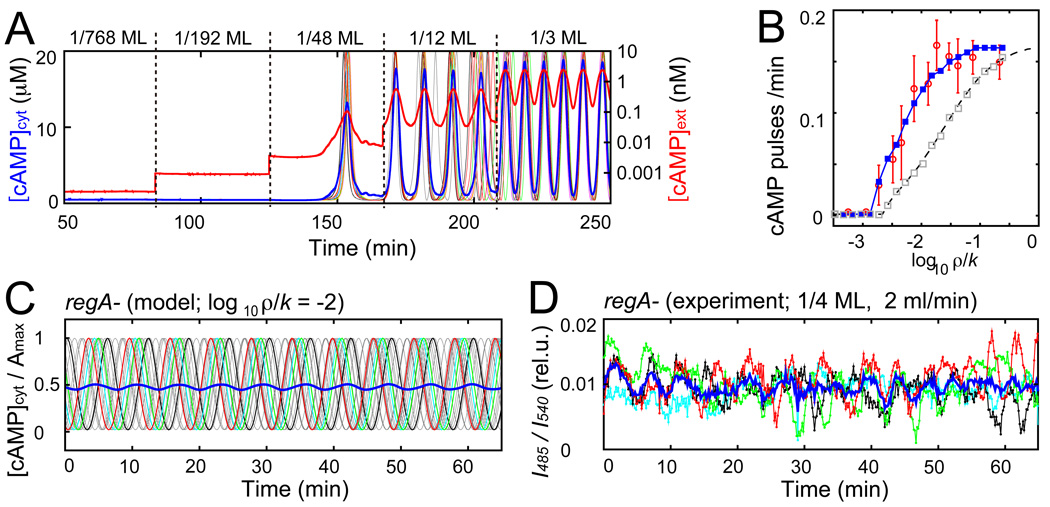
To determine quantitatively the origin of synchronized pulses in the population, we incorporated the observed response behavior into Eq. 1. To this end, the single-cell level dynamics of cytosolic cAMP is described by a phase equation (eqs. S1 and S2; fig. S6A) that reproduces the pulsatile cAMP output observed in Fig. 3 (fig. S6B). When such cellular elements are coupled (eq. S5), the population switches from a quiescent to an oscillatory state at a critical cell density (Fig. 4A). The model can accurately reproduce the frequencies of the synchronized oscillations (Fig. 4B; blue line and red circles) only when the random pulsing observed at sub-nanomolar concentrations (Fig. 3A and fig. S4) is taken into account. Without random pulsing the curve appears slanted and shifts towards higher ρ/k (Fig. 4B; grey). Hence our model confirms the importance of sporadic random firing at the onset of synchronized pulses in the population, as observed experimentally in fig. S5. When extracellular cAMP is at sub-nanomolar concentrations, the probability that a cell is randomly excited increases (Fig. 3A and fig. S4), enhancing the chance for other cells to fire (fig. S6C). A chain reaction of excitation is thus generated that can give rise to synchronized pulses even at concentrations below the threshold (Fig. 4A (1/48ML) and fig. S6C). Thus the question whether specialized cells initiate synchronized pulses is ill posed; the initiation process is inherently collective and stochastic.

Fig. 4.

Dynamical quorum sensing-type transition in a population of excitable/oscillatory switch elements. (A) Representative simulated time courses of average cAMP concentrations (cytosolic [cAMP]_cyt and extracellular [cAMP]_ext in linear and logarithmic scales, respectively). Thin colored lines indicate [cAMP]_cyt in individual cells. Cell densities are raised in incremental steps of 1/768ML, 1/192ML, 1/48ML, 1/12ML, and 1/3ML at k = 5ml/min. (B) Firing rate as a function of ρ/k as predicted by the coupled phase model with (blue line; Eq. S5) or without (grey squares; eq. S5) incorporation of stochastic pulsing. For comparison: experimental data from Fig. 2C (red circle) and mean-field approximation (dashed black line; eq. S6). (C) Model prediction of de-synchronization at elevated cytosolic cAMP levels (A_max and A_bas increased 10 times; eq. S1). [cAMP]_cyt normalized by A_max in individual cells (thin gray lines; four cells are highlighted by colors). Blue line indicates population average. (D) Poorly synchronized population-level oscillations in regA- mutants whose degradation of intracellular cAMP is reduced (1/4 ML; 2mL/min). Colors indicate average signals by cells in four 100µm × 100µm regions separated by ~150µm. Blue line indicates average of the four regions.

Synthesis of intracellular cAMP requires a receptor-mediated activation of adenylyl cyclase ACA (fig. S1, D to G) – the main enzyme responsible for converting ATP to cAMP during this stage of Dictyostelium development. Binding of cAMP to the membrane bound receptor induces production of phosphatidylinositol (3,4,5)-trisphosphate (PIP₃) that recruits an activating factor containing a specific PIP₃-binding domain (PH-domain) to the plasma membrane (24). Given the very small number of extracellular cAMP necessary to elicit a response in cytosolic cAMP (Fig. 3C), the stochastic nature of the pulsing may originate from random binding of cAMP to the membrane-bound cAMP-receptor. However, the threshold value in the response (0.5±0.1 nM in Fig. 3C; blue curve) are an order of magnitude below the affinities of the receptor (22). Since a similar dosage dependence of membrane translocation of a PH-domain containing protein has been observed (25), our input/output relationship most likely reflects the kinetics downstream of the membrane receptors but upstream of PIP₃.

The fact that cells can be oscillatory even at the single cell level in the perfusion setup (Figs. 3B, 3D and 3E) might indicate that the emergence of synchronized oscillations in the population is not a collective phenomenon. However, these cell-intrinsic oscillations only appear when the levels of extracellular cAMP are kept elevated above 1nM (Fig. 3B and fig. S9). Before extracellular cAMP can rise to this level spontaneously in a cell population, synchronized pulses must emerge. In our perfusion experiments, at low ρ/k the population remains in a state where pulses are emitted sporadically. In contrast, when extracellular cAMP is elevated to a sufficiently high level, cells become transiently oscillatory. This occurs at high ρ/k where the pulsing frequency reaches a plateau (Fig. 2C). At that level, pulse-timing is no longer dictated by the occurrence of random pulses in the population, but rather by an oscillatory mechanism at the single-cell level that gates and paces the timing. As a result, the pulses appear regularly at ~6 min intervals (Fig. 2A). One would expect that disruption of intracellular PDE (RegA) (26) should have a strong deleterious effect if these cell-intrinsic oscillatory dynamics involve a feedback regulation via cytosolic cAMP (20). In contrary, if the main effect of disrupting RegA is simply to elevate the overall level of cAMP secreted into extracellular space, regA- cell populations should still be able to oscillate albeit only with partial synchrony (Fig. 4C) because extracellular cAMP levels should almost saturate the dynamic range of the input/output relationship (Fig. 3C and fig. S6B). In agreement with this model prediction, we observe that regA- cells oscillate but they are poorly synchronized (Fig. 4D). Furthermore, since intrinsic oscillations observed at saturating dose of extracellular cAMP are also present in isolated regA-cells (fig. S10B), the newly discovered oscillations at the single cell level do not require a RegA-mediated feedback loop.

Finally, the entire sequence of events in an intact cell population (Fig. 1) beginning from the onset of sporadic firing to determination of the final periodic signaling center can be inferred from the perfusion experiments. The key enzymes that determine the rates of secretion (r) and of cAMP decay (k) in Eq. 1 are ACA and extracellular PDE, respectively (figs. S1, S2 and S10A), both of which are expressed at very low levels but are induced during the first 4 hours following starvation (13, 27). When cAMP slowly begins to accumulate in the extracellular space, initial pulses are randomly elicited due to the stochastic sub-threshold dynamics at the single cell level. While several centers compete for dominance, the results in Figs. 2C and 4B predict that sites which accumulate more extracellular cAMP than others are able to pulse at a higher frequency.

Such sites will entrain other sites that fire less often (10) and therefore survive. Thus, the first site that accumulates enough extracellular cAMP to support the saturating frequency (~6 min period) is the one that is able to become the persistent oscillatory center. This not only allows aggregation of more cells to the same location, but it may also facilitate later development as cAMP is required for cell differentiation (28).

To conclude, the signaling centers in Dictyostelium discoideum are dynamical entities that self-organize in the population. The onset of synchronized pulses occurs by a switch-like response of individual cells to an external threshold concentration. The initiation is highly dynamic and collective, since the threshold and the frequency of the response cannot be attributed solely to those at the single-cell level. As random cells continue to emit pulses sporadically, extracellular cAMP accumulates so that, at the peak of the synchronized pulses, cells become transiently oscillatory. The combination of these two strategies – one global and the other local – may allow cells to first determine the global maximum of extracellular cAMP concentration, and then aggregate as the pulses are now self-sustainable and periodically emitted from such locations.