NMR characterization of general compartment size distributions

Abstract

The influence of molecular diffusion on the nuclear magnetic resonance (NMR) signal can be exploited to estimate compartment size distributions in heterogeneous specimens. Theoretical relationships between the NMR signal intensity at long diffusion times and the moments of a general distribution of isolated pores with characteristic shapes (planar, cylindrical or spherical) are established. A numerical method based on expressing a general diffusion-attenuated NMR signal profile in a series of complete orthogonal basis functions is introduced and subsequently employed to estimate the moments of the compartment size distribution. The results on simulated and real data obtained from controlled water-filled microcapillaries demonstrate the power of the approach to create contrast based not only on the mean of the compartment size but also its variance. The technique can be employed to address a variety of problems such as characterizing distributions of droplet sizes in emulsions and of apparent axon diameters in nerve fascicles.

1. Introduction

In heterogeneous media, one frequently encounters molecules of one kind trapped within isolated compartments of the host medium. For example in porous media, the vacant regions (pores) in a solid matrix may be filled by a fluid. In emulsions, globules of one fluid exist in another immiscible liquid, yielding a distribution of droplets. The physical properties of the resulting heterogeneous medium critically depend on the distribution of pore or globule sizes. Of the numerous methods to measure compartment size distribution, NMR offers significant advantages, probing pore geometry in large domains non-invasively. NMR's exquisite sensitivity to molecular diffusion makes it particularly useful in restricted domains. For example, one approach, originally proposed by Packer and Rees [1], assumes a known statistical distribution of compartment sizes, such as a log-normal distribution, and uses NMR-based molecular displacement measurements to infer the parameters of that distribution. Variants of this approach have been used in examining food products [2, 3], oil suspensions [4, 5], and most recently in characterizing axon diameter distributions in white-matter fibers of the brain [6].

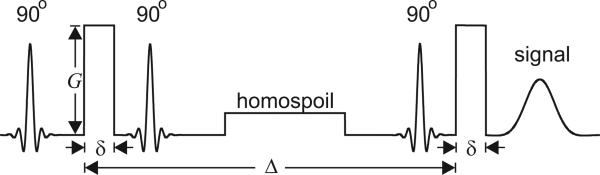
Alternative experimental techniques, exploiting the internal magnetic field induced by susceptibility differences within the porous medium, have also been proposed [7, 8]. However, our approach to determining compartment size distributions involves the sensitization of NMR acquisitions to diffusion via the existence or application of external magnetic field gradients; hence the technique can be employed in the absence of significant susceptibility differences. One such realization of the experiment is depicted in Figure 1, in which a pair of pulsed-field gradients [9] of strength G, duration δ, and separation Δ, are incorporated into a stimulated echo NMR experiment [10].

Figure 1.

The pulsed-field gradient stimulated-echo NMR pulse sequence. The oscillatory shaped radiofrequency pulses rotate the magnetization by 90 degrees. The rectangular pulsed-field gradients encode the displacement of spins.

In this article, we describe a strategy to measure all moments of the compartment size distribution associated with a medium comprising a collection of non-connected pores directly from a single NMR signal attenuation profile, hence obviating the assumed existence [1, 2, 3, 4, 5, 6] of a known parametric size distribution. Compared to other studies that have attempted to bypass the assumption of an underlying parametric distribution [11, 12, 13, 14], our approach does not employ the Gaussian phase approximation, hence it can be used when a significant attenuation of the NMR signal is present. Furthermore, our technique can be used for geometries comprising planar and cylindrical as well as spherical pore shapes albeit a mixture of these pore geometries is not allowed. To this end, theoretical expressions linking the moments of the compartment size distribution to the NMR signal attenuation are derived. Next, we propose to use a complete basis of orthogonal functions to represent the general NMR signal attenuation profiles that makes it possible to estimate the moments of the compartment size distribution accurately and efficiently. We verify these derived expressions and the accuracy of the estimation method via simulations. Finally, we apply the method to real data obtained from controlled distributions of water-filled microcapillaries.

2. Theory

When an ensemble of pores with different sizes are examined via NMR, each pore's contribution to the overall signal is proportional to the number of spins that reside within that pore. In this work, we consider ensembles of parallel plates, coherently oriented cylinders and spheres corresponding to the cases D = 1, 2, and 3, respectively, where D denotes the number of dimensions along which the diffusion process is restricted. The gradients are assumed to be applied perpendicular to the walls. If each pore's size can be characterized by the length, a, then the total signal from the ensemble, as a function of q = (2π)⁻¹γδG, where γ is the gyromagnetic ratio, is given by

$$E\left(q\right)=\frac{{\int }_0^{\infty }da{a}^{D}f\left(a\right)E(q,a)}{{\int }_0^{\infty }da{a}^{D}f\left(a\right)}.$$ (1)

Here E(q, a) is the signal attenuation for a single pore of size a, and f(a) is the pore size distribution function whose features we are interested in extracting. The ensemble average of a quantity X(a) is defined via the relation

$${\langle X\left(a\right)\rangle }_e={\int }_0^{\infty }daf\left(a\right)X\left(a\right).$$ (2)

Clearly, the numerator and denominator in Eq. 1 can be written as 〈a^D E(q, a)〉_e and 〈a^D〉_e, respectively.

Given the E(q) data for the ensemble, estimation of the n-th order moment of the pore size distribution, 〈aⁿ〉_e, is possible by applying an operator ${\mathcal{Q}}_n$ that satisfies the conditions

$${\mathcal{Q}}_{n}E\left(q\right)=\frac{1}{{\langle a^D\rangle }_e}{\int }_0^{\infty }da{a}^{D}f\left(a\right){\mathcal{Q}}_{n}E(q,a),$$ (3)

and

$${\mathcal{Q}}_{n}E(q,a)={\zeta }_n{a}^{n-D},$$ (4)

where ζ_n is a constant. When these conditions are met, the n-th moment of the pore size distribution is given by

$${\langle a^n\rangle }_e=\frac{{\langle a^D\rangle }_e}{{\zeta }_n}{\mathcal{Q}}_{n}E\left(q\right).$$ (5)

Therefore, the problem of calculating all moments of the pore size distribution is reduced to finding a class of operators ${\mathcal{Q}}_n$ that satisfy Eqs. 3 and 4 for n = 0, 1, 2, . . . and n ≠ D.

In this article, we shall consider the long diffusion time $(D_0\Delta \gg a_{\max }^2)$ and the narrow pulse $(D_0\delta \ll a_{\min }^2)$ regimes, where D₀ is the bulk diffusivity of the fluid within the compartments, and a_max and a_min are, respectively, the sizes of the largest and smallest compartments in the ensemble. Under these experimental conditions, three different operators, denoted by $\mathcal{I},\mathcal{D}$, and $\mathcal{K}$ provide all moments of a general pore size distribution. These operators are defined through their action on an arbitrary function F(q) to be

$${\mathcal{R}}_{k}F\left(q\right)={\beta }_k{\int }_0^{\infty }dq{q}^{k-1}F\left(q\right),k=1,2,\dots ,D,$$ (6)

where β₁ = 2, β₂ = 2π, and β₃ = 4π,

$${\mathcal{D}}_{l}F\left(q\right)={\phantom{\mid }\frac{{(-1)}^l}{{\left(2\pi \right)}^{2l}}\frac{d^{2l}F\left(q\right)}{d{q}^{2l}}\mid }_{q=0},l=1,2,3,\dots ,$$ (7)

and

$${\mathcal{K}}_{m}F\left(q\right)={\int }_0^{\infty }dq{\left(\frac{1}{q}\frac{d}{dq}\right)}^{m}F\left(q\right),m=1,2,3,\dots .$$ (8)

To build a physical understanding of these operators, when applied on an arbitrary NMR signal attenuation profile E(q), we recall that E(q) can be envisioned to be the characteristic function of a displacement distribution because of the relationship [15, 16, 17]

$$P\left(x\right)=\int dq{e}^{i2\pi qx}E\left(q\right),$$ (9)

where P(x) is an ensemble-average propagator indicating the likelihood that the spins will undergo a displacement, x, along the gradient direction. More generally, similar definitions for higher dimensional spaces are possible, in which case q and x will be replaced by vectors. The reader is referred to [18] for discussions pertaining to the relations between propagators in different dimensional spaces.

For example, using the three-dimensional version of Eq. 9, the action of the operator ${\mathcal{R}}_3$ in isotropic environments can be shown to yield the return-to-origin probability [19]. Similarly, the result obtained by the application of ${\mathcal{R}}_2$ on axially symmetric environments, when the gradient orientation is perpendicular to the symmetry axis, will yield a return-to-symmetry-axis probability. Finally, the operator ${\mathcal{R}}_1$ reveals the probability that the spins will return to their original plane whose normal is parallel to the gradient direction. The class of operators ${\mathcal{D}}_l$ has a well-defined meaning as well. Taking the Fourier transform of both sides in Eq. 9, and expanding the exponential in a Taylor series, it is straightforward to show that the operator ${\mathcal{D}}_l$ returns the 2l-th order moment of displacements, 〈x^2l〉. It is not clear if the values returned by the operators ${\mathcal{K}}_m$ can be interpreted in a similar way. However, as we show below, they complement the information obtained from the preceding operators.

We now consider ensembles of parallel plates, cylindrical and spherical pores, and apply the above operators to the predicted NMR signal attenuation profiles. The strategy we employ involves the application of ${\mathcal{R}}_D$, which yields the denominator in Eq. 1. Subsequently, all of the remaining operators are applied, each of which returns one of the remaining moments.

2.1. Parallel Plates (D = 1)

We shall start by considering an array of parallel slabs (D = 1) with variable spacings between consecutive plates whose normals are along the gradient direction. The NMR signal attenuation for a single pore with separation L is given by [20]

$$E_1(q,L)=\frac{{\sin }^2\left(\pi qL\right)}{{\left(\pi qL\right)}^2},$$ (10)

where the total NMR signal can be obtained by inserting this expression into Eq. 1 with D = 1, and a = L. Applying the operator ${\mathcal{R}}_1$, followed by the other operators $\mathcal{D}$ and $\mathcal{K}$, all moments of the distribution of separations are obtained to be

$${\langle L\rangle }_e={\left({\mathcal{R}}_1{E}_1\left(q\right)\right)}^{-1}$$ (11a)

$${\langle L^{2l+1}\rangle }_e=(l+1)(2l+1){\langle L\rangle }_e{\mathcal{D}}_l{E}_1\left(q\right)$$ (11b)

$${\langle L^{2m}\rangle }_e=\frac{{(-1)}^m(2m+1)m!}{{\pi }^{2m}{2}^{m-1}}{\langle L\rangle }_e{\mathcal{K}}_m{E}_1\left(q\right).$$ (11c)

2.2. Cylinders (D = 2)

Next, we consider a pack of coherently oriented cylindrical tubes (D = 2) of varying radii. The NMR signal for a single tube of radius r₀ is given by [21]

$$E_2(q,r_0)={\left(\frac{J_1\left(2\pi q{r}_0\right)}{\pi q{r}_0}\right)}^2.$$ (12)

A general distribution of cylinder radii, f(r₀), can be incorporated into Eq. 1, with D = 2, and a = r₀. Starting with the operator ${\mathcal{R}}_2$, all operators are applied on the resulting NMR signal attenuation, E₂(q), revealing all moments of the distribution through the relationships

$${\langle r_0^2\rangle }_e={\left(\pi {\mathcal{R}}_2{E}_2\left(q\right)\right)}^{-1}$$ (13a)

$${\langle r_0\rangle }_e=\frac{3{\pi }^2}{16}{\langle r_0^2\rangle }_e{\mathcal{R}}_1{E}_2\left(q\right)$$ (13b)

$${\langle r_0^{2l+2}\rangle }_e=\frac{(l+1)!(l+2)!}{2(2l-1)!!(2l+1)!!}{\langle r_0^2\rangle }_e{\mathcal{D}}_l{E}_2\left(q\right)$$ (13c)

$${\langle r_0^{2m+1}\rangle }_e=\frac{{(-1)}^m(2m+1)!!(2m+3)!!}{2^{5m+3}{\pi }^{2m-2}m!}{\langle r_0^2\rangle }_e{\mathcal{K}}_m{E}_2\left(q\right).$$ (13d)

2.3. Spheres (D = 3)

The signal for a single spherical pore (D = 3) of radius R₀ is given by [20]

$$E_3(q,R_0)={\left[\frac{3}{{\left(2\pi q{R}_0\right)}^2}\left(\frac{\sin \left(2\pi q{R}_0\right)}{2\pi q{R}_0}-\cos \left(2\pi q{R}_0\right)\right)\right]}^2.$$ (14)

For an ensemble of spheres whose radii are distributed according to f(R₀), all moments of this size distribution are obtained via the application of the operators starting with ${\mathcal{R}}_3$. The moments of f(R₀) are then given by

$${\langle R_0^3\rangle }_e=\frac{3}{4\pi {\mathcal{R}}_3{E}_3\left(q\right)}$$ (15a)

$${\langle R_0\rangle }_e=\frac{8\pi }{9}{\langle R_0^3\rangle }_e{\mathcal{R}}_2{E}_3\left(q\right)$$ (15b)

$${\langle R_0^2\rangle }_e=\frac{5}{3}{\langle R_0^3\rangle }_e{\mathcal{R}}_1{E}_3\left(q\right)$$ (15c)

$${\langle R_0^{2l+3}\rangle }_e=\frac{2l^3+13l^2+27l+18}{9}\frac{2l+1}{2^{2l+1}}{\langle R_0^3\rangle }_e{\mathcal{D}}_l{E}_3\left(q\right)$$ (15d)

$${\langle R_0^{2m+2}\rangle }_e=\frac{(m+1)!(2m+3)(2m+5)}{{(-1)}^m{2}^{3m-1}9{\pi }^{2m}}{\langle R_0^3\rangle }_e{\mathcal{K}}_m{E}_3\left(q\right).$$ (15e)

The derivation of the above expressions for the moments is outlined in Appendix A.

3. Estimation of the moments from sampled data

The above derivations establish the relationships between the moments of the compartment size distribution and a general NMR signal attenuation profile, E(q), which is inherently assumed to be a continuous function that extends to infinity. Since the real data is sparsely sampled and truncated along the q-axis, a method that analytically represents and approximates the discrete data would be useful. However, traditional methods, such as simple function fitting, fail to describe general E(q) profiles, while cumulant expansions suffer from a finite radius of convergence and are very inaccurate at large q-values. Instead, we employ the recently introduced one-dimensional simple harmonic oscillator based reconstruction and estimation (1D-SHORE) method [22], which overcomes these diffculties and is outlined here.

3.1. 1D-SHORE technique

In 1D-SHORE approach, the diffusion-weighted NMR signal intensity is expressed as

$$S\left(q\right)=\sum _{n=0}^{N-1}{a}_n^{\prime }{\varphi }_n(u,q),$$ (16)

with

$${\varphi }_n(u,q)=\frac{i^{-n}}{\sqrt{2^{n}n!}}{e}^{-2{\pi }^2{q}^2{u}^2}{H}_n\left(2\pi uq\right),$$ (17)

where H_n(x) is the n-th order Hermite polynomial and u is a characteristic length. The NMR signal attenuation, E(q) = S(q)/S(0), can also be expressed in this basis as

$$E\left(q\right)=\sum _{n=0}^{N-1}{a}_n{\varphi }_n(u,q),$$ (18)

where

$$a_n=\frac{a_n^{\prime }}{S_0},$$ (19)

and S₀ = S(0) is the non-diffusion-weighted signal, which can be estimated from the coefficients $a_n^{\prime }$:

$$S_0=\sum _{n=0}^{N-1}{a}_n^{\prime }{\varphi }_n(u,0)=\sum _{n=0,2,4,\dots }^{N-1}\frac{\sqrt{n!}}{2^{n∕2}(n∕2)!}{a}_n^{\prime }.$$ (20)

The functions ϕ_n are based on the well-known eigenfunctions of the quantum-mechanical Hamiltonian for the simple harmonic oscillator (SHO), which form a complete orthogonal basis for the space of square-integrable functions [23]. However, our definitions of the eigenfunctions are slightly different from their forms as commonly used in quantum mechanics. Specifically, our basis is not normalized, but the scaling is such that when diffusion is Gaussian, and u² = 2D₀(Δ−δ/3) = 〈x²〉, the coefficients are given by a_n = δ_n0, where δ_ij is the Kronecker delta and D₀ is the diffusion coefficient. Moreover, the phase convention dictated by the factor i⁻ⁿ in Eq. 17 ensures that the real and imaginary parts of E(q) are symmetric and antisymmetric, respectively—a necessary condition for the propagator, P(x) to be real when a_n are real. Despite these minor differences from the basis used in quantum mechanics, our basis functions still satisfy the relationship

$$\mathcal{A}{\varphi }_n(u,q)=\{\begin{array}{cc}0\hfill & ,n=0\hfill \\ \sqrt{n}{\varphi }_{n-1}(u,q)\hfill & ,n\ge 1\hfill \end{array}\phantom{\}},$$ (21)

where $\mathcal{A}$ is the “lowering operator” defined by

$$\mathcal{A}=\frac{i}{\sqrt{2}}\left(2\pi uq+\frac{1}{2\pi u}\frac{d}{dq}\right).$$ (22)

We would like to note that Assemlal et al. [24] have represented the q-space signal in a basis of Gaussian-Laguerre functions and subsequently showed that these functions can be related to the basis functions we have employed in this study.

3.2. Implementation

The problem of transforming a discrete set of measured signals into a set of coefficients can be cast as a set of linear equations. Given an M-dimensional vector of signal values, S, with components S_m = S(q_m), an M × N dimensional matrix, Q, whose components are given by Q_mn = ϕ_n(u, q_m), can be computed. The problem is reduced to a matrix equation S = Qa′, where a′ is the N-dimensional vector of $a_n^{\prime }$ coefficients. In our implementation, we solve this equation by computing the pseudoinverse of Q using singular-value decomposition [25]. Next, S₀ is computed using Eq. 20, which is inserted into Eq. 19 to determine the coefficients a_n.

Note that the above estimation scheme assumes a prior estimate of u. Although the completeness of the basis functions ensures the convergence of the estimates for any u, the rate of this convergence may depend on the particular choice of u. Therefore, in our implementation, we first estimate a maximum value for u obtained from the first few points of S(q) data under the assumption of Gaussianity of the signal. The basis functions are designed such that, when the signal is Gaussian, all coefficients except a₀ vanish yielding the expected behavior E(q) = exp(−2π²q²u²). Starting from this estimate of the maximum u, we gradually reduce the u-value. At each value of u, we estimate the a_n coefficients using the scheme described above and compute the signal attenuation values at the data points, which will be denoted by E^est(u, q). Subsequently, the mean-squared error defined by

$$∊\left(u\right)=\frac{1}{M}\sum _{i=1}^M{(E^{\mathrm{est}}(u,q_i)-E^{\mathrm{data}}\left(q_i\right))}^2,$$ (23)

where E^data(q_i) are the original data points, is computed. The search for the optimal u continued until ∊(u) falls below 1 × 10⁻¹⁵, or a local minimum is achieved, whichever comes first. The last set of u and a_n values are retained for subsequent analysis.

3.3. Actions of the $\mathcal{R}$, $\mathcal{D}$, and $\mathcal{K}$ operators in the SHO basis

Once the a_n coefficients and u are estimated as described above, the actions of the compartment size distribution operators are conveniently expressed in the SHORE basis via the relations

$${\mathcal{R}}_{1}E\left(q\right)=\frac{1}{\sqrt{2\pi }u}\sum _{n=0,2,\dots }^{N-1}\frac{{(-1)}^{n∕2}\sqrt{n!}}{2^{n∕2}(n∕2)!}{a}_n$$ (24a)

$${\mathcal{R}}_{2}E\left(q\right)=\frac{1}{2\pi u^2}\sum _{k=0,2,\dots }^{N-1}\frac{{(-1)}^{k∕2}}{(k-1)!!}\sum _{l=0,2,\dots }^{N-k-1}\frac{2^{(k-l)∕2}\sqrt{(k+l)!}}{(l∕2)!}{a}_{k+l}$$ (24b)

$${\mathcal{R}}_{3}E\left(q\right)=\frac{1}{\sqrt{2}{\pi }^2{u}^3}\sum _{n=0,2,\dots }^{N-1}\sqrt{n!}{a}_n\sum _{m=0,2,\dots }^n\frac{{(-1)}^{(m-n)∕2}{2}^{n-3m∕2}\Gamma \left(\frac{n-m+3}{2}\right)}{(n-m)!(m∕2)!}$$ (24c)

$${\mathcal{D}}_{l}E\left(q\right)=u^{2l}\sum _{k=0,2,\dots }^{N-1}\frac{(k+2l-1)!!}{k!}\sum _{s=0,2,\dots }^{N-k-1}{(-1)}^{s∕2}\frac{\sqrt{2^{k-s}(k+s)!}}{(s∕2)!}{a}_{k+s}$$ (24d)

$${\mathcal{K}}_{1}E\left(q\right)=-2{\pi }^2{u}^2{\mathcal{R}}_{1}E\left(q\right)+{\left(2\pi \right)}^{3∕2}u\sum _{n=2,4,\dots }^{N-1}\sqrt{n!}{a}_n\sum _{m=0,2,\dots }^{n-1}\frac{{(-1)}^{(m+n)∕2}{2}^{-m∕2}}{(n-m-1)\left(\frac{m}{2}\right)!(\frac{n-m}{2}-1)!}.$$ (24e)

The derivations of the above expressions are straightforward but tedious and left out for brevity. All derivations involved writing the Hermite function in the definition of the basis functions as a power series and then carrying out the integrations term-by-term. Note that the SHO basis has the remarkable property that the lowering operator, $\mathcal{A}$, naturally arises within the integrand of the definition for the ${\mathcal{K}}_m$ operator. Therefore, the identity in Eq. 21 was used in the derivation of Eq. 24eK. The action of ${\mathcal{K}}_m$ for m > 1 was not evaluated because they concern high-order moments of the compartment size distribution, which are unlikely to be feasible or useful in practice.

4. Results

4.1. Simulations

To validate the derived expressions for the moments and to assess the accuracy of the 1D-SHORE technique, we simulated distributions of planar, cylindrical, and spherical pores. We assumed that the pore sizes were distributed according to a beta density function because, unlike in the case of more popular functions such as lognormal or gamma distributions, the beta density function is able to accommodate negatively skewed distributions. Here we include the results obtained for cylindrical pores for brevity. To ensure that the radii of cylinders are distributed according to a beta distribution, the interval between 0 and 20 μm was divided into 10,000 segments. The E(q) profile corresponding to each of these radii was computed, then multiplied by the value of the beta distribution,

$$f(r_0;\alpha ,\beta )=\frac{{(r_0∕C)}^{\alpha -1}{(1-r_0∕C)}^{\beta -1}}{CB(\alpha ,\beta )}$$ (25)

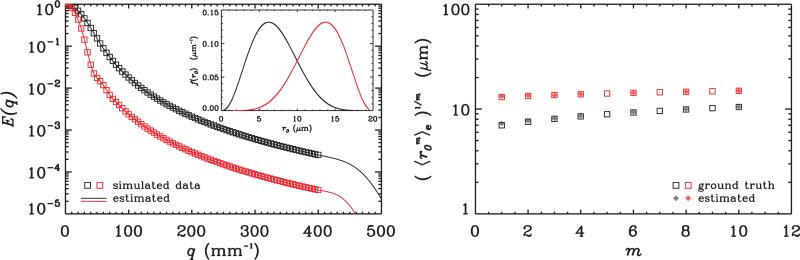
at that radii, where B(α, β) is the beta function and C is the maximum value for the radius, taken to be 20 μm in the simulations. Two such distributions of radii are considered one with (α, β) = (3.5, 6.5), and the other with (α, β) = (6.5, 3.5). The inset on the left panel of Figure 2 illustrates these two probability distribution functions where the first distribution is drawn in black while the second distribution is depicted in red. A total of 81 data points were generated for each ensemble of pores, and the resulting E(q) profiles are illustrated on the left panel of Figure 2. The moments were computed via the 1D-SHORE methodology using Eqs. 24a-24e and 13a-13d. The estimated moments as well as the ground truth values obtained from Eq. 25 are plotted on the right panel of Figure 2. It is clear that excellent agreement is achieved between the predicted and estimated values for the moments in both cases. Obviously, the first moment yields the mean value, i.e., μ = 〈r₀〉_e, while the standard deviation of the ensemble can be obtained via the expression $\sigma ={({\langle r_0^2\rangle }_e-{\mu }^2)}^{1∕2}$. For the first distribution, the predicted values were 7.0 ± 2.9 μm, where the estimates yielded 7.3 ± 2.6 μm. For the second distribution, the predicted and estimated values were 13.0 ± 2.9 μm and 13.2 ± 2.3 μm, respectively.

Figure 2.

The left panel shows the beta distributions simulated (inset) and the E(q) profiles calculated for ensembles of cylinders whose radii are distributed according to those density functions. The right panel depicts the corresponding moments where the hollow squares show the analytical values while the moments estimated from the simulated E(q) profiles are depicted with solid diamonds. The black curves and symbols correspond to the beta distribution with positive skewness (α = 3.5, β = 6.5) whereas the red color is used for the negatively skewed distribution (α = 6.5, β = 3.5).

It may be possible to estimate the higher-order descriptors of the underlying compartment size distribution as well. For example, the skewness of the distribution can be computed via ${\gamma }_1={\sigma }^{-3}({\langle r_0^3\rangle }_e-3\mu {\sigma }^2-{\mu }^3)$. Its expected values are 0.35 and −0.35 for the two distributions. The estimates from the moments yielded γ₁ values of 0.46 and −3.41. Clearly, although the moments are very accurate, measures that depend on the higher-order differences between these moments are not. Therefore, we expect that these higher-order descriptors cannot be reliably estimated from real data though the method performs reasonably well for the mean and standard deviation.

4.2. Experiments on size distribution phantoms

All experiments were performed on an 8.4 T Bruker NMR spectrometer equipped with a Micro5 probe capable of producing gradient strengths up to 1900 mT/m in each direction. The preparation of the size distribution phantoms was described in detail in Ref. [26]. Briefly, hollow microcapillaries with different inner diameters (ID) of 10±1, 13±1, 17±1, 19±1, 20±1, 21±1, or 29±1 μm (Polymicro Technologies, Phoenix, AZ, USA) were immersed in water for several days for filling. Then, one phantom comprising only 19±1 μm tubes (SD000) and three size distribution phantoms (SD001, SD002, and SD003) were prepared by mixing different sized microcapillaries in one NMR tube. The size distribution phantoms were designed to have variations in both the mean diameter and the breadth of the distributions. The microcapillaries were carefully counted to ensure an accurate ratio of fibers needed in each specimen (the volumetric ratios can be found in detail in Table 1 in Ref. [26]. Note that the microcapillaries were packed into a 4 mm glass sleeve, which was then inserted into a 5 mm NMR tube. The 5 mm NMR tube was aligned with the main axis parallel to the z-direction of the NMR magnet. Typical line widths of 4-20 Hz were obtained after shimming for all size distribution phantoms. Pulsed-field gradient experiments were performed using the stimulated echo sequence with the following parameters: 48 q-values were collected with a maximum gradient strength of 1600 mT/m and with Δ/δ=150/3 ms, resulting in a maximum q-value of 204.3 mm⁻¹ and with a number of scans of 32.

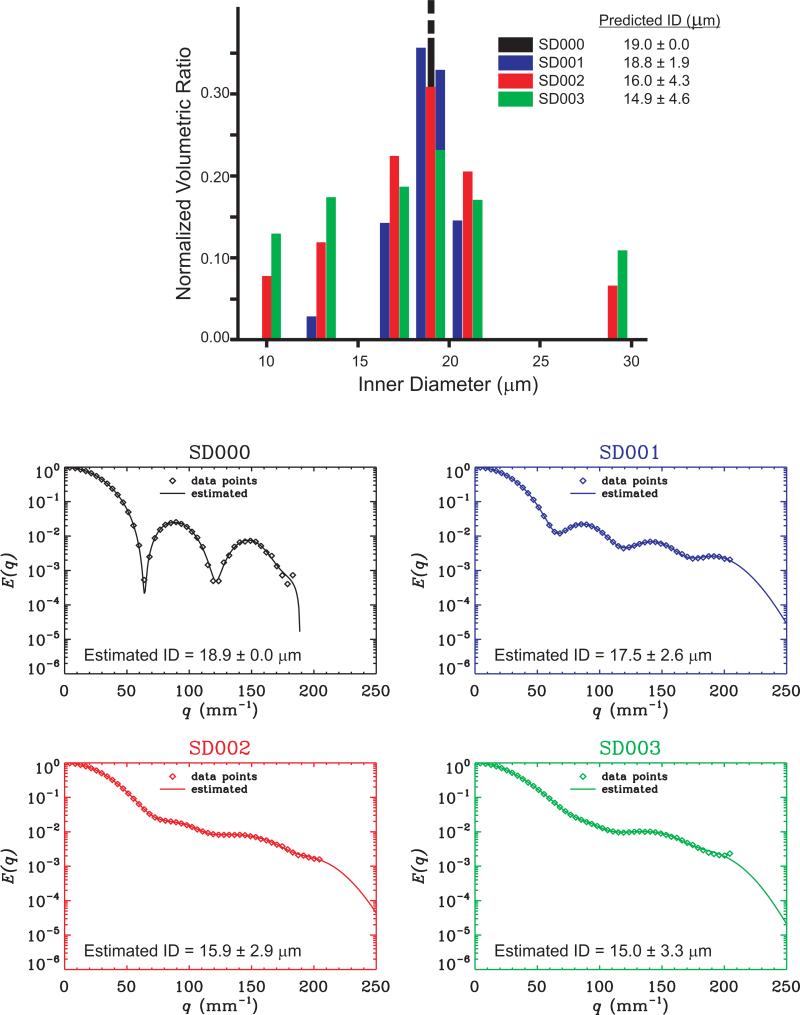
The top panel of Figure 3 illustrates the inner diameter distributions weighted by the number of spins that reside within tubes of their respective IDs, and the predicted ID values. Note that these values are obtained by assuming that the nominal ID values provided by the manufacturer are correct. Previous experiments in similar microcapillaries [27, 28, 29, 30] have demonstrated that there may be some global offset in the actual ID, while no evidence was found to suggest a significant spread within a specimen prepared from tubes of the same ID. Therefore, the standard deviation values of 1 μm reported by the manufacturer seems to represent the uncertainty rather than the variation within one specimen. On the other hand, the standard deviations that are tabulated in Figure 3 quantify the spread of the distributions. Therefore, in the SD000 specimen, we report this value to be 0. We would like to stress that the predicted values may exhibit some inaccuracy due to any offset in the actual ID values, and because some capillaries may be partially filled with water.

Figure 3.

The top panel shows the histograms illustrating the composition of the four different specimens of water-filled microcapillaries. Each color represents one of these specimens. The SD000 specimen contains nothing but the 19 μm tubes. The corresponding real NMR data and the 1D-SHORE fit to them are depicted in the four panels below.

Figure 3 also demonstrates the real data and the 1D-SHORE fit to them. All fits appear to be accurately approximating the signal attenuation curves, and the extrapolations seem to be acceptable. The mean and standard deviation estimates obtained using the theoretical framework introduced in this study are overlaid on the graphs. In the SD000 specimen, the μ² value was very slightly larger than ${\langle r_0^2\rangle }_e$. This observation is consistent with our predicted value of 0 for the standard deviation. The deviations between the predicted and estimated values may be due to the effects discussed above. However, comparing the results for different phantoms, it is clear that the trends in the mean and standard deviation values are consistent with the trends in their predicted values. Therefore, we conclude that it may be possible to create contrast based on the mean and standard deviation values of compartment size distributions using the methodology of this study.

5. Discussion and Conclusion

Accurate estimates of the moments are possible when the narrow diffusion gradient pulse duration (δ) and long pulse separation (Δ) conditions are met. Further, a relatively dense sampling of q-values, large enough to create a significant attenuation of the NMR signal, is necessary. These conditions can be met, for example, in the fringe field of superconducting magnets, or in currently available low-cost mobile NMR systems. When the signal is acquired in a more traditional setting that involves a homogeneous static magnetic field, pulsed-field gradients can be employed to sensitize the signal to diffusion. In such experiments, the long-Δ condition is usually simple to fulfill for microscopic pores. However, it may be more challenging to meet the short-δ condition, the violation of which is expected to yield an underestimation of the moments. This deviation introduced by the diffusion pulse duration is expected to compete against the effect due to the finite range of q-values sampled. Therefore, the value for the mean compartment size may be overestimated or underestimated depending on the experimental design and the underlying pore size distribution.

A similar situation may arise when the surface relaxivity of the restricting walls, which is ignored by our method, is significant. In such environments, molecules may lose their magnetization when they get in contact with the walls. Since such collisions occur more frequently within smaller pores, their contribution to the aggregate signal may be reduced, hence introducing a bias towards larger estimates for the pore size. This effect is expected to be significant when the specimen comprises a broad size distribution and very small compartments. A competing effect becomes apparent when the signal attenuation for a single pore is considered. Although surface relaxation effects tend to attenuate the true signal, the signal attenuation value, E(q), may be increased especially at smaller q-values [31]. In some cases, this effect may act against the effect of surface relaxation mentioned earlier.

As mentioned in the Introduction, this formalism can be employed to characterize compartment size distributions when the pores are isolated. As such, the method can be applied readily to study specimens such as emulsions and many food products. However, in more complex environments such as axonal fiber bundles in white-matter in the nervous system, the accuracy of the results provided by the method needs to be investigated. One particular concern is the presence of extracellular medium in white-matter. In some studies aiming to characterize axon diameter distributions, diffusion of water molecules in the interstitial space has been assumed to be Gaussian [6]. If this assumption is to be employed, the Gaussian component can be removed from the signal profile [32] prior to the estimation of the moments using the introduced technique. For very densely packed cylindrical fibers, the space between the cells can be assumed to be isolated pores as well. Since the size of these “pores” scales with the size of the fibers, the estimated moments can still be used to create contrast that depends on the features of the underlying fiber diameter distribution.

Note that we did not attempt to recover the distribution function from its moments in this study. However, we note that this problem, commonly referred to as the “classical moment problem” is well-studied [33, 34, 35] yet tricky [36], and care must be exercised in such an endeavor. Nonetheless, we recognize that much can be learned about the underlying pore size distribution from an examination of its first few moments.

In conclusion, we presented a method that yields all moments of a general compartment size distribution uniquely from a single NMR signal attenuation profile, E(q), without the need to solve an ill-conditioned problem, invoke an underlying parametric compartment size distribution, or employ empirical statistical methods [37]. This formalism provides new insight into the relations between the features of a compartment size distribution and the NMR signal obtained from it. It is clear that different characteristics of diffusion, such as zero-displacement probabilities and the moments of molecular displacements, lead to different moments of the compartment size distribution. Further, these associations are different for pore spaces of different dimensionality.

Appendix A. The actions of ${\mathcal{R}}_k$, ${\mathcal{D}}_l$, and ${\mathcal{K}}_m$

In the derivation of the expressions for the moments (Eqs. 11a-11c, 13a-13d, 15a-15e,), the values returned by the operators ${\mathcal{R}}_k$ are obtained by evaluating the corresponding integrals in Eq. 6. The action of the operators ${\mathcal{D}}_l$ are given by calculating the moments of the average propagator evaluated using Eq. 7.

Unlike in the cases of ${\mathcal{R}}_k$ and ${\mathcal{D}}_l$ however, the action of the operators ${\mathcal{K}}_m$ is nontrivial. Here, we provide a sketch of the derivations of Eqs. 11c, 13d and K15e, which are all obtained by applying the operator ${\mathcal{K}}_m$ on the NMR signal attenuation functions.

For the purposes of the derivation, we redefine the pore size (a) as equal to L, 2r₀ and 2R₀ for the cases of parallel plates (D = 1), cylinders (D = 2) and spheres (D = 3), respectively. Then, we can define a useful dimensionless variable v = πqa. Note that both a and v are different for different values of D. However, we do not include D in a subscript for brevity. For all three geometries considered, the NMR signal attenuation from a single pore of size a is given by the unified expression

$$E_D(v,a)=F_D{\left(v\right)}^2,$$ (A.1)

where

$$F_D\left(v\right)=C_D{v}^{-D∕2}{J}_{D∕2}\left(v\right),$$ (A.2)

with C₁= (π/2)^1/2, C₂ = 2, and C = (9π/2)^1/2. Note that the following relationship holds [38]

$${\left(\frac{1}{v}\frac{d}{dv}\right)}^n{F}_D\left(v\right)=C_D{(-1)}^n{v}^{-n-D∕2}{J}_{n+D∕2}\left(v\right).$$ (A.3)

Applying the operator ${\mathcal{K}}_m$ on both sides of Eq. A.1, we obtain

$${\mathcal{K}}_m{E}_D(v,a)={\left(\pi a\right)}^{2m-1}{\int }_0^{\infty }dv{\left(\frac{1}{v}\frac{d}{dv}\right)}^m{F}_D{\left(v\right)}^2.$$ (A.4)

The integrand in the above expression can be expanded in a binomial series. Along with Eq. A.3, this procedure yields

$${\mathcal{K}}_m{E}_D(v,a)={(-1)}^m{C}_D^2{\left(\pi a\right)}^{2m-1}\sum _{k=0}^m\frac{m!}{k!(m-k)!}{I}_{kmD},$$ (A.5)

where

$$I_{kmD}={\int }_0^{\infty }dv{v}^{-m-D}{J}_{k+D∕2}\left(v\right)J_{m-k+D∕2}\left(v\right)=\frac{(m+D-1)!}{(2m+2D-1)!!\Gamma (k+\frac{D+1}{2})\Gamma (m-k+\frac{D+1}{2})}.$$ (A.6)

Evaluating the sum in Eq. A.5 and replacing C_D, a and v with their values for D = 1, 2, 3, one obtains the expressions

$${\mathcal{K}}_m{E}_1(q,L)=\frac{{(-1)}^m{\pi }^{2m}{2}^{m-1}}{(2m+1)m!}{L}^{2m-1}$$ (1.7a)

$${\mathcal{K}}_m{E}_2(q,r_0)=\frac{{(-1)}^m{\pi }^{2m-2}{2}^{5m+3}m!}{(2m+1)!!(2m+3)!!}{r}_0^{2m-1}$$ (1.7b)

$${\mathcal{K}}_m{E}_3(q,R_0)=\frac{{(-1)}^{m}9{\pi }^{2m}{2}^{3m-1}}{(m+1)!(2m+3)(2m+5)}{R}_0^{2m-1}.$$ (1.7c)

Applying the operator ${\mathcal{K}}_m$ on both sides of Eq. 1 and using the above equations enables us to establish the relations in Eqs. 11c, 13d, and 15e.