Multivariate Exponential Survival Trees And Their Application to Tooth Prognosis

SUMMARY

This paper is concerned with developing rules for assignment of tooth prognosis based on actual tooth loss in the VA Dental Longitudinal Study. It is also of interest to rank the relative importance of various clinical factors for tooth loss. A multivariate survival tree procedure is proposed. The procedure is built on a parametric exponential frailty model, which leads to greater computational efficiency. We adopted the goodness-of-split pruning algorithm of LeBlanc and Crowley (1993) to determine the best tree size. In addition, the variable importance method is extended to trees grown by goodness-of-fit using an algorithm similar to the random forest procedure in Breiman (2001). Simulation studies for assessing the proposed tree and variable importance methods are presented. To limit the final number of meaningful prognostic groups, an amalgamation algorithm is employed to merge terminal nodes that are homogenous in tooth survival. The resulting prognosis rules and variable importance rankings seem to offer simple yet clear and insightful interpretations.

1. Introduction

Accurate assignment of tooth prognosis is important to dental clinicians for several reasons. Firstly, it is necessary for the periodontist to devise an appropriate periodontal treatment plan to eliminate local risk factors and halt the progression of periodontal destruction. Secondly, a general dentist needs an accurate tooth prognosis in order to determine the feasibility for the long-term success of any extensive restorative dental work, such as endodontic therapy (root canal), multiple crowns, or fixed bridges, all of which can be prohibitively expensive, especially if the underlying periodontal outlook for the teeth involved is questionable. Lastly, insurance companies are increasingly relying upon various indicators of tooth prognosis to determine the cost-effectiveness of benefits paid for particular procedures.

The ultimate outcome for judging a tooth’s condition at any given time is the probability that the tooth will survive in a state of comfort, health, and function in the foreseeable future. Unfortunately, no universal system for assignment of tooth prognosis currently exists. Hence, the assessment of a tooth’s condition can vary widely among dental professionals. Typically, a dental clinician will record and weigh a myriad of commonly taught clinical factors in the process of assigning a prognosis. The relative importance that a practitioner assigns to each factor in assessing a tooth’s condition is based upon the clinician’s training, past clinical experience, and the technical expertise of that particular dentist in treating any condition or pathology present. The subjective nature of this sort of tooth assessment presents difficulty not only for patients, insurance companies, and other third-party payment systems in determining the cost-effectiveness of treatment, but it also creates confusion among dentists since no clear, objective, evidence-based standards have ever been established.

Since teeth within a person are naturally correlated, the resultant data involve multivariate survival times, which require multivariate extensions of established statistical methodology to accurately develop criteria for assignment of tooth prognosis. In addition, predictors of tooth loss include tooth-level factors, such as the presence of calculus or a large amalgam restoration; subject-level factors, such as smoking, poor oral hygiene, and diabetes; and factors that can be considered on both a patient level and a tooth level, such as alveolar bone loss or plaque.

Previous studies investigating tooth prognosis have focused on assessing which clinical factors are statistically significant in predicting tooth loss as a result of periodontal disease. For instance, in a longitudinal study of 100 well-maintained periodontal patients, McGuire and Nunn (1996a, 1996b) found that many commonly taught clinical factors are significantly associated with tooth loss from periodontal disease. In addition, periodontal prognosis based on clearly defined, objective criteria were also significant predictors of tooth loss from periodontal disease. However, assigned periodontal prognosis failed to accurately account for a tooth’s future condition in many cases.

The tree-based method has a nonparametric flavor, making few statistical assumptions. Among its many other attractive features, the hierarchical tree structure automatically groups observations with meaningful interpretation, which renders it an excellent research tool in medical prognosis or diagnosis. Tree-based methods for univariate (or uncorrelated) survival data have been proposed by many authors. See, for example, Gordon and Olshen (1985), Ciampi et al. (1986), Segal (1988), Butler et al. (1989), Davis and Anderson (1989), and LeBlanc and Crowley (1992, 1993). More recently, multivariate (or correlated) survival tree methods have also been proposed. In particular, Su and Fan (2004) and Gao, Manatunga, and Chen (2004) proposed procedures that make use of the semi-parametric frailty model developed by Clayton (1978) and Clayton and Cuzick (1985).

The Dental Longitudinal Study (DLS) contains a large database of subjects from various socioeconomic backgrounds and differing access to medical and dental care, who have been followed for over 30 years. These subjects are volunteers in a long-term Veterans Administration (VA) study of aging health, but they are not VA patients and receive their medical and dental care in the private sector. Such an extended time of follow-up provides a unique opportunity to observe a large number of tooth loss events.

In order to apply the recursive partitioning algorithms to such a large database, computational efficiency becomes particularly challenging. In this article, we propose a multivariate exponential survival tree procedure. It splits data using the score test statistic derived from a parametric exponential frailty model, which allows for fast evaluation of splits. We then adopt the goodness-of-split pruning algorithm of LeBlanc and Crowley (1993) to determine the optimal tree size. In addition, variable importance rankings are established using a novel random forest algorithm similar to Breiman (2001). We note that (1) the proposed tree method can be viewed as a multivariate extension of the exponential survival trees for independent failure time data studied by Davis and Anderson (1989), with dependence among teeth from the same subject accouted for by a frailty term; (2) the semi-parametric frailty model based tree method by Su and Fan (2004) generally does not work for tooth loss data because such data typically contain many identical censoring times and the frailty model estimation encounters convergence problems; (3) it is the fast computation provided by the parametric multivariate exponential approach that allows us to run the random forest algorithm on a large data set.

The remainder of the paper is organized as follows. In Section 2, the proposed tree and random forest procedures are presented in detail. Section 3 contains simulation studies designed for assessing the multivariate exponential survival tree method and the related variable importance method. In Section 4, we apply the proposed tree and random forest procedures to the analysis of the DLS data set for developing rules for assignment of tooth prognosis and for establishing variable importance rankings for tooth loss. Section 5 concludes the paper with a brief discussion. The interested reader may contact Xiaogang Su (xiaosu@mail.ucf.edu) or Juanjuan Fan (jjfan@sciences.sdsu.edu) for the R programs developed for this paper.

2. The Tree Procedure

Suppose that there are n units (i.e., subjects) in the data, with the ith unit containing K_i failure times (i.e., teeth). Let F_ik be the underlying failure time for the kth member of the ith unit and let C_ik be the corresponding underlying censoring time. The data thus consist of {(X_ik, Δ_ik, Z_ik): i = 1, 2,…, n; k = 1, 2,…, K_i}, where X_ik = min(F_ik, C_ik) is the observed follow-up time; Δ_ik = I(F_ik ≤ C_ik) is the failure indicator, which is 1 if F_ik ≤ C_ik and 0 otherwise; and Z_ik ∈ ℛ^p denotes the p-dimensional covariate vector associated with the kth member of the ith unit. The failure times from the same unit are likely to be correlated. In order to ensure identifiability, we assume that the failure time vector (F_i1,…, F_iKi)′ is independent of the censoring time vector (C_i1,…, C_iKi)′ conditional on the covariate vector ${({\mathbf{Z}}_{i1}^{\prime },\dots ,{\mathbf{Z}}_{i{K}_i}^{\prime })}^{\prime }$ for i = 1,…, n.

To build a tree model T, we follow the convention of classification and regression trees (CART; Breiman et al., 1984), which consists of three steps: first growing a large initial tree, then pruning it to obtain a nested sequence of subtrees, and finally determining the best tree size via validation.

2.1. Growing a Large Initial Tree

We formulate the hazard function of failure time F_ik for the kth member of the ith unit by the following exponential frailty model

$${\lambda }_{ik}(t)=exp\{{\beta }_0+{\beta }_1{z}_{ik}\}·w_i$$ (1)

for k = 1,…, K_i and i = 1,…, n, where exp(β₀) is an unknown constant baseline hazard, β₁ is an unknown regression parameter, and z_ik = I(Z_ikj ≤ c) with I(·) being the indicator function. For a constant change point c, Z_ikj ≤ c induces a binary partition of the data according to a continuous covariate Z_j. If Z_j is categorical, then the form of Z_j ∈ A is considered, where A can be any subset of its categories. For simplicity and interpretability, we restrict ourselves to splits on a single covariate.

The frailty w_i is a multiplicative random effect term that explicitly models the intra-unit dependence. It corresponds to some common unobserved characteristics shared by all members in the ith unit. It is assumed that, given the frailty w_i, failure times within the ith unit are independent. The frailty term w_i is assumed to follow the gamma distribution with mean one and an unknown variance v. Namely, w_i ~ gamma(1/v, 1/v) with density function

$$g(w,v)=\frac{w^{(1/v-1)}exp(-w/v)}{\mathrm{\Gamma }(1/v)v^{1/v}},v\ge 0.$$

To split data, we consider the score test for assessing H₀: β₁ = 0. Estimation of the null model (i.e., model (1) under H₀) is outlined in Appendix A. Let l denote the integrated log-likelihood function associated with model (1) and (β̂₀, v̂) the MLE of (β₀, v) from the null model. Also define θ = (β₀, v)′ and $m_i={\sum }_{k=1}^{K_i}{X}_{ik}{z}_{ik}$. Then the score test statistic can be derived as

$${S=\frac{U^2}{i_{{\beta }_1{\beta }_1}-{\mathbf{i}}_{{\beta }_1\mathit{\theta }}^{\prime }{\mathbf{I}}_0^{-1}{\mathbf{i}}_{{\beta }_1\mathit{\theta }}}\mid }_{({\beta }_0,v)=({\widehat{\beta }}_0,\widehat{v})},$$ (2)

where

$$\begin{array}{l}{U=\frac{\partial l}{\partial {\beta }_1}\mid }_{{\beta }_1=0}=\mathrm{\Delta }\mathrm{..}-exp({\beta }_0)\sum _{i=1}^n\frac{m_i{A}_i}{B_i},\\ {i_{{\beta }_1{\beta }_1}=-\frac{{\partial }^{2}l}{\partial {\beta }_1^2}\mid }_{{\beta }_1=0}=exp({\beta }_0)\sum _{i=1}^n\frac{m_i{A}_i{B}_i-exp({\beta }_0)m_i^2{A}_i}{B_i^2},\\ {{\mathbf{i}}_{{\beta }_1\mathit{\theta }}={(i_{{\beta }_1{\beta }_0},i_{{\beta }_{1}v})}^{\prime }={(-\frac{{\partial }^{2}l}{\partial {\beta }_1\partial {\beta }_0},-\frac{{\partial }^{2}l}{\partial {\beta }_1\partial v})}^{\prime }\mid }_{{\beta }_1=0},\\ i_{{\beta }_1{\beta }_0}=exp({\beta }_0)\sum _{i=1}^n\frac{m_i{A}_i}{B_i^2}\{B_i-exp({\beta }_0)X_{i·}\},\\ i_{{\beta }_{1}v}=\frac{exp({\beta }_0)}{v^2}\sum _{i=1}^n\frac{m_i}{B_i^2}(A_i-B_i).\end{array}$$

In the above expressions, I₀ is the Fisher’s information matrix for the null model (see Appendix A for definitions of Δ.., A_i, and B_i). Since z_ik enters S only through m_i, evaluation of the score test statistic for each split is computationally fast. Note that, for a given split, S follows a χ²(1) distribution.

The best split is the one that corresponds to the maximum score test statistic among all permissible splits. According to the best split, the whole data is divided into two child nodes. The same procedure is then applied to either of the two child nodes. Recursively proceeding through these steps results in a large initial tree, denoted by T₀.

2.2. Split-Complexity Pruning

The final tree model could be any subtree of T₀. However, the number of subtrees becomes massive even for a moderately-sized tree. To narrow down our choices, we follow CART’s (Breiman et al., 1984) pruning idea to truncate the “weakest link” of the large initial tree T₀ iteratively. Since we employ the maximum score statistic criterion to grow the tree, which provides a natural goodness-of-split measure of each internal node, this allows us to adopt the split-complexity measure of LeBlanc and Crowley (1993):

$$G_{\alpha }(T)=G(T)-\alpha ·\mid T-\stackrel{\sim }{T}\mid ,$$ (3)

where T̃ denotes the set of all terminal nodes of tree T, T − T̃ is the set of all internal nodes, α is termed as complexity parameter, and G(T) = Σ_h∈T−T̃ S(h) sums up the 7 maximum score test statistic at every internal node of tree T. Here, G(T) provides an overall goodness-of-split assessment, penalized by tree complexity, i.e., |T − T̃| the total number of internal nodes.

As the complexity penalty α increases from 0, there will be a link or internal node h that first becomes ineffective because T_h, the branch whose root node is h, is inferior compared to h as a single terminal node. This link is then termed as the “weakest link” and the branch with the smallest threshold value is truncated first.

We start with the large initial tree T₀. For any link or internal node h of T₀, calculate the threshold

$$g(h)=\frac{{\sum }_{i\in T_h-{\stackrel{\sim }{T}}_h}S(i)}{\mid T_h-{\stackrel{\sim }{T}}_h\mid },$$

where S(i) represents the maximum score test statistic associated with internal node i. Then the “weakest link” h^★ in T₀ is the internal node such that g(h^★) = min_{h∈T0−T̃0} g(h). Let T₁ be the subtree after pruning off h^★, namely, T₁ = T₀ − T_h^*. Also, record α₁ = g(h^★). Then we apply the same procedure to truncate T₁ and obtain the subtree T₂ and α₂. Continuing to do so leads to a decreasing sequence of subtrees T₀ ≻ T₁≻ ··· ≻ T_M, where T_M is the null tree containing the root node only and the notation ≻ means “subtree”, as well as a sequence of increasing α values, 0 = α₀ < α₁ < ··· < α_M < ∞. Note that all the quantities S(i) have been computed when growing T₀, which makes the above pruning procedure computationally very fast.

The optimality of this split-complexity algorithm is established by Breiman et al. (1984) and LeBlanc and Crowley (1993). It can be shown that, for any given α > 0 and tree T, there exists a unique smallest subtree of T that maximizes the split-complexity measure. This unique smallest subtree, denoted as T(α), is called the optimally pruned subtree of T for complexity parameter α. It has further been established that the subtree T_m resulting from the above pruning procedure is the optimally pruned subtree of T₀ for any α such that α_m ≤ α < α_m+1. In particular, this is the case for the geometric mean of α_m and α_m+1, namely ${\alpha }_m^{\prime }=\sqrt{{\alpha }_m{\alpha }_{m+1}}$.

2.3. Tree Size Selection

One best-sized tree needs to be selected from the nested sequence. Again, the split-complexity measure G_α(T) in (3) is the yardstick for comparing these candidates. That is, tree T^★ is the best sized if G_α(T)= max_{m=0,…, m}{(G(T_m) − α|T_m − T̃_m|}. LeBlanc and Crowley (1993) suggests that, for selecting the best-sized subtree, α be fixed within the range 2 ≤ α ≤ 4, where α = 2 is in the spirit of AIC (Akaike, 1974) and α = 4 corresponds roughly to the 0.05 significance level for a split under the χ²(1) curve. However, due to the adaptive nature of greedy searches, the goodness-of-split measure G(T_m) is over-optimistic and needs to be validated to provide a more honest assessment. Two validation methods have been proposed, the test sample method and the resampling method, depending on the sample size available. In the following, the notation G(ℒ₂; ℒ₁, T) denotes the validated goodness-of-split measure for tree T built using sample ℒ₁ and validated using sample ℒ₂.

When the sample size is large, the test sample method can be applied. First divide the whole data into two parts: the learning sample ℒ₁ and the test sample ℒ₂. Then grow and prune the initial tree T₀ using ℒ₁. At the stage of tree size determination, the goodness-of-split measure G(T_m) is recalculated or validated as G(ℒ₂; ℒ₁, T_m) using the test sample ℒ₂. The subtree that maximizes the validated G_α is the best-sized tree.

When the sample size is small or moderate, one may resort to resampling techniques. We adopt a bootstrap method proposed by Efron (1983) for bias correction in the prediction problem (also see LeBlanc and Crowley, 1993). In this method, one first grows and prunes a large initial tree T₀ using the whole data. Next, bootstrap samples ℒ_b, b = 1, …, B, are drawn from the entire sample ℒ. A rough guideline for the number of bootstrap samples is 25 ≤ B ≤ 100, following LeBlanc and Crowley (1993). Based on each bootstrap sample ℒ_b, a tree $T_0^b$ is grown and pruned. Let $T_b({\alpha }_m^{\prime })$, m = 1, … , M, denote the optimally pruned subtrees corresponding to the ${\alpha }_m^{\prime }$ values, where ${\alpha }_m^{\prime }$, m = 1, … , M, are geometric means of the α_m values respectively, obtained from pruning T₀. The bootstrap estimator of G(T_m) is given by

$$G^{(b)}(T_m)=G(\mathcal{L};\mathcal{L},T({\alpha }_m^{\prime }))-\frac{1}{B}\sum _{b=1}^B\{G({\mathcal{L}}_b;{\mathcal{L}}_b,T_b({\alpha }_m^{\prime }))-G(\mathcal{L};{\mathcal{L}}_b,T_b({\alpha }_m^{\prime }))\}.$$ (4)

The rationale behind this estimator is as follows. The first part of (4), G(ℒ; ℒ, $T({\alpha }_m^{\prime })$), uses the same sample for both growing the tree and calculating the goodness-of-split measure, so the resulting estimate G is over-optimistic. The second part of (4) aims to correct this bias. This part is an estimate of the difference between G’s when the same (ℒ_b) vs. different (ℒ_b and ℒ) samples are used for growing/pruning the tree and for recalculating G, and it is averaged over the B bootstrap samples.

2.4. Variable Importance Ranking via Random Forests

Variable importance ranking is another attractive feature offered by recursive partitioning. It is a useful technique if one is interested in answering questions such as which factors are most important for tooth loss/survival. Note that this question can not be fully addressed by simply examining the splitting variables shown in one single final tree structure, as an important variable can be completely masked by another correlated one. There are a few methods available for extracting variable importance information. Here, we develop an algorithm analogous to the procedure used in random forests (Breiman, 2001), which is among the newest and most promising developments in this regard.

The multivariate exponential survival tree presented in previous sections searches for the best split by maximizing between-node difference. In contrast to CART trees which minimize within-node impurity at each split, this kind of trees constructed is generally termed as trees by goodness-of-split. To extend random forests to trees by goodness-by-split, once again we make use of the goodness-of-split measure G(T) for tree T.

Let V_j denote the importance measure of the j-th covariate Z_j for j = 1, …, p. We construct random forests by taking B bootstrap samples ℒ_b, b = 1, …, B and based on each bootstrap sample, growing trees with a greedy search over a subset of randomly selected m covariates at each split. The resultant trees are denoted as T_b, b = 1, …, B. The random selection of m covariates at each split not only helps improve computational efficiency but also produces de-correlated trees. For each tree T_b, the b-th out-of-bag sample (denoted as ℒ − ℒ_b), which contains all observations that are not in ℒ_b, is sent down to compute the goodness-of-split measure G(T_b). Next, the values of the j-th covariate in ℒ − ℒ_b are randomly permuted. The permuted out-of-bag sample is sent down T_b again to recompute G_j(T_b). The relative difference between G(T_b) and G_j(T_b) is recorded. This is done for every covariate. The procedure is repeated for B bootstrap samples. The importance V_j is then the average of the relative differences over all B bootstrap samples. The rationale is that the j-th covariate of the permuted sample contains no predictive value. Hence, a small difference between G(T_b) and G_j(T_b) indicates small predictive power of the original j-th covariate whereas a large difference suggests that the original j-th covariate has large predictive power and hence is important. The complete algorithm is summarized in Appendix B.

3. Simulation Studies

This section contains simulation experiments designed to investigate the performance of the splitting statistic as well as the tree and variable importance procedures under a variety of model configurations. To facilitate the comparison with Su and Fan (2004), we have employed similar model settings.

3.1. Performance of the Splitting Statistic

We first investigate the performance of the splitting statistic. We generated data from the five models given in Table 1 with 4 correlated failure times per unit, i.e., K_i ≡ 4 for all i. Each model involves a covariate Z simulated independently from a discrete uniform distribution over (1/50, …, 50/50) and a threshold covariate effect at cutoff point c.

Table 1.

Models used for assessing the performance of the splitting statistic. The covariate Z_ik’s are generated from a discrete uniform distribution over values (1/50, 2/50, …, 50/50) and c is the true cutoff point.

	Model Form	Name
A	λik(t) = exp (2 + 1{Zik≤c}) · wi, with wi ~ Γ(1, 1)	Gamma-Frailty
B	λik(t) = exp (2 + 1{Zik≤c} + wi), with wi ~ N (0, 1)	Log-Normal Frailty
C	λik(t) = exp (2 + 1{Zik≤c}) not absolutely continuous	Marginal
D	λik(t) = exp (2 + 1{Zik≤c}) absolutely continuous	Marginal
E	λik(t) = λ0(t) exp (2 + 1{Zik≤c} · wi, with wi ~ Γ(1, 1), λ0(t) = αλtα−1, α = 1.5, and λ = 0.1	Non-constant Baseline

Model A is a gamma-frailty model. Model B is a lognormal frailty model. Models C and D are marginal models, in which the correlated failure times marginally have the specified hazard and jointly follow a multivariate exponential distribution (Marshall and Olkin, 1967). This joint multivariate exponential distribution can be absolutely continuous or not, which distinguishes Models C and D. One is referred to Su et al. (2006) on simulating different types of multivariate failure times. Model E involves a baseline hazard function from the Weibull distribution, i.e., a non-constant baseline hazard. Inclusion of Models B, C, D and E is useful for investigating the performance of the splitting statistic under model misspecification.

Two censoring rates were used, no censoring and 50% censoring. The 50% censoring rate was achieved by generating the underlying censoring times from the same model as the underlying failure times. We also tried out two different cutoff points: 0.5 (the middle point) and 0.3 (a shifted one). Only one sample size n = 100 was considered. Each combination was examined for 500 simulation runs and the relative frequencies of the best cutoff points selected by the maximum score test (2) are presented in Table 2.

Table 2.

Results for assessing the splitting statistic: Relative frequencies (in percentages) of the ‘best’ cutoff points identified by the maximum score test statistic in 500 runs. The class intervals, identified by the interval midpoints, are [0, 0.15], (0.15, 0.25], (0.25, 0.35], (0.35, 0.45], (0.45, 0.55], (0.55, 0.65], (0.65, 0.75], (0.75, 0.85], and (0.85, 1], respectively. Also, n = 100 and K = 4.

			Relative Frequencies of the ‘Best’ Cutoff Points
Model	Cutoff c	Censoring Rate	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
A	0.5	0%	0.0	0.0	0.2	4.0	93.6	2.2	0.0	0.0	0.0
		50%	0.0	0.6	2.0	13.6	75.6	6.6	0.6	0.8	0.2
	0.3	0%	0.2	3.2	95.0	1.2	0.4	0.0	0.0	0.0	0.0
		50%	2.8	9.0	80.6	5.0	1.6	0.4	0.2	0.0	0.4
B	0.5	0%	0.0	0.0	0.2	2.8	94.4	2.6	0.0	0.0	0.0
		50%	0.2	0.4	1.6	9.6	76.4	6.0	0.8	0.4	4.6
	0.3	0%	0.6	2.8	95.0	1.6	0.0	0.0	0.0	0.0	0.0
		50%	2.6	9.4	72.8	6.2	0.4	1.0	0.2	0.0	7.4
C	0.5	0%	0.0	0.0	0.0	0.0	99.8	0.0	0.0	0.0	0.2
		50%	0.0	0.0	0.0	0.0	98.2	0.4	0.2	0.0	1.2
	0.3	0%	0.0	0.0	99.2	0.0	0.0	0.0	0.0	0.0	0.8
		50%	0.6	3.6	91.0	0.6	0.2	0.8	1.6	1.0	0.6
D	0.5	0%	0.0	0.0	0.0	0.0	95.8	0.2	0.0	0.0	4.0
		50%	0.0	0.0	0.4	3.6	95.6	0.4	0.0	0.0	0.0
	0.3	0%	0.0	0.0	98.0	0.2	0.0	0.0	0.0	0.0	1.8
		50%	0.0	3.4	95.8	0.8	0.0	0.0	0.0	0.0	0.0
E	0.5	0%	0.0	0.2	0.4	2.6	94.8	1.8	0.2	0.0	0.0
		50%	0.2	1.0	3.6	14.0	70.2	9.0	1.2	0.6	0.2
	0.3	0%	0.0	2.2	95.2	2.4	0.2	0.0	0.0	0.0	0.0
		50%	3.6	14.4	71.8	7.0	2.4	0.4	0.2	0.0	0.2

It can be seen that the maximum score test statistic does very well in selecting the correct cutoff points, even under model misspecifications. The results are comparable to those presented in Su and Fan (2004). It is not surprising that the performance deteriorates a little with heavier censoring. But the location of the true cutoff point does not seem to have much effect.

3.2. Performance of the Tree Method

Next we investigate the efficiency of the proposed multivariate exponential tree procedure in detecting data structure. Data were simulated from the five different models given in Table 3. Four covariates, Z₁, …, Z₄, were generated from a discrete uniform distribution over (1/10, …, 10/10), where Z₁ and Z₃ are unit-specific (mimicking subject-level covariates) and Z₂ and Z₄ are failure-specific (mimicking tooth-level covariates). Note that covariates Z₃ and Z₄ do not have any effect on the failure times but are included in the tree procedure as noise. Models A′ through E′ correspond to those in the previous section, except that each contains two additive threshold effects on Z₁ and Z₂. Only one censoring rate, 50%, was used.

Table 3.

Models used for assessing the performance of the tree procedure. The covariate Z_ik’s are generated from a discrete uniform distribution over values (1/10, 2/10, …, 10/10).

	Model Form
A′	λik(t) = exp (−1 + 2 × 1{Zik1≤0.5} + 1{Zik2≤0.5}) · wi, with wi ~ Γ(1, 1)
B′	λik(t) = exp (−1 + 2 × 1{Zik1≤0.5} + 1{Zik2≤0.5} + wi), with wi ~ N (0, 1)
C′	λik(t) = exp (−1 + 2 × 1{Zik1≤0.5} + 1{Zik2≤0.5}), not absolutely continuous
D′	λik(t) = exp (1 + 2 × 1{Zik1≤0.5} + 1{Zik2≤0.5}), absolutely continuous
E′	λik(t) = λ0(t) exp (−1 + 2 × 1{Zik1≤0.5}) + 1{Zik2≤0.5} · wi, with wi ~ Γ(1, 1), λ0(t) = αλtα−1, α = 1.5, and λ = 0.1

The five models were examined for a sample size of n = 300 and K_i ≡ 4, where the first 200 × 4 observations formed the learning sample ℒ₁ and the remaining 100 × 4 observations formed the test sample ℒ₂. Three different complexity parameters (α = 2, 3, and 4) were used. For each different model and complexity parameter combination, a total of 200 simulation runs were carried out.

Table 4 presents the final tree size (i.e., the number of terminal nodes) selected by the multivariate exponential survival tree procedure. It can be seen that the proposed procedure does fairly well in detecting the true data structure, even in the misspecified cases (models B′ - E′). Also note that α = 4 yields the best performance under models A′ - D′ while values of α = 2 and α = 3 do not seem to impose enough penalty for model complexity. In model E′, α = 3 performs slightly better than α = 4 and both perform better than α = 2. We will use α = 4 when analyzing the DLS data.

Table 4.

Results for assessing the tree procedure: Relative frequencies (in percentages) of the final tree size identified by the multivariate exponential tree procedure in 200 runs. One set of sample sizes was used, 200×4 observations for the learning sample and 100×4 observations for the test sample with K = 4 and 50% censoring rate. Three different complexity parameters (α) were compared: 2, 3, and 4.

		Final Tree Size (in Percentage)
Model	Complexityα	1	2	3	4	5	6	≥ 7
A′
	2	0.0	0.0	0.0	60.0	14.0	7.0	17.0
	3	0.0	0.0	1.0	76.5	10.0	5.0	7.5
	4	0.0	0.0	2.5	87.5	5.5	2.5	2.0
B′
	2	0.0	0.5	2.0	63.5	18.0	5.0	11.0
	3	0.0	0.5	3.5	76.0	13.0	4.5	2.5
	4	0.0	0.5	4.5	81.0	9.5	3.0	1.5
C′
	2	0.0	2.0	3.0	39.0	6.0	9.5	41.5
	3	0.0	2.0	3.0	51.0	9.0	9.0	26.0
	4	0.0	2.0	3.0	62.5	7.5	8.0	17.0
D′
	2	0.0	3.0	1.5	58.5	10.5	12.5	14.0
	3	0.0	3.0	1.5	68.5	9.0	10.0	8.0
	4	0.0	3.0	2.5	70.5	8.0	10.5	5.5
E′
	2	0.0	0.0	8.0	59.5	14.5	8.5	8.5
	3	0.0	0.3	12.5	68.0	8.5	6.0	2.0
	4	0.0	6.0	18.0	65.5	6.0	3.0	1.5

3.3. Performance of the Variable Importance Procedure

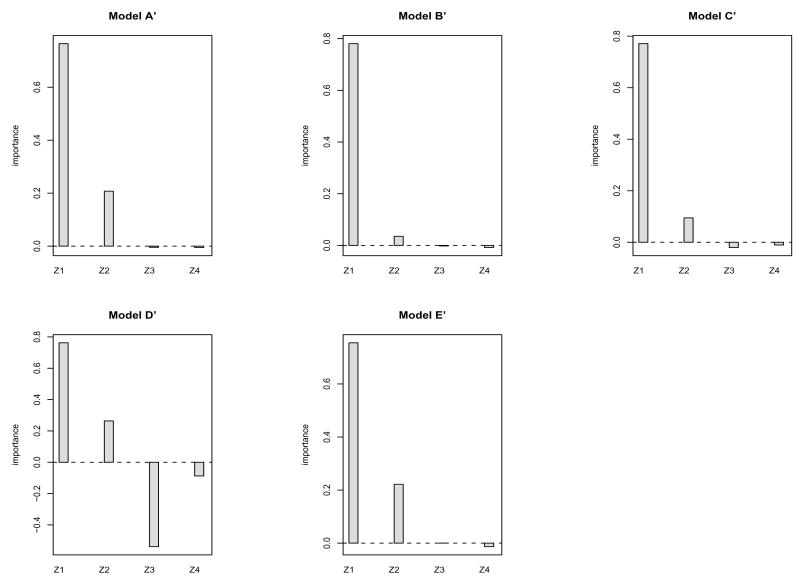
We also evaluated the performance of the variable importance procedure under the same five modles A′ - E′ as presented in Table 3. A sample size of n = 500 and K_i ≡ 4 was used to generate data from each model. The same 50% censoring rate was applied. The algorithm in Appendix B was run with B = 200 bootstrap samples and m = 2 randomly selected inputs at each split. Note that only covariates Z₁ and Z₂ are involved in the five models in Table 3 with Z₁ having a stronger effect than Z₂: the β coefficients are respectively 2 and 1 for the threshold effects based on Z₁ and Z₂. The covariates Z₃ and Z₄ are not involved in these models. Hence, the true variable importance ranks (from most important to least important) are Z₁, followed by Z₂, and followed by Z₃ and Z₄ (equally unimportant). The simulation results presented in Figure 1 reflect the true variable importance ranks with Z₁ having the largest variable importance measure, Z₂ having the second largest variable importance measure, and Z₃ and Z₄ having near zero or negative importance measures. Near zero or negative importance measures signify unimportant variables in our procedure.

Figure 1.

Variable importance measures based on a data set of 500×4 observations generated from each of Models A′–E′: B = 200 bootstrap samples are used in random forests and m is set to 2.

4. Data Example

We now apply the proposed tree method to develop prognostic classification rules using the VA Dental Longitudinal Study (DLS) data. We have compiled a subset of 6,463 teeth (from 355 subjects) that have complete baseline information. Tooth loss was observed for 1,103 (17.07%) teeth during the 30 year follow-up. Table 5 presents a description of 19 prognostic factors that we use in the tree procedure.

Table 5.

Variable description for the baseline measures in the VA Dental Longitudinal Study (DLS).

Variable	Name	Description
V1	loc	tooth type
V2	nteeth	total number teeth present at baseline
V3	age	patient age at baseline
V4	smoke	smoking status
V5	education	educational level
V6	ses	socioeconomic level at NAS cycle
V7	endonum	number of endodontic teeth
V8	bonemm	average bone height (mm)
V9	abl	average alveolar bone loss (ABL) score
V10	plaque	plaque score
V11	mobile	mobility score
V12	calc	calculus score, max of above/below gum
V13	ging	gingival score
V14	maxabl	maximum tooth-level ABL score
V15	pocket	probing pocket depth score, max per tooth
V16	dmfscore	DMF score per tooth at baseline
V17	decay	maximum decay at baseline
V18	endotrt	endodontic treatment
V19	ht	bone height (%)

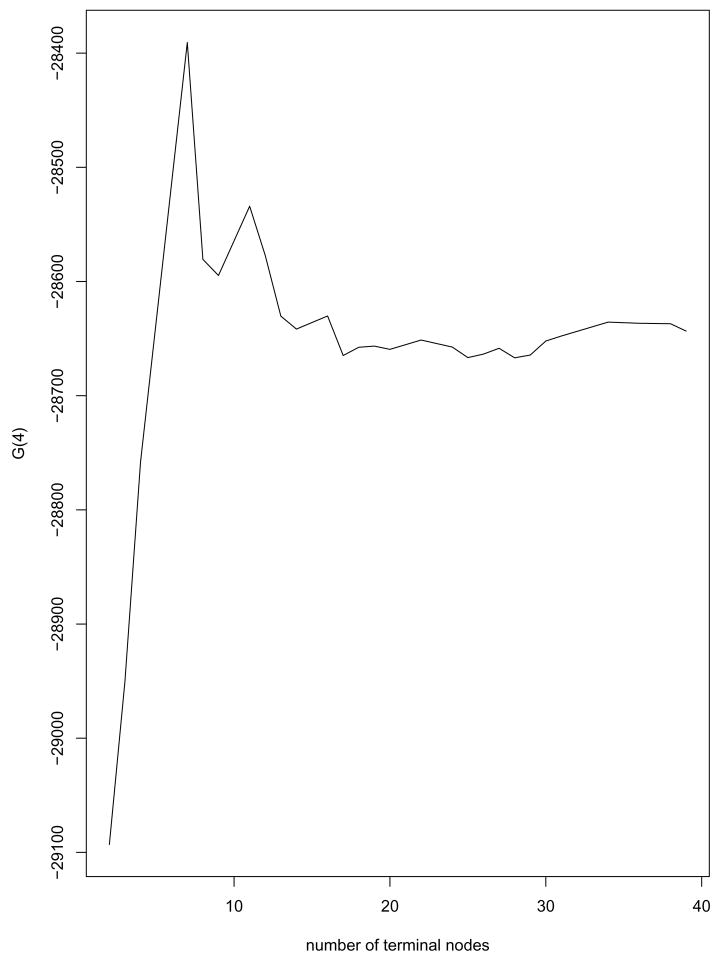
Since the proposed tree method is computationally fast, the bootstrap method was used for selecting the best-sized tree. A large tree was grown using the whole sample with the minimum node size set at 50 teeth. This tree had 39 terminal nodes. Using the pruning algorithm described earlier, a set of 28 optimally pruned subtrees were identified. With tooth as the sampling unit, 30 bootstrap samples were drawn from the data and, for m = 1, …, 28, the goodness-of-split measure G(T_m) was evaluated using equation (4). To obtain a parsimonious tree model, α = 4 was used as the complexity penalty and the G₄(T_m) values for the subtree sequence are presented in Figure 2. The plot of split-complexity statistics has one peak and the tree with 7 terminal nodes has the largest G₄(T_m).

Figure 2.

Tree size selection for the DLS data: Plot of G(4) versus the tree size

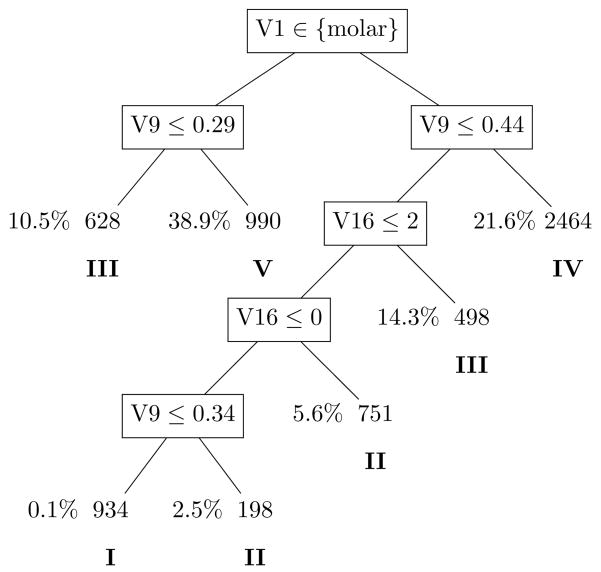
The final tree is plotted in Figure 3, where boxes indicate internal nodes and ovals indicate terminal nodes. Inside each box is the splitting rule for the internal node. Observations satisfying this rule go to the left child node and observations not satisfying this rule go to the right child node. The node sizes of internal nodes are omitted because they can be easily calculated once the terminal node sizes are known. For each terminal node, the node size (i.e., the number of teeth) is given within the oval, and the proportion of teeth that are lost is given on the left of each oval.

Figure 3.

The best-sized tree for the DLS data. For each internal node denoted by a box, the splitting rule is given inside the box. For each terminal node denoted by an oval, the node size (i.e., number of teeth) is given inside the oval, and the percentage of lost teeth on the left. Underneath terminal nodes in Roman numerals are the five assigned prognostic groups: I - good, II - fair, III - poor, IV - questionable, and V - hopeless.

The final tree in Figure 3 divides all the teeth into seven groups. However, some groups have similar tooth loss rates. An amalgamation procedure similar to Ciampi et al. (1986) was run to bring down the final number of prognostic groups. To do this, the whole sample was sent down the best-sized tree in Figure 3 and the robust logrank statistics (Lin, 1996) between every pair of the seven groups were computed. The two terminal nodes giving the smallest robust logrank statistic were merged. This procedure was repeated until the smallest robust logrank statistic was larger than the Bonferroni-adjusted critical value from a χ²(1) distribution. When the algorithm stopped, the number of groups reduced down to five. The amalgamation results are also included in Figure 3, with Roman numeral I indicating a prognosis of “good”, II indicating a prognosis of “fair”, etc. Summary statistics of the five prognostic groups and the pairwise robust logrank statistics among them are presented in Table 6.

Table 6.

Summary measures and pairwise robust logrank statistics for the five prognostic groups.

				Robust Logrank Statistic
Group	Definition	Teeth	Losses (%)	II	III	IV	V
I	good	934	1 (0.11%)	18.48	38.72	71.03	118.82
II	fair	949	47 (4.95%)	·	20.45	45.41	103.67
III	poor	1126	137 (12.17%)	·	·	14.06	66.38
IV	questionable	2464	533 (21.63%)	·	·	·	42.58
V	hopeless	990	385 (38.89%)	·	·	·	·

Although nineteen putative prognostic factors were included in the multivariate exponential survival tree procedure, only three of them appeared in the final tree presented in Figure 3: (1) tooth type: molar vs. non-molar, (2) alveolar bone loss, and (3) tooth-level DMF score: the number of Decayed, Missing, and Filled surfaces for each tooth.

It is particularly interesting to note that the first split was on tooth type with molars having a worse overall outlook than non-molars. This is similar to the results obtained in the studies conducted by McGuire and Nunn (1996a, 1996b), who noted that periodontal prognosis was far more difficult to predict in molars than in non-molars with molars generally having worse overall prognosis than non-molars. One reason for molars having a worse outlook is the potential for the development of furcation involvement. Furcation involvement refers to the situation where alveolar bone loss has progressed to the point on the molar tooth where the roots bifurcate. When furcation involvement develops in a molar, the patient cannot provide adequate oral hygiene to the area which leads to an increased risk of further bone loss as well as an increased risk for dental caries. This sort of furcation involvement only occurs in molars which may explain the model’s distinction between molars and non-molars. In addition, according to the study by McGuire and Nunn (1996b), furcation involvement was one of the most significant factors for predicting tooth loss as a result of periodontal disease. Unfortunately, no measures of furcation involvement were available from the DLS so the only related measure available for the current analysis was tooth type. Hence, it is likely that tooth type in the current study is a proxy measure for furcation involvement, which has long been established to be a significant local etiological risk factor for tooth loss.

The next splits for both molars and non-molars were for average alveolar bone loss. In this case, average alveolar bone loss refers to the subject-level average Schei score. Schei scores range from 0 for “no alveolar bone loss” to 5 for “>80% alveolar bone loss” with values assigned to the mesial and distal areas of each tooth by a trained, calibrated examiner on the basis of examination of the subject’s radiographs. The minimum, median, and maximum of the average ABL score in these data are 0, 0.47, and 2.50, respectively. Three other measures of bone loss that were considered for the model included maximum tooth-level alveolar bone loss, subject-level average bone height, and tooth-level bone height. The maximum tooth-level alveolar bone loss was the maximum Schei score for each tooth. In other words, the maximum Schei score is the maximum of the mesial and distal Schei scores for each tooth. In contrast, the subject-level average bone height and the tooth-level bone height were based on digitized radiography. It is not surprising that alveolar bone loss is a significant predictive factor for tooth loss. However, it is surprising that the “best” measure of alveolar bone loss for predicting tooth loss was the average Schei score since a Schei score has always been considered to be less accurate and more subjective than digitized radiography. In addition, since the subject-level average Schei score was selected over the maximum tooth-level Schei score, it would appear that overall bone loss across one’s mouth is a far stronger predictor of tooth loss than an isolated area of vertical bone loss.

The next two splits for non-molars were for tooth-level DMF score. DMF score is actually the number of Decayed, Missing, Filled surfaces for each tooth with values ranging from 0 for a completely sound tooth to 5 for a posterior tooth with all 5 surfaces exhibiting caries experience. In the first split, non-molars with 3 or more surfaces with a positive DMF were assigned a prognosis of “Poor” while non-molars with 1 or 2 surfaces with a positive DMF were assigned a prognosis of “Fair”. Completely sound non-molars (i.e., DMF=0) were split again according to average alveolar bone loss with sound non-molars with less average alveolar bone loss assigned a prognosis of “Good” while sound non-molars with more average alveolar bone loss were assigned a prognosis of “Fair”.

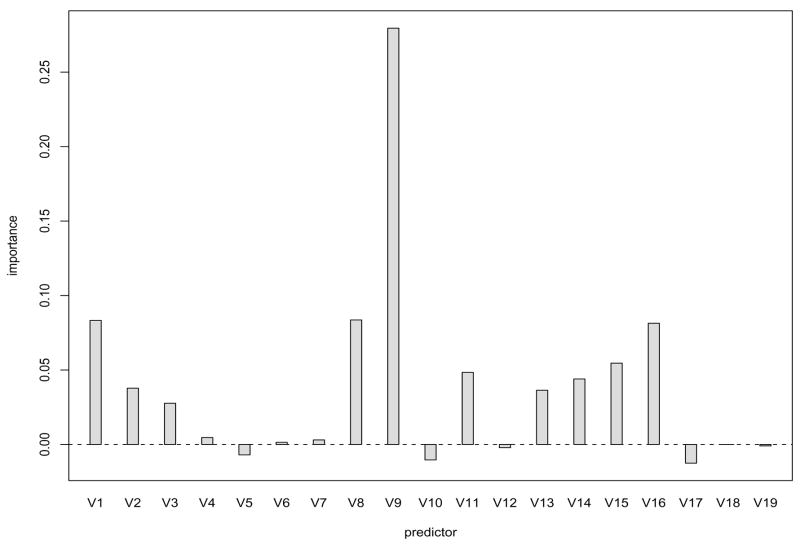
Finally, Figure 4 plots the variable importance scores from B = 200 bootstrap samples. According to Breiman (2001), variable importance results are “insensitive” to the number of covariates selected to split each node. A choice of m = 3 was used in our algorithm. It can be seen that V₉ ( abl) stands out as the most important, followed by V₈ ( bonemm), V₁ ( loc), and V₁₆ ( dmfscore). This matches well with the final tree structure presented in Figure 3, except that V₈ ( bonemm) has been masked out in Figure 3. Variables V₉ ( abl) and V₈ ( bonemm) are both measures of average alveolar bone loss across the entire mouth and are essentially different methods for assessing alveolar bone loss with V₉ ( abl) being the average Schei score that is assessed by a clinician examining a radiogaph and V₈ ( bonemm) being the average alveolar bone height from using digitized radiography. Hence, because of the high correlation between V₉ ( abl) and V₈ ( bonemm), it is expected that only one of these two variables to appear in the final “best tree” model.

Figure 4.

Variable importance measures in the DLS data obtained via random forests.

From a clinical standpoint, three of the four measures that rank as the most important variables in predicting tooth loss are good indicators of the breakdown of the tooth, as represented by V₁₆ ( dmfscore), and breakdown of the periodontium, as represented by V₉ ( abl) and V₈ ( bonemm). Since it is well-known that the two leading causes of tooth loss are dental caries and periodontal disease, the statistical importance agrees quite well with widely-held beliefs about clinical importance. The importance of V₁ ( loc) reinforces the findings from studies by McGuire and Nunn that show molars are quite different from non-molars when predicting tooth loss. Nevertheless, the method based on random forests provides a more comprehensive evaluation of variable importance by automatically taking into account both the linear and nonlinear effect of a variable and its interaction with others.

It is interesting to note that the two most important variables are both measures of subject-level average alveolar bone loss while the two variables for tooth-level alveolar bone loss, V₁₄ ( maxabl) and V₁₉ ( ht), are much less important. From a clinical perspective, the fact that subject-level average alveolar bone loss is substantially more important in predicting tooth loss than tooth-level alveolar bone loss demonstrates that generalized periodontal disease is a stronger predictor of tooth loss than isolated areas of periodontal involvement. The greater importance of subject-level average alveolar bone loss compared to tooth-level alveolar bone loss is also an indication that horizontal bone loss is a more important etiological factor in tooth loss than vertical bone loss since subject-level average alveolar bone loss is a reflection of horizontal bone loss while tooth-level alveolar bone loss is a reflection of vertical bone loss.

5. Discussion

In this paper, we have proposed a multivariate survival tree method. It is an extension of the exponential survival trees by Davis and Anderson (1989) for univariate survival data, but uses a frailty term to adjust for the correlation among survival times from the same cluster. The adoption of the exponential baseline hazard makes it possible to derive a closed-form score test statistic for fast evaluation of tree performance. This paper builds on our work in Su and Fan (2004), but the computational speed gained from the proposed approach is essential for a frailty model based tree method to be applied to large data sets such as the DLS data because the estimation of a general frailty model is slow and a tree algorithm is feasible only if each model fitting is reasonably fast. Not to mention that it is the computational efficiency achieved by the proposed method that affords the implementation of the random forest algorithm. Though we assume a gamma frailty term and a constant baseline hazard, simulation studies show that the proposed method works reasonably well under departure from these assumptions.

The application of the proposed tree method to the DLS data yielded five prognostic groups. Three factors were involved in the final tree structure: tooth type (molar vs. non-molar), subject-level average alveolar bone loss score, and tooth-level DMF score. Molars were found to have worse overall prognosis than non-molars. Greater alveolar bone loss was associated with an increased risk of tooth loss. Similarly, the more broken down a tooth is (i.e., the greater the DMF score is), the more likely that the tooth will be damaged further and thus, eventually lost. The application of the variable importance algorithm to the DLS data ranked the subject-level average alveolar bone loss score as the most important variable in predicting tooth loss, followed by the average alveolar bone height, tooth type (molar vs. non-molar), and tooth-level DMF score. The variable of average bone height is another measure of average alveolar bone loss across the entire mouth and hence is masked out in the final tree structure. From a clinical standpoint, the criteria for assignment of prognosis and the variable importance rankings make sense.

APPENDIX A

Estimation of the Null Model

Under H₀: β₁ = 0, the null frailty exponential model becomes

$${\lambda }_{ik}(t)=exp({\beta }_0)·w_{i·}$$

We first define

$$A_i=1/v+{\mathrm{\Delta }}_{i·}\text{and}{B}_i=1/v+X_{i·}exp({\beta }_0),$$

where ${\mathrm{\Delta }}_{i·}={\sum }_{k=1}^{K_i}{\mathrm{\Delta }}_{ik},X_{i·}={\sum }_{k=1}^{K_i}{X}_{ik}$, and $\mathrm{\Delta }\mathrm{..}={\sum }_{i=1}^n{\mathrm{\Delta }}_{i·}$.

Due to the parametric form of the model, the involved parameters (β₀, v) can be estimated by maximizing the following integrated likelihood

$$L_0=\prod _{i=1}^n{\int }_0^{\infty }\left[g(w_i,v)\prod _{k=1}^{K_i}{\{{\lambda }_{ik}(X_{ik})\}}^{{\mathrm{\Delta }}_{ik}}exp\left\{-{\int }_0^{X_{ik}}{\lambda }_{ik}(t)dt\right\}\right]d{w}_{i·}$$

After integrating w_i out, the resultant log-likelihood function for the null model can be written as

$$l_0={\beta }_0\mathrm{\Delta }\mathrm{..}+\sum _{i=1}^{n}ln\mathrm{\Gamma }(A_i)-nln\mathrm{\Gamma }(\frac{1}{v})-\frac{n}{v}lnv-\sum _{i=1}^n{A}_{i}ln{B}_{i·}$$ (5)

Optimization of the log-likelihood is done using standard Newton-Raphson procedures. Its gradient components are given by

$$\begin{array}{l}\frac{\partial l_0}{\partial {\beta }_0}=\mathrm{\Delta }\mathrm{..}-\sum _{i=1}^n\frac{A_i}{B_i}{X}_{i·}exp({\beta }_0)\\ \frac{\partial l_0}{\partial v}=\frac{1}{v^2}\left\{-\sum _{i=1}^n\frac{{\mathrm{\Gamma }}^{\prime }(A_i)}{\mathrm{\Gamma }(A_i)}+n\frac{{\mathrm{\Gamma }}^{\prime }(1/v)}{\mathrm{\Gamma }(1/v)}-n+\mathit{n}ln\mathit{v}+\sum _{i=1}^{n}ln{B}_i+\sum _{i=1}^n\frac{A_i}{B_i}\right\}.\end{array}$$

The components in the Fisher’s information matrix, denoted as I₀, are given by

$${\mathbf{I}}_0=\left(\begin{array}{cc}{i}_{{\beta }_0{\beta }_0}& i_{{\beta }_{0}v}\\ i_{v{\beta }_0}& i_{vv}\end{array}\right),$$

where

$$\begin{array}{l}{i}_{{\beta }_0{\beta }_0}=-\frac{{\partial }^2{l}_0}{\partial {\beta }_0^2}=\frac{exp({\beta }_0)}{v}\sum _{i=1}^n\frac{A_i}{B_i^2}{X}_{i·},\\ i_{{\beta }_{0}v}=-\frac{{\partial }^2{l}_0}{\partial {\beta }_0\partial v}=\frac{exp({\beta }_0)}{v^2}\sum _{i=1}^n\frac{X_{i·}(A_i-B_i)}{B_i^2}=i_{v{\beta }_0},\\ i_{vv}=-\frac{{\partial }^2{l}_0}{\partial v^2}=\frac{2n}{v^3}\frac{{\mathrm{\Gamma }}^{\prime }(1/v)}{\mathrm{\Gamma }(1/v)}-\frac{3n}{v^3}+\frac{2\mathit{n}ln\mathit{v}}{v^3}+\frac{n}{v^4}\frac{{\mathrm{\Gamma }}^{″}(1/v)}{{\mathrm{\Gamma }}^{\prime }(1/v)}-\frac{n}{v^4}{\left\{\frac{{\mathrm{\Gamma }}^{\prime }(1/v)}{\mathrm{\Gamma }(1/v)}\right\}}^2-\\ +\sum _{i=1}^n\left[\frac{2{\mathrm{\Gamma }}^{\prime }(A_i)}{v^3\mathrm{\Gamma }(A_i)}-\frac{2ln{B}_i}{v^3}-\frac{2A_i}{v^3{B}_i}+\frac{1}{v^4}\frac{{\mathrm{\Gamma }}^{″}(A_i)}{\mathrm{\Gamma }(A_i)}-\frac{1}{v^4}{\left\{\frac{{\mathrm{\Gamma }}^{\prime }(A_i)}{\mathrm{\Gamma }(A_i)}\right\}}^2-\frac{2}{v^4{B}_i}+\frac{A_i}{v^4{B}_i^2}\right].\end{array}$$

APPENDIX B

Algorithm for Computing Variable Importance via Random Forests

Initialize all V_j’s to 0.

For b = 1, 2, …, B, do

• Generate bootstrap sample ℒ_b and obtain the out-of-bag sample ℒ − ℒ_b.

• Based on ℒ_b, grow a tree T_b by searching over m randomly selected inputs at each split and without pruning.

• Send ℒ − ℒ_b down T_b to compute G(T_b).

• For all predictors Z_j, j = 1, …, p, do

• ○ Permute the values of Z_j in ℒ − ℒ_b.

• ○ Send the permuted ℒ − ℒ_b down to T_b to compute G_j(T_b).

• ○ Update $V_j\leftarrow V_j+\frac{G(T_b)-G_j(T_b)}{G(T_b)}$.

  End do.

End do.

Average V_j ← V_j/B.