Bayesian Multiple Quantitative Trait Loci Mapping for Recombinant Inbred Intercrosses

Abstract

The Collaborative Cross (CC) is a renewable mouse resource that mimics the genetic diversity in humans. The recombinant inbred intercrosses (RIX) generated from CC recombinant inbred (RI) lines share similar genetic structures to those of F₂ individuals. In contrast to F₂ mice, genotypes of RIX can be inferred from the genotypes of their RI parents and can be produced repeatedly. Also, RIX mice do not typically share the same degree of relatedness. This unbalanced genetic relatedness requires careful statistical modeling to avoid a large number of false positive findings. For complex traits, mapping multiple genes simultaneously is arguably more powerful than mapping one gene at a time. In this article, we describe how we have developed a Bayesian quantitative trait locus (QTL) mapping method that simultaneously deals with the special genetic architecture of RIX and maps multiple genes. The performance of the proposed method is evaluated by extensive simulations. In addition, for a given set of RI lines, there are numerous ways to generate RIX samples. To provide a general guideline on future RIX studies, we compare several RIX designs through simulations.

THIS study was motivated by the mouse Collaborative Cross (CC) project. As its main thrust, the CC project seeks to overcome several of the severe limitations of human complex trait studies. One major limitation of such studies is that only the simplest genetic models can be resolved with confidence. Many other models are plausible, but difficult or impossible to resolve. Because it is closely related to humans, the mouse serves as a great model organism for studying human diseases. Most human genes have functional mouse counterparts, and genomes of both organisms are organized similarly. Traditional RI lines are generated by crossing only two inbred parental strains, resulting in extensive blind spots where a sizable proportion of the genome is identical by decent (IBD) and a low percentage of genetic variation (15%). In contrast, the CC recombinant inbred (RI) lines are derived from a genetically diverse set of eight founder inbred strains (Chesler et al. 2008; Iraqi et al. 2008). This selection of founder strains was predicted to result in uniform genome-wide high levels of variation. Genetic variation is randomized in the CC lines so that the causal relationships can be established. Another major advantage of the CC mice is that they are retrievable and extensible, which supports data integration over space and time and at all levels—from molecules and cells to physiological systems and environments.

Recombinant inbred intercross (RIX) panels are created by generating diallel F₁ progeny from a set of RI lines. Given a population of L RI lines, this approach can potentially produce L(L – 1)/2 genetically distinct RIX individuals. Subsets of RIX can be used to evaluate biological predictions of the ways in which an individual would respond to environmental perturbations and provide statistical support for prediction accuracy. Because RI mice are homozygote at each locus, the genotypes of the derivative RIX mice can be imputed in advance from the genotypes of the parental RI lines. RIX mice with identical genotypes can be regenerated whenever needed. Therefore the CC mice provide us with an ideal platform to generate testable hypotheses that can be used for accurate probability-based whole-organism biological predictions. Preliminary data from the CC strains and their derivative RIX progenies are now being generated. Developing appropriate analysis tools for mapping CC data is critical for the success of the CC project.

Though at the individual level, the genome of each RIX mouse has similar genetic structures to those of F₂ individuals, statistical analyses for F₂ data cannot be applied directly to RIX data. Backcross or F₂ subjects used in traditional quantitative trait locus (QTL) mapping have the same genetic relatedness to each other, which may not be the case for RIX data. Some RIX mice may share common parental RI lines, making them more related to each other than the RIX mice that do not share parental RI lines. Past investigations (Tsaih et al. 2005; Zou et al. 2005) have shown that careful statistical analyses that correctly handle the unbalanced relatedness in RIX are important to achieve valid results.

Over the last decade, mapping genes of human diseases has been an important research area. The vast majority of genes, however, have been limited to simple Mendelian inheritance patterns and well-defined quantitative traits with relatively large and consistent effects. Recent emphasis has shifted from mapping simple Mendelian traits to complex traits with complex genetic causes. Complex traits have proved far more resistant to genetic analysis. Many available QTL mapping methods map only one or a few QTL at a time and may not be efficient for complex traits. Variable selection methods are useful in selecting variables that are not necessarily individually important but that are, in fact, jointly important. By treating multiple QTL mapping as a model/variable selection problem (Broman and Speed 2002), forward and stepwise selection procedures have been proposed to search for multiple QTL. Although simple, these methods have limitations, such as uncertainty about the number of QTL and difficulty in assessing the significance of associated tests due to their sequential model building nature. Bayesian QTL mapping methods (Satagopan et al. 1996; Sillanpää and Arjas 1998; Stephens and Fisch 1998; Yi and Xu 2000, 2001; Hoeschele 2007) have been developed, in particular, to detect multiple QTL by treating the number of QTL as a random variable and modeling it specifically using reversible-jump Markov chain Monte Carlo (MCMC) (Green 1995). Due to the variable dimensionality of the parameter spaces associated with different models (different numbers of QTL), one must take care of acceptance probabilities for such changes in dimension, which in practice may not be handled correctly (Ven 2004). One leading approach to variable selection in QTL analysis is the Bayesian analysis based on the composite model space framework (Godsill 2001, 2003), first introduced by Yi (2004) to the genetic mapping community. Reversible-jump MCMC (Green 1995) and stochastic search variable selection (SSVS) (George and McCulloch 1993) are special cases of this analysis. An alternative to variable selection with SSVS is shrinkage methods (e.g., the lasso method of Tibshirani 1996), which shrink the effects of unimportant variables near zero. The Bayesian shrinkage methods of Xu (2003) and Wang et al. (2005) place simple normal priors on QTL effects. While they can be modified easily, the specific priors used in Xu (2003) and Wang et al. (2005) induce improper posteriors (Ter Braak et al. 2005).

In this article, for RIX data, we extend the fixed-effect model of Xu (2003) to a mixed-effects model, where the complex relationship structure among RIX samples is specifically dealt with through random polygenic effects. To avoid improper posteriors, we apply the prior modification of ter Braak et al. (2005). To the best of our knowledge, this is the first simultaneous multiple-QTL mapping method specifically designed for RIX data. This article is organized as follows. In statistical method, we first introduce the RIX experiment, and then we propose a mixed-effects model and describe a Bayesian variable selection procedure. In simulation study, extensive simulations are performed to evaluate the proposed model and to compare several RIX designs. Summary comments are given in the discussion.

STATISTICAL METHOD

In this section, after describing the RIX design, we propose the multiple-QTL model and introduce the Bayesian variable selection procedure.

RIX design:

The RIX panel is created as F₁ progenies of RI intercross. For L RI lines, a total of L(L – 1) reciprocal RIX and L(L – 1)/2 nonreciprocal RIX can be generated (see Figure 1 in Zou et al. 2005). For simplification and without loss of generality, in the sequel, we consider the nonreciprocal RIX. Let the parental RI lines be RI₁, RI₂, … , RI_L, respectively, and denote the derived RIX from the RI_i × RI_j mating as RIX_ij, where i, j = 1, … , L with i < j or, alternatively, as RIX_k, where k = 1, 2, … , L(L – 1)/2 for ease of notation. Let n (≤L(L – 1)/2) be the total number of RIX sampled and p be the total number of genetic markers. Further, let the phenotypes (the dependent variable) be y_i (i = 1, … , n) and the discrete marker genotypes be m_ij (i = 1, … , n, j = 1, … , p). We set m_ij to −1, 0, and 1, referring to genotypes aa, Aa, and AA, respectively.

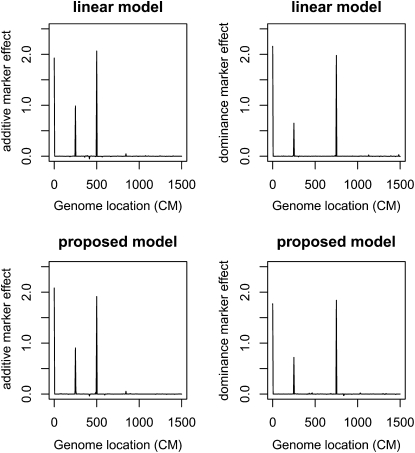
Figure 1.—

Bayesian QTL estimates from data simulated under case 1 where no polygenic effect exists (i.e., ${\mathit{\sigma }}_a^2=0$). The top two panels are from the linear model, and the bottom two panels are from the proposed mixed-effects model. The height of each vertical line refers the posterior mean estimate of each marker.

Model:

It is often acknowledged that quantitative traits are controlled by both major genes and polygenes, that is, genes with intermediate and small effects, respectively. The aggregating effect of polygenes may greatly reduce our ability to map major genes if not modeled carefully. Visscher and Haley (1996) modeled polygenic effects for data derived from commonly used experimental crosses. Methods using Wright's relationship matrix to accommodate different correlations between related individuals have also been developed for pedigree data and diallel data (Goldgar 1990; Amos 1994; Zhu and Weir 1996; Xu 1998).

RIX data can be viewed as the last generation of a large pedigree that originated from a set of inbred founder strains. Therefore, methods for analyzing pedigree data can be directly applied. In our model, we assume that major QTL and polygenes affect the trait of interest independently, and the aggregating polygenic effect is normally distributed. For simplicity, we assume that all putative QTL are located on markers, a reasonable assumption with dense maps. For sparse maps, we can employ interval mapping ideas of Wang et al. (2005) and Huang et al. (2010). Specifically, we fit the mixed-effects model

$$y_i=\mathit{\mu }+{\displaystyle \sum _{j=1}^p\left[x_{ij}{a}_j+w_{ij}{b}_j\right]}+{\displaystyle \sum _{k=1}^L{a}_{ik}}{\mathit{\alpha }}_k+e_i,$$ (1)

where μ is the overall mean, a_j and b_j are the additive and dominant effects of the jth putative QTL with $x_{ij}=\sqrt{2}{m}_{ij}$ and w_ij = 1 − 2|m_ij|, a_ik is the number of parents of RIX_i that are equal to RI_k, and the random polygenic effect α_k follows $N\left(\mathrm{0,}{\mathit{\sigma }}_a^{\mathrm{2}}\right)$ (k = 1, 2, … , L) and the random error e_i follows $N\left(0,{\mathit{\sigma }}_{\mathrm{0}}^{\mathrm{2}}\right)$ (i = 1, 2, … , n) and they are independent of each other. Let A be an n × L matrix whose (i, k)th element equals a_ik. Clearly, ${\displaystyle {\sum }_{k=1}^L{a}_{ik}}\equiv 2$ for all i = 1, 2, … , n since each RIX has two and only two parents. In the model above, we assume that the polygenic effect is additive, which can be easily extended by adding a random dominance polygenic term in model (1).

In the above model, the observed data are y = {y_i}, marker genotypes M = {m_ij}, and parental RI information (i.e., matrix A). The unobserved variables include $\mathit{\mu },{\mathit{\sigma }}_0^2,\text{and}{\mathit{\sigma }}_a^2;$ the regression coefficients a = {a_j}, b = {b_j}; and the random effects α = {α_k}. Below we describe the prior distributions of the unobserved variables.

Prior specifications:

1. For μ: p(μ) ∝ 1.

2. For the a_j’s and b_j’s: $a_j\mathrm{\sim }N\left(0,{\mathit{\sigma }}_j^2\right),b_j\mathrm{\sim }N\left(0,v_j^2\right)$.

3. For ${\mathit{\sigma }}_0^2:p\left({\mathit{\sigma }}_0^2\right)\mathrm{\propto 1/}{\mathit{\sigma }}_{\mathrm{0}}^{\mathrm{2}}$.

4. For ${\mathit{\sigma }}_a^2:p\left({\mathit{\sigma }}_a^2\right)\mathrm{\propto }{\left({\mathit{\sigma }}_a^2\right)}^{\mathit{\delta }\mathrm{-1}}.$

Further, for hyperparameters ${\mathit{\sigma }}_j^2$ and $v_j^2,$ we assign the following priors:

1. $p\left({\mathit{\sigma }}_j^2\right)\mathrm{\propto }{\left({\mathit{\sigma }}_j^2\right)}^{\mathit{\delta }\mathrm{-1}}$ and $p\left({\mathit{v}}_j^2\right)\mathrm{\propto }{\left({\mathit{v}}_j^2\right)}^{\mathit{\delta }\mathrm{-1}}.$

Here δ (0 < δ ≤ $\frac{1}{2}$) is used to ensure that the posterior distribution is proper (ter Braak et al. 2005).

$\mathrm{Let}{\sigma }^2=\left\{{\sigma }_j^2\right\}\mathrm{and}{v}^2=\left\{{\mathrm{v}}_{\mathrm{j}}^2\right\}$.

The specific priors above result in known marginal conditional distributions for all variables; therefore simple Gibbs sampling can be performed, which we describe below.

MCMC algorithm for posterior computation:

We first initiate μ, a, b, ${\mathit{\sigma }}_0^2,$ ${\mathit{\sigma }}_a^2,$ σ², and v². Since the joint posterior distribution

$$\begin{array}{l}p(\mathit{\mu },\mathbf{a},\mathbf{b},\mathbf{\alpha },{\mathbf{v}}^{\mathbf{2}},{\mathbf{\sigma }}^2,{\mathit{\sigma }}_0^2,{\mathit{\sigma }}_a^2|\mathbf{y})\\ \propto p\left(\mathbf{y}\right|\mathit{\mu },\mathbf{a},\mathbf{b},\mathbf{\alpha },{\mathbf{v}}^2,{\mathbf{\sigma }}^2,{\mathit{\sigma }}_0^2,{\mathit{\sigma }}_a^2\left)p\right(\mathit{\mu },\mathbf{a},\mathbf{b},\mathbf{\alpha },{\mathbf{v}}^2,{\mathbf{\sigma }}^2,{\mathit{\sigma }}_0^2,{\mathit{\sigma }}_a^2),\end{array}$$

where

$$\begin{array}{l}p\left(\mathbf{y}\right|\mathit{\mu },\mathbf{a},\mathbf{b},\mathbf{\alpha },{\mathbf{v}}^2,{\mathbf{\sigma }}^2,{\mathit{\sigma }}_0^2,{\mathit{\sigma }}_a^2)\propto ({\mathit{\sigma }}_0^2)-n/2\\ \times \exp {\displaystyle \left\{-\frac{{\sum }_{i=1}^n{(y_i-\mathit{\mu }-{\displaystyle {\sum }_{j=1}^P[}{x}_{ij}{a}_j+w_{ij}{b}_j]-{\displaystyle {\sum }_{k=1}^L{a}_{ik}}{\mathit{\alpha }}_k)}^2}{2{\mathrm{\sigma }}_0^2}\right\}},\end{array}$$

we perform the following Gibbs sampling steps. Superscripts (t) and (t + 1) signify the MCMC iteration steps and we set t = 0 for all initial values.

• Step 1. Updating μ: μ^(t+1) is drawn from the normal distribution with mean $\left(1/n\right){\displaystyle {\sum }_{i=1}^n\left(y_i-{\displaystyle {\sum }_{j=1}^P\left[x_{ij}{a}_j^{\left(t\right)}+w_{ij}{b}_j^{\left(t\right)}\right]-{\displaystyle {\sum }_{k=1}^L{a}_{ik}}{\mathit{\alpha }}_k^{\left(t\right)}}\right)}$ and variance ${\mathit{\sigma }}_0^{2\left(t\right)}\mathrm{/}n.$

• Step 2. Updating a_j and b_j (j = 1, … , p), a_j^(t+1) is sampled from the normal distribution with mean

$$\begin{array}{l}{\left({\displaystyle \sum _{i=1}^n{x}_{ij}^2}+\frac{{\mathit{\sigma }}_0^{2\left(t\right)}}{{\mathit{\sigma }}_j^{2\left(t\right)}}\right)}^{-1}{\displaystyle \sum _{i=1}^n{x}_{ij}}(y_i-{\mathit{\mu }}^{(t+1)}-{\displaystyle \sum _{j=1}^P{w}_{ij}}{b}_j^{\left(t\right)}-{\displaystyle \sum _{k=1}^L{a}_{ik}}{\mathit{\alpha }}_k^{\left(t\right)}\\ -{\displaystyle \sum _{l<j}{x}_{il}}{a}_l^{(t+1)}-{\displaystyle \sum _{l>j}{x}_{il}}{a}_l^{\left(t\right)})\end{array}$$

and variance

$${\left({\displaystyle \sum _{i=1}^n{x}_{ij}^2}+\frac{{\mathit{\sigma }}_0^{2\left(t\right)}}{{\mathit{\sigma }}_j^{2\left(t\right)}}\right)}^{-1}{\mathit{\sigma }}_0^{2\left(t\right)},$$

while b_j^(t+1) is drawn from the normal distribution with mean

$$\begin{array}{l}{\left({\displaystyle \sum _{i=1}^n{w}_{ij}^2}+\frac{{\mathit{\sigma }}_0^{2\left(t\right)}}{v_j^{2\left(t\right)}}\right)}^{-1}{\displaystyle \sum _{i=1}^n{w}_{ij}}(y_i-{\mathit{\mu }}^{(t+1)}-{\displaystyle \sum _{j=1}^P{x}_{ij}}{a}_j^{(t+1)}-{\displaystyle \sum _{k=1}^L{a}_{ik}}{\mathit{\alpha }}_k^{\left(t\right)}\\ -{\displaystyle \sum _{l<j}{w}_{il}}{b}_l^{(t+1)}-{\displaystyle \sum _{l>j}{w}_{il}}{b}_l^{\left(t\right)})\end{array}$$

and variance

$${\left({\displaystyle \sum _{i=1}^n{w}_{ij}^2}+\frac{{\mathit{\sigma }}_0^{2\left(t\right)}}{v_j^{2\left(t\right)}}\right)}^{-1}{\mathit{\sigma }}_0^{2\left(t\right)}.$$

• Step 3. Updating ${\sigma }_0^2:$ The residual variance is sampled from the scale-inverted χ²-distribution, ${\displaystyle {\sum }_{i=1}^n{\left(y_i-{\mathit{\mu }}^{(t+1)}-{\displaystyle {\sum }_{j=1}^P{x}_{ij}}{a}_j^{(t+1)}-{\displaystyle {\sum }_{k=1}^L{a}_{ik}}{\mathit{\alpha }}_k^{\left(t\right)}-{\displaystyle {\sum }_{j=1}^P{w}_{ij}}{b}_j^{(t+1)}\right)}^2}/{\chi }_n^2.$

• Step 4. Updating σ_j² and v_j² (j = 1, … , p), ${\sigma }_j^{2\left(t+1\right)}$ is sampled from the scale-inverted χ²-distribution, $a_j^{2(t+1)}/{\mathrm{\chi }}_{1-2\mathit{\delta }}^2,$ and $v_j^{2\left(t+1\right)}$ is sampled from the scale-inverted χ²-distribution, $b_j^{2\left(t+1\right)}/{\mathrm{\chi }}_{1-2\mathit{\delta }}^2.$

• Step 5. Updating α_k (k = 1, … , L), α_k^(t+1) is drawn from the normal distribution with mean

$$\begin{array}{l}{\left({\displaystyle \sum _{i=1}^n{a}_{ik}^2}+\frac{{\mathit{\sigma }}_0^{2(t+1)}}{{\mathit{\sigma }}_a^{2\left(t\right)}}\right)}^{-1}{\displaystyle \sum _{i=1}^n{a}_{ik}}(y_i-{\mathit{\mu }}^{(t+1)}-{\displaystyle \sum _{j=1}^P{x}_{ij}}{a}_j^{(t+1)}-{\displaystyle \sum _{j=1}^P{w}_{ij}}{b}_j^{(t+1)}\\ -{\displaystyle \sum _{l<k}{a}_{il}}{\mathit{\alpha }}_l^{(t+1)}-{\displaystyle \sum _{l>k}{a}_{il}}{\mathit{\alpha }}_l^{\left(t\right)})\end{array}$$

and variance

$${\left({\displaystyle \sum _{i=1}^n{a}_{ik}^2}+\frac{{\mathit{\sigma }}_0^{2(t+1)}}{{\mathit{\sigma }}_a^{2\left(t\right)}}\right)}^{-1}{\mathit{\sigma }}_0^{2(t+1)}.$$

• Step 6. Updating ${\mathit{\sigma }}_a^2$, the random effect variance is sampled from the scale-inverted χ²-distribution, ${\displaystyle {\sum }_{k=1}^L{\mathit{\alpha }}_k^{2\left(t+1\right)}}/{\mathrm{\chi }}_{L-2\mathit{\delta }}^2.$

After this round of sampling, we complete one sweep of the MCMC and are ready to continue our sampling for the next round by repeating steps 1–6 with the new parameter values. When the chain converges, the sampled parameters approximately follow the joint posterior distribution. For any parameter of interest, one can easily obtain, for example, its posterior means and variances from the joint posterior sample.

SIMULATION STUDY

In this section, we ran extensive simulations to evaluate the performance of the proposed Bayesian method. Specifically, we compared the proposed mixed-effects model with the linear regression model, which ignores the polygenic effect. We also investigated several RIX designs and compared their abilities in mapping major QTL.

Parental RI genotypes were simulated in R/qtl (Broman et al. 2003), from which RIX genotypes and phenotypes were generated accordingly. For all simulations, we set the true population mean (μ) and residual variance $\left({\mathit{\sigma }}_0^2\right)$ to 5.0 and 10, respectively. A single chromosome with total length 15 M was simulated, on which 301 evenly spaced markers (resulting in 300 5-cM intervals) are located. The number of QTL simulated was 4 or 11, and their corresponding genetic effects and locations are summarized in Tables 1 and 2. Three ${\mathit{\sigma }}_a^2$ values, 0, 1, and 8, were simulated, representing the situations where no, low, and high polygenic effects exist, respectively.

TABLE 1.

Locations and sizes of the four simulated QTL

QTL no.	Position (cM)	Additive effect	Dominant effect
1	0	2	2
2	250	1	1
3	500	2	0
4	750	0	2

TABLE 2.

Locations and sizes of the 11 simulated QTL

QTL no.	Position (cM)	Additive effect	Dominant effect
1	0	$\sqrt{10}$	$\sqrt{10}$
2	150	$\sqrt{5}$	$\sqrt{5}$
3	300	$\sqrt{2.5}$	$\sqrt{2.5}$
4	450	$\sqrt{2}$	$\sqrt{2}$
5	600	$\sqrt{1.25}$	$\sqrt{1.25}$
6	750	$\sqrt{1.25}$	$\sqrt{1.25}$
7	900	$\sqrt{0.625}$	$\sqrt{0.625}$
8	1050	$\sqrt{0.625}$	$\sqrt{0.625}$
9	1200	$\sqrt{0.25}$	$\sqrt{0.25}$
10	1350	$\sqrt{0.25}$	$\sqrt{0.25}$
11	1500	$\sqrt{0.25}$	$\sqrt{0.25}$

From 100 RI parental lines, a total of 5000 unique nonreciprocal RIX can be produced. For a realistic sample size n that we set to 300 unless specified, we considered the following five designs: (1) the complete-pair design, selecting 25 RI lines randomly and generating all 300 possible nonreciprocal RIX; (2) the loop design (a clockwise mating scheme described in Zou et al. 2005), ordering the 100 RI lines randomly to form a circle and then mating each RI line (clockwise) with the next 3 RI lines after it (i.e., RI₁ mated with RI₂, RI₃, and RI₄ and RI₂ mated with RI₃, RI₄, and RI₅, and so on); (3) the 50 complete-independent design, ordering the 100 RI lines randomly and mating RI₁ with RI₂, RI₃ with RI₄, RI₅ with RI₆, and so on. The maximal number of RIX that can be generated from this design is L/2. To achieve the sample size of 300, we may alternatively employ (4) the replicated-complete-independent design, sampling six offspring instead of one from each RI_i × RI_j mating in design 3, or (5) the 300 complete-independent design, generating 300 independent RIX samples from 600 RI lines as in design 3.

For each simulated datum, the MCMC sampler was run for a total of 63,000 cycles. We set the initial values of μ, a, and b to 0. The initial values of ${\mathit{\sigma }}_0^2,{\mathit{\sigma }}_a^2,{\mathbf{\sigma }}^2,$ and v² were all set to 1. We further set δ to 0.001. The first 3000 cycles were discarded as burn-in, and the remainder of the chain was thinned by keeping 1 of every 50 samples, resulting in a total of 1200 samples for post-MCMC analysis. All the analysis was done in MATLAB and the MATLAB source code is available at http://bios.unc.edu/∼fzou/software/BayesianRIX.

We also analyzed each datum with the linear model

$$y_i=\mathit{\mu }+{\displaystyle \sum _{j=1}^p[}{x}_{ij}{a}_j+w_{ij}{b}_j]+e_i,$$ (2)

the gold model for RIX data when the true polygenic effect is zero. All the priors in this linear model were set the same as their counterparts in model (1).

• Case 1. Four QTL and ${\mathit{\sigma }}_a^2=0:$ Under this setup, we expect model (2) to perform better than the mixed-effects model (1). The question, more specifically, concerns how much better the linear model (2) is. Figure 1 displays the posterior mean estimates for one simulated datum. The two models perform nearly the same, indicating very little power loss of the proposed mixed-effects model.

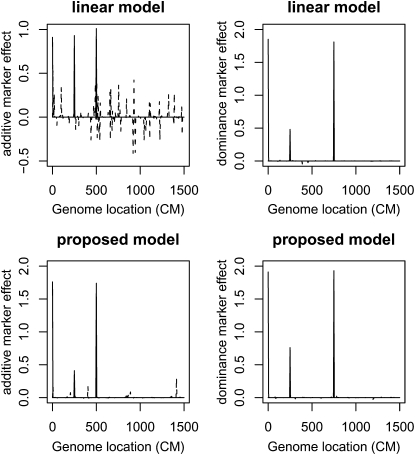
• Case 2. Four QTL and ${\mathit{\sigma }}_a^2=8:$ When the polygenic effect is not zero, Zou et al. (2005) and Tsaih et al. (2005) have shown that linear models that ignore the unbalanced relatedness of RIX result in high false positive rates. Figure 2 clearly reflects this. The linear model produces large estimated additive effects for many null markers. In contrast, the four simulated QTL are mapped successfully by the mixed-effects model and most of the null markers have their posterior means close to 0. Table 3 shows that for the four simulated QTL, their estimated genetic effects from the mixed-effects model are close to those simulated. The second QTL located at 250 cM is the weakest and its estimated genetic effects depart most from its true genetic values.

Figure 2.—

Bayesian QTL estimates from data simulated under case 2 where polygenic effect exists $\left({\mathit{\sigma }}_a^2=8\right).$ The solid lines are for the markers located at the simulated QTL and the dashed lines are for the rest of the markers. See Figure 1 legend for details.

TABLE 3.

Estimated QTL effects from data under case 2 with four QTL and ${\mathit{\sigma }}_{\mathit{a}}^2=8$

		Additive effect				Dominant effect
QTL	Position (cM)	True	a	aL	aU	True	b	bL	bU
1	0	2	1.76	0.52	2.86	2	1.91	1.54	2.28
2	250	1	0.41	0	1.17	1	0.77	0.40	1.14
3	500	2	1.75	0.65	2.74	0	0	0	0
4	750	0	0	0	0	2	1.93	1.57	2.29

a, posterior mean of additive effect; a_L and a_U, the 5th and 95th percentiles of posterior samples for the additive effect. Similarly, b, b_L, and b_U are defined for the dominant effect.

In summary, the mixed-effects model performs substantially better than the linear model. Interestingly, there is no significant difference between the two models for detecting dominance effects. This may be attributed to the fact that the simulated polygenic effect is additive, which is less likely confounded with the dominance QTL effects.

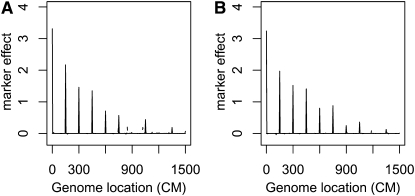
• Case 3. Eleven QTL and ${\mathit{\sigma }}_a^2=1:$ Under this setup, the heritabilities of 11 QTL decrease from left to right. Figure 3 summarizes the analysis results. The estimated genetic effects of the top 6 QTL are significantly different from 0, and the smallest QTL that the proposed method identified explains ∼2% of the phenotypic variation.

Figure 3.—

Bayesian QTL estimates from data simulated under case 3. (A) The additive effect; (B) the dominant effect. See Figure 2 legend for details.

All the above results are based on data generated from the loop design. Next, we compared the loop design with the other four designs. For each design, we simulated 100 data sets with the genetic configuration from case 2 (i.e., four QTL and ${\mathit{\sigma }}_a^2=8$). The data from the two complete-independent designs were analyzed by the linear model, the correct model for the data. For analysis of the data from the loop, the 300 replicated-complete-independent, and the complete-pair designs, we used the mixed-effects model. For the data generated from the 300 replicated-complete-independent design, we also averaged the phenotypes across the six offspring from each RI_i × RI_j mating and analyzed the 50 independent averages by the linear model. Table 4 summarizes the mean squared error (MSE) of the posterior mean estimates of the additive QTL effects. As expected, the data from the 300 complete-independent design perform the best. The loop design is ranked second best and has much higher efficiency than the rest of the designs. Interestingly, though the sample size of the complete-pair design is 300, its power for mapping major QTL is only slightly higher than that of the 50 complete-independent design where the sample size is 50. This is largely due to the fact that we have a large polygenic effect. In summary, for a fixed sample size, we recommend sampling as many independent RIX as possible. If the number of independent RIX is too small, the loop design should be our next choice. One advantage of the loop design over the independent RIX design is that it allows estimation of the polygenic effect but the independent RIX design does not.

TABLE 4.

Comparison of the five designs based on 100 simulations under case 2

Design	Position (0 cM)	Position (250 cM)	Position (500 cM)
300 complete independent	0.17	0.57	0.19
Loop	1.30	0.89	1.46
Replicated complete independenta	3.36	0.94	3.33
Replicated complete independentb	3.45	0.95	3.34
Complete pair	3.50	0.98	3.38
50 complete independent	3.54	1.00	3.58

For each QTL, the mean squared error (MSE) of the posterior mean estimate of the additive effect is reported.

^aIndividual phenotypes of RIX samples were analyzed via the proposed mixed-effects model (1).

^bAverage phenotypes of replicated RIX samples were analyzed via the linear model (2).

DISCUSSION

Recombinant inbred intercrosses, produced by generating all or a subset of the potential F₁ hybrids between pairs of RI lines, increase the number of available genotypes from L RI lines to L(L − 1)/2 nonreciprocal RIX and L(L − 1) reciprocal RIX. Unlike the parental RI lines whose genotypes are homozygous, the genetic structure of RIX resembles that of F₂ animals, reducing the phenotypic anomalies associated with inbred genomes. One of the great achievements of using RIX animals for QTL mapping is the ongoing CC project (Threadgill et al. 2002). The CC project plans to generate and maintain ∼1000 CC RI lines for scientific research. With such large numbers of RI lines available, our ability to map complex traits can be greatly increased. Because RIX genotypes can be directly inferred from the genotypes of their parental RIs, the genotyping effort required for the CC project is to genotype only the CC RI lines. Further, due to the renewability of CC mice, new RIX mice can be selectively produced for testing the accuracies of estimated genetic architectures.

In all our simulations, the parameter δ is set to 0.001 to ensure a proper posterior distribution. We have also analyzed the simulated data with δ = 0. The new analysis results are shown in supporting information, File S1, Figure S1, and Figure S2. Though in theory, the posterior distribution from the priors with δ = 0 is improper (ter Braak et al. 2005), this adjustment makes very little difference in practice.

In this article, we have compared several RIX designs. For a given sample size, the complete-independent design performs the best. But the complete-independent design is limited by the number of available RI lines and lacks ability in estimating polygenic effects. In contrast, the loop design and the complete-pair design can generate large numbers of RIX. Between the two, the loop design performs better. We highly recommend the use of the loop design when the number of RI lines is limited. The loop design also provides estimation of polygenic effects for the heritability calculation.

For simplicity, our model assumes no maternal or paternal effects and we consider only nonreciprocal RIX. One major advantage of RIX over RI or F₂ populations is that parent-of-origin effects can be tested with reciprocal RIX. Now we briefly describe how to extend the proposed model for parent-of-origin effects. For the jth QTL with additive parent-of-origin effect, we replace the term x_ija_j in (1) with x_ij(p)a_jp + x_ij(m)a_jm, where x_ij(p) [and x_ij(m)] = 0 or 1 depending on whether RIX_i gets an A allele from its father (and mother). Any deviation of |a_jp – a_jm| from 0 suggests a parent-of-origin effect. Polygenic parent-of-origin effects can be similarly modeled. Further, our model basically considers only nucleotide effects, which can be extended as well for modeling founder allelic effects. For example, for the additive effects of the eight CC founder alleles, we can replace the term x_ija_j + w_ijb_j in (1) with x_ijβ_j, where β_j = (β_1j, … , β_8j)^T and the kth element of x_ij is 2, 1, or 0 depending on whether RIX_i inherits 2, 1, or 0 copies of the kth founder allele (k = 1, … , 8) at the jth locus. Therefore, β_kj represents the kth founder allelic effect. Similarly, for a codominant QTL model, we set β_j as a vector of length 36 (corresponding to the 36 genotypes formed by the eight CC founder alleles). We can further treat the QTL effects as random as traditionally done for pedigree data. For example, for an additive model, we let ${\mathbf{\beta }}_j\sim N(0,{\mathit{\sigma }}_{aj}^2\mathbf{I})$. This would potentially increase the mapping power as the number of parameters is dramatically reduced.