How geometry and internal bias affect the accuracy of eukaryotic gradient sensing

Abstract

Many motile eukaryotic cells determine their direction by measuring external chemical gradients through the binding of ligands to membrane bound receptors. This process is limited by fluctuations arising from the binding process and from the diffusion of the ligand molecules. Here, we apply estimation-theoretic methods to determine the physical limits of gradient sensing for cells that are non-circular and for cells that have an internal bias. Specifically, we derive theoretical expressions for the accuracy of gradient sensing in elliptical cells. This accuracy for highly elliptical cells can significantly deviate from the gradient sensing limits derived for circular cells. Furthermore, we find that a cell cannot improve its sensing of the gradient steepness and direction simultaneously by elongating its cell body. Finally, we derive a lower bound on the accuracy of gradient sensing for cells that possess an internal bias and compare our analytical results with recent experimental findings.

I. INTRODUCTION

The response in biological systems to external stimuli is often limited by the inherent stochasticity of these stimuli. For example, the accuracy of human (and other vertebrate) vision at low light intensities approaches a fundamental limit set by statistical fluctuations of the number of absorbed photons [1, 2]. Another example includes the embryo patterning along the anterior-posterior axis of the fly Drosophila melanogaster which is primarily determined by concentration profiles of certain morphogens [3]. The accuracy of the resulting pattern is limited by the noise levels in these profiles. A final example is provided by chemotaxis, the directed movement of cells up or down a chemical gradient. In both prokaryotic chemotaxis, where cells measure and compare concentration signals over time [4, 5], and in eukaryotic chemotaxis, where cells measure concentration differences in space [6, 7], the precision of gradient sensing is limited by the stochastic binding of diffusing chemical molecules (ligands) to specific chemoreceptors on the cell membrane.

In this paper, we will apply techniques from estimation theory, which attempts to estimate the values of parameters based on measured data that contain a random component [8], to eukaryotic gradient sensing. Even though our approach and results are applicable in a general way, we will focus mainly on the social amoeba Dictyostelium discoideum, a well-characterized model system [9, 10]. Specific G-protein coupled receptors on the Dictyostelium cell membrane bind and detect the chemoattractants in the surrounding medium. This results in an asymmetric distribution of ligand-occupied receptors, which further activates multiple second-messenger pathways inside the cell and drive the extension of pseudopods preferentially in the direction of the chemoattractant gradient. Due to fluctuations in the ligand binding to chemoreceptors, the receptor signal is inherently noisy, as demonstrated by recent single-molecule imaging experiment [11]. Surprisingly, Dictyostelium cells exhibit extremely high sensitivity to gradients, as they have been observed to be able to detect a 1 – 2% difference in chemical concentration across the cell length [12, 13]. The difference in receptor occupancy between the front and back halves of a cell in these shallow gradients can be calculated to be 10–30. This raises a puzzle about eukaryotic chemotaxis: how can cells reliably acquire the gradient information from such a noisy receptor signal?

In 1977, Berg and Purcell analyzed bacterial chemotaxis and demonstrated that the limit of uncertainty of concentration sensing is set by the diffusion of ligand particles [14]. Their seminal work has been extended by many others [15–19]. The results of Berg and Purcell, however, do not completely carry over to eukaryotic cells, which employ a spatial sensing mechanism. In this mechanism, and in contrast to prokaryotic chemotaxis, cells use the spatial asymmetry (including the gradient steepness and direction) to direct their motion. A number of studies have been carried out to reveal the limits to spatial gradient sensing, but are either only applicable to idealized mechanisms that ignore the receptor kinetics [18], adopt heuristic signaling models [20, 21] or use a simplified geometry [22]. We recently addressed this problem for circular cells using a general statistical mechanical approach, where we view the surface receptors as a (possibly coupled) spin chain and treat the chemical gradient as a perturbation field [23]. By calculating the system’s partition function, we were able to derive the gradient sensing limits for either independent receptors or receptors exhibiting cooperativity. Furthermore, using information theoretical concepts and comparing theoretical results with experiments of chemotaxing Dictyostelium cells, we have shown that for shallow gradients and low background concentrations, the accuracy of gradient sensing is upper-bounded by fluctuations at the receptor level [13, 24].

In this paper, we will first revisit the spatial gradient sensing problem for circular cell shapes using purely estimation-theoretic methods (Section II). This will be the foundation for our extension to the elliptical cell shapes in the next section (Section III). Finally, we will examine how a possible intracellular bias can affect the perceived gradient and compare our results with recent experimental data (Section IV).

II. GRADIENT SENSING FOR A CIRCULAR CELL

We revisit the gradient sensing problem which we have examined in our previous paper using the method of maximum likelihood estimate (MLE) [8, 19, 23]. Consider a circular cell with diameter L placed in a chemoattractant gradient and assume that there are N receptors uniformly distributed on the cell perimeter. The angular coordinates of these receptors are denoted by ϕ_n for n = 1, …, N, which satisfy the uniform distribution P(ϕ_n) = 1/(2π). We further assume that the gradient field takes an exponential profile as has recently been realized in experiments [13, 25]. Then the local concentration at the n-th receptor can be expressed as $C_n=C_{0}exp\left[\frac{p}{2}cos({\varphi }_n-\phi )\right]$, where C₀ is the ambient (mean) concentration, $p\equiv \frac{L}{C_0}\mid \overrightarrow{\nabla }C\mid$ defines the gradient steepness that quantifies the percentage concentration change across the cell length L, and φ denotes the gradient direction. Each receptor switches independently between two states, either empty (0) or occupied (1), with transition rates determined by the local concentration and the relevant chemical kinetics. Therefore, these receptors in a single snapshot constitute a series of independent Bernoulli random variables, represented by

$$x_n=\{\begin{array}{lll}1,\hfill & \text{with}\text{probability}\hfill & P_n,\hfill \\ 0,\hfill & \text{with}\text{probability}\hfill & 1-P_n,\hfill \end{array}$$ (1)

for n = 1, …, N. For simple ligand-receptor kinetics, the occupancy probability of the n_th receptor is P_n = C_n/(C_n + K_d), where K_d = k₋/k₊ is the dissociation constant. The probability mass distribution for Eq. (1) can be expressed as:

$$f_n(x_n\mid \mathbf{\Theta })=P_n^{x_n}{(1-P_n)}^{1-x_n},\text{for}{x}_n\in \{0,1\},$$ (2)

where Θ ≡ {p, φ} represents the parameters to estimate. Therefore, the likelihood function for a sample of N independent receptors is given by

$$\mathcal{L}(\mathbf{\Theta }\mid x_1,\dots ,x_N)=f(x_1,\dots ,x_N\mid \mathbf{\Theta })=\prod _{n=1}^N{f}_n(x_n\mid \mathbf{\Theta }),$$ (3)

and the log-likelihood function is

$$\begin{array}{l}ln\mathcal{L}=\sum _n\left[x_{n}ln\frac{C_n}{C_n+K_d}+(1-x_n)ln\frac{K_d}{C_n+K_d}\right]\\ =\sum _n{x}_{n}ln\frac{C_n}{K_d}+\sum _{n}ln\frac{K_d}{C_n+K_d}\\ =\frac{1}{2}\sum _n{x}_{n}pcos({\varphi }_n-\phi )+ln\frac{C_0}{K_d}\sum _n{x}_n+{\int }_0^{2\pi }\frac{N}{2\pi }ln\left[\frac{K_d}{C_{0}exp[\frac{p}{2}cos(\varphi -\phi )]+K_d}\right]d\varphi \\ =\frac{pcos\phi }{2}\sum _n{x}_{n}cos{\varphi }_n+\frac{psin\phi }{2}\sum _n{x}_{n}sin{\varphi }_n+ln\frac{C_0}{K_d}\sum _n{x}_n-\frac{N{C}_0{K}_d{p}^2}{16{(C_0+K_d)}^2}+\mathcal{O}(p^4).\end{array}$$ (4)

Here, we introduce the transformation Θ_α = (α₁, α₂)^T ≡ (p cos φ, p sin φ)^T and define (z₁, z₂) ≡ (Σ_n x_n cos ϕ_n, Σ_n x_n sin ϕ_n) which measures the spatial asymmetry in the receptor occupancy. Then, we have $p^2={\alpha }_1^2+{\alpha }_2^2$, and for shallow gradients the log-likelihood function becomes

$$ln\mathcal{L}\approx \frac{{\alpha }_1{z}_1+{\alpha }_2{z}_2}{2}+ln\frac{C_0}{K_d}\sum _n{x}_n-\frac{N{C}_0{K}_d({\alpha }_1^2+{\alpha }_2^2)}{16{(C_0+K_d)}^2}.$$ (5)

The method of maximum likelihood estimates the unknown parameters by finding a value of Θ_α that maximizes 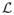(Θ_α|x₁, …, x_N), i.e.,

$${\widehat{\mathbf{\Theta }}}_{\alpha ,\mathbf{mle}}=arg\underset{{\mathbf{\Theta }}_{\alpha }}{max}\mathcal{L}({\mathbf{\Theta }}_{\alpha }\mid x_1,\dots ,x_N),$$ (6)

where the subscript “mle” denotes the maximum likelihood estimator. Since the logarithm is a continuous strictly increasing function over the range of the likelihood, the values which maximize the likelihood will also maximize its logarithm. Thus, the MLE can be found from ∂_α1 ln 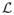= 0 and ∂_α2 ln 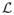= 0, with the following solution

$${\widehat{\mathbf{\Theta }}}_{\alpha ,\mathbf{mle}}=\left(\begin{array}{c}{\widehat{\alpha }}_1\\ {\widehat{\alpha }}_2\end{array}\right)=\frac{1}{\mu }\left(\begin{array}{c}{z}_1\\ z_2\end{array}\right),\text{where}\mu \equiv \frac{N{C}_0{K}_d}{4{(C_0+K_d)}^2}.$$ (7)

This solution is indeed the maximum of the likelihood function since it is the only turning point in Θ_α and the second derivative is strictly less than zero. By the properties of MLE, both α̂₁ and α̂₂ are asymptotically unbiased and normal as the sample size N goes to infinity, i.e., ${\widehat{\alpha }}_1\stackrel{d}{\to }\mathcal{N}({\alpha }_1,{\sigma }_1^2)$ and ${\widehat{\alpha }}_2\stackrel{d}{\to }\mathcal{N}({\alpha }_2,{\sigma }_2^2)$, where “ $\stackrel{d}{\to }$” denotes convergence in distribution. The asymptotic variances ${\sigma }_1^2$ and ${\sigma }_2^2$ can be derived from the inverse of the Fisher information matrix [8, 19]. This matrix has to be diagonal here as α₁ and α₂ are independent of each other. Thus, we have

$$\frac{1}{{\sigma }_{1,2}^2}=\langle {\left(\frac{\partial ln\mathcal{L}}{\partial {\alpha }_{1,2}}\right)}^2\rangle =-\langle \frac{{\partial }^{2}ln\mathcal{L}}{\partial {\alpha }_{1,2}^2}\rangle =\frac{\mu }{2},$$ (8)

where <> represents the expectation and the proof of the second equality can be found in [8]. This equality holds because ln 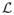is twice differentiable with respect to α₁ and α₂. From the relation α̂_1,2 = z_1,2/μ, we can see that < z_1,2 >= μα_1,2 and that the asymptotic variances of z₁ and z₂ are equal:

$${\sigma }^2={\mu }^2{\sigma }_{1,2}^2=2{\mu }^2/\mu =2\mu .$$ (9)

In addition, one can check that the covariance is Cov[z₁, z₂] = 0, as reflected in the affine form of the log-likelihood: ln = α₁z₁/2 + α₂z₂/2 + …. Thus, for small p, the joint probability density of z₁ and z₂ is [23, 25]:

$$P(z_1,z_2\mid {\mathbf{\Theta }}_{\alpha })=\frac{1}{2\pi {\sigma }^2}exp\left[-\frac{{(z_1-\mu {\alpha }_1)}^2+{(z_2-\mu {\alpha }_2)}^2}{2{\sigma }^2}\right].$$ (10)

As the one-to-one transformation of Θ̂_α,mle, the MLE of Θ = (p, φ)^T is given by

$${\widehat{\mathbf{\Theta }}}_{\mathbf{mle}}=\left(\begin{array}{c}\widehat{p}\\ \widehat{\phi }\end{array}\right)=\left(\begin{array}{c}{\mu }^{-1}\sqrt{z_1^2+z_2^2}\\ arctan(z_2/z_1)\end{array}\right).$$ (11)

If we introduce the complex random variable Z ≡ z₁+iz₂, then Z follows the complex Gaussian distribution, and in the polar coordinates Z = μp̂exp(iφ̂). Eq. (10) suggests that we can define a signal-to-noise (SNR) ratio

$$\kappa \equiv \frac{{\mu }^2{p}^2}{{\sigma }^2}=\frac{\mu p^2}{2}=\frac{N{p}^2{C}_0{K}_d}{8{(C_0+K_d)}^2}.$$ (12)

Again, by the properties of MLE, both p̂ and φ̂ tend to be unbiased and normal in the large N limit, i.e., $\widehat{p}\stackrel{d}{\to }\mathcal{N}(p,{\sigma }_p^2)$ and $\widehat{\phi }\stackrel{d}{\to }\mathcal{N}(\phi ,{\sigma }_{\phi }^2)$. It has been found numerically that the asymptotic normality becomes excellent when the SNR is larger than 9 [25, 26]. Similarly, the asymptotic variances ${\sigma }_p^2$ and ${\sigma }_{\phi }^2$ can be computed from the inverse of the Fisher information matrix with respect to Θ = (p, φ). The matrix is still diagonal due to the orthogonality of p and φ. Thus, we have

$$\frac{1}{{\sigma }_p^2}=\langle {\left(\frac{\partial ln\mathcal{L}}{\partial p}\right)}^2\rangle =-\langle \frac{{\partial }^{2}ln\mathcal{L}}{\partial p^2}\rangle =\frac{\mu }{2},$$ (13)

$$\frac{1}{{\sigma }_{\phi }^2}=\langle {\left(\frac{\partial ln\mathcal{L}}{\partial \phi }\right)}^2\rangle =-\langle \frac{{\partial }^{2}ln\mathcal{L}}{\partial {\phi }^2}\rangle =\frac{\mu p^2}{2},$$ (14)

or equivalently

$${\sigma }_p^2=\frac{8{(C_0+K_d)}^2}{N{C}_0{K}_d}\text{and}{\sigma }_{\phi }^2=\frac{8{(C_0+K_d)}^2}{N{p}^2{C}_0{K}_d}=\frac{1}{\kappa }.$$ (15)

The above results are identical to the ones we have recently derived in [23]. According to the Cramér-Rao inequality, the variances ${\sigma }_p^2$ and ${\sigma }_{\phi }^2$ represent the minimal uncertainties of gradient measurements from an instantaneous sampling of the receptor states [8].

If the cell in question integrates receptor signals over some time interval , then averaging over multiple measurements should obviously reduce the errors of gradient sensing. However, the error-reduction via temporal averaging is limited by the expected time it takes to perform an independent measurement. As shown in [17, 27], the time to make a single measurement is roughly twice the receptor correlation time τ. Hence, the number of independent measurements a cell can make within is about /(2τ). The correlation time can be decomposed as τ = τ_rec + τ_diff, where τ_rec = 1/(k₋ + C₀k₊) is the time-scale of receptor-ligand reaction and τ_diff ≅ N/(2πDLK_d) describes the diffusion noise correlation time [15, 17, 20, 21, 23]. Let η ≡ τ_diff/τ_rec, then the measurement is said to be reaction-limited if η ≪ 1 and diffusion-limited if η ≫ 1 [28]. Combining the above arguments, we find that integrating signals over yields better gradient estimate,

$${\sigma }_{p,\mathcal{T}}^2\simeq \frac{2\tau }{\mathcal{T}}{\sigma }_p^2=\frac{4{\tau }_{\mathit{rec}}(1+\eta )}{\mu \mathcal{T}}=\frac{16(1+\eta )(C_0+K_d)}{N\mathcal{T}k\_C_0}$$ (16)

We can derive similar results for the direction inference, since ${\sigma }_{\phi ,\mathcal{T}}^2={\sigma }_{p,\mathcal{T}}^2/p^2$. For typical eukaryotic cells, it has been estimated [17, 28] that η ≪ 1, which implies that ${\sigma }_{\phi ,\mathcal{T}}^2\simeq 16(C_0+K_d)/(N{p}^2\mathcal{T}k\_C_0)$.

An implicit assumption in the above derivation as well as in our previous paper [23] is that a cell can tell the location of each individual receptor. This is reflected in (z₁, z₂) ≡ (Σ_n x_n cos ϕ_n, Σ_n x_n sin ϕ_n) which keeps track of every individual receptor and its spatial position. Since the density of receptors on the cell surface can be high, one may argue that the cell cannot distinguish between receptors that are very close to each other. We can, however, easily relax this assumption by taking advantage of the Central Limit Theorem (CLT). To see this, we divide the cell surface into M small sensory sectors such that receptors in the same sector are responding to an almost identical chemical concentration. Therefore, receptors in the same sector can be regarded as independent and identically distributed (Bernoulli) random variables, and the state of each sector is represented by its receptor occupancy number which follows the binomial distribution. One can think of M as a quantity that reflects to what extent the cell can spatially distinguish its receptors. Of course, we want to ensure that the number of receptors in each sector N_s = N/M is large enough for the application of CLT. Here, we will choose M = 1000 and N = 40, 000, leading to N_s = 40. Now the local concentration at the m_th sector with angular position ϑ_m = 2πm/M is given by $C_m=C_{0}exp[\frac{p}{2}cos({\vartheta }_m-\phi )]$ for m = 1, …, M. Using the CLT, the number of occupied receptors in the m_th sector in a single snapshot, y_m, is approximately y_m = N_sC_m/(C_m + K_d) + η_m (m = 1, …, M), where the Gaussian random component η_m satisfies 〈η_m〉 = 0 and 〈η_mη_n〉 = δ_mnN_sC_mK_d/(C_m + K_d)² ≈ δ_mnN_sC₀K_d/(C₀ + K_d)² [20, 21, 28]. For small gradients, we can expand y_m around p:

$$y_m\approx \frac{N_s{C}_0}{K_d+C_0}+\frac{N_s{K}_d{C}_0}{2{(C_0+K_d)}^2}pcos({\vartheta }_m-\phi )+{\eta }_m.$$ (17)

We can see that the sector states, denoted by Y = {y₁, y₂, …, y_M}^T, constitute a vector of independent Gaussian random variables with space-dependent means but approximately identical variance ${\sigma }_s^2\equiv N_s{K}_d{C}_0/{(C_0+K_d)}^2$. Hereafter, the superscript symbol ^T means transpose. Eq. (17) suggest that one can view Y = {y₁, y₂, …, y_M}^T as observations of a sinusoidal signal corrupted by some white Gaussian noise. The likelihood function of Y conditional on Θ reads,

$$P(\mathbf{Y}\mid \mathbf{\Theta })\approx \frac{1}{{(2\pi {\sigma }_s^2)}^{M/2}}exp\left[-\frac{J(\mathbf{Y}\mid \mathbf{\Theta })}{2{\sigma }_s^2}\right],$$ (18)

where

$$J(\mathbf{Y}\mid \mathbf{\Theta })=\sum _{m=1}^M{\left(y_m-\frac{N_s{C}_0}{C_0+K_d}-\frac{{\sigma }_s^2}{2}pcos({\vartheta }_m-\phi )\right)}^2.$$ (19)

To maximize P(Y|Θ) is equivalent to minimize J(Y|Θ) which can be converted to a quadratic function by the one-to-one transformation Θ_α = (α₁, α₂)^T = (p cos φ, p sin φ)^T:

$$J(\mathbf{Y}\mid {\mathbf{\Theta }}_{\alpha })={(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}-\mathbf{H}{\mathbf{\Theta }}_{\alpha })}^T(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}-\mathbf{H}{\mathbf{\Theta }}_{\alpha }),$$ (20)

with

$${\mathbf{Y}}_{\mathbf{0}}=\frac{N_s{C}_0}{C_0+K_d}\left(\begin{array}{c}1\\ 1\\ \dots \\ 1\end{array}\right)\text{and}\mathbf{H}=\frac{{\sigma }_s^2}{2}\left(\begin{array}{cc}cos{\vartheta }_1& sin{\vartheta }_1\\ cos{\vartheta }_2& sin{\vartheta }_2\\ \dots & \dots \\ cos{\vartheta }_M& sin{\vartheta }_M\end{array}\right)$$

We can apply the formula of ordinary least squares (OLS) estimate to find the MLE solution that minimizes the quadratic objective function J(Y|Θ_α) and hence maximizes the likelihood function P(Y|Θ_α):

$${\widehat{\mathbf{\Theta }}}_{\alpha ,\mathbf{mle}}={({\mathbf{H}}^T\mathbf{H})}^{-1}{\mathbf{H}}^T(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}).$$ (21)

For large M, we have $\frac{1}{M}{\sum }_{m}cos{\vartheta }_m\approx \frac{1}{M}{\sum }_{m}sin{\vartheta }_m\approx 0,\frac{1}{M}{\sum }_{m}cos{\vartheta }_{m}sin{\vartheta }_m\approx 0$, and $\frac{1}{M}{\sum }_m{cos}^2{\vartheta }_m\approx \frac{1}{M}{\sum }_m{sin}^2{\vartheta }_m\approx 1/2$. Thus,

$$\begin{array}{l}{\widehat{\mathbf{\Theta }}}_{\alpha ,\mathbf{mle}}=\left(\begin{array}{c}{\widehat{\alpha }}_1\\ {\widehat{\alpha }}_2\end{array}\right)\approx \frac{4}{{\sigma }_s^4}{\left(\begin{array}{cc}M/2& 0\\ 0& M/2\end{array}\right)}^{-1}{\mathbf{H}}^T(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}})\\ =\frac{4{(C_0+K_d)}^2}{N{K}_d{C}_0}\left(\begin{array}{c}{\sum }_m{y}_{m}cos{\vartheta }_m\\ {\sum }_m{y}_{m}sin{\vartheta }_m\end{array}\right)\simeq \frac{1}{\mu }\left(\begin{array}{c}{z}_1\\ z_2\end{array}\right),\end{array}$$

where in the last line we have noticed that z₁ = Σ_n x_n cos ϕ_n ≃ Σ_m y_m cos ϑ_m and z₂ = Σ_n x_n sin ϕ_n ≃ Σ_m y_m sin ϑ_m for sufficiently large M. By inverse mapping, we recover the MLE of Θ given in Eq. (11). According to the asymptotic properties, ${\widehat{\mathbf{\Theta }}}_{\mathbf{mle}}={(\widehat{p},\widehat{\phi })}^T\stackrel{d}{\to }\mathcal{N}(\mathbf{\Theta },\mathbf{I}{(\mathbf{\Theta })}^{-1})$, with the Fisher information matrix:

$$\begin{array}{l}\mathbf{I}(\mathbf{\Theta })=\langle \frac{\partial lnP(\mathbf{Y}\mid \mathbf{\Theta })}{\partial {\mathbf{\Theta }}_i}\frac{\partial lnP(\mathbf{Y}\mid \mathbf{\Theta })}{\partial {\mathbf{\Theta }}_j}\rangle \\ \approx \left(\begin{array}{cc}M{\sigma }_s^2/8& 0\\ 0& M{\sigma }_s^2{p}^2/8\end{array}\right)\\ =\left(\begin{array}{cc}\mu /2& 0\\ 0& \mu p^2/2\end{array}\right).\end{array}$$ (22)

Then, we recover our main MLE results:

$$\widehat{p}={\mu }^{-1}\sqrt{z_1^2+z_2^2}\stackrel{d}{\to }\mathcal{N}\left(p,{\sigma }_p^2=\frac{2}{\mu }\right),$$ (23)

$$\widehat{\phi }=arctan(z_2/z_1)\stackrel{d}{\to }\mathcal{N}\left(\phi ,{\sigma }_{\phi }^2=\frac{2}{\mu p^2}\right).$$ (24)

III. GRADIENT SENSING FOR AN ELLIPTICAL CELL

Motile eukaryotic cells can become polarized and exhibit elongated shapes, which may affect the capacity of gradient sensing. In this section, we analyze a chemotactic cell with an elliptical geometry (Fig. 1). The ellipse can be described in parametric form (X(ω), Y(ω)) = (a cos ω, b sin ω), where a is the semi-major axis, b is semi-minor axis (thus b ≤ a) and 0 ≤ ω ≤ 2π. With ϑ = 0 measured from the major axis, the ellipse can also be described in polar coordinates by

FIG. 1.

Schematic representation of our model: an elliptical cell, covered with receptors, is placed in an exponential gradient. The angle between the direction of the gradient and the major axis of the elliptical cell is denoted by φ. The forward and backward rates k_± control the transition between the bound and unbound states for the receptors.

$$r(\vartheta )=\frac{ab}{\sqrt{{(asin\vartheta )}^2+{(bcos\vartheta )}^2}}=\frac{b}{\sqrt{1-{(\epsilon cos\vartheta )}^2}},$$ (25)

where $\epsilon \equiv \sqrt{1-{(b/a)}^2}$ is the eccentricity of the ellipse and measures how much the geometry deviates from being circular. Obviously, ω and ϑ are related through

$$tan\vartheta =tan\left[\frac{Y(\omega )}{X(\omega )}\right]=\frac{b}{a}tan\omega =\sqrt{1-{\epsilon }^2}tan\omega ,$$ (26)

$$\begin{array}{l}r(\vartheta )=b/\sqrt{1-{\epsilon }^2{cos}^2\vartheta }=\sqrt{X{(\omega )}^2+Y{(\omega )}^2}\\ =a\sqrt{1-{\epsilon }^2{sin}^2\omega }=r(\omega ).\end{array}$$ (27)

As before, we distribute the receptors uniformly along the cell circumference and divide the cell’s circumference into M sectors with identical arc lengths (containing N_s = N/M receptors). In the exponential gradient, the local concentration at the m_th sector with polar angle ϑ_m and radius r_m is

$$\begin{array}{l}{C}_m=C_{0}exp\left[\frac{\mid \overrightarrow{\nabla }C\mid }{C_0}{r}_{m}cos({\vartheta }_m-\phi )\right]\\ =C_{0}exp\left[\frac{p}{2}\frac{r_m}{a}cos({\vartheta }_m({\omega }_m)-\phi )\right]\\ =C_{0}exp\left[\frac{p}{2}cos({\vartheta }_m-\phi )\sqrt{1-{\epsilon }^2{sin}^2{\omega }_m}\right],\end{array}$$ (28)

where φ is the gradient direction measured from the major axis and p ≡ 2a|∇→C|/C₀ is the gradient steepness that quantifies the percentage concentration change across the major axis 2a. Here, we have used that

$$\begin{array}{l}{r}_m=r({\omega }_m)=a\sqrt{1-{\epsilon }^2{sin}^2{\omega }_m}\\ =r({\vartheta }_m)=b/\sqrt{1-{\epsilon }^2{cos}^2{\vartheta }_m}.\end{array}$$ (29)

As before, the receptor occupancy number is y_m = N_sC_m/(C_m + K_d) + η_m, for m = 1, …, M. For shallow gradients, we can expand y_m to leading order in p:

$$y_m\approx \frac{N_s{C}_0}{K_d+C_0}+\frac{N_s{K}_d{C}_0}{2(C_0+K_d)}\frac{r_m}{a}pcos({\vartheta }_m-\phi )+{\eta }_m.$$ (30)

where the random component η_m is approximately normal: 〈η_m〉 = 0 and $\langle {\eta }_m{\eta }_n\rangle ={\delta }_{mn}{N}_s{C}_m{K}_d/{(C_m+K_d)}^2\approx {\delta }_{mn}{N}_s{C}_0{K}_d/{(C_0+K_d)}^2={\delta }_{mn}{\sigma }_s^2$. Thus, the likelihood function of Y = {y₁, y₂, …, y_M}^T is $P(\mathbf{Y}\mid \mathbf{\Theta })\approx {(2\pi {\sigma }_s^2)}^{-M/2}exp[-\stackrel{\sim }{J}/(2{\sigma }_s^2)]$, where

$$\begin{array}{l}\stackrel{\sim }{J}=\sum _{m=1}^M{\left[y_m-\frac{N_s{C}_0}{C_0+K_d}-\frac{{\sigma }_s^2{r}_m}{2a}pcos({\vartheta }_m-\phi )\right]}^2\\ ={(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}-\stackrel{\sim }{\mathbf{H}}{\mathbf{\Theta }}_{\alpha })}^T(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}-\stackrel{\sim }{\mathbf{H}}{\mathbf{\Theta }}_{\alpha }),\end{array}$$ (31)

with Θ_α = (α₁, α₂)^T = (p cos φ, p sin φ)^T and

$$\stackrel{\sim }{\mathbf{H}}=\frac{{\sigma }_s^2}{2a}\left(\begin{array}{cc}{r}_{1}cos{\vartheta }_1& r_{1}sin{\vartheta }_1\\ r_{2}cos{\vartheta }_2& r_{2}cos{\vartheta }_2\\ \dots & \dots \\ r_{M}cos{\vartheta }_M& r_{M}sin{\vartheta }_M\end{array}\right).$$ (32)

Thus, the MLE of Θ_α is

$${\stackrel{\sim }{\mathbf{\Theta }}}_{\alpha ,\mathbf{mle}}={({\stackrel{\sim }{\alpha }}_1,{\stackrel{\sim }{\alpha }}_2)}^T={({\stackrel{\sim }{\mathbf{H}}}^T\stackrel{\sim }{\mathbf{H}})}^{-1}{\stackrel{\sim }{\mathbf{H}}}^T(\mathbf{Y}-{\mathbf{Y}}_{\mathbf{0}}).$$ (33)

Due to symmetry, one can directly find that

$$\sum _{m=1}^M{r}_{m}cos{\vartheta }_m=\sum _{m=1}^{M}r({\vartheta }_m)cos{\vartheta }_m=0,$$ (34)

$$\sum _{m=1}^M{r}_{m}sin{\vartheta }_m=\sum _{m=1}^{M}r({\vartheta }_m)sin{\vartheta }_m=0,$$ (35)

$$\sum _{m=1}^{M}r{({\vartheta }_m)}^{2}cos{\vartheta }_{m}sin{\vartheta }_m=0.$$ (36)

For convenience, we define the following two functions which we will evaluate later on:

$$\begin{array}{l}{\mathrm{\Lambda }}_1(\epsilon )\equiv \frac{1}{M}\sum _{m=1}^M\frac{r_m^2}{a^2}{cos}^2{\vartheta }_m=\frac{1}{M}\sum _{m=1}^M\frac{r{({\omega }_m)}^2/a^2}{1+{tanh}^2{\vartheta }_m}\\ =\frac{1}{M}\sum _{m=1}^M\frac{1-{\epsilon }^2{sin}^2{\omega }_m}{1+(1-{\epsilon }^2){tan}^2{\omega }_m},\end{array}$$ (37)

$$\begin{array}{l}{\mathrm{\Lambda }}_2(\epsilon )\equiv \frac{1}{M}\sum _{m=1}^M\frac{r_m^2}{a^2}{sin}^2{\vartheta }_m\\ =\frac{1}{M}\sum _{m=1}^M\frac{(1-{\epsilon }^2{sin}^2{\omega }_m)(1-{\epsilon }^2){tan}^2{\omega }_m}{1+(1-{\epsilon }^2){tan}^2{\omega }_m}.\end{array}$$ (38)

Then, the MLE of Θ_α is given by

$$\begin{array}{l}\left(\begin{array}{c}{\stackrel{\sim }{\alpha }}_1\\ {\stackrel{\sim }{\alpha }}_2\end{array}\right)\approx \frac{4}{{\sigma }_s^4}{\left(\begin{array}{cc}M{\mathrm{\Lambda }}_1(\epsilon )& 0\\ 0& M{\mathrm{\Lambda }}_2(\epsilon )\end{array}\right)}^{-1}{\stackrel{\sim }{\mathbf{H}}}^T(\mathbf{Y}-{\mathbf{Y}}_0)\\ =\frac{1}{2\mu a}\left(\begin{array}{c}{\mathrm{\Lambda }}_1^{-1}{\sum }_m{y}_m{r}_{m}cos{\vartheta }_m\\ {\mathrm{\Lambda }}_2^{-1}{\sum }_m{y}_m{r}_{m}sin{\vartheta }_m\end{array}\right).\end{array}$$ (39)

The expectations and variances of α̃_1,2 are

$$\begin{array}{l}<{\stackrel{\sim }{\alpha }}_1>=\frac{{\sigma }_s^{2}p}{4\mu {\mathrm{\Lambda }}_1}\sum _m\frac{r_m^2}{a^2}cos{\vartheta }_{m}cos({\vartheta }_m-\phi )={\alpha }_1,\\ <{\stackrel{\sim }{\alpha }}_2>=\frac{{\sigma }_s^{2}p}{4\mu {\mathrm{\Lambda }}_2}\sum _m\frac{r_m^2}{a^2}sin{\vartheta }_{m}cos({\vartheta }_m-\phi )={\alpha }_2,\\ {\sigma }_{{\stackrel{\sim }{\alpha }}_1}^2(\epsilon )=\frac{{\sigma }_s^2}{4{\mu }^2{\mathrm{\Lambda }}_1^2}\sum _m\frac{r_m^2}{a^2}{cos}^2{\vartheta }_m=\frac{1}{\mu {\mathrm{\Lambda }}_1(\epsilon )},\\ {\sigma }_{{\stackrel{\sim }{\alpha }}_2}^2(\epsilon )=\frac{{\sigma }_s^2}{4{\mu }^2{\mathrm{\Lambda }}_2^2}\sum _m\frac{r_m^2}{a^2}{sin}^2{\vartheta }_m=\frac{1}{\mu {\mathrm{\Lambda }}_2(\epsilon )}.\end{array}$$

One can also check that their covariance Cov[α̃₁, α̃₂] = 0.

Next, we evaluate Λ_1,2(ε). Each sector has an arc length equal to 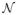/M, where 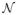= 4aE(ε) is the circumference of the ellipse and $\text{E}(\epsilon )={\int }_0^{\pi /2}\sqrt{1-{(\epsilon sin\omega )}^2}d\omega$ is the complete elliptic integral of the second kind. The arc length of the ellipse between ϑ = 0 and ϑ = ϑ(ω₀) is given by $s({\omega }_0)={\int }_0^{{\omega }_0}\sqrt{{(asin\omega )}^2+{(bcos\omega )}^2}d\omega ={\int }_0^{{\omega }_0}a\sqrt{1-{(\epsilon sin\omega )}^2}d\omega$. Then, $ds=a\sqrt{1-{(\epsilon sin\omega )}^2}d\omega$. For sufficiently large M, we can approximate:

$$\frac{1}{M}\sum _{m=1}^{M}g({\omega }_m)\approx {\int }_0^{\mathfrak{L}}\frac{g(\omega )}{\mathfrak{L}}ds(\omega )=\frac{1}{4\text{E}(\epsilon )}{\int }_0^{2\pi }g(\omega )\sqrt{1-{(\epsilon sin\omega )}^2}d\omega .$$ (40)

where g(·) represents a general integrable function. Therefore, we have

$$\begin{array}{l}{\mathrm{\Lambda }}_1(\epsilon )\approx \frac{1}{4\text{E}(\epsilon )}{\int }_0^{2\pi }\frac{{(1-{\epsilon }^2{sin}^2\omega )}^{3/2}}{1+(1-{\epsilon }^2){tan}^2\omega }d\omega \\ =\frac{(1+{\epsilon }^2)E(\epsilon )-(1-{\epsilon }^2)K(\epsilon )}{3{\epsilon }^{2}E(\epsilon )},\end{array}$$ (41)

where $\text{K}(\epsilon )={\int }_0^{\pi /2}\frac{d\omega }{\sqrt{1-{(\epsilon sin\omega )}^2}}$ is the complete elliptic integral of the first kind. Similarly, one can find

$${\mathrm{\Lambda }}_2(\epsilon )\approx \frac{(1-{\epsilon }^2)\left[(-1+2{\epsilon }^2)E(\epsilon )+(1-{\epsilon }^2)K(\epsilon )\right]}{3{\epsilon }^{2}E(\epsilon )}.$$ (42)

Since Λ_1,2(ε = 0) = 1/2, we have ${\sigma }_{{\stackrel{\sim }{\alpha }}_{1,2}}^2(\epsilon =0)=2/\mu$, consistent with Eq. (8). Therefore, α̃_1,2 → α̂_1,2 as the cell shape tends to be circular. In the other extreme, we have lim_{ε → 1} Λ₁(ε) = 2/3 and lim_{ε → 1} Λ₂(ε) = 0.

The MLE of Θ = (p, φ)^T can be found directly,

$${\stackrel{\sim }{\mathbf{\Theta }}}_{\mathbf{mle}}=\left(\begin{array}{c}\stackrel{\sim }{p}\\ \stackrel{\sim }{\phi }\end{array}\right)=\left(\begin{array}{c}\sqrt{{\stackrel{\sim }{\alpha }}_1^2+{\stackrel{\sim }{\alpha }}_2^2}\\ arctan({\stackrel{\sim }{\alpha }}_2/{\stackrel{\sim }{\alpha }}_1)\end{array}\right)\stackrel{d}{\to }\mathcal{N}\left(\mathbf{\Theta },\stackrel{\sim }{\mathbf{I}}{(\mathbf{\Theta })}^{-1}\right),$$ (43)

where the last line is due to the asymptotic normality of MLE: as the sample size increases, the distribution of the MLE tends to the Gaussian distribution with mean Θ and covariance matrix equal to the inverse of the Fisher information matrix,

$$\begin{array}{l}\stackrel{\sim }{\mathbf{I}}{(\mathbf{\Theta })}^{-1}={\langle \frac{\partial lnP(\mathbf{Y}\mid \mathbf{\Theta })}{\partial {\mathbf{\Theta }}_i}\frac{\partial lnP(\mathbf{Y}\mid \mathbf{\Theta })}{\partial {\mathbf{\Theta }}_j}\rangle }^{-1}\\ \approx \frac{1}{\mu }{\left(\begin{array}{cc}{\mathrm{\Xi }}_1(\epsilon ,\phi )& p·{\mathrm{\Xi }}_0(\epsilon ,\phi )\\ p·{\mathrm{\Xi }}_0(\epsilon ,\phi )& p^2·{\mathrm{\Xi }}_2(\epsilon ,\phi )\end{array}\right)}^{-1},\end{array}$$ (44)

where

$${\mathrm{\Xi }}_0(\epsilon ,\phi )\equiv \frac{1}{M}\sum _{m=1}^M\frac{r_m^2}{a^2}cos({\vartheta }_m-\phi )sin({\vartheta }_m-\phi ),$$ (45)

$${\mathrm{\Xi }}_1(\epsilon ,\phi )\equiv \frac{1}{M}\sum _{m=1}^M\frac{r_m^2}{a^2}{cos}^2({\vartheta }_m-\phi ),$$ (46)

$${\mathrm{\Xi }}_2(\epsilon ,\phi )\equiv \frac{1}{M}\sum _{m=1}^M\frac{r_m^2}{a^2}{sin}^2({\vartheta }_m-\phi ).$$ (47)

Again, one can use Eq. (40) to calculate the above three functions. Here, we will skip all the intermediate technical steps and will only present the final results:

$$\begin{array}{l}{\sigma }_{\stackrel{\sim }{p}}^2(\epsilon ,\phi )=\frac{{\mu }^{-1}{\mathrm{\Xi }}_2(\epsilon ,\phi )}{{\mathrm{\Xi }}_1(\epsilon ,\phi ){\mathrm{\Xi }}_2(\epsilon ,\phi )-{\mathrm{\Xi }}_0{(\epsilon ,\phi )}^2}\\ =\frac{1}{\mu }·\frac{A_1(\epsilon )[A_2(\epsilon ,\phi )-A_3(\epsilon ,\phi )]}{A_6(\epsilon )+A_7(\epsilon )+A_8(\epsilon )},\end{array}$$ (48)

$$\begin{array}{l}{\sigma }_{\stackrel{\sim }{\phi }}^2(\epsilon ,\phi )=\frac{{(\mu p)}^{-1}{\mathrm{\Xi }}_1(\epsilon ,\phi )}{{\mathrm{\Xi }}_1(\epsilon ,\phi ){\mathrm{\Xi }}_2(\epsilon ,\phi )-{\mathrm{\Xi }}_0{(\epsilon ,\phi )}^2}\\ =\frac{\sqrt{1-{\epsilon }^2}}{\mu p^2}\frac{A_1(\epsilon )[A_4(\epsilon ,\phi )-A_5(\epsilon ,\phi )]}{A_6(\epsilon )+A_7(\epsilon )+A_8(\epsilon )},\end{array}$$ (49)

where

$$\begin{array}{l}{A}_1=3{\epsilon }^{2}E(\epsilon )/[2(1-{\epsilon }^2)],\\ A_2=2E(\epsilon )[(2{\epsilon }^2-{\epsilon }^4)-(1-{\epsilon }^2+{\epsilon }^4)cos(2\phi )],\\ A_3=(1-{\epsilon }^2)[{\epsilon }^2-(2-{\epsilon }^2)cos(2\phi )]K(\epsilon ),\\ A_4=2E(\epsilon )[(2{\epsilon }^2-{\epsilon }^4)+(1-{\epsilon }^2+{\epsilon }^4)cos(2\phi )],\\ A_5=(1-{\epsilon }^2)[{\epsilon }^2+(2-{\epsilon }^2)cos(2\phi )]K(\epsilon ),\\ A_6=(-1+{\epsilon }^2+2{\epsilon }^4)E{(\epsilon )}^2,\\ A_7=(2-3{\epsilon }^2+{\epsilon }^4)E(\epsilon )K(\epsilon ),\\ A_8=-{(1-{\epsilon }^2)}^{2}K{(\epsilon )}^2.\end{array}$$

It is easy to check that ${\sigma }_{\stackrel{\sim }{p}}^2(0,\phi )=2/\mu$ and ${\sigma }_{\stackrel{\sim }{\phi }}^2(0,\phi )=2/(\mu p^2)$, consistent with our results for the circular cell (Eqns. 13, 14). Also, we find that the covariance of p̃ and φ̃ can be written as Cov[p̃, φ̃] = A₀(ε) sin(2φ), which vanishes at φ = 0, ±π, ±π/2. For the special case φ = 0, Eq. (48) reduces to ${\sigma }_{\stackrel{\sim }{p}}^2(\epsilon ,0)={[\mu {\mathrm{\Lambda }}_1(\epsilon )]}^{-1}$. As b → 0 such that ε → 1, the ellipse becomes a one-dimensional segment of length 2a, which can measure the gradient steepness with an accuracy ${\sigma }_{\stackrel{\sim }{p}}^2(\epsilon \to 1,\phi =0)=3/(2\mu )$.

To determine how the eccentricity affects the accuracy of gradient estimates and to compare with our results for the circular cell, we fix the area of the elliptical cell, i.e., let $S\equiv \pi ab=\pi a^2/\sqrt{1-{\epsilon }^2}$ be constant. We also keep the gradient profile identical by fixing p₀ ≡ |∇→C|/C₀. Then, the gradient is proportional to the major axis: p = 2ap₀ = p(a). These assumptions allow us to define the following ratios as a measure how the eccentricity will change the gradient sensing limits:

$$\begin{array}{l}{\mathrm{\Delta }}_p(\epsilon ,\phi )\equiv \frac{{\sigma }_{\stackrel{\sim }{p}}^2(\epsilon ,\phi )/p{(a)}^2}{{\sigma }_{\stackrel{\sim }{p}}^2(0,\phi )/p{(\sqrt{S/\pi })}^2}=\frac{\mu S}{2\pi a^2}{\sigma }_{\stackrel{\sim }{p}}^2(\epsilon ,\phi )\\ =\frac{\sqrt{1-{\epsilon }^2}}{2}\frac{A_1(\epsilon )[A_2(\epsilon ,\phi )-A_3(\epsilon ,\phi )]}{A_6(\epsilon )+A_7(\epsilon )+A_8(\epsilon )}\\ =\{\begin{array}{ll}{(2{\mathrm{\Lambda }}_1)}^{-1}\sqrt{1-{\epsilon }^2}\hfill & \text{for}\phi =0,\hfill \\ {(2{\mathrm{\Lambda }}_2)}^{-1}\sqrt{1-{\epsilon }^2}\hfill & \text{for}\phi =\pm \pi /2,\hfill \end{array}\end{array}$$ (50)

$$\begin{array}{l}{\mathrm{\Delta }}_{\phi }(\epsilon ,\phi )\equiv \frac{{\sigma }_{\stackrel{\sim }{\phi }}^2(\epsilon ,\phi )}{{\sigma }_{\stackrel{\sim }{\phi }}^2(0,\phi )}=\frac{\mu p^2}{2}{\sigma }_{\stackrel{\sim }{\phi }}^2(\epsilon ,\phi )\\ =\frac{\sqrt{1-{\epsilon }^2}}{2}\frac{A_1(\epsilon )[A_4(\epsilon ,\phi )-A_5(\epsilon ,\phi )]}{A_6(\epsilon )+A_7(\epsilon )+A_8(\epsilon )}\\ =\{\begin{array}{ll}{(2{\mathrm{\Lambda }}_2)}^{-1}\sqrt{1-{\epsilon }^2}\hfill & \text{for}\phi =0,\hfill \\ {(2{\mathrm{\Lambda }}_1)}^{-1}\sqrt{1-{\epsilon }^2}\hfill & \text{for}\phi =\pm \pi /2,\hfill \end{array}\end{array}$$ (51)

with Λ₁(ε) and Λ₂(ε) given by Eq. (41) and Eq. (42).

In Fig. 2 we have plotted, as solid and dashed lines, these ratios for different values of φ (the gradient direction measured from the major axis). In the same figure, we have also plotted as symbols the results of our Monte-Carlo simulations. In these simulations, the ellipse of a given eccentricity ε was divided into M = 1000 sectors with equal arc lengths. Each sector contained N_s = 40 receptors and the receptor occupancy number for each sector, y_m, was assigned a Gaussian random variable with mean N_sC_m/(C_m + K_d) and variance N_sC_mK_d/(C_m+K_d)². After plugging these random numbers into Eq. (39) and Eq. (43) for 10⁴ realizations, we computed the numerical values for the sample variances of p̃ and φ̃. As shown in the figure, the agreement between our analytical and numerical results is excellent.

FIG. 2.

Δ_p and Δ_φ as a function of the eccentricity ε for different values of φ (lines: analytical expressions; symbols: Monte-Carlo simulations).

In the case where the gradient direction points along the major axis of the elliptical cell (φ = 0 and Fig. 2A), we see that Δ_p is a decreasing function of the eccentricity ε. This can be intuitively understood by realizing that for an elongated cell pointing in the gradient direction, the difference in concentration, and thus the difference in occupied receptors between the back and front sectors becomes large. Therefore, the more elongated the cell is along the gradient direction, the more accurately the cell is able to measure the gradient steepness. In contrast, Δ_φ increases with ε such that more elongated cells are less accurate in estimating the gradient direction than circular cells. When the external gradient is parallel to the cell’s minor axis (φ = ±π/2 and Fig. 2C), we have exactly the opposite: Δ_p increases with ε while Δ_φ decreases with ε. Finally, for the intermediate case φ = ±π/4 (Fig. 2B), we have Δ_p = Δ_φ and they both increase with ε. Depending on the gradient angle φ, the ratios can be even non-monotonic with ε; for example, Δ_p at φ = π/6 will first decrease and then increase with ε (data not shown).

It is noteworthy that gradient sensing generally fails in the line segment limit (ε → 1), except for the special cases of steepness sensing at φ = 0, ±π and direction sensing at φ = ±π/2. As a vector, the concentration gradient can be decomposed into two orthogonal components, one along the major axis of the cell p_major = p cos φ and the other along the minor axis p_minor = p sin φ. When sensing the gradient magnitude (steepness), the line-segment cell is only able to detect the magnitude of p_major. But there is unlimited uncertainty in the other component p_minor (except for vanishing p_minor at φ = 0 or ±π). This explains why Δ_p always diverges as ε → 1 except for φ = 0 and ±π. Similar arguments hold for directional sensing: a line-segment cell can only tell the direction of the gradient component perpendicular to itself (i.e., p_minor) but has unlimited uncertainty about p_major which disappears only for φ = ±π/2.

Our analytical and numerical results reveal that, for every gradient direction φ, a cell cannot improve the gradient steepness and direction estimates simultaneously by elongating its cell body. It is difficult to connect this result to the experimental measurements of the accuracy of chemotaxis. This is mostly done in the form of the chemotactic index (CI), defined as the distance traveled by the cell in the direction of the gradient divided by the total distance traveled. Clearly, the CI is a function of both the accuracy in gradient steepness and gradient direction. To determine the relative importance of these two parameters would require a precise knowledge of the gradient sensing and cell motility process, both of which are currently absent.

Even in the absence of such precise knowledge, however, we can conclude that elongated cell shapes can strongly affect the cell’s accuracy of gradient sensing. In experiments, the cell shape varies depending on the precise conditions. Chemotactic neutrophils, for example, are found to have eccentricities up to 0.8 [29, 30]. For these values, we find that the variances of estimating gradient steepness and direction in the elliptical cells differ by a factor of 2 compared to the ones in circular cells. Furthermore, Dictyostelium cells can have much higher eccentricities (ε ≈ 0.95) [31]. Such highly elliptical geometries are expected to have even more significant effects on the accuracy of gradient sensing. Thus, the sensing limits derived using a circular geometry are a good approximation only for cells that are not significantly elongated.

IV. DIRECTIONAL SENSING IN THE PRESENCE OF AN INTRACELLULAR BIAS

A large number of experiments have revealed that an external cue can induce spatial localization of several signaling proteins along the plasma membrane during eukaryotic directional sensing [7, 10, 32]. The membrane localization of these signaling molecules enables a cell to polarize and migrate toward the external chemical source. Samadani et. al. have quantitatively monitored the spatial and temporal localization of one of the key signaling component fused to GFP [33]. Their data provides evidence for inherent asymmetries in the intracellular signaling network of cells prior to stimulation. The magnitude of this asymmetry was found to vary significantly from cell to cell. This naturally raises the question: what is the accuracy of directional sensing in the presence of such an intracellular bias?

To address this question, we can use a nonuniform prior distribution P(φ) to represent this internal bias and apply the maximum a posteriori (MAP) estimation. Specifically, we assume that the prior distribution follows the circular normal (CN) distribution in directional statistics, P(φ) = exp[κ_ε cos(φ − φ_ε)]/(2πI₀(κ_ε)), where φ_ε denotes the bias direction, κ_ε controls the magnitude of the bias, and I₀(·) is the modified Bessel function of order zero. We have plotted the CN distribution in Fig. 3A for various values of κ_ε.

FIG. 3.

A: The circular normal distribution for different values of κ_ε. B: The lower bound on the variance in gradient sensing ${\phi }_{\phi ,\mathit{map}}^2$ as a function of the direction of the bias φ_ε (relative to the gradient direction) for different values of the strength of the bias κ_ε. Parameter values are N = 40, 000 and C₀ = K_d, resulting in a SNR of κ = 12.5.

The MAP estimate of φ is

$$\begin{array}{l}{\widehat{\phi }}_{\mathit{map}}=\underset{\phi }{argmax}P(\mathbf{Y}\mid \phi )P(\phi )\\ =\underset{\phi }{argmin}\left[\frac{1}{2{\sigma }_s^2}J(\mathbf{Y}\mid \mathbf{\Theta })-{\kappa }_{\epsilon }cos(\phi -{\phi }_{\epsilon })\right]\\ =arctan\left(\frac{{\sum }_m{y}_{m}sin{\vartheta }_m+\gamma sin{\phi }_{\epsilon }}{{\sum }_m{y}_{m}cos{\vartheta }_m+\gamma cos{\phi }_{\epsilon }}\right)\\ =arctan\left(\frac{z_1+\gamma sin{\phi }_{\epsilon }}{z_2+\gamma cos{\phi }_{\epsilon }}\right),\end{array}$$ (52)

with γ ≡ 2κ_ε/p. This expression is similar to the maximal polarization angle derived from the geometric model in [33]. In the limit κ_ε → 0, the prior distribution becomes uniform and the MAP estimate recovers the MLE of the gradient direction, i.e., φ̂_map → φ̂. In the other extreme that κ_ε → ∞, the prior distribution becomes a delta function and φ̂_map → φ_ε. Let z̃₁ ≡ z₁ + γ cos φ_ε and z̃₂ ≡ z₂ + γ sin φ_ε. Then, by Eq. (10), they are independent and both normal: z̃₁ ~ (α₁ + γ cos φ_ε, σ²) and z̃₂ ~ (α₂ + γ sin φ_ε, σ²). If we define Z̃ = z̃₁ + iz̃₂, then Z̃ follows the complex Gaussian distribution and its phase variable is just the MAP estimator, i.e., φ̂_map = arctan(z̃₂/z̃₁). As demonstrated in [25, 26], the phase of a complex Gaussian random variable has a distribution symmetric about the expected value of the phase. In our case, this implies that the MAP estimator φ̂_map is symmetrically distributed about its mean

$$\begin{array}{l}\langle {\widehat{\phi }}_{\mathit{map}}\rangle =arctan\frac{\langle {\stackrel{\sim }{z}}_2\rangle }{\langle {\stackrel{\sim }{z}}_1\rangle }=arctan\left(\frac{\mu pcos\phi +\gamma cos{\phi }_{\epsilon }}{\mu psin\phi +\gamma sin{\phi }_{\epsilon }}\right)\\ \approx \{\begin{array}{ll}{\phi }_{\epsilon }\hfill & \text{if}{\kappa }_{\epsilon }\gg \kappa ,\hfill \\ \phi \hfill & \text{if}{\kappa }_{\epsilon }\ll \kappa .\hfill \end{array}\end{array}$$ (53)

One can see that the value of 〈φ̂_map〉 is largely determined by the ratio γ/(μp) = 2κ_ε/(μp²) = κ_ε/κ, where κ is the signal-to-noise ratio defined in Eq. (12).

In statistics, the bias function of an estimator is the difference between this estimator’s expected value and the true value of the parameter being estimated. In our case, the bias function of the MAP estimator is

$$b_{\mathit{map}}(\phi )\equiv \langle {\stackrel{\sim }{\phi }}_{\mathit{map}}\rangle -\phi =arctan\left(\frac{\kappa sin\phi +{\kappa }_{\epsilon }sin{\phi }_{\epsilon }}{\kappa cos\phi +{\kappa }_{\epsilon }cos{\phi }_{\epsilon }}\right)-\phi .$$ (54)

Obviously, φ̂_map is a biased estimator of φ due to bias in P(φ). The squared estimation error of φ̂_map is

$$\begin{array}{l}{\sigma }_{\phi ,\mathit{map}}^2=\langle {({\widehat{\phi }}_{\mathit{map}}-\phi )}^2\rangle \\ =\langle {({\widehat{\phi }}_{\mathit{map}}-\langle {\widehat{\phi }}_{\mathit{map}}\rangle +\langle {\widehat{\phi }}_{\mathit{map}}\rangle -\phi )}^2\rangle \\ =\langle {({\widehat{\phi }}_{\mathit{map}}-\langle {\widehat{\phi }}_{\mathit{map}}\rangle )}^2\rangle +b_{\mathit{map}}{(\phi )}^2.\end{array}$$ (55)

According to the Cramér-Rao inequality for biased estimators [34] the first term is bounded by

$$\langle {({\widehat{\phi }}_{\mathit{map}}-\langle {\widehat{\phi }}_{\mathit{map}}\rangle )}^2\rangle \ge {\left(1+\frac{\partial b_{\mathit{map}}(\phi )}{\partial \phi }\right)}^2{I}_{\phi }^{-1},$$ (56)

where the Fisher information has been calculated before, $I_{\phi }=\langle {({\partial }_{\phi }ln\mathcal{L})}^2\rangle ={\sigma }_{\phi }^{-2}=\mu p^2/2=\kappa$. Therefore,

$$\begin{array}{l}{\sigma }_{\phi ,\mathit{map}}^2\ge {\left(1+\frac{\partial b_{\mathit{map}}(\phi )}{\partial \phi }\right)}^2{I}_{\phi }^{-1}+b_{\mathit{map}}{(\phi )}^2\\ =\kappa {\left[\frac{\kappa +{\kappa }_{\epsilon }cos(\phi -{\phi }_{\epsilon })}{{\kappa }^2+2\kappa {\kappa }_{\epsilon }cos(\phi -{\phi }_{\epsilon })+{\kappa }_{\epsilon }^2}\right]}^2+{\left[arctan\left(\frac{\kappa sin\phi +{\kappa }_{\epsilon }sin{\phi }_{\epsilon }}{\kappa cos\phi +{\kappa }_{\epsilon }cos{\phi }_{\epsilon }}\right)-\phi \right]}^2\\ =\{\begin{array}{ll}\kappa /{(\kappa +{\kappa }_{\epsilon })}^2\hfill & \text{if}{\phi }_{\epsilon }=\phi ,\hfill \\ \kappa /{(\kappa -{\kappa }_{\epsilon })}^2\hfill & \text{if}{\phi }_{\epsilon }=\phi \pm \pi .\hfill \end{array}\end{array}$$ (57)

In Fig. 3B we have plotted the lower bound of σ_φ,map as a function of the direction of the bias φ_ε for different values of the bias strength κ_ε. As expected, directional sensing is most accurate when the intracellular bias direction coincides with the extracellular gradient direction (φ_ε = φ) and becomes less accurate it differs significantly from the gradient direction. This is consistent with the experimental findings in [33] which showed that the GFP polarization is strongest at φ_ε = φ and weaker at φ_ε = φ± π. Of course, we have chosen a fixed value for the parameter κ_ε, corresponding to a single cell. To deal with a population averaged as in typical experiments, one would have to assign a probability distribution to κ_ε (arising from cell individuality). This quenched randomness is expected to enlarge the cell-to-cell variability of directional sensing response, as observed in [33].

V. SUMMARY

In this paper we have used various concepts and techniques in estimation theory to investigate the physical limits of eukaryotic gradient sensing. We have derived explicit formulas for the variances of estimating both the gradient direction and steepness for an elliptical cell. Our theoretical and numerical results suggest that a cell cannot improve its sensing of both the gradient steepness and direction at the same time by simply elongating itself. We also show that highly eccentric cell shapes can significantly change the gradient sensing limits, which may be relevant in experimental observations for chemotactic eukaryotes like neutrophils and Dictyostelium. Finally, we examined how an intracellular bias may distort the cell’s perception of external stimuli. As expected, the accuracy of gradient detection increases when the internal bias aligned with the external gradient but decreases when the direction of the internal bias is significantly different from the external gradient direction. Our approach is general and in principle can be extended to cases including non-uniformly distributed receptors or more complicated cell shapes.