Homeostasis of Brain Dynamics in Epilepsy: A Feedback Control Systems Perspective of Seizures

Abstract

In an effort to understand basic functional mechanisms that can produce epileptic seizures, some key features are introduced in coupled lumped-parameter neural population models that produce “seizure”-like events and dynamics similar to the ones during the route of the epileptic brain towards seizures. In these models, modified from existing ones in the literature, internal feedback mechanisms are incorporated to maintain the normal low level of synchronous behavior in the presence of coupling variations. While the internal feedback is developed using basic feedback systems principles, it is also functionally equivalent to actual neurophysiological mechanisms such as homeostasis that act to maintain normal activity in neural systems that are subject to extrinsic and intrinsic perturbations. Here it is hypothesized that a plausible cause of seizures is a pathology in the internal feedback action; normal internal feedback quickly regulates an abnormally high coupling between the neural populations, whereas pathological internal feedback can lead to “seizure”-like high amplitude oscillations. Several external seizure-control paradigms, that act to achieve the operational objective of maintaining normal levels of synchronous behavior, are also developed and tested in this paper. In particular, closed-loop “modulating” control with predefined stimuli, and closed-loop feedback decoupling control are considered. Among these, feedback decoupling control is the consistently successful and robust seizure-control strategy. The proposed model and remedies are consistent with a variety of recent observations in the human and animal epileptic brain, and with theories from nonlinear systems, adaptive systems, optimization, and neurophysiology. The results from the analysis of these models have two key implications, namely, developing a basic theory for epilepsy and other brain disorders, and the development of a robust seizure-control device through electrical stimulation and/or drug intervention modalities.

INTRODUCTION

Epilepsy is the second most common neurological disorder after stroke and affects at least 50 million people worldwide. It is characterized by recurrent seizures. Seizures are associated with a sudden development of synchronous firing in a massive group of neurons, and its duration can range from seconds to minutes. Electroencephalogram (EEG) recordings from the epileptic brain show that seizures may begin locally in portions of the cerebral hemispheres (partial/local seizures) or begin simultaneously in both cerebral hemispheres (generalized seizures). Seizures cause temporary disturbances in brain functions such as motor control, cognition and responsiveness. If seizures are left untreated, permanent and extensive damage in the brain may occur.

With the current knowledge of neuro(patho)physiology, and evidence from experimental studies, it is still difficult to explain why and how seizures occur. This is primarily due to the large number of factors and complexity of their interaction that may be responsible for the manifestation of seizures. They can range from genetic and cellular-level factors, such as excitatory/inhibitory behavior, ionic conductances, number of synaptic connections etc., to high-level properties, such as coupling (interaction) level between neural populations and the presence of feedback loops. The sheer number and range of factors and their interactions, make experimental studies to quantify their effects very difficult. In this context, computational neurophysiological models have become attractive due to their ability to model, at least partially, complex neurological phenomena with a relative ease by “tuning” and analyzing the effect of various neurological factors. This is evident from the large number of computational models that have been developed to study epileptic activity in neurological systems. Such computational models are especially useful as test-beds to design and compare seizure control techniques.

In this paper we develop our feedback systems-based approach to epileptic seizure modeling and control, and apply it to the following lumped-parameter models from the literature: cortical^39,84 and thalamocortical⁶⁶ neural population models that model the neuroelectrophysiology of cortical and thalamic neural populations. The basic motivation for our approach stems from the dynamical systems view of the transition to epileptic seizures proposed by Iasemidis and collaborators.^32–38 From epileptic seizure-prediction studies using nonlinear dynamical analysis of EEG, they observed that seizures are characterized by a progressive recruitment (coupling) of brain sites (i.e., a dynamical entrainment) in an abnormal hypersynchronization. Combining these observations with theoretical results from burst phenomena in adaptive systems, Tsakalis and Iasemidis,^74,75 postulated the existence of feedback action in a model of coupled chaotic oscillators, that enables the appearance of seizure-like behavior. Here we generalize and extend this feedback systems perspective to model epileptic seizures in coupled neural populations by incorporating an internal feedback mechanism. The choice of coupled neural populations, on one hand, is motivated by the observations of preictal dynamical entrainment and progressive coupling between brain sites, and is also in conformance with neuroanatomy. The internal feedback, on the other hand, is introduced from a feedback systems- theoretic viewpoint and can be interpreted as a functional model of neural homeostasis. In other words, the function of internal feedback is similar to neural homeostasis mechanisms that are essential for normal (“healthy” asynchronous) operation of neural populations despite being subjected to a variety of extrinsic or intrinsic perturbations. We postulate epileptogenesis as the result of pathology in the feedback action. Our analysis of this model indicates that one manifestation of the pathology is an apparent increase in coupling and synchronization between neural populations, preceding complete system destabilization in the form of a seizure in cases of complete failure. It is worthwhile to note that this viewpoint is consistent with the concept of Highly Optimized Tolerance proposed by Carlson and Doyle^8,21 and where feedback, optimization, and evolution can all give rise to severe system failures. In our case, it is the feedback that is responsible for homeostasis whose failure can produce epileptic seizure type of phenomena.

At this point we should emphasize that we do not aim to reproduce the exact brain output (e.g., EEG recordings). Instead, the objective is to capture the essential functional parts of the operation that leads to epileptic seizures, and incorporate effective control strategies to prevent their occurrence. This is in sharp distinction with a majority of the approaches presented in the literature wherein the objective is to model the precise structure and function of neurophysiological entities which are considered to be important for epileptogenesis. In these approaches, the occurrence of epileptic seizures is typically conjectured to be the result of bifurcations due to changes in key system parameters. While the knowledge gained from these studies about the structure and function of factors involved in epileptic seizures is important, highly detailed and specific neurophysiological models could obscure the basic mechanisms of seizure generation. In this context, the feedback systems perspective for epileptogenesis that we present here is generic in the sense that the occurrence of seizures results from pathologies in the implementation of the general operational objectives of the system.

Beyond a systems-level interpretation of seizures, the proposed mechanism is useful for the development and testing of strategies to control seizures, e.g., via electrical stimulation. The use of neurophysiological models is important to identify neurophysiologically plausible response and control variables. Thus, the design of an external controller incorporates theoretical (e.g., controllability) and practical (e.g., membrane potential and current stimulus as response and control variables respectively) constraints. We study closed-loop control with predefined stimuli and propose a control scheme termed “feedback decoupling” wherein the control signal is a function of the system state. For the former, we show that modulating closed-loop control with predefined stimuli, which are carefully chosen based on the underlying system, is successful in mitigating seizures in certain simple pathological networks. For the general case the proportional-integral feedback decoupling controllers are consistently successful across several pathological configurations in the models tested for various system parameters, and do not critically depend on the accuracy of the system’s model.

This paper is organized as follows. In section “Modeling approach”, we discuss the motivation of our feedback systems-oriented approach for modeling epileptic seizures. We present an overview of the cortical and thalamocortical neural population models in section “Neural population models”, followed by details about the internal feedback function, in section “Neural populations with internal feedback”, that we introduced in order to model normal and pathological (“epileptic”) behavior. Feedback control paradigms to control “seizure” occurrence in the models are presented in the section “Seizure control”. In the discussion sections, we present some limitations of the current modeling framework and propose extensions to it, and finally draw conclusions in section “Conclusion”.

MODELING APPROACH

Control theoretic perspectives have been applied to several physiological systems such as the circulatory, respiratory, visual, muscular and cardiovascular systems. ⁵⁰ In the case of epilepsy, although a control-theoretic approach to understanding epileptiform activity has been advocated,⁴⁰ it has not been a prevalent one in unraveling the structure and function of the multitude of neurological factors and mechanisms responsible for epilepsy. Due to the high complexity of the underlying system (epileptic brain), resolving the causes for epileptic seizures in terms of a large number of interacting factors is a highly nontrivial undertaking. On the other hand, a theoretical approach that addresses the basic dynamics of neurophysiological models seems feasible. Such an approach can provide functional models for the generation and insight for the control of epileptic seizures.

Here, we use coupled neural population models with internal (i.e., part of the overall system) feedback. We present specific motivation for the use of (i) coupled neural population models in section “Why coupled systems?” and (ii) internal feedback structure in section “Why internal feedback?” and the overall model structure in section “Overall model structure”.

Why Coupled Systems?

The generic motivation to consider coupled neural populations stems from the brain’s anatomy and functional organization. Anatomically, there is abundant connectivity within and between neuron populations. For example, in mammalian neocortex, cortical columns are regarded as fundamental units of neural organization.⁴¹ In addition to intra-columnar neural interaction, the cortical columns also exhibit functionally specific inter-columnar connectivity.⁵³ From a high-level brain-function standpoint (e.g., cognition, perception), communication between distinct brain areas that perform specific tasks is also required for normal brain functioning. Thus, the study of cooperative activity between brain areas is necessary to understand normal and pathological brain function, and this forms a general motivation for studying coupled neural populations.

Specific motivation to model epileptic seizures with coupled neural population models originates with the results on seizure prediction by Iasemidis and collaborators.^32–38 Their central concept from nonlinear dynamical analysis of EEG from patients with temporal lobe epilepsy was that seizures represent transitions of the epileptic brain from its normal, less-ordered (chaotic) interictal (between seizures) state to an abnormal, more-ordered, ictal (seizure) state and back to a normal postictal (after seizure) state. Based on this concept, they achieved seizure prediction by monitoring the level of dynamical entrainment, a form of dynamical synchronization, between brain sites. These observations of preictal dynamical entrainment suggest that the various brain sites interact with each other, and that the level of interaction (i.e., inter-areal coupling) is a key bifurcation parameter. This forms a specific motivation for considering coupled neural population models to study epileptic seizures. This approach of studying epileptogenesis as a network-driven event involving neural populations is in agreement with a number of experimental and theoretical studies^34,40 but differs from modeling approaches in the literature that attempt to model seizure behavior as the result of individual system parameterizations.

Why Internal Feedback?

In addition to the generic justification for a feedback-systems viewpoint for epileptic seizures,⁴⁰ a specific motivation to consider feedback structures as part of the coupled neural models comes from adaptive systems theory and neurological observations.

In search of a model and mechanism to explain the preictal dynamical entrainment of the epileptic brain, Iasemidis et al.³⁴ postulated that brain sites could be viewed as chaotic oscillators connected with each other via diffusive coupling. An increase in the coupling strength results in progressive synchronization between the oscillators, and the model’s dynamical entrainment characteristics were consistent with the preictal behavior of the epileptic brain. However, this model did not produce the explosive growth of signals observed during seizures. In order to obtain such a seizure-like behavior, and motivated by analysis and results of burst phenomena in adaptive systems, ^4,61,69,70 Tsakalis and Iasemidis^74,75 postulated the existence of feedback action in the oscillator network. Adaptive bursts are caused by parameter drift or maladjustment, and they are a fundamental limitation of a wide class of adaptive systems.^69,70 When adaptation is part of a feedback loop, as in adaptive control, adaptive bursts are exacerbated by a simultaneous destabilization of the feedback loop.

Although this approach of incorporating feedback as part of the system was developed on basic engineering principles, it is also strongly substantiated by neurological studies. Various experimental and computational studies have reported the existence of fundamental neurophysiological mechanisms, namely “neural homeostasis” and “homeostatic plasticity”, that control and stabilize the level of neural activity. ^{1–3,13,16–19,24,25,29,30,43,45–47,51,52,54,55,58,59,62,64,67,76–81,86}

At the individual neuron-level, activity (e.g., firing rate) is maintained at the neuron’s characteristic level by homeostatic mechanisms despite perturbations such as neural degradation, cell growth, channel turnover, variable extracellular conditions, and synthesis and loss of synaptic and ionic channels. Such a dynamical model with self-regulated activity is in contrast to classical static models wherein neuronal parameters such ionic conductances are considered to be constant. At the neural network level, events such as learning and development are carried out through changes in the synaptic strength via Hebbian mechanisms. Hebbian mechanisms, which tend to destabilize the network,^52,76,81 are opposed in action through homeostatic plasticity mechanisms. Thus neural network activity has also been identified as consisting of two complementary mechanisms: a destabilizing or perturbation mechanism and a regulatory or homeostatic one.

It is not always possible to differentiate the effect of homeostasis as occurring only at the neuronal or neural-network level. One can broadly classify homeostatic processes as occurring at the neuron-level, when single cell characteristics are maintained through the regulation of neuron parameters such as ionic conductance and ion channel number. The main modeling technique for neuron-level homeostasis has been implemented through the use of dynamically regulated ionic conductances and intrinsic excitability. ^{1,16,18,19,25,43,45–47,62,77} Typically a neuron’s excitability, (e.g., firing rate) measured in terms of an intrinsic ionic concentration (e.g., Ca²⁺), is maintained at a setpoint for normal activity by regulating the maximal ionic conductances (controller). In addition to these computational studies, such neuron-level homeostasis was also observed experimentally in cultured neurons via a rise in the intracellular calcium concentration,⁷⁷ conductance regulation,²⁵ changes in neuronal excitability,^18,86 synaptic regulation of ion channel function (number of synapses, synaptic size, synaptic strength) depending on cell activity, cell size and innervation¹⁶ and via neuromodulatory systems.⁴⁷ The effect of neuron-level regulation on neuron-network activity has also been studied.^25,46,47 One can classify homeostasis at the “network-level” when homeostatic synaptic plasticity mechanisms are involved.^{2,3,13,17,24,29,30,47,51,52,54,55,58,59,64,67,76,78–80,81} Broadly speaking, homeostatic synaptic plasticity corresponds to neuron-level synaptic parameters or neuron network-level characteristics such as excitation and inhibition via neurotransmitter release that regulate the level of neural interaction. Synaptic and intrinsic properties must be tuned in order to maintain stable ongoing activity in neural circuits in general, and recurrent excitatory and inhibitory circuits in particular, which, left unregulated, tend to destabilize the neural network activity. Several experimental studies have considered network-level homeostatic mechanisms. Researchers have shown that one possible mechanism by which firing-rates are adjusted, is via a global regulation of synaptic strengths.^{17,55,59,78,79} Homeostatic mechanisms regulate the total synaptic strength (synaptic drive) of a neuron by scaling all its excitatory synapses, in order to maintain constant firing rates.^17,78 Other studies consider homeostatic mechanisms through which both the levels of excitation and inhibition in a network are regulated.^3,24,54 In these experiments, excitatory synapses in cortical neurons were observed to become more depressed when compared to inhibitory synapses, in response to prolonged activity. Other factors affecting synaptic regulation such as molecular, genetic and neuromodulator effects,^13,16,47 and several other kinds of homeostatic mechanisms such as spike-timing dependent plasticity⁶³ and synaptic redistribution⁴⁸ have also been studied.

Homeostatic plasticity mechanisms are functionally modeled in computational studies since their exact forms are unknown. Examples of computational models for homeostasis include activity-dependent excitatory depression,⁶⁷ activity-dependent modification of inhibitory synaptic strengths,⁶⁴ spatial memory modeling through synaptic scaling,⁵⁸ upregulation of excitatory synapses and downregulation of inhibitory synapses to model trauma-induced epileptogenesis,²⁹ and dynamical adjustment of inter-nodal strengths in a neural network.³⁰

While the above homeostatic mechanisms are at a neurophysiologically “low” level, the necessity for regulatory mechanisms at a “high” level (brain level) for normal brain function has also been proposed. The collective behavior and interdependence between coupled systems can be characterized by changes in the synchronization level as a function of coupling.^6,57 The functional and behavioral consequences of neural synchrony are very important for normal and pathological brain activity.⁶⁰ For example, gamma band oscillatory synchronization, and temporally precise balanced pattern of synchronization and desynchronization have been proposed as pertinent factors for normal cognition.^28,83 In parallel, abnormal synchronization patterns in the motor system appears to be a key pathophysiological mechanism behind motor symptoms such as tremors in Parkinson’s disease.⁷ There is emerging evidence that “a delicately balanced patterns of synchronization and desynchronization is functionally and behaviorally important” for normal brain activity, and that abnormalities in neural synchrony are related to a number of neuropsychiatric disorders including epilepsy,⁶⁸ schizophrenia⁸² and Parkinson’s disease.³¹ Hence, it is logical to consider an interplay of synchronization and desynchronization processes in order to model normal and pathological brain dynamics. The exact neuroanatomy and structure of the internal (brain) operations that maintain normal brain activity by balancing synchronization and desynchronization, is unknown. Nevertheless, one can functionally model this balance with a feedback structure which provides appropriate desynchronizing feedback during periods of abnormally high synchrony. The above factors provide “low”-level and “high”-level motivation to consider feedback structures as part of neurophysiological models.

Overall Model Structure

In the variety of homeostasis mechanisms, from the individual neuron level to neural network level, the basic functional components of homeostasis can be seen as a simple feedback loop: a System (neuron/neuron population) whose Output (i.e., a response variable like firing rate or ionic concentration) is maintained at a normal Set-point (homeostasis) through an Internal Feedback Mechanism (homeostatic mechanism). From this viewpoint, in this paper we consider the overall model structure shown as a schematic diagram in Fig. 1. The “coupled neural populations” (i.e., System) block represents two neural populations and their inter-population coupling processes. The “internal feedback” (i.e., Internal Feedback Mechanism) block functionally represents neural homeostasis processes that maintain “normal” activity (i.e., Set-point Output) despite changing interactions between the coupled neural populations. Here, based on the motivation presented in sections “Why coupled systems?” and “Why internal feedback?”, the internal feedback mechanism maintains the synchronization (ρ) between neural populations below a threshold ρ_* (normal homeostasis level). The fact that synchrony is related to the mean activity levels of neural populations¹¹ justifies the selection of the synchronization level as the controlled variable.

FIGURE 1.

Schematic diagram of coupled neural populations with internal feedback. The synchronization level (ρ) between the coupled populations is maintained below a “normal” threshold (ρ_*) by internal feedback action. This internal feedback is functionally equivalent to the brain’s homeostatic mechanisms which maintain normal (asynchronous) behavior despite destabilizing perturbations.

The two coupled neural populations with internal feedback can be described as follows

$$\begin{array}{l}{\stackrel{.}{X}}_1=f_1(X_1)+K(t)C_{2\to 1}(X_2,X_1)+\epsilon (t)B_{2\to 1}(X_2,X_1)\\ {\stackrel{.}{X}}_2=f_2(X_2)+K(t)C_{1\to 2}(X_1,X_2)+\epsilon (t)B_{1\to 2}(X_1,X_2)\end{array}$$ (1)

where X₁ and X₂ denote the states. Ẋ₁ = f₁(X₁) + K(t) C_2→1(X₂,X₁) and Ẋ₂ = f₂(X₂) + K(t)C_1→2(X₁,X₂) represent the dynamics of the coupled neural populations 1 and 2 respectively where C_2→1(X₂,X₁) (C_1→2(X₁,X₂)) denotes the interaction from neural population 2 to 1 (1 to 2) and K(t) denotes the interaction (coupling) strength. ε(t)B_2→1(X₂,X₁) and ε(t)B_1→2(X₁,X₂) denote internal feedback mechanism where B_2→1(X₂,X₁) and B_1→2(X₁,X₂) are the internal feedback terms, and ε(t) denotes the internal feedback strength. ε(t) is altered by the internal feedback mechanism in order to maintain normal synchronization between the two populations.

When C_2→1(X₂,X₁) and B_2→1(X₂,X₁) (or C_1→2 (X₁,X₂) and B_1→2(X₁,X₂)) are different functions of the system states, the internal feedback mechanism can be considered as internal feedback compensation (e.g., balance of excitatory and inhibitory synapses). The internal feedback compensation through the balance of excitatory and inhibitory synapses was considered in Chakravarthy et al.¹⁰ In the case C_2→1(X₂,X₁) = −B_2→1(X₂,X₁) (and C_1→2(X₁,X₂) = −B_1→2 (X₁,X₂)), we will refer to the internal feedback mechanism as internal feedback regulation, and let ε(t) = ε_R(t). The internal feedback regulation of excitatory synapses is considered in this paper.

NEURAL POPULATION MODELS

We employ the feedback-systems approach to show the manifestation of epileptic seizure behavior in cortical and thalamocortical neural population models reported previously in the literature. In comparison with our previous works,^10,72 the dynamics of the models considered here are based on cortical and thalamocortical neural populations, and the observed and controlled variables are constrained by the neurophysiology of these neural populations. Thus, the use of these models helps highlight the generality of our feedback-systems approach and also helps identify physiologically plausible response and control variables that can be used for subsequent external seizure control. An overview of the lumped-parameter cortical population model (section “Cortical population model”), lumped parameter thalamocortical population model (section “Thalamocortical population model”) and details regarding their respective inter-population coupling are presented next.

Cortical Population Model

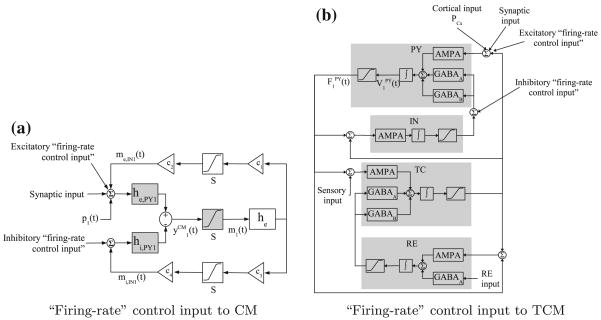
Jansen and Rit³⁹ proposed a cortical neural population Model (CM) consisting of interacting subpopulations of neurons (excitatory pyramidal neurons) and interneurons (excitatory and inhibitory). (A neural subpopulation is termed excitatory when its action potentials cause depolarization, and inhibitory when the action potentials cause hyperpolarization to the target subpopulation.) This model was also used by Wendling and collaborators to simulate epileptic EEG activity.⁸⁴ The interaction strength between the subpopulations is given by the constant gains c₁, c₂, c₃ and c₄, and the system is driven by white noise p(t) that simulates the excitatory input from other cortical areas to the pyramidal cells (see Fig. 2a). Each subpopulation k (i.e., pyramidal neurons and interneurons) is described by the average membrane potential v_k(t) and average action potential output firing rate m_k(t) across cells in the subpopulation. In each subpopulation, the conversion of the incoming action potential firing rate M_k(t) to average excitatory/inhibitory postsynaptic membrane potential is through a linear transformation, i.e., v_k(t) = h_e,i(t) * M_k(t), where h_e,i(t) = (H_e,i/τ_e,i)te^−t/τ_e,i is the excitatory (e)/inhibitory (i) synaptic impulse response (assumed to be the same for all subpopulations), and * denotes convolution. Different values of H_e,i and τ_e,i are chosen to model excitatory and inhibitory postsynaptic potential characteristics. A static nonlinearity transforms the subpopulation average membrane potential v_k(t) to firing rate m_k(t), i.e., m_k(t; v_k(t)) = e₀/(1 + e^{r(v₀−v_k(t))}), where e₀ is the maximum firing rate, and v₀ and r determine the sigmoid shape of the conversion (e₀, v₀ and r are also assumed to be the same for all subpopulations).

FIGURE 2.

Cortical neural mass model. (a) Block diagram of the basic cortical model CM. (b) Block diagram of coupled CMs. The shaded blocks correspond to the pyramidal neuron subpopulation. Inside each CM, h_e = h_e,PY. The model parameters in the two CM populations are dissimilar. $y_1^{CM}(t),y_2^{CM}(t)$ are the observed CM outputs. S denotes the nonlinear relation between the average membrane potential and firing rate. Inter-CM excitatory coupling (bold lines) is based on m₁(t), m₂(t).

In the oscillatory mode, this model produces a narrow band output which depends on the subpopulation impulse responses. With a constant H_e,iτ_e,i, and by varying τ_e and τ_i, the above model was shown by David and Friston¹⁵ to generate oscillatory signals in the delta to gamma band. The schematic diagram of a single neural population model is shown in Fig. 2(a), where y^CM(t) is the model output, and h_e,PY, h_i,PY correspond to the excitatory and inhibitory synaptic transmission of its pyramidal cells respectively. The parameters used for a CM are given in Table 1 and are the same as in Wendling et al.⁸⁴

TABLE 1.

Basic set of parameter values for the cortical model.

Parameter	Value
Heτe	3.25 × 10−2
Hiτi	44 ×10−2
e0	2.5
v0	6
r	0.56
c1	135
c2	108
c3	33.75
c4	33.75
p	Mean = 90
	Variance = 900

In the Coupled Cortical Model (CCM), we model inter-population coupling between the two CMs exclusively via excitatory connections between pyramidal cells of each CM population, which is consistent with neurophysiology.⁴⁴ A synaptic gain factor K represents the coupling level changes, along the lines of Jansen³⁹ and Wendling.⁸⁴ (While we consider here the interaction only between 2 populations, extensions to multiple populations are straightforward.) Let m₁(t), m₂(t) (see Fig. 2b) correspond to the firing rates of pyramidal cells in CM populations 1 and 2 respectively. The coupling from population 2 to population 1 is: K_2→1(t)m₂(t). Similarly, the coupling from population 1 to population 2 is: K_1→2(t)m₁(t). (For simplicity, henceforth we use equal bidirectional coupling, i.e., K_1→2(t) = K_2→1(t) = K(t), where K(t) is the time-varying coupling strength.) The coupling signal K(t)m_i(t) affects the pyramidal cells in the target CM via excitatory synapses. This form of coupling is slightly different from that employed by Jansen³⁹ and Wendling,⁸⁴ where the coupling signal K(t)m_i(t) was filtered to model transmission delays. For simplicity, we do not include this detail here. Note that although with coupling of the form K(t)m_i(t) the DC level of the CM outputs ( $y_1^{CM}(t),y_2^{CM}(t)$) changes with K(t), we retain this form of coupling here since the results are qualitatively similar to those obtained when using a mean-removed coupling signal.

For the sake of clarity, we consider the coupling between 2 dissimilar CMs. The values of H_e,i are adjusted to maintain constant H_e,iτ_e,i (see Table 1). In our simulations, τ_e = 10 ms, τ_i = 20 ms in CM 1 and τ_e = 9.8 ms, τ_i = 16.7 ms in CM 2. (Similar results to the ones we will present here were obtained for several other intrapopulation parameters as well.) Independent noise sources drive the two CMs. All other parameter values are the same as in Wendling et al.⁸⁴ (see also Table 1). Finally, the model was implemented in Simulink using a fixed step solver, executed using Real-Time Workshop, and the output was sampled every 1 ms.

Thalamocortical Population Model

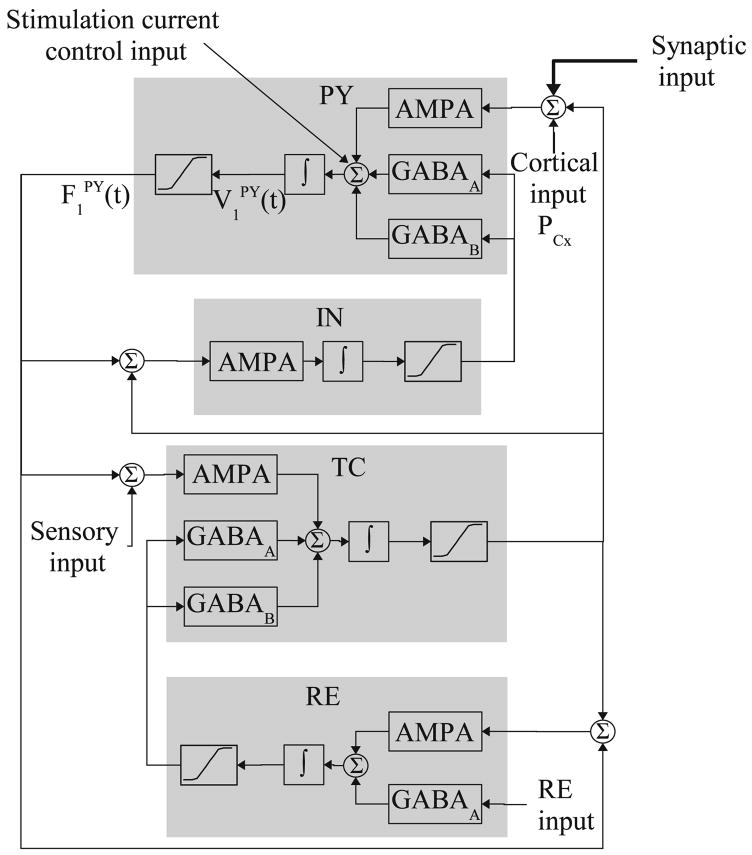
Suffczynski et al. described in detail a thalamocortical model (TCM) with mutually interconnected cortical and thalamic neuron subpopulations in Suffczynski et al.⁶⁶ The TCM consists of 4 cell subpopulations: pyramidal cells (PY) and cortical interneurons (IN) that belong to the cortical module, and thalamocortical cells (TC) and reticular cells (RE) that belong to the thalamic module. The interaction between these subpopulations is via AMPA-mediated (AMPA: α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) excitatory synapses, and GABA_A and GABA_B-mediated (GABA: γ-aminobutyric acid) inhibitory synapses. The schematic diagram of the TCM population is shown in Fig. 3a.

FIGURE 3.

Thalamocortical neural population model. (a) Block diagram of a single TCM population. (b) Block diagram of coupled TCMs. The pyramidal cell average membrane potentials ( $V_1^{PY}(t),V_2^{PY}(t)$) are the observed outputs. The AMPA-mediated excitatory interaction between TCM populations (bold lines) is via pyramidal cells ( $F_1^{PY}(t),F_2^{PY}(t)$). The nonlinear function relating average membrane potential and firing rate are implemented differently in the cortical and thalamic modules.

Each neural subpopulation is described via two variables—membrane potential and firing rate. The synaptic transmission (i.e., firing rate to membrane potential conversion) is described by the following equation for the transmembrane potential V(t) for neurons in each of the above four subpopulations.

$$C_{\text{m}}\stackrel{.}{V}(t)=-\mathrm{\sum }{I}_{\text{syn}}(t)-g_{\text{leak}}(V(t)-V_{\text{leak}})$$ (2)

where the synaptic currents, corresponding to AMPA, GABA_A and GABA_B receptors, are I_syn(t) = g_syn(t) (V(t) − V_syn); C_m is the membrane capacitance, g_leak, g_syn(t) are the leak and synaptic current conductances, and V_leak, V_syn are corresponding reversal potentials. The synaptic conductances are obtained by convolving the incoming action potential firing rate F(t) with the synaptic impulse response h_TCM,syn(t) = A_syn[e^−a_1,synt − e^−a_2,synt], a_2,syn>a_1,syn. Different values for V_syn, A_syn, a_1,syn and a_2,syn are used to model synaptic transmission mediated by AMPA, GABA_A and GABA_B (fast and slow synaptic kinetics). GABA_B receptors have nonlinear activation properties, which are modeled by sigmoid-type nonlinearity based on the afferent firing rate. In the cortical module, a sigmoidal static nonlinearity is used to transform the membrane potentials into firing rates: F(t;V(t)) = G_s/(1 + e^{(V(t)−Θ _s)ζ_s}), where G_s is the maximal firing rate, and Θ_s, ζ_s are the sigmoid threshold and slope parameters. In the thalamic module, this conversion is modeled in greater detail by taking into account the low-threshold calcium current that underlies burst firing in thalamic cells. The intra-TCM interactions, that is the ones between the cortical and thalamic modules, are modeled using constant coupling gains. Cortical and sensory inputs are modeled by non-zero mean white noise. The observed model output is the mean membrane potential of the pyramidal cells V^PY(t), which simulates experimental recordings of local field potentials. We refer the reader to Suffczynski et al.⁶⁶ for further implementation details.

We have modified this population model as follows. In Suffczynski et al.,⁶⁶ the authors show the existence of non-convulsive epileptic phenomena in the TCM as manifestations of a bistable system. In particular, their model exhibits two system states, “spindle-like” oscillations (normal, on-going activity) and high amplitude “seizure-like” oscillations (paroxysmal activity), depending on the values of intrinsic parameters. Here we are interested to investigate transition to seizures due to interactions between neural populations and not due to changes in the intrinsic system parameters of a population. Therefore, we consider each TCM population in the normal activity state, which achieved by reducing its cortical input level 〈P_Cx〉.

In the Coupled Thalamocortical Model (CTCM), we have used a coupling scheme similar to the one we used for CMs. In particular, the coupling between two nonidentical TCMs was assumed to be AMPA-mediated (Fig. 3b). The coupling signal is K(t)F^PY(t) where F^PY(t) denotes the pyramidal cells’ firing rate, and affects the other TCM’s pyramidal cells via excitatory AMPA-mediated synapses. Two TCMs were made nonidentical by setting 〈P_Cx〉 at different values (in particular, for simulations herein, 8 pps (pulses per second) and 10 pps per respective TCM), and with “small” perturbations to the AMPA, GABA_A, GABA_B amplitude, decay and rise times, and with different intrapopulation coupling gains within each TCM population. (It is noteworthy that similar results to the ones we report herein were obtained with a large range of the parameters we utilized to make the TCMs nonidentical). All other parameters were similar to Suffczynski et al.⁶⁶ We implemented the coupled TCM populations in Simulink using a fixed step solver, and the output was sampled every 1 ms.

NEURAL POPULATIONS WITH INTERNAL FEEDBACK

Our hypothesis of the existence of internal feedback mechanisms which maintain low synchrony levels in a neuronal network (section “Why internal feedback?”) suggests the following scheme for normal brain operation: (a) the network is in normal (low synchrony) behavior, (b) an external stimulus or intrinsic change enables spatial coupling, (c) the spatial coupling produces spatial correlations, (d) the spatial correlations activate the internal feedback mechanism, which removes or assimilates the changes in spatial coupling, (e) the network returns to normal (low synchrony) activity. Here we consider internal feedback regulation of excitatory synapses, which bears resemblance to neurophysiological mechanisms.

For simulation expedience, the synchronization level is quantified with an asymptotically unbiased estimate of the correlation coefficient between the population outputs. The correlation ρ_y1y2 (t) between signals y₁(t), y₂(t) is computed in an exponentially weighted manner:

$$\begin{array}{l}{\rho }_{y_1{y}_2}(t)=x_{y_1{y}_2}(t)/\sqrt{x_{y_1{y}_1}(t)x_{y_2{y}_2}(t)}\\ {\stackrel{.}{x}}_{y_1{y}_2}(t)=-a_{\text{f}}{x}_{y_1{y}_2}(t)+a_{\text{f}}(y_1(t)-\langle y_1(t)\rangle )\\ \times (y_2(t)-\langle y_2(t)\rangle )\end{array}$$ (3)

where x_y1y2 (t) is an estimate of the cross-covariance between y₁(t) and y₂(t). 〈.〉 denotes the mean of a signal. a_f affects the memory of the above “correlation filter” (smaller a_f corresponds to a longer correlation window). Since we are interested in slowly varying synaptic interactions and coarse time-scale synchronization properties which is typical for homeostatic processes, we use a low value for a_f. The correlation ρ(t) with a_f = 0.05 is computed between the pyramidal cell membrane potentials, i.e., $y_1^{CM}(t)$ and $y_2^{CM}(t)$ in coupled CMs, and between $V_1^{PY}(t)$ and $V_2^{PY}(t)$ in coupled TCMs.

The CCMs and CTCMs tend to become more correlated with increasing inter-population excitatory coupling (synaptic) strength K(t). However, the internal feedback in these models regulates K(t), i.e., generates ε_R(t) to decrease K(t) by ε_R(t), and maintains an effective coupling K(t) − ε_R(t) for normal synchronization. The internal feedback ε_R(t) is not explicitly shown for coupled CMs in Fig. 2b or coupled TCMs in Fig. 3b. (A more generic, effective coupling formulation would be K̇(t) = g(K(t)) + ε(K(t)), where the kinetics of the coupling process are affected. This is similar to a constrained Hebbian learning model.⁵²)

The internal feedback is modeled as a proportional-integral (PI) feedback action:

$${\epsilon }_R(t)={PI}_I[\rho (t)-{\rho }_{\ast }]$$ (4)

where PI_I denotes the proportional-integral action, ρ(t) is the correlation coefficient (see Eq. 3) between the pyramidal cell populations’ membrane potentials, and ρ_* is a threshold that defines normal synchronous activity. The subscript I in PI_I denotes that the feedback regulation is an internal integral part of the network that models normal brain activity. Despite the highly nonlinear nature of the CCM and CTCM, it was observed that a simple PI regulator was sufficient to maintain a normal level of synchrony. For the PI tuning we followed a simple PI design procedure (for example, see Ogata⁵⁶), although the design can also be carried out rigorously.²⁶ The PI_I is restricted to produce nonnegative signals and it employs limited integration as an anti-windup mechanism (e.g., see Astrom and Rundqwist⁵). This guarantees that when the correlation between the two signals is below the threshold ρ_*, no PI feedback is generated. Thus, the PI_I generates an output that attempts to cancel the effect of the excessive coupling in the neural network and maintain the correlation between the respective two oscillators below a given threshold ρ_*. For all simulations here, we set ρ_* = 0.1 as the “normal” synchrony range. From a feedback point of view, the PI function is to desynchronize the coupled neural populations by reducing their coupling.

Normal Internal Feedback Regulation

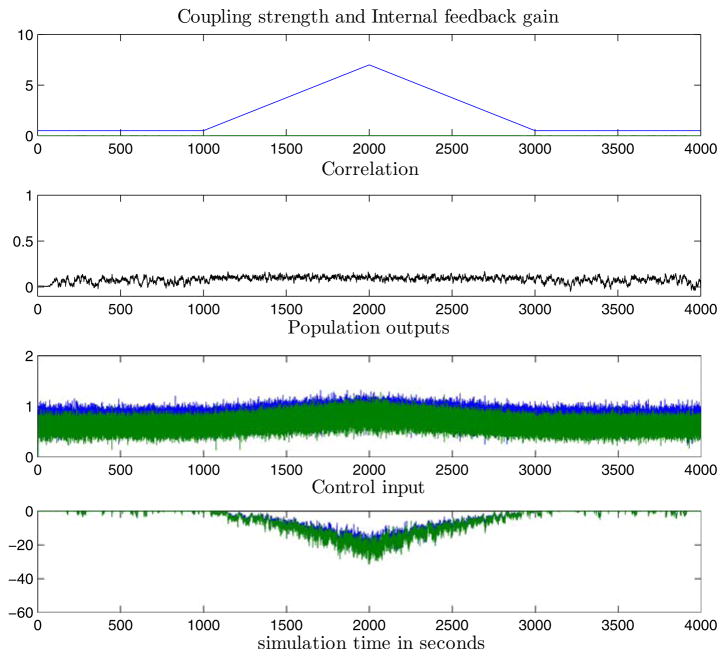
Results from coupled CMs and coupled TCMs with normal internal feedback regulation are presented in Fig. 4. The PI_I that corresponds to a closed loop bandwidth of 0.05 rad/s (that is, twice the open loop bandwidth) for CCMs is modeled with transfer function 2.9 + 1.7/s. Figure 4a shows the response of the coupled CMs with a well-tuned internal PI_I feedback (“normal brain”). The PI produces a feedback gain ε_R(t) that tracks the changing network coupling coefficient K(t) reasonably well to maintain ρ(t) ≤ 0.1. Notice the limited feedback action shown in the ε_R(t) plots; feedback action occurs only when the synchronization is abnormal (here when ρ(t)>0.1). Similar results from CTCMs are shown in Fig. 4b, where the PI’s transfer function is PI_I = 1.7 + 0.44/s, that corresponds to a bandwidth of 0.08 rad/s.

FIGURE 4.

Normal internal feedback regulation of inter-population excitatory coupling in coupled CMs (a) and coupled TCMs (b). The correlation between the neural populations remains low throughout (i.e., ρ_i,j (t)< ρ*) despite the increase of coupling K(t), since normal internal feedback can track these changes and maintain “normal” correlation by constraining the effective coupling K(t) − ε_R(t). (a) and (b) panel legends (top to bottom): Panel I. Coupling K(t) (blue) and regulating feedback gain ε_R(t) (green). Panel II. Correlation between population outputs. Panel III. Population outputs (population 1 in blue, population 2 in green).

Pathological Internal Feedback Regulation

We hypothesize that one pathology of the epileptic brain lies in the pathology of the internal feedback mechanism which does not provide the necessary feedback action (e.g., adequate neurotransmitter release or correct timing) to regulate the excessive increases in the network coupling, which is a pathology within the shaded block in Fig. 1. This may occur when the correction from a malfunctioning (e.g. improperly tuned) internal feedback regulator gets out of phase with the coupling.

In the case of either the CCM or CTCM, if the effective coupling K(t) − ε_R(t) exceeds a critical value K_c (whose value depends on the transfer functions used to model the neural populations), it destabilizes the overall neural network, causing its output to exhibit self-sustained high-amplitude oscillations that resemble a “seizure-like” behavior. (Similar behavior was observed for CM²⁷ and TCM,⁶⁶ and analyzed by a bifurcation analysis, where the CM or TCM populations start exhibiting low-dimensional self-sustained oscillations for certain critical values of their parameters.) A precursor to the seizures in our CCMs and CTCMs appears to be an abnormal increase in the excitatory coupling that is not regulated quickly enough by an existing internal feedback mechanism. This manifests as an abnormal increase in the interpopulation synchronization.

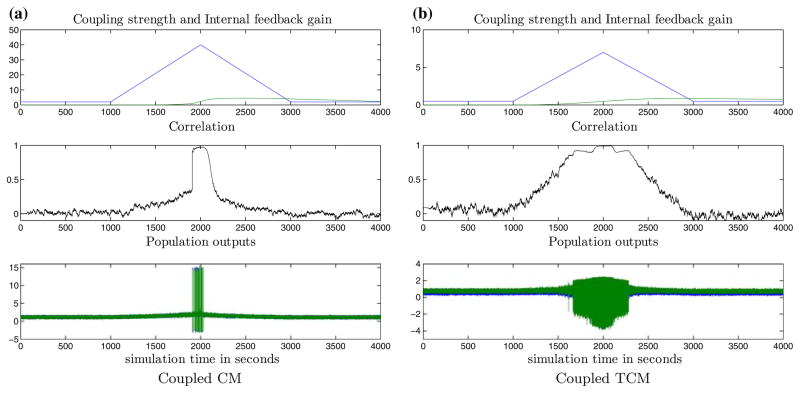
One way to model such a pathological feedback is to use a de-tuned PI_I in the modeling of the network. In contrast to the previously described normal PI_I, the pathological version has orders of magnitude smaller gains. Therefore, to simulate pathological internal regulation, we used PI_I = 0.029 + 0.017/s for the coupled CM and PI_I = 0.0085 + 0.0022/s for the coupled TCM. Results from de-tuned internal feedback regulation are shown in Figs. 5a and 5b for coupled CM and coupled TCM respectively. In these cases, the de-tuned PI_I is out of phase with the coupling change K(t) and the effective coupling K(t) − ε_R(t) keeps increasing. When K(t) − ε_R(t) exceeds a critical value K_c, it destabilizes the neural network, causing its output to exhibit self-sustained high-amplitude oscillations. This “seizure”-like behavior persists until K(t) − ε_R(t)>K_c.

FIGURE 5.

Pathological internal feedback regulation of inter-population excitatory coupling in coupled CMs (a) and coupled TCMs (b). With reduced internal feedback gain, the internal regulator can no longer follow coupling changes closely. “Seizure”-like bursts appear soon after the net coupling K(t) − ε_R(t) exceeds a threshold K_c (K_c ≈ 40 for coupled CM and K_c ≈ 6 for coupled TCM). Notice the significant increase in signal correlation preceding the “seizures”, that bears similarities to the entrainment observed in actual epileptic EEG prior to seizures. Panel legends as in Fig. 4.

Discussion

Several conserved physiological quantities (i.e., controlled variables) for homeostasis have been proposed in the literature (see Turrigiano and Nelson⁸¹ for a review). Our hypothesis for conservation of normal synchronization between neuronal populations as a necessary condition for a normal operation of the epileptic brain represents a novel homeostatic condition. Here we have considered the case of a generic internal feedback mechanism which regulates inter-population coupling based on the resulting inter-population synchronization. Pathology of such an internal controller leads to “epileptic seizures”. It is important to note that the dynamical behavior of the above models bears similarities to the EEG data in real seizures, where preictal dynamical entrainment between critical brain areas, have been observed and reported.^32–38,65 Pre-seizure entrainment similar to the one observed prior to actual seizures was seen in both models presented here (see “pre-ictal” period in Fig. 5). The underlying cause was the inability of the de-tuned PI_I to track the changes in the coupling, which then causes the correlation between the two neural population outputs to increase considerably before a network “seizure”.

Implicit in the above concept of pathological internal feedback is the dependence of occurrence of network “seizures” on the variations of the coupling between neural populations. Thus, while the epileptic neural network may be susceptible to seizures due to its internal pathological feedback (e.g. existence of an epileptogenic focus), the exact onset of seizures remains unknown and depends on external or internal processes (external inputs or internal system modifications) that would eventually cause variations to its coupling. One can generally view such a situation as a pathology in the implementation of the overall operational objectives of a system. Such a viewpoint, that seizures can be caused by pathologies in the implementation of the system’s overall operational objective to maintain normal synchrony between neural populations is clear from (i) the simulation results from the biologically plausible lumped-parameter neural population networks presented above, where excess network excitation may result from failure in the homeostatic mechanisms regulating the synaptic connections, and (ii) previous results¹⁰ from neuronal networks, wherein excess network excitation at neuron- level populations may result from the failure in the homeostatic mechanisms regulating excitatory synapses or the balance of the level of excitation and inhibition in the network. In both cases, excess excitation and network “seizures” are accompanied by the failure to maintain normal synchronous behavior. The simulation results presented here are in conformance with the neurophysiological viewpoint that runaway excitation in neural populations is a cellular mechanism for epileptic seizure generation.⁴⁹

In terms of extensions to the model presented here, while our modeling framework considered internal feedback to compensate for excess coupling at the network (inter-population) level, we would like to point out that such a mechanism could occur at multiple levels, such as individual synapses, neuronal membrane, neuron, neuron-neuron (population) level etc.⁸¹ Also, in the models herein we considered only equal and bidirectional coupling between populations, although unequal (directional) interactions in the brain could generally occur. A straightforward extension of our models could include such interactions, as well as appropriate measures for directional synchronization.

SEIZURE CONTROL

In addition to serving as a functional model for epileptic brain operation, the developed models can be utilized to provide insight into application of feedback control strategies to suppress or avert seizures in the epileptic brain. In these models, a natural goal for a prospective seizure control scheme is the disruption of correlation/synchronization patterns observed prior to seizures with minimal side-effects. We present a hypothesis-driven paradigm for successful seizure control in simulation studies that employ these neural population models. The objective was to externally provide appropriate feedback control stimulation to achieve low (normal) synchronization levels between the populations, when such levels cannot be maintained by the existing internal, but pathological, feedback.

The electrical stimulation-based control paradigms we have studied can be broadly classified as:

1. Open-Loop or Closed-Loop Discrete-Time, where a predefined stimulation (form and duration-wise) is delivered at predetermined regular intervals (open-loop) or when a warning of an impending seizure is issued, typically close to a seizure’s onset (closed-loop).

2. Closed-Loop Continuous-Time, where a control stimulation is applied whenever and until seizure susceptibility is high, not necessarily only in a preictal period. Closed-loop continuous-time control can be further classified based on the type of the stimulation waveform used:

   1. Predefined stimulus, where the stimulation waveform has predefined parameters (e.g., square or sinusoidal, duty cycle etc.) that are determined via experimentation.

   2. Not-a-predefined stimulus, whose characteristics are automatically determined by appropriate analysis of the system’s global current state. We have called this scheme “Feedback Decoupling”, and it is the one that outperformed all above seizure control schemes.

Open-loop and closed-loop discrete-time control schemes with a predetermined stimulus may have the advantage of a simpler implementation but both clinical studies⁴² and our past simulation studies^71–75 have shown that they are mostly ineffective. Therefore, in our simulations herein, we only studied the performance of the closed-loop continuous-time control strategies via either a predefined stimulus or a feedback decoupling stimulus.

Closed-Loop Continuous-Time Feedback Decoupling Control

Feedback decoupling control is inspired from adaptive control. The feedback decoupling controller basically takes advantage of the hypothesized internal feedback structure and generates stimulation signals as a function of the system state in order to quickly return the system at a low a level of synchrony that is considered normal (not pathologic). Although the success of this strategy depends on how realistic our assumed internal feedback structure is, it is a fundamental property of feedback control that it reduces certain aspects of sensitivity to model accuracy. We therefore expect that the requirements on model accuracy are less stringent than the ones for open-loop control.

Conceptually, excess excitatory synaptic coupling in the CCM and CTCM systems can be either directly removed by subtracting an estimate of the excitatory coupling signal, or indirectly compensated through inhibition that would eventually decouple the neural populations. To show the method’s performance, we present examples of both cases first in CCM and then in CTCM. The pyramidal cell subpopulation membrane potential in CM 1 (see Fig. 2b) is $y_1^{CM}(t)=h_{e,PY1}{(t)}^{\ast }(p_1(t)+m_{e,IN1}(t))-h_{i,PY1}{(t)}^{\ast }{m}_{i,IN1}(t)+h_{e,PY1}{(t)}^{\ast }(K(t)-{\epsilon }_R(t))m_2(t)$, where the internal feedback regulation ε_R(t) is pathological (similarly for CM 2). The effect of excessive excitatory coupling to CM 1 (similarly for CM 2) can be:

1. removed with an input of the form −K_E(t)m̂₂(t), where K_E(t) is an externally manipulated control gain and m̂₂(t) is an estimate of the coupling signal (pyramidal cell firing-rate in CM 2). The excitatory synapse of pyramidal cells in CM 1 then becomes: h_e;PY1(t) * ((K(t) − ε_R(t)) m₂(t) − K_E(t)m̂₂(t))

2. compensated with an input K_E(t) m̂₂(t) which affects the inhibitory synapses of the pyramidal cells as h_i;PY1(t) * (m_i;IN1(t)) K_E(t)m̂₂(t))

Implementation-wise it is not possible to stimulate coupled CMs by action potentials with “negative firing rate”, and it may not be feasible to activate only particular kinds of synapses (e.g. the inhibitory ones) with “action potential” control inputs. Nevertheless, we will show that the generated results are insightful for further implementations.

Coupled CMs

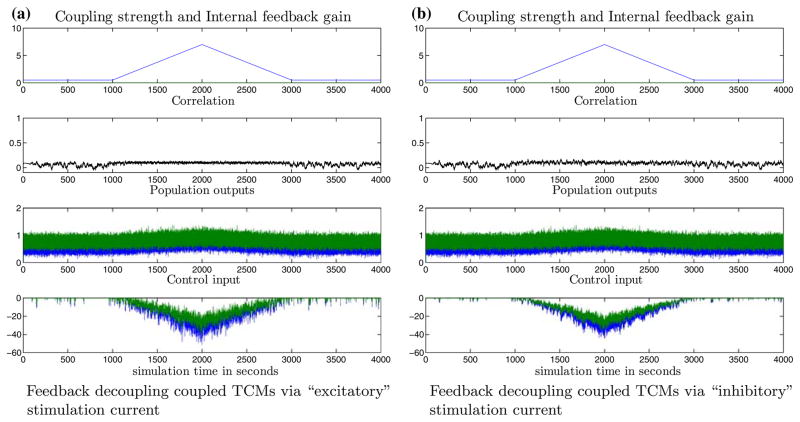
The results of applying the above concept of decoupling through excitatory stimulation via “excitatory firing-rate input” and through compensatory inhibitory stimulation via “inhibitory firing rate input” (see block diagram in Fig. 6a) are presented in Fig. 7. Here, m̂₁(t) and m̂₂(t) are estimated via a rectifier from the observed signals $y_1^{CM}(t)$ and $y_2^{CM}(t)$ respectively, i.e., ${\widehat{m}}_i=y_i^{CM}$ if $y_i^{CM}\ge 0$; and m̂_i = 0 otherwise. Such an approximation of the nonlinear conversion of membrane potential to action potential firing rate turns out to be sufficient for feedback decoupling control. The gains K_E(t) are manipulated by an external PI controller (PI_E), i.e., K_E(t) = PI_E(ρ_i,j(t)− ρ_*), where PI_E = 8.3 + 2.2/s. PI_E provides feedback stimulation when ρ_i;j(t)>ρ_* and compensates for the lack of the model’s internal feedback. From the results, it is evident that such a control approach maintains low levels of correlation and averts network “seizures”.

FIGURE 6.

Schematic diagram of “firing-rate” control inputs to coupled CMs and coupled TCMs. The schematic diagrams show one of the two coupled neural populations with firing-rate control inputs. (a) Conceptually, excess excitatory coupling to CM 1 can be removed with an input −K_E(t)m̂₂(t) to h_e,PY1 or compensated with an “inhibitory firing-rate input” K_Em̂₂(t) to h_i,PY1, and similarly for CM 2. (b) In the case of coupled TCMs, excess excitatory coupling to TCM 1 can be removed with an input $-K_E(t){\widehat{F}}_2^{PY}(t)$ to AMPA receptors or compensated with an “inhibitory firing-rate input” $K_E(t){\widehat{F}}_2^{PY}(t)$ to GABA_A and GABA_B receptors, and similarly for TCM 2. It is not possible to input negative firing-rates, and it may not be feasible to activate only certain synapses. However this setup is useful in providing insight for implementing plausible feedback decoupling control schemes.

FIGURE 7.

Successful feedback decoupling control of epileptic coupled CMs via “firing-rate” control. Conceptually, it is possible to control abnormal synchronization and avoid seizures with (a) “subtractive firing-rate input” to excitatory synapses h_e,PY(t), and (b) compensatory “additive firing-rate input” to inhibitory synapses h_i,PY(t). (a) and (b) Panel legends (top to bottom): Panel I. Coupling K(t) (blue) and internal feedback gain ε_R(t) (green). Panel II. Correlation between population outputs. Panel III. Population outputs (population 1 in blue, population 2 in green). Panel IV. “Firing-rate” control inputs to pyramidal cells in population 1 (blue) and population 2 (green).

Coupled TCMs

Similar to CCMs, excess excitatory coupling input to TCM 1 (or TCM 2) can be removed with excitatory control inputs of the form $-K_E(t){\widehat{F}}_2^{PY}(t)$ to AMPA receptors in the PY subpopulation, or inhibitory inputs to GABA_A and GABA_B receptors in the PY subpopulation (see block diagram in Fig. 6b). ${\widehat{F}}_2^{PY}(t)$, which is an estimate of pyramidal cell firing-rate in TCM 2, is estimated from $V_2^{PY}(t)$ with a rectifier similar to the one for the CCM. The gains K_E(t) are manipulated by an external PI controller, i.e., K_E(t) = PI_E(ρ_i,j(t) − ρ_*), where PI_E = 1.7 + 0.44/s. The results of successful excitatory and inhibitory firing-rate feedback decoupling control are shown in Fig. 8.

FIGURE 8.

Successful feedback decoupling control of epileptic coupled TCMs via “firing-rate” control. Conceptually, it is possible to control abnormal synchronization and avoid seizures with (a) “subtractive firing-rate input” to AMPA-mediated synapses, and (b) compensatory “additive firing-rate input” to GABA_A and GABA_B-mediated synapses. The external control gains are manipulated by a PI controller which is activated when ρ_1,2(t)>ρ*. Panel legends as in Fig. 7.

While firing-rate control is a conceptual development, we next present the implementation aspects of a realistic feedback decoupling control with stimulation currents as control inputs. For illustration purposes we will present the results below only from coupled TCMs. With an external control stimulation current u^E(t), the pyramidal cell subpopulation average membrane potential is described by

$${\stackrel{.}{V}}^{PY}(t)=-\mathrm{\sum }{I}_{int}(t)+u^E(t)$$ (5)

where ΣI_int(t) is the sum of intra-population and interpopulation synaptic and leak currents (see Eq. 2). The block diagram of this is depicted in Fig. 9 and the setup could be implemented with neural stimulation electrodes. The effect of excessive excitatory synaptic coupling current from TCM 2 to TCM 1 can be either removed (case A) or compensated (case B). In case A, the excitatory stimulation current u^E(t) to pyramidal cells in TCM 1 is then:

$$u_1^E(t)=-K_E(t)({\widehat{h}}_{\mathit{TCM},\mathit{AMPA}}(t)\ast {\widehat{F}}_2^{PY}(t))(V_1^{PY}(t)-V_{\mathit{AMPA}})$$ (6)

and similarly for TCM 2. ĥ_TCM;AMPA is an estimate of the AMPA synaptic kinetics, V_AMPA is the synaptic reversal potential, F̂^PY(t) is an estimate of the pyramidal cell firing rate and K_E(t) is the externally manipulated control gain. While ĥ_TCM;AMPA and V_AMPA could be obtained empirically (for example, see Chapter 5 in Destexhe and Sejnowski²⁰), we observed that ĥ_TCM;AMPA can be approximated as a low-pass filter (bandwidth 20 Hz). The accuracy of the synaptic kinetics (for example, rise and settling times) was not observed to be critical in this implementation. F̂^PY(t) is estimated from V^PY(t) with a rectifier similar to the one mentioned above, and K_E(t) is manipulated with an external PI_E = 1.7 + 0.44/s.

FIGURE 9.

Schematic diagram of control stimulation current input to a TCM. The figure shows one the two coupled TCM populations wherein the stimulation current u^E(t) is the control input affecting pyramidal cells.

In case B, the inhibitory stimulation current to TCM 1 is

$$u_1^E(t)=K_E(t)({\widehat{h}}_{\mathit{TCM},{\mathit{GABA}}_A}(t)\ast {\widehat{F}}_2^{PY}(t))(V_1^{PY}(t)-V_{{\mathit{GABA}}_A})$$ (7)

and similarly for TCM 2. The GABA_A kinetics, which is denoted by ĥ_TCM;GABAA, is approximated with a low-pass filter (bandwidth 20 Hz). K_E(t) is obtained from an external PI_E = 1.7 + 0.44/s. Successful seizure control in each case is shown in Fig. 10. In Fig. 10a, an estimate of the excitatory synaptic coupling current (bottom panel) is used as the control input to maintain normal correlation (second panel) and avoid “seizures” (third panel) despite the pathological internal feedback. In Fig. 10b, compensatory control stimulation by the inhibitory synaptic coupling current (bottom panel) is used to control seizures and maintain normal levels of synchrony. These results remained robust with respect to changes in intra-population system parameters and using the same external control stimulation setup.

FIGURE 10.

Successful closed-loop control of the epileptic coupled TCMs with feedback decoupling electrical stimulation. Excess internal excitatory coupling is (a) removed by subtracting its estimate or, (b) through inhibitory compensation. (a) and (b) panel legends (top to bottom): Panel I. Coupling K(t) (blue) and internal feedback gain ε_R(t) (green). Panel II. Correlation between population outputs. Panel III. Population outputs (population 1 in blue, population 2 in green). Panel IV. Stimulation current control input u^E(t) to pyramidal cells in population 1 (blue) and population 2 (green).

Finally, it was also possible to achieve feedback decoupling control of the network seizures without using stimulation currents that precisely mimic the internal synaptic currents described in (6) and (7). Again, this is indicative of the generic nature of the proposed type of feedback decoupling control. In this scheme, we used a “quasi-diffusive”¹ stimulation current to TCM 1 (and similarly TCM 2) $u_1^E(t)=-K_E(t)V_2^{PY}(t)$. The gains K_E(t) are manipulated with an external PI_E = 95 + 7/s. This control scheme is important because the exact synaptic kinetics and currents in the constituent neural populations need not to be known. The results of successful feedback decoupling with quasi-diffusive stimulation current are shown in Fig. 11.

FIGURE 11.

Feedback decoupling control of epileptic coupled TCMs via “quasi-diffusive” control stimulation. The two pathologically coupled TCMs can be decorrelated with stimulation currents which are essentially modulated versions of the observed membrane potentials. Panel legends as in Fig. 10.

Note that the above implementations of the external controller are based on the actual observed membrane potentials. The use of actual membrane potentials implies that for implementation, such a controller would require an observer to estimate those values from available measurements. Observers must be carefully designed so as to avoid unnecessary deterioration of closed loop performance, and modern control theory offers several techniques to achieve this. Other potentially feasible therapeutic implementations of such a closed-loop control action include the local release of GABA enhancing drugs that also effectively may result in increased inhibition.^14,22

Closed-Loop Continuous-Time Predefined Stimulus-Based Control

This control technique involves feedback stimulation with predetermined stimulus such as pulse or sinusoidal waveforms during the high seizure-susceptibility periods (i.e., when the synchronization measures ρ are greater than the threshold ρ_*). The control inputs are phase shifted by π radians with respect to each other and then applied to each pathological neural population pair. Since the TCM is amenable to current stimulation, we here consider the control of pathologically coupled TCMs (same pathology as in section “Pathological internal feedback regulation”) using predefined stimulation currents. The control currents affect the pyramidal cell subpopulations in each TCM (see Eq. 5).

Let u_P,i(t) denote the predefined stimulus to neural population i. Two simple ways to apply the predefined stimulation during periods of high seizure-susceptibility are: (i) switching control, where the control stimulus is applied whenever ρ>ρ_*, i.e., the external control signal $u_i^E(t)=U_S(t)u_{P,i}(t)$, where U_S(t) = 1 (“switched on”) when ρ>ρ_*,U_S = 0 (“switched off”) otherwise. This technique did not produce successful control of seizures in the simulation model, despite using a broad set of parameters (e.g. frequency, duty cycle, amplitude) for the predefined waveforms. (ii) “modulating” control where the predefined waveform’s amplitude is modulated with an external controller, i.e., $u_i^E(t)=U_M(t)u_{P,i}(t)$, where U_M(t) = PI_E(ρ(t) − ρ_*). Based on experiments, we selected monophasic sinusoidal currents at a frequency of 80 Hz, and modulated its amplitude for modulating control (see Eq. 8). It was found that the stimulus waveform frequency was critical for the success of the closed-loop controller. The control input to the coupled TCMs were

$$\begin{array}{l}{u}_1^E(t)=U_M(t)(-0.5+0.5sin(160\pi t))\\ u_2^E(t)=U_M(t)(-0.5+0.5sin(160\pi t+\pi ))\end{array}$$ (8)

The external control gain U_M(t) = PI_E(ρ_1,2(t) − ρ_*), with PI_E = 72 + 25/s. The results of this control are shown in Fig. 12. It is possible to maintain normal levels of synchrony (second panel from top) and mitigate seizure occurrences (third panel from top), but at the expense of higher intensity of control stimulation (bottom panel). It is worthy to compare these results with the ones from the feedback decoupling control cited in Fig. 10. In comparison with feedback decoupling, the use of closed-loop continuous-time predefined current stimulus to control pathological CTCMs was also inferior in terms of control efficacy (seizure mitigation vs. suppression), as well as the required intensity of the control input for the control of seizures, which in turn could give rise to serious physiological side-effects. Based on our past simulation results, the necessity of continuous closed-loop control and the advantages of feedback decoupling strategies remain valid and are often amplified for general network topologies, involving many oscillators with one or more pathological interconnections, see Tsakalis et al.^71–73 and Tsakalis and Iasemidis.⁷⁵

FIGURE 12.

Closed-loop “modulating” control of pathological TCMs using bidirectional “monophasic” sinusoidal stimulation. Without appropriate intervention, the pathological internal feedback can lead to “seizures” as in Fig. 5(b). With “modulating” control using carefully chosen predefined stimulus waveforms, it is possible to maintain “normal” synchrony and mitigate “seizure” occurrence. In comparison with feedback decoupling control in Fig. 10, the use of predefined stimulus-based “modulating” controller required greater control effort. Panel legends (top to bottom): Panel I. Coupling coefficient K(t) (blue) and internal feedback regulating gain ε_R(t) (green). Panel II. Correlation between the population outputs. Panel III. Population outputs (population 1 in blue, population 2 in green). Panel IV. Control input $u_1^E(t)$ (see Eq. 8) to population 1 pyramidal cells ( $u_2^E(t)$, which is a 180° phase-shifted version of $u_1^E(t)$, is not shown).

It is also interesting to point out that the used stimulation frequency (80 Hz) is in the range of that used to stimulate the anterior nucleus of the thalamus for intractable epilepsy in humans.⁴² It is also in the frequency range for studies which reported that stimulating the cerebellar dentate nucleus and centromedial thalamic nucleus desynchronized the EEG.¹² Even in animal studies, stimulation frequency in the range of 50 to 230 Hz has been reported to be effective. On the other hand, in VNS studies in humans, open loop stimulation at 30 pulses per second has been used.²³ Further, Yamamoto et al.⁸⁵ reported that low frequency stimulation has an inhibitory effect.

Discussion

In summary, the control results from simulations of neuronal populations in the brain show that the operational objective of decorrelating excessively coupled neural populations with internal pathological feedback loops can be achieved based on retrieved information about the location, level and direction of this coupling without precise knowledge about their internal interaction mechanisms. Of all control schemes tried on these models so far (herein and elsewhere), the feedback decoupling control appears to be: (a) more effective for seizure control (e.g. seizure suppression vs. mitigation by other methods at best), (b) less interfering because the resulting state-depending control signals are in the range of the actual interpopulation coupling signals (it was found to be 5 times less than the effective predetermined stimulus-based control method—compare Fig. 12 and Fig. 10), and (c) applicable to a wide variety of pathologies in terms of their structural complexity and spatial extent (see more details on this aspect in Chakravarthy⁹).

Next, in terms of limitations and extensions to the external controller, firstly, the neurophysiological effect of electrical stimulation on neural population is not precisely modeled. In other words, current stimulation may in reality induce physiological changes and alter system dynamics in ways that may not be captured in the simplified models. Secondly, the controllers developed here focus on a theoretical (“controllability”) requisite of avoiding “seizure” occurrence, whereas neurophysiological requisites such tissue damage and charge balance, should be considered during practical implementation. For instance, “monophasic” predefined stimulation was used for controlling “seizures” in some models, but such a stimulus waveform may not be preferable in practice. Thirdly, the accuracy of measurements may be critical for certain controllers that generate control inputs which approximate synaptic currents. Hence as mentioned above, observers must be carefully designed so as to avoid unnecessary deterioration of closed loop performance, and modern control theory offers several techniques to achieve this. In this respect we also note that external controllers similar to the “quasi-diffusive” feedback decoupling controller that do not require precise models should also be practically tested. Finally, in order to test the generality and efficacy of the control paradigms, an obvious, albeit computationally expensive, extension of the current overall model would be to include detailed neurophysiological details.

CONCLUSION

Motivated by the existence of a pathological dynamical entrainment (synchronization) between critical brain sites prior to epileptic seizures,^32–38 we sought to discover similar transitions in coupled chaotic oscillators^71–75 and biologically plausible coupled neuron-level populations.^9,10 In this paper, we extended those results to the next class of biologically plausible models. Towards this goal, we first modified two neurophysiological lumped-parameter population models from the literature, the cortical and thalamocortical models, by introducing a physiological coupling between the populations of each of the two models. We called the resulting models coupled cortical models (CCMs) and coupled thalamocortical models (CTCMs) respectively. In each of these models an internal functional feedback of similar form was then implemented, which essentially regulated the coupling between the populations in a model. In particular, normal feedback action could maintain the degree of synchronization between the populations at an acceptable level, i.e., the homeostasis of brain dynamics at the level of population coupling. We showed that, while the presence of normal internal feedback action could compensate for transients of excessive coupling between any two populations, a pathological one (e.g. a detuned internal feedback) could not, and this resulted in “epileptic seizures” in the models that was preceded by “entrainment” periods similar to the ones observed prior to actual epileptic seizures. In search of an effective external controller, capable of compensating the inadequate (pathological) internal feedback action, we tried two closed-loop continuous-time control schemes. One control scheme used an “optimized” (through trial-and-error) predetermined stimulus. The other control scheme used an adaptive state-dependent controller (feedback decoupling). It was shown that the feedback decoupling scheme was superior in terms of its flexibility (across models), efficacy for “seizure” abatement and the low current intensity it was using towards this goal. This implies that the potential use of such a control scheme for seizure control could have four advantages: (a) efficacy, (b) generality, (c) economy in required power (e.g., battery power), and (d) reduced side effects.

A theoretical modeling approach like the one presented here, developed on basic engineering principles of control, is by default only a first step in the investigation of the control of basic dynamics of epileptogenic networks. However, it is an essential step because it provides valuable insights for subsequent testing of novel and refinement of the few currently existing seizure control strategies in animal and human studies. It is noteworthy that the performance of our predetermined stimulus controller for seizure control in our models is in agreement with the poor performance similar controllers have exhibited for seizure control in recent clinical trials. The validation of the performance of the feedback decoupling controller for epileptic seizures in animal studies is underway.