Abstract
Epileptic seizures are manifestations of intermittent spatiotemporal transitions of the human brain from chaos to order. Measures of chaos, namely maximum Lyapunov exponents (STLmax), from dynamical analysis of the electroencephalograms (EEGs) at critical sites of the epileptic brain, progressively converge (diverge) before (after) epileptic seizures, a phenomenon that has been called dynamical synchronization (desynchronization). This dynamical synchronization/desynchronization has already constituted the basis for the design and development of systems for long-term (tens of minutes), on-line, prospective prediction of epileptic seizures. Also, the criterion for the changes in the time constants of the observed synchronization/desynchronization at seizure points has been used to show resetting of the epileptic brain in patients with temporal lobe epilepsy (TLE), a phenomenon that implicates a possible homeostatic role for the seizures themselves to restore normal brain activity. In this paper, we introduce a new criterion to measure this resetting that utilizes changes in the level of observed synchronization/desynchronization. We compare this criterion's sensitivity of resetting with the old one based on the time constants of the observed synchronization/desynchronization. Next, we test the robustness of the resetting phenomena in terms of the utilized measures of EEG dynamics by a comparative study involving STLmax, a measure of phase (ϕmax) and a measure of energy (E) using both criteria (i.e. the level and time constants of the observed synchronization/desynchronization). The measures are estimated from intracranial electroencephalographic (iEEG) recordings with subdural and depth electrodes from two patients with focal temporal lobe epilepsy and a total of 43 seizures. Techniques from optimization theory, in particular quadratic bivalent programming, are applied to optimize the performance of the three measures in detecting preictal entrainment. It is shown that using either of the two resetting criteria, and for all three dynamical measures, dynamical resetting at seizures occurs with a significantly higher probability (α = 0.05) than resetting at randomly selected non-seizure points in days of EEG recordings per patient. It is also shown that dynamical resetting at seizures using time constants of STLmax synchronization/desynchronization occurs with a higher probability than using the other synchronization measures, whereas dynamical resetting at seizures using the level of synchronization/desynchronization criterion is detected with similar probability using any of the three measures of synchronization. These findings show the robustness of seizure resetting with respect to measures of EEG dynamics and criteria of resetting utilized, and the critical role it might play in further elucidation of ictogenesis, as well as in the development of novel treatments for epilepsy.
Keywords: Quadratic binary programming, Dynamical Synchronization, Spatiotemporal transitions, Epileptic seizure dynamics
1 Introduction
Epilepsy is a disorder characterized by recurrent seizures. The seizures (ictal states) cause temporary disturbances of brain functions (e.g. motor control, responsiveness, recall), for periods ranging from seconds to minutes. Seizures may be followed by a postictal period of confusion or impaired sensorium that can last several hours. Seizures occur when a massive group of neurons in the cerebral cortex suddenly begin to discharge in a highly organized rhythmic pattern. This pattern usually begins and terminates spontaneously, without external intervention. This seemingly abrupt initiation and termination of epileptic seizures reflect intrinsic, but poorly understood properties of the epileptic brain.
Research into the neuro(patho)physiology of epileptic seizures has largely focused upon discovering factors that are responsible for seizure initiation. Several neurophysiological (microscopic) and mathematical modeling studies have attributed genetic and cellular-level factors (e.g. intrinsic neuronal properties such as type, number and distribution of voltage and ligand-gated channels, biochemical modification of receptors, modulation of gene expressions) (Gwinn et al. 2002; McCormick and Contreras 2001; Zhou et al. 2007), and synaptic-level factors (e.g. extrinsic neuronal properties such as changes in extracellular ion concentrations, modulation of excitatory/inhibitory synaptic coupling levels between neural populations, presence or absence of inter-neuronal feedback loops) to the spontaneous nature of seizure initiation (Traub et al. 2005; Wendling et al. 2002; Chawla et al. 1999; Prince and Jacobs 1998). However, little is known about the spontaneous arrest of seizures and the postictal period that follows the end of a seizure. Although it has been postulated that termination of seizures are facilitated by the ictal and postictal activation and/or release of endogenous anticonvulsant mechanisms, the lack of which during the preictal period creates conditions conducive for seizure elicitation (Prince and Jacobs 1998; Lee et al. 1984), no single hypothesis unequivocally implicates a unifying framework within which initiation as well as termination of epileptic seizures can be clearly understood.
Using higher-level (macroscopic) dynamical analysis of electroencephalographic signals (EEG), we have found that seizures are not abrupt transitions in and out of an abnormal ictal (seizure) state, instead they follow a dynamical transition that evolves over minutes to hours (Iasemidis and Sackellares 1991; Iasemidis et al. 1997). During this preictal dynamical transition, multiple regions of the cerebral cortex progressively approach a similar dynamical state, a phenomenon we have called preictal dynamical entrainment or dynamical synchronization. The dynamics of the preictal transition are complex. Even in the same patient, the participating cortical regions and the duration of the transition vary from seizure to seizure. Understanding these dynamics requires analytic methods capable of identifying anatomical regions where critical state changes occur. After the seizure (postictal state), brain dynamics revert to a more disordered state in which previously entrained (synchronized) cortical areas become disentrained (desynchronized). The epileptic brain repeats this series of state transitions intermittently, at seemingly irregular but, in fact, time-dependent intervals (Iasemidis et al. 1994; Olson et al. 1989). This implies that the transition into seizures is not a random process. Thus, the question as to why seizures occur should be addressed. Based on the analysis of a small sample of seizure recordings, we postulated that seizures may serve as intrinsic mechanisms to desynchronize brain areas that were dynamically synchronized in the immediate preictal periods (Iasemidis et al. 2003b, 2004; Shiau et al. 2000). We have defined this phenomenon as “resetting” of the epileptic brain via recurrent seizures.
The clinical implications of such a resetting are many. In particular, it may be possible to exploit the knowledge gained about these endogenous dynamical transitions to instigate a rational seizure control approach that aims at dynamically resetting the brain early in the preictal period, i.e., disentrain entrained critical brain sites and alleviate the need for a seizure to occur. Furthermore, the concept of resetting may also provide some insights into the mechanisms underlying a life-threatening emergency, status epilepticus. In “status epilepticus”, seizures occur successively, at brief intervals, without recovery of consciousness between seizures. If, as we suggest, ictal resetting is a mechanism for the brain to reverse a pathological state, one could postulate that, in status epilepticus, successive seizures occur because the previous seizure fails to dynamically reset critical brain sites.
Recent studies on dynamical analysis of seizure control via drug-based stimulation in rodent models of chronic epilepsy, as well as clinical data from patients treated with anti-epileptic drugs (AED), have shown a significant increase in the brain dynamical disentrainment immediately after drug administration (Good et al. 2004). In particular, it appears that the applied stimulation dynamically resets (disentrains or desynchronizes) the entrained brain sites. This constitutes evidence that drug-based stimulation can actually reset the spatio-temporal dynamics of the brain, and hence could be used as actuation in a control scheme for epileptic seizure prevention (Good et al. 2004; Tsakalis et al. 2006). Preliminary results on seizure control with electrical stimulation also point to the same conclusion (Good 2007). Also, in computer simulations of biologically plausible models that consist of networks of coupled chaotic oscillators and exhibit “seizure-like” behaviors, we have shown that an increase in the strength of coupling between these oscillators result in a progressive dynamical entrainment that leads to “seizures” if the existing internal feedback loops in those networks fail to compensate for it (Iasemidis et al. 2003b; Prasad et al. 2005; Tsakalis et al. 2006; Tsakalis and Iasemidis 2006). Our subsequent studies on the control of the above models by external input (electrical stimulation) show that “seizures” can be avoided only if the stimulus successfully resets the dynamically entrained sites (Tsakalis and Iasemidis 2006; Chakravarthy et al. 2007). These findings have motivated us to further quantify the resetting of the human epileptic brain.
Elucidation of the mechanisms of the resetting process from EEG data is a challenging task. In this paper, we utilize two metrics of this process: (a) Level of Resetting (LR), quantified by the difference of the average entrainment (synchronization) value of critical brain sites at 10 min before a seizure's onset (immediate preictal state) and 10 min after a seizure's end (immediate postictal period); (b) Resetting Ratio of Time constants involved (RRT), quantified by the ratio of the time it takes the critical sites to disentrain postictally (desynchronization period) over the time they were entrained preictally (synchronization period). Based on these two metrics of resetting, we test the hypothesis that seizures occur in order to negate the long-term, excessive preictal synchronization and revert to a desynchronization state postictally. In order to show the robustness of this phenomenon with respect to the measures used to measure synchronization, we compare three different measures of dynamical synchronization/entrainment, namely amplitude, phase and STLmax on the basis of their ability to detect resetting at seizure points using the LR and RRT metrics. Due to the current interest in the field, and the proposed measures of energy and phase as alternatives to STLmax for the study of EEG dynamics and seizure prediction (Iasemidis et al. 2005), it was deemed important to comparatively evaluate all three measures' seizure resetting detection capabilities in a retrospective study. Quadratic integer programming techniques of global optimization were applied to select critical electrode sites per measure for every recorded seizure. Results following such an analysis with 43 seizures recorded from two patients with temporal lobe epilepsy demonstrated that: (1) Brain resetting of critical cortical sites synchronized in phase, energy and STLmax, as measured by LR or RRT, occurs much more frequently at seizure points than at randomly selected points in the available days of interictal EEG recordings in both patients; (2) Dynamical resetting of STLmax synchronization using the RRT criterion consistently resulted to higher probability of resetting at seizures than the other two measures. Among the other two measures, the phase-based synchronization measure outperformed the energy-based synchronization in the detection of resetting at seizures using the RRT criterion. On the other hand, no consistent difference between the dynamical resetting performance of the three measures of synchronization could be established by using the LR criterion at seizures; (3) Interictal periods are intermittent states where the transition from a prolonged synchronization of critical sites to faster desynchronization is a rare phenomenon. The implications of these findings for the understanding of ictogenesis, seizure prediction and control are discussed.
The organization of the paper is as follows. In Sect. 2, the three measures of synchronization utilized in the analysis of the EEG are described. In Sect. 3, we explain the formulation of a quadratic integer programming problem to select critical electrode sites for monitoring the epileptic brain's synchronization. Section 4 describes the two metrics used on the measures of synchronization to detect resetting. In Sect. 5, the EEG data and the results of their analysis are presented. Discussion of the results and conclusions are provided in Sect. 6.
2 Measures of EEG synchronization
2.1 Measure of energy (E) profiles
A classical measure of a signal's strength is calculated as the sum of its amplitude squared over a time period T,
| (1) |
where xi are the amplitude values of the scalar, real-valued x signal in consideration. For EEG analysis, the energy (E) values are calculated over consecutive non-overlapping windows of data, each window of T second in duration (here T = 10.24 s), from different locations x in the brain over an extended period of time. Examples of E profiles over time from two electrode sites that show entrainment before a seizure are given in Fig. 1(a) (left panel) for Patient 1. The highest E values were observed during the ictal period. This pattern roughly corresponds to the typical observation of higher amplitudes in the original EEG signal ictally (during a seizure) (Esteller et al. 2005). As we show below (Sect. 3), even though no other discernible trends exist in each individual E profile per electrode, synchronization trends between the E profiles across electrodes over time in the preictal period do exist.
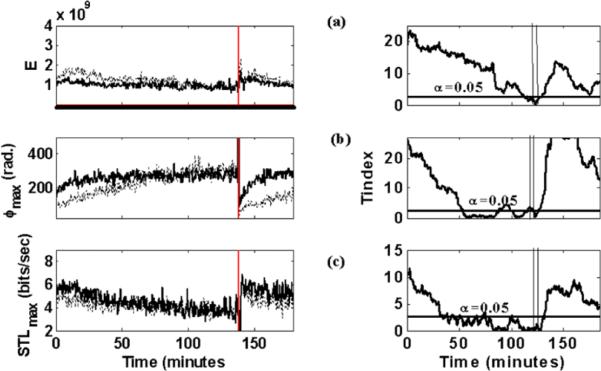
Fig. 1.
Long-term synchronization prior to a seizure (Patient 1; seizure 15). Left Panels (vertical lines here denote seizure onset-seizure duration was two minutes): (a) E profiles over time of two electrode sites (LST1, LOF2) selected to be mostly synchronized 10 min prior to the seizure. (b) ϕmax profiles of two electrode sites (RST1, ROF2) selected to be mostly synchronized 10 min prior to the seizure. (c) STLmax profiles of two electrode sites (RTD3, LOF2) selected to be mostly synchronized 10 min prior to the seizure (seizure's onset is depicted by a vertical line). Right Panels: Corresponding T-index curves for the sites and measures depicted in the left panels. Vertical lines here illustrate the period over which the effect of the ictal period is present in the estimation of the T-index values, since 10-min windows move every 10.24 s over the values of the measure profiles in the left panels and the seizure lasted for 2 minutes, hence period between vertical lines is 12 minutes
2.2 Measure of maximum phase (ϕmax) profiles
The notion of phase synchronization was introduced by Huygens (Hugenii 1986) in the 17th century for two coupled frictionless harmonic oscillators oscillating at different angular frequencies ω1 and ω2 respectively, such that . In this classical case, phase synchronization is usually defined as locking of the phases of the two oscillators:
| (2) |
where n and m are integers, ϕ1 and ϕ2 denote the phases of the oscillators, and φn,m is defined as their relative phase. In order to investigate synchronization in chaotic systems, Rosenblum et al. (1996) relaxed this condition of phase locking by a weaker condition of phase synchronization (since may be an irrational real number and each system may contain power at many frequencies around one dominant frequency):
| (3) |
The estimation of instantaneous phases ϕ1(t) and ϕ2(t) is nontrivial for many nonlinear model systems, and even more difficult when dealing with noisy time series of unknown characteristics. Different approaches have been proposed in the literature for the estimation of instantaneous phase of a signal. In the analysis that follows, we take the analytic signal approach for phase estimation, (Panter 1965), that defines the instantaneous phase of an arbitrary signal s(t) as
| (4) |
where
| (5) |
is the Hilbert Transform of the signal s(t) (P.V. denotes the Cauchy Principal Value that avoids the singularities at τ = t). From (5), the Hilbert transform of the signal can be interpreted as a convolution of the signal s(t) with a non-causal filter h(t) = 1/πt. The Fourier transform H(ω) of h(t) is − jsgn(ω) where sgn(ω) is often called the signum function where
| (6) |
Hence, Hilbert transformation of s(t) is equivalent to a type of filtering of s(t) in which amplitudes of its spectral components are left unchanged, while their phases are altered by ±π/2, positively or negatively according to the sign of ω. Thus, can then be obtained by the following procedure. First, a one-sided Fourier spectrum Z(ω) (in which the negative half of the spectrum is equal to zero) is created by multiplying the Fourier transform S(ω) of the signal s(t) with that of the filter H(ω) (i.e. Z(ω) = S(ω)H(ω)). Next, the inverse Fourier transform of Z(ω) is computed to obtain the complex-valued “analytic” signal z(t). Since Z(ω) only has a positive-sided spectrum, z(t) is given by:
| (7) |
The imaginary part of z(t) then yields . Mathematically, can be compactly represented as
| (8) |
It is important to note that the arctangent function used to estimate the instantaneous phase in (4) could be either a two-quadrant inverse tangent function (ATAN function in MATLAB) or a four-quadrant inverse tangent function (ATAN2 function in MATLAB). The ATAN function gives phase values that are restricted to the interval [−π/2,+π/2) and, on exceeding the value of +π/2, fall to the value of −π/2 twice in each cycle of oscillation, while the ATAN2 function when applied to the same data gives phase values that are restricted to the interval [−π,+π) and, on exceeding the value of +π, fall to the value of −π once every oscillation's cycle. In order to track instantaneous phase changes over long time intervals, this generated disjoint phase sequence has to be “unwrapped” (Rosenblum et al. 1998) by adding either π, when using the ATAN function, or 2π, when using the ATAN2 function, at each phase discontinuity. Thus, a continuous phase profile ϕ(t) over time can be generated.
The ϕ(t) from EEG data were estimated also within non-overlapping moving windows of 10.24 second in duration per electrode site. In the calculation of phase, to avoid edge effects in the estimation of the involved Fourier transforms, each EEG segment was tapered with a Hamming window before taking the Fourier transform. Per EEG segment, a set of phase values are generated that are equal in number to the number of data points in this window. The maximum phase value (ϕmax), minimum phase value (ϕmin), mean phase value (ϕmean) and the standard deviation of the phase values (ϕstd) were estimated per window. Only the dynamics of ϕmax were subsequently followed over time herein, because they were found to be more sensitive than the other three phase measures to dynamical changes before as well as after seizures.
Examples of synchronized ϕmax profiles over time around a seizure in Patient 1 are given in the left panel of Fig. 1(b). The preictal, ictal and postictal states corresponded to medium, high and low values of ϕmax respectively. The highest ϕmax values were observed during the ictal period, and higher ϕmax values were observed during the preictal period than during the postictal period. Interestingly, this pattern roughly corresponds to the typical observation of higher frequencies in the original EEG signal ictally, and lower EEG frequencies postictally.
2.3 Measure of chaos (STLmax) profiles
Under certain conditions, through the method of delays described by Packard et al. (1980) and Takens (1980), sampling of a single variable of a system over time can determine all state variables of the system that are related to the observed state variable. In the case of the EEG, this method can be used to reconstruct a multidimensional state space of the brain's electrical activity from a single EEG electrode that records referentially from a corresponding brain site. Thus, in such an embedding, each state in the state space is represented by a vector X(t), whose components are the delayed versions of the original single-channel EEG time series x(t), that is:
| (9) |
where τ is the time delay between successive components of X(t), and d is a positive integer denoting the embedding dimension of the reconstructed state space. Plotting X(t) in the thus created state space produces the state portrait of a spatially distributed system using the subsystem (brain's site) where x(t) is recorded from. The most complicated steady state a nonlinear deterministic system can have is a strange and chaotic attractor, whose complexity is measured by its dimension D, and its chaoticity by its Kolmogorov entropy (K) and Lyapunov exponents (Ls) (Grassberger and Procaccia 1983a, 1983b). A steady state is chaotic if at least the maximum of all Lyapunov exponents (Lmax) is positive.
According to Takens, in order to properly embed a signal in the state space, the embedding dimension d should at least be equal to (2D + 1). Of the many different methods used to estimate D of an object in the state space, each has its own practical problems (Kostelich 1992). The measure most often used to estimate D is the state space correlation dimension ν. Methods for calculating ν from experimental data have been described in (Abarbanel 1996) and were employed in our work to approximate D in the ictal state. The brain, being nonstationary, is never in a steady state at any location in the strict dynamical sense. Arguably, activity at brain sites is constantly moving through steady states, which are functions of certain parameter values at a given time. According to bifurcation theory (Haken 1996), when these parameters change slowly over time, or the system is close to a bifurcation, dynamics slow down and conditions of stationarity are better satisfied. In the ictal state, temporally ordered and spatially synchronized oscillations in the EEG usually persist for a relatively long period of time (for e.g., the range of minutes for TLE). Dividing the ictal EEG into short segments ranging from 10.24 to 50 s in duration, estimation of ν from ictal EEG has produced values between 2 and 3 (Iasemidis et al. 2000; Sackellares et al. 2000), implying the existence of a low-dimensional manifold in the ictal state, which we have called “epileptic attractor”. Therefore, an embedding dimension d of at least 7 has been used to properly reconstruct this epileptic attractor.
Although d of interictal (between seizures) “steady state” EEG data is expected to be higher than that of the ictal state, a constant embedding dimension d = 7 has been used to reconstruct all relevant state spaces over the ictal and interictal periods at different brain locations. The advantages of this approach are that (a) existence of irrelevant information in dimensions higher than 7 would not influence the estimation of the dynamical measures, and (b) reconstruction of the state space with higher d requires longer moving windows and non-stationary data. The disadvantage is that possibly relevant information about the transition to seizures in higher dimensions than d = 7 may not be captured.
The Lyapunov exponents measure the information flow (bits/sec) along local eigenvectors as the system moves within such attractors. Theoretically, if the state space is of d dimensions, we can estimate up to d Lyapunov exponents. However, as expected, only D + 1 of these will be real. The others are spurious (Panter 1965). Methods for calculating these dynamical measures from experimental data have been published in (Iasemidis and Sackellares 1991; Sackellares et al. 2000). The estimation of the largest Lyapunov exponent (Lmax) in a chaotic system has been shown to be more reliable and reproducible than the estimation of the remaining exponents (Vastano and Kostelich 1986), especially when D is unknown and changes over time, as in the case of high-dimensional and nonstationary data (e.g. interictal EEG). A method to estimate an approximation of Lmax from nonstationary data, called STL (Short-Term Lyapunov) (Iasemidis and Sackellares 1991; Iasemidis et al. 2000), has been developed via a modification of Wolf's algorithm that has been used to estimate Lmax from stationary data (Wolf et al. 1985). The STLmax, defined as the average of local maximum Lyapunov exponents in the state space, can be calculated as follows:
| (10) |
where δXi,j (ti) = X(ti) − X(tj) is the perturbation of X(ti), that is the point on the fiducial orbit at ti (X(tj) is the nearest neighbor to X(ti)), and δXi,j (ti + Δt) = X(ti + Δt) − X(tj + Δt) is the evolution of this perturbation after time Δt. Δt is the evolution time for δXi,j, that is, the time one allows for δXi,j to evolve in the state space. If the evolution time Δt is given in seconds, STLmax has units of bits per second. Na is the number of local Lyapunov exponents that are estimated within a duration T of the data segment. Therefore, if Δt is the sampling period for the time domain data, T = (N − 1)Δt ≈ NaΔt + (d − 1)τ. The STLmax algorithm is applied to sequential EEG epochs of 10.24 seconds recorded from electrodes in multiple brain sites to create a set of STLmax profiles over time (one STLmax profile per recording site) that characterize the spatio-temporal chaotic signature of the epileptic brain. Long-term profiles of STLmax, obtained by analysis of continuous EEG at two electrode sites in Patient 1, are shown in the left panel of Fig. 1(c). The figure shows the evolution of STLmax as the brain progresses from interictal to ictal to postictal states. There is a gradual drop in STLmax values over tens of minutes preceding a seizure at some sites, with no observable gradual drops at other sites. The seizure itself is characterized by a sudden drop in STLmax values with a consequent steep rise in STLmax. This behavior of STLmax indicates a gradual preictal reduction in chaoticity at some sites, reaching a minimum within the seizure state, and a postictal rise in chaoticity that corresponds to the reversal of the preictal behavior. What is most interesting and consistent across seizures and patients is an observed synchronization of STLmax values between electrode sites prior to a seizure. We have called this phenomenon preictal entrainment (dynamical synchronization), and it has constituted the basis for the development of epileptic seizure prediction algorithms (Iasemidis et al. 2001, 2002, 2003c).
2.4 T-index as an index of synchronization of measures of EEG dynamics
A statistical measure of synchronization between two electrodes i and j, with respect to a measure (e.g. STLmax, E or ϕmax) of their dynamics, has been developed before (e.g. Iasemidis et al. 2000) and is described below. Specifically, the Tij between electrode sites i and j for each measure STLmax, E and ϕmax at time t is defined as:
| (11) |
where and denote the sample mean and standard deviation respectively of all m differences between a measure's values at electrodes i and j within a moving window wt = [t, t − m · 10.24 s] over the measure profiles. If the true mean of the differences is equal to zero, and are independent and normally distributed, is asymptotically distributed as the t-distribution with (m − 1) degrees of freedom. We have shown that these independence and normality conditions are satisfied (Iasemidis et al. 2003c). Therefore, we define desynchronization between electrode sites i and j when Tij is significantly different from zero at a significance level. The desynchronization condition between the electrode sites i and j, as detected by the paired t-test, is
| (12) |
where tα/2,m−1 = Tth is the 100(1 − α/2) critical value of the t-distribution with m − 1 degrees of freedom. If (which means that we do not have satisfactory statistical evidence at the α level for the differences of values of a measure between electrode sites i and j to be non-zero within the time window wt), we consider sites i and j synchronized with each other at time t. Using α = 0.01 and m = 60, the threshold Tth = 2.662. It is noteworthy that similar STLmax, E or ϕmax values at two electrode sites do not necessarily mean that these sites also interact. However, when there is a progressive convergence over time of the measures at these sites, the probability that they are unrelated diminishes. This is exactly what occurs before seizures, and it is illustrated in the right panels of Fig. 1 for all the three measures considered herein. A progressive synchronization in all measures, as quantified by Tij, is observed preictally. Note that synchronization occurs at different sites per measure. The sites per measure are selected according to the optimization procedure described below in Sect. 3.
3 Quadratic integer optimization of spatial synchronization
Not all brain sites are progressively synchronized prior to a seizure. The selection of the ones that do (critical sites) is a global optimization problem that minimizes the distance between the dynamical measures of synchronization at these sites. For many years, the Ising model (Domb and Green 1974) has been a powerful tool for studying phase transitions in statistical physics. The model is described by a graph G(V, E) having n vertices {v1,…,vn}, with each edge e(i, j) ∈ E having a weight Jij (interaction energy). Each vertex vi has a magnetic spin variable σi ∈ {−1,+1} associated with it. A spin configuration σ of minimum energy is obtained by minimizing the Hamiltonian:
| (13) |
This optimization problem is equivalent to the combinatorial problem of quadratic bivalent programming. Its solution gives vertices with proper spin at the global minimum energy. Motivated by the application of the Ising model to phase transitions, we have adapted quadratic bivalent (zero-one) programming techniques to optimally select the critical electrode sites during the preictal transition (Iasemidis et al. 2001, 2003c) that minimize the objective function of the distance of STLmax, E or ϕmax between pairs of brain sites.
More specifically, we considered the integer bivalent 0–1 problem:
| (14) |
where n is the total number of available electrode sites, k is the number of sites to be selected, and xi are the (zero/one) elements of the n-dimensional vector x. The elements of the T matrix, Tij, i = 1,…,n and j = 1,…,n were previously defined in (11). If T is a positive semidefinite matrix, then the objective function is a convex function. In this case the quadratic program has a global minimizer if there exists at least one vector x satisfying the constraints and the objective function is bounded below on the feasible region. If the matrix T is positive definite then this global minimizer is unique. If T is zero, then the problem becomes a linear program. From optimization theory, a necessary condition for a point x to be a global minimizer is for it to satisfy the Karush-Kuhn-Tucker (KKT) conditions. The KKT conditions are also sufficient when the objective function is convex. On the other hand, if the matrix T is not positive definite, the optimization problem becomes NP-hard since the objective function becomes non-convex (Pardalos and Rosen 1987). If the constraint in (12) is included in the objective function xtTx by introducing the penalty
| (15) |
the above optimization problem in (12) becomes equivalent to an unconstrained global optimization problem
| (16) |
Note here that since the objective function is a quadratic function, it is easy to combine the Lagrangian term with the quadratic term. Therefore, we square the constraint before adding it to the objective function, as shown in (16). The electrode site i is selected if the corresponding element in the n-dimensional solution x* of (14) is equal to 1. The optimization for the selection of critical sites was performed in the preictal windows w1(t*) = [t*, t* − 10 min) over a measure's profiles, where t* is the time of a seizure's onset, separately for each of the three considered measures. After the optimal sites selection, the average T-index across all possible pairs of the selected sites is generated and followed backward in time from each seizure's onset t*. In the following sections, for simplicity, we denote these spatially averaged T-index values by “T-index”. For demonstration purposes, the corresponding T-indices between two critical sites (k = 2) for each measure were depicted in Fig. 1 (right panel) before and after one of the recording seizures in Patient 1. After the optimal sites selection from each of the three measures E, STLmax and ϕmax profiles within the preictal window w1(t*) per seizure, the average T-index of the selected sites was estimated backward and forward in time with respect to t*. The resetting characteristics of a seizure are then estimated from these T-index profiles by using the procedure described below in Sect. 4.
4 Resetting characteristics
4.1 Level of resetting (LR)
One way to quantify the observed differences in the level of synchronization of the critical sites around seizure onset points t* is to estimate a statistically significant difference between their preictal synchronization and postictal desynchronization levels. Thus, the synchronization level (Lsyn(t*)) per each considered measure is defined as the average value of its differences among all pairs of selected critical sites within the 10-minute preictal window w1(t*) (see Fig. 2(a)). In analogy, the desynchronization level (Ldesyn(t*)) is defined as the average value of a measure's differences among the pairs of the previously selected preictal critical sites within a 10 minute postictal window after the end of a seizure, that is w1(t* + seizure duration + 10 min) (see Fig. 2(b) for an illustration of this procedure). The hypothesis was that higher levels of preictal synchronization are reduced significantly during the corresponding postictal period, and that this phenomenon occurs more often around seizure points t* than around any other point t of the recording.
Fig. 2.
Estimation of the preictal synchronization level Lsyn and postictal desynchronization level Ldesyn of critical sites per seizure. (a) The average difference between the measure values (here STLmax) within the 10-min preictal window w1(t) is set equal to Lsyn. Similarly, the average difference between the measure values within the 10-min postictal window after the end of a seizure, that is w1(t* +seizure duration+ 10 min), is set equal to Ldesyn. (b) Magnification of (a) around the seizure
Criterion for resetting hypothesis based on LR
We define a resetting occurring at time t if the statistical difference between Ldesyn(t) and Lsyn(t) is significant i.e. if the null hypothesis of Ldesyn(t) = Lsyn(t) is rejected in favor of the alternative hypothesis Ldesyn(t) > Lsyn(t) at a significance level of α 0.01 using a two-sample one tailed t-test (Tth = 2.662 with parameters as in Sect. 2.4). The assumptions of normality and indepedance of the Lsyn(t*) and Ldesyn(t*) values per measure were validated using the well-known Shapiro-Wilks test for normality and the Ljung-box test for independence of observations. We refer the reader to the paper by Iasemidis et al. (2004) for further details about these tests. If pLR is the probability of resetting based on LR at a time point t, and we denote by xl the random variable of the number of resettings observed at l time points, xl follows the binomial (l, pLR) distribution with mean lpLR and variance lpLR(1 − pLR), where pLR can be estimated by the maximum likelihood estimate as
| (17) |
The sample estimates of are calculated from l randomly (following a uniform random distribution) chosen time points t (l-tuple of time points) within the available time interval of recordings from each patient, excluding ictal periods (on average 2.5 minute ictal duration per seizure for the two analyzed patients). It is important to note that the sampling distribution of is closely related to the distribution of xl. While xl follows the distribution of the count of total number of resettings observed at l time points, follows the distribution of the proportion of resettings observed at l time points (total number of resettings observed at l time points divided by l). Therefore, by the multiplicative properties of mean of probability distributions, the sample mean of is related to the mean of xl by dividing the mean of xl by l, i.e. lpLR/l = pLR. Thus, is an unbiased estimate of the probability of resetting pLR. Using the same properties as above, the variance of is equal to the variance of xl divided by l2, i.e. lpLR(1 − pLR)/l2 = pLR(1 − pLR)/l. This indicates that the variance of this estimator decreases with increase in sample size l. Therefore, is a consistent estimate of pLR. A Monte-Carlo estimation of the probability distribution of is then performed by generating the histogram of from 25,000 l-tuples (l differs from Patient 1 to Patient 2, being equal to the number of recorded seizures per patient). The at seizure points t*, denoted by , is then compared to the distribution of at time points t to statistically decide if .
4.2 Resetting ratio of time constants (RRT)
One way to quantify the observed differences in the rates of synchronization of the critical sites around seizure points t* is to estimate the synchronization and desynchronization periods from the corresponding average T-index profile, using the same statistical threshold Tth = 2.662 for both periods. Thus, the synchronization period (Tsyn) is defined as the period before the time point t, during which the average T-index values of the critical sites selected within w1(t) (see Fig. 2(a)), remain continuously below 2.662 within the windows w2(t) = [t, t − 10 min). For seizure points, t = t* and Tsyn = Tp (prediction time). In analogy, the desynchronization period (Tdesyn) was defined as the period after time t + 2.5 minutes (allowing for a virtual seizure duration of 2.5 minutes i.e., comparable to a typical seizure duration in our data) during which the average T-index values of the selected sites remain continuously below 2.662 within the windows w2(t) = (t + 2.5 min + 10 min, t)(see Fig. 3). The hypothesis was that preictal entrainment lasts significantly longer than the corresponding postictal disentrainment and, in accordance with the previously observed phenomenon of hysteresis and the theory of nonlinear dynamics at points of critical transitions (Iasemidis 2003), this phenomenon occurs more often at seizure points than at any other time points. This phenomenon is consistent with what is called “critical slowing down” in the literature of the dynamics of phase transitions (Haken 1996).
Fig. 3.
Estimation of the preictal synchronization time Tsyn and postictal desynchronization time Tdesyn. The average T-index of the critical sites within the moving window w2(t) is continuously estimated moving backwards from the seizure onset. When the average T-index > Tth = 2.662, Tsyn is set equal to the right endpoint of w2(t). Similarly, the average T-index within the moving window w2(t) of critical sites is continuously estimated moving forward from the end of the seizure and when the average T-index > Tth = 2.662, Tdesyn is set equal to the left endpoint of w2(t)
Criterion for resetting hypothesis based on RRT
We define a resetting occurring at time t if Tsyn(t) < Tdesyn(t). If pRRT is the probability of such a resetting at a time point t, and we denote by xl the random variable of the number of such resettings observed at l time points, xl follows the binomial (l, pRRT) distribution, where pRRT can be estimated by the maximum likelihood estimate as
| (18) |
The are estimated from l randomly (following a uniform random distribution) chosen time points t (l-tuple of time points) within the available time interval of recordings from each patient, excluding ictal periods, as before. A Monte-Carlo estimation of the probability distribution of is performed by generating the histogram of from 25,000 l-tuples. The at seizure points t*, denoted by , is then compared to the distribution of at time points t to statistically decide if . Both null resetting hypotheses in Sect. 4.1 and 4.2 were tested and rejected (see next section)—assuming that the involved distributions were binomial. Therefore, it appears that resetting of the epileptic brain at seizures manifests itself as a reversal of the pathology of long-term excessive entrainment (synchronization), and that this reversal occurs mostly at seizures than at any other time points.
5 Results
5.1 EEG data
A total of 43 seizures (see Table 1) from two epileptic patients with temporal lobe epilepsy were analyzed by the methodology described above. These patients were the ones for whom we had the most number of recorded seizures. A large scale analysis of the resetting methodology using more patients is currently underway. The EEG signals were recorded from 6 different areas of the brain by 28 electrodes (see Fig. 4) for the electrode montage). Typically, a 3 hour before (preictal period) and 1 hour after (postictal period) each seizure were analyzed with the methods described in Sects. 2, 3 and 4, in search of dynamical synchronization/desynchronization and estimation of seizure resetting characteristics.
Table 1.
Patients and EEG data characteristics
| Patient ID | Number of electrode sites | Location of epilep-togenic focus | Seizure types | Duration of EEG recordings (days) | Number of seizures recorded |
|---|---|---|---|---|---|
| 1 | 28 | RTD | C * | 9.06 | 24 |
| 2 | 28 | RTD | C* & SC** | 6.07 | 17 |
C for clinical seizures
SC for subclinical seizures
Fig. 4.

Schematic diagram of the depth and subdural electrode placement. This view from the inferior aspect of the brain shows the approximate location of depth electrodes, oriented along the anterior-posterior plane in the hippocampi (RTD—right temporal depth, LTD—left temporal depth), and subdural electrodes located beneath the orbitofrontal and subtemporal cortical surfaces (ROF—right orbitofrontal, LOF—left orbitofrontal, RST—right subtemporal, LST—left subtemporal)
The patients in the study underwent a stereotactic placement of bilateral depth electrodes (RTD1 to RTD6 in the right hippocampus, with RTD1 adjacent to right amygdala; LTD1 to LTD6 in the left hippocampus with the LTD1 adjacent to the left amygdala; the rest of the LTD, RTD electrodes extended posterioriliy through the hippocampi). Two subdural strip electrodes were placed bilaterally over the orbitofrontal lobes (LOF1 to LOF4 in the left and ROF1 to ROF4 in the right lobe, with LOF1, ROF1 being most mesial and LOF4, ROF4, most lateral). Two subdural strip electrodes were placed bilaterally over the temporal lobes (LST1 to LST4 in the left and RST1 to RST4 in the right, with LST1, RST1 being more mesial and LST4 and RST4 being more lateral). Video/EEG monitoring was performed using the Nicolet BMSI 4000 EEG machine. EEG signals were recorded using an average common reference with band pass filter settings of 0.1–70 Hz. The data were sampled at 200 Hz with a 10-bit quantization and recorded on VHS tapes continuously over days via 3 time-interleaved VCRs. Decoding of the data from the tapes and transfer to computer media (hard disks, DVDs, CD-ROMs) was subsequently performed off-line. The seizure resetting analysis was performed retrospectively (off-line).
5.2 Resetting results
For each of the 43 recorded seizures, the T-index profiles over time for each dynamical measure per pair of recording sites were estimated, thus generating T-index matrices over time. The 5 most synchronized sites within 10 minutes prior to each seizure onset were selected by the optimization procedure described in Sect. 3 (critical sites per seizure). We then tested the following two null hypotheses for each dynamical measure: (1) versus the alternative hypothesis , and (2) versus the alternative hypothesis . This is performed by comparing the observed probability of resetting at seizures with the distribution of the values at time points in non-seizure periods, for each of the two criteria of resetting. Then, at the 99% confidence level, we can reject the two H0 if the p-value of the tests is less than 0.01. Having previously shown (Iasemidis et al. 2004) that the optimal selection of brain sites increases the sensitivity of detection of resetting, we test both hypotheses using only the optimally selected sites. In Figs. 5 and 6, the probability distribution of resetting at non-seizure points using optimal groups of electrode sites per measure for all three dynamical measures is shown for Patient 1 and 2 respectively. Figure 7 shows the overall distribution from seizures of both patients combined. The probability of resetting at the l seizure points, using either of the two criteria, was significantly greater than the corresponding values at l randomly selected points in interictal periods for all three dynamical measures (see Table 2). Such an observation is consistent with our previous findings that seizures are characterized by a progressive spatiotemporal preictal entrainment of dynamical measures estimated at brain sites that may last for minutes to hours, and then reset postictally. The consistent observation of resetting at seizure points across all three dynamical measures considered herein, reflects the robustness of this phenomenon with respect to the measures of dynamics utilized. Nevertheless, it is noteworthy that using the measure of STLmax, we obtain the maximum sensitivity for detection of resetting (e.g. in Fig. 4(a) right panel). Also, it seems that using the LR criterion versus the RRT, we obtain the maximum specificity (most statistical significance).
Fig. 5.
Probability distributions of resetting (blue) at non-seizure points versus probability of resetting at seizure points (red) in Patient 1. Left Panels: Probability distributions of resetting using LR on the measures of (a) STLmax-based synchronization. (b) E-based synchronization. (c) ϕmax-based synchronization. Right Panels: Corresponding probability distributions of resetting using RRT on the same three measures of synchronization depicted in the left panels. Red arrow in each sub-panel indicates the corresponding probability of resetting at seizure points
Fig. 6.
Probability distributions of resetting at non-seizure points versus probability of resetting at seizure points in Patient 2. Left Panels: Probability distributions of resetting using LR on the measures of (a) STLmax-based synchronization. (b) E-based synchronization. (c) ϕmax-based synchronization. Right Panels: Corresponding Probability distributions of resetting for the same three measures depicted in the left panels. Red arrow in each sub-panel indicates the corresponding probability of resetting at seizure points
Fig. 7.
Overall probability distributions of resetting at non-seizure points versus probability of resetting at seizures across both patients. Left Panels: Probability distributions of resetting using LR on the measures of (a) STLmax-based synchronization. (b) E-based synchronization. (c) ϕmax-based synchronization. Right Panels: Corresponding probability distributions of for the same three measures depicted in the left panels. Red arrow in each sub-panel indicates the probability of resetting at seizure points
Table 2.
Probability values of resetting at epileptic seizures and their statistical significance per resetting criteria and dynamical measure
| Patient | LR |
RRT |
||||
|---|---|---|---|---|---|---|
| Resetting of dynamical synchronization (STLmax synchronization) | ||||||
| 1(22 seizures) | 0.50 | (0.06, 0.039) | P <0.0005 | 0.86 | (0.41, 0.13) | P <0.001 |
| 2(19 seizures) | 0.47 | (0.05, 0.04) | P <0.0005 | 0.74 | (0.37, 0.15) | P <0.01 |
| Overall | 0.485 | (0.055, 0.0395) | P <0.0005 | 0.80 | (0.39, 0.14) | P <0.001 |
| Resetting of amplitude synchronization (E synchronization) | ||||||
| 1(22 seizures) | 0.79 | (0.165, 0.072) | P <0.0005 | 0.59 | (0.40, 0.11) | P <0.055 |
| 2(19 seizures) | 0.47 | (0.14, 0.07) | P <0.0005 | 0.68 | (0.40, 0.15) | P <0.03 |
| Overall | 0.63 | (0.15, 0.071) | P <0.0005 | 0.635 | (0.40, 0.14) | P <0.05 |
| Resetting of phase synchronization (ϕmax synchronization) | ||||||
| 1(22 seizures) | 0.49 | (0.16, 0.068) | P <0.0005 | 0.63 | (0.40, 0.138) | P < 0.05 |
| 2(19 seizures) | 0.37 | (0.12, 0.07) | P <0.0005 | 0.63 | (0.40, 0.157) | P <0.052 |
| Overall | 0.43 | (0.14, 0.069) | P <0.0005 | 0.63 | (0.40, 0.14) | P <0.05 |
Comparative performance of resetting criteria
The RRT criterion for resetting was more significant than the LR criterion in detecting resetting of phase and STLmax synchronization at seizures overall (both patients). The mean of across the two patients for the phase and STLmax measures of dynamics was 0.63 and 0.80 respectively, and that of overall (across both patients) for the same measures was 0.43 and 0.485 respectively (see Table 2). No resetting criterion was found to be more significant over the other when detecting resetting at seizures using the E measure of dynamics. Interestingly, within the interictal periods, the probability distributions of resetting were very similar irrespective of the measures of dynamics utilized. For the RRT criterion, the overall mean of the distribution of across both patients, for the measures of phase, Energy and STLmax, were 0.40, 0.40 and 0.39 respectively. On the other hand, for the LR criterion, the overall mean of the distribution of across both patients, for the measures of phase, Energy and STLmax, were 0.14, 0.15 and 0.055 respectively. Note here that, since for a binomial distribution a probability of 0.5 maximizes its variance and produces the largest uncertainty in its mean, the finding of an overall mean probability of less than 0.5 for resetting during the inter-ictal periods (using either of the two resetting criteria on any of the three dynamical measures) implies that the brain does not reset randomly during the interictal periods. More specifically, such an observation defines the interictal period as a state where the transition from a prolonged synchronization to a faster desynchronization is a rare phenomenon. These results point out that resetting at a seizure can be characterized by the time constant, level and/or level and time constant of resetting during the peri-ictal (around seizures) period. Further investigation into optimally combining the level and time constant criteria for seizure resetting might reveal new insights into the mechanisms underlying the phenomenon of seizure resetting.
Comparative performance of energy, phase and STLmax measures of EEG dynamics for the detection of resetting
Dynamical resetting of STLmax synchronization using the RRT criterion consistently resulted to higher probability of resetting at seizures than of the other two measures (see Table 2). Also, the phase synchronization measure outperformed the energy-based synchronization in the detection of resetting at seizures using the RRT criterion. Using the LR criterion, no consistent difference in the resetting performance of the three measures of synchronization at seizures was observed (see Table 2). This result was consistent across both patients. Previous studies by our group on seizure predictability have shown that dynamical synchronization using STLmax measure consistently results to longer seizure predictability times than using other measures like Energy and phase (Sabesan et al. 2003, 2007; Iasemidis et al. 2003a). Since the RRT criterion of resetting compares the duration of synchronization in the preictal period with that of the postictal period, it appears reasonable that STLmax-based resetting shows the largest probability of occurrence at seizure points, followed by phase and then by Energy. It was also observed that dynamical resetting in the interictal period, using either of the resetting criteria, resulted to similar low values of probability of resetting for any of the three dynamical measures.
6 Conclusion
We have described a method for analysis of characteristic spatiotemporal transitions in complex dynamical systems. It involves the application of dynamical synchronization measures in the time domain, the use of global bivalent optimization in the discrete spatial domain and subsequent estimation of probability of dynamical resetting of synchronization in the time domain. The results of the application of this methodology to the epileptic brain show that the majority of analyzed epileptic seizures demonstrate a high probability of resetting the pathology of brain dynamics, that is the pathological preictal synchronization of normal brain sites with the epileptogenic focus. The underlying key principle is the existence of long-term, excessive dynamical entrainment of critical brain sites prior to seizures, and a reversal to desynchronization postictally. Resetting during interictal periods did occurr but with significantly lower probability (p < 0.05). Furthermore, this study showed that the observed resetting phenomenon at seizures is consistent across three measures of brain dynamics and two criteria of resetting utilized, and therefore it appears to be robust.
This study also demonstrates that a concrete neurophysiological function may be attributed to epileptic seizures themselves. We showed that seizures occur after sustained dynamical entrainment of the electrical activity of the brain. Further, we can seizures occur in order to reset this entrainment. Indirect support for such a hypothesis can be found in the literature of electroconvulsive therapy (ECT). The effect of the seizures induced by ECT, as well as possible causes for the long-term anticonvulsive effect of ECT, were reviewed (Fink 2000). According to this line of thought, a biochemical basis for the resetting of the brain may lie in the release of brain's neuromodulators following seizures (Gwinn et al. 2002; Medvedev 2002). Thus, seizures appear to play a homeostatic role in order to restore the balance between the synchronization and desynchronization mechanisms underlying seizure generation (for simulation along these lines see Tsakalis et al. 2006; Tsakalis and Iasemidis 2006). Interestingly, this balance is maintained during the inter-ictal periods as it is suggested by the low resetting probability in the interictal periods. These results also suggest that interventions, in the form of either electromagnetic stimulation or administration of low doses of AEDs early in the preictal period, with the goal of dynamically resetting the brain, may alleviate the need for a seizure to occur. If this latter hypothesis proves true, it could lead to a revolutionary approach to seizure control.
Acknowledgements
This work was supported in part by the American Epilepsy Research Foundation and the Ali Paris Fund for LKS Research and Education, and NSF Grant ECS-0601740 and the grant from Science foundation of Arizona and Stardust foundation (CAA 0281-08).
References
- Abarbanel H. Analysis of observed chaotic data. Springer; Berlin: 1996. [Google Scholar]
- Chakravarthy N, Sabesan S, Iasemidis LD, Tsakalis K. Controlling synchronization in a neuron-level population model. Int J Neural Syst. 2007;17(2):123–138. doi: 10.1142/S0129065707000993. [DOI] [PubMed] [Google Scholar]
- Chawla D, Lumer ED, Friston KJ. The relationship between synchronization among neuronal populations and their mean activity level. Neural Comput. 1999;11(6):1389–1411. doi: 10.1162/089976699300016287. [DOI] [PubMed] [Google Scholar]
- Domb C, Green M. Phase transitions and critical phenomena. Academic Press; New York: 1974. [Google Scholar]
- Esteller R, Echauz J, D'Alessandro M, Worrell G, Cranstoun S, Vachtsevanos G, Litt B. Continuous energy variation during the seizure cycle: towards an on-line accumulated energy. Clin Neurophysiol. 2005;116(3):517–526. doi: 10.1016/j.clinph.2004.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fink M. Electroshock revisited. Am Sci. 2000;88:162–167. [Google Scholar]
- Good L. PhD thesis. Arizona State University; 2007. Automated seizure prediction and control in a rat model of chronic epilepsy. [Google Scholar]
- Good L, Sabesan S, Iasemidis L, Tsakalis K, Treiman D. Brain dynamical disentrainment by a nti-epileptic drugs in rat and human status epilepticus. 26th annual international conference of the engineering in medicine and biology society; 2004. pp. 1–4. [DOI] [PubMed] [Google Scholar]
- Grassberger P, Procaccia I. Characterization of strange attractors. Phys Rev Lett. 1983a;50(5):346–349. [Google Scholar]
- Grassberger P, Procaccia I. Measuring the strangeness of strange attractors. Phys D: Nonlinear Phenom. 1983b;9(1–2):189–208. [Google Scholar]
- Gwinn R, Kondratyev A, Gale K. Time-dependent increase in basic fibroblast growth factor protein in limbic regions following electroshock seizures. Neuroscience. 2002;114(2):403–409. doi: 10.1016/s0306-4522(02)00265-8. [DOI] [PubMed] [Google Scholar]
- Haken H. Principles of brain functioning: a synergetic approach to brain activity. Springer; New York: 1996. [Google Scholar]
- Hugenii C. Muguet, Paris; reprinted in English as: The pendulum clock. Iowa State UP; Ames: 1986. Horoloquim oscilatorium. [Google Scholar]
- Iasemidis L. Epileptic seizure prediction and control. IEEE Trans Biomed Eng. 2003;50(5):549–558. doi: 10.1109/tbme.2003.810705. [DOI] [PubMed] [Google Scholar]
- Iasemidis L, Sackellares J. Measuring chaos in the human brain. World Scientific; Singapore: 1991. The temporal evolution of the largest Lyapunov exponent on the human epileptic cortex; pp. 49–82. [Google Scholar]
- Iasemidis L, Olson L, Savit R, Sackellares J. Time dependencies in the occurrences of epileptic seizures. Epilepsy Res. 1994;17(1):81–94. doi: 10.1016/0920-1211(94)90081-7. [DOI] [PubMed] [Google Scholar]
- Iasemidis L, Principe J, Czaplewski J, Gilmore R, Roper S, Sackellares J. Spatiotemporal transition to epileptic seizures: a nonlinear dynamical analysis of scalp and intracranial EEG recordings. In: Silva FL, Principe JC, Almeida LB, editors. Spatiotemporal models in biological and artificial systems. 1997. pp. 81–88. [Google Scholar]
- Iasemidis L, Principe J, Sackellares J. Measurement and quantification of spatio-temporal dynamics of human epileptic seizures. In: Akay M, editor. Nonlinear biomedical signal processing. vol 2. 2000. pp. 294–318. [Google Scholar]
- Iasemidis L, Pardalos P, Sackellares J, Shiau D. Quadratic binary programming and dynamical system approach to determine the predictability of epileptic seizures. J Comb Optim. 2001;5(1):9–26. [Google Scholar]
- Iasemidis L, Shiau D, Chaovalitwongse W, Pardalos P, Carney P, Sackellares J. Adaptive seizure prediction system. Epilepsia. 2002;43:264–265. [Google Scholar]
- Iasemidis L, Pardalos P, Shiau D, Chaovalitwongse W, Narayanan K, Sabesan S, Carney P, Chris Sackellares J. Prediction of human epileptic seizures based on optimization and phase changes of brain electrical activity. Optim Methods Softw. 2003a;18(1):81–104. [Google Scholar]
- Iasemidis L, Prasad A, Sackellares J, Pardalos P, Shiau D. On the prediction of seizures, hysteresis and resetting of the epileptic brain: insights from models of coupled chaotic oscillators. In: Bountis T, Pneumatikos S, editors. Order and chaos. vol 8. Publishing House; Thessaloniki: 2003b. pp. 283–305. [Google Scholar]
- Iasemidis L, Shiau D, Chaovalitwongse W, Sackellares J, Pardalos P, Principe J, Carney P, Prasad A, Veeramani B, Tsakalis K. Adaptive epileptic seizure prediction system. IEEE Trans Biomed Eng. 2003c;50(5):616–627. doi: 10.1109/TBME.2003.810689. [DOI] [PubMed] [Google Scholar]
- Iasemidis L, Shiau D, Sackellares J, Pardalos P, Prasad A. Dynamical resetting of the human brain at epileptic seizures: application of nonlinear dynamics and global optimization techniques. IEEE Trans Biomed Eng. 2004;51(3):493–506. doi: 10.1109/TBME.2003.821013. [DOI] [PubMed] [Google Scholar]
- Iasemidis L, Tsakalis K, Sackellares J, Pardalos P. Comment on “Inability of Lyapunov exponents to predict epileptic seizures”. Phys Rev Lett. 2005;94(1):19801. doi: 10.1103/PhysRevLett.94.019801. [DOI] [PubMed] [Google Scholar]
- Kostelich EJ. Problems in estimating dynamics from data. Physica D: Nonlinear Phenom. 1992;58(1–4):138–152. [Google Scholar]
- Lee K, Schubert P, Heinemann U. The anticonvulsive action of adenosine: a postsynaptic, dendritic action by a possible endogenous anticonvulsant. Brain Res. 1984;321(1):160–164. doi: 10.1016/0006-8993(84)90694-2. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Contreras D. On the cellular and network bases of epileptic seizures. Annu Rev Physiol. 2001;63:815–846. doi: 10.1146/annurev.physiol.63.1.815. [DOI] [PubMed] [Google Scholar]
- Medvedev A. Epileptiform spikes desynchronize and diminish fast (gamma) activity of the brain an “anti-binding”-mechanism. Brain Res Bull. 2002;58(1):115–128. doi: 10.1016/s0361-9230(02)00768-2. [DOI] [PubMed] [Google Scholar]
- Olson L, Iasemidis L, Sackellares J. Evidence that interseizure intervals exhibit low dimensional non-random dynamics. Epilepsia. 1989;30(5):644. [Google Scholar]
- Packard N, Crutchfield J, Farmer J, Shaw R. Geometry from a time series. Phys Rev Lett. 1980;45(9):712–716. [Google Scholar]
- Panter P. Modulation, noise, and spectral analysis: applied to information transmission. McGraw-Hill; New York: 1965. [Google Scholar]
- Pardalos P, Rosen J. Constrained global optimization: algorithms and applications. Springer; New York: 1987. [Google Scholar]
- Prasad A, Iasemidis L, Sabesan S, Tsakalis K. Dynamical hysteresis and spatial synchronization in coupled non-identical chaotic oscillators. Pramana J Phys. 2005;64(4):513–523. [Google Scholar]
- Prince D, Jacobs K. Inhibitory function in two models of chronic epileptogenesis. Epilepsy Res. 1998;32(1–2):83–92. doi: 10.1016/s0920-1211(98)00042-4. [DOI] [PubMed] [Google Scholar]
- Rosenblum M, Kurths J. Analysing synchronization phenomena from bivariate data by means of the Hilbert transform. In: Kantz H, Kurths J, Mayer-Kress G, editors. Nonlinear analysis of physiological data. Springer; Berlin: 1998. pp. 91–99. [Google Scholar]
- Rosenblum M, Pikovsky A, Kurths J. Phase synchronization of chaotic oscillators. Phys Rev Lett. 1996;76(11):1804–1807. doi: 10.1103/PhysRevLett.76.1804. [DOI] [PubMed] [Google Scholar]
- Sabesan S, Narayanan K, Prasad A, Spanias A, Sackellares J, Iasemidis L. Predictability of epileptic seizures: a comparative study using Lyapunov exponent and entropy based measures. Biomed Sci Instrum. 2003;39:129–35. [PubMed] [Google Scholar]
- Sabesan S, Chakravarthy N, Good L, Tsakalis K, Pardalos P, Iasemidis L. Global optimization and spatial synchronization prior to epileptic seizures. In: Pardalos P, Alves C, Vicente L, editors. Optimization in biomedicine. Springer optimization and its applications series. vol 12. Springer; Berlin: 2007. pp. 103–125. [Google Scholar]
- Sackellares J, Iasemidis L, Shiau D, Gilmore R, Roper S. Epilepsy when chaos fails. In: Lehnertz K, Arnhold J, Grassberger P, Elger CE, editors. Chaos in the brain? World Scientific; Singapore: 2000. pp. 112–133. [Google Scholar]
- Shiau D, Luo Q, Gilmore R, Roper S, Pardalos P, Sackellares J, Iasemidis L. Epileptic seizures resetting revisited. Epilepsia. 2000;41(Suppl 7):208. [Google Scholar]
- Takens F. Dynamical systems and turbulence. proc symp; Coventry: 1980. Detecting strange attractors in turbulence. [Google Scholar]
- Traub RD, Contreras D, Whittington MA. Combined experimental/simulation studies of cellular and network mechanisms of epileptogenesis in vitro and in vivo. J Clin Neurophysiol. 2005;22(5):330–342. [PubMed] [Google Scholar]
- Tsakalis K, Iasemidis LD. Control aspects of a theoretical model for epileptic seizures. Int J Bifurc Chaos. 2006;16(7):2013–2027. [Google Scholar]
- Tsakalis K, Chakravarthy N, Sabesan S, Iasemidis LD, Pardalos PM. A feedback control systems view of epileptic seizures. Cybern Syst Anal. 2006;42(4):483–495. [Google Scholar]
- Vastano J, Kostelich E. Comparison of algorithms for determining Lyapunov exponents from experimental data. In: Mayer-Kress G, editor. Dimensions and entropies in chaotic systems: quantification of complex behavior. 1986. pp. 100–107. [Google Scholar]
- Wendling F, Bartolomei F, Bellanger JJ, Chauvel P. Epileptic fast activity can be explained by a model of impaired gabaergic dendritic inhibition. Eur J Neurosci. 2002;15(9):1499–1508. doi: 10.1046/j.1460-9568.2002.01985.x. [DOI] [PubMed] [Google Scholar]
- Wolf A, Swift J, Swinney H, Vastano J. Determining Lyapunov exponents from a time series. Physica D. 1985;16(3):285–317. [Google Scholar]
- Zhou J, Lenck-Santini P, Holmes G. Postictal single-cell firing patterns in the hippocampus. Epilepsia. 2007;48(4):713–719. doi: 10.1111/j.1528-1167.2006.00942.x. [DOI] [PubMed] [Google Scholar]