Combining Two-Dimensional Spatially Selective RF Excitation, Parallel Imaging, and UNFOLD for Accelerated MR Thermometry Imaging

Abstract

MR thermometry can be a very challenging application, as good resolution may be needed along spatial, temporal as well as temperature axes. Given that the heated foci produced during thermal therapies are typically much smaller than the anatomy being imaged, much of the imaged FOV is not actually being heated and may not require temperature monitoring. In the present work, many-fold improvements were obtained in terms of temporal resolution and/or 3D spatial coverage by sacrificing some of the in-plane spatial coverage. To do so, three fast-imaging approaches were jointly implemented with a spoiled gradient echo sequence: 1) two-dimensional spatially-selective RF excitation, 2) unaliasing by Fourier-encoding the overlaps using the temporal dimension (UNFOLD), and 3) parallel imaging. The sequence was tested during experiments with focused ultrasound heating in ex-vivo tissue and a tissue-mimicking phantom. Temperature maps were estimated from phase-difference images based on the water proton resonance frequency shift. Results were compared to those obtained from a spoiled gradient echo sequence, using a t-test. Temporal resolution was increased by 24-fold, with temperature uncertainty less than 1°C, while maintaining accurate temperature measurements (mean difference between measurements, as observed in gel, = 0.1°C ± 0.6; R = 0.98; P > 0.05).

INTRODUCTION

Thermal ablation using RF, microwave, laser, or focused ultrasound (FUS) devices offers minimally-invasive alternatives to surgical resection. Magnetic resonance thermometry based on the temperature sensitivity of the water proton resonant frequency (PRF) (1,2) is currently the most practical means available to map quantitative temperature changes in vivo. PRF imaging enables online, closed-loop feedback during thermal ablation in near real-time (3). Temperature-induced shifts in the water PRF can be measured relatively rapidly via phase mapping using a gradient echo (GRE) sequence (4).

MR thermometry is associated with difficult challenges in terms of imaging performance, because of the large thermal gradients and rapid temperature changes produced during thermal ablation. Temporal resolution must be sufficient to capture important temporal variations, both temperature- and motion-induced. Furthermore, spatial resolution must be reasonably high to accurately locate the edges of the ablated volume (where thermal gradients are large). For example, the focal region produced by the ExAblate 4000 TcMRgFUS system (InSightec, Haifa, Israel) is roughly 3.0×3.0×5.8 mm³ (as provided by the manufacturer), and resolution should thus be significantly below 3 mm to resolve it. Spatial coverage may also be important, to detect possible secondary (unintended) heating sites and avoid damage to healthy tissues. Several approaches have been proposed to speed-up the image acquisition process in temperature mapping. For example, echo-planar (5,6) and spiral (7) techniques can achieve sub-second temporal resolution for one image plane, with temperature sensitivity comparable to the gradient echo technique. The use of fast imaging sequences such as PRESTO (8,9) and SSFP (10–12) has also been investigated, and parallel imaging has been proposed to accelerate the image acquisition process (13,14). However, especially in the presence of motion and despite promising recent developments (15), further imaging speed is still very much needed in PRF thermometry, to achieve 3D coverage with sufficient spatial and temporal resolution.

Three existing fast-imaging strategies were combined here in a synergistic manner: two-dimensional spatially-selective RF (2DRF) excitation (16,17), unaliasing by Fourier encoding of the overlaps using the temporal dimension (UNFOLD) (18), and parallel imaging (19). These strategies were implemented on a GRE imaging sequence, and acceleration factors up to 24 were obtained here for temperature mapping. In previous work, the combination of UNFOLD with either 2DRF excitation (20) or SENSE parallel imaging (21) and the combination of 2DRF excitations with parallel imaging (22) was shown to perform substantially better than either of the individual techniques alone. With 2DRF-UNFOLD, the 2DRF excitation suppressed the signal outside the region of interest (ROI) thus allowing the use of a smaller field-of-view (FOV), and any remaining artifacts from the vanishing tails of the excitation profiles were removed by UNFOLD. In the UNFOLD-SENSE method, UNFOLD provided significant suppression of the artifacts and amplified noise sometimes produced by parallel imaging. A 2DRF reduced-FOV (rFOV) approach proves particularly well suited for temperature monitoring during thermal ablation, as the large FOV required to avoid aliasing is often substantially larger than the heated volume. Parallel imaging and UNFOLD are used here to avoid artifacts that might result from imperfect 2DRF profiles, and enable the use of shorter 2DRF pulse durations. All three methods were fused in such a way as to combine their strengths and mitigate their weaknesses. The resulting hybrid pulse sequence was tested in experiments in a tissue-mimicking phantom and in ex-vivo tissue using FUS heating.

THEORY

Reduced FOV imaging using 2DRF Pulse

In MRI, when only a small portion of the FOV is of interest and the Signal-to-Noise Ratio (SNR) is not the main limiting factor, it would make sense to reduce the FOV along the phase-encoding direction to reduce acquisition time by acquiring fewer k-space lines. Doing so, however, leads to aliasing artifacts from the signal outside the desired FOV. A relatively straightforward method to avoid artifacts is to use a 2DRF pulse to limit the excitation in the phase-encoding direction to only the desired region.

A small-tip-angle model has been used for 2DRF pulse design (17). By applying the RF field B₁(t), composed of a series of subpulses weighted with the k-space weighting function W(k⃗), in conjunction with magnetic field gradient G⃗(t), the excitation profile M(r⃗) can be expressed as:

$$M(\overrightarrow{r})=i\gamma M_0{\displaystyle \int W}(\overrightarrow{k})S(\overrightarrow{k})\text{exp}(i\overrightarrow{r}·\overrightarrow{k})d\overrightarrow{k},$$ [1]

where γ and M₀ represent the gyromagnetic ratio and the original longitudinal magnetization, respectively. S(k⃗) is the sampling function in excitation k-space, and $\overrightarrow{k}(t)=-\gamma {\displaystyle {\int }_t^T\overrightarrow{G}(\tau )d\tau }$. The weighting function W(k⃗) is defined as the ratio of RF field B₁(t) to the product of the gyromagnetic ratio γ and gradient field G⃗(t):

$$W(\overrightarrow{k}(t))=\frac{B_1(t)}{\gamma |\overrightarrow{G}(t)|}.$$ [2]

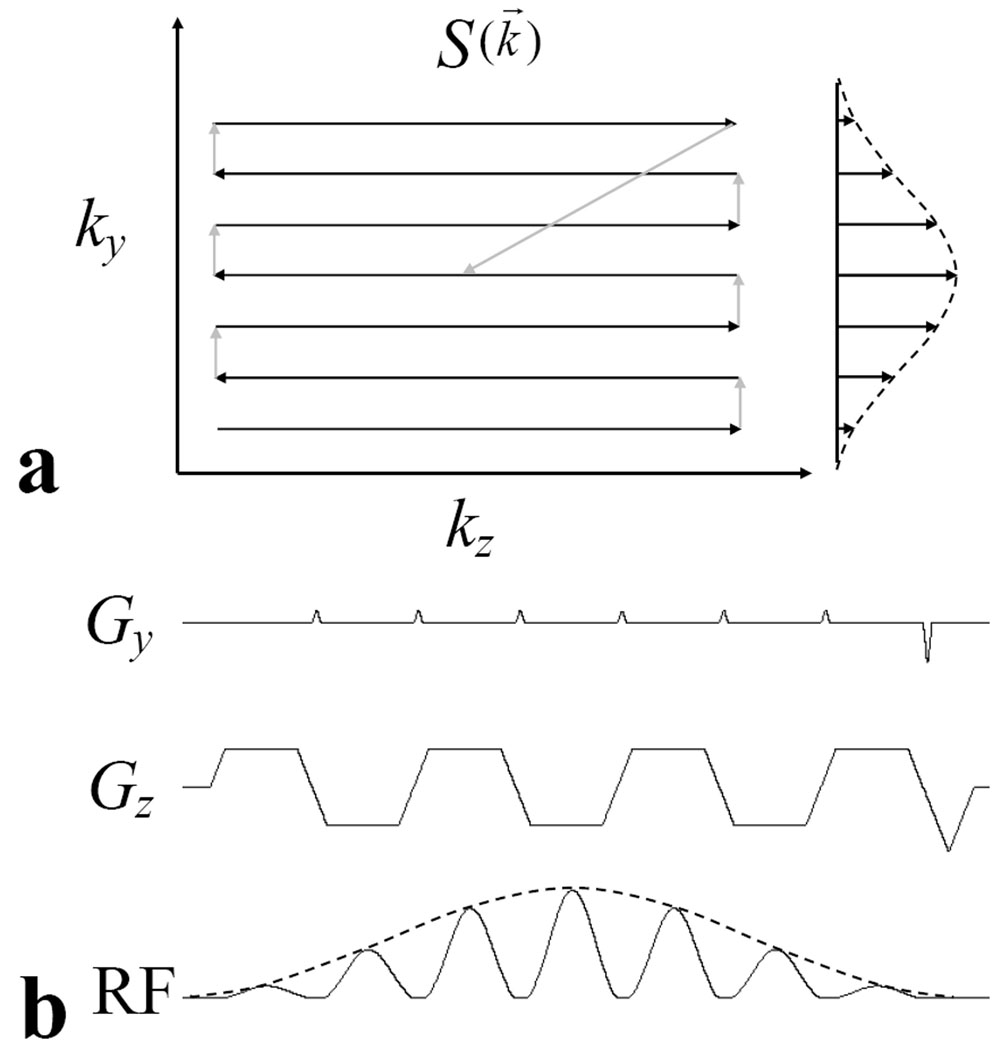
From Eq. [1], the excitation profile M(r⃗) can be viewed as the Fourier transform of the product of k-space weighting function W(k⃗) and k-space sampling function S(k⃗), which is a weighted trajectory in excitation k-space. As shown in Fig. 1a, a Cartesian trajectory can be used in excitation k-space, for 2DRF excitation pulses. The corresponding gradient waveforms and spatially selective RF pulse are shown in Fig. 1b. The slice (G_z) and phase (G_y) gradients are employed to produce the sampling function S(k⃗), and the RF pulse envelope produces the spatial frequency weighting function W(k⃗). For the pulse shown in Fig. 1b, each subpulse has a Gaussian-shaped envelope. To reduce the overall pulse duration, the subpulses are played out during both the plateaus and ramp sections of the G_z waveform, and during both the positive and negative parts of the waveform.

Fig. 1.

a) Gaussian-modulated, Cartesian excitation k-space trajectory of 2DRF pulse used in experiments. The modulation envelope, the distance between lines (Δk_y), the number of k_y lines, and the phase values of each line are user-defined parameters. b) Gradient waveforms and RF pulse waveforms for excitation k-space trajectory shown in a. The area of phase (G_y) blip gradient is used to control Δk_y and determines the distance between lines along the k_y direction. Rephasing gradients at the end of the G_y and G_z rewinds the sampling trajectory to the center of k-space. Subpulses are played out during both positive and negative G_z and also during both the plateau and ramp parts of G_z to reduce pulse duration.

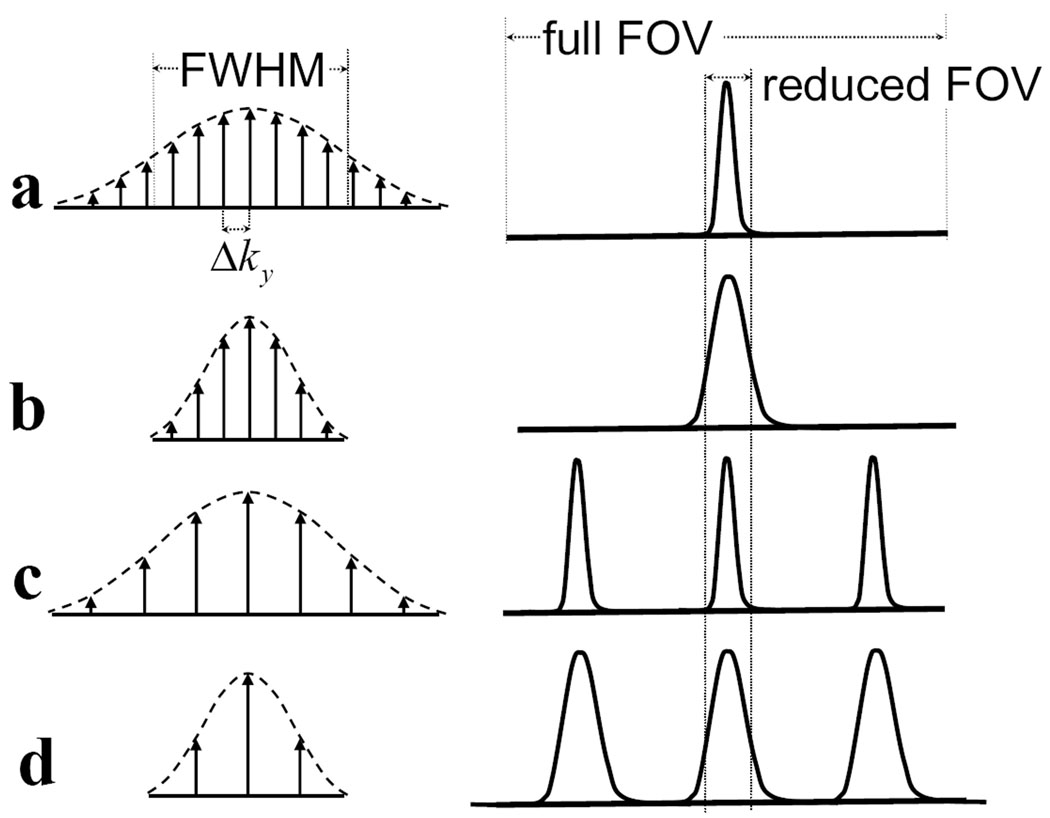
In principle, to completely avoid any aliasing artifacts, an RF pulse is required to create one (and only one) excitation lobe within the FOV. This usually results in a long RF pulse, which is undesirable not only because it increases the minimum TR and may prolong scan time, but also because it makes the RF pulse more sensitive to susceptibility effects. If shorter RF pulses were used for 2DRF excitation, the corresponding excitation profile would either become wider, or the excitation lobe would repeat itself within the FOV. Fig. 2 explores this tradeoff and depicts different schemes for 2DRF excitation along with corresponding excitation profiles. The length of a 2DRF pulse is determined by the number of subpulses it contains, and in Fig. 2 each subpulse is represented by an arrow. As compared to the 2DRF pulse in Fig. 2a, the number of subpulses can be reduced by using a sharper Gaussian modulation (Fig. 2b) or by decreasing the sampling density in excitation k-space (Fig. 2c). In Fig. 2a, a narrow single-lobed excitation profile is obtained at the cost of a relatively long pulse featuring 13 subpulses. An RF pulse nearly twice as short (7 subpulses) can be obtained using a sharper Gaussian modulation (Fig. 2b) or a larger Δk_y (Fig. 2c), although both cases would lead to significant aliasing artifacts in an image acquired with the indicated reduced FOV. The present work involves using a very short 2DRF pulse, as shown in Fig. 2d, and suppressing any aliasing artifact through a combination of UNFOLD and parallel imaging algorithms.

Fig. 2.

2DRF excitation profiles depend on 2DRF-pulse parameters. The figures on the left represent 2DRF pulses with different timing parameters, and the figures on the right represent corresponding excitation profiles. Arrows under the dashed lines represent the amplitudes of subpulses, and dashed lines represent the Gaussian modulation envelop of the 2DRF pulses. a) 2DRF is composed of 13 subpulses, where the excitation k-space increment in phase encoding direction is Δk_y, and the Full-Width Half-Maximum of its modulation is FWHM. This long RF pulse excites one narrow lobe within the FOV with width proportional to 1/FWHM. b) RF pulse is shortened with sharper Gaussian modulation (cutting FWHM in half) and the same sampling density in excitation k-space (same Δk_y). The excitation profile of this pulse is twice the width of the lobe in a. Wraparound aliasing will result if the FOV is reduced as shown. c) With the same Gaussian modulation width as in a, but decreasing the sampling density in excitation k-space (increasing Δk_y), side lobes will be excited within the FOV. d) Changes are made to both Gaussian modulation and sampling density, thus the excitation lobes are wider and there are side excitation lobes within the FOV, resulting in severe aliasing artifact when reduced FOV images are acquired.

Wraparound removal using UNFOLD and parallel imaging

UNFOLD manipulates the time evolution of aliased signals by changing the sampling function from time frame to time frame in acquisition k-space. The effect of UNFOLD can be readily explained in the temporal frequency domain (23). The value of a given image voxel may vary from one time frame to the next in a dynamic set of images, and the fast Fourier Transform (FFT) of this function with respect to time gives a temporal frequency spectrum for the voxel. The “true” or non-aliased signal tends to appear centered around the DC frequency in this temporal frequency spectrum, and UNFOLD can move aliased signal away from DC, to regions in the spectrum that tend to be left mostly unused by the non-aliased signal. After the aliased signal is filtered away, the non-aliased signal is recovered with an inverse FFT. UNFOLD displaces aliased signals in the temporal frequency domain by shifting the k-space sampling function by a fraction f of a line (the distance between two lines in acquisition k-space, or Δk_y) from one time frame to the next. In this study, the shift is equal to Δk_y/2, thus moving aliased signals all the way to the Nyquist frequency, where they may be filtered out.

Parallel imaging makes use of the sensitivity profile of the different elements in a phased array coil to speed up imaging acquisition and correct the artifacts caused by undersampling k-space. While different approaches have been developed, the Cartesian version of SENSE (24) remains commonly used due to its simplicity and relatively short reconstruction time. Its processing is performed in the object domain, using aliased images along with receiver sensitivity maps.

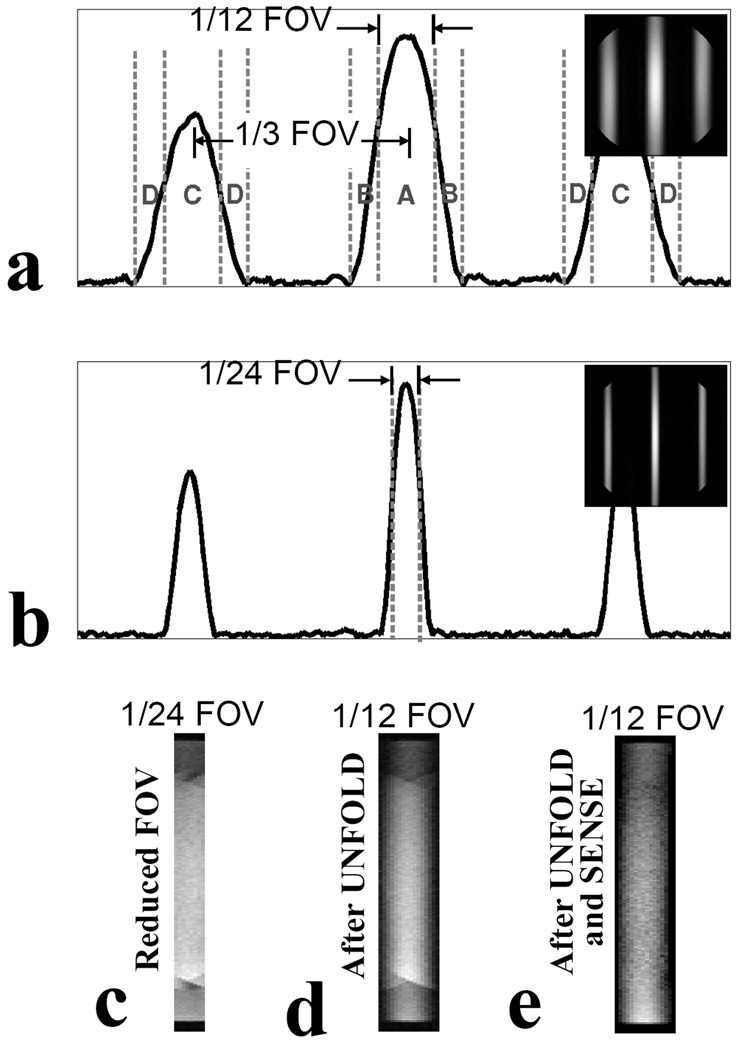
Figure 3 provides an example of the proposed approach, and of the various steps involved. A 2DRF pulse is employed to excite a reduced FOV, and SENSE as well as UNFOLD are used to correct deficiencies in the excitation profile. The very imperfect profile from a short 2DRF pulse is shown in Fig. 3a, where three smooth lobes appear within the FOV, rather than a single sharp one. These three lobes consist of the main excitation lobe in the center with side lobes an equal distance away on each side. The distance between the main lobe and side lobes can be adjusted to a multiple of the reduced-FOV size, so that all lobes overlap onto each other without spatial shifts in the acquired rFOV images (Fig. 3c). Parallel imaging is well suited for removing the signal from regions labeled ‘C’ in Fig. 3a, as there is a large spatial separation between them and the main lobe. It is not as useful, however, for separating the signal from the ‘B’ (and ‘D’) regions from that of the ‘A’ (and ‘C’) regions because they are physically close and are likely to feature similar coil sensitivity. Unlike parallel imaging, UNFOLD is well suited to separate signals from regions that are in close physical proximity. The signal from the transition zones (B and D regions) can be removed using UNFOLD (20), as seen in Fig. 3d, and the main bulk of the signal from excitation side lobes (C regions) can be removed using parallel imaging, leaving only the non-aliased signal from region A, as seen in Fig. 3e.

Fig. 3.

2DRF excitations and SENSE plus UNFOLD filtering were tested on a GE 3T scanner by imaging a homogeneous doped water phantom. The number and width of excitation lobes are adjusted by manipulating the 2DRF subpulse modulation and excitation k-space sampling density. a) Excitation profiles obtained with a short 2DRF pulse (3.6 ms) composed of 7 subpulses. The lobe width including transition regions is 1/6 of the full FOV and the distance between central and side lobes (1/3 FOV) are multiple of desired reduce FOV (1/12 FOV). b) Excitation profile obtained with 17 subpulses (duration 8.8 ms). c) With 17 subpulses, the FOV was reduced to 1/24 of the full FOV, for a 24-fold improvement in temporal resolution. d) Aliasing onto the central lobe from regions B and D was removed by UNFOLD e) The main bulk of the signal from the side lobes (region C) was eliminated using parallel imaging, leaving only the central lobe.

METHODS

Imaging Pulse Sequence

All studies were performed on a 3T GE Signa scanner (General Electric Medical System, Milwaukee, WI, USA) with twin-speed gradients (maximum gradient strength 40 mT/m, maximum slew rate of 150 T/m/s). A GE product 2D spoiled-GRASS (SPGR) gradient-echo sequence was used to measure the PRF shift using phase-mapping, and was modified to incorporate the acceleration method outlined herein. The 2DRF modification was accomplished using functions from a freely available 2DRF pulse library developed within our group (National Center for Image Guided Therapy, or NCIGT, http://www.ncigt.org). Functions in the library enable one to implement an echo planar type of 2DRF excitation pulses with options that include the number of subpulses, the subpulse durations, the modulation envelope (sinc or Gaussian), and the number of cycles within the envelope. The excitation profile can also be controlled through adjustments in blip gradient strength and phase for each subpulse, through user-defined parameters. The UNFOLD modification involved shifting the acquisition k-space lines by Δk_y/2 from one time frame of the dynamic image series to the next, where Δk_y represents the increment between trajectories in acquisition k-space.

FUS Experimental Set-up

The ultrasonic fields were generated by a single-element, spherically curved, piezoelectric transducer with resonance frequency 1.5 MHz (radius of curvature = 100 mm and diameter = 100 mm). The transducer produced an ellipsoid focal spot whose half-maximum intensity length and diameter were 10 mm and 5 mm, respectively. It was driven by a function generator (Model 396, Fluke, Everett, WA) and RF amplifier (model 240L, E and I, Rochester, NY). RF power was monitored using a power meter (model 438A, Hewlett Packard, Palo Alto, CA) and dual directional coupler (model C1373, Werlatone, Brewster, NY). For all experiments, 30-s continuous wave sonications were delivered. The acoustic power ranged from 10–20 W with an aim of achieving a peak temperature change of less than 15°C, so that consecutive experiments could be performed at the same location without causing thermal damage to the tissue samples. The transducer was mounted on the bottom of an acrylic tank, which was filled with degassed and de-ionized water. The tank fit into a standard GE 8-channel head coil. Tissue samples or phantoms were placed on a plastic holder above the transducer and were thick enough to reach the focal depth. The gel phantom used here had rotational symmetry, and its axis was aligned with the main magnetic field to minimize susceptibility effects.

2D Temperature Imaging Experiments in Gel Phantom

Heating experiments were performed in a tissue-mimicking phantom (ATS Laboratories, Bridgeport, CT, see reference (25) for properties) heated with FUS. As part of scan prescription, the focal spot was located by imaging temperature changes during short-duration sonications. Excitation profiles from our 2DRF pulse were measured (e.g., see Fig. 3b) based on full-FOV SPGR images (FOV: 16×16 cm, TR/TE: 40/20 ms, matrix size: 192×192, flip angle: 30°, slice thickness: 5 mm, bandwidth: ±15.6 kHz, high order shim applied). The 2DRF pulse used here consisted of 17 subpulses modulated with a Gaussian envelope, with total duration of 8.8 ms. The location and size of the central excitation lobe was adjusted so as to cover the FUS focal spot (by adjusting the blip gradient size and the phase of the subpulses). Sonication parameters such as RF power, pulsing period, duty cycle, and duration were set at the FUS workstation, outside the scanner room.

During the heating experiment, our modified SPGR sequence was used for temperature mapping purposes. Dynamic images were acquired continuously for 90 s, using the same imaging parameters as described above except for the FOV size, which was reduced by a factor of 24 in the phase-encoding direction (matrix size: 192×8). An acoustic power of 12 W was delivered throughout a 30 s period, after which transmission was stopped and the phantom was allowed to cool. Images before heating were used as baselines in post-processing. Image reconstruction, phase-difference calculations and data analysis were all performed in the MATLAB programming language (MathWorks, Natick, MA).

Temperature measurements obtained using our accelerated approach were compared with results obtained using the same SPGR sequence with regular RF pulse and full FOV (called ‘full SPGR’ below). Comparisons involved different heating experiments performed with identical sonication parameters. A ten-minute cooling period separated consecutive sonications to allow the temperature to return near baseline. Overall, 5 different heating locations and a total of 14 sonication experiments in the gel phantom were imaged using 2D thermometry.

2D Temperature Imaging Experiments in Bovine Muscle

Additional tests were performed in ex vivo bovine muscle. Fresh, never-frozen bovine muscle from a grocery store was used. Each specimen was degassed in a saline solution under vacuum (650 mmHg) for at least one hour before use. Areas free of large vessels and fat were selected for sonication to avoid distortion of the ultrasound beam and imaging artifacts. The same prescription steps as described above were performed, and the same imaging parameter and 2DRF pulse parameters were used. Results were again compared to those obtained from a ‘full SPGR’ sequence.

3D reduced-FOV Temperature Imaging Experiments

A GE product 3D SPGR sequence was modified to incorporate our proposed hybrid acceleration method. As compared to the 2D experiments described above, a very different excitation profile along z was obtained in the present 3D implementation (slab excitation rather than slice excitation) but, on the other hand, the excitation profile along the phase-encoding direction y remained essentially unchanged. Accelerated 3D acquisitions were performed in a gel phantom, which was heated for 30 s with FUS at an acoustic power of 20 W. The 3D rFOV images were acquired during heating and cooling (FOV: 0.7×16.0×12.0 cm, TR/TE: 40/20 ms, matrix size: 192×8×24, flip angle: 30°, slice thickness: 5 mm, bandwidth: ±15.6 kHz). The first 8 s of scanning, before sonication started, were used to establish a pre-heating baseline. All measurements were compared to those obtained using the GE product 2D SPGR sequence. The slice position for the 2D sequence was set to coincide with the center of the imaged volume for the 3D sequence.

Real-time Processing and Display

An implementation of the proposed approach with real-time reconstruction and display was tested during FUS heating of the gel phantom. The real-time implementation required the integration of three separate systems: the MRI scanner, our Dynamic Adaptive Real-Time Software System (DARTS), and 3D-Slicer. Both DARTS and 3D-Slicer are publicly available software packages available through the NCIGT. DARTS involves low-level software written in the C language, which enables real-time acquisition and reconstruction of MRI images. Written in C++, 3D-Slicer is primarily a display and post-processing software package. An external workstation loaded with both DARTS and Slicer was connected to the MR scanner via an Ethernet cable. Reconstruction modules were added to DARTS, to handle UNFOLD and SENSE reconstructions.

Prior to the heating experiment, a 3D FGRE image dataset was acquired for the volumetric display in Slicer. The 2DRF pulse consisted of 5 subpulses, for a total duration of 2.6 ms. As usual, the main excitation lobe was made to coincide with the FUS focal point. The 2D implementation of our proposed thermometry approach was used, over a 20-min period, to follow the temperature changes that occurred as sonication (16 W, 30 s duration) was turned on and off (FOV: 2.3×18.0 cm, TR/TE: 40/17 ms, matrix size: 128×16, flip angle: 30°, slice thickness: 8 mm, bandwidth: ±5 kHz, imaging plane: axial). Acquired data were fed into DARTS for reconstruction with UNFOLD and SENSE algorithms, and the resulting images were then passed on to Slicer for display.

Image Reconstruction

The data acquired with our modified pulse sequences were reconstructed using SENSE and UNFOLD algorithms, and the resulting images were processed to generate dynamic temperature maps. A 24-fold acceleration was obtained by using a 2DRF pulse that significantly excites only about a fraction 6/24 of the FOV along the phase-encoding direction (see Fig. 3b), along with UNFOLD (2-fold acceleration) and parallel imaging (3-fold acceleration). In the actual reconstruction programs, the 24-fold acceleration was obtained through a 2-fold UNFOLD acceleration and a nominal 12-fold SENSE acceleration, but since no more than 3 of the 12 layers separated by SENSE are ever non-zero, the actual SENSE acceleration is 3.0 (not 12.0). The UNFOLD implementation differed slightly between the non real-time and real-time experiments. For non real-time experiments, all images in the time series were employed during the UNFOLD processing (i.e., non-causal implementation), whereas for real-time experiments, only the most recent 12 time frames were employed (i.e., causal implementation). For the ‘full SPGR’ data, a non-accelerated SENSE algorithm (acceleration factor = 1) was used to combine images from different coil elements in an SNR-optimum fashion (26).

The Phase difference between a (coil-combined) image Z_t acquired at time t and a pre-heating baseline Z₀ was calculated by:

$$-\pi \le \mathrm{\Delta }\Phi =\mathit{\text{phase}}(Z_t/Z_0)=\mathit{\text{phase}}(Z_t/{Z_0}^{*})\le \pi$$

where * denotes complex conjugation. Maps of temperature change were generated, using TE values along with the known temperature dependence of the PRF (−0.01 ppm/°C, or −1.28 Hz/°C at 3T) (27). For display purposes, an ROI of 3×5 voxels (2.5×4.2 mm² in size) centered within the FUS focal spot (full-width-half-maximum 5×10 mm² in size) was selected when plotting temperature curves for 2D imaging experiments, while a single voxel ROI was selected for 3D experiments. Temperature-to-Noise Ratio (TNR) analysis was performed by acquiring data without actual heating. To cancel the effects of any slow phase drift, consecutive temperature time frames were subtracted two-by-two. The temperature noise was then taken as the standard deviation along the time axis over all pixels in the same ROI as described above.

Statistical Analysis

Temperature data from fourteen 2D imaging experiments performed in our gel phantom were employed toward evaluating the precision and accuracy of our proposed approach. Linear regression analysis (calculation of slope, y intercept, and correlation coefficient) was used to compare temperature changes obtained from the present accelerated hybrid method and those obtained from a ‘full SPGR’ reference. As a 24-fold higher temporal resolution was reached using our accelerated hybrid method, only the time points that corresponded most closely with the time locations sampled in the ‘full SPGR’ reference were actually involved in the comparison. Since there were 12 time points per experiment in the reference datasets, the total number of time points available for analysis was 168. The Bland-Altman technique was used to evaluate the agreement, and the limits of agreements were defined as the mean difference ±1.96 standard deviations (28). Furthermore, using a Student t-test, the hypothesis that no significant difference exists between results from our method and the ‘full SPGR’ reference was tested, and the correlation coefficient was calculated. We repeated these tests after temporally averaging the results from our hybrid method (24-fold, sliding window), so its temporal resolution would be lowered to the same level as that of the ‘full SPGR’ reference. Doing so allowed an SNR-equivalent comparison of our approach and the reference. As compared to the first set of tests described above, in which time points were simply picked rather than averaged, one would expect the deviation in Bland-Altman plots to become smaller and the mean difference to remain unchanged.

RESULTS

2D Temperature Imaging Experiments

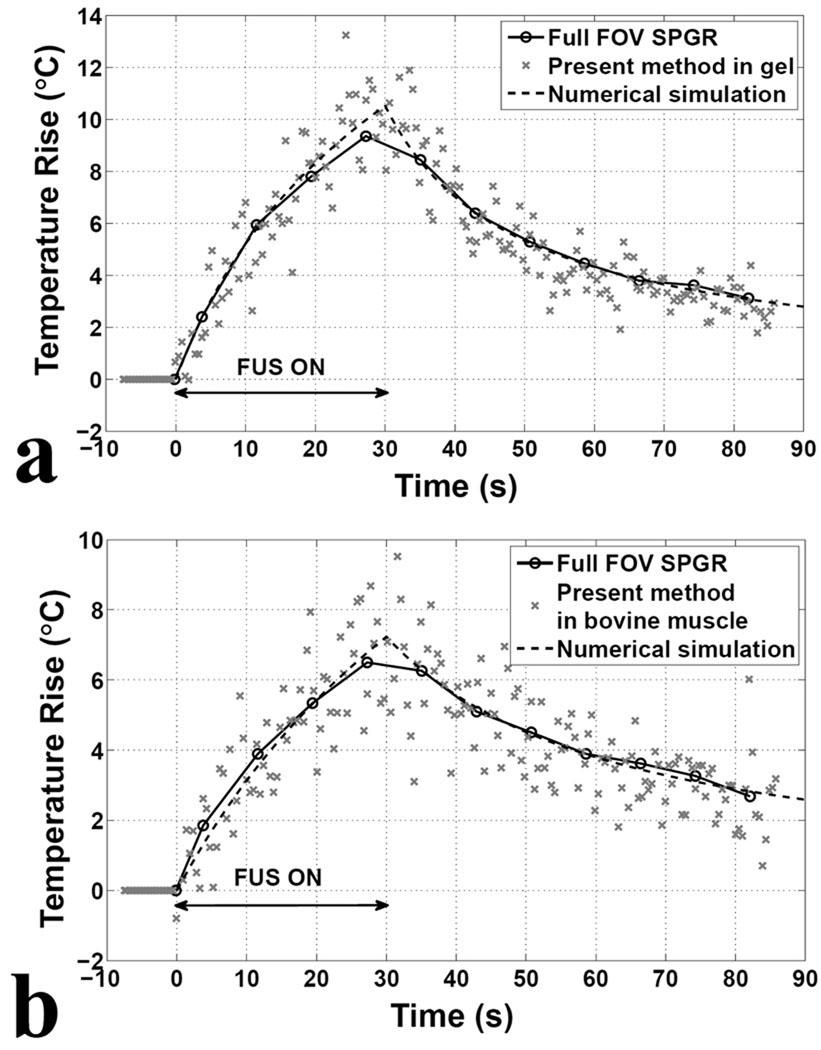
Examples of MR temperature measurements, with our proposed accelerated hybrid approach and with a ‘full SPGR’ reference, are shown in Fig. 4 for both gel and bovine muscle experiments. Temperature changes in a 3×5 ROI at the focus of heating are displayed during ‘x’ markers for our proposed method and ‘o’ markers for the reference. It can be seen from Fig. 4 that both measurements appear to agree, although results from our method clearly have much higher temporal resolution and, as a direct consequence, greater noise levels. Both methods used the same settings for TR/TE (40/20 ms), and the temporal resolution for ‘full SPGR’ was 192 × TR=7.68 s while for our proposed approach it was 0.32 s instead (i.e., 24-fold improvement). In theory, a noise penalty by a factor of $\sqrt{24}$, = 4.9, might be expected, which is roughly consistent with the noise levels that were measured (in gel: ±0.7°C for the accelerated method and ±0.1°C for the reference, in bovine muscle: ±0.8°C for the accelerated method and ±0.2°C for the reference).

Fig. 4.

MR temperature measurements and numerical simulations from the ROI at the focus of heating during and after FUS treatment of a gel phantom (a) and a bovine muscle (b). The graph shows the temperature changes for the modified sequence using a 2DRF pulse consisting of 17 subpulses in reduced FOV imaging (cross markers) compared to the results using a 2DRF pulse consisting of 1 subpulse in full FOV imaging (circle markers). Data from full FOV imaging were fitted using Pennes’ bioheat transfer equation (dashed lines). For comparison, the same TR/TE (40/20ms) and matrix size (192×192) were used for both sequences. The temporal resolution of the full FOV imaging is 7.68 s, compared to 0.32 s for the modified sequence, giving a 24-fold improvement. The modified sequence with SENSE-UNFOLD reconstruction substantially improves temporal resolution with tolerable temperature uncertainty of 0.7°C in gel phantom and 0.8°C in bovine muscle.

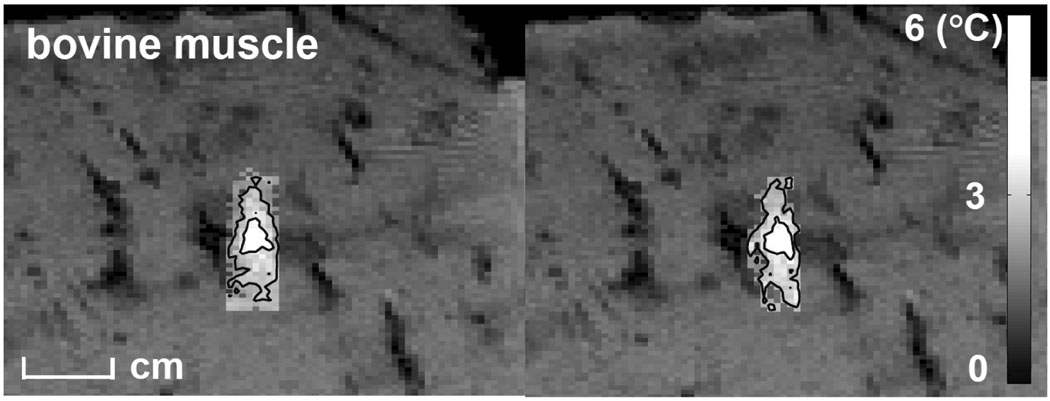
To spatially compare the present approach with the ‘full SPGR’, temperature maps, overlaid on full FOV magnitude images, of the time frames with maximum heating in an ex-vivo experiment were shown at Fig. 5. Temporal averaging was performed in the accelerated approach to make the SNR comparable to that of ‘full SPGR’. Result showed similar heating envelopes. Small differences between the two examples in voxels with low-level heating are expected from noise considerations.

Fig. 5.

Temperature maps, overlaid on full FOV magnitude images, of the time frames with the maximum heating obtained from the present approach (right) and a SPGR sequence (left) in an ex-vivo experiment. The map obtained from the present approach was averaged over 24 time frames. Threshold temperature of 2°C was applied on both maps. Iso-temperature was shown in two-level contours where temperature rises were greater or equal to 2.6°C and 5.2°C. Results show similar heating profiles.

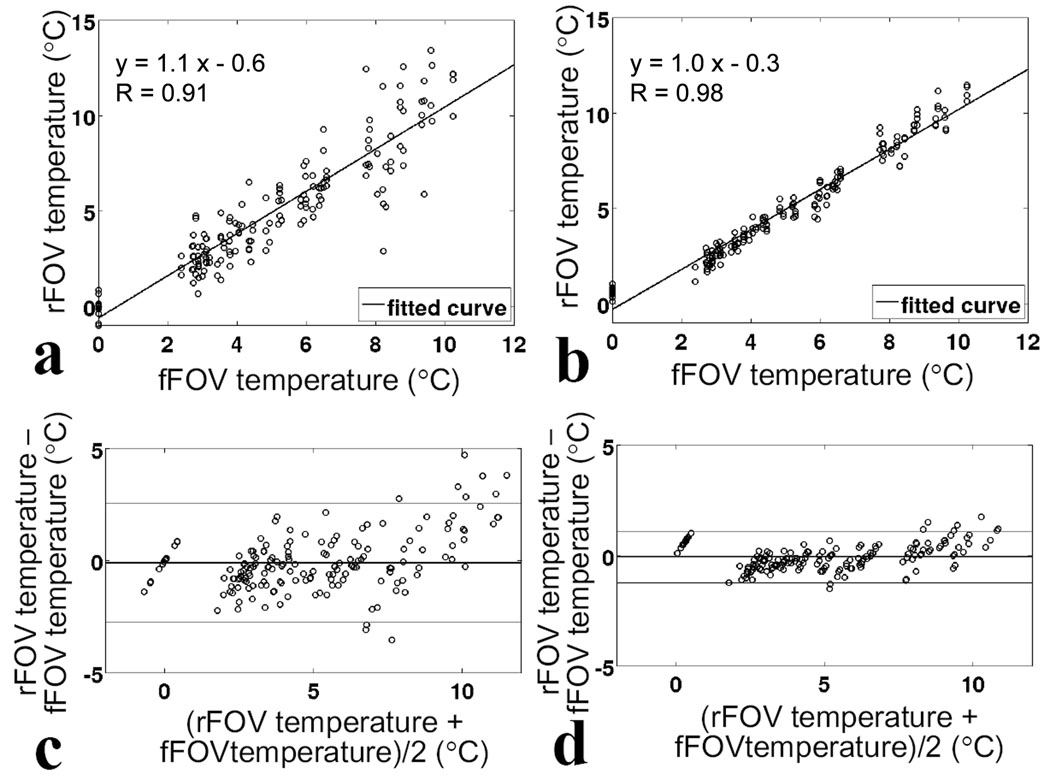
While Fig. 4 features results from only one of the fourteen experiments that were performed in the gel phantom using our modified 2D imaging sequence, in contrast, Fig. 6 is meant to aggregate and analyze data from all fourteen experiments. As explained above, the analysis was performed twice: once on data where one time point every 24 was picked from the high-temporal resolution datasets (Fig. 6a,c) and once on data where temporal averaging was used to reduce temporal resolution by 24-fold, down to the level of the reference dataset (Fig. 6b,d). Good correlation was found through linear regression (R = 0.91 in Fig. 6a, R = 0.98 in Fig. 6b) and the mean difference was small (0.1°C in both Fig. 6c and d). While the standard deviation of the difference was larger in Fig. 6c (1.4°C) due to relatively high noise levels in the accelerated results, a smaller deviation was observed as expected in Fig. 6d (0.6°C) when using averaged data. The 1.4/0.6 = 2.33-fold reduction in standard deviation was similar to its theoretically expected value of 2.47-fold, as obtained through noise propagation considerations, as listed in Table 1 (line 9 divided by line 10, $\sqrt{54/48}/\sqrt{9/48}=2.47$).

Fig. 6.

Scatterplots (a, b) and Bland-Altman plots (c, d) comparing of temperature measurements obtained using the present accelerated method with those obtained using full FOV SPGR sequence for 168 measurements acquired during 14 sonications. a),c), comparison using individual measurements from accelerated sequence. b),d), comparison using time-averaging over 24 frames in the rFOV measurements. The mean difference between measurements for the time-averaging scenario remained at 0.1°C, while standard deviation was reduced from 1.4°C to 0.6°C. In a and b, solid lines represents linear regression. In c and d, solid lines represent average difference, upper and lower lines represent ±1.96 standard deviations (95% confidence intervals).

Table 1.

Noise propagation considerations for Bland-Altman plots.

Dataset	Variance	Relative Standard Deviation
1. Dataset for rFOV (24-fold acceleration)	σ2	1
2. Dataset for averaged rFOV (average over 24 frames)	σ2/24	0.20
3. Baseline for rFOV (average over 16 preheating dataset)	σ2/16	0.25
4. Temperature mapping for rFOV (difference b/w 1 and 3)	σ2+σ2/16	1.03
5. Temperature mapping for averaged rFOV (difference b/w 2 and 3)	σ2/24+σ2/16	0.32
6. Dataset for fFOV (no acceleration)	σ2/24	0.20
7. Baseline for fFOV (1 preheating image)	σ2/24	0.20
8. Temperature mapping for fFOV (phase difference b/w 6 and 7)	σ2/24+σ2/24	0.29
9. rFOV temperature – fFOV temperature (difference b/w 4 and 8)	σ2+σ2/16+σ2/24+σ2/24	1.07
10. averaged rFOV temperature – fFOV temperature (difference b/w 5 and 8)	σ2/24+σ2/16+σ2/24+σ2/24	0.43

Based on data from Fig. 6d, for 95% of the measurements (159 of 168), temperature values from our proposed approach and the reference agreed within ±1.2°C. Furthermore, a Student t-test performed on both time-averaged and non-time-averaged data showed that measurements from the proposed approach and from the reference did not significantly differ (p-values of 0.1 and 0.4, respectively).

As can be observed in Fig. 6d, the difference between accelerated and non-accelerated datasets tended to have a bias toward positive values for higher temperatures, i.e., near the peak temperature. We suspect this might be caused by the lower temporal resolution of the reference ‘Full SPGR’ data, too low to accurately catch the peak temperature. Accordingly, the reference datasets would provide peak temperature estimates that are systematically too low, due to temporal averaging effects. Simulations were performed to verify this point. Data from the reference sequence were fitted using two distinct heating models: one based on simple rising and then decaying exponentials, and one more complex based on Pennes’ bioheat transfer equation (fitted thermal properties were k=0.1×10⁻⁷m²/s and c_v=3.8×10⁶ J/m³/°C, where k is the thermal diffusivity and c_v is the heat capacity per unit volume). Fitting based on Pennes’ model is shown in Fig. 4. Using averaging windows that correspond to both the reference and accelerated temporal resolutions, we found a peak-temperature difference of about 0.3 °C (exponential model) or 0.8 °C (Pennes’ model). While we cannot be sure that the bias as observed in Fig. 6d is entirely caused by the effect described here, we note that the bias has the correct polarity (the accelerated values are higher), and roughly the correct size, suggesting the bias near peak temperatures might indeed be caused by differences in temporal resolution and corresponding averaging effects.

3D Temperature Imaging Experiments

While the present acceleration method can be employed to increase temporal resolution (e.g., Fig. 4), doing so comes at a price in TNR. On the other hand, the proposed method can alternately be used to improve 3D spatial coverage instead, at no cost in terms of SNR. In Fig. 7, reduced in-plane FOV 3D temperature measurements (solid lines) are compared to results using a ‘full SPGR’ 2D sequence (dashed line). With the proposed rFOV 3D sequence, in-plane coverage is reduced by a factor of 24 and through-plane coverage is increased by the same amount. Accordingly, the ROI (focus) was imaged in 3D. Note that temporal resolution and TNR are the same as with the ‘full SPGR’ 2D sequence, but that spatial coverage has the shape of an elongated box rather than a slice. Temperature measurements in the central slices of the acquired 3D volume (slices #11 and #12 out of 24) were similar to those obtained using the single-slice reference sequence, while other slices in the 3D volume featured much smaller temperature changes (Fig. 7).

Fig. 7.

Temperature changes of the hottest voxel of 6 middle slices in 3D gel experiments were plotted in solid lines. The dashed line shows temperature measurements for the full-FOV SPGR sequence. The full SPGR sequence gave the similar result to slices #11 and #12 of the accelerated 3D sequence since they were around the same slice location. Inset: three-dimensional isosurface where the temperature rise was greater or equal to 9°C. These temperatures were reached in slices #11 and #12.

Real-time Processing and Display Experiments

The term ‘real time’ is used here to convey the fact that acquired data were displayed, with reasonably small latency, as the multi-frame scan progressed. It should be noted however that a fully real-time implementation would further include real-time control of sequence parameters and of the FUS beam in terms of steering and output power, which was not the case here.

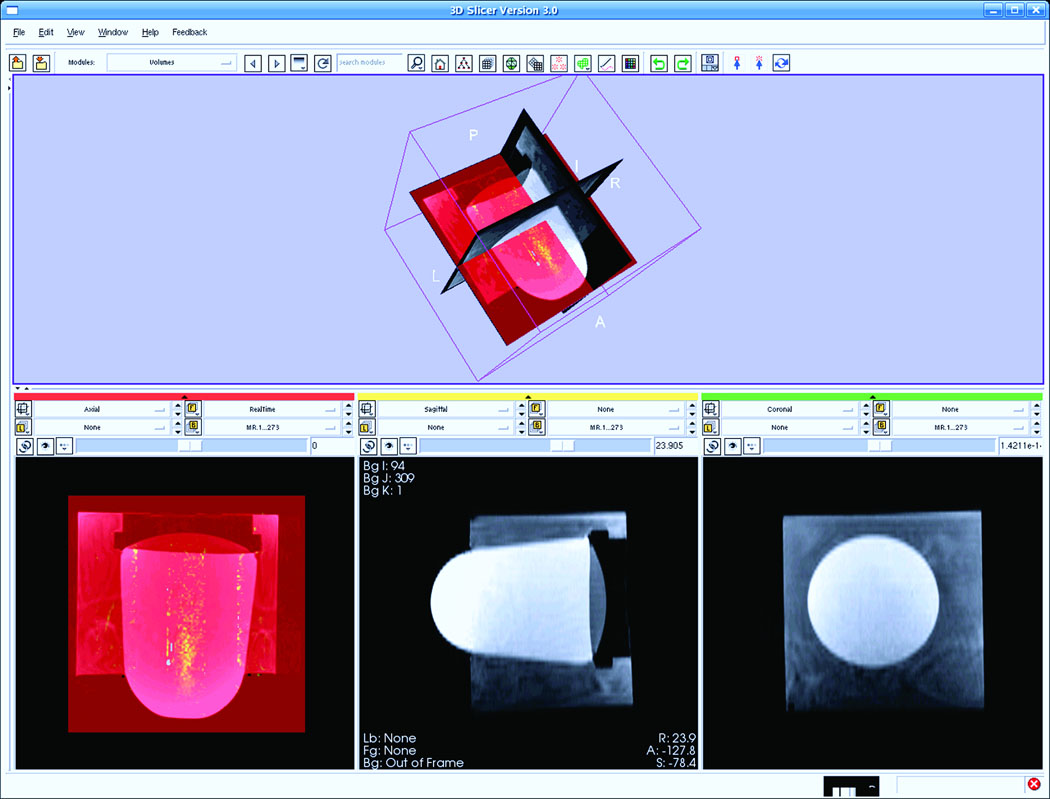
Fig. 8 shows a screen snapshot of the Slicer display 30 s into a phantom heating experiment during which temperature maps were continuously acquired, processed, and displayed. The top panel displays the 3D object, overlaid with a temperature-sensitive image in the axial plane. Three orthogonal tomographic planes from the 3D images were displayed in the bottom panel. The bottom middle and bottom right images are sagittal and coronal baseline images from the gel phantom, respectively. The bottom left image is in the axial orientation, the transducer can be seen in the upper portion, and temperature changes are displayed as a color overlay. Images were acquired at a rate of about 1 fps, and the corresponding temperature maps were reconstructed and displayed with a latency of less than one frame.

Fig. 8.

Screen snapshot of 3D-Slicer, the display software package. The bottom left image displays a snapshot during the real-time imaging, processing, and display. The FUS heating effect, which is updated in real-time, is shown in yellow superimposed on the baseline axial image of the gel. The transducer is located in the upper portion of the bottom left of the image.

DISCUSSION AND CONCLUSIONS

The present work was aimed at accelerated imaging, and more specifically at accelerated MR thermometry imaging. Using the proposed approach, we demonstrated that acquisitions could be substantially accelerated in FUS temperature mapping experiments, with acceleration factors as high as 24-fold. To account for the effect of the UNFOLD temporal filter (FWHM = 90% of the bandwidth), it is often useful to define an “effective acceleration” factor, equal here to 0.9×24 = 21.6-fold. This 21.6-fold acceleration can then be spent in a number of different ways. The method was used here either to improve temporal resolution (at an SNR cost), or to enable 3D coverage (at essentially no SNR cost). In one particular experiment a product SPGR sequence provided a temporal resolution of only 7.68 s/frame, while our accelerated version of this same sequence achieved 0.32 s/frame in both gel and ex-vivo experiments. Improvements in temporal resolution do, however, come at a price in terms of SNR. Alternately, we also implemented our approach onto a 3D sequence, and showed how acceleration could be used here to enable 3D coverage, with essentially no reduction in SNR. Results were obtained with the same temporal resolution and noise properties as in the 2D non-accelerated case, but with 24-slice 3D coverage. In this example, full-FOV coverage in the y phase-encoding direction was sacrificed to generate through-slab coverage in the z direction, leading to an elongated box-like coverage arguably better suited to monitor heating from an FUS beam than a more usual 2D-slice coverage. When used in this fashion, the technique essentially provides flexibility toward tailoring the imaged volume to the heated zone. In cases where peripheral heating may be expected, for example when the ribs or skull are on the path of the FUS beam, especially careful thought should be given to the shape and orientation of the desired FOV.

While the present method was implemented on a regular gradient-echo sequence, with a single k-space line acquired per TR period, it could be combined instead with fast pulse sequences such as echo-planar (6) or spiral (7) imaging, for example. The present method is based on RF pulse (2DRF) design, receiver coils (SENSE), and a temporal strategy (UNFOLD); as such, it is not limited to the gradient-echo sequence used here. For example, Stafford et al. (7) reported a temporal resolution 0.58 s/image with a spiral sequence, and the proposed approach could be used to further improve temporal resolution (as far as SNR permits). Similarly, in a recent study by Holbrook et al. (15) EPI has been used to achieve 3.43 frames per second, with temperature noise below 0.5 °C. When combined with EPI, the present approach could enable a reduction in the number of shots and/or a reduction in the echo-train-length, for reduced distortion. As compared to the present implementation based on a regular gradient-echo sequence, an EPI implementation would not feature any SNR or TNR advantage, but rather a spatial-coverage advantage. SNR is proportional to $V\times \sqrt{T}$, where V is the voxel volume and T the total sampling time, given by T = N_tr × N_e × τ, where N_tr is the number of TR periods required to build an image, N_e is the number of echoes per TR period, and τ is the readout period. With SPGR, N_e = 1, and our method speeds up the acquisition process by reducing N_tr. With interleaved EPI, N_e > 1, τ is reduced by a factor N_e, and the factor N_e × τ is thus left mostly unchanged. Just like with our method, interleaved EPI reduces scan time by reducing N_tr, with essentially the same effect on SNR, for equivalent acceleration. We have measured the TNR for accelerated SPGR and interleaved EPI in a gel phantom, confirming that with equivalent voxel size, bandwidth, TR and temporal resolution, the TNR of the present method was comparable to that from gradient-echo EPI. Table 2 shows different acquisition scenarios along with expected and measured TNR values. For each line in the table, datasets were acquired both with a full-FOV SPGR sequence and with the sequence listed in the leftmost column, in a gel phantom. Temperature maps were generated and temperature noise was evaluated. The rightmost column gives the measured TNR, normalized by that measured in the corresponding full-FOV SPGR dataset. In line with the explanation above, the advantage of interleaved EPI compared to our proposed approach is not SNR or TNR, but spatial coverage. Our method provides a limited FOV, while EPI could provide a full FOV. On the other hand, interleaved EPI is not without weakness. For example, interleaved EPI often suffers from distortions, signal voids, and ghosting. Our accelerated SPGR method can be seen as an alternative to interleaved EPI, where some spatial coverage is sacrificed in order to avoid EPI-related problems, at no cost in TNR. The implementation of the present approach with EPI sequences, although potentially useful, is beyond the scope of the present work.

Table 2.

TNR estimation for scenarios involving different sequences and parameters.

	Matrix Size	Temporal Resolution	Acceleration Factor	Expected TNR	Measured TNR
a) Full-FOV SPGR (2D)	192x192x1 1 average	7.68 s	1	1	1*
b) Proposed rFOV method (2D)	192x8x1 1 average	0.32 s	24	0.20	0.18
c) Proposed rFOV method (3D)	192x8x24 1 average	7.68 s	1	1	0.86
d) Full-FOV EPI (ETL=4)	192x192x1 4 averages	7.68 s	1	1	0.95

^*Temperature noise of Full-FOV SPGR in a gel was 0.1°C.

Even though the proposed accelerated method requires longer (2D) RF pulses than the (1D) pulses typically employed, it should be noted that TR and thus imaging time were not affected. Since TE in PRF temperature imaging is usually relatively long (equal to T2* of the tissue for higher SNR (29)), it is possible to play out a somewhat longer RF pulse without having to increase TR. However, with TE defined as the time between the middle of the RF pulse and the echo, longer RF pulses may lead to shorter TE values and slightly reduced temperature-to-noise-ratios. Furthermore, when using long RF pulses (about 10 ms here) susceptibility-related effects can be a concern. These problems can, however, be mitigated to a large degree through the use of high order shimming.

It should also be noted that for accurate temperature measurements in vivo, the 2DRF excitations used here should further allow fat suppression. We recently implemented pulses that exploit the chemical-shift sensitivity of 2DRF pulses to obtain spatially-varying water-fat excitation patterns and fat-suppressed regions, toward reduced-FOV accelerated imaging (30,31). In a cheese phantom (about 20% of fat), accurate temperature measurements were obtained through to successful suppression of fat signals. A method by K Sung, et al, was also proposed to remove fat signal in conjunction with 2DRF excitations (32). Although clearly not a trivial problem, we believe the present method to be quite compatible with robust fat suppression at 3T.

To conclude, an accelerated imaging method was presented that combines 2DRF excitations, UNFOLD, and parallel imaging. The method was targeted toward fast MR thermometry imaging, and acceleration factors up to 24-fold were obtained to increase temporal resolution and/or through-plane spatial coverage. We demonstrated a real-time implementation with low acquisition-reconstruction-display latency. The method showed good temperature accuracy, is reasonably easy to implement (using our 2DRF library) and to prescribe (2DRF parameters were adjusted from the console). The proposed approach can allow faster imaging for better motion tracking, and/or flexible 3D coverage to more closely adapt the image FOV to the shape of the heated region.