The wisdom of the crowd playing The Price Is Right

Abstract

In The Price Is Right game show, players compete to win a prize, by placing bids on its price. We ask whether it is possible to achieve a “wisdom of the crowd” effect, by combining the bids to produce an aggregate price estimate that is superior to the estimates of individual players. Using data from the game show, we show that a wisdom of the crowd effect is possible, especially by using models of the decision-making processes involved in bidding. The key insight is that, because of the competitive nature of the game, what people bid is not necessarily the same as what they know. This means better estimates are formed by aggregating latent knowledge than by aggregating observed bids. We use our results to highlight the usefulness of models of cognition and decision-making in studying the wisdom of the crowd, which are often approached only from non-psychological statistical perspectives.

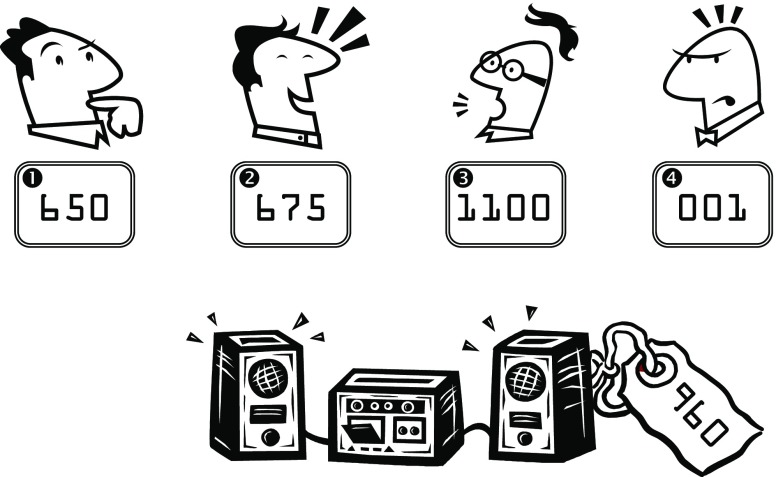
The Price Is Right is a well-known game show involving a number of different competitions. The most frequent competition is caricatured in Fig. 1 and involves four players placing bids to win a prize. Bids are placed sequentially—from Player 1 to Player 4—with all players knowing the value of preceding bids. Once all bids have been made, the winner is the player whose bid is closest to, without exceeding, the true value of the prize. In Fig. 1, the winner is Player 2 because, although Player 3’s bid of $1,100 is closer to the true price of $960, it goes over the true price.

Fig. 1.

A Price Is Right competition, with four players placing bids to win a stereo. Player 2 is the winner, because their bid of $675 is the closest to the true price of $960, without having exceeding the true price

This competition provides an interesting “real-world” source of competitive decision-making data and has occasionally been used to study human decision-making (e.g., Bennett & Hickman, 1993; Berk, Hughson, & Vandezande, 1996). Those previous studies come from behavioral economics and are largely concerned with assessing the rationality of people’s bids.

Our research question is different: We are interested in whether it is possible to combine the knowledge of the four players to provide a good estimate of the true value of the prize. Each player is likely to have some knowledge that helps estimate a price, but it is unlikely that any player knows the exact answer. Under these circumstances, it should be possible to combine the individual knowledge to form a group answer that improves the estimate of the true value of the prize. This idea is essentially a miniature form of the “wisdom of the crowd” phenomenon, in which estimates formed by aggregating individual answers are superior to even those provided by the best individuals in the group (Surowiecki, 2004).

The wisdom of crowds is an interesting psychological phenomenon closely related to classic areas of psychological inquiry, including group decision-making (e.g., Hastie & Kameda, 2005; Kerr & Tindale, 2004), memory and knowledge representation (e.g., Altmann, 2003; Norman, Detre, & Polyn, 2008), and heuristics and biases in estimation (e.g., Gigerenzer & Todd, 1999; Kahneman & Tversky, 2000). It provides a fresh and interesting set of theoretical questions and behavioral tasks linking these sometimes disparate areas of psychology, and so has become a topic of recent research focus.1 Wisdom-of-the-crowd research within psychology has considered issues such as whether it is possible to combine multiple estimates from a single person to generate better decisions (e.g., Herzog & Hertwig, 2009; Vul & Pashler, 2008) or how to combine decisions, like rank orders or sequences of decisions, that are more complicated than a single numerical estimate (e.g., Steyvers, Lee, Miller, & Hemmer, 2009; Zhang & Lee, 2010).

The wisdom-of-the-crowd issue we address is whether combining the knowledge of Price Is Right contestants can be done most effectively by using a model of their decision-making processes. Because of the competitive nature of the task, what people say when they bid is different from what they believe the price to be. A good example is provided by the sequence of bids in Fig. 1, which comes directly from a real competition from the show. The fourth player does not bid $1 because they believe that is the value of the stereo. Rather, their bid reflects a clever strategy designed to improve their chance of winning: If Player 4 believes that the three previous bids are all likely to exceed the true price, the rules of the competition mean that the best final bid is $1.

The net effect of strategies like this is that aggregating bids by, for example, finding their average is not necessarily the best way to combine the knowledge of the contestants. Rather, the goal should be to combine the knowledge about prices that led to the observed bids. For the most useful aggregation of information across people, we have to average what they know, not what they say. This requires the ability to infer price knowledge from bid behavior, which, in turn, requires a model of the strategy or decision-making process that converted each player’s price beliefs into bids. In this sense, the applied question of aggregating bids to form accurate group estimates provides both a challenge for cognitive modeling and an opportunity to test theoretical and modeling ideas on real-world data.

In this article, we explore a set of methods for aggregating bids in the Price Is Right competition. These methods include simple heuristic and statistical methods using the bids themselves and more complicated methods based on decision-making models. We evaluate the ability of all of the approaches to estimate the true value of prizes, using a data set from the real game show, and find that the use of decision models can substantially improve aggregate estimation. We then discuss what our results mean both theoretically and practically, considering the role of decision-making models in studying group decision-making, and discuss the advantages of using competitions to extract and combine people’s knowledge.

Data

Our data are sequences of bids and true prize prices collected from 72 competitions from the U.S. version of The Price Is Right game show, screened between March and June 2009. A few competitions that included extreme outlier bids (greater than $5,000) were removed, as were those competitions in which every player bid above the true price. In the latter situation, within the game show, the competition is repeated with the same prize and same contestants, and we used the second version for our data.

Aggregation methods

We considered a total of 11 different aggregation methods as ways of using the players’ bids to form a group estimate. Seven of these methods are simple, based directly on the bids themselves. The remaining 4 come from decision-making models. Together, these aggregation methods let us begin to explore the importance of cognitive modeling in achieving the wisdom-of-the-crowd effect.

The 11 methods are summarized in Table 1, where a concrete example of their application is also shown. In particular, we detail how they combine the bids shown in Fig. 1—$650, $675, $1,100, and $1—to produce an aggregate estimate. We also measure how that estimate fares in relation to the true price of $960, in terms of both the absolute error between the estimate and the truth and the relative error (i.e., the absolute error normalized by the true price).

Table 1.

The performance of the 11 methods, in terms of absolute error and relative error, on a competition with bids of $650, $675, $1,100, and $1 and a true price of $960

Method	Description	Estimate	Abs Error	Rel Error
First bid	Use the first bid as the estimate	650	310	0.32
Second bid	Use the second bid as the estimate	675	285	0.30
Third bid	Use the third bid as the estimate	1,100	140	0.15
Fourth bid	Use the fourth bid as the estimate	1	959	1.0
Random bid	Use one of the bids at random	{650, 675, 1,100, 1}	{310, 285, 140, 959}	{0.32, 0.30, 0.15, 1.0}
Average bid	Use the average of the four bids as the estimate	607	353	0.37
Middle two	Use the average of the middlemost bids	663	297	0.31
Nonstrategic	Assume that players choose between bounds nonstrategically, and use the inferred mean between the bounds as the estimate	551	409	0.43
Nonstrategic with individual differences	Assume that players choose between different bounds centered on the same mean nonstrategically, and use the common mean as the estimate	674	286	0.30
Last player optimal	Assume first that three players choose between bounds nonstrategically but the last one bids according to probability of winning, and use the inferred mean between the bounds as the estimate	818	142	0.15
Last two players optimal	Assume that first two players choose between bounds nonstrategically but the last two bid according to their probability of winning, and use the inferred mean between the bounds as the estimate	900	60	0.06

Simple methods for aggregating

There are many obvious and simple ways to use the bids provided by contestants to estimate the price of prizes. One approach is just to take a bid directly as an estimate. This can be done separately for each of the players. It can also be done by picking a player at random, as a way of getting average performance at the level of individual bids.

Another obvious approach based on the bids is to take their arithmetic average, and the final simple approach we considered was to take the average of the middlemost two bids. That is, we removed the highest and lowest bids (as in some sports scoring systems) and averaged the remaining two, as a way of dealing with outlier bids like $1. Of course, it is easy to think of other simple methods based on the bids, but these seemed sufficient to provide a baseline level of accuracy.

Decision-model methods for aggregating

The four methods for aggregation we consider based on decision models make the same basic representational and decision-making assumptions. We now describe those assumptions and the four specific models we developed, and outline the inference process that let us apply the models to a set of bids to produce an aggregate price estimate. The Discussion section considers limitations and extensions of the basic assumptions, and the Appendix gives formal details of the decision models and inference process.

Two modeling assumptions

Our interest is whether using models of decision-making can lead to improved estimates of the true values of the prizes. To build decision models, we relied on two key assumptions. The first is that, following the basic motivation for the wisdom-of-the-crowd effect, people have shared but inexact knowledge about the prices of the prizes. To make this idea concrete, we assume that uncertain knowledge of prices can be represented by simple ranges, defined by upper and lower values that bound the true price. While this is not the only possible assumption, it is a reasonable one. People often seem to think of uncertainty in prices in terms of bounded ranges (e.g., “What is the maximum you are willing to pay?”). The bounds could be very precise, such as believing a stereo’s price is between $950 and $1,000, or they could be very broad, putting the price between $500 and $1,500. We also allow for the possibility that people’s knowledge may be quite wrong, perhaps putting the price between $200 and $500. The important aspects of the assumption are that the uncertain knowledge is in some sense shared, because there is a single true price underlying the inexact knowledge people have, and that this knowledge can be quantified by upper and lower bounds.

Our second assumption is that players make decisions in one of two ways. Perhaps they bid nonstrategically, and simply choose a number between their lower and upper bounds as their bid. Alternatively, we allowed for the possibility that some players bid strategically, according to the probability that a bid will result in them winning the competition. A look at our raw data gives reason to believe that this might sometimes be the case. For example, in 79 of the 272 competitions (about 30%), the final bid was $1 greater than the bid made by one of the previous players. This is consistent with an optimal strategy for the last player.

Of course, we do not believe that everybody who plays The Price Is Right bids optimally, nor do we believe that people are even capable, in most cases, of working out what corresponds to an optimal bid through any explicit process. But we do believe, especially for the third and fourth players in the sequence, that at least part of their bidding decisions can be understood as driven by strategies or heuristics to help them win. This position that rationality provides a framework for understanding decision-making is consistent with many previous analyses of The Price Is Right and other game shows (e.g., Gertner, 1993; Metrick, 1995). It is also consistent with recent influential work in cognitive science that has aimed for a rational or “computational-level” explanation of human cognition (e.g., Chater, Tenenbaum, & Yuille, 2006; Griffiths, Kemp, & Tenenbaum, 2008).

Four decision models

Based on these representational and decision-making assumptions, we considered four aggregation models. The first uses the simplest possible account of decision-making, which is that all four players bid nonstrategically, and so choose a random bid between the lower and upper bounds. In this account, the bounds are the same for all players.

The second model also assumes that players choose nonstrategically from their range, but it allows each player to have a different range. This approach allows for individual differences in the accuracy of players’ knowledge and assumes instead that the shared information about the true price means that each range is centered on that true price. This model is a natural adaptation of the Thurstonian model for the wisdom-of-the-crowd analysis presented by Steyvers et al. (2009).

The third and fourth models are quite different, because they allow for strategic bidding by some players. The third model assumes that Players 1–3 continue to choose nonstrategically between their bounds but that Player 4 chooses strategically. We adopt a probability-matching definition of what it means to be rational (see Vulkan, 2000). This means that Player 4 chooses a particular bid in proportion to the probability of that bid winning, based on their knowledge about the upper and lower bounds and their knowledge of the first three bids. This sort of assumption has limitations that we address in the Discussion, but it is used in some cognitive models of decision-making (e.g., Busemeyer & Stout, 2002; Griffiths & Tenenbaum, 2009; Lee & Sarnecka, 2010; Nosofsky, 1984) and is consistent with theories of decision-making by sampling (e.g., Stewart, Chater, & Brown, 2006; Vul, Goodman, Griffiths, & Tenenbaum, 2009).

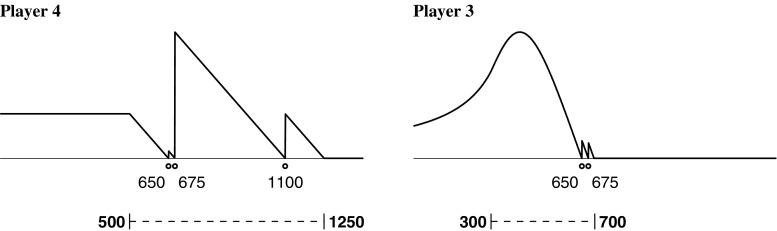
An example of strategic bidding for the fourth player in shown in the left panel of Fig. 2. The previous bids of $650, $675, and $1,100 are shown by circles. Also shown by the dashed bounded line beneath is an example of the price knowledge that the fourth player might have. In this example, the fourth player believes the prize costs between $500 and $1,250. The solid line above the bids then shows the probability that the fourth player will win for any possible bid made. This probability peaks at bids of $1 and of $1 above any of the existing bids and measures the proportion of the hypothesized true price range that falls above the bid of the fourth player and below the next highest bid. In the example in Fig. 2, the best bid the fourth player can make is $676, since it is most likely that the true price lies between $675 and $1,100, when compared to the possibilities of less than $650, between $650 and $675, and greater than $1,100.

Fig. 2.

Rational decision-making for the fourth (left panel) and third (right panel) players, given the existing bids, shown by circles, and bounded price knowledge, shown by the dashed-line interval

Our fourth and final model assumes that only the first two players choose nonstrategically and that the third and fourth bid strategically. As before, the fourth player makes a bid that maximizes their probability of winning, given all of the earlier bids. But now, the third player also bids according to their probability of winning, assuming that the fourth player is going to see their bid and then also bid strategically. An example of strategic bidding for the third player is shown in the right panel of Fig. 2. Now, only the first two bids of $650 and $675 are known, and we consider a different assumption about price knowledge, with bounds of $300 and $700. Under this scenario, the third player believes the existing bids are likely too high, but this player cannot simply bid $1, because they know that the fourth player will then immediately “cut them off” with a $2 bid. Instead, the third player must judge how low their bid can go without being “cut off.” The curve in Fig. 2 shows how this balance is reflected in the probabilities of the third player winning, and guides their strategic bidding.

Note that both of the analyses in Fig. 2 are based on the specific price range that is assumed. For other beliefs about price, what would constitute strategic behavior would be different, because the probabilities of winning with various bids would change. For example, the right panel of Fig. 2 makes it clear that if Player 3 in Fig. 1 is behaving strategically by bidding $1,100, this player does not believe the price range is anything like $300–$700. This link between latent price knowledge and observed bidding is what we exploited to do model-based inference about what people know, based on what they bid.

Aggregation by inference

All four decision models can be used in the same basic way to form an aggregate price estimate from the observed bids. The Appendix gives formal details, but the intuitions are discussed here. The key idea is to use each model to make an inference about the upper and lower bounds, based on the bids. That is, we take the assumptions made by the model about how people use the bounds to generate bids, and then invert them. Rather than starting with the bounds to generate the bids, we start with the bids to infer the bounds. This can be done using standard Bayesian statistical inference. In terms of conditional probabilities, Bayes’s theorem provides the bridge to go from the probability of bids given bounds, which is what the decision models define, to the probability of bounds given bids, which is what we want in order to form an aggregate estimate.

It is helpful to summarize how inference proceeds for the concrete example we have been using throughout, with bids of $650, $675, $1,100, and $1. For the simplest decision model, with nonstrategic bidding from a single range, the observed bids force that range to extend from $1 to $1,100. That is, the only way to explain the disparity in the bids is to infer that the players have a very uncertain knowledge, spanning all the way from the smallest to the largest bid. This leads to an inferred estimate of the price, and mean of the inferred range, of $551, as shown in Table 1.

The nonstrategic bidding with individual differences model can explain the variety of bids by inferring different ranges, but these ranges must center on the inferred true price. For the concrete example, it turns out that the inferred ranges center on $674 and extend from $650 to $698, $673 to $675, $248 to $1,100, and $1 to $1,348, respectively, for the four players. In this way, the final bid of $1 is explained as coming from a player with very poor knowledge of the true price. A natural property of the individual differences model is that bids from players with poor knowledge are “downweighted” in forming the aggregate. From this perspective, the inferred group value of $674 can be viewed as a weighted sum of the individual bids, with weights reflecting the inferred certainty of knowledge. It is also reasonable to view this weighting process as a form of model-based outlier detection, with extreme bids like $1 in the example contributing very little to the final inference.

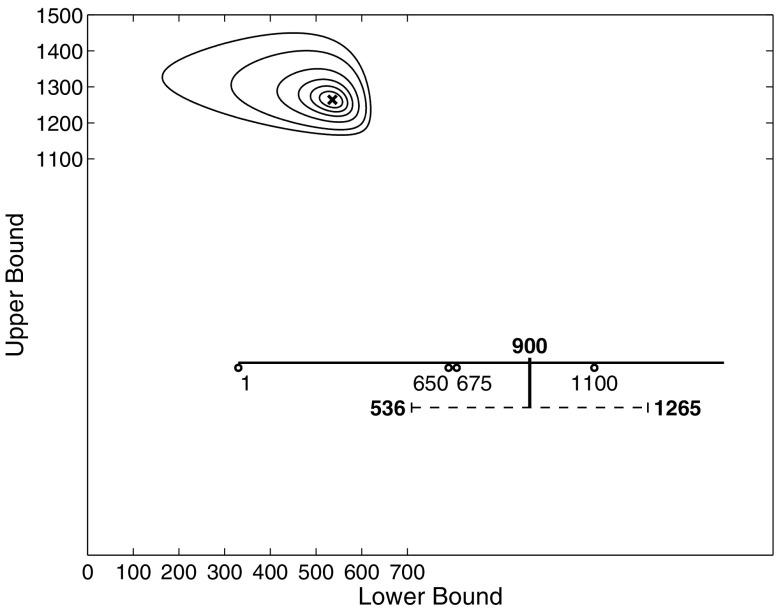
The two strategic decision models treat the extreme bids as goal-driven competitive behavior. To understand the inference process for these models, Fig. 3 summarizes the process for the model in which the final two players bid strategically. The contour plot shows the relative probability of each possible combination of lower and upper bounds producing these bids. The single most likely combination is shown by the cross and corresponds to a price range from $536 and $1,265. Given this inferred knowledge of range, it is natural to take the halfway point as the aggregate estimate of the true price, which is $900. The linear inset in Fig. 3 summarizes this analysis, showing that the decision model allows us to take the observed bids, infer the underlying knowledge about the price range that most likely generated those bids, and summarize that price range as a group estimate.

Fig. 3.

Forming an aggregate estimate from bids, based on inference using a decision-making model. The contour plot shows the distribution over inferred lower and upper bounds for the price range knowledge shared by players. The inset shows the actual bids (circles), the most likely bounds ($536 and $1,265), and the center of these price bounds ($900), which corresponds to the model-based aggregate of the bids

Results

We applied all 11 aggregation methods to all of the competitions in our data set. For each competition and each method, we measured the mean error between the aggregate estimate and the true price in the different ways presented in Table 1. The mean absolute difference quantifies how many dollars away from the true price each estimate was on average. The mean relative absolute difference quantifies the proportion of the true price that an estimate differs from the true price on average.

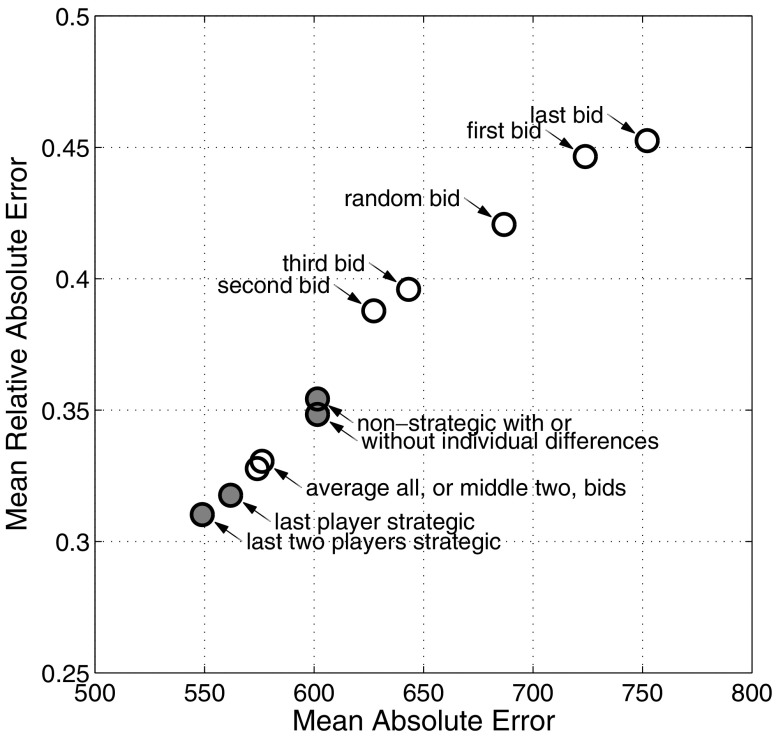
Our results are summarized in Fig. 4, which shows the performance of all 11 methods on both measures simultaneously. Obviously, lower mean and relative mean absolute deviations are better, so methods closer to the lower-left corner give more accurate estimates of the true price of the prize. Figure 4 thus reveals a clear ordering of the performance for the methods, which is robust across both measures.

Fig. 4.

Pverformance of the simple (unshaded circles) and model-based (shaded circles) methods for aggregate estimation, in terms of both mean absolute error and mean relative absolute error

The model-based approach in which the last two players bid strategically provides the best performance; the second best performance comes from assuming that only the bid of the last player is strategic. The simple approaches of averaging all bids or the middlemost two bids give extremely similar performance, and they are followed by the two model-based averaging methods (one allowing for individual differences, one not) that do not incorporate strategic bidding. All of the simple measures based on a single bid perform much worse, although there is a clear order for each player. The best individual bid comes from the second player, followed by the third, the first, and the last players.

Discussion

Present findings

There are really three factors underlying our 11 methods, and they build on each other in a logical way. The first factor is whether information is aggregated across players. The second is, if there is aggregation, whether it is done directly on the bids or on a decision-model-based inference of a latent price estimate. The third is, if there is model-based aggregation, whether people are assumed to follow a simple nonstrategic decision process or to behave strategically according to their probability of winning.

In terms of these three factors, our results show that aggregation improves performance. The best six methods all involve aggregation, and the worst five do not. This finding provides clear support for the wisdom-of-the-crowd phenomenon applying to our small groups in a competitive bidding task. The same basic conclusion was reached by Lee and Shi (2010) from controlled laboratory data, and it is interesting to see it confirmed with real-world game show data.

The second finding is that decision-model approaches can improve a simple aggregation of bids, but only if the right assumptions about the decision processes and goals are embedded within a model. The model-based averages that rely on nonstrategic decision-making (with or without individual differences) perform worse than the simple mean of the bids (or of the middlemost two bids).

Only when we assume that one or more players are bidding strategically do the decision models begin to outperform simple aggregation.

Limitations and future directions

There are three ways in which the models we chose to consider were constrained by issues of computational feasibility. The most obvious is that we never allowed the first or second players to choose strategically. The computational effort that would be involved in considering these models is prohibitive, because of the recursive nature of the optimization problem facing early players in the bidding sequence. We would like to find more efficient computational methods to explore methods assuming fully strategic bidding. We suspect that they would not improve substantially on the best model we have implemented here, because we think early players in the real Price Is Right game struggle even to approximate strategic bidding. But we might be wrong, and it would be interesting to find out.

Our assumption that uniform distributions characterize uncertainty about prices was also made partly on grounds of computational convenience. From this assumption, we were able to make some analytic derivations that helped make the inference process tractable.2 We think this is a reasonable assumption, but we would like to explore alternative representations of knowledge, such as normal distributions.

Finally, we needed the assumption of probability matching in decision-making in order to make inference tractable. In particular, we were not able to consider a model of decision-making in which players bid to maximize the probability of winning, even though this seems a compelling psychological possibility. Deterministic rules like choosing the unique maximum are not easily analyzed within the probabilistic approach to inference we have adopted. There are possible modeling solutions to this problem, involving such statistical methods as entropification (e.g., Grünwald, 1999; Lee, 2004) or an extended exponentiated version of the decision rule (e.g., Kruschke, 1992; Lee & Vanpaemel, 2008), but they present significant computational challenges.

Beyond these technical challenges, there are other extensions, refinements, and improvements to our approach that are also worth trying. Almost all of our basic assumptions—that players have a common belief about the price distribution, that beliefs center on the true price, or that players choose their bids based entirely on either strategic or nonstrategic bases—could be improved. We would like to extend our ability to allow for more detailed forms of individual differences in knowledge, especially in the models using strategic bidding.

Applications and implications

While The Price Is Right game show is geared toward entertainment, it does raise issues that are relevant for important applied problems. The competitive nature of the estimation task mirrors such real-world devices as auctions (e.g., Krishna, 2002) and prediction markets (e.g., Christiansen, 2007) for estimating values and probabilities. In such contexts, we think our results support the idea that competition is an effective way to extract information from people. Often expertise needs to be combined in situations where there are only a few experts and their knowledge is not independent. In the military, a few domain experts might be asked to estimate how many missiles an enemy country has, and their estimates will be based on shared intelligence information. In business, estimating the probability a merger will be successful might be a task given to a few key managers, and their advice will be based on similar training and data. Under such circumstances, the large-scale aggregation and independence assumptions for standard wisdom-of-the-crowd effects do not apply. Our case study suggests that competitions between the few experts might be an effective way of combining their knowledge.

Theoretically, we think our results give some credence to the idea that finding the wisdom in crowds will often require theories and models from the cognitive sciences. Sometimes the wisdom-of-the-crowd effect is viewed as a statistical one, involving the amplification of signal and removal of noise by statistical methods. What this perspective misses is that the observed data in wisdom-of-the-crowd studies are very often estimates, judgments, preferences, bids, opinions, or guesses made by people. This means that the available data can be best understood through the window of goal-directed human decision-making. Indeed, most generally, we think the present study highlights a general malaise in how cognitive psychology treats its relationship to statistics, machine learning, and other fields that adopt quantitative approaches to decision-making and inference. Too often, we think, psychology does not become involved in problems where its contribution could be critically useful.

A good example of this issue is provided by a recently finished Netflix competition. Netflix is a company that rents DVD movies to customers, who provide ratings of the movies they watch. Using these data, Netflix uses a statistical model to provide recommendations of other movies a user is likely to rate highly. The Netflix competition involved large cash prizes—including a grand prize of one million dollars—for quantitative methods that significantly improved recommendation accuracy, based on a corpus of real rating data. We think that, in large part, the Netflix competition asked a fundamentally psychological question—how people rated richly structured aesthetic stimuli—and offered a million-dollar reward for predictive capabilities based on understanding this process. Yet, with perhaps one notable exception (Potter, 2008), the entrants to the competition were primarily trained in, and applied, nonpsychological methods from statistics and machine learning.

Against this context, we think the present study supports a different perspective. Our ability here to apply cognitive decision models and thereby achieve better aggregate price estimates from competitive Price Is Right bids shows the fundamental role of psychological models in complicated applied statistical problems involving people. Most especially, we think that research into wisdom-of-the-crowd phenomena should not just be a domain for the development and application of innovative and useful statistical methods, but also a motivating problem for the understanding of human cognition and decision-making.

Appendix

In this appendix, we formalize the decision-making models, and how they are used to infer group estimates. The decision models we used for inference make two key classes of assumption. The first is a representational assumption, which is that all of the players have partial knowledge of the price of a prize and that their uncertainty can be represented by the same upper and lower bounds u and l. The second is a decision-making assumption, which is that players either bid strategically, according to their probability of winning the game, or nonstrategically, choosing a number consistent with their knowledge but independent of other bids. For each decision-making model, our inferential goal is to find the mean of the upper and lower bounds, since it represents the average price based on the players’ knowledge.

Nonstrategic bidding

Both of the nonstrategic models are straightforward. If the xth player believes that the true price lies between a lower bound l _x and an upper bound u _x, then every choice between those bounds is equally likely. Thus, the probability that the xth player will bid y, for all possible bids l _x ≤ y ≤ u _x, is

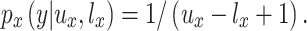For the first model, where each player has the same knowledge, l _x and u _x are the same for all players. The extension to individual differences in the second model means that there is a common mean, μ, but a separate range r _x for the xth player, so that l _x = max(1, μ − r _x) and u _x = min(5,000, μ + r _x).

Optimal bidding

Modeling strategic bidding is more complicated. Our approach is similar to that presented by Lee and Shi (2010), but different in several important ways. The first difference is that we assume that people’s knowledge of prices is defined by upper and lower bounds, rather than by normal distributions. A second difference is that we consider mixtures of strategic and nonstrategic bidding, rather than just strategic bidding. A final difference is that our analyses extend to the 4 participants in a Price Is Right game, rather than the 3 participants in the laboratory data collected by Lee and Shi (2010).

Win functions

Formally, given u and l, we can define a “win” function w _x(a, b, c, d, u, l) for the probability that the xth player will win, given bids a, b, c, and d for Players 1, 2, 3, and 4, respectively. This win probability is just the area under the uniform distribution between the bid of the xth player and the next highest bid (or the maximum possible bid, if it is the highest bid).

A concrete example is given in Fig. 5, using the bids 650, 675, 1,100, and 1 in the case where the true price distribution is between 500 and 1,250. Under these circumstances, the fourth player (bidding $1) will win if the true price turns out to be below $650. Given the belief about where the true price may fall, this means that 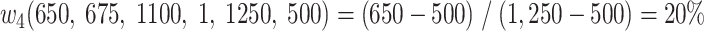. The probabilities for the other bids are found similarly and are shown in Fig. 5. Note that the win function captures the “closest without going over” rule of the competition. Different rules, such as simply being as close as possible to the true price or being as close as possible without going under, could be considered by changing the win function appropriately.

Fig. 5.

The win function probabilities for bids of 1, 650, 675, and 1,100 when the price distribution is bounded between 500 and 1,250

Decision-making

On the basis of the win function, we can formalize what constitutes strategic decision-making for each player. Player 4 knows about the existing bids a, b, and c, so the probability that this player will win if they made the bid d is just

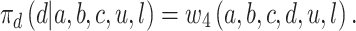Thus, formalizing what it means to be a strategic player in terms of probability matching, they will choose according to these probabilities, so that

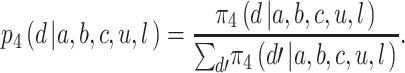The analysis is a little more complicated for Player 3. They know only about the earlier bids a and b but can assume that if they bid c, Player 4 will subsequently behave strategically and bid according to p ₄(d | a, b, c, u, l) above. Under this assumption, the probability of Player 3 winning by bidding c is

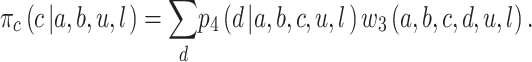So, Player 3 will bid according to the probabilities

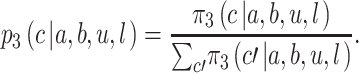It is straightforward to derive strategic decision-making for Players 1 and 2 using the same conceptual approach, but as we noted, these derivations proved too hard for our inference calculations.

Final inference

The different decision-model methods we consider make different assumptions about whether each player makes nonstrategic or strategic choices. Given these assumptions, our goal is to make an inference about an underlying “group” value based on the observed bids. We do this using the joint posterior distribution over the upper- and lower-bound parameters that represent people’s knowledge. This is given by Bayes’s rule as

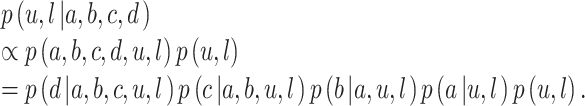We put a simple flat prior on p(u, l), and all of the other likelihood terms are available from the decision-making models—either nonstrategic or strategic—used by the model for each player.

There are many potential ways that p(u, l | a, b, c, d) could be used to estimate the final group price. We use a simple but reasonable approach, first finding the mode (u*, l*) | a, b, c, d, which gives the most likely values for the bounds, and then using the midpoint of these bounds (u* + l*)/2 as the group estimate.