Inflow-based Vascular-Space-Occupancy (iVASO) MRI

Abstract

Vascular-space-occupancy (VASO) MRI, a blood nulling approach for assessing changes in cerebral blood volume (CBV), is hampered by low SNR because only 10-20% of tissue signal is recovered when using non-selective inversion for blood nulling. A new approach, called inflow-VASO (iVASO), is introduced in which only blood flowing into the slice has experienced inversion, thereby keeping tissue and CSF signal in the slice maximal and reducing CSF partial volume effects. SNR increases of 198±12% and 334±9% (mean±SD, n=7) with respect to VASO were found at TR values of 5s and 2s, respectively. When using inflow approaches, data interpretation is complicated by the fact that signal changes are affected by vascular transit times. An optimal TR-range (1.5-2.5s) was derived in which the iVASO response during activation predominantly reflects arterial/arteriolar CBV (CBV_a) changes. In this TR-range, perfusion contributions to the signal change are negligible because arterial label has not yet undergone capillary exchange, and arterial and precapillary blood signals are nulled. For TR=2s, the iVASO signal change upon visual stimulation corresponded to a CBV_a increase of 58±7%, in agreement with arteriolar CBV changes previously reported. The onset of the hemodynamic response for iVASO occurred 1.2±0.5s (n=7) faster than for conventional VASO.

Introduction

Vascular-space-occupancy (VASO) MRI is an approach in which cerebral blood volume (CBV) changes are assessed by nulling blood signal (1). In VASO, a spatially non-selective inversion pulse is followed by a delay time (TI) after which the longitudinal magnetization of blood is expected to be zero, while that of tissue is slightly positive. Detection at this time point leads to a negative VASO fMRI signal change (ΔS/S) during vascular dilatation, attributed to a decrease in the detectable tissue signal consequential to the CBV increase (1).

One major disadvantage of VASO MRI is its low signal to noise ratio (SNR), because only 10-20% of gray matter magnetization is recovered at the TI for blood nulling at 3T. At higher fields, residual tissue signal will be even lower since the longitudinal relaxation times (T₁) of blood and tissue water increase and the signal difference between tissue and blood reduces at the time of blood nulling (2). The dependence of VASO MRI on the T₁ relaxation time of tissue also confounds the detection of blood volume effects in cases where this T₁ would change, e.g. for certain pathological conditions. A third point of concern for VASO MRI is whether blood signals in capillaries and draining venules and veins are actually nulled, which is uncertain in view of exchange occurring between capillaries and tissue that may affect the T₁ of postcapillary blood. Fourth, the VASO signal change is strongly affected by the presence of cerebrospinal fluid (CSF) (3). Finally, the conventional VASO effect reflects total CBV change. Recent brain physiology studies during functional activation point to larger relative increases in blood volume in arterioles (33-79%) (4-12) than in capillaries and venules (5,6,8,9,12,13). The design of an MRI method sensitive mainly to arterial blood volume (CBV_a) changes could be a useful tool for physiological and functional studies.

Here we show that VASO experiments can be performed while retaining maximum tissue signal by inverting the blood water spins outside the imaging slice and acquiring images when the spins flowing into the slice are nulled. The pulse sequence is similar to the double inversion recovery (DIR) technique used in MR angiography (MRA) for coronary and carotid imaging (14). What is different when studying brain microvasculature compared to large vessels is that the blood velocity is much slower and the blood nulling efficiency and location will depend on the relationship between inversion nulling time and vascular transit time. The vascular territory to be nulled can be regulated experimentally by adjusting the TR-based steady-state blood nulling time (TI) or the gap between the detection slice and the inversion labeling plane. The arterial transit time is the sum of the times for inverted blood water spins to reach the imaging slice (Δ) and perfuse the arterioles (δ_a). In the visual cortex, even during activation, this time has been measured to be longer than 800ms (Table 1 (10,15-18)), which is in the range of the TI values (300-1150ms) used in VASO MRI (19), allowing regulation of the spatial extent of the blood nulling. The new VASO approach, dubbed inflow VASO or iVASO, is based predominantly on arterial and arteriolar blood nulling by keeping TI below Δ+δ_a. Here we demonstrate the principles of the iVASO approach during visual activation at 3T, where vascular expansion is expected to be restricted mainly to the microvasculature, as well as during hyper- or hypocapnia, between which CBV changes are of opposite sign. A theoretical framework is developed to describe the dual influence of transit time and CBV, and to derive an optimal TI/TR-range for dominant arterial/arteriolar CBV (CBV_a) effects. This work has been partially published in abstract form (20).

Table 1.

Literature data on arterial transit times^* in human visual cortex.

Gap a (mm)	baseline (ms)			activation (ms)			Ref.
	Δ	δ a	Δ + δa	Δ	δ a	Δ + δa
5	420±80			380±80			(16)
6	423±33	573±62	996±70	340±78	495±52	835±94	(10)
30	540±20						(18)
41			1393.4±116.7b				(17)
45	607±320			446±234			(15)

^*Δ = time needed for inverted blood to traverse the gap between inversion and image planes; δ_a = mean time for blood to traverse the arterial compartment in region of interest before reaching capillaries. The sum of the two (Δ + δ_a) is defined as the arterial transit time.

^agap between inversion and image planes

^bOnly the sum of Δ and δ_a was reported.

Materials and Methods

Pulse sequences

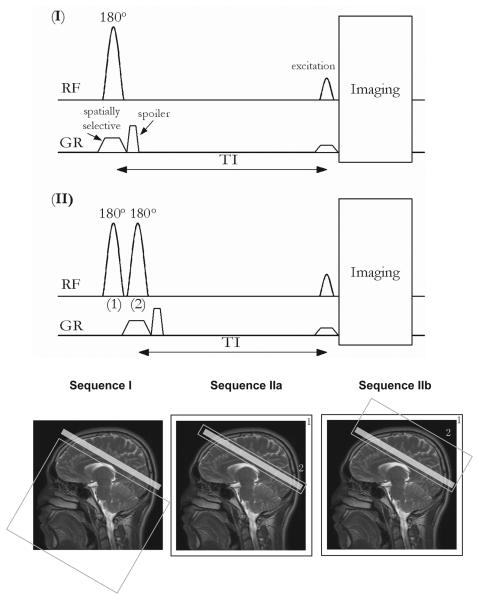
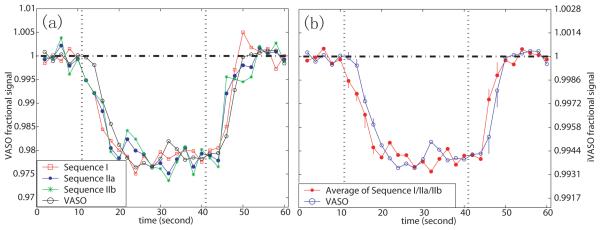
Two possible iVASO schemes are illustrated in Fig.1. In Scheme I (slab-selective iVASO), a slice-selective adiabatic inversion inverts a slab directly beneath the imaging slice. In Scheme II (flip-back iVASO), non-selective adiabatic inversion is followed by slice-selective adiabatic inversion of spins within the imaging slice. In Sequence IIa only the image slice is flipped back, while, in Sequence IIb, a larger volume covering the imaging slice and the superior brain is flipped back. For proper blood nulling in all iVASO sequences, it is important to assure that inflowing blood water spins have reached steady state when they enter the imaging slice. Based on recent work, steady state can be achieved in visual cortex as long as the inversion slab extends more than 150mm below the imaging slice (21), which is achieved when using the body coil for transmission, as done in all of our experiments here.

Fig. 1.

Pulse sequences and spatial depictions of possible iVASO labeling schemes, where blood flowing into the slice is inverted and subsequently nulled through appropriate choice of TI. “RF” and “GR” indicate radio frequency and gradient pulses, respectively. The light-gray shaded box on the image indicates the imaging slice. The box labeled “1” outside the image (sequences IIa and IIb) indicates spatially non-selective inversion. Gray boxes (non-shaded) within the images outline spatially selective inversion. Sequence I: slab-selective inversion below the imaging slice. Sequence IIa: spatially non-selective inversion (“1”) followed by slice-selective flip-back (“2”) over the imaging slice. Sequence IIb: spatially non-selective inversion (“1”) followed by slab-selective flip-back (“2”) covering the imaging slice and the brain above. In all sequences, imaging is initiated at nulling time TI. A spoiler gradient is applied to eliminate the residual transverse magnetization. Note that the sizes of slabs/slices in the figure do not represent the exact geometry used in our experiments, which is described in Methods.

The inversion schemes in iVASO resemble those used in the labeling scans of existing pulsed ASL techniques. These are EPISTAR (22), PICORE (23) and DIPLOMA (24) for sequence I, and UNFAIR (25,26), EST (27) and IDOL (28) for sequence II. However, ASL and iVASO differ fundamentally with respect to their contrast mechanisms. ASL measures tissue perfusion (i.e. cerebral blood flow (CBF)), which is defined as the amount of blood water that is delivered into tissue per unit time, based on the exchange between magnetically labeled blood water spins and tissue spins in the capillary bed, and usually eliminates the unwanted arterial blood effects by applying crusher gradients or a long post-labeling delay (29-31). On the other hand, depending on the TI values used, iVASO can be sensitized predominantly to arterial and arteriolar blood effects, where no exchange between blood and tissue water can occur due to limited permeability of the vessel wall. In addition, the inflowing blood magnetization is always nulled at the time of detection, thus avoiding unwanted signal contributions from potential changes in the concentration of labeled blood water spins upon neuronal activation.

Theory

When discussing CBV effects, the terminology is often confusing between macro- and microvasculature. We define CBV (ml blood/ml parenchyma) as microvascular blood volume, with the term microvasculature representative of blood vessels that can dilate or constrict, i.e. arterioles, capillaries and venules. Of these, the capillaries are the only vasculature where exchange with tissue can occur. In iVASO, which employs inflow labeling, the effects measured will depend on the relationship between the time of measurement and the time of label arrival, the so-called arterial transit time (7) or capillary arrival time. This is the sum of the time needed for the leading edge of inverted blood to reach the imaging slice, Δ, and the mean time for blood to traverse the arterial compartment before entering the capillaries, δ_a. Typical arterial transit times in visual cortex (10,15-18) range from 800–1400ms (Table 1), which is of comparable magnitude to the blood nulling inversion times (TI) used in VASO MRI at 3T (19). Therefore, in iVASO, if TI is set in a range shorter than or close to arterial transit times, the amount of blood nulled reflects predominantly arterial blood volume effects.

I. Steady state magnetization in blood and tissue compartments

In iVASO, the steady state magnetizations for inflowing (before-slice) and in-slice blood water spins differ. Depending on the inversion volume (we use the body coil), TR, and blood velocity, the inflowing blood may have experienced several inversion pulses before reaching the slice. When the inversion volume is sufficiently large (21), the steady state for inflowing blood water magnetization at TI after multiple inversions is (see Appendix I):

$$M_{\mathit{ss},\mathit{inv}}\left(TI\right)=M_0\left(1-2e^{-\mathit{TI}∕T_{1b}}+e^{-\mathit{TR}∕T_{1b}}\right)/\left(1+e^{-\mathit{TR}}∕T_{1b}\right)$$ [1]

in which M₀ is the equilibrium magnetization and T_1b the longitudinal relaxation time of blood, assumed to be the same for arterial, capillary and venous blood compartments, which is reasonable within error at 3T (32). On the other hand, the in-slice blood magnetization is only affected by the excitation pulses for readout. The steady state signal for these spins is (see Appendix I):

$$M_{\mathit{ss},\mathit{ex}}=M_0(1-e^{-\mathit{TR}∕T_{1b}})$$ [2]

Eq. [2] applies to capillary and venular blood when TI ≤ Δ +δ_a (no inverted blood has reached capillaries and venules).

Using Eqs. [1,2], we can derive the steady state signal equations (Table 2) for blood during the three relevant time periods, namely for blood nulling before the slice is reached (TI < Δ), during arteriolar transit (Δ < TI < Δ + δ_a), and after arteriolar transit (TI > Δ + δ_a). This is done for the three microvascular blood compartments: arterioles (“a”), capillaries (“c”), and venules (“v”). Notice that the TI for blood nulling can never be more than 1.13s (when TR is infinitely long) at 3T. In view of the arterial transit times for GM in Table 1 (≈ 800ms during activation and ≈ 1000ms at baseline), the capillary compartment, which takes about 500-1000ms to traverse (33,34), can only be partially nulled, while the venular compartment is not nulled. At longer TRs, the inflowing blood enters the capillary bed, which may cause a small tissue perfusion contribution. Table 2 also contains the steady state equations for extravascular tissue (i.e. parenchyma without blood) and CSF. To determine the parenchymal iVASO signal changes, the relevant contributions from the different compartments (rows) need to be added. For instance, for Δ ≤ TI ≤ Δ + δ_a, this will be the residual arterial signal, all of the capillary and venular signal, and the gray matter (GM) tissue signal.

Table 2.

Steady state expressions¹,² for MRI signal (S) in iVASO and VASO³ experiments.

Signal Origin	TI < Δ	Δ ≤ TI ≤ Δ + δa	Δ + δa ≤ TI ≤ Δ + δa + δc
BLOOD
iVASO
a, nulled4	0	$\left(\frac{\mathit{TI}-\mathrm{\Delta }}{{\delta }_a}\right){\mathit{CBV}}_a{C}_b{M}_0\left(\frac{1-2e^{-\mathit{TI}∕T_{1b}}+e^{-\mathit{TR}∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)$	${\mathit{CBV}}_a{C}_b{M}_0\left(\frac{1-2e^{-\mathit{TI}∕T_{1b}}+e^{-\mathit{TR}∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)$
a, residual5	CBVaCbM0(1 − e−TR/T1b)	$\left(\frac{{\delta }_a-(\mathit{TI}-\mathrm{\Delta })}{{\delta }_a}\right){\mathit{CBV}}_a{C}_b{M}_0\left(1+e^{-\mathit{TR}∕T_{1b}}\right)$	0
c, nulled4	0		$\left(\frac{\mathit{TI}-\mathrm{\Delta }-{\delta }_a}{{\delta }_c}\right){\mathit{CBV}}_c{C}_b{M}_0\left(\frac{1-2e^{-\mathit{TI}∕T_{1b}}+e^{-\mathit{TR}∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)$
c, residual5	CBVcCbM0(1 − e−TR/T1b)		$\left(\frac{{\delta }_c-(\mathit{TI}-\mathrm{\Delta }-{\delta }_a)}{{\delta }_c}\right){\mathit{CBV}}_c{C}_b{M}_0\left(1+e^{-\mathit{TR}∕T_{1b}}\right)$
v, residual5	CBVvCbM0(1 − e−TR/T1b)
VASO nulled4	CBV * CbM0(1 − 2e−TI/T1b + e−TR/T1b)
Tissue
iVASO5	(Ctis − CBV * Cb)M0(1 − e−TR/T1tis)
VASO6	(Ctis − CBV * Cb)M0(1 − 2e−TI/T1tis + e−TR/T1tis)
CSF
iVASO	CCSFM0(1 − e−TR/T1CSF)
VASO	CCSFM0(1 − 2e−TI/T1CSF + e−TR/T1CSF)

a: arteriolar; c: capillary; v: venular; b: blood; tis: tissue (GM or WM), which is defined as parenchyma without blood contribution. C_i is the water density in ml water/ml compartment volume, summarized in Table 3. CBV = CBV_a + CBV_c + CBV_v.

¹All terms need to be multiplied by their compartmental T₂ contribution (e^−TE/T_2i, in which i = b, tis, CSF).

²A single longitudinal relaxation time, T_1b, is used for all blood compartments.

³In VASO experiments, negligible exchange between blood and tissue is assumed.

⁴Parenchymal signal reduction due to blood nulling.

⁵Terms contributing to parenchymal MRI signal in iVASO.

⁶Parenchymal MRI signal in VASO.

II. Relative signal change during functional activation in GM parenchyma

The relative signal change (ΔS/S) in GM parenchyma (blood+tissue) between baseline (base) and activation (act) can be calculated using the expressions in Table 2. In general, the iVASO ΔS/S following activation reflects alterations in CBV_a and the transit delays Δ and δ_a, making the effect TR/TI dependent. A simplified analytical expression for ΔS/S can be derived for 1s<TR<3s, approximately Δ < TI < Δ + δ_a. Starting from the full equations for GM signal in Table 2 and assuming that: (1) the effects from the T₂ terms (mainly BOLD effect) are negligible for short TE (≤6ms); (2) the term $\left[C_{\mathit{GM}}-{\mathit{CBV}}_{\mathit{GM}}^{\mathit{base}}\cdot C_{\mathit{blood}}\right]\cdot \left(1-e^{-\mathit{TR}∕T_{1\mathit{GM}}}\right)$, which is an order greater than the other terms, dominates the denominator; and (3) for TR>1s, the term (e^−TR/T_1GM− e^−TR/T_lb) is negligible compared to (1−e^−TR/T_1b), we can derive:

$$\begin{array}{cc}\hfill \frac{\mathrm{\Delta }{S}_{\mathit{GM}}}{S_{\mathit{GM}}^{\mathit{base}}}& =\frac{\left[\left({\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\right)+{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}\left(\mathit{TI}-{\mathrm{\Delta }}^{\mathit{base}}-{\delta }_a^{\mathit{base}}\right)∕{\delta }_a^{\mathit{base}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\left(\mathit{TI}-{\mathrm{\Delta }}^{\mathit{act}}-{\delta }_a^{\mathit{act}}\right)∕{\delta }_a^{\mathit{act}}\right]\cdot C_{\mathit{blood}}\cdot \left(1-e^{-\mathit{TR}∕T_{1b}}\right)}{\left[C_{\mathit{GM}}-{\mathit{CBV}}_{\mathit{GM}}^{\mathit{base}}\cdot C_{\mathit{blood}}\right]\cdot \left(1-e^{-\mathit{TR}∕T_{1\mathit{GM}}}\right)}\hfill \\ \hfill & =\frac{\left[{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}\left(\mathit{TI}-{\mathrm{\Delta }}^{\mathit{base}}\right)∕{\delta }_a^{\mathit{base}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\left(\mathit{TI}-{\mathrm{\Delta }}^{\mathit{act}}\right)∕{\delta }_a^{\mathit{act}}\right]\cdot C_{\mathit{blood}}\cdot \left(1-e^{-\mathit{TR}∕T_{1b}}\right)}{\left[C_{\mathit{GM}}-{\mathit{CBV}}_{\mathit{GM}}^{\mathit{base}}\cdot C_{\mathit{blood}}\right]\cdot \left(1-e^{-\mathit{TR}∕T_{1\mathit{GM}}}\right)}\hfill \end{array}$$ [3a]

When choosing a suitable TI that zeroes the term ${\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}\left(\mathit{TI}-{\mathrm{\Delta }}^{\mathit{base}}-{\delta }_a^{\mathit{base}}\right)/{\delta }_a^{\mathit{base}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\left(\mathit{TI}-{\mathrm{\Delta }}^{\mathit{act}}-{\delta }_a^{\mathit{act}}\right)/{\delta }_a^{\mathit{act}}$, Eq. [3a] becomes:

$$\frac{\mathrm{\Delta }{S}_{\mathit{GM}}}{S_{\mathit{GM}}^{\mathit{base}}}=\frac{\left({\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\right)\cdot C_{\mathit{blood}}\cdot \left(1-e^{-\mathit{TR}∕T_{1b}}\right)}{\left(C_{\mathit{GM}}-{\mathit{CBV}}_{\mathit{GM}}^{\mathit{base}}\cdot C_{\mathit{blood}}\right)\cdot \left(1-e^{-\mathit{TR}∕T_{1\mathit{GM}}}\right)}$$ [3b]

This means that when the TR-based TI is adjusted so that the amount of residual arterial blood (not nulled) is the same during baseline and activation, the signal change in iVASO is proportional to the real CBV_a change. The “optimal” TI needed to achieve this is:

$$\begin{array}{cc}\hfill {\mathit{TI}}_{\mathit{optimal}}& =\frac{{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}\cdot ({\mathrm{\Delta }}_{\mathit{GM}}^{\mathit{base}}+{\delta }_{a,\mathit{GM}}^{\mathit{base}})\cdot {\delta }_{a,\mathit{GM}}^{\mathit{act}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\cdot ({\mathrm{\Delta }}_{\mathit{GM}}^{\mathit{act}}+{\delta }_{a,\mathit{GM}}^{\mathit{act}})\cdot {\delta }_{a,\mathit{GM}}^{\mathit{base}}}{{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{base}}\cdot {\delta }_{a,\mathit{GM}}^{\mathit{act}}-{\mathit{CBV}}_{a,\mathit{GM}}^{\mathit{act}}\cdot {\delta }_{a,\mathit{GM}}^{\mathit{base}}}\hfill \\ \hfill & =\frac{f_{\mathit{GM}}^{\mathit{base}}\cdot ({\mathrm{\Delta }}_{\mathit{GM}}^{\mathit{base}}+{\delta }_{a,\mathit{GM}}^{\mathit{base}})-f_{\mathit{GM}}^{\mathit{act}}\cdot ({\mathrm{\Delta }}_{\mathit{GM}}^{\mathit{act}}+{\delta }_{a,\mathit{GM}}^{\mathit{act}})}{f_{\mathit{GM}}^{\mathit{base}}-f_{\mathit{GM}}^{\mathit{act}}}\hfill \end{array}$$ [4a]

where

$$f={\mathit{CBV}}_a∕{\delta }_a$$ [4b]

The quantity f represents CBF if CBV_a is arteriolar CBV (7,10,29). This TI, and the corresponding TR will be called optimal TI/TR in the following text. Under this “optimal” condition, the signal change in iVASO reflects a predominant CBV_a change, i.e. ΔS_GM ~ ΔCBV_a,GM. Equations [3] and [4] are useful for the estimation of relative CBV_a changes. Several potential confounding factors are further discussed in Simulations and Discussions.

III. Partial volume effects

The expressions in Table 2 for tissue apply to both GM and white matter (WM). The arterial transit time for WM (35) is longer than the inversion times used in iVASO and no contributions are expected from this compartment, except for a reduction of the overall iVASO signal change due to partial volume effects. To account for these, the theory can be extended to a multi-compartment model (19). For voxels consisting of GM parenchyma, WM parenchyma, and CSF, the total signal is:

$$S_{\mathit{Total}}=(1-X_{\mathit{CSF}}-X_{\mathit{WM}})\cdot S_{\mathit{GM}}+X_{\mathit{WM}}\cdot S_{\mathit{WM}}+X_{\mathit{CSF}}\cdot S_{\mathit{CSF}}$$ [5]

in which X_i and S_i are the compartmental fractions and signal intensities, respectively.

IV. Comparison with VASO fMRI

To allow comparison of iVASO with VASO fMRI, Table 2 also lists the steady state equations for VASO. From these, ΔS/S in VASO can be derived to be (1):

$$\frac{\mathrm{\Delta }{S}_{\mathit{GM}}}{S_{\mathit{GM}}^{\mathit{base}}}=\frac{\left({\mathit{CBV}}_{\mathit{GM}}^{\mathit{base}}-{\mathit{CBV}}_{\mathit{GM}}^{\mathit{act}}\right)\cdot C_{\mathit{blood}}}{\left(C_{\mathit{GM}}-{\mathit{CBV}}_{\mathit{GM}}^{\mathit{base}}\cdot C_{\mathit{blood}}\right)}$$ [6]

The signal change in VASO is proportional to total CBV change during activation. It has been demonstrated that CBF alteration during activation also influences the VASO contrast at short TR, which makes ΔS/S in VASO TR dependent as well. The readers are referred to the work from Donahue et al (19) for the details of the VASO theory including CBF effects.

Simulations

The parameters used in simulations are summarized in Table 3. In addition, baseline CBV_a, CBV_c, and CBV_v were taken as 21%, 33%, and 46% of total CBV (36,37). Arteriolar dilation during neuronal activation has been reported to be 33-79% in the cortex (4-12). Therefore, we assumed an overall increase in CBV of 25% during activation, consisting of a 60% $(\mathrm{\Delta }{\mathit{CBV}}_a∕{\mathit{CBV}}_a^{\mathit{base}})$ increase in CBV_a (4), a 20% $(\mathrm{\Delta }{\mathit{CBV}}_c∕{\mathit{CBV}}_c^{\mathit{base}})$ increase in CBV_c (33,34), and the remaining 12% $(\mathrm{\Delta }{\mathit{CBV}}_v∕{\mathit{CBV}}_v^{\mathit{base}})$ increase in CBV_v. The arterial transit times from visual activation studies in (10) were used (Table 1), as the experimental settings (the gap between label and imaging slices) were comparable. The capillary transit time (δ_c) was assumed to be 900ms at baseline (33) and 578ms during activation (34). Transit times may not be uniform across voxels as the regional vascular geometry in the cortex varies. Nevertheless, they have generally been found to differ significantly only between separate brain lobes (17,18,23,38), since nearby regions within a lobe are supplied with shared upstream arteries and arterioles, and a variation of less than 100ms is commonly observed (18,38). We therefore simulated ΔS/S for arterial transit times 100ms longer or shorter than the mean values used. In the VASO simulations, GM CBF values at baseline and during activation were assumed to be 55 and 85ml/100g/min, respectively (19).

Table 3.

MR constants and physiological parameters used in the simulations.

	T1 (ms)	T2 (ms)		C (ml water /ml tissue)	X (%)	CBV (ml blood /ml parenchyma)
		base.	act.			base.	act.
GM	1209a	70.8c	71.4c	0.89e	84.5c	0.0525c	0.0655f
WM	758a	81a	81a	0.73e	5c	0.0210c	0.0210c
CSF	4300a	1442c	1442c	1c	10.5c
Arterial blood	1627b	102d	102d	0.87e		0.0110g	0.0176h
Capillary blood	1627b	63.3d	80.1d	0.87e		0.0173g	0.0208h
Venous blood	1627b	36.2d	55.3d	0.87e		0.0242g	0.0271h

^aLu et al. (62).

^bLu et al. (32). No significant difference was found between arterial and venous blood.

^cDonahue et al. (19). The GM T₂ values are for extravascular tissue only, not including the blood compartment.

^dZhao et al. (63), based on oxygenation levels at baseline/activation of: arterial = 98%/98%, capillary = 77%/85%, venous = 61%/73%.

^eHerscovitch et al. (64).

^fA 25% total CBV change is assumed.

^gVolume fractions: arteriolar, capillary, venular = 21%, 33%, 46%, are assumed (36,37).

^hA 60% increase in CBV_a (4), a 20% increase in CBV_c (33,34), and the remaining 12% increase in CBV_v are assumed.

To investigate partial volume effects from WM and CSF, we assumed 5% WM and 10.5% CSF volume (Table 3), based on work by Donahue et al. (19). Currently it is not entirely clear whether local CSF volume changes occur in the cortex during neuronal activation. Several studies have reported different results: in human visual cortex, no significant change (19) and 5-6% decrease in CSF volume from a 20×20×20mm³ voxel (39) during visual stimulation, increase of 2% during hypercapnia (3), and most recently, in cat visual cortex 2.45% CSF volume reduction during activation (40). We therefore simulated four cases (no change, +2%, −2% and –6%) to get an impression of possible CSF influences. To demonstrate the TR dependence of the signal change, all simulations are carried out with TR ranging from 1ms to 10s with a step of 500ms, while keeping TE fixed at 6ms.

MRI

Experiments were performed on a 3.0 Tesla (3T) MRI scanner (Philips Medical Systems, Best, The Netherlands), using body coil (approximately 650mm in length) transmit and 8-channel head coil receive. Four functional experiments were conducted per subject in a pseudo-randomized order: 1) Sequence I: inversion slab thickness=150mm, gap between the leading edge of the inversion slab and the bottom edge of the imaging slice=10mm; 2) Sequence IIa: flip-back slab thickness=23mm (thick enough to ensure complete inversion in the slice and keeping the gap the same as the other sequences); 3) Sequence IIb: flip-back slab thickness=80mm, trailing edge of the flip-back slab is 10mm (the gap) beneath the imaging slice; 4) VASO with a non-selective adiabatic inversion. For all sequences, the inversion volume for both non-selective and slab-selective inversion were sufficiently large (>150mm beneath imaging slice) to ensure a steady state for inflowing blood water spins entering the imaging slice, according to the recent work by Donahue et al. (21). A single-shot turbo spin echo (TSE) readout with a low-high profile order (lower frequency k-space lines acquired first) was employed to minimize the fat shift artifact typically seen in single-shot gradient echo (GE) echo planar imaging (EPI) readout and to reduce extravascular BOLD signal contamination (41). Three TRs were used: TR/TI=5000/1054ms, 2000/711ms, 1000/424ms. The blood nulling times (TI) were calculated using a blood T₁ of 1627ms (average of arterial and venous blood T₁). Note that arterial and venous T₁ values at 3T are not significantly different (32) and that both signals are sufficiently nulled in VASO and arterial signal is nulled in iVASO. Only one TR was used per session and the three sets of experiments for each subject were conducted on different days. In addition, in order to compare signal changes between different TR/TI combinations within the same regions of interest, functional experiments using iVASO sequence IIb with all three TR/TI combinations were performed (n=2) during the same session. Other common imaging parameters were: TE=5.9ms, flip angle (FA)=90°, imaging matrix=64×64, voxel volume=3 × 3 × 3mm³, reconstruction matrix=256×256, single-slice, SENSE=2.5, halfscan=0.525. First-order volume shimming was employed to establish a homogenously shimmed area throughout the coil, which is needed to have all tissue resonate within the applied inversion bandwidth. Each functional experiment was 4′30”, during which 54/135/270 images were acquired for TR=5000/2000/1000ms.

The profiles of spatially selective inversion pulses are extremely important in this method. As the inversion slab becomes thicker, the transition ramp (distance between the completely inverted region and the unaffected region) widens. We therefore used frequency offset corrected inversion (FOCI) pulses that are known to produce sharper edges than conventional hyper-secant (HS) pulses at the same peak coil voltage (42). The parameters for the C-shaped FOCI pulse (42) optimized for our purpose were: μ (the side-to-width parameter)=6, β =1023, cutoff (maximum) value of the modulation function=5, duration=14.86ms and bandwidth=1953Hz. We used a conventional HS adiabatic pulse as the non-selective inversion pulse. HS and FOCI pulses were calibrated on a saline phantom and inversion profiles were confirmed.

Functional MRI

All subjects (n=7, age 25-46) gave written informed consent before participating in this Johns Hopkins Institutional Review Board (IRB)-approved, Health Insurance Portability and Accountability Act (HIPAA)-compliant study. A black-white flashing checkerboard (frequency=8Hz, visual angle=25°) was projected onto a screen in the back of the magnet for visual stimulation. An angled axial imaging slice was carefully selected to cover the primary visual cortex, mainly the calcarine fissure. For visual stimulation experiments (n=7), a block paradigm of 30s stimulus-off interleaved with 30s stimulus-on was used. In addition, two subjects performed a breath-hold and a hyperventilation session, with a block paradigm of 55s normal breathing (stimulus-off) interleaved with 15s breath-hold/hyperventilation (stimulus-on), during which only Sequence IIb was used. Each fMRI experiment consists of four interleaved off and on periods with one extra off period in the end.

Data Analysis

Images were co-registered using the Automated Image Registration (AIR) algorithm (43). Baseline drift of the time course for each voxel was corrected using a cubic spline interpolation algorithm. In order to allow the subject to reach a hemodynamic steady state, images acquired during 20s at the beginning of the first off period and 10s at the beginning of the following on and off periods were not used for activation detection. The images not analyzed in the first 20s of the first off period also serve as dummy scans to reach steady state. A hypothesis test (two-tailed Z-test) with statistical significance of 0.01 was engaged to detect activated voxels. Requirements for voxel activation were Z-score<-2.5, cluster size≥4, and SNR>20 (19). The fractional signal (S) in each voxel was computed by normalizing to the average baseline signal. The relative signal change (ΔS/S) was calculated by subtracting the average fractional signals during baseline from those during activation. Two types of SNR were calculated: SNR of the MR images and the functional time courses (tSNR) (44,45). In both cases, the signal is defined as the intensity of the iVASO images (S). The standard deviation of a difference map from two baseline images in the middle of the paradigm was used to estimate the noise level (N) in one image. The noise in the time courses was estimated by the temporal standard deviation of the MR signal intensities in each voxel. The CNR per minute for each voxel was defined as tSNR ×|ΔS/S|×√N_a (N_a = number of images acquired over the minute). A region of interest (ROI) was carefully drawn to cover the visual cortex for each subject. Programs were coded in Matlab 6.0 (Mathworks, Natick, MA, USA).

Results

Simulations

Contribution of CBV_a and arterial transit times

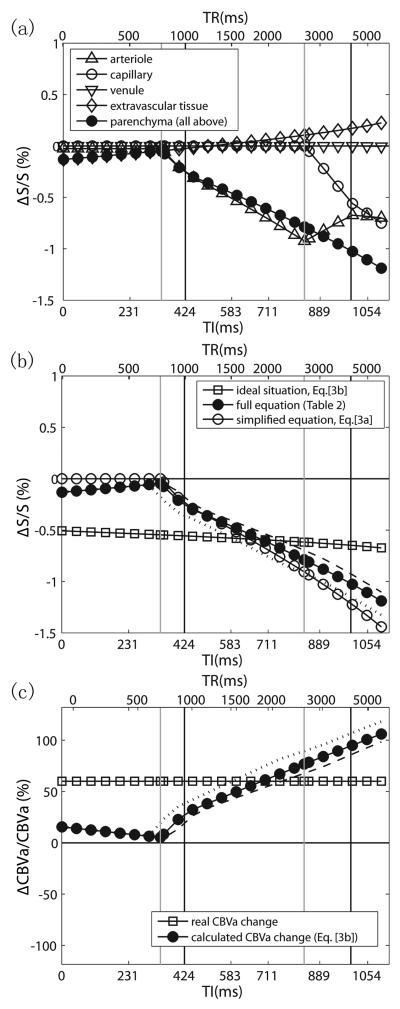
First, it is important to notice that the iVASO ΔS/S is less intuitive to interpret than ASL, because it is not directly proportional to the relative change of the intended physiological parameter, i.e. $\mathrm{\Delta }{\mathit{CBV}}_a∕{\mathit{CBV}}_a^{\mathit{base}}$. In iVASO, the inflowing blood signal is nulled and it is the signals from extravascular tissue and postarterial compartments that are measured to infer CBV_a change, while in ASL where a control scan is performed, the difference signal between label and control is proportional to CBF change. The true relationship between iVASO ΔS/S and $\mathrm{\Delta }{\mathit{CBV}}_a∕{\mathit{CBV}}_a^{\mathit{base}}$ is described in Theory. In Fig. 2a, the relative signal changes (ΔS/S) in iVASO during activation are plotted as a function of TI (and TR) to illustrate the contributions from different compartments. These simulations include the small spin echo (SE) BOLD effect for TE=6ms, calculated from different T₂ values during baseline and activation known from the literature (Table 3). A first observation is that a small tissue signal change would be visible even without blood nulling. There are two compensating effects behind this, a negative component because of the T₁-difference between blood and gray matter tissue, and a positive small BOLD effect. The combined BOLD/CBV effect is slightly negative at short TI and slightly positive at longer TI, both negligible compared to the total S/S. Upon the introduction of nulled blood in the arterioles, the signal change becomes larger (more negative), similar to the original VASO. The most important difference between iVASO and conventional VASO is that the blood nulling fraction now depends on the vascular transit times. As demonstrated in Fig. 2a, this leads to a strong increase in the iVASO effect for the TI range from 340ms (Δ^act, left gray vertical line) to 994ms ({Δ+δ_a}^base, right black vertical line), which corresponds to a TR range from about 0.77 to 4s. The increase in (ΔS/S) for Δ^act<TI<{Δ+δ_a}^act is due to both the reduced transit time and increased CBV_a upon activation.

Fig. 2.

Simulations of relative iVASO signal changes (ΔS/S) (a,b) and calculated CBV_a changes (ΔCBV_a/CBV_a) from ΔS/S (c) in gray matter during neuronal activation as a function of TI (TE=6ms). The corresponding TR values (not linear with respect to TI) are indicated at the top. The black and gray vertical lines mark the transit times used in the simulations during baseline and activation, respectively, with the two left lines corresponding to Δ and the two right lines to Δ + δ_a. In (b) and (c), simulations are shown for a range of baseline arterial transit times (the broken line for +100ms, the dotted line for −100ms). (a) Contributions from different blood compartments and pure tissue to total parenchymal signal change. (b) Comparison of exact equations (Table 2) and approximated and ideal expressions (Eqs. [3a,b]). (c) Relative CBV_a changes calculated using the ideal equation (Eq. [3b]) from simulated ΔS/S with full equations (dark dot curve in (b)). The curve through the squares indicates true CBV_a change assumed when simulating ΔS/S. It can be seen that CBV_a change is the dominant effect when TI/TR is in the optimal range (1.5s<TI<2.5s).

In Fig. 2b, the TR dependence of ΔS/S for the simplified equation (Eq. [3a]) and the ideal equation for pure arteriolar blood volume effects (Eq. [3b]) are compared with the simulation for the full equation (Table 2). The simplified and full equation results compare well for TR<about 2.5s. The full equation curve crosses with the ideal curve at TI/TR=646/1734ms, which indicates the optimal parameters to accomplish pure arteriolar blood volume effects. Since the transit times may vary between subjects, these optimal numbers will encompass a range. To get an impression of this range, the TR dependence of ΔS/S was simulated for a ± 100ms variation in baseline arterial transit times, leading to an optimal TI range of 589-757ms, corresponding to a TR range of 1.52-2.52s. The difference between the ideal and full equation curves represents the arterial transit time contribution. Within the optimal TI/TR range, CBV_a change is the dominant effect in the iVASO ΔS/S, while the contribution from arterial transit time changes becomes greater with shorter or longer TIs outside the optimal range. A substantial change in baseline arterial transit time (± 100ms) would alter its contribution by 7-24% (around 10% on average).

To make things more intuitive, in Fig. 2c, we illustrate what $\mathrm{\Delta }{\mathit{CBV}}_a∕{\mathit{CBV}}_a^{\mathit{base}}$ will look like when calculating it using the ideal equation (Eq. [3b]) from the ΔS/S simulated with full equations (dark dot curve in Fig. 2b) assuming a certain CBV_a change (60% increase here). It can be seen that within the optimal TI/TR range (1.5s<TR<2.5s), the calculated CBV_a changes are within experimental error range compared to the real CBV_a change assumed when simulating ΔS/S. Outside the optimal range, simply attributing iVASO ΔS/S to CBV_a changes using the ideal equation (Eq. [3b]) would result in significant underestimate or overestimate with shorter or longer TIs, because substantial transit time effects are involved. In that case, Eq. [3a] should be used with assumed or measured transit time values to correct for the discrepancy.

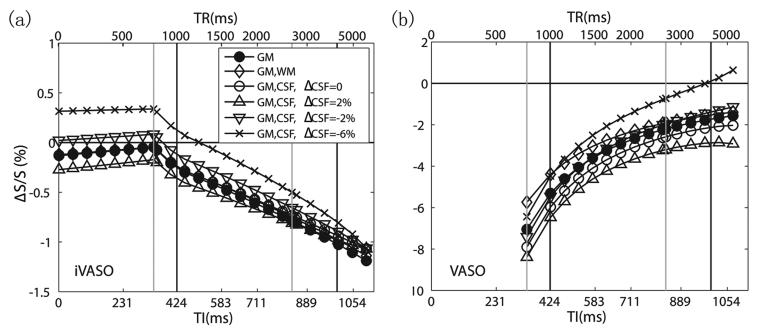
Partial volume effects and comparison with VASO

The partial volume effects from WM and CSF in iVASO are simulated in Fig. 3a. The first observation is that increases in baseline volume fraction of CSF (10.5%) and WM (5%) have the effect of flattening the curve, thus reducing the TR dependence. Secondly, these effects are very small in the 1-4s TR range and most likely are indistinguishable within experimental error. On the other hand, increases or decreases in CSF content during activation will affect the curve strongly for TR<1.5s, with an effect of up to 25% for ± 2% alteration and 30-70% for −6% change around the optimal TR.

Fig. 3.

Influence of partial volume effects from WM (5%) and CSF (10.5%) and from changes in CSF volume during activation on the relative GM parenchymal signal change in iVASO (a) and VASO (b). Note that the vertical scale for VASO is greater than for iVASO. The corresponding TIs and TRs are indicated at the bottom and top, respectively. The black and gray vertical lines mark the transit times used in the simulations during baseline and activation, respectively, with the two left lines corresponding to Δ and the two right lines to Δ + δ_a.

To illustrate the different contrast mechanisms, the theoretical VASO ΔS/S is simulated in Fig. 3b using the CBF-inclusive theory described in (19). The relative signal changes in VASO are greater than iVASO (notice vertical scale difference), mainly because VASO reflects total CBV change while iVASO is dominated by arterial blood effects. The partial volume effects from WM and CSF are larger in VASO than iVASO. Particularly, a 10.5% CSF partial volume would result in 15-50% increase in ΔS/S, whereas a ± 2% alteration in CSF volume during activation would lead to 20-60% change in ΔS/S for TR<4s and up to 130% for TR>4s. Notice that the TR dependence of the VASO ΔS/S is largely due to the CBF contribution at short TR (19), whereas the TR dependence in iVASO is mainly caused by the transit time effects.

Functional MRI results

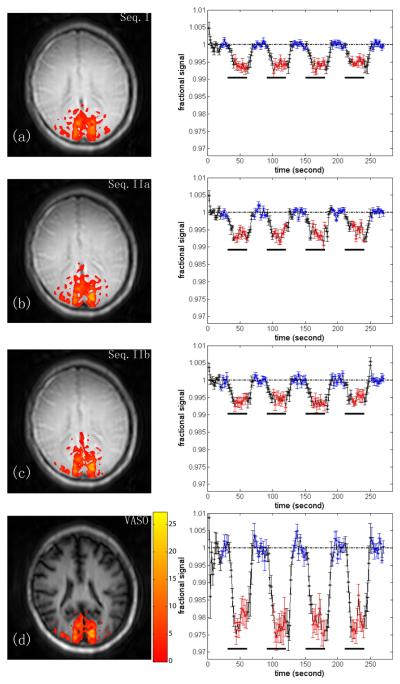
Fig. 4 shows visual activation maps and averaged hemodynamic responses (n=7) at TR=2s for iVASO sequences I, IIa, IIb (Figs. 4a-c) and VASO (Fig. 4d). The conventional VASO images are heavily T₁-weighted, and the darkening of big blood vessels (e.g. sagittal sinus) verifies that the blood is nulled. On the contrary, iVASO images have much less T₁-weighting especially at long TR, showing that the static tissue signal in the imaging slice remains mostly in steady state equilibrium. For iVASO, the blood in the sagittal sinus should not be nulled, which is confirmed experimentally for sequences I and IIb. However, some nulling occurred for Sequence IIa, which we attribute to inverted venous blood flowing in from above the slice when flipping back only a narrow slice after nonselective inversion. The regions of activation are comparable for all sequences.

Fig. 4.

Visual activation results for TR= 2s. Representative activation maps and subject-averaged hemodynamic responses (n=7) for sequences I, IIa, IIb and VASO, respectively. The color overlays indicate Z-score according to the bar displayed beside the bottom image. The error bar indicates the inter-subject standard deviation. The black bars underneath indicate the stimulus periods. Red and blue points indicate points included in activation detection and baseline signal calculation, respectively.

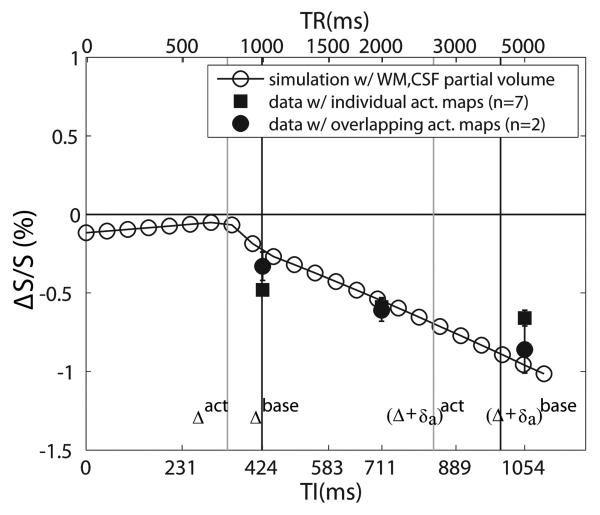
Table 4 summarizes the functional activation data averaged over voxels activated in all four experiments at the same TR in the visual experiments (n=7), which are well reproduced between the three iVASO sequences at each individual TR (no significant difference P>0.1). The VASO signal changes agreed well with the simulations (Fig. 3b) and previous studies (1,19). At long TR (5s), iVASO sequences had slightly more activated voxels than VASO (all P<0.1), while these numbers were comparable (P>0.1) at TR of 2s. Using iVASO, negative signal changes during activation could still be reliably detected at TR=1s, which was not the case for VASO, where significant positive signal change was detected in 1757 ± 143 voxels (n=7). The relative signal changes in iVASO were smaller than those in VASO (P<0.01). For iVASO, ΔS/S significantly reduced (P<0.1) from TR=5s, to TR=2s, to TR=1s, in line with expectations based on the simulations. In Fig. 5, the experimental results are compared with the theoretical curve predicted from simulations with the full equations and partial volume effects (assuming 5% WM, 10.5% CSF and no CSF volume change during activation). ΔS/S at TR=2s, which is within the optimal TR range, agrees reasonably well with the simulated value, whereas ΔS/S from the other two TRs deviated from the simulated values. We attribute this to the fact that ΔS/S was calculated over individual activation maps for each TR, because the scans with different TRs were performed on different days. To properly compare signal changes between different TRs, the same ROI has to be used. We therefore repeated the same experiments using iVASO sequence IIb with all three TR/TI combinations on two subjects (n=2) during the same session. A common activation map consisting of voxels activated for all TR values was used to calculate ΔS/S for each subject. The average ΔS/S values found were −0.86±0.15%, – 0.61±0.07% and −0.33±0.09% for TR of 5s, 2s and 1s, respectively, which matched the theoretical curve in Fig. 5 within experimental error.

Table 4.

Visual stimulation data¹,² for the three iVASO methods and conventional VASO.

TR/TI (ms)	Method	Activated Voxels3	ΔS/S (%)	SNR	tSNR	CNR
5000/1054	Seq. I	2731±204	−0.62±0.04	347±8	313±11	6.56±0.51
	Seq. IIa	2388±224	−0.66±0.06	308±16	290±10	6.54±0.36
	Seq. IIb	2698±220	−0.69±0.04	308±16	287±9	6.96±0.36
	VASO	1910±213	−1.46±0.15	104±4	99±10	4.88±0.54
2000/711	Seq. I	2219±183	−0.59±0.06	319±9	283±10	9.09±0.89
	Seq. IIa	2286±168	−0.60±0.07	288±8	254±13	8.58±0.80
	Seq. IIb	2102±230	−0.59±0.05	302±7	282±6	8.92±0.89
	VASO	2252±216	−2.16±0.32	66±3	63±5	7.32±1.07
1000/424	Seq. I	2294±108	−0.47±0.03	227±9	201±11	7.22±0.47
	Seq. IIa	2053±211	−0.48±0.03	207±6	188±8	6.74±0.61
	Seq. IIb	2210±134	−0.51±0.03	196±6	181±9	7.29±0.42
	VASO	893±131	N/A	N/A	N/A	N/A

¹n=7, mean ± standard deviation.

²All ΔS/S, SNR, tSNR and CNR are averaged over voxels that were activated in all four experiments of the same TR/TI. Therefore, SNR and tSNR reported here is per image per voxel based. CNR is per voxel per minute based.

³The number of voxels is based on the reconstructed image resolution (256×256).

Fig. 5.

Comparison of experimental and simulated data for iVASO, displayed as a function of TI. The corresponding TR values (not linear with respect to TI) are indicated at the top. The simulated curve was obtained by using the full equations and assuming partial volume fractions of 5% and 10.5% for WM and CSF, respectively. Results from two individuals in which the signal changes for different TR values were measured for overlapping voxels during the same study (black circles) correspond well to the simulations. Data from Table 4, representing signal changes averaged over all activated voxels in each TR (scanned on different days) (black squares) also agree, but deviate more from simulation when TR is outside the optimal range. The black and gray vertical lines mark the transit times used in the simulations during baseline and activation, respectively, with the two left lines corresponding to Δ and the two right lines to Δ + δ_a.

The SNR, tSNR and CNR values for all iVASO sequences were significantly greater than those for VASO at each TR (all P<0.01). The SNR/tSNR values averaged over all iVASO sequences were 3.04 ± 0.11/2.98 ± 0.12 and 4.41 ± 0.11/4.34 ± 0.09 (mean ± SD, n=7) times the VASO SNR values at TR values of 5s and 2s, respectively. Note that all SNR values were slightly higher than respective tSNR values (P<0.05), mainly because the former includes only thermal noise while the latter has both thermal and physiological noise (44,45). The enhancement in SNR was also slightly greater than in tSNR (P<0.05), which can be expected as only physiological noise grows with the actual MR signal intensity (44,45). The iVASO ± values averaged over results from the three iVASO sequences were only 45 ± 2% and 28 ± 1% (mean ± SD, n=7) in magnitude of the corresponding VASO ΔS/S at TR of 5s and 2s, which is consistent with the simulations and attributed to the additional vasodilation in capillaries and venules as well as CBF contributions at short TR in VASO. The CNR (proportional to the product of ΔS/S and SNR) in iVASO was thus less enhanced than SNR, but still increased by factors of 1.37 ± 0.03 and 1.21 ± 0.02 (mean ± SD, n=7) with respect to VASO at these two TRs. In all sequences, SNR increased with TR as a result of increased steady state signal. Note, however, that the number of images acquired per minute differs in each TR and that CNR (per unit time) does not increase with TR as a consequence.

In Fig. 6a the averaged hemodynamic responses of the three iVASO sequences are compared with the VASO response. This was done for overlapping voxels within subjects. To allow temporal comparison, the fractional signal changes were normalized between VASO and iVASO. Since no significant difference was found among iVASO sequences, they were averaged for each subject and then over all subjects (Fig. 6b). To test for temporal differences between iVASO and VASO, a paired student T-test was conducted to detect ΔS/S differences for data points in the transition periods after the start (4 points) and cessation (2 points) of the stimulus. These points are labeled by their standard deviations (error bars) in Fig. 6b. The P-values (n=7) were (in the order of time): 0.0008, 0.016, 0.192, 0.026, 0.030, 0.272. Using a P-value threshold of 0.05, ΔS/S in iVASO is significantly smaller than in VASO for the first, second and fourth pairs of points after the start of stimulus. The dropping and rising rates, which were calculated by a linear fitting of the transitional points, were comparable between the two methods (P>0.1). The times for ΔS/S to reach half maximum after stimulus onset and cessation were 3.31s/4.54s (iVASO/VASO) and 3.73s/5.26s, respectively. Together these results show that the hemodynamic response detected by iVASO uniformly preceeds the one measured by conventional VASO by 1.23-1.53s.

Fig. 6.

Hemodynamic responses for visual activation detected by iVASO and VASO at TR=2 s. In each time course, four blocks were averaged. The points during 20 s in the beginning of the first block and 10 s in the end of the fourth block were not included. (a) Time courses from all sequences. (b) Comparison of average time course from iVASO sequences I-II with VASO. Time courses were scaled by the ratio of mean ΔS/S between VASO and iVASO to have coinciding maximal effects. True amplitudes of VASO and iVASO ΔS/S are on the left and right vertical legends, respectively. The vertical dotted lines mark the start and cessation of the stimulus. In (b), the points during the transition periods show error bars describing the inter-subject standard deviation (n=7).

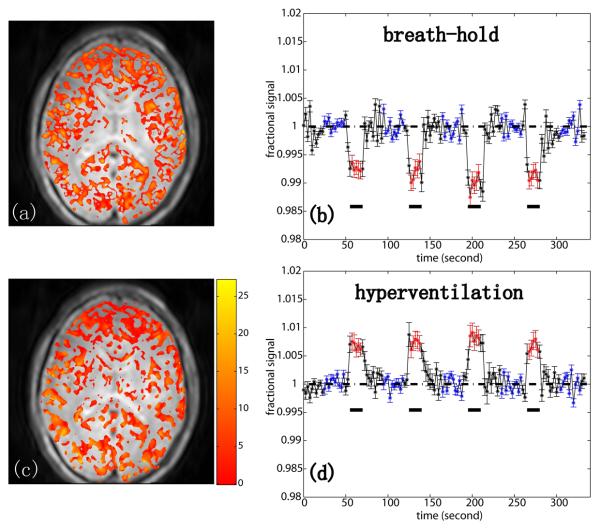
To illustrate the potential of iVASO for detecting CBV-based changes, we also performed breath holding and hyperventilation experiments with iVASO sequence IIb, for which CBV and transit time effects are of opposite sign and in which all GM regions within the slice should be affected. The results in Fig. 7 confirm the expectations.

Fig. 7.

iVASO (Sequence IIb) activation maps and corresponding hemodynamic time courses (n=2) for breath hold (a,b) and hyperventilation (c,d) paradigms at TR=2.5s. The data show the expected reversal of sign of ΔS/S due to the occurrence of vasodilatation and vasorestriction, respectively. The color overlays indicate Z-score according to the bar displayed beside the bottom image. The error bar indicates the inter-subject standard deviation. The black bars underneath indicate the stimulus periods. Red and blue points indicate points included in activation detection and baseline signal calculation, respectively.

Discussion

A new inflow based VASO fMRI method was designed that greatly increased SNR and CNR with respect to the conventional VASO approach, which suffers from low SNR due to the small residual tissue signal after a non-selective inversion. Recently, there have been several efforts to design VASO approaches with higher SNR. One approach in which VASO SNR can be enhanced by 50-60% is by acquiring data at a time that blood is not nulled (46-48). However, the theoretical description of those methods becomes more sophisticated, mainly due to the need to include substantial intravascular BOLD effects. Another method achieved SNR enhancement of about 40% by using magnetization transfer (MT) effects to accelerate T₁ recovery of tissue signal (MT-VASO) (49). However, MT-VASO has increased RF power deposition, which may become a limiting factor at high magnetic fields. As another alternative, Jin and Kim proposed the use of a narrow slab-selective inversion (SI-VASO) (2) including the imaging slice, allowing SNR to be magnified by about 70%. The key in SI-VASO is to choose the slab thickness so that all blood water spins flowing into the imaging slice are fresh and experience only one inversion pulse before leaving the imaging slice, allowing images to be acquired at the equilibrium TI, which is longer than the steady state TI. However, fulfillment of such condition depends on various experimental and physiological parameters.

All current VASO approaches invert the tissue signal in the imaging slice, a fundamental constraint for SNR. In iVASO, the tissue signal is not affected by the blood-nulling preparation and SNR and CNR do not depend on the difference between T₁ of blood and tissue. At 3T, iVASO showed a 3-4 times higher SNR than VASO, a factor that is expected to increase with field strength, where diminishing T₁ difference will adversely affect the other VASO approaches. The two techniques measure complementary contrasts in that iVASO reflects predominately arteriolar effects and VASO total CBV. The arteriolar blood volume is only about 20% of total CBV at baseline. Therefore, even though relative increases in blood volume are reportedly much larger in arterioles than in capillaries and venules (5,6,8,9,12,13), the size of the signal change is reduced in absolute magnitude. Despite this, there is an overall CNR increase of 20-40% in iVASO with respect to VASO. In addition, a temporal resolution up to 1s could be achieved for iVASO, which is not possible in VASO due to overwhelming fresh blood effects that cancel out the small negative signal change at short TR (21). Even though such fresh blood effects still affect the iVASO signal change at short TR (see Technical Considerations), they are less detrimental as for VASO due to the larger tissue signal in iVASO.

The fact that blood nulling in iVASO is achieved without inverting the imaging slice may be advantageous when detecting blood volume effects in diseased tissue. For instance, T₁ increases have been found in many pathologies (cancer, ischemia), rendering it difficult to separate disease tissue from blood that also has a long T₁ when using conventional VASO.

Another advantage of not inverting tissue signal is a strong reduction in partial volume effects with CSF and WM. Assuming a typical scenario of 10.5% CSF (19) for GM voxels, our simulations show a decrease in ΔS/S magnitude by about 10% (Fig. 3a). This effect increases with TR, but still less than the experimental error range for TR<3s. In VASO, on the other hand, this same partial volume contribution increases ΔS/S magnitude by 15-50% in our simulations, in line with previous reports (19). The main reason for this large discrepancy between the methods is that, in iVASO, the CSF magnetization is positive with a short-TR magnitude much smaller than that of the GM magnetization, while, in VASO, the CSF magnetization is negative with an absolute magnitude that is larger than that of the positive GM magnetization (19). When including increases or decreases in CSF volume during activation (Fig. 3a), the size of the iVASO effects changes more dramatically at short TR but not at long TR. For instance, for a 2% change in CSF volume, the effect on signal change during activation can be up to 25%. Nevertheless, when comparing the experimental data with the simulations (Fig. 5), the data fall close to the curve for 10.5% CSF contamination with no CSF change upon activation. At TR of 1s, simulations show that a 6% CSF volume reduction during activation would result in a slightly positive ΔS/S. Our measured ΔS/S was significantly negative (P<0.01), which seems to imply that such large CSF volume reduction is not likely in the cortical regions that we were measuring. For WM, the magnetization is positive in both iVASO and VASO, and partial volume effects reduce ΔS/S in both approaches. However, the WM magnetization is comparable in magnitude to that of GM in iVASO, while it is about three times more intense than GM magnetization in VASO, which leads to a more noticeable partial volume effect (19).

Signal origins and spatial and temporal specificity

The signal origin of the proposed iVASO approach is different from the conventional VASO technique. Despite simulations showing negligible effects of exchange (1), conventional VASO has been criticized in that exchange of water protons between tissue and blood may affect CBV quantification because capillary and venular spins may not be perfectly nulled. A major advantage of iVASO is that a proper choice of TR range (Fig. 2) allows it to be predominantly sensitive to arteriolar blood effects, where no exchange between blood and tissue can occur due to limited permeability of the vessel wall. At longer TR/TI, the inflowing blood water spins may reach the capillary bed where exchange can occur. However, considering the fact that the longest iVASO TI at 3T is about 1.1s and typical arterial transit times are 0.8-1s, the inflowing spins can be in the capillaries for at most 300ms by the time images are acquired. On the other hand, the water exchange between capillary blood and tissue does not occur instantaneously, but takes on average 0.5-1s (50,51). These all imply that the exchange effect in iVASO should be very small, although further investigation is needed to incorporate this effect in the equations and quantify its contribution to the overall iVASO signal change.

In general, the interpretation of iVASO signal changes is complicated by vascular transit time effects that are strongly TR/TI dependent. However, an optimal TI/TR range of 1.5–2.5s could be derived for which the arteriolar blood volume effect is dominant (Eqs. [3a,b]), and at which partial volume effects from WM and CSF (Fig. 3a) are minor. Using these equations for our data at TR=2s, a Δ CBV_a/CBV_a of 58 ± 7% (mean ± SD, n=7) could be estimated. This arteriolar volume change is consistent with the range of values reported in previous studies, including MRI in animal (79% (5), 41% (9), 46% (11), 35% (12)), MRI in humans (33% (7), 61% (10)), and high resolution optical imaging studies (59% (4), 39% (6), 37% (8)).

Depending on the inflow time, the blood nulled in iVASO includes blood in arterial vessels of all sizes as well as in capillaries before the blood water exchanges with tissue water. As neuronal activation related vasodilation occurs mostly in microvasculature (52), the signal change in iVASO is expected to reflect predominately arteriolar blood effects at short TR (<2.5s where TI ≈ {Δ + δ_a}^act) and will contain some capillary blood effects at longer TR. When very high spatial resolution is available (such as in the animal studies by Kim et al. (2,9,12)), iVASO should be able to provide arteriolar/capillary specificity. However, for the typical human fMRI resolution we used in this study (3mm isotropic voxel), even though the mechanistic specificity is arteriolar and capillary, the experimental spatial specificity for iVASO is expected to be similar to VASO, in which total microvascular blood volume changes are measured (1,2). This is confirmed by the finding of comparable numbers of activated voxels (Table 4) and similar appearance of the activation maps (Fig. 4) between the two methods.

The iVASO hemodynamic response for visual stimulation at TR=2s was significantly faster and returned to baseline more rapidly than the one for conventional VASO, which provides additional support for the arteriolar origin of the iVASO contrast in the optimal TR range. The half maximum time difference (1.23-1.53s) between iVASO and VASO responses probably reflects the difference in delay between arteriolar and combined (average) microvascular compartments. This accords with recent high-resolution optical imaging results in rat somatosensory cortex (8), where prompt stimulus onset and post-stimulus decay in the arteriolar response and delayed return in capillary and venular compartments were observed. Vanzetta et al (53) reported a uniform lag (~0.5-1s) of blood volume change in capillaries, venules and veins after the arterioles and arteries in the cat superficial cortical vasculature. They also observed that the response of larger arteries is slower than that of arterioles, which strengthens our belief that large artery dilation has limited contribution to the iVASO signal change during visual stimulation.

A major limitation of the current iVASO approach is that estimation of CBV_a changes requires the derivation of an optimal TR/TI range based on a priori knowledge of the arterial transit time (Δ + δ_a) and CBF (Eq. [4]). Depending on the cortical region studied, the optimal TR/TI range would need to be adjusted accordingly. Therefore, in general, the application of the current iVASO approach seems to be confined to detecting predominantly CBV_a-weighted signal changes. For more accurate CBV_a quantification, it will be necessary to perform multiple experiments with different TR/TI and numerically fit the signal changes to the exact theory, which is the topic of future work. Besides, due to the existence of residue arterial blood at the optimal TI, it is possible that the temporal and spatial responses in iVASO may not be exactly the same as the actual physiological CBV_a change. This potential discrepancy remains to be investigated and characterized at a higher spatial resolution and possibly with the aid from multi-modality neuroimaging techniques such as optical imaging.

Comparison of iVASO and ASL

There are multiple MRI approaches to measure CBF and CBV effects and most of these use inversion approaches. Actually, the preparatory inversion schemes in iVASO are similar to those used in the labeling scans of some ASL techniques such as EPISTAR (22), PICORE (23), DIPLOMA (24), UNFAIR (25,26), EST (27), and IDOL (28). However, ASL and iVASO differ fundamentally with respect to the contrast mechanism used. ASL measures tissue perfusion based on the exchange between magnetically labeled blood water spins and tissue water spins in the capillary bed. As such, its quantification is hampered by residual arteriolar blood label, which can be eliminated using crusher gradients or a long post-labeling delay (29-31). VASO employs blood labeling (nulling) to monitor changes in blood volume. Particularly, by using a short delay (TI<1s), iVASO is designed to be predominantly sensitive to arterial blood effects, where no exchange between blood and tissue can occur due to limited permeability of the vessel wall. Besides, iVASO images are acquired only at the blood nulling time, so that the vascular contribution is highlighted.

Comparison of iVASO and existing CBV_a methods

Noninvasive determination of CBV_a has been shown to be possible by using ASL techniques with and without crusher gradients (54-57). A more recent approach (7,10) combines pulsed ASL (PASL) with Look-Locker echo-planar imaging (LL-EPI) with high flip angle and short pulse spacing to accelerate the acquisition while suppressing the tissue perfusion signal and quantifying CBV_a with an intravoxel arterial signal model at a temporal resolution of 6s. The modulation of tissue and vessel (MOTIVE) (58) method exploits the difference in MT effects between tissue and blood to modulate tissue signal and calculate CBV_a and CBF. A model-free ASL approach named quantitative STAR labeling of arterial regions (QUASAR) (57) employs deconvolution like that used in dynamic susceptibility contrast (DSC) MRI to calculate CBV_a and CBF. While all these approaches have been demonstrated useful in various applications, they all involve acquiring two series (label and control) of images at different post-labeling time and sophisticated numerical post-processing procedures including fitting to a quantitative model or deconvolution. On the other hand, the proposed iVASO approach in this paper, which employs inversion recovery to zero out blood signal in order to monitor blood volume alteration, does not require a control scan and acquires images only at the blood nulling TI. When detection of a relative CBV_a change is the only requirement, for instance for detecting neuronal activity or impaired perfusion in diseases, iVASO is expected to provide a useful alternate with improved SNR/CNR and temporal resolution (up to 1 s).

Technical Considerations

It is important to discuss the effects from fresh inflowing blood on the blood magnetization steady state in VASO and iVASO, which may lead to an erroneously large ΔS/S (19,21). A recent VASO study (21) has shown that for the blood water spins to experience sufficient inversion pulses for reaching steady state when entering the imaging slice in the cortex, the thickness of the inversion slab below imaging slice has to be greater than 150mm for TR longer or equal than 2s. In our iVASO experiments, the inversion slab is 7mm below the bottom of imaging slice and at least 150mm thick (body coil excitation), which is expected to cover the large arteries (e.g. carotid arteries) as well as smaller arteries proximal to arterioles, which have a large heterogeneity of flow velocity and trajectory. In addition, as the static tissue signal in iVASO is much larger than that in VASO, the influence from fresh inflowing blood should be smaller. Therefore, the contamination from fresh inflowing blood in iVASO is expected to be minimal, especially for TR of 5s and 2s. This is reflected in Fig. 5, which shows a reasonable match between the measured ΔS/S and theory developed for steady state inflowing blood. Furthermore, such fresh blood effects can be alleviated by applying spatially non-selective saturation following the readout module (47,59), which resets the magnetization in all blood so that steady state is built immediately after the first TR. To evaluate the residual influence from fresh inflowing blood in our experiments, we repeated the visual stimulation experiments with iVASO sequence IIb on 3 subjects using a 90° RF pulse followed by crusher gradients immediately after the imaging module. The average ΔS/S from voxels activated for all TRs were −0.83±0.11%, −0.62±0.09% and −0.27±0.10% for TR of 5s, 2s and 1s, respectively. Only ΔS/S from the shortest TR (1s) showed a trend of being smaller (P<0.1) in absolute magnitude than the value measured without the global saturation after readout (−0.33±0.09%, see Results for Fig. 5). It is therefore recommended to incorporate this magnetization reset (47,59) technique in short-TR iVASO sequences in order to minimize the contamination from fresh inflowing blood.

Three different preparatory inversion schemes (I, IIa, IIb) were compared with respect to nulling inflowing blood while leaving the static tissue in the imaging slice unaffected. Sequence I is the simplest with only one inversion pulse. Based on recent work, the thickness of the inversion slab has to be greater than 150mm to ensure the inverted inflow blood being in steady state (21). However, such a broad slab results in less sharp edges of the inversion profile, requiring the use of a wider gap between the inversion slab and imaging slice. In sequence II, the gap can be narrower since the flip-back slab is much slimmer. Both sequences I and IIb ensure that only blood flowing in from the inferior direction is nulled. In sequence IIa, blood from both superior (mostly venous) and inferior (mostly arterial) direction is nulled, which may introduce some venous inflow effects, as confirmed by signal detected in the sagittal sinus. However, this is not expected to affect ΔS/S as large-vessel venous flow is not expected to change during activation (5,6,8,9,12,13), an expectation borne out by the result of comparable signal changes for all three iVASO pulse sequences (Table 4).

BOLD effects reduce the negative signal change detected in both iVASO and VASO. In iVASO, where the signal change is only a few tenths of a percent while the blood in capillaries and venules is not nulled, the combined intra and extravascular BOLD contribution can be detrimental. When performing the same functional experiments with a gradient echo (GE) echo planar imaging (EPI) readout (data not shown), the number of voxels with negative signal change was much reduced. Therefore, TSE with short TE (6ms) was used to mitigate BOLD effects. Unfortunately compared to EPI, TSE has the disadvantages of longer acquisition time and higher specific absorption rate (SAR). For the future development of multi-slice sequences and application at higher magnetic field, gradient spin echo (GraSE) sequence would probably be a better choice (60,61). Another way to filter out the BOLD contamination is to acquire multiple echo EPI data and extrapolate the signal change to TE of 0.

In this proof-of-concept paper, we demonstrated the features of iVASO as a single-slice technique. It is not trivial to develop multi-slice sequence for inflow based approaches because the optimal inflow time may differ per slice, requiring the acquisition of a transit time map. However, the current single-slice approach has potential for the noninvasive study of mechanisms of microvascular activation patterns during brain activation in humans in a way similar to optical spectroscopy in animals.

Conclusions

We demonstrated a novel VASO technique (iVASO) with improved SNR, CNR, and temporal resolution, as well as reduced partial volume effects from WM and CSF compared to conventional VASO. The contrast in iVASO can have contributions from arterial, arteriolar, and capillary CBV effects combined with the influence of arterial and capillary transit times. An optimal TR-range could be defined in which the contrast is predominantly based on arterial/arteriolar blood volume effects. During visual stimulation, our data acquired in this TR-range showed an immediate hemodynamic response to visual activation, which was significantly faster than the VASO response, supporting this interpretation.

APPENDIX I: The two steady states for inverted inflowing blood

Consider a bolus of blood flowing from arteries into the microvasculature. Before reaching the imaging slice (TI < Δ), the blood water spins experience a series of inversion pulses, namely one or more depending on the inversion volume, TR, and the velocity of the blood. A recent study by Donahue et al. (21) has shown that in human visual cortex, when the thickness of the inversion slab beneath the imaging slice is 150mm or greater and TR is 2s or longer, inflow of fresh blood can be neglected and the blood magnetization will reach a steady state before it enters the imaging slice. Such a wide inversion can be achieved using body coil transmit, which is now standard on many clinical scanners. This steady state in the absence of inflow of fresh blood can be derived by solving the Bloch equation:

$$\frac{{\mathit{dM}}_z}{\mathit{dt}}=-\frac{M_z-M_0}{T_{1b}}$$ [A1]

to get:

$$M_z\left(t\right)=M_0\cdot (1-e^{-\left(t-t_0\right)∕T_{1b}})+M_z(t-t_0)\cdot e^{-\left(t-t_0\right)∕T_{1b}}$$ [A2]

in which M₀ and M_z(t=t₀) are the equilibrium and initial longitudinal magnetizations, respectively. Note that in the following derivation, for M_z(t) at discontinuous time points (e.g. before and after an inversion/excitation pulse), t⁻ and t⁺ are used to represent the time instances before and after the pulse, respectively. The steady state magnetization M_ss before each inversion can be derived by setting M_z(t= t₀⁻+TR) = M_z(t=t₀⁻) = M_ss in Eq. [A2]:

$$M_{\mathit{ss}}=M_0\cdot \left(\frac{1-e^{-\mathit{TR}∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)$$ [A3]

After inversion, substituting M_z(t=t₀⁺) = −M_ss back into Eq. [A2], the blood magnetization can be written as:

$$M_{\mathit{ss},\mathit{inv}}(t-t_0)=M_0\cdot \left(\frac{1-2e^{-(t-t_0)∕T_{1b}}+e^{-\mathit{TR}∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)=M_0\cdot \left(1-\frac{2e^{-(t-t_0)∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)$$ [A4]

Eq. [A4] describes the magnetization during inversion recovery between two consecutive inversion pulses (t₀<t<t₀+TR, t₀ being the time point right after an inversion pulse). Notice that with the extra scaling factor 1+ e^−TR/T_1b, Eq. [A4] is not the signal equation for an inversion recovery (IR) pulse sequence. In a normal IR sequence, each inversion pulse is followed by a readout excitation pulse, while in our case only inversion pulses with time intervals of TR are applied. The steady state is of course different. Nevertheless, the blood nulling point (TI) is still the same since it is determined simply by the numerator:

$$1-2e^{-\mathit{TI}∕T_{1b}}+e^{-\mathit{TR}∕T_{1b}}=0$$ [A5]

Now consider the blood leaving the inversion slab with this steady state, which will be nulled at the first TI afterwards. When TI > Δ, this blood nulling effect starts to contribute to the images acquired at the first TI. Note that the readout excitation pulse at this TI does not affect the blood magnetization itself since it is zero. After the first TI, the blood keeps perfusing the rest of microvasculature. In the meantime, the blood water spins also undergo T₁ relaxation, which is still governed by Eq. [A4]. As the blood is now inside the imaging slice, the inversion pulse at t=t₀+TR does not invert its magnetization. At t = t₀⁻+TR+TI, just before the second TI, the blood magnetization can be calculated from Eq. [A4]:

$$M_z(t_0^{-}+\mathit{TR}+\mathit{TI})=M_0\cdot \left(1-\frac{2e^{-(\mathit{TR}+\mathit{TI})∕T_{1b}}}{1+e^{-\mathit{TR}∕T_{1b}}}\right)$$ [A6]

which can be simplified by substituting TI defined by Eq. [A5]:

$$M_z(t_0^{-}+\mathit{TR}+\mathit{TI})=M_0\cdot (1-e^{-\mathit{TR}∕T_{1b}})$$ [A7]

This is the blood magnetization at the second TI (image acquisition point) after the blood leaves the inversion slab (not nulled any more). After the excitation pulse at the second TI, the blood magnetization is set to zero. It may take more than one TR for blood to eventually flow out of the imaging slice, which depends on the slice thickness, TR and the blood velocity. Using Eq. [A2] (M_z(t=t₀⁺)=0), the magnetization between two consecutive excitation pulses at TI (t₀<t<t₀+TR, t₀ being the time point right after an excitation pulse, which is different from Eq. [A4]) can be described by:

$$M_{\mathit{ss},\mathit{ex}}\left(t\right)=M_0\cdot \left(1-e^{-(t-t_0)∕T_{1b}}\right)$$ [A8]

At each TI (t = t₀⁻+TR) when an image is acquired, the blood magnetization is exactly the same in Eqs. [A7] and [A8].

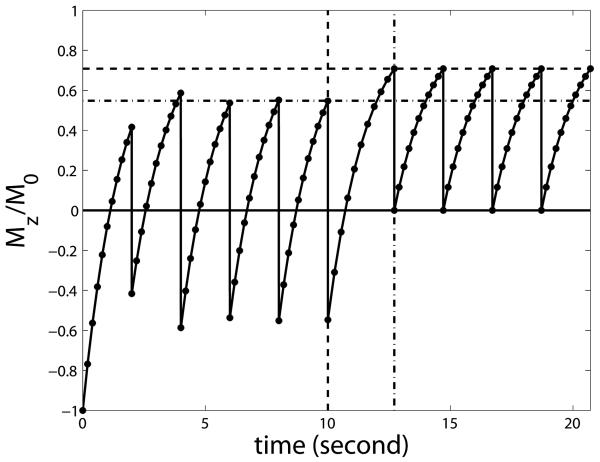
This process was verified by numerical simulation using Eq. [A1], which is shown in Fig. A1 using blood T₁=1627ms, TR/TI=2s/711ms. This figure illustrates the general situation for steady state inflow blood and the timing does not correspond to any specific inversion geometry. The horizontal dash dot and dashed lines indicate the first and second steady states calculated by Eqs. [A3] and [A7], respectively. The vertical dashed line marks the time point when the blood leaves the inversion slab, before which it experiences a series of inversion pulses equally spaced by TR. The vertical dash dot line indicates the second TI after the blood leaves the inversion slab, after which it experiences a series of excitation pulse with intervals of TR until it flows out of slice. During the period between the two vertical lines (TR+TI), no RF pulse affects the blood magnetization. Importantly, this figure indicates that when a steady state is built after a few scans, the inverted inflowing blood is nulled only at the first TI after entering the slice when most of it resides in the arterial compartment, and at its steady state full signal at consecutive TIs when it reaches the capillary and venous compartments.

Fig. A1.

Numerical simulation of the steady state buildup process for inverted inflowing blood using the Bloch equation. The vertical axis is the normalized longitudinal magnetization. The horizontal dash dot and dashed lines indicate the first (Eq. [A3]) and second (Eq. [A7]) steady states derived in the Appendix I, respectively. The vertical dashed line marks the time point when the blood leaves the inversion slab. The vertical dash dot line indicates the second TI after the blood leaves the inversion slab. Note that this figure is intended to show the general situation for steady state inflow blood and the timing does not correspond to any specific inversion geometry.