Duplication count distributions in DNA sequences

Abstract

We study quantitative features of complex repetitive DNA in several genomes by studying sequences that are sufficiently long that they are unlikely to have repeated by chance. For each genome we study, we determine the number of identical copies, the “duplication count,” of each sequence of length 40, that is of each “40-mer.” We say a 40-mer is “repeated” if its duplication count is at least 2. We focus mainly on “complex” 40-mers, those without short internal repetitions. We find that we can classify most of the complex repeated 40-mers into two categories: one category has its copies clustered closely together on one chromosome, the other has its copies distributed widely across multiple chromosomes. For each genome and each of the categories above, we compute N(c), the number of 40-mers that have duplication count c, for each integer c. In each case, we observe a power-law-like decay in N(c) as c increases from 3 to 50 or higher. In particular, we find that N(c) decays much more slowly than would be predicted by evolutionary models where each 40-mer is equally likely to be duplicated. We also analyze an evolutionary model that does reflect the slow decay of N(c).

I. INTRODUCTION

The term genome refers to the complete DNA sequence of an organism and is typically represented as a sequence of bases denoted A, C, G, and T. The length of a genome can range from several million bases, for bacteria, to billions, as in a mammalian genome, and may be separated into chromosomes. Typically, a genome contains a variety of highly similar subsequences, too similar to have occurred by chance. Such subsequences, whether they match each other exactly or with occasional differences, are collectively called repetitive DNA.

Repetitive DNA forms a significant fraction of the genomes of many organisms (for example, [1–4]), including more than half of the human genome [5–8]. While most repetitive DNA has no known function, numerous studies (for example, [8–10]) have found evidence that some types of repetitive sequence are involved with important processes. As James Shapiro wrote, “…the distribution of repetitive DNA sequence elements is a key determinant of how a particular genome functions (i.e., replicates, transmits to future generations, and encodes phenotypic traits).” [11].

Some types of repetitive DNA, such as transposable elements, have known mechanisms of duplication. Transposable elements can be from several hundred to several thousand bases in length. These sequences are sometimes referred to as “jumping genes” because they are capable of creating additional copies of themselves within a genome (see [10,12,13]). Another common type of duplication is a tandem duplication where a copy of a sequence is created adjacent to the original location. For example, microsatellites (see [12,14]) are low complexity subsequences consisting of a short sequence concatenated many times, such as “ATATATATAT.…” The length of these sequences is known to fluctuate due to the insertion (or deletion) of the same short sequence.

Duplications are an important part of the evolutionary process; it is well-known that duplication of a gene is a way that a species can acquire new abilities. If a gene is duplicated, the copy can mutate in ways that provide new functionality while preserving the old function in one copy. As an example, a gene duplication, followed by mutations, was the mechanism by which primates acquired the ability to see in three colors rather than two [15].

The availability of published genomes for a variety of organisms has allowed substantial statistical analysis of repetitive DNA. One quantity of interest is the number of occurrences of a particular “word” (a short sequence of bases such as “AGCCGTAAAT”) as a subsequence of a genome, and the distribution of this number across different words [16–21]. We call the number of occurrences of a word within a particular genome its “duplication count,” and we call a word “repeated” if its duplication count is at least 2 [22]. A word of length k is also called a “ k-mer.”

We study the distribution of duplication counts of long words (so long they are very unlikely to be repeated by chance) for several organisms whose published genomes have stabilized [23]. Our goal is to determine factors contributing to the duplication count distributions in the genomes we study and to determine plausible models of the evolution of these distributions. Specifically, we analyze the human genome, the genomes of C. elegans, A. thaliana, and D. melanogaster, using 40-mers. We choose the word length k = 40 to be representative of word lengths 20 ≤ k ≤ 100, and we find qualitatively similar duplication count distributions for other values of k in this range. In particular, the power-law-like decay we observe below for k = 40 also occurs for 20 ≤ k ≤ 100. Notice that for k ≥ 20, the number of possible k-mers is considerably larger than the lengths of the genomes we study. Most previous work on duplication counts, e.g., [16–19], study considerably shorter word lengths (k ≤ 10).

When a DNA sequence is duplicated within a genome, the copies will begin to differ through mutations. After enough mutations, the copies may no longer have any identical 40-mers in common. By studying 40-mers that are duplicated exactly within a genome, we focus on repetitive DNA that has not been highly mutated since it was duplicated. This subset of repetitive DNA contains information about the duplication processes that are responsible for repetitive DNA as a whole.

Throughout most of this paper we restrict our attention to complex repeated 40-mers, where by “complex” we mean that each 10-mer occurs only once within the 40-mer. In Sec. IV we consider the remaining “simple” repeated 40-mers, which include microsatellites but represent a small fraction of the repeated 40-mers [24].

In Sec. II we show that duplication counts for complex 40-mers in the genomes we study have a long-tailed distribution with a power-law-like decay. To study properties of duplication processes creating high count duplications, we partition complex repeated 40-mers into different categories. We argue that one category consists primarily of 40-mers that were duplicated by a process that copies subsequences to a nearby location in the same chromosome, while the other category consists primarily of transposable elements, which are duplicated widely across multiple chromosomes. Within each category, we find a power-law-like decay in the duplication count distribution. These results indicate that multiple processes have created the complex 40-mers with high duplication counts. We discuss differences in the relative contribution of these processes to the entire set of complex repeated 40-mers in a genome.

In Sec. III we show that the power-law-like tail in the duplication count distribution is not reproduced by a model in which all subsequences are equally likely to be duplicated. Thus, in order to model the duplication processes that give rise to repeated 40-mers in genomes, one must allow variability in the likelihood of duplication for different subsequences. We show that a simple model of this type does produce power-law-like decay of the duplication count distribution for a general class of distributions of duplication probabilities. We also considered a Markov model that generates a genomic sequence with the same distribution of short k-mers (k ≤ 10) as in a real genome, but find that such a model does not produce a significant number of complex repeated 40-mers. In Sec. IV we discuss our results and related work, in particular power-law-like distributions observed previously for duplication counts of short k-mers (k ≤ 10) [16–21] and gene families [25]. We also show that the distribution of duplication counts for simple 40-mers has power-law-like decay for the genomes we study.

II. DUPLICATION COUNT DISTRIBUTIONS

As discussed above, we find there are at least two kinds of duplication processes that produce power-law-like decay in duplication count distributions: one creating duplications on multiple chromosomes and the other creating copies within a small distance from one another. To distinguish between these processes, we subdivide the repeated 40-mers into categories based on their sequence complexity and distributions within the genome.

Our categorization is complicated by the fact that some 40-mers can occur independently on multiple chromosomes, in the sense that they were created independently by a local duplication process within each chromosome. Such 40-mers consist of relatively simple sequences, largely microsatellites, like “CATCATCAT…” or “AAAA….” These microsatellites have been well-studied and modeled (see [12,14]); these sequences change due to a “slippage” mechanism that can increase or decrease the length of the microsatellite. To avoid such 40-mers, we restrict our attention to 40-mers that are not internally repetitive. Recall that we call a 40-mer complex if each 10-mer within it occurs only once [22], and we call it simple otherwise [24]. By showing power-law-like decay in the duplication count distributions of complex 40-mers, we ensure that these distributions are not dominated by 40-mers associated with microsatellites. (In fact, for the genomes we study most repeated 40-mers are complex, as we will see in Table I and Fig. 4.) We then divide the complex repeated 40-mers into those that occur in multiple chromosomes and those that occur only within one chromosome, and find that each category has a power-law-like decay in its duplication count distribution. In the remainder of Sec. II, we discuss duplication count distributions only for complex 40-mers; we consider simple 40-mers in Sec. IV A.

TABLE I.

Fraction of positions beginning a repeated 40-mer. The table lists the lengths of the genomes we study and the percentage of positions (bases) that begin a repeated 40-mer and that begin a complex repeated 40-mer.

Genome	Length ×106	% positions with count ≥ 2
		All 40-mers	Complex 40-mers
C. elegans	100	7.44	6.74
A. thaliana	119	5.84	5.20
Human genome	3000	11.23	10.69
D. melanogaster	180	5.03	4.85

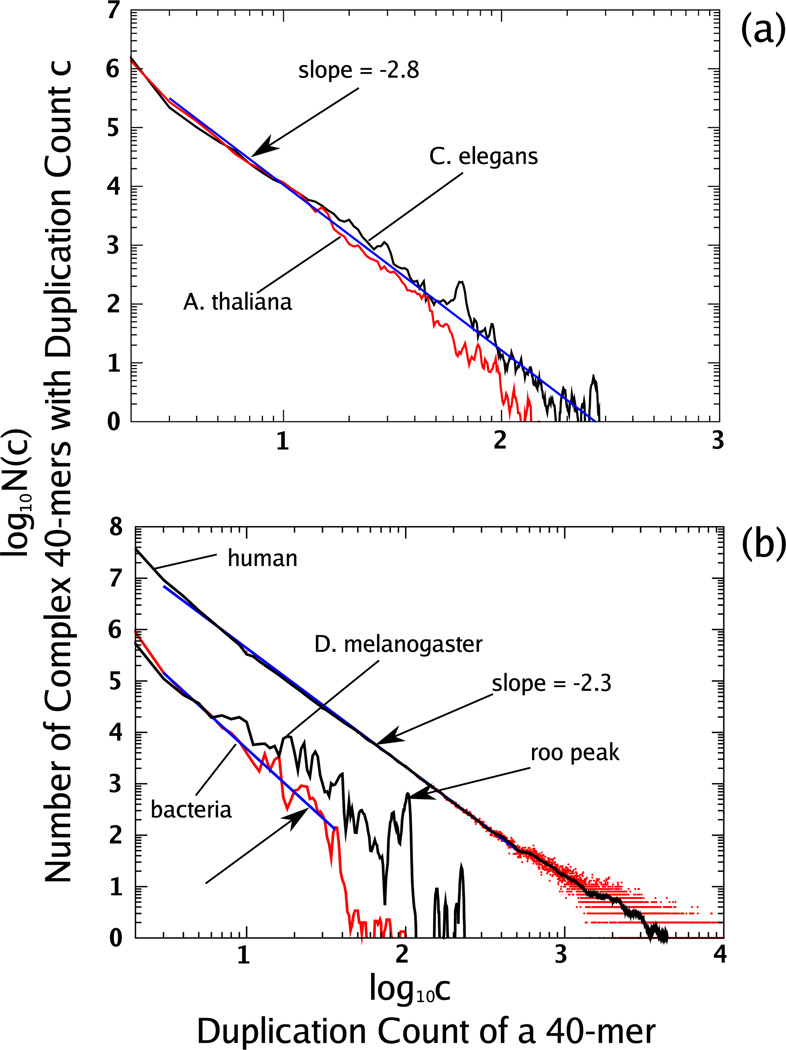
FIG. 4.

(Color online) We show both the simple and complex 40-mer duplication count distributions for the human genome and C. elegans with a moving average as in Fig. 1. All simple and complex distributions follow similar power-law-like distributions for the range of 3 ≤ c ≤ 100.

A. Complex 40-mer duplication count distributions

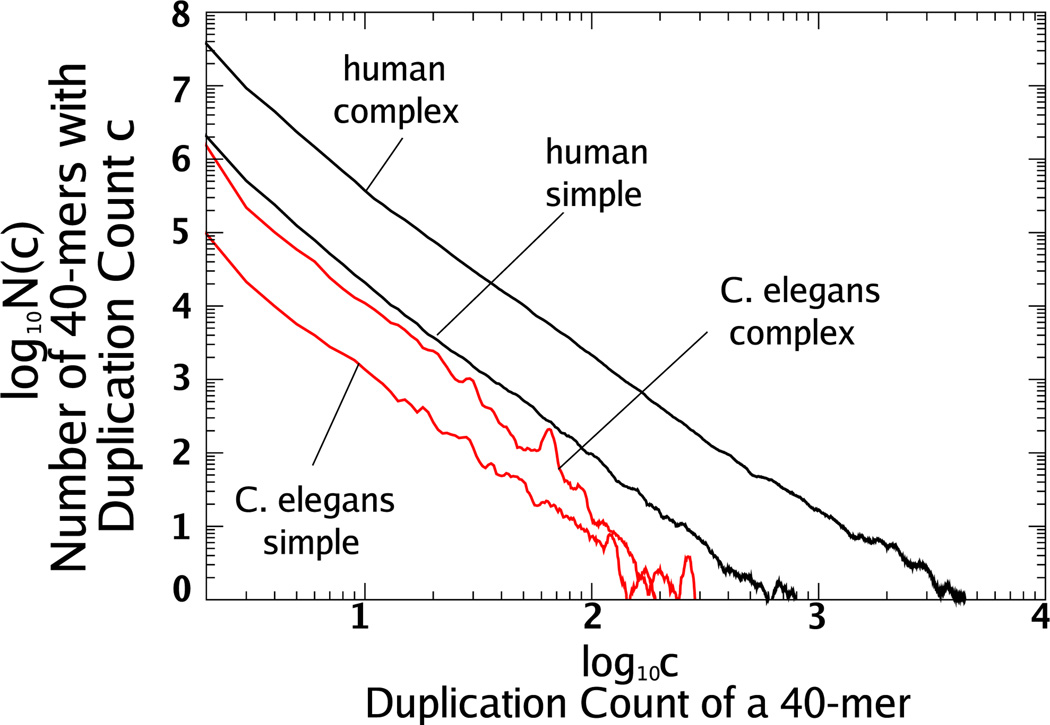
We determined the distribution of duplication counts for complex 40-mers in the human genome and the genomes of C. elegans, A. thaliana, and C. melanogaster, whose sequences we obtained from GenBank [26,27]. These data sets represent the best available, most complete DNA sequences for large genomes. For these genomes, between 5% and 11% of all bases begin a repeated 40-mer. Of these bases, over 88% begin a complex repeated 40-mer (see Table I). In Fig. 1 we graph the number of complex 40-mers, N(c), with duplication count c for these genomes. (The line segments we show with the distributions are intended as only rough approximations.)

FIG. 1.

(Color online) We plot duplication count distributions for complex 40-mers on a logarithmic scale for (a) A. thaliana and C. elegans and (b) human and D. melanogaster. To reduce small-scale fluctuations, we use a moving average of ±5%—that is, for each c we graph the average of N(c) over (0.95c, 1.05c). In (a) we superimpose a line segment with slope −2.8 to approximate the distributions of C. elegans and A. thaliana. In (b) we illustrate the effect of the moving average by showing averaged (solid curve) and unaveraged (dots) duplication count distributions for the human genome. We plot a line segment with slope −2.3 that approximates the human distribution. Even with averaging, the data for D. melanogaster fluctuates more than the other genomes. Several of the peaks in the distribution of D. melanogaster are caused by transposable elements (see text).

C. elegans and A. thaliana

In Fig. 1(a) we plot the duplication count distributions for C. elegans and A. thaliana. We also plot a line segment with slope −2.8 that approximates both distributions well for about 3 ≤ c ≤ 50 and continues to follow the distribution for C. elegans until around c = 200. For A. thaliana beyond c = 50 the distribution drops faster than predicted by a power law.

Human

In Fig. 1(b) we show N(c) for complex 40-mers in the human genome and the genome of D. melanogaster. The data for the human genome also displays a power-lawlike decay over a large range. We plot a line segment with slope −2.3 approximating the duplication count distribution over the range 3 ≤ c ≤ 500.

D. melanogaster

For D. melanogaster, the decay of N(c) can be approximated roughly by a line segment over the range 3 ≤ c ≤ 70. However, N(c) fluctuates more than for the other genomes, especially for c ≥ 70. We find that several of the peaks in the graph of N(c) for c ≥ 70 are due to high fidelity copies of transposable elements. As mentioned previously, transposable elements, or transposons, are a class of repetitive DNA that can create additional copies of their sequence [12]. For example, the deviation from power-law-like decay near duplication count c = 100 is due to 40-mers from the so-called roo element [28], the transposable element in D. melanogaster that has the greatest number of copies and high sequence conservation as described in [29].

Transposable elements also account for some of the deviations from the power-law-like decay for other genomes. For example, we found that 40-mers causing the peak near duplication count c = 70 for C. elegans have high sequence similarity with transposable elements from C. elegans (see Sec. II B).

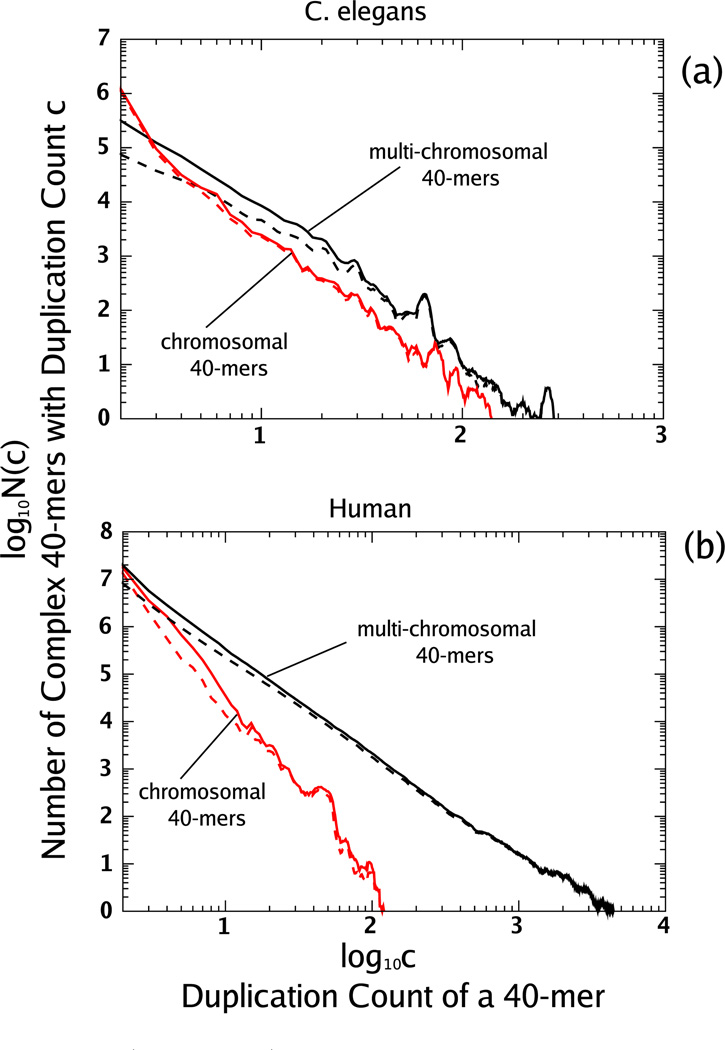
B. Chromosomal versus multichromosomal duplications

We can gain insight into the processes responsible for the duplication count distribution by separating complex 40-mers into two categories depending on where their copies occur. We call a complex repeated 40-mer “chromosomal” if all its copies occur within the same chromosome, and “multichromosomal” otherwise.

In Fig. 2, we show the duplication count distributions for the two categories of complex 40-mers for the human genome and C. elegans. For C. elegans, both distributions follow a power-law-like decay with similar exponents. We observed the same behavior for the genomes of A. thaliana and D. melanogaster when we partition into chromosomal and multichromosomal 40-mers. For the human genome, although both distributions have a power-law-like decay, the chromosomal distribution decays significantly faster. Although some human chromosomes are more than ten times as long as those of C. elegans, the counts of chromosomal 40-mers have nearly the same range. As a result, the tail of the aggregate distribution for the human genome [see Fig. 1(b)] is dominated by multichromosomal 40-mers.

FIG. 2.

(Color online) We show the duplication count distributions for chromosomal and multichromosomal complex 40-mers separately for the C. elegans (a) and the human genome (b). These distributions are shown with a moving average as in Fig. 1. For C. elegans (a), both distributions are qualitatively similar beyond c = 2 and follow approximate power-law distributions with similar exponents. For the human genome (b), the duplication count distribution for chromosomal 40-mers decays like a power law but at a faster rate than multichromosomal 40-mers. We indicate with dashed curves the duplication count distributions for proximate chromosomal 40-mers and for multichromosomal 40-mers that match transposable elements (see text). For both the human genome and C. elegans these dashed lines merge with the chromosomal and multichromosomal distributions as c increases, indicating that the long-tailed power-law-like decay for chromosomal 40-mers is dominated by a proximate sequence and for multichromosomal 40-mers by transposable elements.

Proximate 40-mers

As observed in [30–32], duplications of count exactly 2 in the genome have a strong tendency to occur not only in the same chromosome but very close together. In [30] we observed that for C. elegans nearly 90% of all chromosomal 40-mers with count 2 occurred within 0.3% of the chromosome length. To generalize this idea to higher counts, we define a complex 40-mer to be “proximate with respect to a chromosome” if it has more than one copy within the chromosome and all copies lie within a subsequence of length less than 3% of the length of that chromosome. A complex repeated 40-mer is “proximate” if it is proximate with respect to each chromosome on which it has multiple copies. We have found that much of the proximate sequence consists of a tandemly duplicated sequence, where a sequence is duplicated adjacent to itself.

As shown in Table II, the majority of chromosomal 40-mers in the genomes we study are proximate, while most multichromosomal 40-mers are not. Furthermore, the tendency of chromosomal 40-mers to be proximate, and multichromosomal 40-mers not to be, grows as their duplication counts increase from c = 3 (see Fig. 2 in addition to Table II). We will discuss the case c = 2 in Sec. IV B.

TABLE II.

Proximate fraction. The table shows the fraction of complex repeated 40-mers in a given category that are proximate, i.e., have all their copies within 3% of the length of each chromosome on which they occur more than once. For all genomes, the majority of chromosomal 40-mers are proximate, whereas most multichromosomal 40-mers are not.

	Chromosomal			Multichromosomal
Genome	c = 2	c ≥ 3	c ≥ 10	c ≥ 3	c ≥ 10
C. elegans	0.92	0.84	0.92	0.23	0.04
A. thaliana	0.85	0.89	0.99	0.23	0.04
Human genome	0.76	0.50	0.59	0.20	0.02
D. melanogaster	0.97	0.95	0.96	0.13	0.01

Transposable elements

While proximate duplication strongly influences the chromosomal 40-mers, transposable elements characterize the majority of multichromosomal 40-mers. We compare the complex repeated 40-mers for the genomes we study with the library of known transposable elements as annotated in RepBase [33]. We say that a 40-mer “matches” a transposable element if they share an identical 18-mer. This simple criterion is designed to capture 40-mers that lie within inexact copies of a transposable element throughout the genome, but of course it misses some inexact matches (see [34]).

In all cases, except C. elegans, we find that a majority of multichromosomal 40-mers match a transposable element even when considering very low count multichromosomal 40-mers (see Table III). In fact, as shown for the human genome and the genome of C. elegans in Fig. 2, transposable elements are the dominant mechanism contributing to the long-tailed power-law-like decay for multichromosomal 40-mers.

TABLE III.

Fraction matching transposable elements. Fraction of complex repeated 40-mers in a given category that match a known transposable element (in the sense that they share an identical 18-mer). For each genome, the majority of multichromosomal 40-mers with c ≥ 10, and only a small fraction of chromosomal 40-mers, match a known transposable element.

	Chromosomal			Multichromosomal
Genome	c = 2	c ≥ 3	c ≥ 10	c = 2	c ≥ 3	c ≥ 10
C. elegans	0.09	0.16	0.13	0.24	0.42	0.62
A. thaliana	0.23	0.18	0.05	0.53	0.78	0.91
Human genome	0.10	0.06	0.05	0.41	0.59	0.75
D. melanogaster	0.17	0.19	0.08	0.73	0.93	0.99

For some of the genomes we study, A. thaliana and the human genome, there is substantial evidence of other types of multichromosomal duplication. The species A. thaliana underwent a duplication of the entire genome [2], and thus there are some multichromosomal 40-mers that are neither proximate nor transposable elements. In the human genome there are many segmental duplications ranging in length from a few hundred bases to thousands, such as a duplication of over 2 × 10⁶ bases within chromosome 21 [35]. However, these duplications typically have counts c ≤ 3 and do not contribute to the tail of the duplication count distributions.

The data for chromosomal and multichromosomal complex 40-mers indicates that there are at least two types of processes that independently create a power-law-like decay in duplication count distributions: one that operates primarily within a chromosome, and includes tandem duplication, and another that creates duplications on multiple chromosomes in the genome, and includes transposable elements. We consider in more detail the relative contribution of each category to the repetitive content of the genomes we study in the next section.

C. Position counts

Each position (or base) in the genome is the beginning of a 40-mer (except near the end of a chromosome), so we can refer to its “position count” (meaning the duplication count of its 40-mer). A 40-mer with duplication count c corresponds to c positions with duplication count c. Thus the number of positions with duplication count c is cN(c), where N(c) as above is the number of 40-mers in a given category with duplication count c. Notice that the power-law-like behavior we observe for N(c) applies also to cN(c) with an exponent one greater.

We say that a position is “repetitive” if its position count is at least 2, and that a position is “complex” if its 40-mer is. Although the count of a typical complex repeated 40-mer is relatively low for all our genomes, the count of a typical complex repetitive position is somewhat higher (see Table IV). For example, in the human genome, the median count of a complex repetitive position is 9 and the median count for a complex repeated 40-mer is 2. For all the genomes we study, most complex repetitive positions have a count of at least 3. Thus the power-law behavior we observe for c ≥ 3 in Fig. 1 and Fig. 2 reflects a majority of the complex repetitive positions in the genomes we study.

TABLE IV.

Duplication counts and position counts for complex repeated 40-mers. Mean and median duplication and position counts (see Sec. II C) for the genomes we study.

	Position count		Duplication count
Genome	Median	Mean	Median	Mean
C. elegans	3	12.53	2	3.25
A. thaliana	3	6.50	2	3.05
Human genome	9	706	2	5.10
D. melanogaster	15	29.34	2	6.11

In Sec. II B we argued that the power-law-like decay for complex chromosomal 40-mers is dominated by proximate 40-mers and for complex multichromosomal 40-mers by transposable elements. We now consider the proportion of repetitive positions in the genome that fall into each of these categories. In Table V we show, for each genome, the fraction of repetitive positions that fall into each of five categories. We observe that for all genomes the majority of repetitive positions are either chromosomal and proximate or multichromosomal and match a transposable element. As illustrated in Fig. 2 and Table II and Table III, these categories become even more prevalent for 40-mers with high duplication counts.

TABLE V.

Fraction of repetitive positions. Fraction of repetitive positions in each genome that begin a 40-mer in each of five categories. We classify complex repetitive positions that begin a chromosomal 40-mer according to whether that 40-mer is proximate. We classify complex repetitive positions that begin a multi-chromosomal 40-mer according to whether that 40-mer matches a known transposable element as described in Sec. II B

	Complex chromosomal			Complex multichromosomal
Genome	Simple	Proximate	Not proximate	Transposable	Not transposable
C. elegans	0.10	0.41	0.05	0.18	0.26
A. thaliana	0.11	0.36	0.05	0.35	0.13
Human genome	0.05	0.12	0.07	0.54	0.21
D. melanogaster	0.04	0.26	0.01	0.67	0.03

Notice that for the D. melanogaster and human genome over 2/3 of the repetitive positions begin multichromosomal 40-mers, whereas for the genomes of C. elegans and A. thaliana this proportion is less than half. In the former genomes a majority of the repetitive positions begin multichromsomal 40-mers that match transposable elements, while in the latter genomes repetitive positions that begin proximate chromosomal 40-mers are more common.

III. MODELING DUPLICATION COUNT DISTRIBUTIONS

We next demonstrate that the duplication count distributions discussed in Sec. II are not reproduced by an evolutionary model where duplications are equally likely for all 40-mers. On the other hand, we find that a model allowing variation in the probability of duplication can produce power-law-like distributions. We also consider a Markov model that generates random genomes with the same distribution of short genomes as an actual genome, but find that it produces vastly fewer repeated 40-mers than in the genome.

A. Homogeneous duplication model

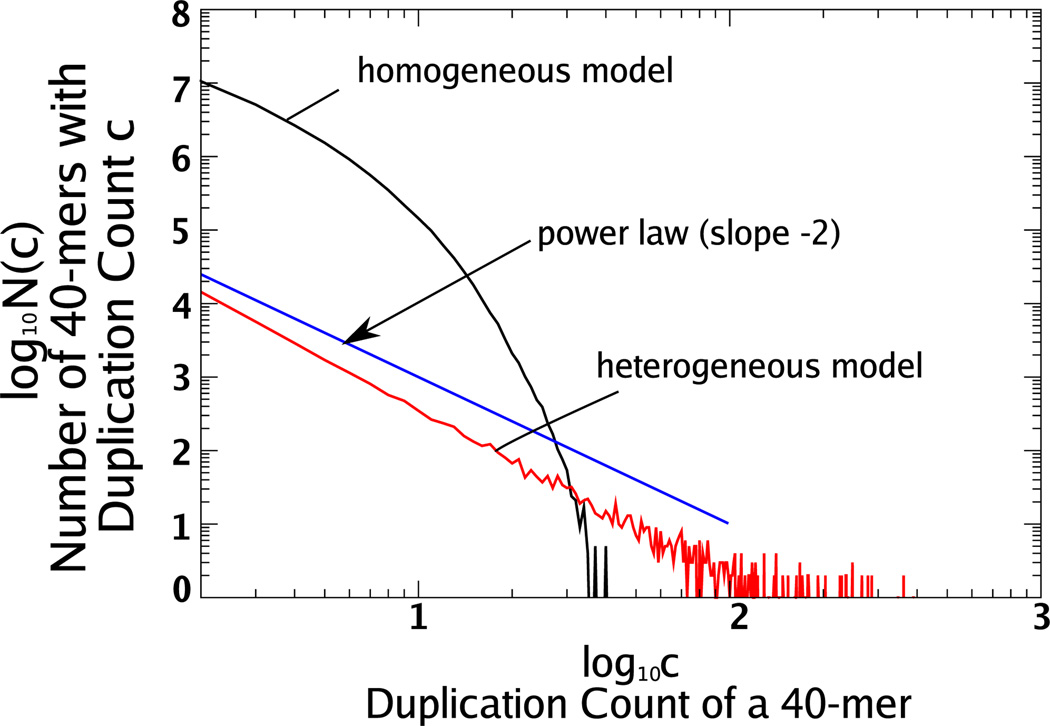
In a homogeneous duplication model, duplications are equally likely to be chosen at any position in the genome. There is a natural way to model such duplications and their long-term evolution. Begin with a random genome of specified size and a distribution of lengths; according to that distribution, select a random segment of the appropriate length from the genome and create an extra copy somewhere else in the genome. To preserve the length of the genome, delete a randomly chosen segment of the same length. To incorporate isolated point mutations, change a fixed number of randomly selected bases in the genome. Then, repeat this combination of duplication, deletion, and point mutations until a stationary distribution of duplication counts is reached.

When we implement this strategy [30], the distribution of 40-mer counts converges quickly to an exponential distribution. In Fig. 3 we plot the distribution of duplication counts for a genome generated by this model. We show the resulting duplication count distribution for a numerical simulation where the initial genome length was 100 × 10⁶ bases (roughly the size of C. elegans) and we chose duplication lengths uniformly between 0 and 2 × 10⁴; we performed 10² point mutations for every duplication and repeated the procedure 1 × 10⁶ times. Although this model does not capture the same power-law-like decay in duplication counts as shown in Fig. 1, it reproduces other significant features of the duplication structure as discussed in [30].

FIG. 3.

(Color online) We show the distribution of duplication counts from numerical simulations of two different random models. In the homogeneous model 40-mers are duplicated at random with the 40-mer at each position in the genome equally likely to be duplicated. In the heterogeneous model, the probability of duplication varies according to the particular 40-mer. The stationary distribution for the homogeneous model is an exponential distribution. The particular form we have chosen for the heterogeneity of duplications leads to a stationary distribution approximately proportional to 1 /(c² log c) (see text). To compare the heterogeneous model with a pure power law, we plot a line segment with slope −2.

The exponential decay that we observe for the duplication count distribution in the model above can be explained with a related model, detailed in [36], that is more abstract and simpler to analyze. This abstract model starts with a population of disjoint 40-mers, each with count 1. The count of each 40-mer evolves in time independently of the other 40-mers. A 40-mer with count c has its count increase to c + 1 with probability δc per unit time, where the constant δ represents the probability per unit time that a particular copy of the 40-mer is duplicated. This reflects homogeneous duplication probabilities; a 40-mer that occurs c times in the genome is c times more likely to be duplicated than a 40-mer that occurs once. In the abstract model, a 40-mer with count c has its count decrease to c − 1 with probability μc per unit time, where the constant μ represents the probability per unit time that a particular copy of the 40-mer is lost due to a point mutation or segmental deletion.

Let N(c) be the number of 40-mers with count c. The stationary count distribution for this model can be determined by setting the flux, δcN(c), of 40-mers from count c to count c + 1 equal to the flux, μ(c + 1)N(c + 1), of 40-mers from count c + 1 to count c, yielding N(c + 1)/N(c) = (δ/μ)c/(c + 1). This implies that N(c) = (δ/μ)^c−1N(1)/c. Thus N(c) decays exponentially for δ < μ. For δ ≥ μ, there is no stationary distribution with Σ_c≥1N(c) < ∞, though formally setting δ = μ yields a power-law distribution with exponent −1.

B. Heterogeneous duplication model

As observed in [36], it is possible to get power-law decay for N(c) with any exponent less than −1 by modifying the abstract model, described above, to allow a given copy of a 40-mer to be more likely to be duplicated the higher the count of that 40-mer. This can be done by replacing the constant δ with an appropriate increasing function of c. In order to obtain a pure power law for N(c), this increasing function must approach μ as c → ∞ at a particular rate.

We observe that a power law can also be obtained by assuming heterogeneous duplication rates for the initial population of 40-mers. (Over time, this causes 40-mers with higher counts to be more likely to duplicate.) We do this by regarding δ to be constant over time for each 40-mer, but to vary among different 40-mers. (A similar evolutionary model for gene family size distribution is discussed in [37].) The resulting stationary count distribution N(c) will then be a weighted average over δ of the exponential distributions we derived for fixed δ, where the weighting depends on the distribution of δ values.

For this model we find that distributions that allow δ to be arbitrarily close to μ generally yield a power-law-like decay for N(c). For example, taking a simple unweighted average over δ between 0 and μ yields

$$N(c)=\frac{1}{\mu }{\displaystyle {\int }_0^{\mu }{\left(\frac{\delta }{\mu }\right)}^{c-1}\frac{N(1)}{c}}d\delta =\frac{N(1)}{c^2}.$$ (1)

Notice this calculation does not reflect a uniform distribution of δ values because we have not normalized the fixed-δ distributions. Doing so, before averaging over δ, yields a correction that is logarithmic for large c; that is N(c) ~ 1 / (c² log c) as c → ∞ if the model is initialized with δ uniformly distributed between 0 and μ (see the Appendix).

We plot a numerical simulation of the heterogeneous duplication model in Fig. 3. In this simulation we begin with 10⁶ 40-mers in the population and μ =10⁻³; duplication probabilities are assigned to each of the 40-mers randomly from the uniform distribution on [0, μ]. The simulation is carried out for 5 × 10⁶ iterations. Along with the simulation results, we plot a line with slope −2 to show the resemblance of the distribution to a pure power law. The slope is somewhat steeper for the simulation results due to the logarithmic correction.

In the Appendix we show that for different a priori distributions of the duplication probability δ, this heterogeneous duplication model can yield a variety of power-law distributions for N(c). Because N(c) is the average over δ of distributions that decay like (δ/μ)^c, the average will itself decay exponentially if δ is bounded away from μ. For N(c) to be a power law, the distribution must allow δ to be arbitrarily close to μ, but not to exceed μ. In this case we find that only the form of the distribution of δ near μ is important in determining the asymptotic decay rate of N(c). In particular, if the density function is approximately proportional to (μ -δ)^α for δ near μ, where α > −1, then N(c) ~ 11 (c^2+α log c) as c → ∞.

These models suggests that the power-law-like decay we observed for N(c) in Sec. II is due to parts of the genome that have duplicated nearly as fast as they have mutated. In the genomes we study, we hypothesize that this property is characteristic of the transposable elements and proximate sequence that dominate the high duplication counts (see Fig. 2 and Table II and Table III).

C. Markov genome model

In addition to studying evolutionary models, we considered Markov models in which the transition probabilities from one short k-mer to the next are derived by the actual distribution of short k-mers in a particular genome. Although numerous studies, such as [20], analyzed distributions of counts of specified words in random sequences of {A,C,G,T} generated by a Markov process, the duplication counts we analyze in this paper have not been widely studied for Markov models, except for short words such as k ≤ 8 [21]. The duplication counts we observe for 40-mers are not reproduced in sequences generated by a Markov process of lower order. The genomes are far more repetitive than these types of models would suggest.

For example, we used a ninth order Markov process to generate sample random genomes of length 10⁸, approximately the same length as C. elegans. We use the actual distribution of 10-mers in C. elegans to determine the transition probabilities from each 9-mer to the next (overlapping) 9-mer. (Generating random genomes using a much higher order Markov model is not feasible because the genomes we study are not long enough to estimate the parameters; only a fraction of all k-mers, for k ≥ 15, actually occur in the genomes.)

For each of the random genomes, the number of simple repeated 40-mers was less than 300 and the number of complex repeated 40-mers was at most 3. By comparison there are over 10⁵ simple repeated 40-mers and over 2 × 10⁶ complex repeated 40-mers in the genome of C. elegans.

IV. DISCUSSION

In this paper, we have shown for a variety of genomes that duplication count distributions have a long-tailed, power-law-like decay, both for complex chromosomal and for complex multichromosomal 40-mers (Fig. 2). In Sec. IV A we show that the same is true for the remaining category of simple 40-mers. We have argued that these categories correspond to distinct duplication processes, so the distributions we observe are characteristic of multiple duplication processes. In Sec. III we have shown that these distributions are not reproduced by models of evolution where each 40-mer is equally likely to be duplicated, while it is possible to reproduce a power-law-like decay from models in which some 40-mers are more likely to be duplicated than others. Thus we feel that when modeling a variety of genomic duplication processes, it is important to take into account “preferential duplication” in which some subsequences of a given length are more likely to be duplicated than others. However, we do not mean to suggest that preferential duplication is characteristic of all important duplication processes. Indeed in Sec. IV B we argue that our chromosomal data suggests a combination of preferential and nonpreferential duplication processes. In Sec. IV C we discuss other work where power-law-like decay has been observed in count distributions.

A. Duplication count distribution for simple 40-mers

In Fig. 4 we show the duplication count distributions for both simple and complex 40-mers for the human genome and the genome of C. elegans. We observe that most repeated 40-mers are complex, but that the duplication counts for simple 40-mers have a similar power-law-like distribution. This indicates that the processes (like those discussed in [12,14]) that produce simple repeated 40-mers are also capable of generating a power-law-like behavior.

B. Chromosomal duplication processes

A close look at our data for complex chromosomal 40-mers suggest that at least two different duplication processes contribute substantially to the duplication count distribution. In Fig. 2, N(2) in the chromosomal distribution of C. elegans lies well above what would be predicted by a pure power-law distribution; we found that the same is true for genomes of A. thaliana and D. melanogaster (as is reflected in the aggregate distributions in Fig. 1). As shown in Table II, chromosomal 40-mers with count c = 2 have a high tendency to be proximate, even for the human genome. In [32], Thomas identifies a class of duplications, called “doublets,” that have count c = 2 and occur within a small separation on the same chromosome. Thomas argues that, unlike microsatellites that have internal repetitions, any sequence could potentially be duplicated to create a doublet. In Sec. III A, we show that when sequence duplication likelihood is homogeneous the duplication count distribution decays very rapidly. While homogeneous duplication cannot be responsible for the entire distribution of chromosomal 40-mers, we conjecture that a similar type of process is responsible for the creation of most of the chromosomal 40-mers with count c = 2 in the genomes of C. elegans, A. thaliana, and D. melanogaster.

C. Previous work

1. Duplication counts for k-mers with k ≤ 10

Previous studies, such as [18], have observed a power-law decay in the distribution of duplication counts for much shorter k-mers, k ≤ 10. Others analyzed the distribution of ranked word counts; that is, the counts of k-mers plotted in decreasing order (see [16,17]). Both of these types of analysis reflect the distribution of the most frequently occurring words, those with counts in the hundreds or thousands. (Some properties reported in [16,17] have been found to hold for randomly generated sequences [38].)

For the genome of C. elegans, roughly 100 × 10⁶ bases, the average duplication count of a 10-mer is about 190. (There are roughly 2¹⁹ ≈ 5 × 10⁵ distinct 10-mers [22].) Thus duplications with a count of much less than 100 will not have a noticeable effect on the distribution of 10-mer duplication counts. Indeed, the power laws in [18] do not emerge until beyond a count of 200. That is, the power-law distribution is not reflective of the range of counts of the majority of long high fidelity repetitive sequences. Because only a small fraction of all 40-mers appear in the genomes we study, we are able to detect high fidelity duplications with a low count.

In addition, these previous studies did not attempt to discuss the types of duplication processes responsible for generating the long-tailed behavior of the duplication counts. Indeed, we have shown that there are two different types of processes that impact the distribution of complex duplications in DNA sequences and that each alone can generate a long-tail decay.

Some studies have suggested that many such power-lawlike distributions in genomics are better fit by a function with more parameters, such as the Yule distribution [17]. Our interest is not in the precise form of the decay, but rather what the slow decay indicates about modeling genomic duplications.

2. Power-law distribution in gene families

A power-law distribution has been observed for the number of members in gene families [25]. Recent papers have developed models of the evolution of gene families (see [36,37,39]) to explain these distributions. Obviously, gene families are under considerable selective pressure that may hide the underlying physical duplication process. The distribution of counts in gene families would certainly impact the duplication count distribution of 40-mers, but the relationship would be indirect. The length distribution of the genes as well as sequence similarity (fidelity) between duplicate genes would also effect the 40-mer distribution. The power-law exponents determined for gene families [18] are distinct from the exponents we determine for complex 40-mers.

To study the relationship between repeated 40-mers and duplicated genes, we determined the distribution of 40-mers contained in the genes of C. elegans according to current gene annotations [26]. The distribution of duplication counts for 40-mers in genes is consistent with power-law-like behavior of a similar exponent, but represents less than 10% of the repetitive content in the genome for duplication counts c ≥ 10. It is possible that similar processes could be responsible for both the power-law distribution in gene families and complex 40-mers.

APPENDIX

In Sec. III B we introduce a heterogeneous duplication model that evolves the counts of a collection of elements (e.g., 40-mers) that have the same mutation probability, μ, but distinct duplication probabilities δ, δ ≤ μ. Here we discuss the relationship between the a priori distribution of δ values and the stationary distribution of counts to which the model evolves. We consider only values of δ between 0 and μ.

We assume that the elements each evolve independently according to the duplication-mutation process described in Sec. III A. For each element, we assume that its duplication probability remains constant in time and that its minimum count is 1. Thus mutating an element of count 1 alters neither the distribution of counts nor the distribution of duplication probabilities.

If M is the total number of elements in the full collection and the distribution of duplication probabilities has density function g(δ), then the expected number of elements with duplication probability between δ and δ+dδ is Mg(δ)dδ. Let N(c, δ) represent the stationary joint distribution of c and δ, in the sense that the expected number of elements with count c and duplication probability between δ and δ+dδ is N(c, δ)dδ.

In Sec. III A, we showed that for a homogeneous population of duplication probabilities,

$$N(c,\delta )={(\delta /\mu )}^{(c-1)}\frac{N(1,\delta )}{c}.$$

Summing this equation over c yields

$$\begin{array}{c}Mg(\delta )={\displaystyle \sum _{c\ge 1}N(c,\delta )=}{\displaystyle \sum _{c\ge 1}{\left(\frac{\delta }{\mu }\right)}^{(c-1)}\frac{N(1,\delta )}{c}}\\ =N(1,\delta )\left(\frac{-\text{log}\left(1-\frac{\delta }{\mu }\right)}{\frac{\delta }{\mu }}\right).\end{array}$$

These two equations determine N(1, δ) in terms of Mg(δ). The stationary distribution of counts is then given by

$$N(c)={\displaystyle {\int }_0^{\mu }N(c,\delta )d\delta =\frac{M}{c}{\displaystyle {\int }_0^{\mu }{(\delta /\mu )}^c\left(\frac{g(\delta )}{-\text{log}(1-\delta /\mu )}\right)d\delta .}}$$ (A1)

This equation determines N(c) in terms of the a priori distribution of δ with density function g(δ). In the remainder of the Appendix we discuss how the asymptotic decay rate of N(c) as c → ∞ depends on g(δ).

First we observe that N(c) decays exponentially if g(δ) is identically 0 for δ near μ. To be precise, if g(δ) = 0 for λ < δ ≤ μ then

$$N(c)={\displaystyle {\int }_0^{\lambda }N(c,\delta )d\delta \le \frac{M}{c}{(\lambda /\mu )}^c{\displaystyle {\int }_0^{\lambda }\frac{g(\delta )}{-\text{log}(1-\delta /\mu )}d\delta .}}$$

By the same argument, changing g(δ) on an interval that is bounded away from μ changes N(c) by at most an exponentially decaying term. Thus if N(c) decays more slowly than an exponential function of c, the decay rate depends only on the form of g(δ) for δ near μ.

Consider the case that g(δ) behaves like a power of (μ − δ) as δ → μ. To be precise, assume that

$$g(\delta )=h(\delta ){(\mu -\delta )}^{\alpha }$$

where α > −1 and h(δ) is continuous and bounded with h(μ) > 0. We claim that N(c) ~ 1/(c^α+2 log c). The case α = 0 corresponds to g(μ) > 0 and finite. In particular, the uniform distribution that we considered in Sec. III B falls into this category.

To verify our claim, we start by performing a change of variables to Eq. (A1), x=1 − δ/μ, and arrive at the following:

$$N(c)=\frac{M\mu }{c}{\displaystyle {\int }_0^1\frac{{(1-x)}^{c}g(\mu (1-x))}{-\text{log}x}dx.}$$

The integrand is small except when x is of order 1/c. To see this, notice that for 0 < x < 1 we have

$$\frac{{(1-x)}^c}{-\text{log}x}\le {(1-x)}^{(c-1)}\le e^{-(c-1)x}.$$

Here we have used the inequalities (1 − x) ≤ (−logx) and (1 −x) ≤ e^−x. We next re-normalize x in terms of c so the range over which the integrand is significant will be roughly independent of c as c → ∞. Letting x = t/c we have the following:

$$N(c)=\frac{M\mu }{c^2}{\displaystyle {\int }_0^c\frac{{(1-t/c)}^{c}g(\mu (1-t/c))}{\text{log}(c/t)}dt.}$$ (A2)

First consider the case α = 0, for which g(δ) = h(δ) is continuous and bounded. To show that N(c) ~ 1/(c² log c), we multiply Eq. (A2) by c² log c, yielding

$$c^2(\text{log}c)N(c)=M\mu {\displaystyle {\int }_0^c\frac{\text{log}c}{\text{log}(c/t)}{(1-t/c)}^{c}g(\mu (1-t/c))dt.}$$

Formally, we can take the limit as c → ∞ as follows:

$$\begin{array}{l}\underset{\mathrm{c}\to \infty }{\text{lim}}{c}^2(\text{log}c)N(c)\hfill \\ =M\mu {\displaystyle {\int }_0^{\infty }\underset{c\to \infty }{\text{lim}}\frac{\text{log}c}{\text{log}(c/t)}{(1-t/c)}^{c}g(\mu (1-t/c))dt}\hfill \\ =M\mu {\displaystyle {\int }_0^{\infty }{e}^{-t}g(\mu )dt=M\mu g(\mu ).}\hfill \end{array}$$

Below we justify exchanging the limit with the integral with the Lebesgue dominated convergence theorem. If g(μ) > 0, then we have shown that N(c) ~ 1/(c² log c).

We treat the case g(δ) = h(δ)(μ − δ)^α for other values of α > − 1 in a similar fashion. First, multiplying Eq. (A2) by c^2+α log c yields

$$\begin{array}{l}{c}^{2+\alpha }(\text{log}c)N(c)\hfill \\ =M{\mu }^{\alpha +1}{\displaystyle {\int }_0^c\frac{\text{log}(c)}{\text{log}(c/t)}{(1-t/c)}^{c}h[\mu (1-t/c)]t^{\alpha }dt.}\hfill \end{array}$$

Taking the limit as c → ∞ formally yields

$$\begin{array}{ll}\underset{c\to \infty }{\text{lim}}{c}^{2+\alpha }(\text{log}c)N(c)\hfill & =M{\mu }^{\alpha +1}h(\mu ){\displaystyle {\int }_0^{\infty }{e}^{-t}{t}^{\alpha }dt}\hfill \\ \hfill & =M{\mu }^{\alpha +1}h(\mu )\mathrm{\Gamma }(1+\alpha ).\hfill \end{array}$$

Notice that other forms of N(c) are also possible. For example, if

$$g(\delta )=h{(\delta )(\mu -\delta )}^{\alpha }[-\text{log}(1-\delta /\mu )],$$

where α > −1, h(δ) is continuous and bounded with h(μ) > 0, then by the same argument N(c) ~ 1/ c^α+2. The following proposition uses the Lebesgue dominated convergence theorem to justify the formal arguments above.

Proposition 1. If the distribution of duplication probabilities in the heterogeneous duplication model has density function g(δ) = h(δ)(μ − δ)^α, where α > −1 and h(δ) is continuous and bounded on the interval 0 ≤ δ ≤ μ, and h(μ) > 0, then the stationary distribution of duplication counts is given by

$$N(c)=\beta /(c^{2+\alpha }\text{log}c)+o[1/(c^{2+\alpha }\text{log}c)],$$

where β = M/μ^α+1h(μ)Γ(1 + α).

Proof. In order to justify the formal evaluation of the limit as c → ∞ of c^2+αN(c) above, we need to show that

$$\begin{array}{l}\underset{c\to \infty }{\text{lim}}{\displaystyle {\int }_0^c\frac{\text{log}c}{\text{log}(c/t)}{(1-t/c)}^{c}h[\mu (1-t/c)]t^{\alpha }dt}\hfill \\ ={\displaystyle {\int }_0^{\infty }\underset{c\to \infty }{\text{lim}}\frac{\text{log}c}{\text{log}(c/t)}{(1-t/c)}^{c}h[\mu (1-t/c)]t^{\alpha }dt.}\hfill \end{array}$$

In other words, we need to show that ${\text{lim}}_{c\to \infty }{\displaystyle {\int }_0^{\infty }{F}_c(t)dt={\displaystyle {\int }_0^{\infty }{\text{lim}}_{c\to \infty }{F}_c(t)dt}}$, where F_c(t) is defined as follows:

$$F_c(t)=\frac{\text{log}c}{\text{log}(c/t)}{(1-t/c)}^{c}h[\mu (1-t/c)]t^{\alpha },$$

when t < c and F_c(t) = 0 when t ≥ c. This follows from the Lebesgue dominated convergence theorem provided we can show that, for c sufficiently large, there is a function independent of c, G(t), with finite integral such that F_c(t) ≤ G(t). We claim that a suitable G(t) is given by

$$G(t)=2e^{-t/4}H{t}^{\alpha },$$

where H is an upper bound on h(δ) for 0 ≤ δ ≤ μ. Notice that G(t) indeed has finite integral when α > − 1 and the inequality F_c(t) ≤ G(t) holds when t ≥ c. Because we trivially have h[μ(1 − t/c)]t^α ≤ Ht^α, it remains to be shown that

$$\frac{\text{log}c}{\text{log}(c/t)}{(1-t/c)}^c\le 2e^{-t/4}$$ (A3)

for sufficiently large c and 0 ≤ t ≤c.

Case 1. When $0\le t\le \sqrt{c}$, we have the following:

$$\frac{\text{log}c}{\text{log}(c/t)}=\frac{\text{log}c}{\text{log}c-\text{log}t}\le \frac{\text{log}c}{(1/2)\text{log}c}=2.$$

Also, using the inequality (1−x) ≤ e^−x, we have (1 − t/c)^c ≤ e^−t ≤ e^−t/4. Together these inequalities establish Eq. (A3) in this case.

Case 2. For $\sqrt{c}\le t\le c$ we write the left-hand side of Eq. (A3) as the product of three terms:

$$\frac{1-t/c}{\text{log}(c/t)}\times {(1-t/c)}^{(c-1)/2}\text{log}c\times {(1-t/c)}^{(c-1)/2}.$$

For the first term, we use the inequality (1 − x) ≤ −logx to obtain

$$\frac{1-t/c}{\text{log}(c/t)}\le 1.$$

Next we consider the second term (1 − t/c)^(c−1)/2 log c. This is a decreasing function of t that attains its maximum value when $t=\sqrt{c}$. Thus (1 − t/c)^(c−1)/2 log c ≤ (1 − c^−1/2)^(c−1)/2. We again use the inequality (1 − x) ≤ e^−x to arrive at

$${(1-t/c)}^{(c-1)/2}\text{log}c\le e^{-(c-1)/(2\sqrt{c})}\text{log}c.$$

The right-hand side is at most 2 when 1 ≤ c ≤ e² and is decreasing for c ≥ 2, as can be shown by differentiation. Thus we have

$${(1-t/c)}^{(c-1)/2}\text{log}c\le 2.$$

Finally, we bound the third term (1 − t/c)^(c − ^1)/2 ≤ e^{−(t/c)(c−1)/2} ≤ e^−t/4 when c ≥ 2. Combining these three inequalities we have demonstrated Eq. (A3) for c ≥ 2 when $\sqrt{c}\le t\le c$.