Reproducibility Analysis of Diffusion Tensor Indices and Fiber Architecture of Human Calf Muscles in vivo at 1.5 Tesla in Neutral and Plantarflexed Ankle Positions at Rest

Abstract

Purpose

To investigate the reproducibility of diffusion tensor imaging (DTI) derived indices and fiber architecture of calf muscles at 1.5 Tesla, to establish an imaging based method to confirm ankle position, and to compare fiber architecture at different ankle positions.

Materials and Methods

Six subjects were imaged at 1.5T with the foot in neutral and plantarflexed positions. DTI indices were calculated in four muscle compartments (medial and lateral gastrocnemius (MG, LG), superficial and deep anterior tibialis (AT-S, AT-D). Two subjects were scanned on three days to calculate the coefficient of variability (CV) and the repeatability coefficient (RC).

Results

DTI indices were close to the values obtained in earlier 3T and 1.5 T studies. FA decreased significantly in the MG and increased significantly in the AT-S and AT-D compartments while fiber orientation with respect to the magnet Z-axis increased significantly in the MG and decreased significantly in the AT-S compartment with plantarflexion. The CV and RC for the DTI indices and fiber orientations were comparable to 3T studies. Fiber lengths and orientation angles in the MG matched corresponding measures from ultrasound studies.

Conclusion

DTI at 1.5 Tesla provides reproducible measures of diffusion indices and fiber architecture of calf muscle at different muscle lengths.

INTRODUCTION

Diffusion tensor imaging (DTI) of skeletal muscle is emerging as a promising technique to study muscle architecture in normal and diseased states (1 – 8). A small number of studies have been conducted that monitor the changes in fiber orientation and DTI indices as a function of ankle position (dorsiflexion, neutral, plantarflexion) under passive ankle positions at 3 Tesla and during flexion at 1.5 Tesla (9– 12). However, rigorous reproducibility studies have been performed for the DTI indices (fractional anisotropy, ADC, eigenvalues) as well as for fiber orientation/pennation angles only at 3 Tesla (12, 13). It is important to evaluate the DTI indices and fiber reproducibility of calf muscle at 1.5 T as well. The main limitation to imaging at lower field strengths is the loss in signal-to-noise (SNR), a factor critical in musculoskeletal diffusion tensor imaging. However, there are several advantages of imaging at 1.5 Tesla including wider clinical availability, lower susceptibility induced artifacts, and better fat suppression. Incomplete fat suppression adversely affects image quality of diffusion images but is a practical reality at any field strength, especially when large fields of view are employed. However, lower field strengths offer the advantage of a smaller chemical shift of fat voxels in the event of incomplete fat suppression. In general, susceptibility artifacts are not as big a concern in calf muscle DTI as in brain DTI. However, susceptibility artifacts from bone/tissue and air/tissue interface effects on a 3.0T MR scanner are up to four times greater than those on a 1.5T scanner (14). Echo planar based DTI is extremely sensitive to susceptibility artifacts due to the low bandwidth of the phase-encode direction and thus higher fields (such as 3T) can cause geometric distortions at bone/tissue interfaces. The reduction in susceptibility induced artifacts at 1.5 T (compared to 3T) has important consequences in that the diffusion tensor images have higher geometric fidelity and enable larger volume imaging without the need for repositioning and centering in the magnet volume. Studies at 1.5 Tesla have monitored changes in DTI during active plantar- and dorsiflexion (10,11). Deux et al assessed calf muscle contraction under active conditions at 1.5 Tesla and monitored the three eigenvalues, fractional anisotropy (FA) and apparent diffusion coefficient (ADC) quantitatively, whereas the fibers were classified qualitatively (10). Okamoto et al use active controlled conditions to study the calf muscle DTI at 1.5 T and to monitor the changes in the eigenvalues, ADC and FA (11). However, a comprehensive study of reproducibility of DTI indices, fiber lengths and orientations in the different muscle compartments and under different ankle positions has not been reported as yet at 1.5 Tesla. In particular, it is important to assess the reproducibility of the fiber orientation changes as it is very sensitive to the noise in the acquired data and further, depends on the accuracy with which the ankle position can be measured.

The clinical applications of DTI measurements in muscle have been explored only recently (15–17). Zariaskaya et al used DTI in the evaluation of muscle injury resulting from trauma and found decreased measures of FA and increased measures of ADC which is consistent with cellular damage and inflammation resulting in a less ordered tissue microstructure (17, 18). Similar results have been found for DTI changes in skeletal muscle injury due to ischemia (15, 16). In contrast, atrophy resulting from denervation was reported to cause a significant increase in FA and no significant change in ADC (19). The latter study did not evaluate muscle fiber architecture; however the clinical potential for mapping fiber pennation angles and lengths is significant. It will enable a better understanding of physiological changes with atrophy and provide the ability to correlate muscle functional changes to architectural changes, to monitor recovery, and to optimize rehabilitation paradigms. Fan and Doe reported compartmental T2 relaxation and DTI measurements in carrageenan induced edema in rat skeletal muscle (18). The latter study showed that edematous rat muscle showed compartmental diffusion that reflected intra-and extra-cellular water and the potential to explore architectural changes with muscle injury.

In this study, we estimate the reproducibility at 1.5 Tesla of estimates of DTI indices and fiber length and orientation of different muscles of the calf at two foot positions, plantarflexed and neutral, both at rest. In an effort to reduce scan time, investigations were also performed to compare a 6 direction diffusion gradient acquisition with a 13 direction diffusion gradient acquisition. Further, using the body coil to accurately measure ankle/foot position, DTI indices were measured at four ankle angle positions. To date, studies have used an external device to change and maintain the foot in different ankle positions. However, external devices do not provide a method as accurate as does imaging to monitor the ankle position. The latter is defined as the angle subtended by the longitudinal axis of the tibia and the line through the head of the second metatarsal, intersecting at the center of rotation on the talus (20). Inaccuracies in determining the ankle position (when measured with external device) will then translate to variability in the measured DT indices and fiber architecture (length and orientation) changes. In this study, we confirm ankle position using the body coil to image the foot (without change in foot position from the DTI scan).

MATERIALS AND METHODS

Image Acquisition

Studies were performed on six healthy subjects (5 males, 1 female with an average age of 40 years). Two subjects were scanned under conditions of rest with the foot in neutral and plantarflexed positions on three separate days to determine the coefficient of variation (CV) and the repeatability coefficients (RC) of the diffusion tensor derived indices. Studies were conducted after the subjects signed the appropriate consent form reviewed and approved by the Institutional Review Board. Images in the axial view were acquired from the mid-calf region on a 1.5T system (GE; GE Medical Systems), using the 8-channel phased array knee coil. The subject lay in a supine position with the leg in a relaxed state; care was taken to position the subjects with the long axis of the leg placed parallel to the magnetic field by aligning the laser line with the tibia, with the center of the coil approximately 10 cm below the tibial head. The foot was taped with a surgical band to an adjustable plastic cradle which ensured that the foot was immobile and comfortably held during the acquisition in the neutral (+5° to +10°) and plantarflexed (+126° to +134°) ankle positions. Here 0° (neutral) corresponds to the position when the angle subtended by the longitudinal axis of the tibia and the line through the head of the second metatarsal, intersecting at the center of rotation on the talus is 90° and ‘+’ refers to the ankle rotated away from the neutral toward the plantarflexed direction. Two of the subjects were also imaged with the foot in two different ankle positions in addition to the above neutral and plantarflexed positions.

Sagittal images were first acquired in the body coil with the foot taped in position. The foot position was confirmed from these images and adjusted to the desired ankle angle. The rest of the study was conducted using the knee coil without any change in the foot position. The spin echo planar imaging (SE-EPI) based DTI acquisition consisted of a baseline and 13 diffusion-weighted axial images (b factor: 500 s/mm²) along 13 non-collinear gradient directions. A 6 diffusion direction scan was also performed with the same parameter settings as for the 13 diffusion direction scan. The optimum directions for the 6- and 13-diffusion gradients were obtained based on the electrostatic repulsion algorithm proposed by Jones et al (21). Image acquisition parameters were as follows: TE/TR/FOV/matrix: 46 ms/5000 ms/24 cm/128 × 128 with SENSE parallel imaging and a reduction factor of 2. Images were reconstructed to a matrix size of 256×256. The in-plane resolution for all the studies was 0.94 mm × 0.94 mm in the reconstructed images while the slice thickness was 5 mm and the number of slices ranged from 21 to 23. Each DTI acquisition was performed with 8 averages which resulted in a scan time of ~9 mins (13 directions) and ~4.6 mins (6 directions). The volume of interest was also shimmed using the autoshim utility prior to the DTI acquisition. Fat was suppressed by preferentially exciting water using a spectral-spatial RF pulse. High-resolution images that matched the anatomical location of the DTI images were also acquired using T2-weighted fast spin echo (FSE) sequence. The above three image sequences were repeated for each foot position.

Rationale for DTI Sequence Parameters

It is important to note the low TE value of 46 ms for diffusion weighted imaging used in the current study. As the T2 of muscle is short, it is critical to have a low TE to ensure sufficient SNR for DTI measurements. This was achievable on the GE 1.5 T scanner with the fast gradient option which is available on most clinical systems. In addition, the dual 180° refocusing pulse for eddy current compensation was not used as this would have prolonged the minimum echo time. The eddy current induced distortions due to the diffusion gradients were not more than 1–2 pixels even without the dual 180° pulses. Further, the residual eddy current distortions were corrected in the post-processing. The other factor that enabled a low TE of 46 ms was the choice of b at 500 s/mm² (contrast with b values of 1000 s/mm² or greater for brain imaging). The choice of low b values also implies lower eddy current effects.

Numerical simulations have shown that the variance in the trace, fractional anisotropy and tensor orientations decreased for a greater number of diffusion gradient directions (22). For tissue with high FA (>0.7), like that of white matter, the optimum number of gradient directions was estimated at 30 with the directions optimized using the electrostatic repulsion algorithm. For tissue with low FA values (~0.4), the benefits of going to higher number of gradient directions was not that pronounced and the variances in the DTI indices did not change much for gradient directions greater than 14 (22). It should be noted that the simulation study found a greater sensitivity to the number of diffusion gradients as the SNR decreased. Since muscle FA is low (~0.25), 13 diffusion gradients were applied in directions optimized by the electrostatic repulsion algorithm. However, a detailed study of the tradeoff between averages, diffusion directions and SNR will be required to elucidate the optimal strategies.

Brain DTI studies are usually acquired with a b value of 1000 s/mm² whereas a lower value of 400–600 s/mm² is chosen for muscle imaging since one focus of the sequence design is to minimize TE in order to maximize SNR of the low T2 muscle. The theoretical optimum value for b for a two point acquisition is given by 1.11/ADC (=580 s/mm²), where ADC is the diffusion coefficient of muscle (23). Numerical simulations using muscle tissue have also shown that optimum ‘b’ values in terms of minimizing variance in DTI indices are 580±145 s/mm²(23); thus the choice of 500 s/mm² in the current study.

Image Analysis

Motion and eddy current correction

The quality of the diffusion weighted images was first visually inspected for motion and other artifacts. The eddy current correction was modeled as an affine transform while the motion correction was modeled by a rigid transform. Since the affine includes the rigid transform, the two transformations were combined into a single affine transform. The baseline DTI image (with b of 0 s/mm²) was taken as the reference image and each diffusion weighted volume was aligned to it using a 12 parameter affine transform. Diffusion gradient directions were also rotated using the rotational component of the affine transform matrix obtained from the alignment.

The tensor model of diffusion assumes that the underlying diffusion transport can be represented by a single symmetric Gaussian displacement distribution (24). The 3×3 symmetric diffusion tensor, D, is calculated at each voxel from:

$$ln\left(\frac{S_b}{S_{b=0}}\right)=\sum _{i=x,y,z}\sum _{j=x,y,z}exp(b_{ij}{D}_{ij})=-(b_{xx}{D}_{xx}+2b_{xy}{D}_{xy}+2b_{xz}{D}_{xz}+b_{yy}{D}_{yy}+2b_{yz}{D}_{yz}+b_{zz}{D}_{zz})$$

where S_b is the signal intensity in the diffusion weighted image and S_b=0 is the baseline image without any diffusion weighting. The diffusion tensor can be visualized as a ellipsoid whose principal axes are in the ratio of the three eigenvalues (λ₁, λ₂, λ₃). With the current acquisition scheme, this leads to 13 equations which are fitted to a linear regression model to extract the tensor components. The calculated value at each voxel is then the value of the signal intensity corresponding to the fitted line to the tensor model.

Difference images are obtained by a voxel based subtraction of the calculated and acquired diffusion weighted images. Images/voxels that are corrupted by motion and/or other artifacts will deviate from the tensor model and will not be close to the fitted line and will show up in the difference images with non zero pixel intensities, thus enabling identification of the distortions. Diffusion gradient induced eddy current artifacts are usually detected at edges along the phase encode direction with artifact location varying with the diffusion gradient direction. Difference images of each subject were verified to confirm that the data was artifact free. It should be noted that the difference images were not used to drive the registration program; the latter algorithm uses its own cost function (standard deviation of ratio images) to drive the registration. The difference images were used to visualize that the registration had corrected motion and eddy current artifacts. This was only a qualitative estimation and the registration was repeated when the difference images did not show any improvement or showed larger regions of mismatch compared to the unregistered data.

The eddy current and motion correction was performed on the averaged image. It is true that the optimum method is to perform the correction on each dataset before averaging. In practice though, our preliminary comparisons of correcting each dataset before averaging and correcting the the averaged data showed that the two methods were not significantly different. Given that the averaged data was faster to process than each separate dataset, the averaged datasets were used. It should however be noted that large distortions from eddy currents were not seen due to the low b values and motion artifacts were minimized by the lower leg immobilizing device.

Denoising

The SNR of the current data was measured in the baseline images by the subtraction of two identical scans; this is the method recommended by Dietrich et al for parallel imaging (25). The latter method consists of acquiring two scans with the same DTI protocol and pre-scan settings. Two baseline (no diffusion weighting) images at the same location were analyzed using data from ROIs placed in each muscle compartment. The SNR was calculated as the quotient of the mean value (in the ROI) of the signal in the sum image and the SD (evaluated in the same ROI) of the signal in the difference image, divided by a factor of √2. The method assumes a Gaussian noise distribution within the ROI in the difference image and thus all the ROIs were placed in high signal regions (muscle).

The DTI acquisition is inherently noisy and a denoising algorithm was used to decrease the noise in the calculated tensor data. The tensor smoothing was performed using the log-Euclidean anisotropic filter available from the software package, MedINRIA (26). This method is based on the anisotropic diffusion filter which smooths in homogeneous regions but preserves the edges in the image. The actual degree of smoothing is controlled by the gradient threshold for smoothing (kappa) and the number of iterations. In this study, kappa was set at 0.2 and the number of iterations to 250. These values were selected based on the balance between smoothing and blurring.

Tracking

Fibers were tracked from the smoothed tensor using the fractional anisotropy and the lead eigenvector. Seed points were placed interactively: close to and shifted by 1–2 pixels from the aponeurosis of origin on the resliced coronal images for the MG. Inter-observer variability in fiber tracking was assessed based on two observers placing seed voxels as described above. In this study, the focus is on evaluation of the MG fibers (mean fiber length, fiber orientation and average CV and RC values of the same). Fibers were traced from the middle of the MG muscle. Tracking was performed using the free software package, DTIStudio (27). The FA threshold was set at 0.1 to avoid missing fibers in regions of low FA and the angular threshold was set low at 20° (i.e., the fiber tracking stopped if the fiber orientation changed by greater than 20° in adjacent voxel locations in the track). This latter condition is in conformance with the knowledge that muscle fibers do not exhibit a high curvature. The fiber orientation was calculated as the mean of the fiber orientations of all the voxels in the fiber track.

Statistical Analysis

The image(s) with the maximal cross-section of the muscle compartments were chosen for analysis. The ROIs were traced for the following four compartments: Medial gastrocnemius (MG), Lateral Gastrocnemius (LG), Anterior Tibialis, superficial (AT-S) and Anterior Tibialis, deep (AT-D) using the anatomic T2-FSE images as guide; care was taken to avoid blood vessels. ROIs were adjusted to be 1–2 voxels within the anatomic border and ranged from 115 mm² (in the AT, Deep) to 759 mm² (in the MG). The lead eigenvector orientation was calculated with respect to the magnet X-, Y- and Z-axis. Values of the DTI indices and the fiber orientations are reported as mean and standard deviation (SD) of the six subjects. The coefficient of variation (CV) was calculated as the ratio of the within subject standard deviation, S_w to the mean value expressed as a percentage (estimated from the three repeat measures). The mean of the CVs for each subject is reported for each DTI index in the four muscle compartments.

The repeatability coefficient, RC, which represents the threshold value below which the absolute differences between 2 measurements on the same subject is expected to lie for 95% of the measurement pairs was also calculated (28). With the assumption of normal distribution, the difference between two measurements on the same subject (the repeatability coefficient) is expected to be less than 1.96 × standard deviation of the difference for 95% of all pairs of measurement. However, the standard deviation for the difference values (of repeat measurements) is equal to √ 2 times the within-subject standard deviation (S_w); this results in a factor of 1.96*√2*S_w; the first of these two terms equal 2.77. Since the coefficient of variation (CV) is defined as (S_w/mean)*100, RC can also be formulated as 0.0277*mean*CV.

CV is a dimensionless quantity and is a useful index when S_w varies with the measurement level (mean values). When S_w is constant over the measurement range, then RC is useful. Both values are reported here as measures of reproducibility. However, as RC provides absolute values it directly allows one to disambiguate the intrinsic variance of the method from real effects (as from shortening of the muscle). Another measure reported here is the limits of agreement (mean±1.96 SD), where the mean is the mean of the differences of repeat measurements and the SD is the standard deviation of the differences. The limits of agreement (LOA-lower (L) and upper (U)) provides a measure of the differences (in the DTI values) in repeated measurements on the same subject. The changes in DTI indices between the neutral and plantarflexed states were tested for significance using a paired t-test. The significance of differences in CV between 13 and 6 directions was evaluated by a paired t-test on the CV for each muscle calculated from repeated 13 gradient or the 13- and 6- gradient directions.

RESULTS

Image Quality

The overall image quality was good and no data set or images had to be discarded due to the presence of artifacts. Motion artifacts were not seen in any of the data confirming that the restraining device worked effectively. Further, fat images shifted into the water image were not seen; this is a common artifact in muscle imaging at 3T when the fat suppression is sub-optimal. In the current study, peripheral fat was incompletely suppressed in one subject, but the fat image was not shifted into the muscle regions, so the data could be used in the analysis.

Tensor Denoising

The SNR was evaluated in two subjects, each SNR assessment required two identical acquisitions. The average baseline image SNR (of both subjects) measured in the compartments using the same ROIs as for the DTI indices ranged from 102.1±2.3 in the MG/LG to 68.4± 1.2 in AT superficial and deep compartments. The baseline image SNR values in the AT at 3T are ~ 109 for the superficial and 147 for the deep compartments, so that the MG/LG SNRs of the current study are comparable but that of the AT compartments is less than that of the 3T study (13). Images of the lead eigenvector in the plantarflexed ankle position for one of the subjects (axial and coronal views) are shown in Figure 1. The lead eigenvector images from the acquired datasets (prior to denoising) are shown in the left column, Figure 1 and that from the denoised tensor in the right column, Figure 1. The noise in eigenvector directions derived from the acquired images can be seen within homogeneous muscle compartments and arises from the noise in the raw echo-planar based diffusion weighted images. The improvement in eigenvector orientation within a muscle compartment after denoising can be readily seen in these images. Comparing the borders of the muscle compartments, it can be appreciated that the anisotropic diffusion filter based smoothing used in the current study does not introduce blurring of the eigenvectors across the muscle compartments (Figure 1). The denoising decreased the FA value by an average of 4%) measured in all muscle compartments and subjects. However, this decrease in FA was offset by the much larger decrease in variance of FA (and eigenvector orientations). Thus, overall, the robustness of the tracking improved with the denoising.

Figure 1.

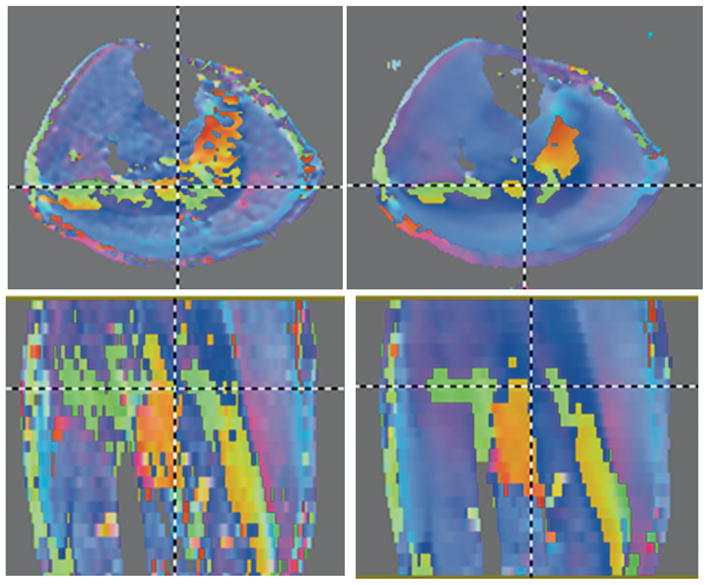
Axial (top row) and coronal (bottom row) images of the color map of the lead eigenvector of the diffusion tensor from images acquired at plantarflexion Left column: prior to denoising and right column: corresponding after tensor denoising. The effect of tensor denoising on reducing noise in the lead eigenvector can be readily appreciated. Further, the smoothing algorithm preserves the boundaries between muscle regions. The color map is encoded as: Superior to Inferior: Blue; Right to Left: Red; and Anterior to Posterior: Green. Unsuppressed fat shows as regions around the muscle but was easily avoided in ROI measurements since the fat signal was very much reduced compared to muscle in the b0 images and could be readily identified. The fat was not thresholded during tensor fitting in order to ensure that small low intensity regions in the muscle were not inadvertently thresholded.

Eigenvalues, Fractional Anisotropy, fiber orientations at neutral and PF ankle positions (Mean, STD, CV and RC)

Table 1 lists the mean (AV) and standard deviations (STD) of the DTI indices (eigenvalues: λ₁, λ₂, λ₃; fractional anisotropy (FA) and fiber orientations with respect to the magnet X-axis, Y-axis, Z-axis for the four muscle compartments (MG, LG, AT-S and AT-D) in the neutral (N) and plantarflexion (PF) positions). The mean and standard deviation values are the average/standard deviation of the six subjects while the CV-av and RC-av are the averages of the CV and RC for the two subjects with the three repeated measurements. The ROI data was tested for the normality of the distribution prior to estimating the mean value of each ROI; the skew of the ROI data was close to 0, indicating a symmetric distribution. The kurtosis of the data was slightly less than 3 in many of the ROis, indicating that the distributions were not as peaked as a normal distribution. However, all the ROI distributions were sufficiently close to normal distribution to allow one to use mean and standard deviation as meaningful descriptors.

TABLE 1.

Reproducibility of DTI indices in Calf Muscle Compartments at 1.5 T

MG	λ1		λ2		λ3		FA		x-axis		y-axis		z-axis
	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF
AV	1.98*	1.84	1.44	1.46	1.30	1.33	0.23*	0.18	83.25	78.80	89.92	84.91	12.08*	20.88
STD	0.02	0.05	0.07	0.04	0.09	0.04	0.04	0.03	3.48	5.69	5.67	4.54	2.64	3.71
CV-av	1.28	2.73	1.50	2.14	3.68	3.13	6.93	3.27	3.80	4.46	5.68	4.79	14.24	14.87
RC-av	0.07	0.14	0.06	0.09	0.13	0.12	0.04	0.02	8.80	9.78	13.95	11.18	4.92	8.08
LOA-L	−0.03	−0.10	−0.02	−0.03	−0.06	−0.06	−0.04	−0.03	−7.85	−5.06	−5.18	−11.28	−1.48	−7.80
LOA-U	0.05	0.06	0.04	0.07	0.08	0.08	0.02	−0.01	4.61	8.78	14.56	4.54	5.48	3.63
LG	λ1		λ2		λ3		FA		x-axis		y-axis		z-axis
	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF
AV	2.10	2.06	1.42	1.43	2.03	2.09	0.27	0.25	106.21	106.95	87.35*	81.05	20.02	22.41
STD	0.11	0.12	0.06	0.08	0.80	0.90	0.02	0.03	3.53	1.61	6.62	3.23	4.16	3.38
CV-av	3.30	4.49	1.92	5.72	4.12	4.63	8.98	9.80	2.32	1.14	3.17	3.02	13.87	14.66
RC-av	0.19	0.26	0.07	0.23	0.14	0.16	0.07	0.07	6.84	3.37	7.46	6.75	7.90	8.99
LOA-L	−0.12	−0.24	0.05	0.00	0.04	−0.02	−0.10	−0.12	−0.42	0.11	−7.01	−5.76	−1.70	3.83
LOA-U	0.08	0.12	0.21	0.32	0.20	0.22	−0.02	−0.02	7.33	4.88	4.30	3.79	15.78	16.56
AT-S	λ1		λ2		λ3		FA		x-axis		y-axis		z-axis
	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF
AV	1.96	1.96	1.5*	1.42	1.25*	1.11	0.24*	0.29	93.54*	85.28	107.58*	99.20	19.42*	11.52
STD	0.04	0.05	0.05	0.05	0.02	0.04	0.02	0.01	5.38	2.92	6.32	3.25	6.19	3.09
CV-av	1.65	1.97	3.53	3.93	3.87	4.25	9.36	3.65	4.60	2.82	4.45	2.50	26.21	27.08
RC-av	0.09	0.11	0.15	0.15	0.13	0.13	0.06	0.03	11.91	6.61	13.06	6.94	13.25	8.65
LOA-L	−0.02	−0.06	0.00	−0.05	−0.19	−0.17	0.01	0.01	−2.31	0.75	−3.56	−4.51	−1.18	−9.10
LOA-U	0.10	0.10	0.20	0.17	−0.01	0.01	0.09	0.05	14.55	10.11	14.92	5.32	17.57	3.14
AT-D	λ1		λ2		λ3		FA		x-axis		y-axis		z-axis
	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF	N	PF
AV	2.01	2.00	1.49*	1.43	1.27*	1.17	0.24*	0.27	85.34	85.62	94.59	93.87	8.37	6.86
STD	0.03	0.02	0.06	0.03	0.06	0.02	0.01	0.01	3.15	2.09	4.01	1.71	3.41	1.11
CV-av	1.25	2.19	4.28	3.69	3.99	1.35	6.50	2.14	3.35	2.32	2.32	2.06	37.41	18.71
RC-av	0.07	0.12	0.18	0.15	0.14	0.04	0.04	0.02	7.89	5.50	6.21	5.36	8.75	3.55
LOA-L	−0.07	−0.05	−0.02	−0.04	−0.22	−0.07	0.00	0.00	−5.93	−2.84	3.67	−0.65	1.00	−0.99
LOA-U	0.03	0.13	0.22	0.16	−0.02	−0.01	0.06	0.02	5.24	4.94	12.47	6.94	13.38	4.03

Eigenvalues are x10⁻³ mm²/sec; FA is dimensionless and the fiber orientations with the x-, y-, and z-axis are in degrees.

^*significant differences between neutral and plantarflexed foot positions are shown with * (p<0.05)

λ₁, λ₂, λ₃ are the eigenvalues, FA is the fractional anisotropy, x-axis, y-axis, z-axis refers to the lead eigenvector angle (in degrees) with the x-, y-and z-axis; N: neutral and PF: plantarflexed foot position; MG: medial gastrocnemius, LG: lateral gastrocnemius, AT-S: anterior tibialis, superficial compartment, AT-D: anterior tibialis, deep compartment; AV: average, STD: standard deviation, CV-av: average coefficient of variation, RC-av: average repeatability coefficient; LOA-L: limit of agreement (lower), LOA-U: limit of agreement (upper).

The CV-av and RC-av values are less than 5% for the eigenvalues and less than 10% for the fractional anisotropy. The fiber orientation with the Z-axis has the maximum variability (14% to 37%) among the orientation angles; however it should be noted that since the fibers were aligned predominantly with the Z-axis, this resulted in relatively small values for the repeatability coefficients. In fact, it should be noted that CV is the largest for the fiber that has the smallest angle with the Z-axis (anterior tibialis, deep; Table 1).

Comparison of the 6 - with the 13 - diffusion gradient direction acquisition

Table 2 lists the CV-av and RC-av comparing the six gradient diffusion direction acquisition to the thirteen gradient diffusion direction acquisition; units of the eigenvalues and angles are the same as for Table 1. Values reported are the average of two subjects. The CV was evaluated in the MG, LG, AT-S and AT-D compartments in the two ankle positions from the same ROI in the 6- and 13-gradient schemes and compared with the CV derived from repeated scans acquired with the 13-gradient scheme alone (Table 1). If the two CVs are comparable, then it can be inferred that the 6-diffusion gradient method yields values similar to the 13-diffusion gradient scheme. The CV of the eigenvalues and FA from the 6-diffusion gradient direction (Table 2) is almost similar to that found for the 13-diffusion gradient direction (Table 1). The highest values of the CV are, as before, associated with the fiber orientation with the Z-axis. The latter values are larger than corresponding values for the 13-diffusion gradient direction scans; however differences in the CV of the eigenvector orientations are not significant (p=0.28).

TABLE 2.

Coefficient of Variation (CV) and Repeatability coefficient (RC) of the DTI indices between the 6- and 13- diffusion gradient directions (top panel) compared to those using the repeated 13-diffusion gradient directions^* (bottom panel).

13–6	MG		LG		AT-S		AT-D
	CV-av	RC-av	CV-av	RC-av	CV-av	RC-av	CV-av	RC-av
λ1	2.29	0.06	0.70	0.04	0.36	0.02	1.04	0.06
λ2	1.89	0.10	4.50	0.14	4.56	0.18	4.00	0.16
λ3	2.11	0.08	6.53	0.27	3.94	0.12	3.13	0.10
FA	0.00	0.02	9.43	0.09	4.88	0.04	9.59	0.08
x-axis	1.75	4.59	1.32	2.57	0.53	1.30	0.81	1.98
y-axis	0.46	0.56	3.39	5.73	5.30	14.11	3.15	8.12
z-axis	19.24	11.34	9.64	4.06	53.45	12.06	35.72	4.59
*13–13	MG		LG		AT-S		AT-D
	CV-av	RC-av	CV-av	RC-av	CV-av	RC-av	CV-av	RC-av
λ1	1.28	0.07	3.30	0.19	1.65	0.09	1.25	0.07
λ2	1.50	0.06	1.92	0.07	3.53	0.15	4.28	0.18
λ3	3.68	0.13	4.12	0.14	3.87	0.13	3.99	0.14
FA	6.93	0.04	8.98	0.07	9.36	0.06	6.50	0.04
x-axis	3.80	8.80	2.32	6.84	4.60	11.91	3.35	7.89
y-axis	5.68	13.95	3.17	7.46	4.45	13.06	2.32	6.21
z-axis	14.24	4.92	13.87	7.90	26.21	13.25	37.41	8.75

^*The values for the repeated 13-gradients are also in Table 1 and are shown again here for ease of comparison.

CV is dimensionless percentage, the RC has the same dimensions as the corresponding parameter.

DTI indices and fiber orientations for four ankle positions

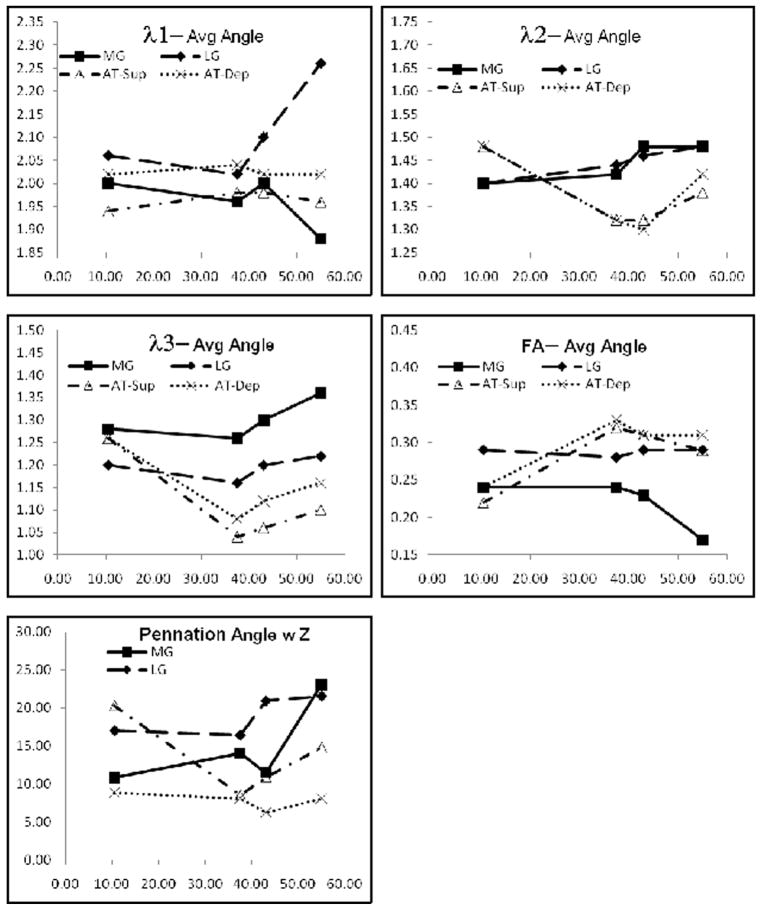
Figure 2 shows the images of the ankle acquired with the body coil with the ankle angle measurements overlaid on the ankle images at each position. The body coil scan is a reliable, quick, and accurate method of quantifying the ankle position. Figure 3 is a graph of the DTI indices as a function of the ankle angle for one subject. A trend from these graphs indicates that large changes occur close to the neutral ankle position and/or at the extreme plantarflexed ankle position.

Figure 2.

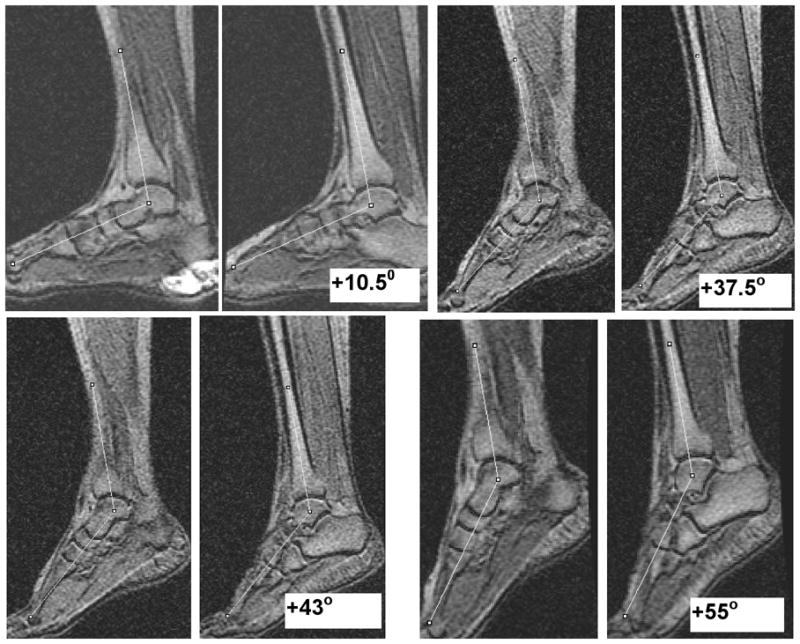
Anatomical images of the ankle acquired in the body coil at four ankle positions with ankle angle as the average of the measurements in two slices at each position. Positive ankle angle values shown in the images are the deviations from the neutral position (0⁰) in the plantarflexed direction. This imaging based assessment allowed accurate positioning and determination of the ankle angle.

Figure 3.

Graphs of the variation of the DTI indices and fiber orientation in the four compartments with ankle angle. The lines are not fits to the underlying data but serve as a guide to the eye. The variation is clearly non-linear.

Fiber orientations and lengths in the neutral and plantarflexed ankle positions

Figure 4 shows typical images for fibers tracked form the MG (in neutral and PF) from seed points positioned (on coronal images) 45–55 mm from the most distal aspect of the MG and just adjacent to the aponeurosis of insertion in a coronal view. Seed points chosen at this level produced consistent fibers in the neutral and plantarflexed positions. Seed selection was performed by two observers (on all the subjects and repeat studies) from the coronal view with seeds located approximately 45–55 mm from the most distal aspect of the MG. The angular threshold and FA threshold for tracking was unchanged between the observers. An analysis of the differences in fiber lengths estimated by the two raters gave a mean difference of 2 mm with limits of agreement (mean± 1.96SD) at 5 mm and −1 mm. Seed voxel selection influenced fiber lengths more than the fiber orientation since many seed voxels lead to early termination of correctly oriented fibers. This was true especially for the most distal regions of the MG. The analysis was thus restricted to 45–55 mm from the most distal point of the MG.

Figure 4.

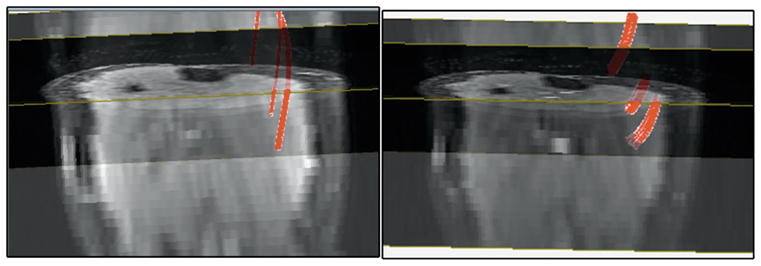
Fibers tracked from seed points in the MG at neutral (left) and at plantarflexion (right) positions of the ankle, shown here superposed on the corresponding 3D b0 volumes. The fiber statistics was derived for seed locations in the middle of the MG as it was possible to obtain fiber tracks in all subjects at this location. The 3D view is shown here with the volume at an angle so that the axial and coronal cross-sections can be seen. Since the 3D view was set interactively, it was not possible to reproduce the exact same view for images.

Table 3 lists the mean and standard deviation of the fiber length (in mm) and fiber orientation (in degrees) of the six subjects and the CV-av and RC-av as the average for the two subjects (each scanned three times). The mean and standard deviation (STD) values are the averages for all the subjects while the CV-av and RC-av are the averages for the two subjects’ repeated scans.

TABLE 3.

Reproducibility of Medial Gastrocnemius Fiber Architecture at 1.5 T

	Fiber Length (mm)		X(degrees)		Y(degrees)		Z(degrees)
	N	PF	N	PF	N	PF	N	PF
Mean	44.56	29.86	79.88	71.78	99.88	98.40	16.13	26.33
STD	3.71	5.26	2.24	5.94	3.69	4.80	3.58	5.68
CV-av	6.34	10.35	2.80	8.20	3.94	4.78	22.59	16.57
RC-av	7.68	8.83	6.19	16.27	10.92	12.98	10.18	12.69

DISCUSSION

Eigenvalues, Fractional Anisotropy at neutral and PF ankle positions

The DTI indices at the neutral position agree with that reported for the muscle compartments at 1.5 and 3 T (10–13). However, the FA values in the current study are at the lower limit of values reported earlier (e.g. a range of 0.24–0.31 for the anterior tibialis from literature compared to the mean value of 0.24±0.01 in the current study). A small reduction in FA was introduced by the denoising algorithm; however we optimized the denoising algorithm parameters as a tradeoff between noise reduction and not significantly changing the FA.

Significant decreases in λ₂, λ₃ with no significant change in λ₁ and a significant increase in FA were observed in both compartments of the anterior tibialis (deep and superficial) for a change of the ankle position from neutral to plantarflexed. This change is similar to that observed in an earlier work with passive ankle plantarflexion by Schwenzer et al at 3T (12). The latter study also reported for the AT, a decrease in λ₂, λ₃ of approximately the same magnitude as reported here (Table 1). Deux et al (10) and Okamoto et al (11) performed measurements during plantarflexion (as opposed to the passive conditions of the current study) and found that all three eigenvalues increased during PF while FA decreased marginally in the AT. The differences in the observed changes in the DTI indices may reflect the ‘passive’ and ‘active’ conditions of flexion. In the latter condition, there are likely confounding contributions from regional blood flow and temperature increase due to the muscle activity.

In the current study, DTI indices in the MG showed a significant decrease in λ₁ and small (though not significant) increases in λ₂ and λ₃. In contrast, Schwenzer et al observed no change in λ₁, and significant increases in λ₂ and λ₃ (12). However the significant decrease in FA with ankle position change to plantarflexion is in agreement in both studies. The lateral gastrocnemius showed no significant changes in any of the DTI indices with ankle position change; this is possibly because the LG is resting flat on a support in the supine position.

Lead eigenvector orientation at neutral and PF ankle positions

Of the prior studies that monitor DTI changes with ankle position (active or passive), only Schwenzer et al (12) report the fiber orientation changes in the different compartments. Heemskerek et al (13) have studied, in detail, the pennation angles of the superficial and deep compartments of the anterior tibialis in the neutral position. However, as the reference frame is different between the latter study (aponeurosis) and the current study (magnet frame), it is difficult to make direct and quantitative comparisons. In the rest of the discussion, the fiber orientation with respect to the Z-axis is referred to as the complementary of the angle of elevation (c-elevation). The angle of elevation is defined here as the fiber ‘elevation’ from the X-Y plane.

The c-elevation angle of the MG in the neutral and PF ankle position reported in Ref. 12 is: 13±4° (N) and 19±5° (PF)) and this agrees well with the values of the current study: 12±3° (N) and 21±4° (PF). The increase in the c-elevation angle of the MG with ankle change was significant in the current study. The c-elevation angle of the lateral gastrocnemius fibers also agreed with that of the Schwenzer et al study (12): compare current values of 20±4° (N) and 22±3° (PF) to the earlier report of 17 ±3° (N) and 17±5° (PF). The small increase in LG c-elevation angle found in the current study was not significant. In the current study, the anterior tibialis was analyzed separately for the superficial and deep compartments in contrast to the Schwenzer study (12) that analyzed them as one. The orientation angles averaged over both compartments are: 14 ±4° (N) and 9 ±2° (PF) in the current study and are close to that obtained by Schwenzer et al in both neutral and PF states: 10±3° (N) and 11±3° (PF). However, the c-elevation angle of the AT increased only marginally on plantarflexion in the Schwenzer et al study (12). The physiological model for elongation (as in the AT muscle on plantarflexion) would imply smaller c-elevation angles for the AT fibers. Consistent with this model, smaller c-elevation angles were found in both AT compartments in the plantarflexed ankle position compared to the neutral ankle position; though only the superficial compartment showed significant changes in the angle.

It is also interesting to make a comparison of the fiber orientation c-elevation angles (i.e., the orientation with the magnet Z-axis) with the pennation angles reported by Heemskerk et al (13). Assuming that the aponeurosis is approximately parallel to the Z-axis, the pennation angles and fiber c-elevation angles should be in the same range. The middle segment AT analysis from Ref. 13 shows that the pennation angles in the superficial compartment are around 20° (compare to 19° for the c-elevation angle in current study for the neutral position, Table 1) and in the deep compartment, the pennation angles are smaller at 6–10° (compare to 8.4° for the c-elevation angle in current study for the neutral position, Table 1).

Coefficient of Variation (CV) and Repeatability Coefficients (RC) of DTI indices and fiber orientations

Heemskerk et al (13) have reported the CVs and RCs of the three eigenvalues and FA for the anterior tibilais (at neutral position) at 3 Tesla; the CVs and RCs for the muscle compartments in the current study are comparable (Table 1). The CVs of MG and AT have also been reported at 3 Tesla by Schwenzer et al (12) in the neutral and plantarflexed ankle positions. The latter study found the CV of FA for the muscle compartments to be lower than that determined in the current study (and in Ref. 13); this may arise from methodological differences in pulse sequence as well as the lower resolution of the images in (12) which allows for higher SNR, and consequently a lower CV.

An important finding of the reproducibility study is that the CV (and RC) of the eigenvalues and FA in the plantarflexed position is not significantly different from that of the neutral position (p=0.48, Table 1). Two factors can potentially lower the reproducibility of the values found in the plantarflexed position including (i) difficulty in maintaining the ankle position without any gross motion for the duration of the scan, and (ii) difficulty in reproducing exactly the plantarflexed angle for each session. These two factors were addressed in the current study: motion was minimized by an appropriate restraining device, residual motion between different baseline/diffusion weighted images were corrected prior to tensor calculations, and motion correction was verified by examining the subtracted images of the acquired and fitted images. Reproducibility of plantarflexed ankle position was ensured for each session by imaging the ankle in the body coil and repositioning the ankle, if necessary.

Heemskerk et al (13) have reported higher values for the CVs of the pennation angles of the anterior tibialis fiber (range: 9.9–52.8) in the neutral position than the CV of the fiber orientation angles in any of the compartments (neutral or plantarflexed ankle position) (range:1.14–37.4) in the current study. The higher values reported in Ref. 13 may arise from the fact that the pennation angles were calculated from 3–4 voxels along the fiber track whereas the fiber orientations calculated in the current study use much larger ROIs (60–120 voxels). The high reproducibility of the eigenvector orientation in the repeated studies in both the neutral and plantarflexed ankle positions shows that the calf can be positioned very consistently (long axis parallel to the Z-axis of the magnet) and that the ankle position can be accurately measured by imaging the foot/ankle. The fact that fiber orientations in the magnet frame of reference are reproducible also implies that these measures can be reliably compared across studies. This circumvents the need for calculating pennation angles and reduces computational burden of tracking the fibers (which have the highest SNR requirements) as well as the manual delineation of the aponeurosis.

In addition to the reproducibility of the ankle position, the SNR of the baseline and diffusion weighted images determine the reproducibility of the DTI indices. The baseline image SNR of the muscle compartments in the current study compares well with the baseline SNR of images acquired at 3T. Further, the post-processing operation of denoising serves to regularize the diffusion tensor and this processing reduces the standard deviation of calculated diffusion indices in homogeneous regions by ~60%. The denoising algorithm thus compensates for the slightly reduced SNR at 1.5 T compared to values reported at 3T, enabling comparable RC and CV values for the DTI indices at both field strengths.

Comparison of the 6 - with the 13 - diffusion gradient direction acquisition

A general consensus in brain DTI regarding the tradeoff between number of diffusion gradient directions and averages is that the best SNR in the diffusion tensor is obtained using larger gradient directions and lower averages than lower gradient directions and higher averages for a given acquisition time (29). In practice, physiological noise and scanner instabilities can reduce SNR for long scan times. The focus in the current study is on decreasing scan times approximately by a factor of 2 and this was accomplished by decreasing the number of diffusion gradients (thus the choice of 13 and 6) while keeping the number of averages the same. The intent was to evaluate the performance at the reduced scan times afforded by the six diffusion gradients. The CVs calculated from a 6- and 13- diffusion gradient acquisitions are not significantly different from that calculated from repeated 13 gradient directions for the eigenvalues and FA (paired t-test of CVs of each muscle calculated from repeated 13 gradients and the 6–13 gradient direction, p=0.99; Table 2). There are also no significant differences in the CVs of the eigenvector orientations (p=0.28) between the two acquisitions. For the 6- diffusion gradient direction acquisition, there are some large CV values for the eigenvector orientation (with respect to the z-axis) of the AT fibers but since the mean values are low, this translates to a relatively smaller RC (Table 2). As fiber orientations are most sensitive to noise as well as to the number of gradient directions (30), it is not surprising that the CVs of the fiber orientation from the 6-diffusion gradient sensitization are larger than that from 13-diffusion gradient sensitization. A more detailed study is required to evaluate the most efficient way of reducing the total scan time by changing the number of averages and/or diffusion gradients.

The repeatability required of a DTI measurement depends on the application: DTI indices change in the range 10–20% in diseased or damaged tissue (15,16, 31). The RC of the DTI indices (eigenvalues, FA) in any compartment using the 6- or 13-diffusion gradient is much less than 10%, and thus either sequence should be capable of detecting changes in muscle DTI indices with disease/damage. Changes in muscle architecture arising from changes in ankle positions or from contraction can be as small as 3° – 5°, so that repeatability coefficients for fiber orientations should be in this range. The average RCs of the fiber orientations in the current study is 8°, which is more than the anticipated changes in fiber orientation with ankle position or from contraction. However, it should be noted that muscle architecture changes are typically monitored without any change in patient position, so that these measurements (same session, no subject repositioning) will have a higher reproducibility than that measured here (separate days, subject repositioning). This is probably the reason that fiber orientation changes of the order of 8° could be detected even when the RC value was in the same range. However, it should be noted that the 6 gradient direction sequence may be best suited for applications that monitor changes in DTI indices whereas the 13 gradient sequence will be more appropriate for monitoring fiber orientation changes as well.

DTI indices and fiber orientations for four ankle positions

The variation of DTI indices with ankle positions between neutral (+10°) to plantarflexed (+55°) does not follow a linear relationship (Fig. 3). Earlier work using ultrasound measurement also shows a non-linear behavior for fiber architecture, with maximum change in fiber length/pennation angle close to the neutral position (0° to +10°) and decreasing for increasing plantarflexed angles (32). Figure 3 shows that the DTI/fiber orientation changes near the neutral position are sometimes high, though large changes are also seen at the highest plantarflexed ankle angles (Figure 3). A more detailed study of the fiber architecture changes with a larger number of ankle positions is required to accurately map the variation. These studies will allow in-vivo determination of fiber architecture at different levels of contraction and these parameters will enable a better determination of force-length characteristics in intact human muscles (32).

Fiber orientations and lengths in the neutral and plantarflexed ankle positions

In the current study, the MG was evaluated in detail for reproducibility of fiber architecture. Fibers could most reliably be generated in the middle section of the MG muscle and further, the fibers in this section terminated in the superficial aponeurosis within the imaged field of view. An important aspect of tracking lay in the selection of the angular threshold: high values generated clearly erroneous fibers whereas low values caused early termination (before the fiber reached the aponeurosis). The mean fiber length and fiber orientation of the tracked fibers in the MG (Table 3) compare well with the ultrasound measurements on MG fiber length and pennation angles in the relaxed and contracted state (33). The latter study reported the fiber length in the relaxed/contracted state as 43.6 ±8.6 mm/27.7 ±5.6 mm which is comparable to values in Table 3. The mean RC values for fiber orientations (average of neutral and plantarflexed values) is ~11°, which is close to the mean RC value for the pennation angle of the AT at 3T for the ‘between day’ condition (13). The mean RC values for fiber length (average of neutral and plantarflexed values) is ~8 mm, which is lower than the mean RC value of 50 mm for the fiber length of the AT at 3T (13). This discrepancy may arise from differences in the fiber tracking algorithm and choice of the threshold parameters as well as there may be differences in the reproducibility of fiber tracks between compartments (AT in Ref 13 vs MG in current study). Simulation studies have shown that the SNR required for single voxel based fiber tracking is quite stringent (23). Values of SNR > 60 are required to accurately track fibers; it should be noted that the SNR for the MG data in the current study is around 102 which is then denoised to increase the SNR to be effectively at a value of 175. This is well over that required for accurate fiber tracking.

The study has some limitations including (i) the small number of subjects, (ii) averaging before eddy current correction/DTI regression analysis, and (iii) the manual placement of the seed voxels for tractography. Averages were performed in the scanner and analysis was performed on the averaged image. A more robust approach is to evaluate each image prior to averaging and reject those with artifacts and further, use every data point in the linear regression. An automated method of seed selection would have removed the need for manual placement; the latter is prone to placement errors. A consistent method of placing the seed voxels on the coronal image was developed (one voxel displaced from the aponeurosis). The inter-observer correlation was high, confirming that the manual method provided consistent muscle fiber tracts. It should be noted that, regardless of the observer, some fibers terminated prematurely before the aponeurosis was reached; this arose from a combination of low FA, low SNR, fat admixture and possible fiber curvature higher than the angular threshold. Increases in SNR in DTI acquisition and more sophisticated tractography methods may be required to provide more consistent muscle fibers along the entire length of the MG muscle.

In summary, the reproducibility of diffusion tensor indices as well as the fiber orientation at 1.5 T is comparable to that measured at 3T. The coefficient of variation and the repeatability coefficients were evaluated in the neutral and plantarflexed positions in four muscle compartments. Fibers tracked in the medial gastrocnemius were also evaluated for reproducibility of fiber length and orientation. The CV and RC of the tracked fibers were very similar to that obtained at 3T. The current paper thus establishes that the reproducibility of DTI at 1.5 Tesla is sufficient to monitor changes with disease state as well as with muscle contraction. Given the widespread availability of 1.5 Tesla scanners, this opens the possibilities for using DTI to monitor muscle architecture in normal and diseased states.