Abstract
In this work, we investigated the frequency-offset dependence of the rotating frame longitudinal (R1ρ) and transverse (R2ρ) relaxation rate constants when using hyperbolic-secant adiabatic full passage pulses or continuous-wave spin-lock irradiation. Phantom and in vivo measurements were performed to validate theoretical predictions of the dominant relaxation mechanisms existing during adiabatic full passage pulses when using different settings of the frequency offset relative to the carrier. In addition, adiabatic R1ρ and R2ρ values of total creatine and N-acetylaspartate were measured in vivo from the human brain at 4 T. When the continuous-wave pulse power was limited to safe specific absorption rates for humans, simulations revealed a strong dependence of R1ρ and R2ρ values on the frequency offset for both dipolar interactions and anisochronous exchange mechanisms. By contrast, theoretical and experimental results showed adiabatic R1ρ and R2ρ values to be practically invariant within the large subregion of the bandwidth of the hyperbolic-secant pulse where complete inversion was achieved. However, adiabatic R1ρ and R2ρ values of the methyl protons of total creatine (at 3.03 ppm) were almost doubled when compared with those of the methyl protons of N-acetylaspartate (at 2.01 ppm) in spite of the fact that these resonances were in the flat region of the inversion band of the adiabatic full passage pulses. We conclude that differences in adiabatic R1ρ and R2ρ values of human brain metabolites are not a result of their chemical shifts, but instead reflect differences in dynamics.
Keywords: transverse and longitudinal relaxations, rotating frame, exchange and dipolar relaxation, adiabatic pulse, ethanol, glycerol, in vivo, human brain metabolites
INTRODUCTION
Longitudinal and transverse relaxation measurements in the rotating frame during radiofrequency (RF) irradiation, with rate constants of R1ρ and R2ρ, respectively, are sensitive to molecular dynamics relevant for the characterization of the functionality of tissue in vivo, especially at high magnetic fields [for a review, see ref. (1)]. Rotating frame relaxations depend on the choice of the RF parameters (i.e. the amplitude and frequency of the RF irradiation), thus providing a basis to generate MR contrast (2,3). Notably, by appropriate modeling of the relaxation processes, the simultaneous analysis of independent measurements of R1ρ and R2ρ, obtained with different experimental RF settings, permits the extraction of fundamental relaxation parameters, which may provide sensitive markers to differentiate healthy from pathological conditions. However, although relaxation processes occurring during RF irradiation are often exploited for in vivo imaging applications, the same does not apply for spectroscopic purposes and, so far, only one study of this kind has been presented in the literature (4). Rotating frame relaxation rate constants measured during a continuous-wave (CW) spin-lock pulse are dependent on the frequency offset (ΔΩ) between the carrier frequency of the RF pulse and the frequency of the isochromat of interest (5–8). This characteristic impairs the time-efficient utilization of CW spin-lock for MRS applications in vivo, as data need to be acquired separately for resonances which are often dispersed over a wide chemical shift range.
As occurs during the CW spin-lock pulse, rotating frame relaxation also takes place in the presence of frequency-modulated irradiation. The frequency-modulated method can offer advantages when using adiabatic full passage (AFP) pulses, especially for in vivo studies. In particular, B0 and B1 inhomogeneities that often persist in vivo, especially when performing studies at high magnetic field (≥ 3 T), create uncertainty in the angle of the CW spin-lock (9). Conversely, adiabatic rotating frame relaxation methods are relatively immune to B0 and B1 inhomogeneities (10). The formalism utilized to describe rotating frame relaxations during AFP pulses considers the relaxation rate constants as an average of time-dependent contributions occurring over the duration of the pulse (11). This formalism has been used to describe quantitatively how adiabatic R1ρ and R2ρ depend on RF parameters, such as the amplitude and frequency modulation functions, peak RF power and bandwidth (BW) of the AFP pulse (2). However, the dependence of the adiabatic relaxation rate constants on ΔΩ remains to be examined, and the validity of the formalism used for the theoretical predictions remains to be tested and generalized for the different isochromats within BW of the AFP pulse. Importantly, recent studies performed in the context of high-resolution NMR have shown that the application of trains of AFP pulses gives frequency-offset-independent relaxation rates, without the need to apply residue-specific corrections (12), thus further substantiating the rationale for the present investigation.
In the present study, we compared the theoretical predictions of the frequency-offset dependence of R1ρ and R2ρ during CW spin-lock irradiation vs a train of hyperbolic-secant (HS) AFP pulses (10). Rotating frame relaxation caused by dipolar interactions in the weak field approximation (i.e. fast motional regime), and anisochronous exchange (i.e. exchange between spins with different chemical shifts, δω ≠ 0) in the fast exchange regime (FXR), were considered specifically. Phantom and in vivo measurements were performed to validate the theoretical predictions of the relaxations during AFP pulses as a function of the offset from the carrier frequency. Finally, adiabatic R1ρ and R2ρ values of total creatine (t-Cr) and N-acetylaspartate (NAA) were measured with localized MRS from the human brain of healthy subjects at 4 T.
THEORY
The theory concerning the description of the relaxation rate constants during either AFP pulses or CW spin-lock irradiation in the presence of dipolar interactions and anisochronous exchange has been developed and reviewed in a number of publications (1,2,5,13). In the following, we summarize the key concepts and formulae which have been used for the simulations in this work.
During RF irradiation, the effective magnetic field (B⃗eff) is tilted from the quantization axis z′ (i.e. the longitudinal axis of the first rotating frame x′y′z′) by the angle α, defined as:
| [1] |
where ω1 is the amplitude of the RF pulse, Δω = (ω0 − ωRF) is the frequency offset, ω0 is the Larmor frequency of the resonance of interest and ωRF is the frequency of the RF pulse. Note that ω1, Δω, ω0 and ωRF are expressed in units of rad/s. The amplitude of the effective frequency ωeff (= γBeff, where γ is the gyromagnetic ratio) is given by:
| [2] |
It should be noted that the dependence of R1ρ and R2ρ on the frequency offset occurs via both ωeff and α.
Although during CW spin-lock pulses, α and ωeff are constant during the pulse, during the application of AFP pulses these two parameters are time dependent. The adiabatic condition is well satisfied when the change in orientation of the effective field is significantly slower than the rotation of the magnetization vector (M⃗) around the effective field: ωeff ≫ |dα/dt|.
The amplitude modulation function of the HS AFP pulse (10,14,15) is given by:
| [3] |
where is the maximum value of ω1(t) during the pulse, t ∈ [0, Tp], β is a truncation factor [sech(β) = 0.01] and Tp is the pulse duration. With respect to the carrier frequency ωc, i.e. the center frequency in the BW of interest, the frequency modulation for the HS pulse is given by:
| [4] |
where A is the amplitude (rad/s) of the frequency sweep; the bandwidth of the pulse is BW = 2A.
One fundamental property of the adiabatic pulse is the time–BW product, given by R = (ATp)/π. It should be noted that, if A is given in Hertz, R = 2ATp and, consequently, BW = R/Tp. Equation (4) suggests that relaxation measurements during AFP pulses are intrinsically an off-resonance measurement for all isochromats (except for the instant in time when the magnetization crosses the x′y′ plane). For clarity, we define the time-independent frequency offset between the isochromat of interest and the carrier frequency of the RF pulse as ΔΩ = (ω0 − ωc), to be conceptually distinguished from the time-dependent Δω. We then investigate how relaxation rate constants are affected when ΔΩ varies within BW of the adiabatic pulse. Obviously, in the CW experiment, the result is always ΔΩ = Δω, as ωRF = ωc.
Similarly to the CW spin-lock experiment, depending on the initial orientation of M⃗ relative to B⃗eff, the relaxation mechanisms occurring during AFP pulses can be governed solely by R1ρ or R2ρ processes, or by a combination of R1ρ and R2ρ. It has been shown (16) that the relaxations during adiabatic rotation can be represented as an average of instantaneous contributions from the different relaxation pathways:
| [5] |
where R1,2ρ,dd(t) and R1,2ρ,ex(t) are the time-dependent contributions of the rotating frame relaxations as a result of dipolar interactions and anisochronous exchange, respectively. This formalism has been used in a number of publications for modeling experimental data acquired with adiabatic relaxation methods (3,11,18); however, in the previous investigations, the resonance of interest (i.e. the water resonance) was placed in the center of BW of the adiabatic pulses, implying ω0 = ωc, and therefore ΔΩ = 0. In the present study, we validate the accuracy of the formalism expressed by eqn (5) for different isochromats within BW of the adiabatic pulse (ΔΩ ≠ 0). Importantly, eqn (5) assumes that the isochromat of interest undergoes full inversion during the adiabatic pulse, a characteristic that is true only for a subregion of BW, provided that the amplitude of ω1 is sufficient to satisfy the adiabatic condition (ωeff ≫ |dα/dt|).
Dipolar relaxations: isolated two-spin description (like spins)
For a system of two equivalent nuclei of spin I and gyromagnetic ratio γ [= 2π × 42.576 × 106 rad/(s T) for protons] in a single site, R1ρ and R2ρ caused by dipolar fluctuations can be described as an isolated two-spin system (1,19):
| [6] |
| [7] |
where b = −μ0ħγ2/(4πr3), μ0 = 4π × 10−7 H/m is the vacuum permeability, ħ = 1.055 × 10−34 J s is Planck’s constant, r is the internuclear distance in meters and τc is the rotational correlation time in seconds characterizing the tumbling of the magnetic dipole. Equations (6,7) are written in a general form in which ωeff and α are time dependent, and can be used to calculate the time courses of R1ρ,dd or R2ρ,dd values during the adiabatic pulses. Equations (6,7) apply also to the CW spin-lock experiment, with the only difference being that ωeff and α are time invariant.
The described dipolar interaction theory assumes a single rotational correlation time. This approximation is an over-simplification for biological tissues where there probably exists a distribution of dipolar interactions. However, this simplified model of relaxation can provide an ‘effective correlation time’ in vivo which is reasonable and useful to describe general features of the tissue, as performed previously (11).
Anisochronous exchange
For simplicity, we consider a two-site equilibrium exchange between sites A and B, . Here, k1 and k−1 represent the forward and backward exchange rate constants obeying the relation , where PA and PB are the fractional populations of sites A and B, respectively. The difference in chemical shifts between sites A and B is defined by δω (rad/s) and, in FXR, , whereτex is the exchange correlation time. Exchange-induced R1ρ,ex and R2ρ,ex under CW spin-lock irradiation in FXR are given by (5,20):
| [8] |
| [9] |
As in the case of dipolar interactions, the time courses of the instantaneous contributions used in eqn (5) during adiabatic rotation in FXR can be evaluated by introducing the time dependence of α(t) and ωeff(t) in eqns (8) and (9), thus giving (1):
| [10] |
and
| [11] |
Under a broad range of experimental conditions typically used for in vivo experiments (B0 < 9.4 T, ω1/(2π) < 10 kHz and BW/(2π) < 10 kHz), the second term in eqn (11) is small when compared with the first term, and R2ρ,ex(t) can be simplified to (16):
| [12] |
Within this approximation, the time dependence of R2ρ,ex(t) during adiabatic pulses originates from the time dependence of α (t) and not from ωeff(t).
METHODS
Theoretical simulations
Numerical calculations of R1ρ,ex,dd and R2ρ,ex,dd were performed using the Mathematica 5.2 platform (Wolfram Research, Inc., Champaign, IL, USA), based on the formulae described in the ‘Theory’ section for CW and adiabatic irradiation. The Larmor frequency was chosen as ω0/(2π) = 200 MHz in order to resemble the experimental conditions utilized for phantom studies (4.7 T). In the case of adiabatic pulses, the time average of the instantaneous contributions to the relaxation rate constants was calculated over the pulse duration, according to eqn (5). For dipolar interactions, we chose r = 0.153 nm, which corresponds to the distance between protons within the methyl group. For anisochronous exchange, we chose PA = PB = 0.5 and δω = 0.85 ppm, which correspond to the chemical shift difference between protons from water and the hydroxyl group of ethanol. For CW spin-lock irradiation, the maximum amplitude was set as or 10 kHz. For HS pulses, or 10 kHz, the pulse duration (Tp) was 6 ms and BW/(2π) ≈ 3.3 kHz. The lower values of for both CW and adiabatic irradiation were chosen to reproduce the common experimental conditions used for in vivo applications in humans, and to provide approximately the same relative specific absorption rate (SAR). It is worth noting that adiabatic pulses are generally employed for in vivo human studies with pulse lengths of a few milliseconds, a typical number being 6 ms, and with the Tp × BW product typically set to 20, thus leading to BW ≈ 3.3 kHz. This is a reasonable choice of RF parameters, which allows the adiabatic condition to be satisfied using a maximum RF amplitude (≈ 1.3 kHz) that complies with SAR guidelines and that is readily attainable with the RF amplifiers and RF coils available for human applications for magnetic fields of 4 T or less.
Phantom experiments
To investigate the dipolar relaxation channel, a 300 mM acetate (Sigma-Aldrich Inc., St. Louis, IL, USA) solutions in glycerol–water mixtures at ratios of 0.9: 0.1 by weight was prepared, and the relaxation measurements were performed on the methyl protons of acetate at 1.9 ppm. The choice of this sample was justified by the high viscosity of the water–glycerol mixture and the lack of exchange between hydroxyl groups with the CH3 functional group of acetate. Glycerol (99.9% grade) was purchased from Fischer Scientific Inc. (Pittsburgh, PA, USA), and was used as received. To investigate the anisochronous exchange pathway, a water–ethanol sample was prepared at an approximate ratio of 50: 50 by volume (measured pH of the phantom was approximately 5.5 when the MR experiments were performed). It is well documented that protons from water and the hydroxyl group of ethanol in the water–ethanol mixture undergo fast exchange, which results in a single line in the NMR spectrum.
Measurements were carried out using a 40-cm bore, 4.7-T magnet (Oxford Magnet Technology Inc., Witney, UK) with a Varian UNITYINOVA console (Varian Inc., Palo Alto, CA, USA). The RF power was transmitted and received using a home-built linear surface coil (diameter, 2 cm). Voxel selection (4 × 4 × 4 mm3) was achieved by localization by adiabatic selective refocusing (LASER), with TE = 29 ms and TR = 5 s. Adiabatic R1ρ and R2ρ measurements were performed as described previously (3,11), by placing a train of AFP pulses prior to or after excitation by an adiabatic half passage (AHP) pulse, respectively. The pulse trains consisted of a variable number of pulses (4, 8, 16 and 32 pulses), with phases prescribed according to Malcolm Levitt scheme (MLEV) −4, −8, −16 and −32 (21). The peak amplitude of the pulse was , with Tp = 6 ms and BW/(2π) ≈ 3.3 kHz. The relaxation measurements were performed by varying the frequency offset ΔΩ between the carrier frequency of the HS pulse and the isochromat of interest (i.e. the water or acetate resonances, depending on the phantom). Finally, another set of experiments was carried out on a 90-cm bore 4-T magnet (Siemens/Oxford Magnet Technology, Witney, UK) with a Varian UNITYINOVA console (Varian Inc.). The same RF coil as used for 4.7-T measurements was retuned for 4 T. The aim of this set of measurements was to explore the dependence of the relaxation rate constants on ΔΩ for different inversion BW profiles. Specifically, the dependence on ΔΩ in R1ρ experiments was investigated for the water–ethanol sample using a variable R value of the HS adiabatic pulse (R = 15, 20, 30 and 40) whilst matching Tp (3, 4, 6 and 8 ms) to keep BW fixed at 5 kHz. The peak amplitude of the pulse was .
In vivo experiments
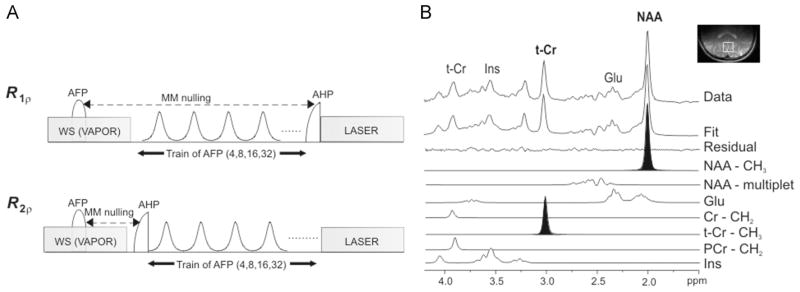
Eleven healthy subjects were investigated on the same 4-T magnet as described above. A half-volume RF coil combined with quadrature hybrids with a fixed 90° phase shift was used for RF irradiation and signal reception. The two geometrically decoupled circular coil loops were 14 cm in diameter. Single-voxel localization (20 × 20 × 20 mm3) was performed as described for phantom experiments, with TE = 39 ms and TR = 5–8 s (depending on the coil loading), and number of averages = 16 (acquired as single scans). The number of pulses in the AFP pulse train was 4, 8, 16 or 32, Tp = 6 ms; BW ≈ 3.3 kHz and . All first- and second-order shim terms were automatically adjusted using FASTMAP with echo planar imaging readout (17). On one of the subjects, the relaxation measurements were performed by varying the frequency offset ΔΩ between the carrier frequency of the HS pulse and the unsuppressed water resonance, similar to that performed for phantom experiments. On the other 10 subjects, MRS measurements were performed on metabolites (Fig. 1A). The macromolecule contribution was minimized by macromolecule nulling using inversion recovery (inversion time TI = 0.18 s), and the signal from water was minimized using VAPOR water suppression (22). The carrier frequency of the AFP pulses was set on water; the resonances of the singlets belonging to the methyl groups of NAA (2.01 ppm) and t-Cr (3.03 ppm) fell into the subregion of BW where complete inversion is achieved. When needed, eddy current correction was performed on the spectra before quantification. The signal intensities of the singlets of t-Cr and NAA were estimated by LCModel (Fig. 1B). Ad hoc basis sets, including 21 metabolites, were generated using a custom-made MATLAB routine (23) with published chemical shifts and J coupling values from ref. (24). This code uses the density matrix formalism, and simulates the evolution of spins under RF pulses, chemical shift and J coupling (the effect of gradients was neglected). For NAA, Cr and phosphocreatine (PCr), CH3 and CH2 resonances were simulated as separate basis spectra in order to accommodate the different relaxation time constants for CH3 and CH2 resonances.
Figure 1.
Schematics of the pulse sequence (A) and post-processing methods (B) for MRS measurements of metabolites in vivo. (A) In the R1ρ configuration, the train of adiabatic full passage (AFP) pulses was placed before the excitation achieved with an adiabatic half passage pulse (AHP). In the R2ρ configuration, the train of AFP pulses was placed after the excitation pulse. Macromolecule (MM) nulling was achieved by inversion recovery with TI = 0.18 s (note that, in the R1ρ configuration, the actual time between the inversion pulse and the excitation pulse was the sum of TI = 0.18 s plus the duration of the AFP train). Localization was performed with localization by adiabatic selective refocusing (LASER), and water suppression (WS) was obtained with VAPOR. (B) Principle of spectral deconvolution operated by LCModel. The resonances of interest in the present study (NAA-CH3 and t-Cr-CH3) are highlighted. Cr, creatine; Glu, glutamate; Ins, Inositol; NAA, N-acetylaspartate; PCr, phosphocreatine; t-Cr, total creatine.
The RF power delivered to the coil was limited to a safe operating range using the hardware monitoring module of the Varian console. In addition, the RF power output over the full range of settings used in these experiments was measured with an oscilloscope connected to the coil port. From these measured values, the average RF power delivered to the coil was computed by integration of all RF pulses in the sequence, and SAR was estimated assuming a tissue load of 2 kg in the coil. When using the longest pulse train, the estimated SAR was always below the Food and Drug Administration limit of 3 W/kg averaged over the head for 10 min (http://www.fda.gov/MedicalDevices/DeviceRe-gulationandGuidance/GuidanceDocuments/ucm072686.htm).
Estimation of rate constants
The relaxation rate constants were calculated from the signal intensity decay curves using a linear regression algorithm with a monoexponential decay function. These routines were developed with Matlab 7.2 (Wolfram Research, Inc.).
Statistical analysis
The statistical significance of the differences in relaxation rates was evaluated using an unpaired t-test, and the level of significance was set at p = 0.05.
RESULTS AND DISCUSSION
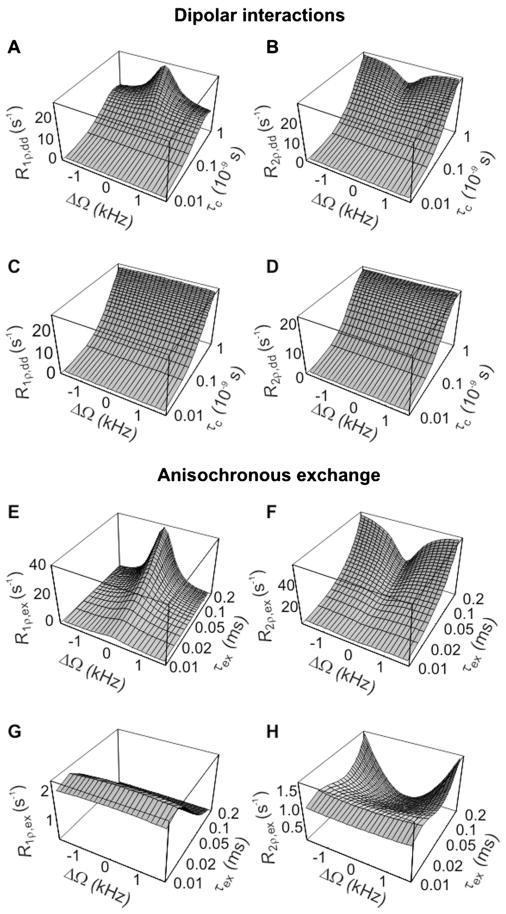
The calculated R1ρ and R2ρ values resulting from dipolar interactions (Fig. 2A–D) or anisochronous exchange (Fig. 2E–H) during CW irradiation, plotted as a function of ΔΩ and correlation times, are shown in Fig. 2. In the case of moderate RF peak power, i.e. , R1ρ R2ρ and caused by dipolar interactions depend strongly on ΔΩ when τc > 10−10 s (Fig. 2A,B). Similar considerations apply for the anisochronous exchange considered in Fig. 2E,F, when τex > 0.05 ms, a situation that occurs when the exchange process is still in FXR, but is slower than the extreme case of the fast exchange limit. When increasing to 10 kHz, R1ρ and R2ρ caused by dipolar interactions (Fig. 2C,D), and R1ρ as a result of anisochronous exchange (Fig. 2G), are minimally affected by ΔΩ in the investigated region of ΔΩ, τc and τex values. However, the exchange-induced R2ρ still exhibits a prominent dependence on ΔΩ for (Fig. 2H). This is a consequence of the fact that the R2ρ,ex formula contains one secular term that depends only on the cosine square of the angle α [given by eqn (1)]; this function becomes independent of ΔΩ when α approaches the asymptotic value of 90°, which occurs at for the chosen ΔΩ range of 3 kHz. Overall, the dependence of rotating frame relaxations on ΔΩ during CW irradiation is a known feature of conventional spin-lock methods, which is often used to generate different MR contrasts.
Figure 2.
Calculated R1ρ and R2ρ values as a function of ΔΩ and correlation times during continuous-wave (CW) irradiation, resulting from dipolar interactions (A–D) and anisochronous exchange (E–H). Relaxation rate constants were calculated according to eqns (6,7) and eqns (8,9), respectively. Simulation parameters were as follows: ω0/(2π) = 200 MHz; r = 0.153 nm; PA = PB = 0.5; δω = 0.85 ppm. The range of rotational correlation times (τc) was chosen in order to satisfy the weak field approximation, and the range of exchange correlation times (τex) was chosen to satisfy the fast exchange regime. In (A,B,E,F), ; in (C,D,G,H), . R1ρ and R2ρ values are plotted over the same chemical shift range as displayed in Fig. 3.
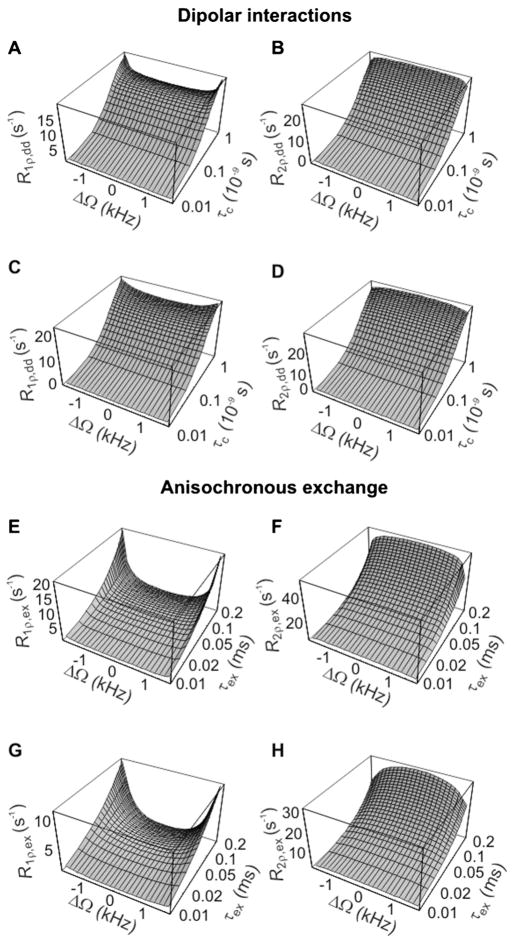
However, the results of the theoretical predictions indicate that R1ρ and R2ρ in the presence of both dipolar interactions (Fig. 3A,B) and anisochronous exchange (Fig. 3C,D) are essentially constant as a function of ΔΩ for all investigated values of correlation times within a subregion of BW of the HS pulse. Contrary to that observed with conventional spin-lock, the simulations showed that the dependence of adiabatic R1ρ and R2ρ on ΔΩ is actually more pronounced for the higher values, resulting in a slightly smaller range of chemical shifts within BW of the adiabatic pulse where the relaxation rates are constant as a function of ΔΩ. This is a clear advantage of adiabatic methods over CW spin-lock for in vivo MRS in humans, because it allows ‘one-shot’ data acquisition over a wide range of chemical shifts without the need to use impractically large RF power, remaining in compliance with the limits imposed by SAR.
Figure 3.
Calculated R1ρ and R2ρ values as a function of ΔΩ and correlation times during adiabatic rotation, resulting from dipolar interactions (A–D) and anisochronous exchange (E–H). Relaxation rate constants were calculated according to eqns (6,7) and eqns (10,11), respectively. The simulation parameters are the same as in Fig. 2. Pulse parameters: hyperbolic-secant (HS) modulation functions; Tp = 6 ms; bandwidth (BW)/(2π) ≈ 3.3 kHz. In (A,B,E,F), ; in (C,D,G,H), . Relaxation rate constants were plotted over the chemical shift range corresponding to BW of the HS pulse.
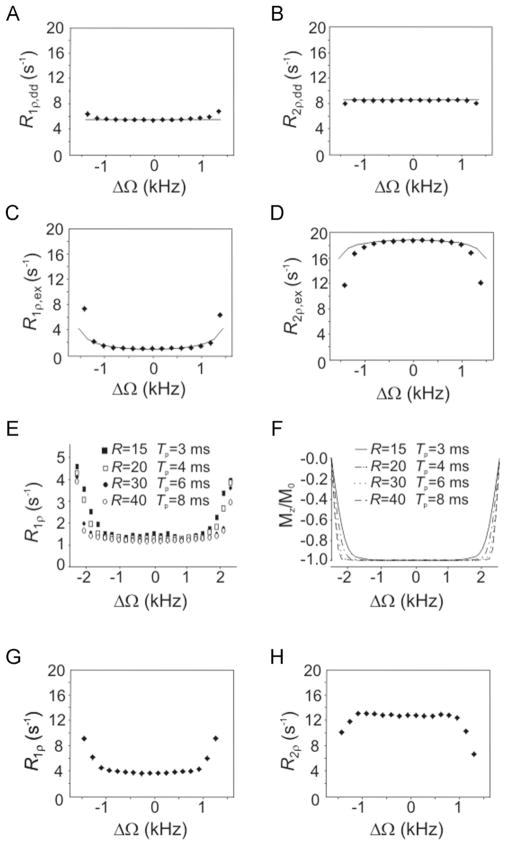
The phantom results confirmed the theoretical predictions for both dipolar interactions (Fig. 4A,B) and anisochronous exchange (Fig. 4C,D). From simulations, the experimentally measured R1ρ and R2ρ values for the glycerol phantom (Fig. 4A,B) yielded τc values of approximately 1.0 × 10−10 s and 1.6 × 10−10 s, respectively, in agreement with previous findings (25). The slight discrepancy between the estimated τc values from R1ρ and R2ρ can be attributed to the complexity of motion of the acetate embedded in the heterogeneous environment of the glycerol matrix (26). The values of PAPB and τex which fitted the R1ρ and R2ρ data (Fig. 4C,D) simultaneously were approximately 0.16 and 1.4 × 10−4 s, respectively, which are in the same range as previously reported τex values (16). These results demonstrate creatine. that the formalism summarized by eqn (5) is adequate for isochromats that undergo full inversion during the adiabatic pulse. Deviations of the experimental findings from the theoretical predictions occur at the edges of the inversion band of the adiabatic pulse. In these regions, the isochromats do not satisfy the adiabatic condition, and therefore do not reach full inversion, which is instead an assumed prerequisite of the theoretical calculations. Notably, in the case of partial inversion, magnetization does not remain locked along B⃗eff in the case of R1ρ, nor does it precess in a plane perpendicular toB⃗eff in the case of R2ρ. Under these circumstances, the rotating frame relaxation rate constants are a combination of R1ρ and R2ρ, and therefore the formalism summarized in eqn (5) can no longer be applied. Importantly, adiabatic pulses with different R values produce different inversion profiles over the same BW. Interestingly, the rotating frame relaxation rate constants measured on the water–ethanol sample as a function of ΔΩ closely resemble the inversion profile of the pulse over BW (Fig. 4E,F), thus confirming that the inversion efficiency of the isochromat of interest is a critical parameter that determines the rotating frame relaxation during adiabatic pulses. In vivo, the coefficient of variations of R1ρ and R2ρ of the water signal (Fig. 4G,H) were 6% and 1.5%, respectively, within a 60% region of BW of the adiabatic pulse (≈ 2 kHz), thus confirming the minimal dependence of the rotating frame relaxation rate constants on ΔΩ in the case of adiabatic pulses, even in the presence of a variety of different relaxation channels and distribution of correlation times.
Figure 4.
Experimental R1ρ and R2ρ values during the adiabatic hyperbolic-secant (HS) pulse with Tp = 6 ms and bandwidth (BW)/(2π) ≈ 3.3 kHz, as a function of ΔΩ. Full lines represent results from simulations. Relaxation rate constants are plotted over BW of the HS pulse. (A,B) Results from acetate in glycerol–water phantom, which represents the dipolar interaction channel, ω0/(2π) = 200 MHz, ; values of τc which fitted the experimental R1ρ and R2ρ data were 1.0 × 10−10 s and 1.6 × 10−10 s, respectively. (C,D) Results from the ethanol–water phantom, which represents the anisochronous exchange relaxation channel, ; values of τex and PAPB which fitted the R1ρ and R2ρ data simultaneously were approximately 1.4 × 10−4 s and approximately 0.16, respectively (δω = 0.85 ppm). (E,F) Dependence of R1ρ on ΔΩ for different BW profiles of the HS pulse: (E) experimental results from the water–ethanol phantom, ω0/(2π) = 169 MHz; (F) inversion profiles over BW for the different HS pulses. R values and Tp are given in the figure. Other parameters: BW/(2π) = 5 kHz; . (G,H) Results from the human brain, ω0/(2π) = 169 MHz, .
Representative spectra used for the estimation of the adiabatic R1ρ and R2ρ values of metabolites are shown in Fig. 5. Our results demonstrate that the adiabatic R1ρ and R2ρ values of the methyl groups of t-Cr and NAA are significantly different (Fig. 2). Specifically, R1ρ and R2ρ of t-Cr are almost doubled when compared with those of NAA (see Fig. 5). As the resonances at 2.01 ppm and 3.03 ppm fell in the ‘flat’ region of BW of the AFP pulses, where adiabatic relaxation rate constants do not depend on the chemical shift, this implies that the observed differences in adiabatic R1ρ and R2ρ values are not a result of different frequency offsets, but rather reflect different dynamic properties of the two metabolites. The faster rate constants of t-Cr are in agreement with previous findings obtained in rat brain, where conventional spin-lock CW T1ρ measurements (4) were performed by placing the peaks of interest on-resonance in separate acquisitions. This observation is consistent with the involvement of NAA and t-Cr in biochemical processes characterized by different rates, with the turnover of NAA being very slow compared with the energetic processes involving t-Cr (27). Interestingly, in contrast with adiabatic R1ρ and R2ρ, longitudinal relaxation time constants do not show any difference between t-Cr and NAA at 4 T (28), thus suggesting enhanced sensitivity of rotating frame relaxation measurements to metabolic processes relative to T1 measurements.
Figure 5.
Adiabatic R1ρ (left) and R2ρ (right) of metabolites measured from the human brain. Top: spectra acquired at different durations (TD) of the adiabatic full passage (AFP) train from one representative subject. MRS data processing: frequency and phase corrections of individual scans; summation of 16 scans; residual eddy current correction; Gaussian multiplication (σ = 0.0865s); fast Fourier transformation and zero-order phase correction. No further post-processing, such as water signal removal and baseline correction, was performed. Bottom: normalized signal intensity (SI) decays plotted as a function of TD. Full lines indicate a monoexponential fit. The values of the measured relaxation rate constants are given in the figure. Data are presented as averages ± standard deviation (n = 10). NAA, N-acetylaspartate; t-Cr, total
CONCLUSION
The results from simulations, phantom and in vivo experiments demonstrate that adiabatic R1ρ and R2ρ values are minimally dependent on the frequency offset under general experimental conditions, unlike CW spin-lock measurements. Measurements performed on metabolites from the human brain using adiabatic methods offer high sensitivity to metabolite dynamics in vivo.
Acknowledgments
The authors thank the following agencies for financial support: Instrumentarium Science Foundation (TL); Orion Corporation Research Foundation (TL); Finnish Cultural Foundation Northern Savo (TL); National Institutes of Health grants P30 NS057091, P41 RR008079, R01NS061866 and R21NS059813. The authors finally thank Dr Jennifer Rees for help with phantom preparations.
Abbreviations used
- AFP
adiabatic full passage
- AHP
adiabatic half passage
- BW
bandwidth
- CW
continuous-wave
- FXR
fast exchange regime
- HS
hyperbolic-secant
- LASER
localization by adiabatic selective refocusing
- MLEV
Malcolm Levitt
- NAA
N-acetylaspartate
- RF
radiofrequency
- SAR
specific absorption rate
- t-Cr
total creatine
- Tp
pulse duration
References
- 1.Michaeli S, Sorce DJ, Garwood M. T2ρ and T1ρ adiabatic relaxations and contrasts. Curr Anal Chem. 2008;4:8–25. [Google Scholar]
- 2.Mangia S, Liimatainen T, Garwood M, Michaeli S. Rotating frame relaxation during adiabatic pulses versus conventional spin-lock: simulations and experimental results at4T. Magn Reson Imaging. 2009;27:1074–1087. doi: 10.1016/j.mri.2009.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Michaeli S, Grohn H, Grohn O, Sorce DJ, Kauppinen R, Springer CS, Jr, Ugurbil K, Garwood M. Exchange-influenced T2ρ contrast in human brain images measured with adiabatic radio frequency pulses. Magn Reson Med. 2005;53:823–829. doi: 10.1002/mrm.20428. [DOI] [PubMed] [Google Scholar]
- 4.Kettunen M, Grohn O, Kauppinen R. Quantitative T1ρ NMR spectroscopy of rat cerebral metabolites in vivo: effects of global ischemia. Magn Reson Med. 2004;51:875–880. doi: 10.1002/mrm.20099. [DOI] [PubMed] [Google Scholar]
- 5.Abergel D, Palmer AG. On the use of the stochastic Liouville equation in nuclear magnetic resonance: application to R1ρ relaxation in the presence of exchange. Concepts Magn Reson Part A. 2003;19A:134–148. [Google Scholar]
- 6.Desvaux H, Berthault P. Study of dynamic processes in liquids using off-resonance RF irradiation. Progr NMR Spectr. 1999;35:295–340. [Google Scholar]
- 7.Palmer A, Kroenke C, Loria J. Nuclear magnetic resonance methods for quantifying microsecond-to-millisecond motions in biological macromolecules. Methods Enzymol. 2001;339:204–238. doi: 10.1016/s0076-6879(01)39315-1. [DOI] [PubMed] [Google Scholar]
- 8.Trott O, Palmer AG., 3rd Theoretical study of R1ρ rotating-frame and R2 free-precession relaxation in the presence of n-site chemical exchange. J Magn Reson. 2004;170:104–112. doi: 10.1016/j.jmr.2004.06.005. [DOI] [PubMed] [Google Scholar]
- 9.Witschey WR, 2nd, Borthakur A, Elliott MA, Mellon E, Niyogi S, Wallman DJ, Wang C, Reddy R. Artifacts in T1ρ-weighted imaging: compensation for B1 and B0 field imperfections. J Magn Reson. 2007;186:75–85. doi: 10.1016/j.jmr.2007.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Garwood M, DelaBarre L. The return of the frequency sweep: designing adiabatic pulses for contemporary NMR. J Magn Reson. 2001;153:155–177. doi: 10.1006/jmre.2001.2340. [DOI] [PubMed] [Google Scholar]
- 11.Michaeli S, Sorce DJ, Springer CS, Jr, Ugurbil K, Garwood M. T1ρ MRI contrast in the human brain: modulation of the longitudinal rotating frame relaxation shutter-speed during an adiabatic RF pulse. J Magn Reson. 2006;181:135–147. doi: 10.1016/j.jmr.2006.04.002. [DOI] [PubMed] [Google Scholar]
- 12.Mangia S, Traaseth NJ, Veglia G, Garwood M, Michaeli S. Probing slow protein dynamics by adiabatic R1ρ and R2ρ NMR experiments. J Am Chem Soc. 2010;132:9979–9981. doi: 10.1021/ja1038787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sorce D, Michaeli S, Garwood M. Relaxation during adiabatic radio-frequency pulses. Curr Anal Chem. 2007;3:239–251. [Google Scholar]
- 14.Silver M, Joseph R, Hoult D. Highly selective π/2 and π pulse generation. J Magn Reson. 1984;59:347–351. [Google Scholar]
- 15.Tannus A, Garwood M. Improved performance of frequency-swept pulses using offset-independent adiabaticity. J Magn Reson A. 1996;120:133–137. [Google Scholar]
- 16.Michaeli S, Sorce DJ, Idiyatullin D, Ugurbil K, Garwood M. Transverse relaxation in the rotating frame induced by chemical exchange. J Magn Reson. 2004;169:293–299. doi: 10.1016/j.jmr.2004.05.010. [DOI] [PubMed] [Google Scholar]
- 17.Gruetter R, Tkac I. Field mapping without reference scan using asymmetric echo-planar techniques. Magn Reson Med. 2000;43:319–323. doi: 10.1002/(sici)1522-2594(200002)43:2<319::aid-mrm22>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 18.Sierra A, Michaeli S, Niskanen JP, Valonen PK, Grohn HI, Yla-Herttuala S, Garwood M, Grohn OH. Water spin dynamics during apoptotic cell death in glioma gene therapy probed by T1ρ and T2ρ. Magn Reson Med. 2008;59:1311–1319. doi: 10.1002/mrm.21600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Blicharski J. Nuclear magnetic relaxation in rotating frame. Acta Phys Pol A. 1972;41:223–236. [Google Scholar]
- 20.Davis D, Perlman M, London R. Direct measurements of the dissociation-rate constant for inhibitor–enzyme complexes via the T1ρ and T2 (CPMG) methods. J Magn Reson B. 1994;104:266–275. doi: 10.1006/jmrb.1994.1084. [DOI] [PubMed] [Google Scholar]
- 21.Levitt M, Freeman R, Frenkel T. Broadband heteronuclear decoupling. J Magn Reson. 1982;47:328–330. [Google Scholar]
- 22.Tkac I, Starcuk Z, Choi IY, Gruetter R. In vivo 1H NMR spectroscopy of rat brain at 1ms echo time. Magn Reson Med. 1999;41:649–656. doi: 10.1002/(sici)1522-2594(199904)41:4<649::aid-mrm2>3.0.co;2-g. [DOI] [PubMed] [Google Scholar]
- 23.Henry PG, Marjanska M, Walls JD, Valette J, Gruetter R, Ugurbil K. Proton-observed carbon-edited NMR spectroscopy in strongly coupled second-order spin systems. Magn Reson Med. 2006;55:250–257. doi: 10.1002/mrm.20764. [DOI] [PubMed] [Google Scholar]
- 24.Govindaraju V, Young K, Maudsley AA. Proton NMR chemical shifts and coupling constants for brain metabolites. NMR Biomed. 2000;13:129–153. doi: 10.1002/1099-1492(200005)13:3<129::aid-nbm619>3.0.co;2-v. [DOI] [PubMed] [Google Scholar]
- 25.Liimatainen T, Sorce DJ, O’Connell R, Garwood M, Michaeli S. MRI contrast from relaxation along a fictitious field (RAFF) Magn Reson Med. 2010;64:983–994. doi: 10.1002/mrm.22372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cowan B. Nuclear Magnetic Resonance and Relaxation. Cambridge University Press; Cambridge: 1997. [Google Scholar]
- 27.Choi IY, Gruetter R. Dynamic or inert metabolism? Turnover of N-acetyl aspartate and glutathione from D-[1-13C]glucose in the rat brain in vivo. J Neurochem. 2004;91:778–787. doi: 10.1111/j.1471-4159.2004.02716.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Posse S, Cuenod CA, Risinger R, Le Bihan D, Balaban RS. Anomalous transverse relaxation in 1H spectroscopy in human brain at 4 Tesla. Magn Reson Med. 1995;33:246–252. doi: 10.1002/mrm.1910330215. [DOI] [PubMed] [Google Scholar]