To transform or not to transform:

Chemical ecology, be it the study of plant volatiles or insect cuticular hydrocarbons, largely involves the analysis of compositions or “blends” of a mixture of compounds. Compositional data have intrinsic properties such as a “constantsum constraint,” which should be taken into account when statistically analyzing these data. The field of compositional data analysis has greatly improved our understanding of the nature of such compositions and has provided us with insights on statistically rigorous ways of analyzing such constrained data. Employment of standard multivariate statistical procedures on compositional data necessitates the use of appropriate transformation procedures, which removes the non-independence of data points, thus rendering the data suitable for such analysis. Here we present the current situation of the analysis of compositional data in chemical ecology; the awareness of this constraint of compositional data; and alternative ways of analyzing such constrained data using Random Forests, a data-mining algorithm that has many features that facilitate the analysis of such data. Two such features of particular relevance to compositional data are that Random Forests does not incorporate implicit assumptions about the distribution of the data and can deal with auto-correlations between data points.

Compositional Data in Chemical Ecology

Plant volatile bouquets or insect cuticular hydrocarbons are usually analyzed as relative proportions or percentages that are always bounded, i.e., all the data points add to a constant of 1 or 100%. Thus any increase in the value of a data point automatically requires the other data points to decrease, demonstrating the “constantsum constraint” of such data.¹ This non-independence of data points makes the data unsuitable for analysis using standard conventional statistical procedures such as multiple pairwise correlations, principal component analysis (PCA), multivariate analysis of variance (MANOVA) and multiple regressions. This is because all these procedures implicitly assume a data distribution, independence of data points, as well as absence of interactions between data points. Additional problems encountered in such data in chemical ecology include log-level differences in the percentage values of the data points, presence of a large number of zeroes and auto-correlations between data points.² These features are natural constraints in chemical ecology since many compounds could share common biosynthetic pathways, have isomeric forms, and also be selectively regulated based on the ecological context, resulting in large absences or large presences based on context.^3,4

The statistical analysis of compositional data saw a surge of improvement borrowing heavily from the field of geological chemistry. The study of mineral compositions usually involved categorisation into “major” elements that are present in percent to tens of percent values, “minor” elements that are present at around 1% concentrations and “trace” elements that are present in parts per million or parts per billion levels.⁵ Such data were analyzed using standard statistical procedures without being aware of the fact that the basic assumptions of normality, among others, were being violated. Although this was pointed out as early as 1897 by Karl Pearson writing on spurious correlations, it was not until the 1960s that such pitfalls were acknowledged and were taken into consideration.¹ Several transformations were proposed to render the data suitable for analysis. These include the centered log ratio transformation (clr), additive log ratio transformation (alr) and isometric log ratio transformation (ilr), of which clr is most often used.^6,7

Transformation of Compositional Data in Chemical Ecology

To understand the extent of transformations of compositional data in chemical ecology, we performed a literature survey using Google Scholar. We limited our search period to 1986–2010, since it was in 1986 that J. Aitchison published the seminal work titled “The statistical analysis of compositional data,” which advocated the use of data transformation.⁸ We employed the key words: (plant + volatiles + “GC-MS”) and (cuticular + hydrocarbons + “GC-MS”) to retrieve citations which we used as surrogates for published literature in this area of chemical ecology. We restricted our search with the keyword (GC-MS) as this would capture the specific subset of studies that identify and analyze compounds in chemical ecology. Along with this search, we were able to retrieve literature that contained the keyword (Aitchison) and literature that did not contain the keyword. The results of this survey revealed a disproportionately small number of studies that actually contained the keyword (Aitchison) and thus by proxy have cited Aitchison's paper and transformed their data as recommended by Aitchison (Fig. 1). We repeated this survey using the phrase (“Random Forests”) to retrieve literature that has used this relatively new algorithm. We found just five results with “plant volatiles” and none with “cuticular hydrocarbons” (Fig. 1).

Figure 1.

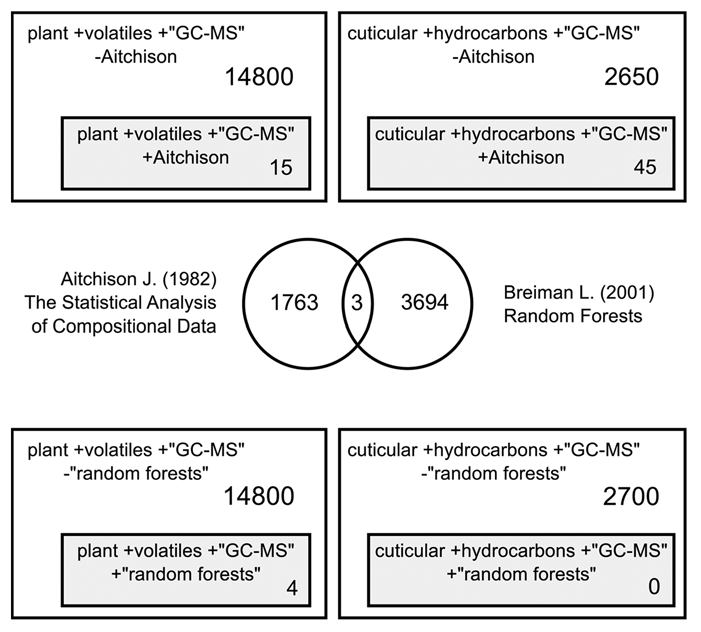
Literature survey using Google Scholar from 1986–2010 to retrieve publications in chemical ecology which transformed their proportion data as recommended by Aitchison in the fields of plant volatile (or) insect cuticular hydrocarbon analysis. The number of publications citing both the Aitchison transformation and Breiman's Random Forests is also shown.

Although dedicated software packages for analyzing compositional data exist, e.g., compositions, robCompositions and MixeR for R software, as well as CoDa developed by Aitchison, many studies use square-root transformations or log transformations with the addition of a constant (ranging from 0.01–0.00001) to accommodate zero data points. The addition of such seemingly arbitrary constant values would greatly affect/alter the projection of such data points in multivariate space.⁹ Thus, if one sets out to study compositional data within the framework of standard multivariate procedures, it is imperative that the researcher be aware of the limitations and/or assumptions of such procedures and uses appropriate transformation procedures to incorporate statistical rigor into the analysis. If the researcher desires not to use such model-based methods with built-in assumptions, alternate algorithm-based methods such as Random Forests are at the researcher's disposal.

Random Forests and Compositional Data

Random Forests¹⁰ is a data-mining algorithm that has many features which make it suitable for analyzing complex data sets.¹¹ For example, there is increasing use of Random Forests in the analysis of complex microarray data since year-wise microarray studies citing this approach that were retrieved using the keywords (microarray + “random forest”) were the following: 2002:10, 2003:30, 2004:70, 2005:130, 2006:280, 2007:472, 2008:706, 2009:1021, 2010:1300. This indicates an increasing adoption of this method by molecular biologists. Of particular interest to chemical ecologists are two features of Random Forests: no implicit assumptions on the structure of the data points and accommodation of any interactions and/or correlations between data points. As Random Forests is a non-parametric method,¹² it can also deal with data points varying in log-scales and with zeroes. Random Forests constructs decision-based trees selecting a subset of samples and variables at random. This combined with bootstrap aggregations gives estimates of classification errors. Such attractive features provide possibilities of using such algorithms for data sets in chemical ecology which have the additional constraint of comprising of compositional data.

We reanalyzed data on volatile organic compounds (VOCs) produced by ripe figs of three species and two sexes within these species (Ficus hispida male and female figs, Ficus exasperata male and female figs, and Ficus tsjahela monoecious figs) that we had analyzed using Random Forests in an earlier paper,^2,13 this time by transforming the data by adding 0.0001 to all values. In comparison with an earlier PCA plot of untransformed VOC values, we found that a PCA with transformed VOC values gave better separation between species and sexes (Fig. 2) in comparison to untransformed data (Fig. 4a of the earlier publication¹³). Furthermore, a multidimensional scaling plot using the MDSplot function in the Random Forests package with untransformed proportions showed the same separation as did the PCA plot with transformed proportions (Fig. 2). This indicates that a PCA with transformed proportions is equivalent to a multidimensional scaling (MDS) plot with untransformed proportions with these data (the MDSplot function does not provide stress values as in other MDS analysis). Furthermore, we used the varSelRF routine¹¹ with Random Forests on transformed data to separate the five classes of figs and found some interesting similarities and differences from our earlier results (Table 1). In the case of male F. hispida and F. tsjahela, there were no differences from our earlier predictor VOC compounds. In the case of F. hispida female, we found that Random Forests had substituted 2-heptyl acetate instead of iso-amyl acetate as a predictor compound (Table 1). In female F. exasperata, Random Forests substituted undecane instead of p-cymene and β-caryophyllene with a lower model frequency of 83% compared to the earlier model frequency of 98% (Table 1). In male F. exasperata, Random Forests added allo-aromadendrene, γ-terpinene and terpinolene to a previous list of predictor VOCs with a now much higher model frequency of 82% compared to the earlier 31% (Table 1).

Figure 2.

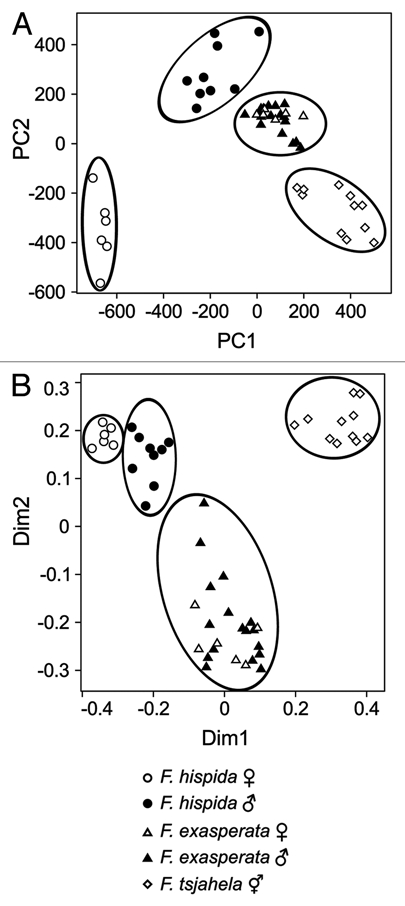
Unsupervised classification of fruit-dispersal volatile organic compounds (VOCs) of three sympatric Ficus species using proportional abundance of VOCs. (A) A PCA plot of VOC proportions after transformation employing the clr (centered log ratio) method as recommended by Aitchison. (B) An MDS plot of the untransformed proportions of the same VOCs using Random Forests.

Table 1.

Comparison of results from Random Forests on ripe fig fruit volatile organic compounds (VOCs) using untransformed and transformed data

Group of interest	Model frequency (untransformed data)a	Predictor VOCs (untransformed data)a	Model frequency (transformed data)	Predictor VOCs (transformed data)	Percentage of VOCs in headspacea	CVa,b
F. hispida female	100	2-amyl acetate	100	2-amyl acetate	63.3	0.3
		iso-amyl acetate			1.3	1.5
				2-heptyl acetate	23.2	0.7
F. hispida male	100	indole	100	indole	32.1	0.6
		α-trans bergamotene		α-trans bergamotene	20.9	0.5
F. tsjahela monoecious	100	α-pinene	100	α-pinene	31.5	0.2
		camphene		camphene	3.1	0.3
F. exasperata female	98	γ-terpinene	83	γ-terpinene	21.7	0.5
		p-cymene			5.4	0.3
		β-caryophyllene			0.2	1.5
				undecane	1.3	1.1
F. exasperata male	31	daucene	82	daucene	2.9	1.0
		β-copaene		β-copaene	0.9	0.9
				allo-aromadendrene	3.3	1.0
				γ-terpinene	7.9	0.6
				terpinolene	0.5	0.9

^aData from Ranganathan & Borges (2010).²

^bCoefficient of variation of VOC headspace percentage.

Should a researcher be more comfortable with the results from transformed or untransformed data in this case? We suggest that since Random Forests coupled with varSelRF employs bootstrapping in which various compounds are selected at random may times over, in various combinations, it should not be necessary to transform the data to employ such algorithms in the search for predictor variables. However, this suggestion needs to be examined and verified statistically. We urge statisticians such as John Aitchison and Leo Breiman to turn their attention to such specific problems that will help to shed light on the genuine dilemma facing researchers in this area: to transform or not to transform?

Addendum to: Ranganathan Y, Borges RM. Reducing the babel in plant volatile communication: Using the forest to see the trees. Plant Biol. 2010;12:735–742. doi: 10.1111/j.1438-8677.2009.00278.x.