The organization of intralimb and interlimb synergies in response to different joint dynamics

Abstract

We sought to understand differences in joint coordination between the dominant and nondominant arms when performing repetitive tasks. The uncontrolled manifold approach was used to decompose the variability of joint motions into components that reflect the use of motor redundancy or movement error. First, we hypothesized that coordination of the dominant arm would demonstrate greater use of motor redundancy to compensate for interaction forces than would coordination of the nondominant arm. Secondly, we hypothesized that when interjoint dynamics were more complex, control of the interlimb relationship would remain stable despite differences in control of individual hand paths. Healthy adults performed bimanual tracing of two orientations of ellipses that resulted in different magnitudes of elbow interaction forces. For the dominant arm, joint variance leading to hand path error was the same for both ellipsis orientations, whereas joint variance reflecting the use of motor redundancy increased when interaction moment was highest. For the nondominant arm, more joint error variance was found when interaction moment was highest, whereas motor redundancy did not differ across orientations. There was no apparent difference in interjoint dynamics between the two arms. Thus, greater skill exhibited by the dominant arm may be related to its ability to utilize motor redundancy to compensate for the effect of interaction forces. However, despite the greater error associated with control of the nondominant hand, control of the interlimb relationship remained stable when the interaction moment increased. This suggests separate levels of control for inter- versus intra-limb coordination in this bimanual task.

Introduction

In everyday tasks, many different combinations of muscles and joint angles can be used to achieve a given movement pattern. Bernstein (1967) has characterized this fact as the problem of mastering the “redundant” degrees of freedom (DOFs). The concept of motor redundancy has motivated significant experimental and theoretical interest in recent years (e.g., Cole and Abbs 1986; McDonald et al. 1989; Cruse et al. 1990; Vereijken et al. 1992; Desmurget and Prablanc 1997; Scholz and Schöner 1999; Schwartz and Moran 2000; Latash et al. 2003). If one considers motor redundancy to be more problematic than beneficial, then performing a task with more DOFs, such as bimanual versus unimanual tasks, compounds the problem. This is because the nervous system needs to consider not only control of DOFs within an arm but also coordination of DOFs across two arms to maintain a stable interlimb relationship. An alternative view is that the nervous system takes advantage of the available redundancy or motor abundance (Latash 2000) to allow for more flexible task performance (Gelfand and Tsetlin 1969; Schöner 1995).

Recent work has demonstrated the use of motor abundance as one important feature of motor coordination (Scholz et al. 2001; Domkin et al. 2002; Latash et al. 2002; Tseng et al. 2003; Krishnamoorthy et al. 2005; Yang and Scholz 2005). For unimanual movements, both dominant and nondominant arms generally demonstrate a similar use of motor redundancy, although coordination of the nondominant arm typically is associated with higher overall variability (Tseng et al. 2002, 2003). In tasks that require simultaneous actions of both arms, however, the use of motor redundancy differs between the two arms (Domkin et al. 2005; Tseng et al. 2006). This difference is most dramatic when the bimanual pattern becomes more difficult (i.e. moving in asymmetry at faster speeds) and the nondominant arm demonstrates inefficient joint coordination patterns that lead to greater performance error in this arm.

Being able to coordinate intersegmental forces is another important feature controlling multijoint movements (Ghez et al. 1995; Sainburg et al. 1995; Bastian et al. 1996; Beer et al. 2000). Sainburg and coworkers have proposed a dynamic-dominance hypothesis (Sainburg 2002) stating that the ability to govern limb dynamics is the key factor to distinguish motor skills between the dominant and nondominant arms. Namely, the dominant arm is better at hand path control, presumably because of the dominant hemisphere’s ability to predict the effect of interaction moments (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg 2002; Sainburg 2002). On the other hand, the nondominant arm is purported to be better at steady-state control, like stabilizing the final reach position (Wang and Sainburg 2007). Because of the ability to anticipate and capitalize on the effect of interaction moments, movements of the dominant arm are produced with less muscle force in comparison to the nondominant arm, and they are associated with straighter hand path (Bagesteiro and Sainburg 2002). Given these observations, one could predict that when moving bimanually, differences between each arm’s ability to coordinate limb dynamics would affect the stability of interlimb coupling especially when intersegmental dynamics becomes more complex.

Because interaction force is a mechanical effect, incomplete compensation or poor anticipation of this effect will disturb the on-going movement. This is especially the case when there is minimal or no redundancy. Having motor redundancy allows the possibility of error compensation by other joints in the event that one joint deviates from its planned path, maintaining stability of the hand path (Latash et al. 2002, 2003). The poorer control exhibited by the nondominant arm in dealing with interaction forces may stem partly from a poorer ability to take advantage of available motor redundancy for error compensation. We previously showed that the nondominant arm exhibited decreased use of motor redundancy when moving very fast (>2 Hz), and this was related to less ability to counteract the effect of interaction forces (Tseng et al. 2006), resulting in a breakdown of movement coordination. In contrast, the dominant arm was able to maintain a stable use of motor redundancy across different speed levels. However, the observed differences could arise, because interaction forces are high when moving fast and the nondominant hand has less force-generating capacity compared to the dominant arm (Crosby et al. 1994).

The first goal of this study was to further investigate how the magnitude of interaction forces affected each arm’s use of motor redundancy to control its hand path. We manipulated the magnitude of interaction moments by changing movement direction to understand the effect of interaction force magnitude when it is independent of movement speed. We selected a bimanual tracing task that required subjects to monitor the hand trajectories continuously to pose a greater challenge to control of the nondominant arm than would a target reaching task. Subjects were asked to trace accurately two ellipses simultaneously when the long axes of both ellipses were oriented either ipsilaterally or contralaterally (see Fig. 1b). The different orientations required different magnitudes of individual joint motions as well as interaction moments (Dounskaia et al. 2002). Tracing the contralaterally orientated ellipses resulted in greater shoulder motion and larger interaction moments at the elbow compared to tracing the ipsilaterally oriented ellipse. We predicted that contralateral tracing would cause more disturbances to control of the nondominant arm compared to tracing the ipsilateral pattern. We also hypothesized that control of the dominant arm would take greater advantage of the available, “abundant” DOFs to compensate for the higher elbow interaction moment when tracing the contralateral pattern.

Fig. 1.

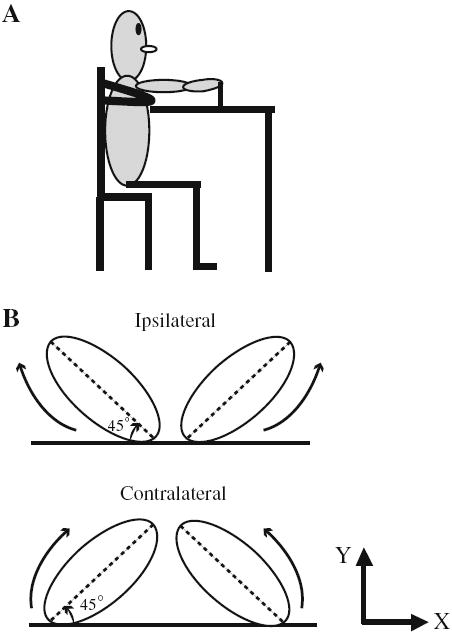
Illustration of the experimental setup: a view from the right side; b the arrangement of the ellipse template. Arrows indicate hand movement direction. See text for details

The second goal of this work was to understand how the ability to deal with interaction forces within a limb affected interlimb coordination, which requires the management of a greater number of DOFs compared to controlling the individual hand paths. Stable interlimb coupling is important for successful performance of the bimanual task. The mode of interlimb coordination (in-phase or antiphase) has been shown to affect the stability of intralimb coordination, whereas the opposite is not necessarily true (Li et al. 2005), indicating that maintaining stable interlimb coupling has a stronger impact on the overall coordination. Trade-offs between controlling an individual hand versus control of the between-hand relationship can also occur in a bimanual task. For example, Ryu and Buchanan showed that when variability of the individual hand paths increased due to changes in movement amplitude or pacing frequency, variability of the relative phasing between the two hands actually decreased (Ryu and Buchanan 2004; Buchanan and Ryu 2005). One advantage of motor redundancy is the possibility to maintain the overall goal when errors in individual components occur by adjusting the output of “redundant” DOFs (Latash et al. 2003). In a bimanual task, it is possible to recruit more joint motions to achieve stable interlimb coupling compared to achieving stable intralimb coordination, because both arms’ joint motions contribute to interlimb coupling. Based on this argument, we hypothesized that there would be greater use of motor redundancy to control the interlimb coupling compared to the control of the individual hand paths.

Materials and methods

Subjects

Ten healthy young subjects (three females and seven males, mean age 23 ± 3.71 years old) volunteered for this study. Subjects were paid for their participation and signed a consent form approved by the University of Delaware’s Human Subjects Review Board. All participants’ were self-identified as right-handers and their hand-dominance was confirmed using the ten-item Edinburgh Handedness Inventory (Oldfield 1971). All subjects were naïve about the purpose of the study. During the experiment, one male subject had difficulty performing the task with his nondominant arm, exhibiting very unstable performance compared to all other subjects. Therefore, we excluded his data from further analyses.

Experimental setup

We used a six-camera VICON motion measurement system (Oxford Metrics Ltd, UK) to record horizontal plane motion of the two arms. Individual reflective markers were attached to the following bony landmarks: (1) sternal notch; (2) just inferior to the lateral edge of acromion process (shoulder); (3) lateral epicondyle of the humerus (elbow); (4) radial styloid process (wrist); (5) distal end of the second metacarpal bone. The marker data was sampled at 120 Hz and the 3D coordinates were reconstructed offline using the VICON software. Reconstructed marker coordinates were filtered at 5 Hz with a bidirectional, second-order Butterworth low-pass filter in MATLAB^® (The MathWorks, MA, USA).

Subjects sat on a high-back chair at a rectangular table (122 cm × 91 cm) (Fig. 1a). Chair height was adjusted so that the upper arm and forearm were horizontal and parallel to the tabletop when holding the tool used to trace an elliptical template, using a power grip. The elliptical template to be traced was drawn with chalk on the tabletop. Subjects used a (4 cm diameter, 11 cm height) cylindrical bottle with a low friction roller to trace each template. The side of the bottle was attached to the subject’s hand with Velcro to prevent movements between the hand and the bottle. The position and size of the elliptical templates ensured that subjects used their scapulae as well as the shoulder, elbow and wrist joints to move the hand. A wide strap that encompassed the subject’s upper trunk and the chair back prevented trunk motion. No significant trunk movement was observed, and further analyses of the sternal marker confirmed this observation (<1 cm in both lateral and forward–backward directions).

The size of each template was scaled to the subject’s arm length. The length of the major axis of the elliptical template was set to 50% of each subject’s arm length (acromion to index finger). The X coordinate of the proximal end of the elliptical template was aligned with the subject’s shoulder (right or left, respectively). The Y coordinate of the proximal end was positioned at a distance equivalent to 50% of the subject’s upper arm length from the edge of the table in the forward direction. Ellipses were oriented at 45° angles to the horizontal. In the starting position, which had the tracing implements positioned at the proximal end of each ellipse, the experimenter measured the elbow and wrist angles of both arms with a goniometer before each trial to ensure a constant initial arm configuration.

Procedures

The task was to trace an elliptical template with both hands simultaneously. A metronome pulse paced the tracing movements at 2.0 Hz. Subjects were instructed to trace the template smoothly and continuously using a symmetrical pattern of hand coordination (demonstrated to the subject), while at the same time following a metronome beat for each 8-s trial. The major axis of the elliptical templates had a tilt angle of either 45° toward the same side of the body (ipsilateral) or 45° toward the opposite side of the body (contralateral) (Fig. 1b). The elliptical template had a ratio of minor to major axis (i.e. aspect ratio) of 0.54. Movement direction was outward (i.e. moving the dominant hand counterclockwise and nondominant hand clockwise), which resulted in an “in-phase” or a mirror-symmetry bimanual pattern. A dot placed midway between the two templates served as a gaze point. Ten randomized trials of tracing each of the elliptical orientations were performed.

Data analysis

Calculation of joint angles

The 2D angle between adjacent limb segments was calculated using a link-segment model. For example, the vector connecting the shoulder and the sternum markers defines the orientation of the clavicle (V1), while the vector connecting the shoulder and elbow markers (V2) defines the orientation of the upper arm segment. The angle between these two vectors, after normalization, defines the shoulder angle (Θ_sho), e.g.

$${\Theta }_{\mathrm{sho}}=\mathrm{Arc}\mathrm{cosine}(\frac{\mathrm{V}1}{\left|\mathrm{V}1\right|}\cdot \frac{\mathrm{V}2}{\left|\mathrm{V}2\right|})$$ (1)

Four angles in each arm were computed: scapular (clavicular) abduction–adduction, shoulder horizontal abduction–adduction, elbow flexion–extension and wrist flexion–extension (Fig. 2). For scapular angle, the line extending to the right side and parallel to the frontal plane was used as the reference axis. Segment lengths were determined by computing the vector length between each adjacent pair of joint markers.

Fig. 2.

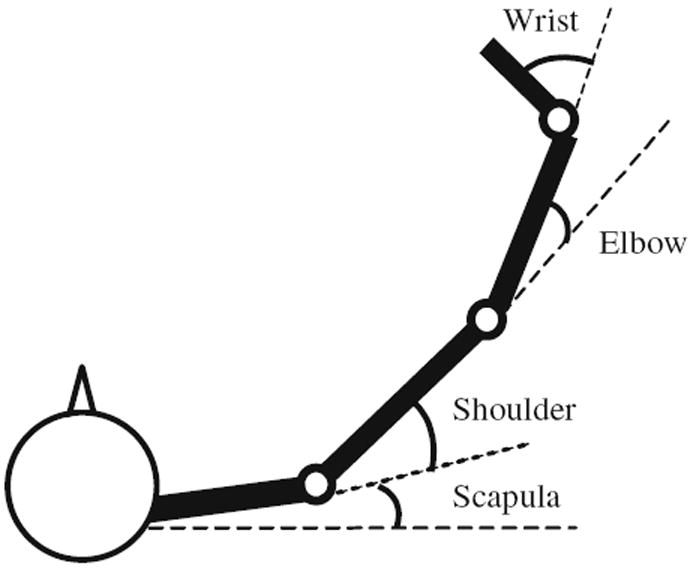
Illustration of joint angle calculation for the dominant arm: scapular abduction–adduction; shoulder horizontal abduction–adduction; elbow flexion–extension; wrist flexion–extension. The same arrangement applies to the nondominant arm

Components of joint configuration variance—uncontrolled manifold approach

We used the uncontrolled manifold (UCM) approach to quantify the extent to which the nervous system uses redundant combinations of joint motions to control two different task variables. These variables were chosen because of their importance to successful performance of this tracing task: the movement path of each hand and the vectorial difference (i.e. position and orientation) between the two hands. Implementation of the UCM approach has been described in detail elsewhere (Scholz and Schöner 1999; Tseng and Scholz 2005). The method is used to provide an operational definition of synergy in the current context: the use of motor redundancy to achieve flexible joint coordination that stabilizes important task-relevant parameters while, at the same time, minimizing joint variance leading to unwanted variations of task-relevant parameters. Another feature of synergies, the average sharing pattern among the motor elements (Latash et al. 2007), is less characteristic and is not addressed here.

Because of motor redundancy, it is possible that subjects use different joint angle combinations to achieve the same hand path when performing the tracing task multiple times. At any given point during the movement, there are likely combinations of joint angles that would result in an identical hand position while others could result in errors in hand position. We used the UCM approach to decompose the cycle-to-cycle variation of joint angle combinations into two components, one leading to the same hand position across cycles at specific points of the movement and the other leading to different hand positions across cycles. This decomposition reveals the extent to which joint variance adversely affects each hand’s path or in the bimanual case, how it affects the relative motion (i.e. vectorial difference) between the hands.

The first step to implement the UCM method was to define a geometric model linking the hand’s path to joint angles. For control of each individual hand path, the geometric model expressed the relationship between four joint angles and the X and Y coordinates of each hand. For example, the geometric model that linked the right hand’s medial–lateral position (X_R) was expressed as a function of segmental length and joint angles on the right arm (l₁ length of clavicle, l₂ length of upper arm, l₃ length of forearm, l₄ length of hand, θ₁ scapula, θ₂ shoulder, θ₃ elbow, θ₄ wrist).

$$\begin{array}{lll}{X}_{\mathrm{R}}& =& l_{1\mathrm{R}}\times \cos ({\theta }_{1\mathrm{R}})+l_{2\mathrm{R}}\times \cos ({\theta }_{1\mathrm{R}}+{\theta }_{2\mathrm{R}})\\ & & +l_{3\mathrm{R}}\times \cos ({\theta }_{1\mathrm{R}}+{\theta }_{2\mathrm{R}}+{\theta }_{3\mathrm{R}})+l_{4\mathrm{R}}\\ & & \times \cos ({\theta }_{1\mathrm{R}}+{\theta }_{2\mathrm{R}}+{\theta }_{3\mathrm{R}}+{\theta }_{4\mathrm{R}})\end{array}$$ (2)

The left hand’s medial–lateral position (X_L) can be similarly expressed:

$$\begin{array}{lll}{X}_{\mathrm{L}}& =& l_{1\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}})+l_{2\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}}+{\theta }_{2\mathrm{L}})\\ & & +l_{3\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}}+{\theta }_{2\mathrm{L}}+{\theta }_{3\mathrm{L}})+l_{4\mathrm{L}}\\ & & \times \cos ({\theta }_{1\mathrm{L}}+{\theta }_{2\mathrm{L}}+{\theta }_{3\mathrm{L}}+{\theta }_{4\mathrm{L}})\end{array}$$ (3)

For control of the vectorial difference (i.e., combined vector length and orientation) between two hands, the geometric model for the left hand was subtracted from the geometric model for the right hand, resulting in a difference in the X and Y coordinates between the two hands.

$$\begin{array}{lll}{X}_{\mathrm{R}-\mathrm{L}}& =& [l_{1\mathrm{R}}\times \cos ({\theta }_{1\mathrm{R}})+l_{2\mathrm{R}}\times \cos ({\theta }_{1\mathrm{R}}+{\theta }_{2\mathrm{R}})+l_{3\mathrm{R}}\\ & & \times \cos ({\theta }_{1\mathrm{R}}+{\theta }_{2\mathrm{R}}+{\theta }_{3\mathrm{R}})+l_{4\mathrm{R}}\\ & & \times \cos ({\theta }_{1\mathrm{R}}+{\theta }_{2\mathrm{R}}+{\theta }_{3\mathrm{R}}+{\theta }_{4\mathrm{R}})]\\ & & -[l_{1\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}})+l_{2\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}}+{\theta }_{2\mathrm{L}})\\ & & +l_{3\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}}+{\theta }_{2\mathrm{L}}+{\theta }_{3\mathrm{L}})\\ & & +l_{4\mathrm{L}}\times \cos ({\theta }_{1\mathrm{L}}+{\theta }_{2\mathrm{L}}+{\theta }_{3\mathrm{L}}+{\theta }_{4\mathrm{L}})]\end{array}$$ (4)

The same computation was performed for the Y dimension, yielding a vector subtraction of {X_R, Y_R} − {X_L, Y_L}. This vectorial difference represented the geometric model linking the relative position between two hands with eight joint angles (four from each arm). We then computed the Jacobian matrix based on the geometric model, which represents the partial derivatives of a given task variable (e.g., X_R) with respect to the joint angles. We used the mean vector of joint angles across cycles to estimate the planned value of the task variable for computing the Jacobian. One could assume that the hand position on the tracing template at each time point represents the planned value of the task variable. However, determining a joint angle combination that corresponds to a given hand position is an ill-posed problem given motor redundancy. The null space of the Jacobian matrix provides a linear estimate of a subspace, or the UCM, within which all joint angle combinations yield the mean value of the task variable to which the joint angles were related by the geometric model.

For each cycle of tracing, we projected experimentally observed joint angle combinations of each cycle at each sampled interval onto the UCM. We then computed the variance of the projection lengths, normalizing this value to the appropriate DOFs. This measure is a reflection of the amount of motor redundancy, i.e. reflecting the use of equivalent joint angle combinations to achieve an identical hand path. We refer to this component as goal-equivalent variance (GEV). Note that GEV would be zero if a system were truly nonredundant. The variance of joint angle combinations projected onto the orthogonal subspace that represents different values of the task variable is referred to as nongoal-equivalent variance (NGEV).

Because GEV is a reflection of the amount of motor redundancy used, GEV ≫ NGEV was expected with respect to control of the hand path or the vectorial difference between two hands, presuming that these variables are important for success of this bimanual tracing task. In contrast, if the nervous system solved the problem of coordinating multiple DOFs by invoking additional constraints to achieve a unique solution to joint coordination, then GEV is expected to be less than or approximately equal to NGEV, while the size of NGEV will reflect the error in tracing the template. A large value of NGEV compared to GEV despite successful task performance will indicate that the hypothesized variable is less crucial for this task, although it may be important for another task.

We also computed the relative difference, D_VAR = (GEV − NGEV)/(total joint configuration variance per DOF) to further quantify the selective use of motor redundancy, i.e. higher GEV than NGEV (Scholz et al. 2003). Total joint configuration variance was the experimentally observed variance of the joint angle vector across cycles at a given normalized time point, and this value was further normalized to the number of joints (n = 4 for control of the individual hand’s position; n = 8 for control of the vectorial difference). D_VAR is the appropriate measure for statistical comparisons between control of the individual hand paths and control of the vectorial difference between the hands, because these hypotheses were associated with different numbers of DOFs. In this case, control of each hand’s path was associated with only four joint motions, whereas control of the vectorial distance between the two hands involved all eight joint motions. A high positive D_VAR indicates a more selective use of motor redundancy, i.e., higher GEV and lower NGEV, compared to a low positive or negative value. Selective use of motor redundancy indicates that variations of joint combinations that contribute to error compensation, i.e. reflect motor redundancy, are allowed, whereas variations of joint combinations tending to cause errors in the task-relevant variables, such as the hand’s path, are suppressed. To allow such selective variation in joint space requires joint coordination.

Kinetic analyses

The moment of force acting at each joint in the horizontal plane was determined using a dynamic link-segment model. Segmental masses, segmental center of mass locations and moments of inertia about the vertical axes passing through the joint centers were estimated using anthropometric data (Hanavan 1964; Winter 1979). The dynamics equations for the four-joint manipulator were derived from the Lagrange’s equation within the screw theory framework (Murray et al. 1994). These equations allowed for partitioning of net joint moments (NM) into an interaction moment (IM) and a muscle moment (MM) (see Appendix for details). The gravitational moment was zero because the movement was restricted to the horizontal plane.

After qualitative examination of the continuous moment profiles to identify the general organization of each component of joint moments, analyses of the sign of the moment and the moment impulse were conducted (Sainburg and Kalakanis 2000). Intervals during which the sign of the interaction or muscle moments were the same or opposite to that of the NM were considered to make a positive (assisting) or negative (resisting) contributions, respectively, to NM. The percentage of these intervals relative to total cycle time was computed; positive or negative moment impulse (moment × time) was computed during intervals where the IM or MM acted in the same or opposite direction compared to NM. All positive and negative impulses were summed for each moment component within each cycle to yield a measure of total moment impulse. We conducted the kinetic analysis for all joint angles, but will only focus on results of the shoulder and elbow due to their primary contribution to the task.

Other kinematic measures

Aspect ratio and tilt angle

Measures that determined the features of each hand’s tracing path were computed following Walters and Carson (1997). An aspect ratio of 1 indicates a perfect circle, while an aspect ratio of 0 indicates a straight line. A vertical ellipse has tilt angle = 90°, while a horizontal ellipse would have tilt angle = 0°.

Cycle period

The time between two successive crossings of the minima in forward–backward dimension of the hand movement determined cycle period.

Constant error

The 2D template path is reconstructed based on the center, length of major axis and the eccentricity of the ellipse. The absolute difference between the template and the 2D resultant $\left(\sqrt{x^2+y^2}\right)$ hand path is computed at each point in time. The subtraction is then summed across time and averaged over trials to represent constant error.

Hand path variability

The standard deviation of the 2D hand path across cycles was computed at each point in time. This measure was then averaged over time to represent the path variability over the entire cycle for each condition.

Vector distance variability

The vectorial distance was first computed by subtracting the two hands’ {X, Y} position, resulting in a 2D vector of relative position. The length of this vector at each point in time could then be computed as the vector norm. The coefficient of variation of this norm over cycles and averaged over time provided the measure of vector length variability. We chose coefficient of variation instead of standard deviation, because the distance between two hands varied between the two elliptical conditions.

Vector direction variability

The cosine angle of the vectorial difference represents vector orientation. The standard deviation of this angle (in degrees) over cycles at each point in time was calculated and then averaged over time to represent the consistency of vector orientation relative to the horizontal line.

Angular excursion

Angular excursion of joint motions was measured as the per-cycle difference between the maximal and minimal positions of each joint.

Statistical analyses

Repeated measures ANOVAs were performed using the SPSS software. For hypotheses about controlling each hand’s path, a 2 × 2 × 2 design was used (arm × elliptical orientation × variance component). For the test of the vector distance between the two hands, we used a 2 × 2 design for analysis (elliptical orientation × variance component). To determine whether D_VAR differed between interlimb and intralimb coordination, we used a 3 × 2 design (vectorial distance, nondominant hand’s path, dominant hand’s path × elliptical orientation). Statistical tests of other kinematic and kinetic variables related to individual hand’s motion used a 2 × 2 design (arm × elliptical orientation). To analyze variations in the length and orientation of the vectorial distance between two hands, we used a single factor ANOVA (elliptical orientation). Planned comparisons based on the experimental hypotheses were also performed using the matrix structure in SPSS. Significance level was set at P < 0.05. To better understand the relationship between the selective use of motor redundancy (D_VAR) and movement performance (constant error), a Pearson correlation was conducted in SPSS. The analysis was performed separately for each arm and elliptical orientation combination, because we hypothesized that the arm might utilize motor redundancy differently when encountering different magnitude of interaction moments.

Results

Task performance

The hand paths of a representative subject are shown in Fig. 3a, b. The average tilt angle of the movement trajectory was 42.7° (±0.31°) across all subjects. There was a significant main effect of ellipse orientation on aspect ratio (F_1,8 = 19.0, P < 0.01). The aspect ratio of the ellipse was higher (more circular) for ipsilateral tracing (0.62 ± 0.02) compared to contralateral tracing (0.50 ± 0.03). Cycle period for contralateral tracing (580 ± 21 ms) was slower than that for ipsilateral tracing (500 ± 17 ms) (F_1,8 = 20.0, P < 0.01). There was no difference in tilt angle, aspect ratio and cycle period between the two arms (all P > 0.1).

Fig. 3.

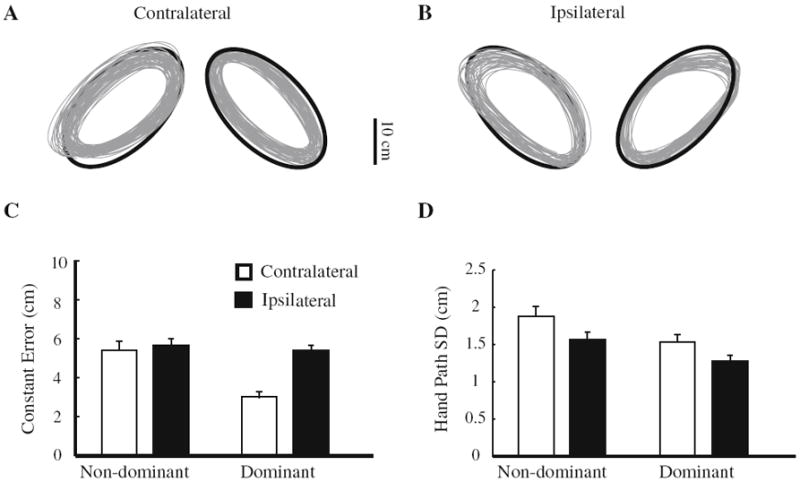
Hand path from one representative subject during (a) contralateral and (b) ipsilateral elliptical tracing; (c) constant error and (d) hand path standard deviation for each tracing condition. Error bars are standard errors of the mean (SEM)

To further quantify the tracing performance, constant error (Fig. 3c) of tracing was computed based on the required hand path defined by the template. The nondominant arm showed higher constant error than did the dominant arm (F_1,8 = 20.8, P < 0.005). Constant error was also higher when tracing the ipsilateral compared to the contralateral orientation (F_1,8 = 19.1, P < 0.005). However, these effects were primarily due to differences in performance of the dominant arm when tracing the contralateral ellipse; constant error was smallest when the dominant (right) arm performed the contralateral tracing compared to all other conditions (constant error: F_1,8 = 8.5, P < 0.05).

Variability of each hand’s path

We found a significant main effect of arm (F_1,8 = 17.0, P < 0.005), indicating that the nondominant hand’s path was more variable than that of the dominant hand regardless of the ellipsis orientation (Fig. 3d). Both hands’ paths were more variable when tracing the contralaterally compared to the ipsilaterally oriented ellipse, supported by a significant main effect of elliptical orientation (F_1,8 = 13.1, P < 0.01). The interaction of arm by elliptical orientation was not significant (P > 0.5).

Variability of relative motion between the hands

Stability of the vectorial distance between the two hands was characterized by the coefficient of variation of vector length and SD of vector orientation. There was a main effect of elliptical orientation when considering both vector length (F_1,8 = 31.5, P = 0.001) and vector orientation (F_1,8 = 49.6, P < 0.001). Both vector length (coefficient of variation 31 ± 1.4% vs. 22 ± 1.9%) and vector orientation (SD 10.6° ± 0.9° vs. 5.9° ± 0.9°) varied more when tracing the ipsilaterally compared to the contralaterally oriented ellipse.

Kinetic analysis

The kinetic analysis was performed to corroborate previously described differences in joint dynamics when tracing a contralateral versus an ipsilateral elliptical pattern (Dounskaia et al. 2002). For all of the variables we examined, there were no effects associated with the arm (P > 0.1). Figure 4 illustrates that the IM was larger and less smooth at the elbow when tracing the contralateral compared to the ipsilateral elliptical template, whereas the opposite appeared to be true for the shoulder joint. The primary contribution to NM was from MM (≥80% cycle period) (Fig. 5a). The exception was for the elbow joint, which, when considering the percentage of the cycle during which IM contributed to NM, had a larger positive IM interval during contralateral tracing compared to ipsilateral tracing (F_1,8 = 63.7, P < 0.001) (Fig. 5b). In contrast, the interval during which IM assisted the shoulder joint did not depend on the orientation of the ellipse (P > 0.1). The analysis of moment impulse showed that higher MM at the shoulder (F_1,8 = 77.5, P < 0.001, Fig. 6a) was accompanied by higher IM impulse at the elbow (F_1,8 = 75.0, P < 0.001, Fig. 6b) during tracing in the contralateral direction. In contrast, MM impulse was higher at the elbow during ipsilateral compared to contralateral elliptical tracing (F_1,8 = 87.6, P < 0.001, Fig. 6a).

Fig. 4.

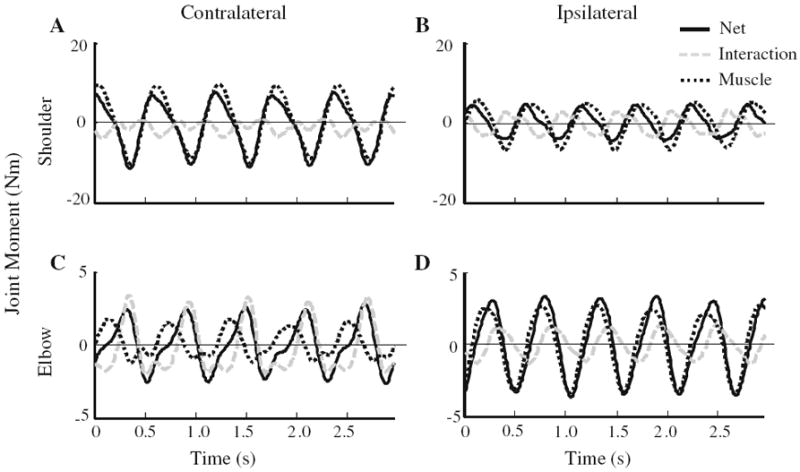
Example components of the individual moments at the shoulder (a, b) and elbow (c, d) during contralateral and ipsilateral tracing. Data from a representative subject is shown. Positive values indicate joint abduction or extension; negative values indicate joint adduction or flexion

Fig. 5.

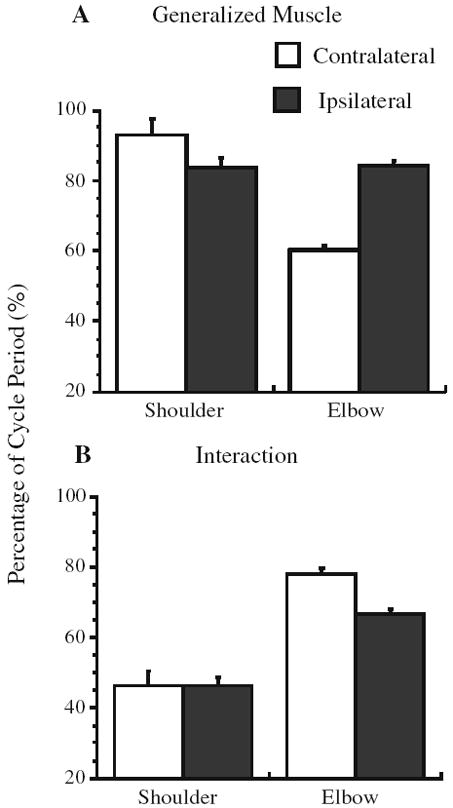
Mean percent of movement cycle during which (a) muscle and (b) interaction moments assisted NM at the shoulder and elbow joints. Interval is expressed as a percentage of the cycle period. Error bars are SEM

Fig. 6.

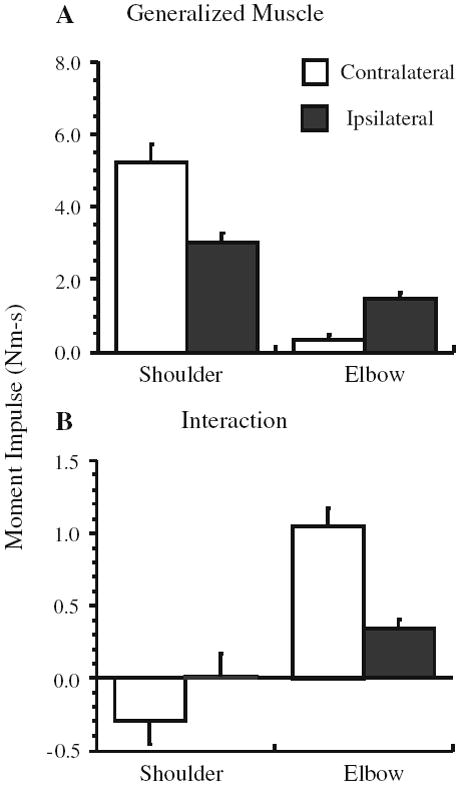
Mean (a) muscle and (b) interaction moment impulses at the shoulder and elbow joints. Error bars are SEM

Joint excursion

Shoulder excursion was significantly larger when tracing the contralaterally (38.2° ± 2.2°) compared to the ipsilaterally oriented ellipse (21.3° ± 0.8°) (F_1,8 = 81.3, P < 0.001). In contrast, elbow excursion was significantly larger when tracing the ipsilaterally (54.1° ± 2.6°) compared to the contralaterally (45.1° ± 2.5°) oriented ellipse (F_1,8 = 24.0, P = 0.001). Compared to the shoulder and elbow excursions, excursions of scapula (9.4° ± 0.7°) and wrist (8.9° ± 0.6°) were smaller. However, there was a significant main effect of orientation, indicating that scapular excursion was larger during contralateral compared to ipsilateral tracing (F_1,8 = 108.2, P < 0.001). Angular excursions did not differ between the arms (P > 0.1).

Use of motor redundancy

Control of the individual hand path

There was a significant effect of variance component (F_1,8 = 48.5, P < 0.001), indicating that GEV was larger than NGEV overall, reflecting the use of motor redundancy to control the individual hand paths (Fig. 7). Although a number of effects were interesting, including more overall joint variance (F_1,8 = 7.3, P < 0.05) and larger NGEV (F_1,8 = 7.5, P < 0.05) for the nondominant compared to the dominant arm, and a trend toward higher overall joint variance when tracing the contralateral pattern (P = 0.06), the effect of primary relevance to our hypothesis was in the interaction between arm, orientation and variance component.

Fig. 7.

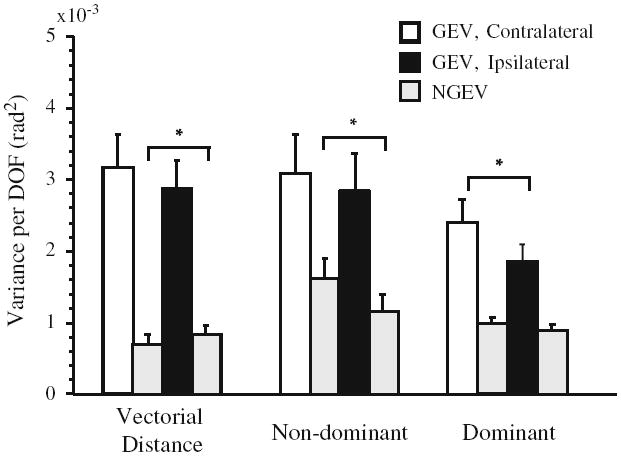
Mean components of joint configuration variance related to control of the vectorial distance between the hands, the nondominant and dominant hands’ paths. GEV is represented by open (contralateral) or black (ipsilateral) bars; NGEV for all control hypotheses is indicated by the light gray bar immediately to the right of the bars representing GEV. Error bars are SEM. *P < 0.05

This interaction was significant (F_1,8 = 5.3, P = 0.05), leading us to make additional comparisons. They revealed that control of the dominant hand’s path was associated with higher GEV when tracing the contralateral compared to the ipsilateral pattern (F_1,8 = 5.4, P < 0.05, Fig. 7, Dominant). NGEV underlying control of the dominant hand’s movement path did not differ between elliptical orientations (P > 0.5). These results suggest that the dominant hemisphere was able to take greater advantage of available motor redundancy in the face of higher elbow interaction moment when tracing the contralateral pattern. For control of the nondominant hand’s path, GEV did not differ between elliptical orientations (P > 0.5), whereas NGEV was higher when tracing the contralateral compared to the ipsilateral pattern (Fig. 7, Nondominant) (F_1,8 = 8.1, P < 0.05). These results suggest that the nondominant arm did not fully compensate for the higher interaction moment associated with tracing the contralateral ellipse, which adversely affected task-relevant coordination (i.e., higher NGEV).

Control of relative motion between the hands

There was a significant main effect of variance component (F_1,8 = 44.3, P < 0.001) reflecting higher GEV than NGEV related to control of the vectorial distance between the hands (Fig. 7). A significant interaction between ellipse orientation and variance component was also found (F_1,8 = 5.7, P < 0.05). This effect indicated a small increase of NGEV related to control of vectorial difference when tracing ipsilaterally oriented ellipses (F_1,8 = 7.3, P < 0.05). GEV did not differ between orientations (P > 0.2). Thus, control of the vectorial distance between the two arms took advantage of the available of joint motions, although this difference was less stable when tracing ipsilaterally oriented ellipses.

Comparison between intralimb and interlimb coordination (D_VAR)

Higher D_VAR indicates more selective use of motor redundancy, i.e., higher GEV relative to NGEV. A significant interaction between the level of coordination (i.e., control of the vectorial difference or the individual hand paths) and ellipse orientation was found (F_2,16 = 5.7, P < 0.05). Post-hoc contrasts revealed that D_VAR related to control of the vectorial difference (interlimb coordination) was higher when tracing the contralateral (0.95 ± 0.04) versus ipsilateral (0.82 ± 0.05) elliptical pattern (F_1,8 = 13.4, P < 0.01). During contralateral tracing, D_VAR related to control of the vectorial difference (0.95 ± 0.04) was higher than that related to control of the nondominant hand’s path (0.59 ± 0.13; F_1,8 = 10.4, P < 0.05), but not for control of the dominant hand’s path (0.77 ± 0.12; P > 0.1). In contrast, there were no significant differences in D_VAR between the different levels of coordination when examining ipsilateral elliptical tracing (interlimb 0.82 ± 0.05, nondominant 0.90 ± 0.07, P > 0.4; dominant 0.66 ± 0.09, P > 0.1). These results indicate that control of the relative motion between the two hands was more stable compared to control of the nondominant hand’s path when movements involved higher interaction moments. Interlimb and intralimb control did not differ when movements involved smaller interaction moments, as observed during ipsilateral tracing.

Correlation analysis

A correlation analysis was conducted to better understand whether selectively utilizing motor redundancy would affect the tracing performance. We chose constant error as an objective measure of performance, because it represented the average deviation of hand path from the template. We found significant correlation between D_VAR and constant error only for the dominant arm’s contralateral tracing (r = −0.9, P = 0.001). This analysis was not significant for other conditions (P > 0.5).

Discussion

We investigated the effect of interaction forces on the arm’s use of motor redundancy to control individual hand paths and to control the relative motion between the hands when participants performed a bimanual tracing task. The use of motor redundancy was found to be a feature of control (i.e. GEV ≫ NGEV). However, the extent of this usage differed depending on the arm and tracing condition. For control of individual hand paths, the dominant arm demonstrated greater use of motor redundancy when interaction forces were high, whereas the magnitude of interaction forces had no effect on the component of joint variance associated with hand path error. These results support the hypothesis that motor redundancy may be used to compensate for the effect of interaction forces on the hand’s path. In contrast, the magnitude of the interaction force had no effect on the use of motor redundancy in the nondominant arm. Instead, higher interaction forces led to a greater amount of joint variance associated with hand path error. Thus, the nondominant hemisphere exhibited poorer decoupling of joint space (see below) needed to take advantage of the available motor redundancy when there were higher interaction forces compared to the dominant arm. Despite these arm differences, however, the vectorial distance between the hands was still stabilized, indicating that the synergy organizing interlimb coordination had precedence over the intralimb synergies in this task. We will discuss the details of these findings below.

Intralimb synergy

Our results indicate that tracing a contralaterally oriented ellipse resulted in greater hand path variability compared to ipsilaterally oriented tracing, suggesting that higher interaction forces posed a greater challenge to control of the hand’s movements. Nonetheless, as summarized above, the greater challenge posed by higher interaction forces during contralateral tracing was associated with differences in each arm’s joint coordination and tracing performance; the dominant arm exhibited a more selective use of motor redundancy and lower constant error than did the nondominant arm. These results provide preliminary evidence that the use of “redundant” joint motions, or motor redundancy, may help compensate for the potentially adverse effect of interaction forces on performance. In contrast, the increase in the component of joint variance associated with hand path error in the nondominant arm when encountering higher interaction forces was associated with higher constant error compared to the dominant arm. The results suggest that this synergy was stronger in the dominant arm, even though both arms exhibited flexibility in joint coordination associated with the intralimb synergy. This arm difference was likely due to more effective joint space decoupling by the dominant hemisphere (see below, Martin et al. 2008; Scholz and Kubo 2008), resulting in better error compensation (Latash et al. 2003).

Intralimb versus interlimb synergy

In this bimanual task, control of the relative motion between the two hands was an important task requirement in addition to control of individual hand motion. It is perhaps surprising that the variability of the vectorial distance between the two hands was lower during contralateral tracing, even though the individual hand paths were more variable, compared to ipsilateral tracing. Consistent with this finding was that the interlimb synergy during contralateral tracing exhibited more selective use of motor redundancy (i.e. higher D_VAR) compared to ipsilateral tracing. This finding suggests that the joint variance within individual limbs is related, in part, to an effort to maintain a more stable interlimb coupling (Kazennikov et al. 1994; Wiesendanger et al. 1994; Wiesendanger and Serrien 2001; Kazennikov et al. 2002). Neurophysiologic studies have suggested that producing bimanual movements requires additional neural resources compared to producing single arm actions (Kermadi et al. 1998; Donchin et al. 2001). Thus, it is possible that the bimanual synergy represents a higher level control that involves neural activations across two hemispheres compared to the unimanual synergy where neural control may be limited within one hemisphere. Interactions between the cerebral hemispheres through the corpus callosum provide a possible link of movement planning and/or movement organization for the two intralimb synergies (Franz et al. 1996; Diedrichsen et al. 2003). Therefore, stable bimanual coordination may be achieved by a higher order synergy by which the nervous system links joint movements of the two limbs together to achieve a stable relationship between the two hands. Such interlimb synergies should be considered as separate from the two intralimb synergies that underlie the control of the individual hand’s movement. This conclusion is consistent with recent investigations of multijoint, multihand force control synergies. Those authors showed that there was a strong synergy uniting the fingers to stabilize the total force output during one-hand tasks. However, during a two-hand force production task, the intralimb synergies were weak, while the interlimb synergy was strong (Gorniak et al. 2007b). When subjects were instructed to switch from a one-hand task to a two-hand task, the interlimb synergy emerged while the previously strong intralimb synergy disappeared (Gorniak et al. 2007a).

We do not mean to imply that the stability of an interlimb synergy always takes precedence over intralimb synergies, however. The nature of synergies ought to be flexible and context-dependent to deal with the complexities of environmental interactions and limb dynamics. One study provides one example where maintaining a stable interlimb synergy is not possible due to task difficulty, in which case the intralimb synergy apparently takes precedence (Buchanan and Ryu 2006). They demonstrated that spontaneous polyrhythmic coordination emerged when the two arms were put in quite disparate tracing conditions, leading to better control of individual limb motions. On the other hand, results from the same laboratory under a different context reported the opposite trade-off in favor of the interlimb synergy (Ryu and Buchanan 2004; Buchanan and Ryu 2005). The elliptical tracing task studied here involved a relatively stable bimanual pattern in the absence of pattern switching and results indicate that the interlimb synergy took precedence over individual intralimb synergies.

When considering differences between intralimb and interlimb coordination, recruiting more joint motions might have advantages. For contralateral tracing, control of the relative movement between the two hands was associated with a stronger synergy (i.e. increased use of motor redundancy as evidenced by higher D_VAR) compared to control of the nondominant hand’s path. This was true even though the interlimb coordination involved more joint motions (eight vs. four). Therefore, having to coordinate a larger number of joints does not necessarily pose a greater challenge to the nervous system if the additional DOFs can be used to provide greater flexibility of task control. How well additional DOFs can be used to enhance control likely depends on the nature of the task, and there may be a limit beyond which the disadvantage of coordinating multiple DOFs outweighs its advantages, an issue requiring further study.

Dominant versus nondominant arm differences

A difference in skill between the dominant and nondominant arms is a classically described motor asymmetry (Hildreth 1949; Flowers 1975). Consistent with previous studies on bimanual rhythmic tasks, we found that tracing movements produced by the nondominant arm were more variable (Franz et al. 2002; Ryu and Buchanan 2004) and showed more deviations in shape (Semjen et al. 1995; Franz et al. 2002) compared to movements produced by the dominant arm. Unlike previous reports (Wuyts et al. 1996; Carson et al. 1997), we did not find speed-related differences between the arms in this experiment, indicating that the observed differences in kinematics could not be explained by slowing down of the nondominant arm. A recent imaging study provided neurophysiological evidence that the performance asymmetry may be associated with different sensorimotor processing ability between the two hemispheres when the task involves constant visual monitoring of movement trajectories (Lavrysen et al. 2008). Coordinated eye–hand movements of the nondominant arm were associated in that study with higher activations in the sensorimotor and frontal areas as well as the cerebellum when compared with neural activations associated with generating eye or hand movements alone. On the other hand, coordinated movements of the dominant arm only involved stronger activations in the occipital cortex (Lavrysen et al. 2008). This finding is consistent with the idea that dominant arm movements require less attention. When participants were asked to selectively attend to one arm’s movement during a bimanual drawing task, the dominant arm’s movements remained similar, whereas the nondominant arm’s drawing performance largely depended on the shift of visual attention, showing less shape deviations when attention was directed to this arm (Wuyts et al. 1996). Similar findings of shifting visual attention have also been reported in a rhythmic task that did not involve the formation of a drawing trajectory (Amazeen et al. 1997). Therefore, perceptual factors, such as shift of visual attention, may enhance the arm-related differences in bimanual tasks because of inherent differences in the ability to process visuomotor information associated with each arm.

Wang and Sainburg proposed that the two arms and their controllers are functionally different (Wang and Sainburg 2007). Presumably, the dominant controller can more efficiently coordinate muscle activity with interaction forces to generate the planned hand path (Sainburg and Kalakanis 2000; Bagesteiro and Sainburg 2002; Sainburg 2002). On the other hand, the nondominant controller appears to be more accurate at controlling final reaching positions (Wang and Sainburg, 2007) by generating effective terminal corrections (Duff and Sainburg 2007). Unlike their results, however, we did not find differences in the amount of muscle and interaction moments between the dominant and nondominant arms in the current study. The discrepancy in findings may be accounted for by several factors. First, Sainburg and coworkers studied discrete reaching movements, while we studied a rhythmic tracing task. Rhythmic movements are not a series of linked discrete movements (Teeken et al. 1996; Wei et al. 2003; Sternad 2007), and the two types of movements appear to involve different neural circuits (Schaal et al. 2004). Many features of manual asymmetries based on aiming movements (Elliott et al. 2001) cannot be readily applied to rhythmic movements, because such tasks do not involve planning of distinctive onset and termination. Secondly, moving bimanually may also assimilate some kinematic features of the two hands (Kelso et al. 1979). This “assimilation” could lead to similarities in joint dynamics, which is consistent with the current finding. Thirdly, a tracking task does not require stabilization of a single “terminal position,” different from aimed reaching where end-point accuracy is crucial to achieving task success. Instead, constant monitoring to ensure that each hand stays on the required template is important for these tracing movements. Because we do not yet fully understand how these candidate factors contribute to arm-related differences in joint dynamics, we cannot conclude whether or not our results support the dynamic dominance hypothesis (Sainburg 2002). Nonetheless, we found that the dominant arm showed a better ability to perform the task when the two arms encountered the same interaction moments, which is consistent with this hypothesis.

Timing versus spatial control

Alternatively, the measured UCM differences related to intralimb versus interlimb coordination could reflect previously proposed differences between spatial and temporal levels of control (Schöner 1995). The intralimb synergy in the current task had both a spatial and temporal component; the hand was required to trace a specified template while at the same time maintaining temporal coordination with the metronome. Coordination between the hands, however, largely required a temporal constraint: to maintain a consistent relative timing between the two hands’ motions regardless of each hand’s path. The higher interaction moment may affect primarily the spatial aspect of intralimb synergy, which was reflected by the analysis related to control of each hand’s path, with minimal effect on the temporal aspect. This would be consistent with the finding of stronger interlimb synergy compared to the nondominant arm’s intralimb synergy during contralateral tracing, although the current analysis did not directly address movement timing. Future efforts should explore UCM-related methods that examine temporal structure more thoroughly.

Unresolved Issues

In this study, the correspondence between the magnitudes of NGEV and actual hand path variability provided some unexpected results and call for further study into the joint variance—hand path variance relationship. In general, higher NGEV is expected to be associated with higher hand path variability. Such a correspondence has been supported in previous studies of neurologically normal and patient populations (e.g., Reisman and Scholz 2003; Tseng et al. 2003). When comparing the two arms, both NGEV and hand path variability were higher for the nondominant arm. However, the relationship was more complicated when comparing across ellipse orientations for a given arm. For the left, nondominant arm, both NGEV and hand path variability were higher when the elbow interaction moment was high. In contrast, the increase in right hand path variability when tracing the contralateral pattern was associated with a smaller and nonsignificant increase in NGEV. This finding highlights the inherently nonlinear nature of the relationship between joint variance and hand path variability and its known dependence on limb geometry (Scholz and Schöner 1999). Thus, future studies will need to minimize differences in arm geometry between conditions designed to examine different effects of interaction moments.

We predicted that subjects would use motor redundancy to compensate for errors due to high elbow interaction moment, which can lead to unwanted hand path deviations unless compensated by changes at other joints (i.e. error compensation). Interestingly, GEV in the nondominant arm was always higher than that in the dominant arm, even though it did not change between directions of tracing. Greater nondominant arm GEV, however, does not necessarily imply better use of redundancy. Specifically, improved task performance occurs only when GEV is accompanied by relatively low NGEV, as observed for control of the dominant arm. That is, skilled action that takes advantage of the flexibility requires a decoupling of joint space to ensure that joint variations that would lead to error in the performance-related parameters are resisted while at the same time allowing for variations that provide for error compensation (Martin et al. 2008; Scholz and Kubo 2008). This mechanism requires a significant degree of joint coordination. The failure to restrict the amount of NGEV while at the same time allowing for higher GEV reflects poorer joint space decoupling in the nondominant arm.

We noted that the amount of motor redundancy in the dominant arm during contralateral tracing was greater than that for ipsilateral tracing. Two factors may explain this difference. First, the elbow interaction moment was lower during ipsilateral tracing (Dounskaia et al. 2002). Thus, there simply may be less need for error compensation. Second, ipsilateral tracing appears to be kinematically more complex than contralateral tracing. During contralateral tracing, the relative motion of the shoulder and elbow joints exhibits an elliptical pattern, being coupled in a near-linear fashion throughout most of the motion. That is, shoulder abduction is primarily coupled with elbow flexion and shoulder adduction with elbow extension (Fig. 8, top panels). Exceptions occur near the motion reversals. In contrast, the shoulder–elbow motion trajectory for ipsilateral tracing (Fig. 8, bottom panels) is more circular with more frequent reversals between shoulder abduction–elbow extension and vice versa. This fact is also illustrated by principal component (PC) analysis performed on the joint data. For contralateral tracing, two PCs explained over 90% of the joint variance with the first PC accounting for at least 75% of the variance. In contrast, for ipsilateral tracing, three PCs were required to explain over 90% of the variance and the first PCs accounted for <65% of the variance. Thus, the component of the arm synergy reflecting the general “sharing” of motion among the joints (Latash et al. 2003) appears to be more complicated for ipsilateral tracing. This may have posed more challenges to control and coordination during ipsilateral tracing, which is independent of the interaction moment magnitude. Future work will require a different design to change the contribution of muscle versus interaction moments within the context of a more identical movement pattern.

Fig. 8.

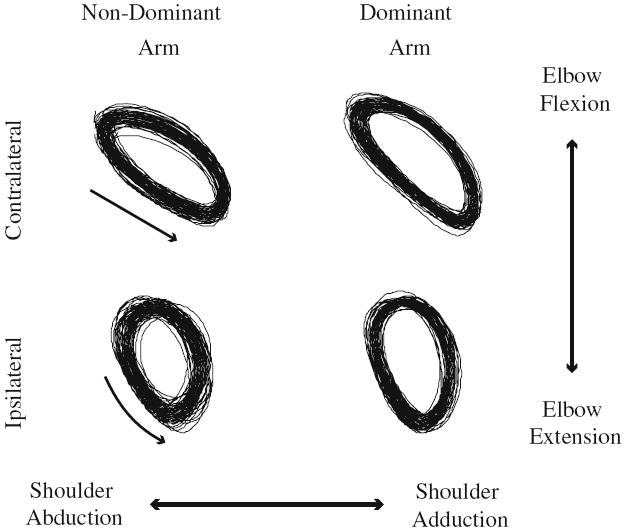
Shoulder–elbow angle–angle plots to illustrate coordination differences when tracing the contralaterally versus ipsilaterally oriented ellipses. Arrows next to the joint paths indicate the direction of joint movements

Appendix

To compute the equations of motion, the Lagrangian of the arm was formulated in terms of joint angles and joint velocities, and then solved analytically using Mathematica^® 5.0 (Wolfram Research, Inc.). The general formulation of equations of motion can be represented as

$$M(\theta )\times \ddot{\theta }+H(\theta ,\dot{\theta })={\tau }_{\mathrm{muscle}}$$ (5)

where H(θ, θ̇) is a combination of Coriolis and centrifugal forces acting at each joint and its magnitude depends on the motion and position of other joints. τ_muscle is the generalized muscle moment (MM) that includes active muscle activity and passive forces arising from the viscoelastic properties of muscles, tendons, ligaments and periarticular soft tissues. There is no gravitational moment, since movement is constrained in a horizontal plane. M(θ) is a 4 × 4, configuration-dependent inertial matrix; θ̈, θ̇ and θ are the vectors of joint acceleration, velocity and angle, respectively. The inertial matrix M(θ) has diagonal entries corresponding to the inertia of a given segment of interest and off-diagonal entries capturing the effect on each joint based on the acceleration of the other joints. By separating out the two components of the inertial matrix, M_d(θ) and M_nd(θ), Eq. 5 can be written as:

$$M_{\mathrm{d}}(\theta )\times \ddot{\theta }=-M_{\mathrm{nd}}(\theta )\times \ddot{\theta }-H(\theta ,\dot{\theta })={\tau }_{\mathrm{muscle}}$$ (6)

Equation 6 can be further represented as the following, by grouping the appropriate terms for interaction moments

$$\mathrm{NM}=\mathrm{IM}+\mathrm{MM}$$ (7)

The net moment (NM) is proportional to joint acceleration and is directly responsible for motion of this joint. IM is the interaction moment that depends on mutual interactions with the other joints. MM represents the generalized muscle moment.

The individual terms of the M and H matrices are listed below. Note that the diagonal terms are M_1,1, M_2,2, M_3,3, M_4,4, while the off diagonal terms are M_i,j, where i ≠ j; i and j = 1, 2, 3, 4. The same arrangement applies to the H matrix. Notation: θ_i angle of the ith joint; l_i length of the ith segment; r_i position of the center of mass of the ith joint from the proximal end of that segment; m_i mass of the ith segment; I_i moment of inertia of the ith segment. The number representing each arm segment and joint angle (in parentheses): 1 clavicle (scapula); 2 upper arm (shoulder); 3 forearm (elbow); 4 hand (wrist).

$$\begin{array}{lll}M{(\theta )}_{1,1}& =& I_1+I_2+I_3+I_4+m_1\cdot r_1^2+(m_2+m_3+m_4)\cdot l_1^2\\ & & +(m_3+m_4)\cdot l_2^2+m_2\cdot r_2^2+m_4\cdot l_3^2+m_3\cdot r_3^2\\ & & +m_4\cdot r_4^2+m_3\cdot (2\cdot l_1\cdot l_2\cdot \cos ({\theta }_2)\\ & & +2\cdot l_1\cdot r_3\cdot \cos ({\theta }_2+{\theta }_3)+2\cdot l_2\cdot r_3\cdot \cos ({\theta }_3))\\ & & +2\cdot m_2\cdot l_1\cdot r_2\cos ({\theta }_2)+m_4\cdot (2\cdot l_1\cdot l_2\cdot \cos ({\theta }_2)\\ & & +2\cdot l_1\cdot l_3\cdot \cos ({\theta }_2+{\theta }_3)+2\cdot l_1\cdot r_4\cdot \cos ({\theta }_2+{\theta }_3\\ & & +{\theta }_4)+2\cdot l_2\cdot l_3\cdot \cos ({\theta }_3)+2\cdot l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)\\ & & +2\cdot l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$\begin{array}{lll}M{(\theta )}_{1,2}& =& I_2+I_3+I_4+m_2\cdot r_2^2+m_3\cdot r_3^2+m_4\cdot r_4^2\\ & & +m_2\cdot l_1\cdot r_2\cdot \cos ({\theta }_2)+(m_3+m_4)\cdot l_2^2+m_4\cdot l_3^2\\ & & +m_3\cdot (l_1\cdot l_2\cdot \cos ({\theta }_2)+l_1\cdot r_3\cdot \cos ({\theta }_2+{\theta }_3)\\ & & +2\cdot l_2\cdot r_3\cdot \cos ({\theta }_3))+m_4\cdot (l_1\cdot l_2\cdot \cos ({\theta }_2)\\ & & +l_1\cdot l_3\cdot \cos ({\theta }_2+{\theta }_3)+l_1\cdot r_4\cdot \cos ({\theta }_2+{\theta }_3+{\theta }_4)\\ & & +2\cdot l_2\cdot l_3\cdot \cos ({\theta }_3)+2\cdot l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)\\ & & +2\cdot l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$\begin{array}{lll}M{(\theta )}_{1,3}& =& I_3+I_4+m_3\cdot r_3^2+m_4\cdot r_4^2+m_4\cdot l_3^2\\ & & +m_3\cdot (l_1\cdot r_3\cdot \cos ({\theta }_2+{\theta }_3)+l_2\cdot r_3\cdot \cos ({\theta }_3))\\ & & +m_4\cdot (l_1\cdot l_3\cdot \cos ({\theta }_2+{\theta }_3)+l_1\cdot r_4\cdot \cos ({\theta }_2+{\theta }_3\\ & & +{\theta }_4)+l_2\cdot l_3\cdot \cos ({\theta }_3)+l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)\\ & & +2\cdot l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$\begin{array}{lll}M{(\theta )}_{1,4}& =& I_4+m_4\cdot r_4^2+m_4\cdot (l_1\cdot r_4\cdot \cos ({\theta }_2+{\theta }_3+{\theta }_4)\\ & & +l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)+l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$M{(\theta )}_{2,1}=M{(\theta )}_{1,2}$$

$$\begin{array}{lll}M{(\theta )}_{2,2}& =& I_2+I_3+I_4+m_2\cdot r_2^2+m_3\cdot l_2^2+m_3\cdot r_3^2\\ & & +2\cdot m_3\cdot l_2\cdot r_3\cdot \cos ({\theta }_3)+m_4\cdot (l_2^2+l_3^2+r_4^2\\ & & +2\cdot l_2\cdot l_3\cdot \cos ({\theta }_3))+2\cdot l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)\\ & & +2\cdot l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$\begin{array}{lll}M{(\theta )}_{2,3}& =& I_4+I_3+m_3\cdot r_3^2+m_3\cdot l_2\cdot r_3\cdot \cos ({\theta }_3)\\ & & +m_4\cdot (l_3^2+r_4^2+l_2\cdot l_3\cdot \cos ({\theta }_3)\\ & & +l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)+2\cdot l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$\begin{array}{lll}M{(\theta )}_{2,4}& =& I_4+m_4\cdot r_4^2+m_4\cdot l_2\cdot r_4\cdot \cos ({\theta }_3+{\theta }_4)\\ & & +m_4\cdot l_3\cdot r_4\cdot \cos ({\theta }_4)\end{array}$$

$$M{(\theta )}_{3,1}=M{(\theta )}_{1,3}$$

$$M{(\theta )}_{3,2}=M{(\theta )}_{2,3}$$

$$\begin{array}{lll}M{(\theta )}_{3,3}& =& I_3+I_4+m_3\cdot r_3^2+m_4\cdot (l_3^2+r_4^2\\ & & +2\cdot l_3\cdot r_4\cdot \cos ({\theta }_4))\end{array}$$

$$M{(\theta )}_{3,4}=I_4+m_4\cdot r_4^2+m_4\cdot l_3\cdot r_4\cdot \cos ({\theta }_4)$$

$$M{(\theta )}_{4,1}=M{(\theta )}_{1,4}$$

$$M{(\theta )}_{4,2}=M{(\theta )}_{2,4}$$

$$M{(\theta )}_{4,3}=M{(\theta )}_{3,4}$$

$$M{(\theta )}_{4,4}=m_4\cdot r_4^2+I_4$$

$$\begin{array}{lll}H{(\theta ,\dot{\theta })}_1& =& (2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_3+2\cdot {\dot{\theta }}_2\cdot {\dot{\theta }}_3+{\dot{\theta }}_3^2)\cdot (-m_3\cdot l_1\cdot r_3\cdot \\ & & \sin ({\theta }_2+{\theta }_3)-m_3\cdot l_2\cdot r_3\sin ({\theta }_3))+({\dot{\theta }}_2^2+2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_2)\cdot \\ & & (\sin ({\theta }_2)\cdot (-m_2\cdot l_1\cdot r_2-m_3\cdot l_1\cdot l_2)\\ & & -m_3\cdot l_1\cdot r_3\cdot \sin ({\theta }_2+{\theta }_3))-m_4\cdot ((2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_4\\ & & +2\cdot {\dot{\theta }}_2\cdot {\dot{\theta }}_4+2\cdot {\dot{\theta }}_3\cdot {\dot{\theta }}_4+{\dot{\theta }}_4^2)\cdot (l_3\cdot r_4\cdot \sin ({\theta }_4)\\ & & +l_2\cdot r_4\cdot \sin ({\theta }_3+{\theta }_4)+l_1\cdot r_4\cdot \sin ({\theta }_2+{\theta }_3+{\theta }_4))\\ & & +(2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_3+2\cdot {\dot{\theta }}_2\cdot {\dot{\theta }}_3+{\dot{\theta }}_3^2)\cdot (l_2\cdot r_4\cdot \sin ({\theta }_3+{\theta }_4)\\ & & +l_1\cdot l_3\cdot \sin ({\theta }_2+{\theta }_3)+l_2\cdot l_3\cdot \sin ({\theta }_3)\\ & & +l_1\cdot r_4\cdot \sin ({\theta }_2+{\theta }_3+{\theta }_4))+(2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_2+{\dot{\theta }}_2^2)\cdot \\ & & ({\mathrm{ł}}_1\cdot r_4\cdot \sin ({\theta }_2+{\theta }_3+{\theta }_4)+l_1\cdot l_3\cdot \sin ({\theta }_2+{\theta }_3)\\ & & +l_1\cdot l_2\cdot \sin ({\theta }_2))\end{array}$$

$$\begin{array}{lll}H{(\theta ,\dot{\theta })}_2& =& {\dot{\theta }}_1^2\cdot \sin ({\theta }_2)\cdot (m_2\cdot l_1\cdot r_2+m_3\cdot l_1\cdot l_2)\\ & & +m_3\cdot r_3\cdot l_1\cdot \sin ({\theta }_2+{\theta }_3)\cdot {\dot{\theta }}_1^2-m_3\cdot l_2\cdot r_3\cdot \\ & & \sin ({\theta }_3)\cdot (2\cdot {\dot{\theta }}_3\cdot {\dot{\theta }}_1+2\cdot {\dot{\theta }}_3\cdot {\dot{\theta }}_2+{\dot{\theta }}_3^2)+{\dot{\theta }}_1^2\cdot \\ & & (m_4\cdot l_1\cdot l_2\cdot \sin ({\theta }_2)+m_4\cdot l_1\cdot l_3\cdot \sin ({\theta }_2+{\theta }_3)\\ & & +m_4\cdot l_1\cdot r_4\cdot \sin ({\theta }_2+{\theta }_3+{\theta }_4))\\ & & -m_4\cdot ((l_2\cdot l_3\cdot \sin ({\theta }_3)+l_2\cdot r_4\cdot \sin ({\theta }_3+{\theta }_4))\cdot \\ & & (2\cdot {\dot{\theta }}_3\cdot {\dot{\theta }}_1+2\cdot {\dot{\theta }}_3\cdot {\dot{\theta }}_2+{\dot{\theta }}_3^2)+(l_2\cdot r_4\cdot \sin ({\theta }_3+{\theta }_4)\\ & & +l_3\cdot r_4\cdot \sin ({\theta }_4))\cdot (2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_4+2\cdot {\dot{\theta }}_2\cdot {\dot{\theta }}_4\\ & & +2\cdot {\dot{\theta }}_3\cdot {\dot{\theta }}_4+{\dot{\theta }}_4^2)\end{array}$$

$$\begin{array}{lll}H{(\theta ,\dot{\theta })}_3& =& ({\dot{\theta }}_1^2+{\dot{\theta }}_2^2+2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_2)\cdot (m_3\cdot l_2\cdot r_3\cdot \sin ({\theta }_3)\\ & & +m_4\cdot l_2\cdot l_3\cdot \sin ({\theta }_3)+m_4\cdot l_2\cdot r_4\cdot \sin ({\theta }_3+{\theta }_4))\\ & & +{\dot{\theta }}_1^2\cdot (m_3\cdot l_1\cdot r_3\cdot \sin ({\theta }_2+{\theta }_3)+m_4\cdot {\mathrm{ł}}_1\cdot l_3\cdot \\ & & \sin ({\theta }_2+{\theta }_3)+m_4\cdot l_1\cdot r_4\cdot \sin ({\theta }_2+{\theta }_3+{\theta }_4))\\ & & -m_4\cdot l_3\cdot r_4\cdot \sin ({\theta }_4)\cdot (2\cdot {\dot{\theta }}_4\cdot {\dot{\theta }}_1+2\cdot {\dot{\theta }}_4\cdot {\dot{\theta }}_2\\ & & +2\cdot {\dot{\theta }}_4\cdot {\dot{\theta }}_3+{\dot{\theta }}_4^2)\end{array}$$

$$\begin{array}{lll}H{(\theta ,\dot{\theta })}_4& =& {\dot{\theta }}_1^2\cdot m_4\cdot l_1\cdot r_4\cdot \sin ({\theta }_2+{\theta }_3+{\theta }_4)\\ & & +{({\dot{\theta }}_1+{\dot{\theta }}_2)}^2\cdot m_4\cdot l_2\cdot r_4\cdot \sin ({\theta }_3+{\theta }_4)\\ & & +m_4\cdot l_3\cdot r_4\cdot \sin ({\theta }_4)\cdot ({({\dot{\theta }}_1+{\dot{\theta }}_2)}^2+2\cdot {\dot{\theta }}_1\cdot {\dot{\theta }}_3\\ & & +2\cdot {\dot{\theta }}_2\cdot {\dot{\theta }}_3+{\dot{\theta }}_3^2)\end{array}$$