Abstract
The shape of the mitral valve annulus is used in diagnostic and modeling applications, yet methods to accurately and reproducibly delineate the annulus are limited. This paper presents a mitral annulus segmentation algorithm designed for closed mitral valves which locates the annulus in three-dimensional ultrasound using only a single user-specified point near the center of the valve. The algorithm first constructs a surface at the location of the thin leaflets, and then locates the annulus by finding where the thin leaflet tissue meets the thicker heart wall. The algorithm iterates until convergence metrics are satisfied, resulting in an operator-independent mitral annulus segmentation. The accuracy of the algorithm was assessed from both a diagnostic and surgical standpoint by comparing the algorithm’s results to delineations made by a group of experts on clinical ultrasound images of the mitral valve, and to delineations made by an expert with a surgical view of the mitral annulus on excised porcine hearts using an electromagnetically tracked pointer. In the former study, the algorithm was statistically indistinguishable from the best performing expert (p = 0.85) and had an average RMS difference of 1.81 ± 0.78mm to the expert average. In the latter, the average RMS difference between the algorithm’s annulus and the electromagnetically tracked points across six hearts was 1.19 ± 0.17mm.
Index Terms: Mitral Valve, Annulus, Segmentation, Ultrasound, Graph Cuts
I. Introduction
The mitral valve annulus is an important cardiac structure that is defined as the fibrous saddle-shaped structure that anchors the mitral leaflets. Characterization of the geometry of the mitral annulus has proven valuable in an array of applications. Clinically, studies on annulus shape have shown that there is a correlation between annular geometry and pathology [1]–[5], and that the annulus can be used in the assessment of valve function [6], [7]. The annulus shape is also commonly used in surgical planning for valve repair [8] and in prostheses design [9]. In modeling, the annulus defines the boundary conditions for models simulating the mechanics of the leaflets during valve closure [10]–[14].
The mitral annulus is most commonly visualized using ultrasound, given that ultrasound is a cheap, portable, and non-ionizing imaging modality capable of capturing the fast moving valve structures. Prior to three-dimensional ultrasound (3DUS), delineating the shape of the annulus was difficult, leading to the assumption that the annulus was planar, instead of saddle-shaped as is now apparent [6]. Even after the advancement from 2D to 3D ultrasound, visualizing the annulus remains a problem due to imaging noise and volume visualization limitations.
Despite widespread use of the annulus in both clinical and research applications, available methods to extract an accurate and reproducible geometry remain limited. One of the most common methods used in research applications is to segment and track implanted fiducials, such as tracking radiopaque markers with fluoroscopy [15]–[18] or tracking sonomicrometry transducers [19]. This is an invasive approach not feasible in a clinical setting. Another common method is manual segmentation of images [2]–[5], [20]–[22], which in addition to being tedious and time consuming, is also prone to inaccuracies. One reason is that the usual practice is to pick points in 2D slices taken from a 3D volume, so the user only has access to a portion of the available information at any given step, forcing the user to mentally interpolate 3D information. The methods presented in [23] and [24] attempt to correct for the deficiencies in these manual slice-based segmentations, but do so by smoothing the segmentations without referring back to the original 3D data from which they were made.
Semi-automatic methods to delineate the 3D annulus from 3DUS are presented in [25] and [26]. The former method segments the annulus by compiling semi-automated annulus point delineations in 2D slices into a 3D annulus structure. As in the case of manual segmentation, this method does not take into account information in neighboring slices, so it suffers from inaccuracies and spatial inconsistencies. The latter method segments the annulus as a consequence of fitting an entire mitral valve model to 3DUS data using learning techniques, which consequently requires a training database of manually delineated points. The resulting accuracy of the method for the purpose of patient-specific annulus segmentation is unclear, as comparisons are only made to published population valve dimensions.
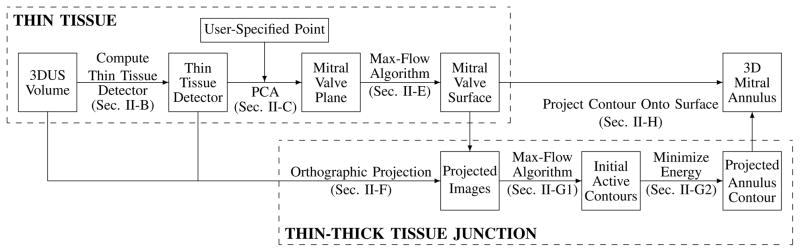
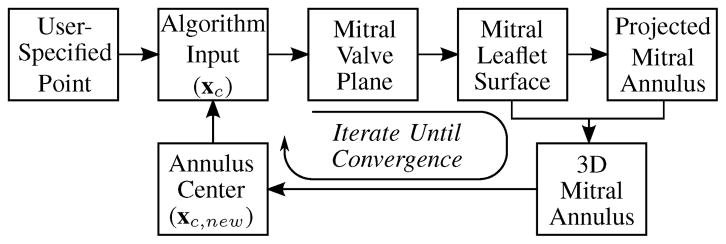
We present in this manuscript an accurate and robust segmentation algorithm (Fig. 1) designed to segment the mitral annulus in an ultrasound volume containing a closed valve. The algorithm begins by first finding a surface at the location of the thin leaflets. The surface is constructed near a user-provided point using a thin tissue detector and the max-flow algorithm. The algorithm then locates the annulus by finding where at the surface the thin leaflet tissue meets the thicker tissue of the surrounding heart wall. This is done using the max-flow algorithm and active contour methods in projection images created from the surface and surroundings. A 3D mitral annulus contour is computed by projecting the annulus contour in the images back onto the mitral leaflet surface.
Fig. 1.
Flow chart for the mitral annulus segmentation algorithm designed for closed valves which locates the annulus by first finding the thin leaflet tissue and then finding where the thin tissue meets the thick tissue of the surrounding heart wall. Specific details for the respective processes can be found in the indicated sections.
The details of the algorithm are described in Section II. An analysis of the algorithm is then presented in Section III, which includes studies which validate the algorithm’s accuracy (Sections III-A and III-B), and an analysis of the sensitivity of the algorithm to the user-provided point (Section III-C).
II. Algorithm Design
A. Ultrasound Data
The acquired data for this study was in the form of full volume reconstructions, allowing for the visualization of the entire mitral valve in a single 3DUS volume (iE33 Echocardiography System with transesophageal, X7-2t, and transthoracic, X7-2, probes, Philips Healthcare, Andover, MA, USA). The condition of the valves ranged from normal to varying types and degrees of pathology. While the position and orientation of a valve within a volume varied, the segmentation algorithm requires that the thin tissue of the leaflets can be seen across the entire valve.
From each 4D data set (3D + time), a single ultrasound frame containing a closed valve was selected. The frame was chosen at or near peak systole, as this is a time in the cardiac cycle when the valve is closed and moving slowly. Restricting the selection to closed valves enabled accurate computation of a surface at the location of the leaflets. The dimensions of the volume were roughly 200×200×200 voxels, with a resolution on the order of 0.5–0.75 mm per voxel. In this manuscript, the selected 3DUS volume is referred to as Ω, and individual voxel locations as vi, where each vi has corresponding (xi, yi, zi) coordinates. For Ω with N voxels, i ∈ {1, …,N}.
B. Thin Tissue Detector
Delineating the location of the annulus directly from 3DUS is difficult, so the algorithm first segments the location of the leaflets using a thin tissue detector. The thin tissue detector (TTD) highlights thin structures at a particular scale in the 3DUS volume. The TTD is computed using characteristics of the gradient field of both Ω and ΩF, where ΩF is a filtered version of Ω, reducing the effects of speckle in the volume. ΩF is computed by convolving Ω with a Gaussian kernel, G(σ), with standard deviation, σ, approximately equal to half the maximum expected thickness of the mitral leaflets, taking into account any abnormal thickness due to disease state. The kernel dimension is 4σ+1 to include two standard deviations.
The TTD is computed using the results of three computations. The first of these
| (1) |
is a measure of the average angle between gradient vectors of ΩF within a neighborhood, where ∇ denotes the gradient operator. A neighborhood at vi is defined as the set of all neighboring voxels, vj, which are contained within the cube of side length p centered at voxel vi, making j ∈ {1, …, J}, with J = p3 for a cubical neighborhood. At the location of the leaflets, there will be opposing gradient fields as a result of the dark blood pools above and below the thin, bright leaflets. Therefore, Θ will have a higher value at the leaflets in comparison to more homogeneous regions, such as in the middle of the blood pool or thick tissue regions.
The gradient vectors at the leaflets should be pointing inward, so
| (2) |
measures the flux of the vectors across the neighborhood boundary faces. In computing Φ, the inward directed unit normal of each boundary face is denoted fq,norm, where q ∈ {1, …, 6} for a cubical neighborhood. Neighbors with a face adjacent to face q are denoted fk, where k ∈ {1, …,K} and K = p2 for a cubical neighborhood.
Θ and Φ are computed using directions of gradient vectors but not their magnitude, meaning they contain no information about edges. However, the mitral leaflets are near two strong edges as a consequence of the thin tissue residing between two blood pools. Therefore, to quantify the number and proximity of strong edges to a voxel
| (3) |
The complete TTD is then (ΘΦ[0–1] Π)[0–1], where (·)[0–1] indicates that the values for that term are normalized to the range of 0 to 1. High TTD values indicate that the voxel is likely part of a thin structure and potentially at the location of the mitral leaflets. The TTD computed for a 3DUS image of a prolapsed mitral valve is shown in Fig. 2, where the TTD is inverted to better show the highlighted thin tissue regions.
Fig. 2.
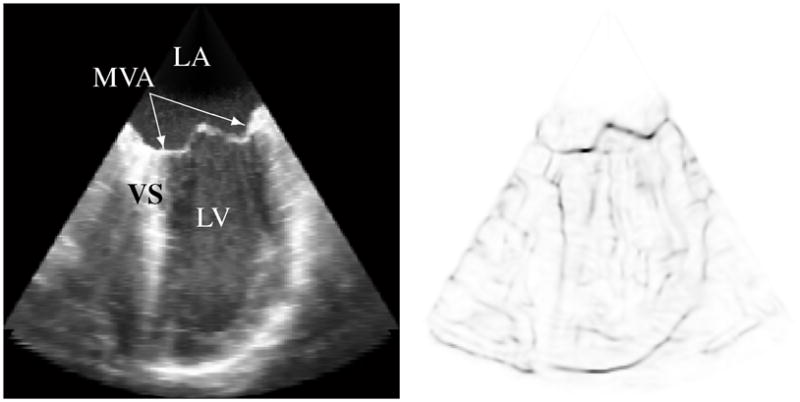
(Left) Slice from a 3DUS volume of a prolapsed mitral valve showing the location of the mitral valve annulus (MVA), left atrium (LA), left ventricle (LV), and ventricular septum (VS). (Right) Corresponding slice from the thin tissue detector (inverted for clarity) computed for the 3DUS volume.
C. Valve Position & Orientation
To accurately construct a surface at the location of the mitral leaflets, an initial estimation of the position and orientation of the mitral valve relative to the volume is needed. In the first iteration of the algorithm, the position is determined by the user, who is asked to provide a point, xc, somewhere near the center of the valve but not necessarily on the valve. In subsequent iterations, assuming they are needed, xc is defined as the center of the computed annulus from the previous iteration.
Given xc near the center of the valve, the orientation of the mitral valve is then estimated by computing a corresponding best-fit mitral valve plane. The idea is to threshold to separate leaflet tissue and blood, then fit a plane to the tissue. This is done by first clustering the values of the TTD from voxels residing in a spherical region of interest of radius rpca centered at xc into two clusters using a k-means algorithm. The sample mean and standard deviation of the TTD at voxels for the cluster likely containing the leaflets, which is the cluster with the higher TTD average, are denoted μhigh and σhigh, respectively. A principle-component analysis (PCA) on the set of voxels vpca: {vi|TTD(vi)>(μhigh − σhigh) ∩ |vi − xc| ≤ rpca} then defines the orientation of the cluster. The mitral valve plane, MVplane, is then the plane passing through xc with normal direction nc equal to the direction of least variance as determined in the PCA.
D. Graph Construction and the Max-Flow Algorithm
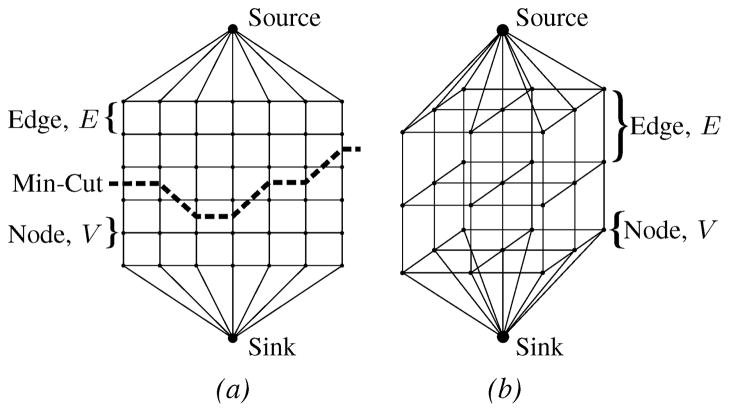
The annulus segmentation algorithm makes extensive use of the max-flow algorithm [27]. Generically, a graph, Γ=〈V,E〉, is a set of nodes, V, connected by edges, E, which have either a directed or undirected capacity. In the case of the max-flow algorithm, there are also two special nodes called the source and the sink. The max-flow algorithm finds the maximum flow which can originate from the source, flow through the edges of predefined capacity, and enter the sink. In doing so, according to the min-cut/max-flow theorem [28], the max-flow algorithm generates a set of saturated edges called the min-cut which separates the graph into two regions – one containing the source and another containing the sink.
A generalization of the graph construction used in the algorithm is shown in Fig. 3, where the 2D and 3D graphs are used to find contours and surfaces, respectively. The graph construction, in particular attaching the source and sink to opposite ends of the graph, allows us to enforce prior knowledge that the min-cut should reside between the opposite ends.
Fig. 3.
Generalized graph structures used in the mitral annulus segmentation algorithm: (a) 2D graph with a min-cut example, (b) 3D rectilinear graph
E. Mitral Leaflet Surface via Max-Flow
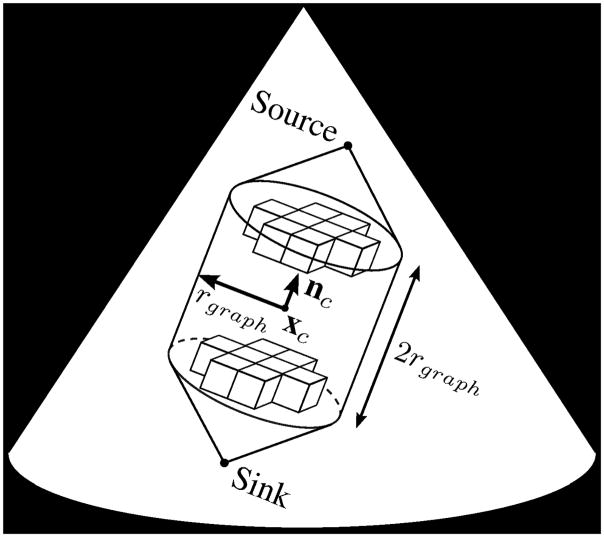
With an estimation of the valve position and orientation, a graph can be constructed on which we implement the max-flow algorithm to find a surface at the location of the mitral leaflets. The graph, Γsurf =〈Vs,Es〉, resides within a cylinder of radius rgraph and height 2rgraph which is centered at xc with an axis directed along nc. The graph consists of nodes Vs located on a rectilinear grid directed along nc with a one voxel spacing, and undirected edges Es which connect the nodes, making Γsurf 6-connected except on the edges of the graph. The source connects to all nodes on one face of the cylinder, while the sink connects to all nodes on the opposite face (Fig. 4).
Fig. 4.
Position, orientation, and cylindrical boundary of the 3D rectilinear graph used to find the mitral leaflet surface
To find a surface at the location of the leaflets, we define the edge capacities, Es,p and Es,o, in (4) and (5), respectively, such that between connected nodes Vs,i and Vs,j
| (4) |
| (5) |
where ωp, ωo, and αs are scalar weights. This form lowers the edge capacity around the leaflets, encouraging the min-cut to be located at the leaflets. Es,p defines the capacity for edges parallel to nc, and Es,o the capacity for all other edges. This is an anisotropic edge capacity assignment [29] used to control the curvature of the surface: ωp < ωo encourages a flat surface, while ωp > ωo allows for a high curvature surface. For those edges where one of the nodes is either the source or the sink, the edge capacity is set to infinity.
The min-cut is found using the max-flow implementation by Kolmogorov [30]. The resulting min-cut defines the mitral valve leaflet surface, MVsurf. Assuming xc is located near the center of the valve and rgraph is sufficiently large, MVsurf extends beyond the leaflets and contains the mitral annulus.
F. Projection Image Formation
The annulus is where the thin leaflets connect to the thicker cardiac walls. We therefore search at and around MVsurf, which contains the annulus, for this location. Because the curvature of MVsurf was controlled using ωp and ωo in the max-flow implementation, MVsurf is a regular surface in ℜ3 that can be described as the graph of a function, Zsurf, described in the x′y′-plane
| (6) |
The x′y′z′-coordinate system is centered at xc with the z′ axis parallel to nc (Fig. 5).
Fig. 5.
(a) Slice normal to the valve plane from 3DUS of a prolapsed mitral valve (same data as shown in Fig. 2) showing MVsurf (black) and adjacent regions (white striped) used to form Pint, (b) intensity projection Pint, and (c) thin tissue detector projection Pttd. Projection images are only defined within the dotted circles.
The annulus, a closed curve on MVsurf, therefore projects to a closed planar curve in the x′y′-plane. To locate this planar curve, two images, Pint and Pttd, are used, where
| (7) |
| (8) |
Examples of the images are shown in Fig. 5. Pint is the value of Ω in regions above and below MVsurf, excluding a band of thickness 2σ where the leaflets are located, and provides information about where the tissue surrounding the leaflets resides. Pttd is the value of the TTD at MVsurf, and provides information about where the thin tissue resides at the surface. It is clear from the example images of Pint and Pttd in Fig. 5 that there exists a centrally located dark region in Pint and a bright region in Pttd. This region corresponds to the location of the mitral valve in the projection space, making the annulus the border of this region.
G. Projected Mitral Annulus Contour
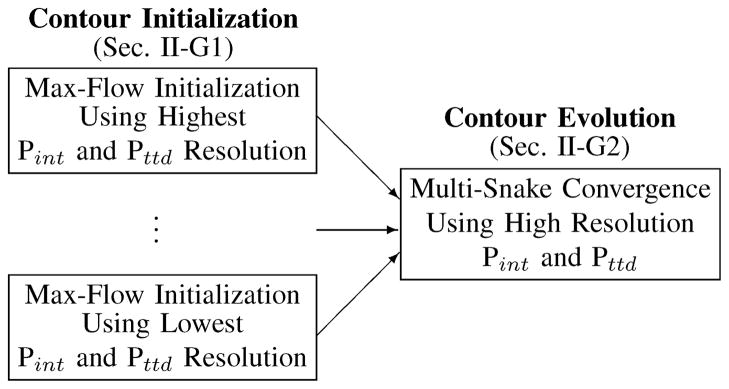
The border that we wish to delineate in the projection space, which corresponds to the projected location of the mitral annulus, is a single closed contour which can be delineated with such methods as snakes [31] or level sets [32]. These methods, however, are sensitive to initial contour position and generally require a manually initialized contour. To avoid the variability inherent in user input, we developed an automated method which initializes contours by computing min-cuts on 2D graphs using the max-flow algorithm, with edge capacities derived from both Pint and Pttd for added robustness. This method is preferred over our preliminary method which initialized generic contours in the projection images [33]. To overcome noise and anatomic variability in Pint and Pttd, multiple spatial scales of the projection images are used to construct multiple resolution-specific contours. Treating these contours as snakes and forcing them to a common location in high resolution versions of Pint and Pttd produces a single contour at the desired location. A summary of the approach is shown in Fig. 6. The advantage of using the method of snakes versus level sets is it allows for a simple integration of an attractive energy between contours and does not allow a contour to split during its evolution.
Fig. 6.
Contour initialization and evolution scheme for finding the annulus in the projection plane
1) Contour Initialization via Max-Flow
The graph, Γcont=〈Vc,Ec〉, used in the max-flow implementation to initialize a contour in the projection space is shown in Fig. 7. The nodes, Vc, are positioned along rays emanating from a center point, xo. The rays span the defined projection space and are evenly spaced at an angular offset of Δγ, while nodes are evenly spaced along the rays at an offset of Δr. The nodes nearest to the center connect to the source, while nodes farthest from the center connect to the sink.
Fig. 7.
Graph used in the max-flow algorithm for contour initialization in the projection space, along with an example of a min-cut
To initialize a contour at a specific resolution of the projection images, Pint and Pttd are first filtered using a Gaussian, G(σn), to generate Fint,n and Fttd,n, respectively. For the case where m different contours will be initialized at m different resolutions, n ∈ {1, …, m}. The values of Fint,n and Fttd,n at the node locations are found using bilinear interpolation and are normalized across all nodes to the range [0–1].
It is assumed that the border of the centrally located regions surrounds the center of the rays, xo. To find this border, we first compute at the node locations
| (9) |
where λint and λttd are scalar weights and R is the direction along a ray. This is a drive image that will help to define the graph edge capacities, with high values at locations that are most likely the desired border. Partial derivatives of Fint,n and Fttd,n are computed along the rays because we would like to find the location where Fint,n changes from dark to light as we travel out from xo along a ray, rather than light to dark. Similarly, we want to find the location where Fttd,n changes from light to dark. Fdrv,n is scaled by the inverse of Fint,n to encourage the contour to be found near the darker regions of Fint,n.
The edge capacities, Ec,s,n and Ec,d,n, of the graph are undirected and defined using Fdrv,n such that between connected nodes Vc,i and Vc,j
| (10) |
| (11) |
where ωs, ωd, and αc are scalar weights. Ec,s,n defines the capacity for edges between nodes on the same ray, and Ec,d,n defines the capacity for edges between nodes on different rays. This is done to control the deviation of a contour from a circle: ωs < ωd encourages a more circular min-cut, while ωs > ωd allows for a less circular min-cut.
Due to the construction of the graph, nodal resolution varies with distance from the center. Minimizing these variations along the min-cut requires iterating the contour initialization to force the ray center to the centroid of the area contained within the min-cut. For the first iteration, xo is the projection of the point xc onto the projection space. The final location of the ray center is xf,n, and the final min-cut is contour Cn, where n is specific to the resolution of the projection images.
2) Contour Convergence via Active Contours
The multiple contours initialized using m different resolutions of Pint and Pttd are forced to converge as snakes. This allows us to find a balance between the expected shape of the contour and the expected location of the contour determined from the images.
We restrict the nodes of the snake to reside on rays emanating from a center point, xs, which is computed as the centroid of the ray centers, xf,n, where n ∈ {1, …,m}. The rays are equally spaced at an angular offset of Δφ (Fig. 8). For snake n, the radial location of the snake node on ray φτ is referred to as Rn(φτ), where τ∈ {1, …, T} and T is the number of rays, and is initially determined from the location of Cn.
Fig. 8.
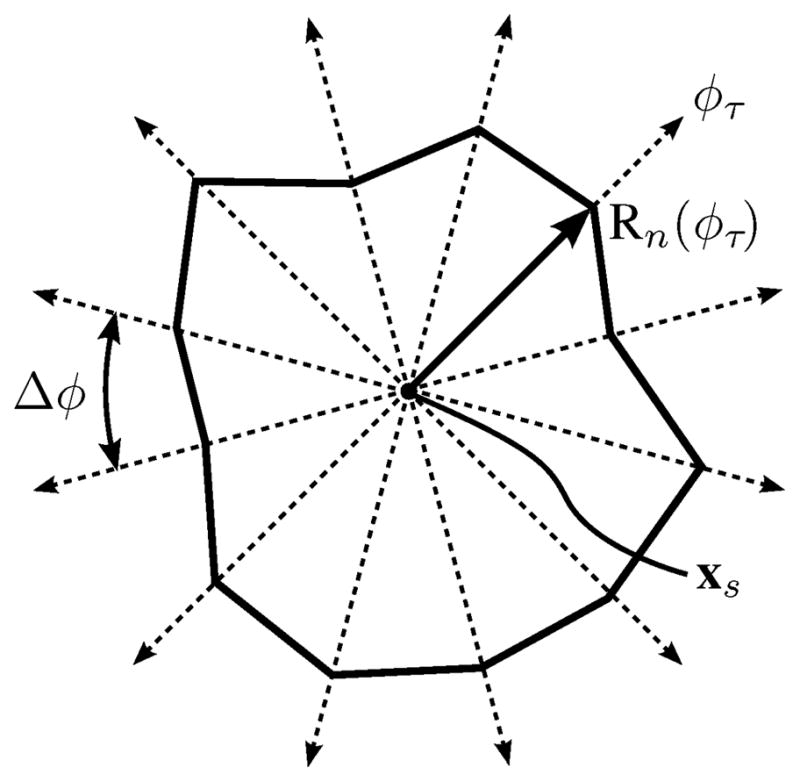
Ray system on which snake nodes are forced to reside during contour refinement and convergence, shown with an example snake
Snakes evolve simultaneously such that they are forced to converge to a single snake. The energy used in the snake evolution is
| (12) |
where ωdrv, ωxy, ωz, and ωatt are scalar weights. Edrv,n is an image energy derived from the projection images, Exy,n is the curvature energy of the snake in the projection plane, Ez,n is the curvature energy of MVsurf at the snake location, and Eatt is an attractive energy which forces the multiple snakes to converge to a single snake.
Image Energy
The image energy, Edrv,n, is derived in much the same way that Fdrv,n is derived for the graph. Pint and Pttd are first filtered using a Gaussian, G(σs), and normalized to the range of [0–1] to generate Fint,s and Fttd,s, respectively. The image energy is then
| (13) |
where λint and λttd are the same scalar weights used in (9), and Edrv,n is normalized so that its magnitude is less than one. Imparting force Udrv,n defined as
| (14) |
on the snake nodes subsequently minimizes the image energy at the location of the snake.
Contour Curvature Energy
To account for contour curvature but avoid undesirable evolution of the snake in the absence of strong image forces, as is common with typical methods [34], we use the method presented in [35]. This method, instead of minimizing the curvature of the snake, minimizes the change in curvature. The energy Exy,n is then
| (15) |
where κ is the curvature of the contour and s is arc length.
Whereas the method in [35] minimizes (15) by moving snake nodes to the perpendicular bisector of neighboring nodes, we restrict the nodes to move along the rays. In doing so, we find Rn,des(φi), which is the desired location of the node from snake n along ray φi which will minimize (15). Snake nodes are forced toward the location of Rn,des(φi) using Uxy,n(φi) = Rn,des(φi) − Rn(φi).
Surface Height Curvature Energy
The shape of the surface at a snake’s location is easily obtained, as it is known that MVsurf can be described as the graph of a function, Zsurf, which is defined in the projection space. Therefore, we can define Zn(φτ ) to be the height of MVsurf above the node on snake n residing on ray φτ. Since the annulus is not flat, but rather saddle-shaped, Ez,n is defined as
| (16) |
This energy is minimized by imparting a force
| (17) |
on the nodes, which encourages a constant local change in elevation of the annulus contour with respect to changes in φ.
Attractive Energy
As a means to allow the snakes to interact - so that a node of one snake which is at the global minimum can draw nodes of other snakes away from local minimums - and consequently force the snakes to converge to a common location, we designed the attractive energy Eatt
| (18) |
Eatt is minimized in each ray by driving the nodes from the different snakes on that ray towards the center of the node range, , using Uatt,n = Rmid − Rn.
Snake Update
Given the described energies which evolve the individual snakes, and the methods designed to minimize the energies, the snakes update according to
| (19) |
where Rn,t+1 is the updated snake, Rn,t is the current snake, and dt is a time step. The snakes are updated until they stabilize to within 0.1 pixels, which occurs in roughly 100 iterations using the parameter values shown in Table I.
TABLE I.
Mitral Annulus Segmentation Algorithm Parameters Used for All Studied Valves
| Parameter | Value | Units | Parameter | Value | Units |
|---|---|---|---|---|---|
| σ | 1 | mm | αc | 25 | |
| p | 3 | voxels | m | 2 | |
| rpca | 12.5 | mm | σn=1 | 2.5 | mm |
| rgraph | 25 | mm | σn=2 | 1 | mm |
| ωp | 1.5 | Δφ | 10 | degrees | |
| ωo | 1 | σs | 1 | mm | |
| αs | 25 | dt | 0.2 | ||
| Δγ | 5 | degrees | ωdrv | 2 | |
| Δr | 0.5 | mm | ωxy | 2 | |
| λint | 5 | ωz | 0.2 | ||
| λttd | 1 | ωatt | 1 | ||
| ωs | 25 | ε | 0.5 | mm | |
| ωd | 1 |
H. 3D Mitral Annulus Contour
The three-dimensional annulus is constructed from the final snake by computing the x′ and y′ coordinates using the angle of the rays and radial location of the nodes, and the z′ coordinates using Zn. We compute a continuous annulus contour in ℜ3 using a cubic interpolation of the defined points.
I. Algorithm Convergence
The point xc which initially positions and orients the graph used to find MVsurf is provided initially by a user who is asked to provide a point near the center of the valve. Therefore, the location of the user-specified point could have an effect on the shape of the 3D annulus contour. However, this dependency is resolved by iterating the algorithm until convergence metrics are satisfied (Fig. 9).
Fig. 9.
Simplified flow chart for the mitral annulus segmentation algorithm; the algorithm iterates until the computed annulus center stops changing.
After the first execution of the algorithm, and in subsequent iterations, the center point of the resulting 3D annulus contour, xc,new, is compared to the location of xc. If |xc,new − xc| > ε, where ε is a pre-defined scalar distance, xc is set equal to xc,new and the algorithm iterates. Otherwise, it is assumed the annulus contour has been accurately segmented. Enforcing this convergence means the resulting annulus segmentation is independent of the initial user-provided point, making the algorithm’s results operator-independent. Section III-C shows that a relatively large region of convergence exists.
III. Validation
To determine the appropriateness of the algorithm for diagnostic applications, we assessed the algorithm’s abilities to accurately locate the mitral annulus in 3DUS compared to a group of experts (Sec. III-A). For surgical planning purposes, we compared the algorithm’s results to the appearance of the mitral annulus as seen in a surgical view (Sec. III-B). We also explored the sensitivity of the algorithm to the initial user-specified point which serves as the algorithm’s input (Sec. III-C).
It is important to note that in these studies, the same parameter values (Table I) were used for every valve and every study. These parameters were found by testing the algorithm on 11 clinical images, none of which were included in the validation studies. The clinical images contained both normal and diseased mitral valves (3 normal, 4 with mitral prolapse, and 4 with mitral regurgitation). Of the 11 images, 10 were acquired with a transesophageal approach (X7-2t probe), and one with a transthoracic approach (X7-2 probe).
The algorithm was coded mostly in MATLAB (The Math-Works, Natick, MA, USA), but used C++ for both computing Φ in the TTD, and for the implementation of the max-flow algorithm. Approximate running times for various portions of the algorithm (64-bit PC, 3.0 GHz Intel Core 2 Duo processor with 4GB of RAM) were 30 seconds to compute the TTD, 30 seconds to compute the mitral leaflet surface, and 15 seconds to subsequently initialize and converge the contours, meaning each iteration took roughly 45 seconds. Typically two iterations were needed for convergence.
A. Validation Study Using Manual Image Delineations
Noise in 3DUS and volume visualization limitations make delineating the annulus from 3DUS difficult. As a result, a ground truth segmentation of the annulus cannot be defined from images. Therefore, to validate the annulus segmentation algorithm, we compared the algorithmic annulus to manual segmentations of the annulus performed by a group (n = 10) of cardiologists and trained echocardiography technicians, who will be collectively referred to as experts. We performed the analysis by first comparing the segmentations made by each expert to the collection of segmentations made by the rest of the experts for each valve. In this way, a measure of the performance for each expert could be quantified. We then compared the algorithm segmentations to the collection of segmentations made by the entire group of experts for each valve.
Experts were provided with 3DUS images of 10 different closed valves. The state of the valve and the nature of the 3DUS acquisition for each valve is summarized in Table II. The images were slices at 10° increments about a mitral valve center point and axis. We asked the experts to delineate the two annulus points in each image of the valve, for a total of 36 annulus points per valve. While the segmentations were performed in a single frame, temporal information in each image was available to the experts to allow them to accurately delineate the location of the annulus. To reduce the effects of training and fatigue in the analysis, we presented the valves to the experts in random order.
TABLE II.
Summary of Clinical Mitral Valve Images Used in Manual Image Delineation Validation Study
| Valve | Mitral Valve State | Acquisition Type | Probe |
|---|---|---|---|
|
| |||
| 1 | Prolapse; Regurgitation | Transesophageal | X7-2t |
| 2 | Normal | Transesophageal | X7-2t |
| 3 | Normal | Transthoracic | X7-2 |
| 4 | Normal | Transesophageal | X7-2t |
| 5 | Cleft Mitral | Transesophageal | X7-2t |
| 6 | Prolapse; Dilated Annulus | Transesophageal | X7-2t |
| 7 | Prolapse; Myxomatous Valve | Transesophageal | X7-2t |
| 8 | Prolapse; Regurgitation | Transesophageal | X7-2t |
| 9 | Normal | Transesophageal | X7-2t |
| 10 | Prolapse | Transthoracic | X7-2 |
The comparison of an expert to other experts, or the algorithm to the group of experts, was done on a point-by-point basis. As some annulus points were better defined than others, it was appropriate to penalize more for deviations of a point from a well-defined annulus location than from a poorly-defined location. The measure of a well-defined and poorly-defined annulus location was based on the collection of segmentations to which a particular segmentation was being compared. Additionally, as the experts could only provide points in the space of the image, points did not deviate out of the image plane. Therefore, the analysis of points was done in ℜ2 space.
When comparing an expert’s segmentation to the collection of segmentations made by the remaining experts, we refer to the ith point of the expert’s segmentation as Ai, where i ∈ {1, …, 36}. The mean and covariance of the ith point as determined from the segmentations from the rest of the group are referred to as Āi and Σi, respectively. A normalized (Mahalanobis) distance was then computed for each Ai, and the performance of an expert quantified as
| (20) |
which is the mean normalized distance (MND) across all points for a valve.
We then analyzed the algorithm results in much the same way we analyzed the segmentations from each expert, where the ith point of the algorithm’s segmentation was Ai, and Āi and Σi were the mean and covariance, respectively, of the ith point from the entire group of experts. The MND computation for the algorithm was then the same as shown in (20).
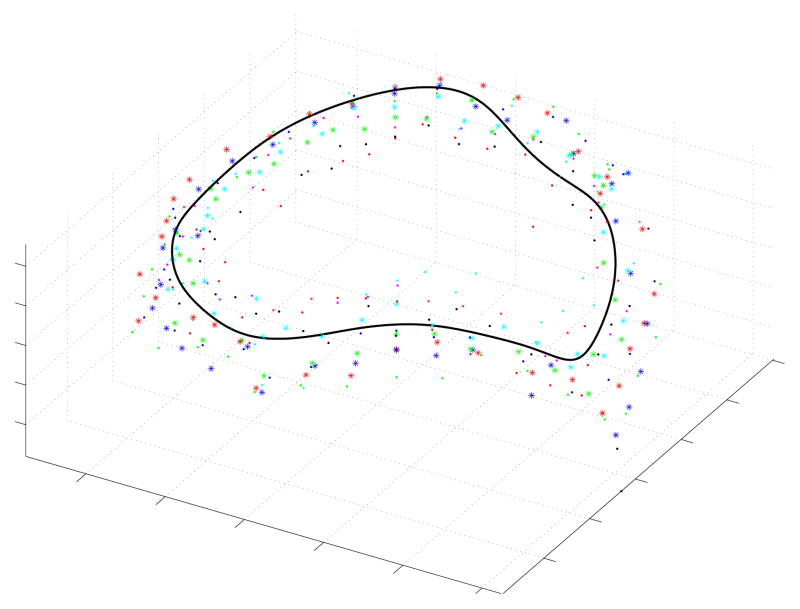
A typical comparison between the algorithm’s resulting annulus and the points manually delineated by the experts can be seen in Fig. 10. Table III shows the MND values for each expert and for the algorithm across all valves, along with the sample mean and standard deviation of the MND values from each group. Based on the distribution parameters of the two groups, we concluded that the algorithm (MND= 1.11 ± 0.19) had a lower mean MND than the group of clinicians (MND= 1.63 ± 0.76), and that this difference was statistically significant (p < 0.001). If instead of looking at the group, we look at the best scoring expert (Expert 6: MND= 1.13±0.33), we found that the algorithm and the best scoring expert were statistically indistinguishable (p = 0.85).
Fig. 10.
Typical comparison between the algorithmic annulus (solid line) and points delineated manually by experts on clinical 3DUS images
TABLE III.
Mean Normalized Distances & Distribution Parameters for the Experts and Algorithm
| Expert | Valve | Mean ± Std. Dev. | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
| 1 | 1.23 | 1.19 | 1.06 | 1.04 | 1.16 | 1.74 | 1.07 | 0.94 | 1.28 | 1.00 | 1.63±0.76 |
| 2 | 1.19 | 1.31 | 1.98 | 1.32 | 1.64 | 1.82 | 1.02 | 1.46 | 1.38 | 2.63 | |
| 3 | 2.68 | 1.50 | 1.69 | 2.68 | 1.92 | 1.62 | 2.71 | 2.61 | 1.85 | 3.80 | |
| 4 | 2.19 | 1.74 | 3.05 | 0.83 | 1.56 | 2.03 | 2.32 | 1.02 | 1.09 | 0.86 | |
| 5 | 1.50 | 1.09 | 1.39 | 1.25 | 1.21 | 0.99 | 1.10 | 0.91 | 1.94 | 0.92 | |
| 6 | 1.03 | 1.79 | 1.19 | 0.88 | 1.65 | 1.10 | 0.96 | 0.95 | 0.81 | 0.93 | |
| 7 | 1.03 | 1.15 | 1.07 | 1.14 | 1.33 | 1.08 | 1.69 | 0.94 | 1.42 | 1.26 | |
| 8 | 1.15 | 1.71 | 1.25 | 1.18 | 1.51 | 0.96 | 1.19 | 2.31 | 2.36 | 1.13 | |
| 9 | 1.44 | 1.73 | 1.40 | 4.16 | 1.01 | 1.23 | 1.49 | 1.36 | 1.34 | 0.98 | |
| 10 | 2.70 | 2.97 | 1.92 | 2.00 | 2.97 | 4.33 | 2.81 | 3.66 | 2.46 | 2.92 | |
|
| |||||||||||
| Algorithm | 1.19 | 0.97 | 1.42 | 0.97 | 1.15 | 1.13 | 1.28 | 1.03 | 1.19 | 0.73 | 1.11±0.19 |
We also compared the algorithm and experts by computing the RMS difference between the algorithm and the expert average (Table IV), as this is a commonly used accuracy metric and allows for comparisons to be drawn to other studies and methods. The average RMS difference between the algorithm and the expert average was 1.81 ± 0.78mm. The larger RMS differences usually coincided with a disagreement among the experts as to the annulus location (i.e. a large spread of experts’ annular points), which could typically be attributed to poor image quality.
TABLE IV.
RMS Difference Between the Algorithmic Annulus and Manual Delineations Made by Experts on Clinical Images
| Valve | RMS Difference (mm) |
|---|---|
|
| |
| 1 | 1.95 |
| 2 | 1.37 |
| 3 | 2.75 |
| 4 | 0.96 |
| 5 | 1.19 |
| 6 | 2.50 |
| 7 | 3.22 |
| 8 | 1.82 |
| 9 | 1.27 |
| 10 | 1.09 |
|
| |
| Mean±Std. Dev. | 1.81±0.78 |
B. Validation Study Using Surgical View Delineations
Given the poor image quality of 3DUS, validating the algorithm by comparing the algorithm’s annulus to manual delineations made in 3DUS only answered the question of whether the algorithm was interpreting the images in the same way as a group of experts. The conclusion could not be made, however, that the annulus was understood to be the same shape as seen in a surgical view. Therefore, we further validated the algorithm by comparing the algorithm results to a fully visible mitral annulus delineated by a pointing device tracked using an electromagnetic (EM) tracker (miniBIRD - Model 800, Ascension Technology Corporation, Burlington, VT, USA).
We performed this validation study using six freshly excised porcine hearts. We removed the left atrium to fully expose the mitral annulus, and to inhibit motion, secured the heart to a plastic frame using suture. After securing the heart in a water tank, to roughly simulate a peak systolic state, we artificially distended the left ventricle by connecting the aorta to a tube from a container of water elevated about two meters above the heart, and by closing the coronary arteries using suture (Fig. 11). An expert acquired a 3DUS volume of the loaded mitral valve with a transthoracic probe, and shortly after, used an EM tracked pointing device to delineate the fully visible mitral annulus with about 30 evenly placed points. Taking into account the sensor resolution and calibration procedure, point locations were computed to within a measured accuracy of 0.21 mm.
Fig. 11.
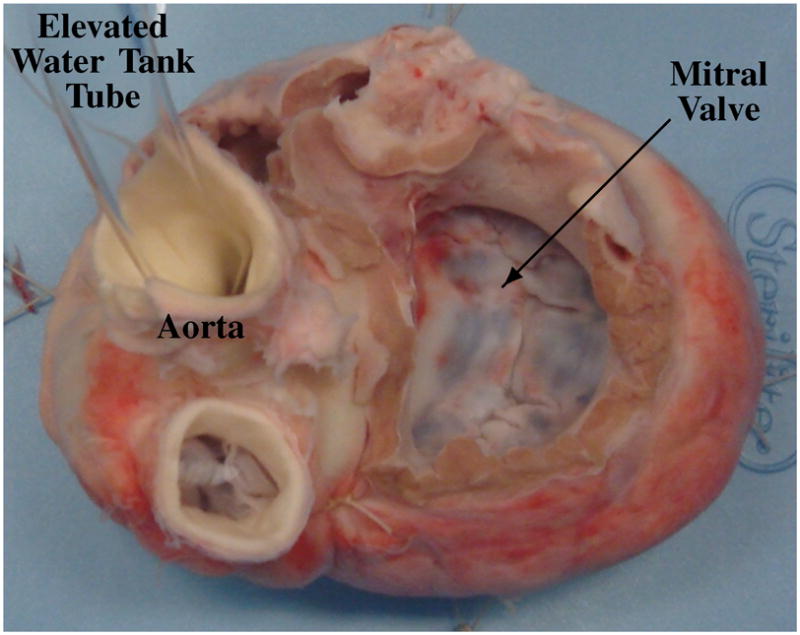
Typical view of a loaded mitral valve in a water tank that was used in the surgical view delineation study.
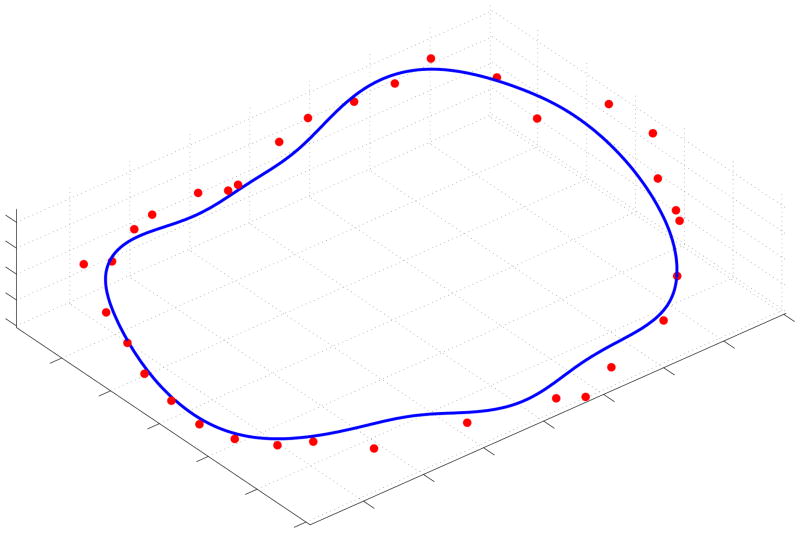
We segmented the annulus from the acquired 3DUS volume using the semi-automatic algorithm, and registered the EM delineated points to the algorithmic annulus by first manually aligning the two segmentations and then using an iterative-closest-point algorithm to refine the alignment. The RMS differences between the two can be seen in Table V, with Fig. 12 showing a typical comparison. The average RMS distance of the EM delineated annulus from the algorithmic annulus was 1.19±0.17mm, where we computed the standard deviation of the RMS distance from three different EM delineations of the annulus made by the expert on each mitral valve.
TABLE V.
RMS Difference Between the Algorithmic and EM Delineated Annulus from Freshly Excised Porcine Hearts
| Valve | RMS Difference (mm) (average ± std. dev.) |
|---|---|
|
| |
| 1 | 1.15 ± 0.04 |
| 2 | 1.35 ± 0.18 |
| 3 | 1.42 ± 0.01 |
| 4 | 1.38 ± 0.12 |
| 5 | 0.95 ± 0.42 |
| 6 | 0.91 ± 0.26 |
|
| |
| Mean | 1.19 ± 0.17 |
Fig. 12.
Typical comparison between the algorithmic annulus (solid line) and points delineated by an expert on a porcine mitral annulus using an EM tracked device.
C. Sensitivity Study
Just as important as the algorithm’s accuracy is the accuracy needed for the algorithm’s input, which is the user-specified point. For this study, we first established a baseline segmentation for each valve, i.e. the algorithm’s segmentation resulting from a carefully placed user-specified point near the center of the valve. The algorithm was then run on test points that were placed in the region around the center point, where we determined the center point from the baseline segmentation. If we refer to a segmentation resulting from a test point as a test annulus, then a test annulus was said to converge to the baseline if all points from the test annulus were less than 0.5 millimeters away from the baseline. The 3DUS images used in this study were the same as those used in the imaging validation study described in Section III-A.
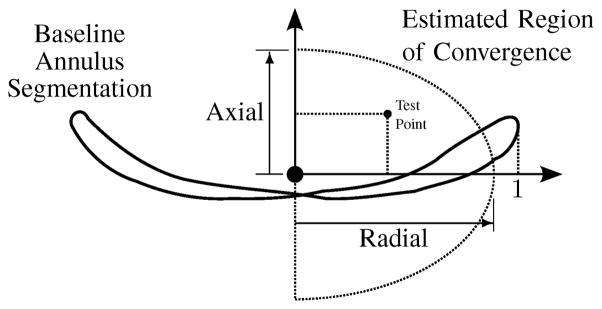
Based on the test points that resulted in the algorithm converging to the baseline, we could then establish a region of convergence. To describe the region of convergence in general terms, we refer to two directions – an axial direction, which is an estimation of the mitral valve axis from the baseline segmentation, and a radial direction, which is any direction perpendicular to the axis extending out from the center point towards the annulus. We represent the location of all test points relative to these axes, and normalize the coordinates by the radius of the baseline annulus in the plane defined by the axis and the test point. We then approximate the region of convergence as the ellipsoidal region shown in Fig. 13. Table VI shows the results of the sensitivity study, where it can be seen that the region of convergence extends to an average of 85% of the annulus radius in the axial direction and 106% of the annulus radius in the radial direction.
Fig. 13.
Estimated shape and size of the region of convergence relative to a baseline segmentation and described using the axial and radial directions
TABLE VI.
Estimated Region of Convergence Dimensions for Each Valve Normalized by the Annular Radius
| Valve | Axial | Radial |
|---|---|---|
| 1 | 0.96 | 1.34 |
| 2 | 0.44 | 0.65 |
| 3 | 0.76 | 1.13 |
| 4 | 1.24 | 1.08 |
| 5 | 0.72 | 1.11 |
| 6 | 0.71 | 0.98 |
| 7 | 0.96 | 1.16 |
| 8 | 0.78 | 0.68 |
| 9 | 1.26 | 1.17 |
| 10 | 0.67 | 1.26 |
|
| ||
| Mean ± Std. Dev. | 0.85 ± 0.26 | 1.06 ± 0.23 |
IV. Discussion
A. Performance and Validation
In both validation studies, the mitral annulus segmentation algorithm accurately and robustly segmented the three-dimensional mitral annulus contour from 3DUS. When comparing the algorithm to a group of experts, results showed that the algorithm consistently segmented the annulus near the location selected by the experts (Table III). The consistency of the algorithm was better than the group of experts, i.e. while the algorithm might not have the lowest MND values for each valve, across all valves, the algorithm had a lower mean MND than the group of clinicians (p < 0.001). Additionally, the algorithm and the best scoring expert were statistically indistinguishable (p = 0.85). We also analyzed the expert segmentations by computing the RMS difference between the algorithm and the expert average, in which we found an average RMS difference of 1.81 ± 0.78mm. Lastly, we compared the computed annulus shape to a fully exposed porcine annulus delineated using an EM tracked pointer. Results showed an average RMS difference of 1.19±0.17mm between the algorithm and the delineated points. This smaller RMS difference, compared to the validation study using the group of experts, is due to the fact that the true annulus could be seen. In contrast, the group of experts could only use 3DUS images to interpret the annulus location. Consequently, when image quality was poor, there was typically a lack of consensus as to the annulus location, resulting in a larger RMS difference between the expert average and the algorithm.
The two validation studies were complimentary. The first study used actual clinical images, which display the full range of noise and distortion encountered in medical practice. Here the performance of the algorithm cannot be compared to a “gold standard” determination of the annulus location; instead, the results were compared to the annulus location determined by a group of practicing clinicians. This approach is most immediately relevant to diagnostic applications, where determination of the annulus shape provides insight into various pathological states [1]–[5]; current clinical practice is based on the expert segmentations which are the standard for comparison here.
In the water tank study, the quality of the 3DUS images is significantly better than in vivo, which may improve algorithm performance compared to clinical images. The annulus location, however, could be directly designated using visual inspection and a pointing device, which is likely to produce a good estimate of the “true” annulus location. This method is particularly pertinent to surgical planning applications [8], as the mitral annulus is viewed from a similar perspective during annuloplasty. While both validation studies have limitations, the results in combination suggests that the algorithm is able to estimate annulus location with an accuracy comparable to current clinical practice.
The sensitivity study suggests that the algorithm is robust to variation in user input. So long as the user-specified point is located within about a half-diameter of the valve’s center, the algorithm converges to the same annulus location. Given that this point is the only information the algorithm requires from the user, the results of the semi-automatic annulus segmentation algorithm are consequently independent of the user as well. Additionally, despite variation in the states and degrees of pathology of the mitral valves, the probe orientation relative to the valve, and the ultrasound machine settings, the algorithm accurately segmented the annulus using the same algorithm parameter values for every image, reinforcing the robustness of the method.
The measured accuracy of this algorithm is difficult to compare to prior work, as previously published semi-automatic mitral annulus segmentation algorithms include minimal validation [25], [26]. In [26], indirect quantitative analysis of the method was performed by comparing measurements from a model to published population valve dimensions. As an example, for average annulus diameter dimensions, the method reported errors of roughly 15%. We measured the annuli from our algorithm and the EM delineations discussed in III-B and found an average diameter difference of under 4%.
B. Algorithm Design
The algorithm uses a thin tissue detector which can be likened to a simplified three dimensional ridge detector [36] for determining the valve orientation, computing the mitral leaflet surface, and finding the location of the projected mitral annulus contour. This is a key reason the algorithm is successful: the only extensive regions of thin tissue in the image volume are the mitral valve leaflets, so the algorithm focuses on the mitral apparatus and ignores the rest of the volume. This generates accurate results despite poor placement of the user input point.
Characterizing the leaflet location using the thin tissue detector, however, does place restrictions on the ultrasound imaging, in that the thin leaflet tissue needs to be visible (Fig. 14(a)). This is not the case when the ultrasound wave propagation is parallel to the leaflet surface orientation (Fig. 14(b) and 14(c)), as this produces little acoustic return. The algorithm will fail on images such as these. However, similar restrictions would also exist for the previous work in annulus segmentation presented in [25] and [26], and is to be expected for algorithms wishing to delineate the mitral annulus from a single ultrasound frame and with no use of temporal information.
Fig. 14.
Mitral valve leaflet appearance of the same valve in several scenarios. (a) Closed mitral valve in a long-axis view (LA - left atrium; LV - left ventricle). Leaflet surface is well defined. Dashed red lines are the approximate border of the LV. (b) Open mitral valve in a long-axis view. Leaflets are poorly defined. (c) Closed mitral valve in a short-axis view shown with the border taken from (a). Leaflet surface is poorly defined and chordae insertions are visible.
With ultrasound imaging, anatomical structures become more or less defined depending on their orientation to the acoustic propagation (Fig. 14). This helps to explain why the presented method cannot be used to find the annulus throughout the cardiac cycle, but rather was designed for just closed valves. For instance, if the probe orientation such as that shown in Fig. 14(a) was used to view the mitral valve throughout the cardiac cycle, when the valve opens (Fig. 14(b)), the leaflets become oriented such that they become poorly defined. Additionally, when the valve opens, the leaflets can become difficult to distinguish from the left ventricle wall that they are pushed against.
The graph cut method (max-flow algorithm) is used in the annulus segmentation algorithm first in a 3D graph to find a surface at the location of the mitral leaflets, and then in a 2D graph to find a contour at the location of the projected mitral annulus in the projection images. There are several reasons why we use the graph cut method. One of the main reasons is the fact that it finds an optimal solution to an energy minimization problem, meaning we will not fall victim to the local minima that many methods are subject to which attempt to find an optimal surface or contour (i.e. active contours [31], level sets [32], etc.). This is especially important in cardiac ultrasound, where anatomic variation along with the noise, artifacts, and inhomogeneities inherent in ultrasound imaging have the potential to create several local minima. Other reasons to use the graph cut method are that it does not require an initialization, and a limited amount of prior knowledge can be enforced through mindful construction of the graph. Therefore, the need for additional user input, for either initialization or to encourage a specific geometry, is eliminated without sacrificing accuracy, and we avoid the variation inherent in any additional user inputs. The combination of these characteristics of the graph cut method helps to make the annulus segmentation algorithm accurate, and also helps to explain why the algorithm has such a large region of convergence relative to the user-provided point.
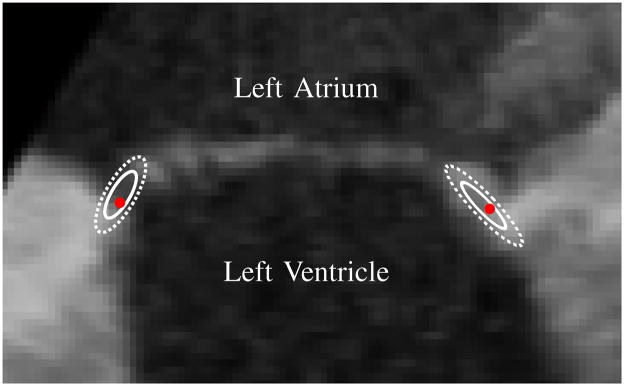
The annulus segmentation algorithm can be simplified to two main steps: find the leaflets, then search along the leaflets to find the annulus. This was consistent with the approach used by the experts (cardiologists and technicians) to delineate the annulus. Fig. 15 shows an example of the distribution of the human selected annular points which are aligned along the leaflets. The main difference was that after finding the leaflets, the human observers had access to temporal information to delineate the annulus location, whereas the algorithm used only a single 3DUS volume.
Fig. 15.
Slice from 3DUS of the mitral valve used in the manual segmentation study showing typical distributions of the annulus points selected by the experts. The first standard deviation (solid line) and second standard deviation (dotted line) are shown. The red point is the location of the algorithm-generated annulus in the slice. This suggests that human observers, much like the algorithm, select annulus points along the leaflet structure.
C. Future Work
One of the most significant improvements to the algorithm would be to integrate temporal information to more accurately and robustly locate the annulus. Currently, the algorithm finds the annulus as the location at the leaflets where the tissue thickness changes abruptly along the computed leaflet surface. A drawback of this approach, however, is that if the TTD is improperly tuned or if the leaflets are severely calcified, the annulus might not be accurately located, which might be ameliorated when temporal information is used.
The large region of convergence for the algorithm makes it an attractive candidate for complete automation. Because the only input to the algorithm is the user-specified point, if this point can be delineated by some automated process, the annulus segmentation algorithm could be made fully automatic. Special care would need to be taken, however, to account for the different appearances of valves due to varying pathologies, ultrasound probe orientations, and ultrasound machine settings. An example of a method that could be used for this automatic selection is the work presented in [37], which automatically segments the mitral valve plane and left ventricular long-axis. The intersection of the plane and the axis could be used to define the user-specified point.
The annulus segmentation algorithm presents many opportunities in clinical studies. The algorithm can help to analyze large clinical databases to explore correlations between pathologies and annular geometries. It can also be used to monitor patient anatomy over time to determine if geometry at an earlier age has any indication as to pathologies that may develop at later ages.
To build on this algorithm, future work will also include segmentation and/or tracking of the annulus over the duration of the cardiac cycle. However, given that the algorithm can segment the mitral annulus whenever the leaflets are coapted, the shape and motion of the annulus throughout most of the cardiac cycle can already be obtained from the present method.
V. Conclusion
The annulus segmentation algorithm accurately and robustly segments the mitral annulus from a 3DUS frame using only a single user specified point. The approach first uses a thin tissue detector to localize the mitral leaflets, and then the graph cut algorithm to define the leaflet surface. The annulus is detected as the curve where the thin leaflet surface meets the thick heart wall using another graph cut implementation and multiscale active contours. Validation using clinical 3DUS images showed that estimated annulus positions were comparable to expert manual segmentation. A second validation study showed that the algorithm matched annulus delineations made by an expert using an EM tracked pointing device, with an RMS error of 1.19 ± 0.17mm across six valves. The algorithm is insensitive to the placement of the user-specified point within about half of the valve radius, and a single set of parameters was used for all valve images, with no fine-tuning required. The algorithm can be used to increase speed and consistency in determining annulus location for diagnostic, surgical planning, and database applications.
Acknowledgments
The authors would like to thank Todd Zickler and Ramin Zabih for helpful discussions on the max-flow algorithm, and Hugo Loyola for discussions on the statistical analysis.
This work was supported in part by the U.S. National Institutes of Health under grants NIH RO1 HL073647-01 and NIH 5 F32 HL084965-03, and by the National Science Foundation’s Graduate Research Fellowship Program.
Contributor Information
Robert J. Schneider, Email: rjschn@seas.harvard.edu, Harvard School of Engineering and Applied Sciences, Cambridge, MA 02138 USA (617-496-9098)
Douglas P. Perrin, Department of Cardiac Surgery, Children’s Hospital Boston, Boston, MA 02115 USA
Nikolay V. Vasilyev, Department of Cardiac Surgery, Children’s Hospital Boston, Boston, MA 02115 USA
Gerald R. Marx, Department of Cardiology, Children’s Hospital Boston, Boston, MA 02115 USA
Pedro J. del Nido, Department of Cardiac Surgery, Children’s Hospital Boston, Boston, MA 02115 USA
Robert D. Howe, Harvard School of Engineering and Applied Sciences and with the Harvard-MIT Division of Health Sciences and Technology, Cambridge, MA 02138 USA.
References
- 1.Levine R, Handschumacher M, Sanfilippo A, Hagege A, Harrigan P, Marshall J, et al. Three-dimensional echocardiographic reconstruction of the mitral valve, with implications for the diagnosis of mitral valve prolapse. Circulation. 1989;80(3):589–598. doi: 10.1161/01.cir.80.3.589. [DOI] [PubMed] [Google Scholar]
- 2.Flachskampf F, Chandra S, Gaddipatti A, Levine R, Weyman A, Ameling W, et al. Analysis of shape and motion of the mitral annulus in subjects with and without cardiomyopathy by echocardiographic 3-dimensional reconstruction. Journal of the American Society of Echocardiography. 2000;13(4):277–287. doi: 10.1067/mje.2000.103878. [DOI] [PubMed] [Google Scholar]
- 3.Kaplan S, Bashein G, Sheehan F, Legget M, Munt B, Li X, et al. Three-dimensional echocardiographic assessment of annular shape changes in the normal and regurgitant mitral valve. American Heart Journal. 2000;139(3):378–387. doi: 10.1016/s0002-8703(00)90077-2. [DOI] [PubMed] [Google Scholar]
- 4.Kaji S, Nasu M, Yamamuro A, Tanabe K, Nagai K, Tani T, et al. Annular Geometry in Patients With Chronic Ischemic Mitral Regurgitation: Three-Dimensional Magnetic Resonance Imaging Study. Circulation. 2005;112(9 Suppl):I409–I414. doi: 10.1161/CIRCULATIONAHA.104.525246. [DOI] [PubMed] [Google Scholar]
- 5.Popovic Z, Martin M, Fukamachi K, Inoue M, Kwan J, Doi K, et al. Mitral annulus size links ventricular dilatation to functional mitral regurgitation. Journal of the American Society of Echocardiography. 2005;18(9):959–963. doi: 10.1016/j.echo.2005.01.011. [DOI] [PubMed] [Google Scholar]
- 6.Jimenez J, Soerensen D, He Z, He S, Yoganathan A. Effects of a saddle shaped annulus on mitral valve function and chordal force distribution: an in vitro study. Annals of Biomedical Engineering. 2003;31(10):1171–1181. doi: 10.1114/1.1616929. [DOI] [PubMed] [Google Scholar]
- 7.Salgo I, Gorman J, Gorman R, Jackson B, Bowen F, Plappert T, et al. Effect of annular shape on leaflet curvature in reducing mitral leaflet stress. Circulation. 2002;106(6):711–717. doi: 10.1161/01.cir.0000025426.39426.83. [DOI] [PubMed] [Google Scholar]
- 8.Fabricius A, Walther T, Falk V, Mohr F. Three-dimensional echocardiography for planning of mitral valve surgery: Current applicability? The Annals of Thoracic Surgery. 2004;78(2):575–578. doi: 10.1016/j.athoracsur.2003.10.031. [DOI] [PubMed] [Google Scholar]
- 9.Ferrazzi P, Iacovoni A, Pentiricci S, Senni M, Iascone M, Borenstein N, et al. Toward the development of a fully elastic mitral ring: Preliminary, acute, in vivo evaluation of physiomechanical behavior. The Journal of Thoracic and Cardiovascular Surgery. 2009;137(1):174–179. doi: 10.1016/j.jtcvs.2008.08.041. [DOI] [PubMed] [Google Scholar]
- 10.Votta E, Caiani E, Veronesi F, Soncini M, Montevecchi F, Redaelli A. Mitral valve finite-element modelling from ultrasound data: a pilot study for a new approach to understand mitral function and clinical scenarios. Philosophical Transactions of the Royal Society London, Series A. 2008;366(1879):3411–3434. doi: 10.1098/rsta.2008.0095. [DOI] [PubMed] [Google Scholar]
- 11.Hammer P, Vasilyev N, Perrin D, del Nido P, Howe R. Fast image-based model of mitral valve closure for surgical planning. MICCAI 2008 Workshop Proceedings: Computational Biomechanics for Medicine III; New York, NY. 2008. pp. 15–26. [Google Scholar]
- 12.Lim K, Yeo J, Duran C. Three-dimensional asymmetrical modeling of the mitral valve: a finite element study with dynamic boundaries. The Journal of Heart Valve Disease. 2005;14(3):386–392. [PubMed] [Google Scholar]
- 13.Einstein D, Kunzelman K, Reinhall P, Nicosia M, Cochran R. Non-linear fluid-coupled computational model of the mitral valve. The Journal of Heart Valve Disease. 2005;14(3):376–385. [PubMed] [Google Scholar]
- 14.Kunzelman KS, Cochran RP, Chuong C, Ring WS, Verrier ED, Eberhart RD. Finite element analysis of the mitral valve. The Journal of Heart Valve Disease. 1993;2(3):326–40. [PubMed] [Google Scholar]
- 15.Glasson J, Komeda M, Daughters G, Niczyporuk M, Bolger A, Ingels N, et al. Three-dimensional regional dynamics of the normal mitral anulus during left ventricular ejection. The Journal of Thoracic and Cardiovascular Surgery. 1996;111(3):574–585. doi: 10.1016/s0022-5223(96)70309-4. [DOI] [PubMed] [Google Scholar]
- 16.Dagum P, Timek T, Green G, Daughters G, Liang D, Ingels N, et al. Three-dimensional geometric comparison of partial and complete flexible mitral annuloplasty rings. The Journal of Thoracic and Cardiovascular Surgery. 2001;122(4):665–673. doi: 10.1067/mtc.2001.116313. [DOI] [PubMed] [Google Scholar]
- 17.Timek T, Dagum P, Lai D, Liang D, Daughters G, Tibayan F, et al. Tachycardia-induced cardiomyopathy in the ovine heart: Mitral annular dynamic three-dimensional geometry. The Journal of Thoracic and Cardiovascular Surgery. 2003;125(2):315–324. doi: 10.1067/mtc.2003.80. [DOI] [PubMed] [Google Scholar]
- 18.Bothe W, Nguyen T, Ennis D, Itoh A, Carlhäll C, Lai D, et al. Effects of acute ischemic mitral regurgitation on three-dimensional mitral leaflet edge geometry. European Journal of Cardio-Thoracic Surgery. 2008;33(2):191–197. doi: 10.1016/j.ejcts.2007.10.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gorman J, Gupta K, Streicher J, Gorman R, Jackson B, Ratcliffe M, et al. Dynamic three-dimensional imaging of the mitral valve and left ventricle by rapid sonomicrometry array localization. The Journal of Thoracic and Cardiovascular Surgery. 1996;112(3):712–726. doi: 10.1016/S0022-5223(96)70056-9. [DOI] [PubMed] [Google Scholar]
- 20.Watanabe N, Ogasawara Y, Yamaura Y, Yamamoto K, Wada N, Okahashi N, et al. Dynamics of mitral complex geometry and functional mitral regurgitation during heart failure treatment. Journal of Echocardiography. 2006;4(2):51–58. [Google Scholar]
- 21.Daimon M, Saracino G, Gillinov A, Koyama Y, Fukuda S, Kwan J, et al. Local dysfunction and asymmetrical deformation of mitral annular geometry in ischemic mitral regurgitation: a novel computerized 3D echocardiographic analysis. Echocardiography. 2008;25(4):414–423. doi: 10.1111/j.1540-8175.2007.00600.x. [DOI] [PubMed] [Google Scholar]
- 22.Qin J, Shiota T, Tsujino H, Saracino G, White R, Greenberg N, et al. Mitral annular motion as a surrogate for left ventricular ejection fraction: real-time three-dimensional echocardiography and magnetic resonance imaging studies. European Journal of Echocardiography. 2004;5(6):407–415. doi: 10.1016/j.euje.2004.03.002. [DOI] [PubMed] [Google Scholar]
- 23.Ratanasopa S, Bolson E, Sheehan F, McDonald J, Bashein G. Performance of a Fourier-based program for three-dimensional reconstruction of the mitral annulus on application to sparse, noisy data. The International Journal of Cardiac Imaging. 1999;15(4):301–307. doi: 10.1023/a:1006184726733. [DOI] [PubMed] [Google Scholar]
- 24.Lei Z, Xin Y, Liping Y, Kun S. Three Dimensional Reconstruction and Dynamic Analysis of Mitral Annular Based on Connected Equi-length Curve Angle Chain. Lecture Notes in Computer Science - International Conference on Medical Biometrics; Springer; 2007. pp. 298–306. [Google Scholar]
- 25.Wolf I, Hastenteufel M, De Simone R, Vahl C, Hagl S, Meinzer H. Computers in Cardiology. 2001. Three-dimensional annulus segmentation and hybrid visualisation in echocardiography; pp. 105–108. [Google Scholar]
- 26.Voigt I, Ionasec R, Georgescu B, Houle H, Huber M, Hornegger J, et al. Model-driven physiological assessment of the mitral valve from 4D TEE. Proc. SPIE - Medical Imaging; SPIE; 2009. [Google Scholar]
- 27.Boykov Y, Kolmogorov V. An experimental comparison of mincut/max-flow algorithms for energy minimization in vision. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2004;26(9):1124–1137. doi: 10.1109/TPAMI.2004.60. [DOI] [PubMed] [Google Scholar]
- 28.Ford L, Fulkerson D. Flows in networks. Princeton University Press; 1962. [Google Scholar]
- 29.Roy S. Stereo without epipolar lines: A maximum-flow formulation. International Journal of Computer Vision. 1999;34(2):147–161. [Google Scholar]
- 30.Kolmogorov V. [[Accessed: October 1, 2008]];“Software”. 2004 http://www.cs.ucl.ac.uk/staff/V.Kolmogorov/software.html.
- 31.Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. International Journal of Computer Vision. 1988;1(4):321–331. [Google Scholar]
- 32.Sethian J. Level set methods and fast marching methods: evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science. Cambridge University Press; 1999. [Google Scholar]
- 33.Schneider R, Perrin D, Vasilyev N, Marx G, del Nido P, Howe R. Mitral annulus segmentation from three-dimensional ultrasound. Proc. IEEE International Symposium on Biomedical Imaging; Boston, MA: IEEE; 2009. pp. 779–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Williams D, Shah M. A fast algorithm for active contours and curvature estimation. CVGIP: Image Understanding. 1992;55(1):14–26. [Google Scholar]
- 35.Wagner C, Perrin D. Efficient curvature estimations for real-time (25Hz) segmentation of volumetric ultrasound data. Proc. SPIE - Medical Imaging; SPIE; 2008. pp. 1–10. [Google Scholar]
- 36.López A, Lumbreras F, Serrat J, Villanueva J. Evaluation of methods for ridge and valley detection. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1999;21(4):327–335. [Google Scholar]
- 37.Van Stralen M, Leung K, Voormolen M, De Jong N, Van der Steen A, Reiber J, et al. Time Continuous Detection of the Left Ventricular Long Axis and the Mitral Valve Plane in 3-D Echocardiography. Ultrasound in Medicine & Biology. 2008;34(2):196–207. doi: 10.1016/j.ultrasmedbio.2007.07.016. [DOI] [PubMed] [Google Scholar]