Abstract
Head motion is a fundamental problem in functional MRI, and is often a limiting factor in its clinical implementation. This work presents a rigid-body motion correction strategy for echo-planar imaging (EPI) sequences that uses micro radio-frequency coil “active markers” for real-time, slice-by-slice prospective correction. Before the acquisition of each EPI-slice, a short tracking pulse-sequence measures the positions of three active markers integrated into a headband worn by the subject; the rigid-body transformation that realigns these markers to their initial positions is then fed back to dynamically update the scan-plane, maintaining it at a fixed orientation relative to the head. Using this method, prospectively-corrected EPI time-series are acquired on volunteers performing in-plane and through-plane head motions, with results demonstrating increased image stability over conventional retrospective image-realignment. Implications of this improvement for BOLD fMRI applications is assessed, as well as the benefit of non-rigid-body distortion-correction to reduce the remaining signal variation.
Keywords: functional magnetic resonance imaging, fMRI, EPI, motion correction, prospective, real-time, active marker, device tracking, RF-coil, micro-coil, geometric distortion
INTRODUCTION
Functional magnetic resonance imaging (fMRI) is playing an increasingly important role in the clinical setting (1). Echo-planar imaging (EPI) is the preferred sequence for fMRI, since a closely sampled time-series of brain volumes is needed. Image stability between time-frames is particularly important, as the measured intensity changes are small relative to baseline levels. Even a few millimeters of movement can cause large signal fluctuations that reduce stability and obscure the small brain activation signal, thereby leading to the generation of inaccurate brain activation maps (1-3). This problem is further compounded in clinical fMRI studies as patients are more likely to move than healthy volunteers (1,3-5). In a survey of 194 functional scans, the 26 failures were correlated to degree of paresis, with head movement artifacts being the most frequent cause of fMRI failure (1).
To compensate for motion, fMRI studies typically employ post-hoc image-based methods to estimate six degrees-of-freedom (6-DOF) rigid-body head movement, and to realign each brain volume in the time-series after the data has already been acquired (2,3). In this work, we use “volume” to refer to a complete multi-slice brain acquired at a single EPI time-frame. These retrospective correction techniques involve interpolation, which can cause image blurring, and are fundamentally limited by their inability to fully correct for the influences of through-plane motion on local spin-history. Additionally, the most common algorithms (6) only correct for inter-volume motion, neglecting potential intra-volume motion between slices in the same time-frame. Retrospective methods may also induce spurious brain activations even without any actual motion (7).
To avoid these deficiencies, prospective strategies compensate for motion in the acquisition stage by keeping the scan-plane at a fixed orientation relative to the head throughout the scan, thereby eliminating the need for interpolation and maintaining the volume's spin-history. Several prospective techniques for fMRI have been proposed, each using different reference data to track the 6-DOF motion. An image-based approach (8), is able to correct for inter-volume motion only. Navigator-based methods (9) acquire extra data along various three-dimensional (3D) k-space trajectories to estimate the 6-DOF (10-14). Prospective correction using multiple orbital navigators require delays of ~ 160 ms per update (11). Cloverleaf navigators reduce the delay to ~ 18 ms, but require an initial 12 s reference map to be acquired while the patient is stationary (13). Alternatively, optical systems use cameras to track external markers (15-19); while there is no extra pulse-sequence load, this comes at the cost of an additional cross-calibration procedure to determine the coordinate transform between camera-space (where markers are tracked) and magnet-space (where scan-plane orientation is defined).
The method described here uses real-time tracking of micro radio-frequency (RF) coils (20-25), or “active markers,” to provide the 6-DOF information for prospective correction. Proof-of-principle was originally demonstrated in an “offline” inter-volume update scheme (26). Krueger et al. presented the first use of active markers for real-time motion correction (27), with successful preliminary demonstrations in moving phantoms (28). Our previous work (29) showed the advantages of active-marker prospective correction in structural brain scans. The current work demonstrates the first use of active markers for real-time, prospective motion correction in 2D-EPI sequences. The scan-plane orientation is dynamically updated between EPI readouts, allowing for intra-volume motion compensation on a slice-by-slice basis (30). Increased image stability is demonstrated in time-series scans of volunteers performing deliberate motions, and the implications of these results for improving the sensitivity of brain activation maps in blood oxygenation level dependent (BOLD) fMRI is addressed. We discuss the issue of motion-induced non-rigid image distortion, which is a remaining source of signal variation; an unwarping algorithm incorporating the complex EPI-data is shown to provide additional retrospective distortion-correction to the prospectively-corrected images.
METHODS
Active Marker Tracking Device and Scan-Plane Update
Details of the tracking hardware and scan-plane update scheme have been previously presented (29), and are briefly reviewed here. Motion tracking was performed using three active markers integrated into a headband worn by the subject. Three non-colinear markers are sufficient to fully describe any arbitrary rigid-body head motion. Each marker is a solenoid inductor, tuned and matched to 64.3 MHz, containing a small (3 mm diameter) glass sphere filled with Gd-doped 1H solution. The markers are attached to a Synergy Multi-Connect (SMC) box (Philips Healthcare, Best, the Netherlands; by IGC Medical Advances), which then connects to the scanner.
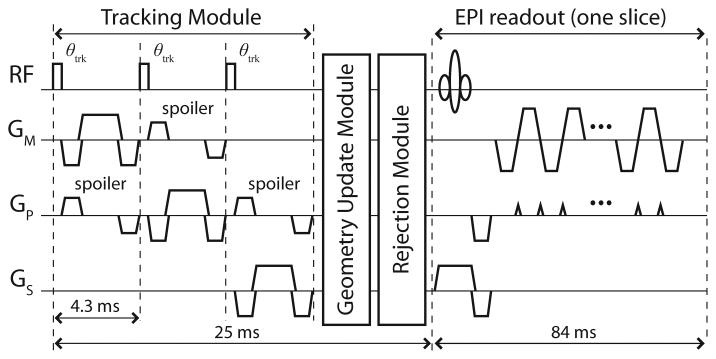
Figure 1 shows the prospective motion correction modules. The tracking module contains a short tracking pulse-sequence of orthogonal 1D projection-readouts, that measures the 3D-positions of the active markers. The markers are measured simultaneously, and unambiguously identified due to the use of separate receive channels. A weak non-selective RF-excitation pulse (θtrk = 4°) minimizes the effects on imaged spins; using this setup, no RF-shadowing effects were observed. A peak search and quadratic fit in frequency is used to estimate each marker's position along the projected axis. Previous studies have demonstrated measurement precision and accuracy with this method to be 0.01 mm and 0.3 mm, respectively (29).
Fig. 1.
Prospective slice-by-slice motion correction scheme for a single-shot EPI sequence. A tracking, geometry update, and rejection module are interleaved into the imaging pulse-sequence before the acquisition of each EPI-slice. Spoiler gradients further enhance the marker's signal relative to any signal from its surroundings (25). Custom modifications to the standard EPI sequence were programmed in the Philips Pulse Programming Environment, and a software patch generated that integrates all prospective correction options (θtrk, resolution, rejection threshold, etc.) into the standard Philips graphical user interface.
In the geometry update module, the current marker positions are compared with their initial reference positions (measured by the first tracking-module at the beginning of the scan), and the 6-DOF rigid-body transform (three rotations θm, θp, θs, and three translations tm, tp, ts, given in the “measurement–phase-encode–slice-selection” (mps) image coordinate-system) is calculated that realigns the markers (31). The transform is then fed back to prospectively update the scan-plane for rotational and translational head motion – by dynamically modifying the relevant imaging RF, gradient, and data acquisition attributes – before the subsequent EPI readout. In the optional rejection module, if the motion between the current and previous tracking modules is greater than a user-defined threshold, then the previous time-frame is discarded and reacquired with updated geometry. If the motion is within the threshold, then the previous data is accepted and the next EPI readout is acquired after geometry update as described above. The total time for each update ~ 25 ms.
In Vivo Tests
Prospective correction was evaluated on volunteers performing a series of naturalistic head motions. Eight EPI studies were performed on seven healthy volunteers (one repeat volunteer on separate days). For each study the volunteer was trained to reproduce three types of motion throughout the scan: a baseline “resting” position, a slow but continuous left-right “head-shake” rotation of < ±5°, and a continuous head-foot “head-nodding” rotation of < ±5°. In one of the studies, the volunteer performed two additional motions: an abrupt left-right “head-jerk” from 0 to 5° in the middle of the scan, and a similarly abrupt motion in the head-foot direction. In axial slices, left-right and head-foot rotations induced in-plane and through-plane motions, respectively. For each motion, two EPI time-series were acquired – with prospective correction ON and OFF – to evaluate correction quality under similar motion conditions. For scans with correction OFF, all tracking and geometry calculations were performed and logged – but not applied to update the scan-plane – to verify reproducibility of volunteer movement. All experiments with human subjects were in accordance with local IRB regulations and informed consent was obtained before each exam.
Experiments were performed on a 1.5T Philips Achieva (Philips Healthcare, Best, The Netherlands). Imaging was performed with a standard quadrature bird-cage coil, and tracking via active-marker headband. Slice-by-slice prospective correction (TE/TR = 1.8/4.3 ms, θtrk = 4°, resolution = 1 mm, rejection threshold = 10 mm) was applied to an axial, single-shot 2D-EPI time-series (TE/TR = 40/1680 ms, θ = 85°, FOV = 192×192 mm, voxels = 3×3 mm, thickness/gap = 5/1 mm, slices = 20, phase-encode direction = right-left, time-frames = 10, shim = first-order (subject-specific), scan time = 38 s). The scanner's standard post-processing pipeline was used for image reconstruction. Scan durations increased due to extensive real-time logging of tracking information required at this developmental stage; with logging disabled, scan times reduce to 23 s. The original scan with prospective correction completely disabled is 18 s.
Analysis
Uncorrected scans were retrospectively realigned to their first (reference) time-frame using a standard image-based analysis package (Statistical Parametric Mapping v5 (SPM5), Wellcome Trust, London, UK) for comparison with prospective correction results; default SPM5 rigid-body realignment settings were used. For visual assessment, difference images were generated by subtracting slices acquired before motion (Ibefore) from those acquired after motion (Iafter), where perfect correction will result in a zero difference-image.
To quantify and provide spatial information of image stability across the time-series, standard deviation maps (σ-maps) were calculated. Binary masks of gray/white matter were segmented from the first time-frame of each scan using SPM5, and applied to the rest of the time-frames so that only voxels containing brain tissue were included. For each voxel, the standard deviation of its intensity across the time-series was then normalized as a percentage of its mean intensity to obtain the σ-map. The average standard deviation σ̄ over all voxels in the σ-map was also calculated. As movement increases the intensity variation of each voxel, the result of perfect motion correction will be reduced values of σ̄ comparable to resting scans.
A simulation was used to evaluate the effects of reducing σ from a BOLD fMRI perspective. A simulated BOLD signal was applied to the time-series acquired with prospective correction both ON, and OFF (after retrospective realignment), as follows. The standard Automated Anatomical Labeling (AAL) template (32) was registered into subject-space using the inverse transform matrix produced by SPM5 segmentation. Based on the AAL-map, the left/right supplemental-motor-area and left/right cuneus-regions (i.e. motor cortex and visual cortex, respectively) were selected as stimulated regions of interest (ROI). Binary masks of these two ROIs were generated in the first time-frame, then propagated through the remaining (prospectively or retrospectively realigned) time-frames of each scan. To simulate a BOLD fMRI signal in these ROIs, the average signal intensity for each ROI was calculated across the time-series, and 2% of this average signal was added to the ROIs in the 1st, 2nd, 5th, 6th, 9th, and 10th time-frames. A boxcar-regressor was then fitted to the data using the standard SPM5 fMRI package, and z-scores calculated for each voxel. This processing stream was repeated for all scans.
Distortion Correction using Field Maps
Complex EPI-data from the prospectively corrected images of one volunteer were saved to generate field-maps, which were used to investigate the benefit of additional retrospective correction for motion-induced non-rigid image distortion, as suggested by (33). Phase images Φn of the nth time-frame were unwrapped (34), and the field-map Bn calculated: Bn = (Φn − Φ1)/(2πTE). Bn thus yields a frequency-difference map (Hz) that represents the relative field inhomogeneity deviation between the nth and reference time-frame due to the different head positions. Since field inhomogeneities cause negligible pixel mis-location in the readout direction for EPI, the distortion correction then simplifies into a series of 1D pixel-shifts in the phase-encode direction; a simplified version of the shifting algorithm presented in (35) was implemented here. To calculate the necessary shifts, Bn is converted into a pixel-shift map rn = Bn/BWpe, where BWpe is the bandwidth per pixel (Hz/pixel) in the phase-encode direction. The average value of each phase-encode line in rn was then used to shift the corresponding image phase-encode line, with linear interpolation used for sub-pixel shifts. In this manner every nth time-frame was undistorted back to the reference. This (non-rigid-body) distortion correction was retrospectively applied to the (rigid-body) prospectively corrected dataset to determine if σ̄ could be further reduced.
RESULTS
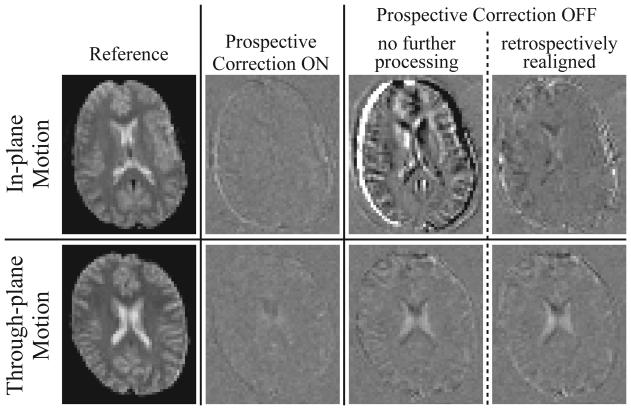
In-plane and through-plane motions, as well as varying degrees of intra-volume motion, were evaluated. Figure 2, row 1 shows difference images from one volunteer performing a continuous in-plane motion. Here the slice Iafter illustrates the effects of a large rotational displacement θs (relative to the initial reference) and moderate intra-volume motion Δθs; Δθs is induced due to the continuous nature of the head rotation, and is the difference in θs between the first and last slice of the volume in which Iafter was acquired. The volunteer reproduced the motion, and the closest matching slice with prospective correction ON (row 1, column 2) and OFF (row 1, columns 3,4) was chosen for comparison. Retrospective realignment (row 1, column 4), while significantly better than no compensation (row 1, column 3), still exhibits some remaining error. Prospective correction results in a near-zero difference image.
Fig. 2.
Difference images (Iafter - Ibefore) obtained from one volunteer performing a continuous in-plane motion (row 1), and a second volunteer performing a continuous through-plane motion (row 2). A zero difference image reflects perfect correction. A reference EPI image (column 1) is shown alongside sample difference images generated from time-series acquired with prospective correction ON (column 2) and OFF (columns 3,4); column 3 images remained completely unprocessed, while column 4 images were retrospectively realigned using SPM. Row 1 was chosen to demonstrate an in-plane motion case with a large rotational displacement θs and moderate intra-volume motion Δθs; the closest matching slices with prospective correction ON (row 1, column 2: Iafter acquired at θs = 3.52°, Δθs = 1.25°) and OFF (row 1, columns 3,4: Iafter at θs = 4.38°, Δθs = 1.07°) are chosen for comparison. Row 2 was chosen to demonstrate through-plane motion with a small rotational displacement θp but a large intra-volume motion Δθp; matching slices with prospective correction ON (row 2, column 2: Iafter at θp = 0.67°, Δθp = 2.37°) and OFF (row 2, columns 3,4: Iafter at θp = 0.46°, Δθp = 2.53°) are compared. The difference image in row 1, column 3 is worse than row 2 column 3 since in this case θs >> θp. For all difference images, the corresponding slice in the first (reference) time-frame was chosen for Ibefore (θs,p, Δθs,p ~ 0°). All difference images are identically windowed.
Figure 2, row 2 displays analogous results for a continuous through-plane motion. Here, Iafter demonstrates the case of small overall rotational displacement θp but large momentary intra-volume motion Δθp. Matching slices with prospective correction ON (row 2, column 2) and OFF (row 2, columns 3,4) are compared. Retrospective realignment (row 2, column 4) does little to improve the uncompensated image (row 2, column 3) while prospective correction again achieves near-perfect correction. No data was rejected in any continuous-motion scans.
Figure 3a shows σ-maps from the same scans used in Fig. 2. The σ-maps of unprocessed scans (column 3) illustrate the spatial distribution of increased variation caused by the motions. After retrospective realignment (column 4) regions of increased intensity variation still remain, particularly at the brain edges and superior slices, and are more pronounced during through-plane motion. Prospective correction (column 2) improves image stability over the time-series, returning standard deviations back to spatially-uniform resting levels of σ̄ ~ 2%.
Fig. 3.
a: Standard deviation maps (σ-maps) generated from the same in-plane (row 1) and through-plane (row 2) scans as used in Fig. 2. For ease of reference, the same layout is used as in Fig. 2. Reference EPI images (column 1) are shown alongside σ-maps generated from time-series acquired with prospective correction ON (column 2) and OFF (columns 3,4); column 3 images remained completely unprocessed, while column 4 images were retrospectively realigned using SPM before generating the σ-maps. The σ-maps provide spatial information of image stability, with perfect correction reducing standard deviations to baseline resting levels of brain activation ~ 2 %. b: Comparison of image stability between correction methods using metric σ̄. For each of the three motions tested, each column represents the average σ̄ over the relevant volunteer scans, while error bars are standard deviations between scans. N = 7, 9, 9 for resting, in-plane, and through-plane motions, respectively; one resting scan was removed due to significant subject movement, while analysis for deliberate motions include all 8 smooth + 1 abrupt motion scans. Prospective correction provides the greatest decrease σ̄ in for both deliberate motions, returning image stability closest to resting levels.
Image stability σ̄ over all subjects is summarized in Fig. 3b. In all 18 cases of deliberate motion, prospective correction significantly improved image stability (i.e. reduced σ̄) compared to the corresponding retrospectively realigned scan without prospective correction (p < 10−6, two-tailed paired student's t-test). For in-plane motions (N = 9), prospective correction improved image stability by an average of ~ 23% and 74% relative to retrospectively realigned and completely unprocessed scans, respectively. For through-plane motions (N = 9), prospective correction improved image stability by an average of ~ 30% and 59% relative to retrospectively realigned and unprocessed scans. As expected, retrospective realignment performed poorer in through-plane vs. in-plane cases. Retrospective realignment applied to prospectively corrected scans showed no visually obvious improvements, with only marginal improvement in σ̄ (data not shown). No statistical significance was found between correction methods in resting scans.
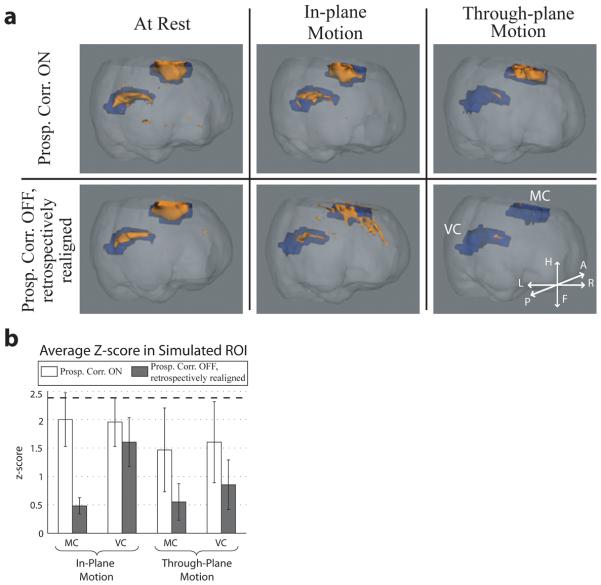
To quantitate the effect that improved image stability has on brain-activation sensitivity, a simulated BOLD fMRI signal was imposed on the continuous-motion scans. Since the z-score – typically used to measure statistical significance in fMRI – is inversely proportional to σ, a decrease in a voxel's background σ (Fig. 3) will increase its sensitivity to brain activation. Figure 4a shows activation maps from one volunteer. Blue ROIs represent areas of the motor (MC) and visual cortex (VC) where the BOLD signal was simulated, while orange ROIs denote areas of measured activation (p < 0.01). Prospective correction during deliberate motions shows an overall increase in true activation, and decrease in false activation (see Fig. 4a, row 2 column 2) vs. retrospectively realigned scans. Average z-scores of voxels within the stimulated ROIs is summarized in Fig. 4b over all subjects. An increase in average z-score, and hence sensitivity to brain activation, is seen between prospective vs. retrospective compensation in the MC and VC during deliberate motions, with an increase in sensitivity of over 300% in the MC of scans during in-plane motions.
Fig. 4.
Analysis of the datasets from a BOLD fMRI perspective. a: Activation maps from one volunteer during resting (column 1), continuous in-plane (column 2), and through-plane (column 3) motions. Blue ROIs represent areas of the motor cortex (MC) and visual cortex (VC) where the BOLD signal was simulated, while orange ROIs denote areas of measured activation (p < 0.01) using the standard SPM5 fMRI package. Prospective correction (row 1) during deliberate motions shows an overall increase in true activation (orange within blue ROIs), and decrease in false activation (orange outside of blue ROIs) vs. retrospectively realigned scans (row 2). Orientation in the patient coordinate system is shown in the bottom-right inset. b: Summary of brain-activation sensitivity, as measured by the average z-scores within the stimulated MC and VC regions (blue ROIs), over all continuous-motion scans. For both in-plane and through-plane motions, each column represents the average z-score over the relevant volunteer scans, while error bars are standard deviations between scans. Comparing average z-scores, prospective correction outperforms conventional retrospective realignment for all conditions of deliberate motion, as expected from the σ̄ results in Fig. 3b. The greatest improvement of brain-activation sensitivity is seen in the MC during in-plane motion, and in both MC and VC during through-plane motion. The average z-score in the MC and VC over all resting scans = 2.48 (best-case scenario) and is depicted by the dashed line; no statistically significant difference was found between resting scans.
The rejection module improves prospective correction during extreme motions. In Fig. 5a Iafter was acquired after a large, quick, through-plane head rotation θp; the volunteer then maintained this position for several seconds, resulting in minimal intra-volume motion Δθp. Since the motion was over the rejection threshold, the time-frame acquired during the movement was rejected and reacquired after the motion was completed. Despite substantial improvement over the uncorrected case a residual, uncorrected shear-like image-distortion is visible, highlighted by black/white arrows. Its cause is suggested by the field maps in Fig. 5b, which were calculated from phase data acquired in an additional case of in-plane and through-plane motion. For similar rotational magnitudes, pixel-shifts did not exceed 0.5 mm for in-plane motions, while pixel-shifts of up to 3 mm were observed for through-plane motions. For the through-plane case, prospective correction followed by retrospective distortion-correction using r reduced σ̄ by an additional 11% relative to prospective correction only. There was no change in σ̄ with distortion correction for the in-plane case (images not shown), since pixel-shifts were minimal. This suggests that non-rigid-body image-distortion due to motion-induced B0 variations is a remaining source of signal variance that can be reduced using an appropriate distortion-correction algorithm.
Fig. 5.
a: Prospective correction with the rejection module enabled. A sample EPI-slice from a volunteer before (column 1) and after (column 2) a large, abrupt through-plane head-nod, with difference images shown (column 3). The example demonstrates a large rotational displacement θp and minimal intra-volume motion Δθp (the opposite of Fig. 2, row 2); matching slices with prospective correction ON (row 1: Iafter at θp = 6.11°, Δθp ~ 0°) and OFF (row 2: Iafter at θp = 6.33°, Δθp ~ 0°) are compared. The uncorrected slice (row 2) moving through the frontal sinus illustrates the extreme nature of the motion, while its position is maintained with correction (row 1). Residual error in the difference image is emphasized by white and black arrows at the corners of the brain that denote areas of positive and negative difference, respectively – this indicates an uncorrected non-rigid-body shear in the left-right phase-encode direction. b: Field maps illustrate the effective shim-change within the brain due to motion. Pixel-shift maps r of prospectively corrected images are shown after in-plane (column 1: Iafter at θs = 4.30°, Δθs = 1.11°) and through-plane (column 2: Iafter at θp = 5.38°, Δθp = 1.76°) rotations. Maps r were windowed so that the background gray-level = 0 mm pixel-shift, while white/black map to +3/−3 mm pixel-shifts. For the in-plane case, pixel-shifts in r did not exceed 0.5 mm. For the through-plane case, pixel-shifts of up to +3 mm and −1.5 mm were observed in the anterior and posterior regions, respectively. The difference image with prospective correction only (column 3) contains the same shear-like distortion in the anterior/posterior regions as present in Fig. 5a. When additional retrospective distortion-correction is applied (column 4), the shear-like artifact is significantly reduced.
DISCUSSION AND CONCLUSIONS
Active-marker tracking possesses several advantages over alternative prospective methods. Unlike the complex k-space trajectories used for 6-DOF navigator tracking, the well-defined geometry of the active markers requires only a series of short 1D-projections for accurate localization, followed by a computationally simple 3-point 3D-realignment algorithm. Optical tracking is limited by direct line-of-sight with the cameras; also, since active-marker tracking and imaging are done in the same magnet coordinate-system, no cross-calibration procedure is needed. Integration of active markers requires little additional hardware and is equivalent to adding three coils, something that modern multi-channel scanners easily accommodate. For scanners with a limited number of receive channels, techniques to use a channel for both imaging and active-marker tracking via fast switches are available. To further decouple tracking and imaging, individually shielded markers with designated transmit/receive chains may be employed (36).
Similar to navigator methods, a designated pulse-sequence is used for active-marker tracking, which adds to the scanner load. In the current work, 25 ms was added to the scan time per track-and-update iteration, which is on-par with the fastest (cloverleaf) navigator techniques; slice-by-slice corrections thus increased scan times by ~ 30%. Decreasing the tracking frequency, e.g., updating every 3 slices will increase times by only 10%. In sequences that contain long “dead times” for magnetization preparation, signal recovery, and/or echo formation, track-and-update modules may be inserted with little cost. For example, in single-slice arterial spin-labeling (ASL) corrections incorporated into the transit time between labeling and imaging will incur no time penalty. The optional rejection module, while adding to the scan time, improves the robustness of prospective correction during extreme motions (see Fig. 5a). In this case the time-frame corrupted by motion was rejected and reacquired; for applications such as fMRI where task-activations and scanning are synchronized, a flag should be set for every rejected time-frame to allow for timing adjustments in the post-processing analysis.
Its low phase-encode bandwidth makes EPI particularly sensitive to field inhomogeneities, which cause residual non-rigid image distortion that cannot be compensated for by either prospective or retrospective rigid-body correction. Field inhomogeneities can be considered as having a static component common to all volumes, and a time-varying component such as caused by changes in the effective shim within the brain as the head moves through the magnetic field (33,37). The latter manifests as a time-varying, shear-like distortion in the phase-encode direction and is clearly more noticeable during through-plane vs. in-plane motions, as expected from the field maps in Fig. 5b. Image stability was further improved when prospective rigid-body correction was followed by retrospective distortion-correction using the saved phase images, demonstrating the benefits of a combined solution. Note that this method only corrects for time-varying field inhomogeneities, as unwarping is performed relative to the first time-frame. To compensate for static inhomogeneities still present in all time-frames (i.e. unwarp to the “true geometry”), one more stage of unwarping may be performed on the time-series by using a single EPI-volume acquired with a different TE (35).
Other retrospective unwarping schemes face the challenge that distortions will be in different directions, depending on the current orientation of the head relative to the initially prescribed phase-encode direction. The approach presented here simplifies the distortion correction to only one dimension since the phase-encode direction prospectively tracks with the head orientation. Moreover, while other unwarping methods rely on field-map predictions (38) and/or susceptibility models of the imaged object (39), the presented method uses the measured phase information itself and requires only that the complex EPI-data is saved. Alternatively, field-map estimates (38) that are modified to incorporate marker tracking-information, as well as real-time shim-update strategies (13,40), may further improve these results. Note, however, that if coil arrays are used for multi-transmit/receive, the effects of head motion relative to the stationary coil elements must also be considered. For example, B1-inhomogeneities during RF-transmit may induce additional time-varying components in the phase images that will affect the distortion model, while change in coil sensitivity relative to the patient orientation during RF-receive will affect parallel imaging reconstruction (41). For our experiments at 1.5T with volume coils, these effects were negligible.
Image stability is critical in EPI-based applications. Motion-induced variation in the time-series data will reduce image stability, and, as a result, reduce sensitivity to signal changes induced by true brain activity. The current work demonstrates improved image stability that will potentially benefit the detection-sensitivity of diffusion, perfusion, and task-activated BOLD fMRI.
ACKNOWLEDGEMENTS
We thank Alex Dresner, Melanie Kotys, Fernando Arias-Mendoza, Robin Goldman, Congju Chen, Mohammad Reza Taei-Tehrani, Jianing Shi, Hamed Mojahed, Xiaowei Zou, Jack Grinband, Xian Zhang, Murat Aksoy, and Roland Bammer for their support.
Grant Sponsor:
NIH R21EB006877, NIH/NCRR UL1RR024156
List of Symbols
- θm, θp, θs
Greek italic lower case ‘theta’, subscript roman lower case ‘em’, ‘pee’, or ‘ess’
- Δθm, Δθp, Δθs
Greek upper case ‘delta’, Greek italic lower case ‘theta’, subscript roman lower case ‘em’, ‘pee’, or ‘ess’
- tm, tp, ts
Italic lower case ‘tee’, subscript roman lower case ‘em’, ‘pee’, or ‘ess’
- σ
Greek italic lower case ‘sigma’
- σ̄
Greek italic lower case ‘sigma-bar’
- Iafter
Bold roman upper case ‘eye’, subscript roman italic lower case ‘after’
- Ibefore
Bold roman upper case ‘eye’, subscript roman italic lower case ‘before’
- rn
Bold roman lower case ‘arr’, subscript roman lower case ‘en’
- Bn
Bold roman upper case ‘bee’, subscript roman lower case ‘en’
- BWpe
Roman upper case ‘bee’ and ‘double-u’, subscript roman lower case ‘pee’ and ‘ee’
- Φn
Bold greek upper case ‘phi’, subscript roman lower case ‘en’
- Φ1
Bold greek upper case ‘phi’, subscript roman ‘number one’
REFERENCES
- 1.Krings T, Reinges MH, Erberich S, Kemeny S, Rohde V, Spetzger U, Korinth M, Willmes K, Gilsbach JM, Thron A. Functional MRI for presurgical planning: problems, artefacts, and solution strategies. J Neurol Neurosurg Psychiatry. 2001;70(6):749–760. doi: 10.1136/jnnp.70.6.749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hajnal JV, Myers R, Oatridge A, Schwieso JE, Young IR, Bydder GM. Artifacts due to stimulus correlated motion in functional imaging of the brain. Magn Reson Med. 1994;31(3):283–291. doi: 10.1002/mrm.1910310307. [DOI] [PubMed] [Google Scholar]
- 3.Friston KJ, Williams S, Howard R, Frackowiak RS, Turner R. Movement-related effects in fMRI time-series. Magnetic Resonance in Medicine. 1996;35(3):346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- 4.Righini A, de Divitiis O, Prinster A, Spagnoli D, Appollonio I, Bello L, Scifo P, Tomei G, Villani R, Fazio F, Leonardi M. Functional MRI: primary motor cortex localization in patients with brain tumors. Journal of Computer Assisted Tomography. 1996;20(5):702–708. doi: 10.1097/00004728-199609000-00003. [DOI] [PubMed] [Google Scholar]
- 5.Steger TR, Jackson EF. Real-time motion detection of functional MRI data. J Appl Clin Med Phys. 2004;5(2):64–70. doi: 10.1120/jacmp.v5i2.1969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ardekani BA, Bachman AH, Helpern JA. A quantitative comparison of motion detection algorithms in fMRI. Magnetic Resonance Imaging. 2001;19(7):959–963. doi: 10.1016/s0730-725x(01)00418-0. [DOI] [PubMed] [Google Scholar]
- 7.Freire L, Mangin JF. Motion correction algorithms may create spurious brain activations in the absence of subject motion. Neuroimage. 2001;14(3):709–722. doi: 10.1006/nimg.2001.0869. [DOI] [PubMed] [Google Scholar]
- 8.Thesen S, Heid O, Mueller E, Schad LR. Prospective acquisition correction for head motion with image-based tracking for real-time fMRI. Magnetic Resonance in Medicine. 2000;44(3):457–465. doi: 10.1002/1522-2594(200009)44:3<457::aid-mrm17>3.0.co;2-r. [DOI] [PubMed] [Google Scholar]
- 9.Ehman RL, Felmlee JP. Adaptive technique for high-definition MR imaging of moving structures. Radiology. 1989;173(1):255–263. doi: 10.1148/radiology.173.1.2781017. [DOI] [PubMed] [Google Scholar]
- 10.Pipe JG. Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magnetic Resonance in Medicine. 1999;42(5):963–969. doi: 10.1002/(sici)1522-2594(199911)42:5<963::aid-mrm17>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- 11.Ward HA, Riederer SJ, Grimm RC, Ehman RL, Felmlee JP, Jack CR., Jr. Prospective multiaxial motion correction for fMRI. Magnetic Resonance in Medicine. 2000;43(3):459–469. doi: 10.1002/(sici)1522-2594(200003)43:3<459::aid-mrm19>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
- 12.Welch EB, Manduca A, Grimm RC, Ward HA, Jack CR., Jr. Spherical navigator echoes for full 3D rigid body motion measurement in MRI. Magnetic Resonance in Medicine. 2002;47(1):32–41. doi: 10.1002/mrm.10012. [DOI] [PubMed] [Google Scholar]
- 13.van der Kouwe AJW, Benner T, Dale AM. Real-time rigid body motion correction and shimming using cloverleaf navigators. Magnetic Resonance in Medicine. 2006;56(5):1019–1032. doi: 10.1002/mrm.21038. [DOI] [PubMed] [Google Scholar]
- 14.White N, Roddey C, Shankaranarayanan A, Han E, Rettmann D, Santos J, Kuperman J, Dale A. PROMO: Real-time prospective motion correction in MRI using image-based tracking. Magn Reson Med. 2010;63(1):91–105. doi: 10.1002/mrm.22176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zaitsev M, Dold C, Sakas G, Hennig J, Speck O. Magnetic Resonance Imaging of Freely Moving Objects: Prospective Real-time Motion Correction Using an External Optical Motion Tracking System. NEUROIMAGE. 2006;31(3):1038–1050. doi: 10.1016/j.neuroimage.2006.01.039. [DOI] [PubMed] [Google Scholar]
- 16.Speck O, Hennig J, Zaitsev M. Prospective real-time slice-by-slice motion correction for fMRI in freely moving subjects. MAGMA. 2006;19(2):55–61. doi: 10.1007/s10334-006-0027-1. [DOI] [PubMed] [Google Scholar]
- 17.Aksoy M, Newbould R, Straka M, Holdsworth S, Skare S, Santos J, Bammer R. A Real Time Optical Motion Correction System Using a Single Camera and 2D Marker; Proceedings of the 16th Annual Meeting of ISMRM; Toronto, ON, Canada. 2008. p. 3120. [Google Scholar]
- 18.Qin L, van Gelderen P, Derbyshire JA, Jin F, Lee J, de Zwart JA, Tao Y, Duyn JH. Prospective head-movement correction for high-resolution MRI using an in-bore optical tracking system. Magn Reson Med. 2009;62(4):924–934. doi: 10.1002/mrm.22076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Forman C, Aksoy M, Hornegger J, Bammer R. Self-encoded marker for optical prospective head motion correction in MRI. Med Image Comput Comput Assist Interv. 2010;13(Pt 1):259–266. doi: 10.1007/978-3-642-15705-9_32. [DOI] [PubMed] [Google Scholar]
- 20.Ackerman JL, Offutt MC, Buxton RB, Brady TJ. Rapid 3D Tracking of Small RF Coils; Proceedings of the 5th Annual Meeting of SMRM; Montreal, QC, Canada. 1986. pp. 1131–1132. [Google Scholar]
- 21.Dumoulin CL, Souza SP, Darrow RD. Real-time position monitoring of invasive devices using magnetic resonance. Magnetic Resonance in Medicine. 1993;29(3):411–415. doi: 10.1002/mrm.1910290322. [DOI] [PubMed] [Google Scholar]
- 22.Zhang Q, Wendt M, Aschoff AJ, Zheng L, Lewin JS, Duerk JL. Active MR guidance of interventional devices with target-navigation. Magnetic Resonance in Medicine. 2000;44(1):56–65. doi: 10.1002/1522-2594(200007)44:1<56::aid-mrm10>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- 23.Flask C, Elgort D, Wong E, Shankaranarayanan A, Lewin J, Wendt M, Duerk JL. A method for fast 3D tracking using tuned fiducial markers and a limited projection reconstruction FISP (LPR-FISP) sequence. J Magn Reson Imaging. 2001;14(5):617–627. doi: 10.1002/jmri.1227. [DOI] [PubMed] [Google Scholar]
- 24.Elgort DR, Wong EY, Hillenbrand CM, Wacker FK, Lewin JS, Duerk JL. Real-time catheter tracking and adaptive imaging. Journal of Magnetic Resonance Imaging. 2003;18(5):621–626. doi: 10.1002/jmri.10402. [DOI] [PubMed] [Google Scholar]
- 25.Krueger S, Wolff S, Schmitgen A, Timinger H, Bublat M, Schaeffter T, Nabavi A. Fast and accurate automatic registration for MR-guided procedures using active microcoils. IEEE Trans Med Imaging. 2007;26(3):385–392. doi: 10.1109/TMI.2006.889748. [DOI] [PubMed] [Google Scholar]
- 26.Derbyshire JA, Wright GA, Henkelman RM, Hinks RS. Dynamic scan-plane tracking using MR position monitoring. Journal of Magnetic Resonance Imaging. 1998;8(4):924–932. doi: 10.1002/jmri.1880080423. [DOI] [PubMed] [Google Scholar]
- 27.Krueger S, Schaeffter T, Weiss S, Nehrke K, Rozijn T, Boernert P. Prospective Intra-Image Compensation for Non-Periodic Rigid Body Motion Using Active Markers.; Proceedings of the 14th Annual Meeting of ISMRM; Seattle, WA, USA. 2006. p. 3196. [Google Scholar]
- 28.Ooi MB, Krueger S, Thomas W, Swaminathan SV, Brown TR. Prospective Motion Correction via Real-Time Active Marker Tracking: An Image Quality Assessment; Proceedings of the 16th Annual Meeting of ISMRM; Toronto, ON, Canada. 2008. p. 209. [Google Scholar]
- 29.Ooi MB, Krueger S, Thomas WJ, Swaminathan SV, Brown TR. Prospective real-time correction for arbitrary head motion using active markers. Magn Reson Med. 2009;62(4):943–954. doi: 10.1002/mrm.22082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ooi MB, Krueger S, Thomas W, Brown TR. Real-Time Intra-Volume Motion Correction in EPI Using Active Markers; Proceedings of the 18th Annual Meeting of ISMRM; Stockholm, Sweden. 2010. p. 5038. [Google Scholar]
- 31.Umeyama S. Least-squares estimation of transformation parameters between two point patterns. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1991;13(4):376–380. [Google Scholar]
- 32.Tzourio-Mazoyer N, Landeau B, Papathanassiou D, Crivello F, Etard O, Delcroix N, Mazoyer B, Joliot M. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single-subject brain. Neuroimage. 2002;15(1):273–289. doi: 10.1006/nimg.2001.0978. [DOI] [PubMed] [Google Scholar]
- 33.Jezzard P, Clare S. Sources of distortion in functional MRI data. Hum Brain Mapp. 1999;8(2-3):80–85. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<80::AID-HBM2>3.0.CO;2-C. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jenkinson M. Fast, automated, N-dimensional phase-unwrapping algorithm. Magn Reson Med. 2003;49(1):193–197. doi: 10.1002/mrm.10354. [DOI] [PubMed] [Google Scholar]
- 35.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. 1995;34(1):65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 36.Barmet C, De Zanche N, Wilm BJ, Pruessmann KP. A transmit/receive system for magnetic field monitoring of in vivo MRI. Magn Reson Med. 2009;62(1):269–276. doi: 10.1002/mrm.21996. [DOI] [PubMed] [Google Scholar]
- 37.Hutton C, Bork A, Josephs O, Deichmann R, Ashburner J, Turner R. Image distortion correction in fMRI: A quantitative evaluation. Neuroimage. 2002;16(1):217–240. doi: 10.1006/nimg.2001.1054. [DOI] [PubMed] [Google Scholar]
- 38.Andersson JL, Hutton C, Ashburner J, Turner R, Friston K. Modeling geometric deformations in EPI time series. Neuroimage. 2001;13(5):903–919. doi: 10.1006/nimg.2001.0746. [DOI] [PubMed] [Google Scholar]
- 39.Boegle R, Maclaren J, Zaitsev M. Combining prospective motion correction and distortion correction for EPI: towards a comprehensive correction of motion and susceptibility-induced artifacts. MAGMA. 2010;23(4):263–273. doi: 10.1007/s10334-010-0225-8. [DOI] [PubMed] [Google Scholar]
- 40.Ward HA, Riederer SJ, Jack CR., Jr. Real-time autoshimming for echo planar timecourse imaging. Magn Reson Med. 2002;48(5):771–780. doi: 10.1002/mrm.10259. [DOI] [PubMed] [Google Scholar]
- 41.Bammer R, Aksoy M, Liu C. Augmented generalized SENSE reconstruction to correct for rigid body motion. Magn Reson Med. 2007;57(1):90–102. doi: 10.1002/mrm.21106. [DOI] [PMC free article] [PubMed] [Google Scholar]