Abstract
Pseudomonas aeruginosa pneumonia remains a most-difficult-to-treat nosocomial bacterial infection. We used mathematical modeling to identify drug exposure targets for meropenem in the epithelial lining fluid (ELF) of mice with Pseudomonas pneumonia driving substantial [2 to 3 log10 (CFU/g)] killing and which suppressed resistant subpopulation amplification. We bridged to humans to estimate the frequency with which the largest licensed meropenem dose would achieve these exposure targets. Cell kills of 2 and 3 log10 (CFU/g) and resistant subpopulation suppression were mediated by achieving time > MIC in ELF of 32%, 50%, and 50%. Substantial variability in meropenem's ability to penetrate into ELF of both mice and humans was observed. Penetration variability and high exposure targets combined to prevent even the largest licensed meropenem dose from achieving the targets at an acceptable frequency. Even a highly potent agent such as meropenem does not adequately suppress resistant subpopulation amplification as single-agent therapy administered at maximal dose and optimal schedule. Combination chemotherapy is likely required in humans if we are to minimize resistance emergence in Pseudomonas aeruginosa pneumonia. This combination needs evaluation both in the murine pneumonia model and in humans.
INTRODUCTION
Pseudomonas aeruginosa pneumonia remains one of the most intractable infections with which the clinician is faced. Partly this is because of the causative pathogen. Pseudomonas aeruginosa is heir to a plethora of resistance mechanisms that allow it to escape the bactericidal effects of many, if not all, of our antimicrobial agents. The second issue is the sort of patient that is stricken with Pseudomonas aeruginosa pneumonia. Often, such patients are not immunity “normal” and also have insults such as plastic catheters that transgress anatomical boundaries. All these factors make Pseudomonas pneumonia among the most challenging infections to successfully treat.
In this evaluation, we will focus on the microbiological issues as well as the pharmacological issues that have an impact on the cell kill and ability to suppress resistant subpopulation amplification seen in a murine model of Pseudomonas aeruginosa pneumonia treated with the carbapenem meropenem. Specifically, we will examine the penetration of meropenem into mouse epithelial lining fluid (ELF) and also determine its variability. We will link this ELF exposure to the ability to kill the pathogen in the lung and suppress resistant mutant subpopulation amplification. This will allow delineation of exposure targets in murine ELF that will accomplish these aims.
Finally, we will examine meropenem penetration into ELF in patients being treated for ventilator-associated pneumonia (VAP). We propose that the variability associated with this penetration will doom the prospects of treating VAP patients infected with Pseudomonas aeruginosa with a high likelihood of success, not because of resistance mechanisms (we have identified an exposure to suppress amplification of resistant mutants) but, rather, because of the variability of penetration of meropenem into ELF in VAP patients. As part of this, we will propose that combination therapy, in this case meropenem plus tobramycin, will allow patients to be successfully treated, achieving excellent log kill as well as suppressing emergence of resistant cell populations.
MATERIALS AND METHODS
Microorganism.
Pseudomonas aeruginosa strain PAO1 was a kind gift of Karen Bush. MIC determination was by CLSI macrobroth methodology for meropenem (2). Mutational frequency to resistance was estimated by plating 1 ml of serial dilutions of strain PAO1 cultures grown overnight on agar without antibiotic and agar containing 3× the baseline MIC of meropenem. The ratio of the two determinations provided the estimate of the mutational frequency to resistance. This estimation was performed on at least three occasions.
Murine pneumonia model.
All animal experimentation was approved by the local institutional animal care and use committee (IACUC). The mouse pneumonia model previously described by Du et al. (7) was used. Female, 24- to 26-g, outbred Swiss-Webster mice (Taconic Farms, Taconic, NY) were provided water and food ad libitum. Mice were rendered transiently neutropenic with 150 mg/kg body weight cyclophosphamide given intraperitoneally (i.p.) 4 days prior to infection plus 100 mg/kg given i.p. 1 day before infection. Anesthetized mice were infected via the intranasal route with a 20-μl volume using 2 × 107 CFU of P. aeruginosa. The bacterial inoculum density was confirmed by quantitative cultures. Five hours after bacterial inoculation, and just prior to therapy initiation, five mice were sacrificed for baseline quantitative cultures of lung homogenates. Five animal cohorts were administered meropenem i.p. at doses of 50, 100, 150, 200, 300, and 450 mg/kg every 4 h for cell kill and resistance suppression studies. Twenty-four hours after treatment initiation, all mice were humanely sacrificed and lungs were aseptically collected. The tissues were homogenized and washed with normal saline to prevent drug carryover. Homogenates were then quantitatively cultured on drug-free agar plates. After incubation of the plates at 35°C for 48 h, colonies were enumerated. For drug-containing plates, colonies were enumerated at 48 h also. We generally wait for 72 h to evaluate drug-containing plates. However, preliminary studies demonstrated meropenem instability in agar at incubator temperatures. Means and standard deviations for the quantitative culture samples were calculated. Estimates of resistant organism numbers were determined by quantitatively plating an aliquot of each homogenate of lung tissue onto plates containing 3× the baseline MIC of meropenem.
Pharmacokinetic studies.
To correlate the doses of drug administered to mice with measures of exposure, single-dose pharmacokinetic studies were conducted in mice with Pseudomonas aeruginosa pneumonia (it should be noted that the pharmacokinetic evaluation took place in a different cohort of mice than the group used for evaluation of microbiological effect). Neutropenic mice were infected via the intranasal route (see above). Single doses of meropenem (doses of 2.4 to 150 mg/kg) were given to four groups of mice 5 h after they were inoculated with P. aeruginosa. Pharmacokinetics in plasma and ELF were determined with 11 sampling times (2 to 3 mice per time point) between 0 and 5 h after an i.p. dose. At time points between 0 and 5 h after i.p. dosing of meropenem, blood was collected by cardiac puncture and allowed to clot on ice. The plasma obtained by centrifugation was stored at −80°C. Bronchoalveolar lavage (BAL) fluid was simultaneously obtained by instilling 0.6 ml of water into lungs and removing 0.6 ml of water from the lungs twice. Plasma and BAL fluid were stored at −80°C until they were assayed for drug content by liquid chromatography (LC) and dual mass spectrometry (MS-MS). The prediluted concentration of antibiotic in the BAL fluid was calculated by comparing the difference in amounts of urea measured in simultaneously collected plasma and BAL fluid.
Meropenem assay.
Mouse plasma samples (0.050 ml) were deproteinated with acetonitrile (0.150 ml). The samples were centrifuged, and an aliquot of the supernatant (0.050 ml) was transferred into an appropriately labeled autosampler vial containing 1.00 ml of high-pressure liquid chromatography (HPLC) water. Samples were analyzed by high-pressure liquid chromatography-tandem mass spectrometry for meropenem concentrations.
Mouse BAL fluid samples (0.050 ml) were diluted with 0.100 ml of HPLC water and were also analyzed by high-pressure liquid chromatography-tandem mass spectrometry for meropenem concentrations. The LC/MS-MS system was comprised of a Shimadzu Prominence HPLC system and an Applied Biosystems/MDS Sciex API5000 LC/MS-MS.
Chromatographic separation was performed using a Thermo Scientific Hypersil Gold column (5 μm, 150 by 4.6 mm) and a mobile phase consisting of 85:15 0.1% formic acid in water:methanol at a flow rate of 0.75 ml/min.
Meropenem concentrations were obtained using LC/MS-MS monitoring the MS-MS transition m/z 384 → m/z 141. Analysis run time was 4.5 min. The assay was linear over a range of 0.005 to 10 μg/ml (r2 > 0.993) for meropenem in mouse plasma and a range of 0.10 to 200 ng/ml (r2 > 0.994) for meropenem in mouse BAL fluid. The interday coefficients of variation (CVs) for the quality control samples, containing meropenem analyzed in replicates of three at three concentrations on each analysis day, ranged from 0.543 to 4.29% for meropenem in mouse plasma and 1.87 to 5.08% for meropenem in BAL fluid. Accuracies (%REC) for these same quality control samples ranged between 92.7% and 103% for meropenem in mouse plasma and between 96.9 and 102% for meropenem in BAL fluid.
Urea assay.
The assay of urea in murine plasma and ELF was performed by employing the BioAssay Systems QuantiChrom urea assay kit (DIUR-500). The kit was purchased from BioAssay Systems (Hayward, CA). The standard curve was linear from 3.1 mg/dl to 50 mg/dl (r2 = 0.999). Within-day CV values were 1.0% at 3.1 mg/dl and 1.1% at 50 mg/dl.
Population modeling approach.
For the population modeling approach, the ELF was its own sampling compartment with its own apparent volume of distribution. It required 17 parameters, five differential equations, and four system outputs [drug concentration in plasma, drug concentration in ELF, log10 (total number of organisms in lung) and log10 (number of meropenem-resistant organisms in the lung)] to define this system:
The plasma concentration equals X2/(Vc/F), the ELF concentration equals X3/VELF, total lung colony counts equal log10(X4) and meropenem-resistant lung colony counts equal log10(X5). Ka is the absorption rate constant, as meropenem was administered via i.p. injection; CL/F is plasma clearance, where F is the bioavailability of the i.p. dose; Vc/F is the apparent volume of the central compartment, where F is the bioavailability of the i.p. dose; K23 and K32 are first-order intercompartmental transfer rate constants; VELF is the apparent volume of the ELF compartment; Kgrowth-s and Kgrowth-r are the first-order growth constants of sensitive and resistant organisms, respectively; POPMAX is the maximal organism concentration (CFU/g) at stationary phase; Kkill-max-s and Kkill-max-r are the maximal kill rate constants for the sensitive and meropenem-resistant organisms, respectively, and are driven by drug concentration; EC50-s and EC50-r are the drug concentrations at which the organism kill rate is half-maximal for sensitive and meropenem-resistant strains, respectively; H-s and H-r are Hill's constants for sensitive and meropenem-resistant organisms, respectively. Not shown are two parameters, IC4 and IC5, which are the initial conditions for the last two differential equations and represent the number of meropenem-susceptible and meropenem-resistant organisms present at baseline, respectively.
The BigNPAG program described previously by Leary et al. (10) was employed for all population modeling. The weighting employed was the inverse of the between-day assay error variance. Bayesian estimates were obtained for each mouse using the “population-of-one” utility in BigNPAG. Model evaluation was performed by predicted-observed plots. The mean error served as the measure of bias. The bias-adjusted mean squared error served as the measure of precision. Separate cohorts of animals were studied for pharmacokinetics (plasma and ELF concentrations) and drug effects (colony counts in lung).
Lung colony counts were linked to the total drug ELF time > MIC through simulation from the identified system parameters (see above). The ELF time > MIC driving 2 and 3 log10 (CFU/g) kills from the static exposure as well as the exposure required to hold the number of resistant colonies at or below the baseline level was calculated.
Bridging to humans.
We generated a 9,999-subject Monte Carlo simulation for the meropenem concentration-time profile in plasma and ELF using a 2,000-mg dose administered over a 3-h intravenous infusion. The mean parameter vector and full covariance matrix from clinical data were embedded in Subroutine PRIOR of the ADAPT II package of programs described previously by D'Argenio and Schumitzky (3). Both normal and log-normal distributions were evaluated and discriminated by the fidelity with which the measures of central tendency and dispersion were recreated by simulation. From this, the distribution of the time > MIC in ELF was calculated, and the target attainments were calculated for 2 and 3 log10 (CFU/g) kills as well as resistance suppression by employing the program SYSTAT for Windows (version 11.0).
RESULTS
MIC and mutational frequency to resistance of meropenem for Pseudomonas aeruginosa PAO1.
On six different occasions, broth microdilution was performed, and the MIC of meropenem for Pseudomonas aeruginosa ranged from 0.5 to 1.0 mg/liter. The mutational frequency to resistance was 1/(3.72 × 107) at 3× MIC.
Fit of the model to all the data simultaneously.
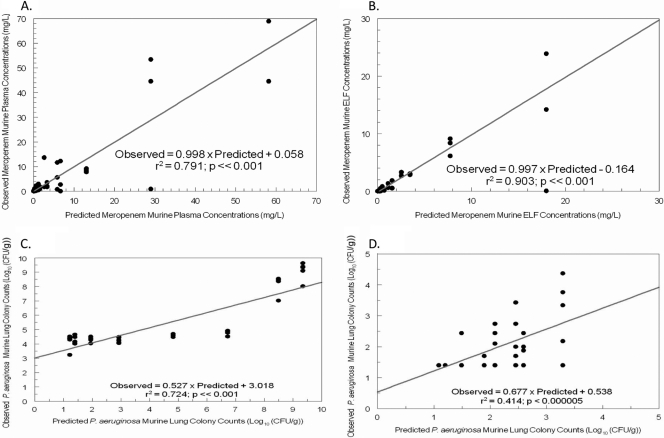
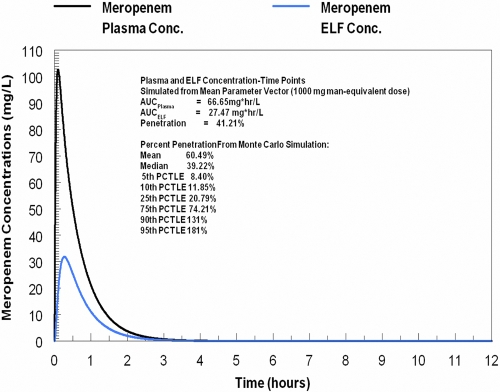
The model fit the data quite well. For each of the four outputs, the predicted-observed plots prior to the Bayesian step are displayed in Fig. 1. These demonstrate that, even with the mean parameter vector, the simulations drive through the center mass of the data. For the post-Bayesian step regressions, the regression equations are shown in Table 1 and are quite acceptable. The mean and median parameter estimates and their standard deviations are displayed in Table 2. These values, along with the covariance matrix, were employed to generate a 9,999-subject Monte Carlo simulation. The mean plasma and ELF curves are displayed, along with the distribution AUC values and their ratio (which gives penetration) in Fig. 2. It is important to note the broad range of penetration, with the 25th-to-75th-percentile range of penetration being 20.8% to 74.2% and the median penetration being 39.2%.
Fig. 1.
Fit of the model to the data (pre-Bayesian step) for all four system outputs. (A) Plasma data. (B) ELF data. (C) Total bacterial population. (D) Meropenem-resistant population.
Table 1.
Observed-predicted regression equations for the system outputs after the Bayesian estimation step for the murine model
| System output | Regression resulta |
||
|---|---|---|---|
| Slope | Intercept | r2 | |
| Meropenem plasma concn | 0.980 | +0.164 | 0.995 |
| Meropenem ELF concn | 0.960 | +0.025 | 0.997 |
| Total bacterial counts | 0.883 | +0.638 | 0.914 |
| Meropenem-resistant bacterial counts | 0.776 | +0.464 | 0.801 |
Observed = slope × output + intercept, where output is one of meropenem concentration in plasma or ELF or total bacterial population counts or drug-resistant population counts.
Table 2.
Parameter estimates from the population pharmacokinetic/dynamic analysis from the murine pneumonia model with Pseudomonas aeruginosa PAO1 as the infecting pathogen
| Parametera | Mean | Median | SD |
|---|---|---|---|
| Vc/F (liters) | 0.00879 | 0.00880 | 0.00266 |
| CL/F (liters/h) | 0.0198 | 0.0179 | 0.00549 |
| K12 (h−1) | 1.13 | 0.992 | 0.443 |
| K21 (h−1) | 5.10 | 5.35 | 1.46 |
| VELF (liters) | 0.00508 | 0.00541 | 0.00268 |
| Ka (h−1) | 19.5 | 18.1 | 7.92 |
| Kgmax-s (h−1) | 0.952 | 0.711 | 0.478 |
| Kkillmax-s (h−1) | 1.86 | 1.70 | 0.745 |
| C50k-s (mg/liter) | 2.08 | 1.65 | 1.25 |
| Hk-s | 17.7 | 19.0 | 4.50 |
| POPMAX (CFU/g) | 1.96 × 109 | 2.21 × 109 | 1.30 × 109 |
| Kgmax-r (h−1) | 0.307 | 0.309 | 0.179 |
| Kkillmax-r (h−1) | 0.498 | 0.605 | 0.252 |
| C50k-r (mg/liter) | 5.38 | 5.57 | 2.75 |
| Hk-r | 20.9 | 20.4 | 5.52 |
| IC4 (CFU/g) | 3.46 × 108 | 4.27 × 108 | 1.59 × 108 |
| IC5 (CFU/g) | 131 | 244 | 98 |
Vc/F, volume of the central compartment; CL/F, plasma clearance; K12, K21, first order intercompartmental transfer rate constants; VELF, volume of the ELF compartment; Ka, first order absorption rate constant; Kgmax-s and Kgmax-r, first order growth rate constants for the susceptible and resistant subpopulations; Kkillmax-s and Kkillmax-r, first order kill rate constants for the susceptible and resistant subpopulations; C50k-s and C50k-r, drug concentration at which the kill rate is half maximal; Hk-s and Hk-r, Hill's constants for the susceptible and resistant subpopulations; POPMAX, maximal population density; IC4 and IC5, initial densities of total pathogens and resistant pathogens.
Fig. 2.
Penetration of meropenem into murine lung infected with Pseudomonas aeruginosa PAO1.
Cell kill and emergence of resistance.
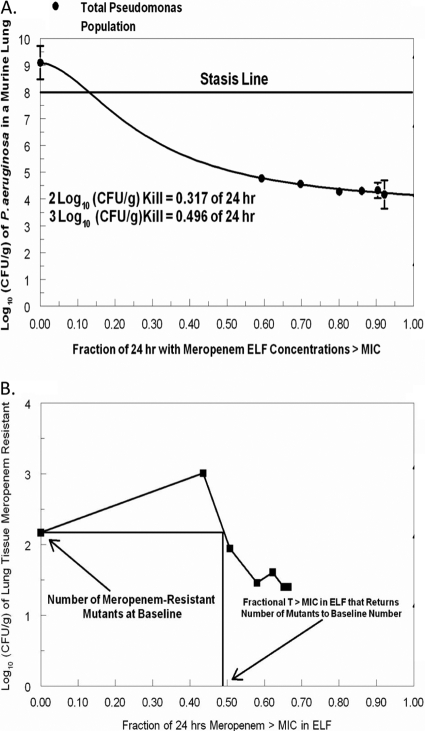
We employed simulation using the parameter values shown in Table 2 and their Bayesian posterior estimates to calculate exposure targets in ELF resulting in 2 log10 (CFU/g) cell kill, 3 log10 (CFU/g) cell kill, and the exposure required to suppress resistance. These are shown in Fig. 3A and B. The exposure targets were 31.7%, 49.6%, and 49.8% of the dosing interval in which meropenem concentrations exceeded the MIC in ELF, respectively, for the three endpoints. It should be noted that the exposure target for the 2 log10 (CFU/g) cell kill is lower than the range actually tested, so that this value must be viewed with some skepticism.
Fig. 3.
Exposure-effect curve for meropenem and Pseudomonas aeruginosa reconstructed from the model parameters. (A) Cell kill targets. (B) Resistance suppression target.
Bridging to humans.
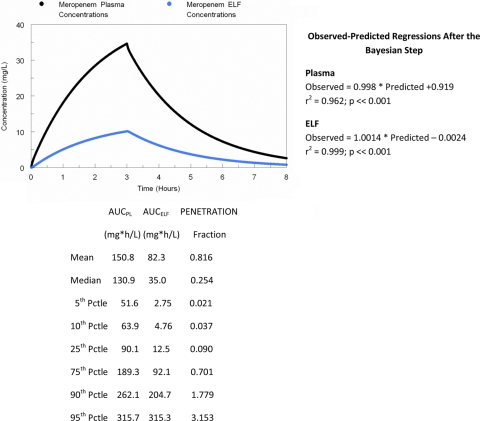
In order to optimally bridge to the therapy of Pseudomonas aeruginosa pneumonia in humans, it is optimal to examine the penetration of the drug in question into ELF in infected patients. We employed a data set available to us previously (12). We conducted a 9,999-subject Monte Carlo simulation from the parameter values displayed in Table 3. The penetration, as calculated from the median parameter vector and its distribution, is displayed in Fig. 4. A 2,000-mg meropenem dose administered as a 3-h infusion was simulated.
Table 3.
Parameter estimates from the population pharmacokinetic analysis from 39 patients with ventilator-associated pneumonia
| Parametera | Vc (liters) | CL (liters/h) | K12 (h−1) | K21 (h−1) | K13 (h−1) | K31 (h−1) | VELF (liters) |
|---|---|---|---|---|---|---|---|
| Mean | 12.6 | 15.2 | 8.32 | 14.1 | 10.1 | 14.2 | 30.4 |
| Median | 6.68 | 13.5 | 3.15 | 11.2 | 8.02 | 15.4 | 24.2 |
| SD | 13.3 | 9.71 | 9.82 | 11.8 | 8.63 | 11.4 | 25.2 |
Vc, volume of the central compartment; CL, plasma clearance; K12, K21, K13, K31, first order intercompartmental transfer rate constants; VELF, volume of the ELF compartment.
Fig. 4.
Penetration of meropenem into epithelial lining fluid (ELF) in 39 patients with ventilator-associated pneumonia. All patient pathogens were recovered in a bronchoalveolar lavage at baseline with more than 104 CFU/ml. A 9,999-subject Monte Carlo simulation was performed to examine variability in penetration.
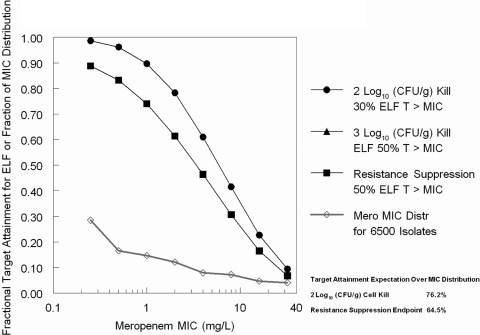
We then employed the targets developed in the murine model to ascertain how well the largest licensed dose of meropenem, administered in a fashion to optimize time > MIC in ELF, would attain these targets, especially the target of suppression of resistant mutant subpopulation amplification. The results are displayed in Fig. 5. Even at 0.25 mg/liter, the achievement of the 3 log10 (CFU/g) cell kill target and resistance suppression target are both below 90% and are less than 75% at an MIC of 1.0 mg/liter. Since most of a Pseudomonas aeruginosa meropenem MIC distribution is greater than 0.25 mg/liter, this result is suboptimal. We used a previously published (12) 6,500-isolate MIC distribution of meropenem for Pseudomonas aeruginosa to take a target expectation for the 2 log10 (CFU/g) target and the resistance suppression target (the latter also being the 3 log kill target). These overall target expectations were 76.2% and 64.5%, respectively.
Fig. 5.
Target attainment of a 2,000-mg meropenem dose administered as a 3-hour infusion for both cell kill targets and resistance suppression targets. The 3 log10 (CFU/g) cell kill marker lies directly under the resistance suppression target marker.
DISCUSSION
We are in a crisis of resistance in which many pathogens are untreatable with current antimicrobials. Over the last 5 to 7 years, we have learned a great deal about the relationship of exposure and microbiological response and, especially, exposure intensity and the likelihood that resistant subpopulation amplification will or will not occur with single-agent therapy (9, 17, 18).
Part of the puzzle of suppressing amplification of resistant subpopulations is recognizing that organisms differ in their mutational frequency to resistance. Indeed, hypermutator phenotypes have been described (15), where frequencies to resistance may increase by more than 100-fold.
The other major issue is the site of infection. While some sites are privileged (e.g., eye, CSF, prostate) because of tight junctions, rendering drug penetration more difficult, it is also true that the majority of infections at these sites do not have large bacterial burdens. In contrast, infections such as VAP can have very large burdens, particularly in patients with multilobar involvement. The large bacterial burden means that whatever the mutational frequency to resistance is for the infecting pathogen, there will be a substantial burden of less-susceptible organisms present at baseline. Consequently, it is not a surprise that studies of hospital-acquired pneumonia (HAP) and VAP have demonstrated that emergence of resistance with Pseudomonas aeruginosa has occurred during therapy with probabilities of 33 to 50%, even with potent agents, such as carbapenems and fluoroquinolones such as ciprofloxacin (1, 8).
In these experiments, we wished to examine meropenem as a single agent against Pseudomonas aeruginosa in a murine pneumonia model. The goal was to identify the penetration of meropenem into murine ELF from plasma and to link the drug exposure in ELF to both microbiological effect and suppression of resistance.
We fit a 17-parameter, five-differential-equation system to all four system outputs (meropenem concentration in plasma and ELF, total organism burden, less-susceptible organism burden) simultaneously. As demonstrated in Fig. 1 and Table 1, the fit of the model to the data was quite acceptable. Even the pre-Bayesian observed-predicted plots demonstrated that the regressions drove through the center mass of the data. After the Bayesian step, the observed-predicted regressions (Table 1) were excellent, with all coefficients of determination (r2) exceeding 0.8.
The model parameters in Table 2 were employed in a Monte Carlo simulation. This simulation allowed us to identify the penetration into ELF and, as importantly, the variability of meropenem penetration into infected ELF. The meropenem concentration-time curves for plasma and ELF (Fig. 2) were derived from the mean parameter vector and demonstrate that in this circumstance, penetration was approximately 40%, with the median penetration from the Monte Carlo simulation being 39%. It is important to note the variability of the penetration, with the 10th percentile being 12% penetration while the 90th percentile was 131%.
The model parameters were also employed to reconstruct a traditional exposure-response curve for microbiological effect and to identify the exposure needed to suppress resistance. It is important to emphasize that the exposure modeled was that at the primary infection site, the ELF. Figure 3A shows the ELF meropenem exposures required for 2 log10 (CFU/g) and 3 log10 (CFU/g) bacterial cell kill. The time > MIC in ELF associated with these effects is 32% of the dosing interval and 50% of the dosing interval, respectively. For resistance suppression, the required ELF exposure was 50% (Fig. 3B).
These exposures can then serve as a target for the use of meropenem in humans in patients with Pseudomonas aeruginosa VAP. This allows direct bridging to humans. We had previously studied 39 patients with VAP receiving meropenem (12). Samples of plasma (39 patients) and ELF (17 patients) were obtained and population modeled with an approach quite similar to that employed in the mouse model (Table 3). The fit of the model to the data was quite acceptable for both plasma and ELF, as shown in Fig. 4, which also demonstrates that the penetration of meropenem into ELF was quite variable, exactly as seen in the infected mouse. The median penetration from a 9,999-subject Monte Carlo simulation was 25%, while the 10th to 90th percentiles ranged from 4% penetration to 178% penetration. The variability of penetration in human is marginally greater than that in mouse, but it should be noted that the median murine penetration into infected ELF was 39%, while in humans the 60th percentile of penetration was 37%. Consequently, the penetration into infected ELF was similar in mouse and human.
The variability of penetration is a central issue regarding the adequacy of single drug therapy of Pseudomonas aeruginosa VAP. We employed the cell kill exposure targets in ELF and performed another Monte Carlo simulation to examine the rate of target attainment. In this, we employed the largest licensed dose of meropenem (2 g) and administered it as a prolonged infusion, as this (prolonged infusion) has been demonstrated to improve outcome in patients seriously infected with Pseudomonas (6, 11, 13). From Fig. 5, we can see that the target attainment for a 2 log10 (CFU/g) cell kill is less than 80% at an MIC value of 2 mg/liter, while the 3 log10 (CFU/g) cell kill and for resistance suppression, the target attainments are less than 90% at an MIC value of 0.25 mg/liter and less than 75% at 1.0 mg/liter. These are clearly suboptimal. Finally, the expected target attainment over the entire meropenem MIC distribution for Pseudomonas aeruginosa is slightly less than two-thirds at 64.5%, which puts the inadequacy of the maximal regimen into proper perspective.
As part of learning about defining exposures to suppress resistant subpopulation amplification, we also learned that this endpoint is different in kind from microbiological effect. For the latter, the effect curve is monotonic, with more drug exposure mediating a greater cell kill, up to a maximal value. However, for resistance suppression our laboratory has noted that the form of the effect curve is nonmonotonic and is, indeed, an “inverted U” (16). Very low exposures have little effect in amplifying resistant subpopulations. Intermediate exposures give the greatest amplification of resistant subpopulations. Only at very large exposures do we gain control of resistant subpopulation amplification (9, 17, 18). The inadequacy of single-agent therapy of Pseudomonas aeruginosa in VAP is then explained by having a large resistant population at baseline because of the large bacterial burden overall in VAP, requiring quite extensive drug exposure in the effect site (ELF), and finally, the variability. If the variability were small, our ability to find a nontoxic drug exposure that would suppress resistance in a large fraction (>90%) of the population would be good. Because of the variability, the drug dose has to get quite large before 90% of the population can have target attainment for resistance suppression and, for meropenem, as for all other antipseudomonal agents of which we are aware, would exceed the highest licensed dose.
Given the inadequacy of single-agent therapy for Pseudomonas aeruginosa VAP, it is clear that combination-agent therapy or administration of an agent directly into the lung will be required to attain the desired outcome of good cell kill accompanied by emergence of resistance. We have seen this interaction before in previous publications, with both meropenem plus tobramycin in vitro in static kill assays (5) as well as meropenem plus levofloxacin in our hollow-fiber infection model (14).
As indicated above, HAP/VAP trials with monotherapy with carbapenems or ciprofloxacin have resulted in 33 to 50% resistance emergence in Pseudomonas aeruginosa during single-agent therapy. The exception to these observations is found in the HAP trial of levofloxacin, where recovery of Pseudomonas caused the addition of a second agent, mostly β-lactams (19). There were 17 patients from whom Pseudomonas aeruginosa was recovered. None of these isolates emerged as resistant during therapy. Part of this may be because hospital-acquired pneumonia (HAP) was studied and not VAP, as patients with the latter generally have larger bacterial burdens and tend to be more ill.
There are two other important things to realize. The first is that the murine model is not as stringent a test of a drug as actually treating patients with VAP. This only makes the need to study combinations to suppress resistance even more important. The second is that this was a neutropenic animal model. Granulocytes would definitely improve cell kill. However, it should be noted that the mouse started with about 8 log10 (CFU/g) of lung tissue. We have recently shown that granulocytes (4) kill, at most, approximately 2.0 log10 (CFU/g) of Pseudomonas aeruginosa cells per day, depending on the initial inoculum. Burdens exceeding 6 log10 (CFU/g) saturated the granulocytes. Since many VAP patients will have burdens even greater than 8 log10 (CFU/g), attaining a 2 log10 (CFU/g) cell kill may be inadequate for outcome and the 3 log10 (CFU/g) resistance suppression exposure target may be needed for clinical outcome and resistance suppression, again underlying the need to properly study combination regimens, specifically against difficult-to-treat pathogens such as Pseudomonas aeruginosa and Acinetobacter spp.
ACKNOWLEDGMENTS
This work was supported by R01AI079578, a grant from NIAID to the Emerging Infections and Pharmacodynamics Laboratory.
The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute of Allergy and Infectious Diseases or the National Institutes of Health.
Footnotes
Published ahead of print on 16 May 2011.
REFERENCES
- 1. Calandra G., Ricci F., Wang C., Brown K. 1986. Cross resistance and imipenem. Lancet ii:340–341 [DOI] [PubMed] [Google Scholar]
- 2. Clinical Laboratory Standards Institute 2006. Methods for dilution antimicrobial susceptibility tests for bacteria that grow aerobically; approved standard, 7th ed. CLSI publication M7-A7 Clinical and Laboratory Standards Institute, Wayne, PA [Google Scholar]
- 3. D'Argenio D. Z., Schumitzky A. 1997. ADAPT II. A program for simulation, identification, and optimal experimental design. User manual. Biomedical Simulations Resource, University of Southern California, Los Angeles, CA: http://bmsr.usc.edu/ [Google Scholar]
- 4. Drusano G. L., et al. 2011. Saturability of granulocyte kill of Pseudomonas aeruginosa in a murine model of pneumonia. Antimicrob. Agents Chemother. 55:2693–2695 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Drusano G. L., Liu W., Fregeau C., Kulawy R., Louie A. 2009. Differing effects of combination chemotherapy with meropenem and tobramycin on cell kill and suppression of resistance of wild-type Pseudomonas aeruginosa PA01 and its isogenic MexAB efflux pump-overexpressed mutant. Antimicrob. Agents Chemother. 53:2266–2273 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Drusano G. L., Sorgel F., Quinn J., Mason B., Melnick D. 2005. Impact of pharmacodynamics dosing of meropenem on emergence of resistance during treatment of ventilator-associated pneumonia; a prospective clinical trial. Abstract K-127 Abstr. 45th Intersci. Conf. Antimicrob. Agents Chemother., 16 to 19 December 2005, Washington, DC [Google Scholar]
- 7. Du X., Li C., Sun H. K., Nightingale C. H., Nicolau D. P. 2005. A sensitive assay of amoxicillin in mouse serum and broncho-alveolar lavage fluid by liquid-liquid extraction and reversed-phase HPLC. J. Pharm. Biomed. Anal. 39:648–652 [DOI] [PubMed] [Google Scholar]
- 8. Fink M. P., et al. 1994. Treatment of severe pneumonia in hospitalized patients: results of a multicenter, randomized, double-blind trial comparing intravenous ciprofloxacin with imipenem-cilastatin. Antimicrob. Agents Chemother. 38:547–557 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Jumbe N., et al. 2003. Application of a mathematical model to prevent in-vivo amplification of antibiotic-resistant bacterial populations during therapy. J. Clin. Invest. 112:275–285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Leary R., Jelliffe R., Schumitzky A., Van Guilder M. 2001. An adaptive grid non-parametric approach to pharmacokinetic and dynamic (PK/PD) models, p. 389–394 In Proceedings of the 14th IEEE Symposium on Computer-Based Medical Systems IEEE Computer Society, Bethesda, MD [Google Scholar]
- 11. Lodise T., Lomaestro B., Drusano G. L. 2007. Piperacillin/tazobactam for Pseudomonas aeruginosa infections: clinical implications of an extended infusion dosing strategy. Clin. Infect. Dis. 44:357–363 [DOI] [PubMed] [Google Scholar]
- 12. Lodise T. P., Sorgel F., Mason B., Melnick D., Drusano G. L. 2011. Penetration of meropenem into epithelial lining fluid of patients with ventilator-associated pneumonia. Antimicrob. Agents Chemother. 55:1606–1610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Lomaestro B. M., Drusano G. L. 2005. Pharmacodynamic evaluation of extending the administration time of meropenem using a Monte Carlo simulation. Antimicrob. Agents Chemother. 49:461–463 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Louie A., et al. 2010. The combination of meropenem and levofloxacin is synergistic with respect to both Pseudomonas aeruginosa kill rate and resistance suppression. Antimicrob. Agents Chemother. 54:2646–2654 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Macia M. D., et al. 2006. Efficacy and potential for resistance selection of antipseudomonal treatments in a mouse model of lung infection by hypermutable Pseudomonas aeruginosa. Antimicrob. Agents Chemother. 50:975–983 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Tam V. H., Louie A., Deziel M. R., Liu W., Drusano G. L. 2007. The relationship between quinolone exposures and resistance amplification is characterized by an inverted U: a new paradigm for optimizing pharmacodynamics to counterselect resistance. Antimicrob. Agents Chemother. 51:744–747 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Tam V. H., et al. 2005. Bacterial population responses to drug selective pressure: examination of garenoxacin against Pseudomonas aeruginosa. J. Infect. Dis. 192:420–428 [DOI] [PubMed] [Google Scholar]
- 18. Tam V. H., et al. 2007. Drug exposure intensity and duration of therapy's impact on emergence of resistance of Staphylococcus aureus to a quinolone antimicrobial. J. Infect. Dis. 195:1818–1827 [DOI] [PubMed] [Google Scholar]
- 19. West M., et al. 2003. Levofloxacin compared with imipenem/cilastatin followed by ciprofloxacin in adult patients with nosocomial pneumonia: a multicenter, prospective, randomized, open-label study. Clin. Ther. 25:485–506 [DOI] [PubMed] [Google Scholar]