Abstract
Much important evolutionary activity occurs in gene clusters, where a copy of a gene may be free to acquire new functions. Current computational methods to extract evolutionary information from sequence data for such clusters are suboptimal, in part because accurate sequence data are often lacking in these genomic regions, making existing methods difficult to apply. We describe a new method for reconstructing the recent evolutionary history of gene clusters, and evaluate its performance on both simulated data and actual human gene clusters.
Key words: algorithms, alignment, gene clusters, genomics, phylogenetic trees
1. Introduction
Because the computational methods considered here in no way rely on the presence of protein-coding segments, in what follows we use gene cluster to refer to any genomic region that contains a number of duplicated segments. In applying the methods developed here, we often focus on regions that contain duplicated protein-coding genes, but the methods are much more generally applicable. A typical case might consist of a megabase-sized region of the human genome that contains dozens of pairs of segments that are hundreds or thousands of basepairs in length, and where the paired segments can be aligned to each other at, say, at least 70% nucleotide identity. Within a gene cluster, some segment pairs might have 70% identity and others have 95% identity, reflecting differing ages of the duplication events that created the pairs. The human genome contains dozens or hundreds of such clusters, depending on what one means by “a number of duplicated segments.”
Mechanistically, these clusters are created by tandem and segmental duplications (as opposed to the events that create interspersed repeats, such as Alu and L1 elements). Tandem duplication arises when replication slippage or unequal crossover copies a genomic region into an adjacent position (Achaz et al., 2000). With segmental duplications, a genomic interval is copied and the copy inserted elsewhere in the genome (Akhunov et al., 2006; Bailey et al., 2006). In the human genome (and other primates), many of these events are caused by Alu-mediated recombination. Segmental duplications have a strong tendency for the copy to be in close proximity on the same chromosome as the original segment; this preference, together with tandem duplications, creates the clusters. Moreover, the presence of highly similar segments in close proximity increases the likelihood of deletion and inversion events, which together with nucleotide substitutions further sculpt these regions (Ohno, 1970; Hurles, 2004).
The computational problem considered in this paper is to infer the large-scale duplication and deletion events that created a given gene cluster, based only on self-alignments of the region, and perhaps alignments involving the corresponding region of another species. How those alignments are produced, and how to use them to map small-scale events such as nucleotide substitutions, is not the subject here, although we will explain how we produced the alignments used in our case studies and will have more to say about the difficulty of creating good alignments in these regions.
One reason for our interest in these regions is that the copied intervals (which we will call just genes) provide the raw material for rapid evolution, as redundant copies of a gene are free to adopt new functions (Ohno, 1970; Lynch and Conery, 2000). A copy may take on a novel, beneficial role that is then preserved by natural selection, a process called neofunctionalization, or both copies may become partially compromised by mutations that keep their total function equal to that of the original gene, called subfunctionalization (Force et al., 1999).
Another reason to focus on changes in gene clusters is that deletions in protein-coding gene clusters are responsible for several human genetic diseases (Lupski, 2007). A major finding of the initial sequencing of the human genome is that 5% of the genome had been involved in recent duplications (Lander et al., 2001). More recently, it has become clear that duplicated regions often vary in copy number between individual humans (Wong et al., 2007). A substantial fraction of what distinguishes humans from other primates, as well as the genetic differences among humans, cannot be understood until we have a clearer picture of gene clusters and of the evolutionary mechanisms that act on them.
One hurdle to this understanding is that recently duplicated regions, say those that retain over 95% identity (so are likely produced within the last 10 million years) resist assembly by the current whole-genome shotgun approach (Green, 2001). Even the so-called “finished” human genome sequence has 300 gaps, most of which are caused by the presence of recent duplications. Moreover, much available mammalian genomic sequence is only lightly sampled, further impeding the analysis of gene clusters. Because of the lack of accurate sequence data in gene clusters, practical computational tools for their analysis are only beginning to emerge.
As mentioned above, analyzing gene clusters requires a marriage of two tasks, one inferring large-scale evolutionary operations (primarily duplication, inversion, segmental deletion, and gene conversion) and the other, fine-scale evolutionary changes (substitutions and very small insertions/deletions). Even the second part is currently not handled well by existing tools though it is essentially just an extension of the familiar problem of multiple sequence alignment. Indeed, what constitutes a proper alignment of gene cluster sequences deserves extended discussion (Blanchette et al., 2004; Raphael et al., 2004). Several programs are available for aligning multiple genomes (Margulies et al., 2007). Although their inference is satisfactory with non-duplicated regions, their performance on gene cluster regions is inadequate (Hou, 2007). Our observations about the quality of current whole-genome alignments (Miller et al., 2007) indicate that it may be worthwhile to align gene clusters using methods designed specifically for them, and then to splice the results into the whole-genome alignments created by the other methods.
Several ideas have been explored for reconstructing large-scale evolutionary history. Some attempt to reconstruct the history of duplication operations on regions with highly regular boundaries (Elemento et al., 2002; Zhang et al., 2003; Sammeth and Stoye, 2006), while others allow inversions (Bertrand et al., 2006; Ma et al., 2008), and/or also deletions (Jiang et al., 2007; Zhang et al., 2008, 2009).
In this article, we describe a new method for analyzing gene cluster data, called CAGE (Combinatorial Analysis of Gene-cluster Evolution), so as to reconstruct large-scale duplication histories. Earlier studies used phylogenetic information from such reconstruction (Elemento et al., 2002; Zhang et al., 2003; Sammeth and Stoye, 2006; Bertrand et al., 2006; Ma et al., 2008). Unlike these, we infer the duplication history using only positional information and similarities from sequence alignments. Our method outputs a plausible duplication history underlying the formation of a gene cluster while Jiang et al. (2007) focused only on identifying duplicated elements. Zhang et al. (2008) used probabilistic techniques, whereas our approach is entirely combinatorial.
2. Methods
During genomic evolution, a duplication event copies a segment to a new genomic position. Genome sequencing and analysis suggest that many protein-coding gene clusters have arisen by recent duplication in the human and other mammalian genomes. We aim to identify the duplication events that generated a gene cluster using a parsimony approach.
2.1. Notations
A duplication is formally defined as follows. Let
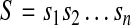 |
be a genomic sequence of length n, where 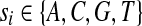 . For any a, b, and c (1 ≤ a ≤ b ≤ n and 1 ≤ c ≤ n), a forward duplication that copies the segment
. For any a, b, and c (1 ≤ a ≤ b ≤ n and 1 ≤ c ≤ n), a forward duplication that copies the segment 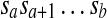 and inserts it between sc−1 and sc is written [a, b] + c. It transforms S into the following sequence
and inserts it between sc−1 and sc is written [a, b] + c. It transforms S into the following sequence
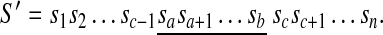 |
If c = b + 1, the forward duplication [a, b] + c forms a tandem duplication in the resulting sequence
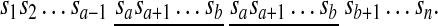 |
Tandem duplications are observed in many important gene clusters in eukaryotic genomes. If a < c < b, then [a, b] + c copies within itself and produces a segment AABB where A and B are non-empty segments in the resulting sequence
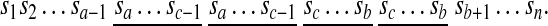 |
A backward duplication inserting the reverse-complement sequence 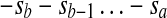 between sc−1 and sc is written [a, b] − c. If c = b + 1, the backward duplication [a, b] − c produces a palindrome. Let
between sc−1 and sc is written [a, b] − c. If c = b + 1, the backward duplication [a, b] − c produces a palindrome. Let 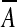 denote the reverse complement of sequence A. If a < c < b, [a, b] − c produces a segment
denote the reverse complement of sequence A. If a < c < b, [a, b] − c produces a segment 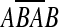 .
.
For simplicity, we say a duplication is an operation that copies a subsequence or its reverse complement into a new position. We call the original segment [a, b] of duplication [a, b] ± c the source region and the inserted copy the target region. Subsequently, the source and target regions evolve independently, e.g., by point mutations and small insertions/deletions, and thus in the present-day sequence, the two regions are generally not identical. However, they do tend to form a strong local alignment (called a match) in a self-alignment of any genomic region that contains them both.
Definition 1
We say a region A is contained in a region B if all bases of A are in B but not vice-versa. We say A and B overlap if they share at least one base but neither contains the other.
Let A be a match region of a duplication event and let B be a match region of another duplication event in S. A nucleotide of location i in S is denoted si.
-
If there exist i, j, k, l (1 ≤ i < k ≤ j < l ≤ n) such that
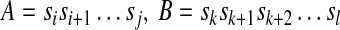
Or vice versa, we say that A overlaps B.
-
If there exist i, j, k, l (i < k < j < l) such that
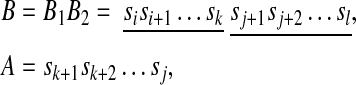
A is said to be inserted into B.
-
If there exist i, j, k, l (i ≤ k ≤ j ≤ l) such that
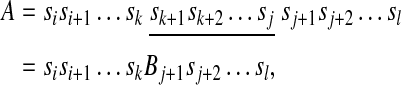
we say that A contains B.
2.2. Problem
We detect a gene cluster by aligning a genomic sequence with itself using the program BLASTZ (Schwartz et al., 2003). Let S be a genomic sequence. We start by running BLASTZ using the parameters T = 2 and Y = 3400 to obtain all local self-alignments of S. The resulting local self-alignments are then processed in a pipeline in which local self-alignments with similarity less than 70% are filtered out, those separated only by small gaps and/or interspersed repeats are merged, and the endpoints of good alignments are determined. Finally, we identify a set of matches, which are visualized as a dot plot and form a gene cluster (Fig. 1b). Note that changing the parameters of BLASTZ may change its output. The problem of inferring the duplication history of the gene cluster is then to find a duplication-free sequence T and the minimum number of duplication events 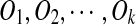 such that
such that
The source and target regions of each Oi consist of one or more match regions.
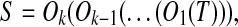 where Oi(S′) denotes the resulting sequence after applying O to sequence S′.
where Oi(S′) denotes the resulting sequence after applying O to sequence S′.
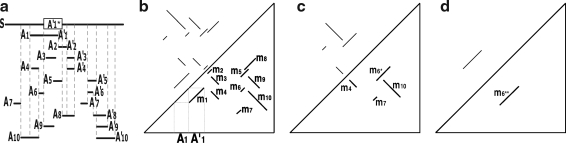
FIG. 1.
An example of duplication inference. (a) The original match regions in a sequence S. S contains 10 matches 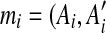 for regions Ai and
for regions Ai and 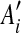 where 1 ≤ i ≤ 10, and the box shows the location of an intraposed duplication which is discussed in Sections 2.4 and 2.5. (b) The self-alignment of the original sequence. (c) The self-alignment after rolling back a duplication. (d) The self-alignment after rolling back another duplication. See Section 2.3 for details.
where 1 ≤ i ≤ 10, and the box shows the location of an intraposed duplication which is discussed in Sections 2.4 and 2.5. (b) The self-alignment of the original sequence. (c) The self-alignment after rolling back a duplication. (d) The self-alignment after rolling back another duplication. See Section 2.3 for details.
Given a sequence of duplications 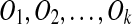 , we call the boundaries of all source and target regions breakpoints. If duplication events occur randomly during genome evolution, two duplications are quite unlikely to share their boundaries. So we assume that no two duplications have a common breakpoint in a duplication history (Nadeau and Taylor, 1984), except for tandem duplication. Tandem duplication (with or without reversal) copies a source region into a location adjacent to its boundary, and happens quite frequently. Thus, it is a special exception to our breakpoint uniqueness assumption.
, we call the boundaries of all source and target regions breakpoints. If duplication events occur randomly during genome evolution, two duplications are quite unlikely to share their boundaries. So we assume that no two duplications have a common breakpoint in a duplication history (Nadeau and Taylor, 1984), except for tandem duplication. Tandem duplication (with or without reversal) copies a source region into a location adjacent to its boundary, and happens quite frequently. Thus, it is a special exception to our breakpoint uniqueness assumption.
2.3. Algorithm
The main idea of our algorithm is, in turns, to identify the latest duplication event in the history of a gene cluster, roll back this latest event by eliminating its target region, and use the resulting sequence as an input for the next iteration. These steps are repeated until we reconstruct the duplication-free sequence.
Figure 1 depicts the overview of our method. Figure 1a shows an example of input data that is a sequence including 10 pairs of matching regions formed by duplication events. Those 10 matches are visualized as a dot plot in Figure 1b. 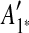 is inferred as the latest duplicated region in Figure 1b, and this duplication is rewound by removing
is inferred as the latest duplicated region in Figure 1b, and this duplication is rewound by removing 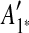 as shown in Figure 1b (note the algorithm for identifying the latest duplicated region is described later in this section). These steps are repeated in Figure 1b, c.
as shown in Figure 1b (note the algorithm for identifying the latest duplicated region is described later in this section). These steps are repeated in Figure 1b, c.
Before determining the most recent duplication, we must identify matches that have been split by a subsequent duplication. Consider a given match (A, A′). If a duplication event inserts a segment C in the region A′, then the match (A, A′) is split into two small matches 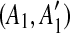 and
and 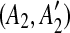 . If this happens, we can correctly identify the original duplication event forming the match (A, A′) only if we first identify the one inserting C. Hence, using a kd-tree data structure, we identify all the pairs of matches
. If this happens, we can correctly identify the original duplication event forming the match (A, A′) only if we first identify the one inserting C. Hence, using a kd-tree data structure, we identify all the pairs of matches 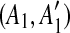 and
and 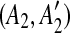 such that A1 and A2 are adjacent but
such that A1 and A2 are adjacent but 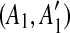 and
and 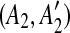 are separated by a region C of some match. To guarantee that
are separated by a region C of some match. To guarantee that 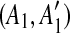 and
and 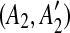 are not examined before removing C from the sequence, we place [A1, C],
are not examined before removing C from the sequence, we place [A1, C], 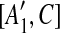 , [A2, C],
, [A2, C], 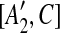 into a suspend list. We call the regions A1,
into a suspend list. We call the regions A1, 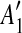 , A2,
, A2, 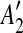 the suspended regions, and the region C on which they depend the inserted region.
the suspended regions, and the region C on which they depend the inserted region.
Theorem 1
Assume a sequence S is transformed from a duplication-free sequence T by a series of duplication events. Then the target region of the latest duplication event does not overlap with the source or target regions of any other duplications, and it is not contained in any match regions of S.
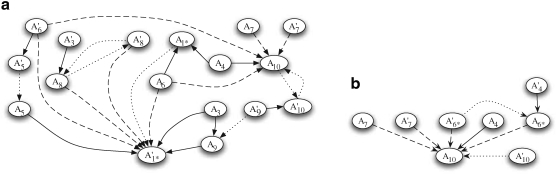
The proof of Theorem 1 follows from the breakpoint uniqueness assumption. Based on Theorem 1, we determine the latest duplication event in the history of a gene cluster as follows. Suppose there are n matches in genomic sequence S. We define the constraint graph G = (V, E) of these matches as follows. G is directed and has 2n nodes representing the 2n regions of the matches. There are three types of arcs. Let (A, A′) be a match. If A overlaps a region B of another match, there is an arc from node A to node A′. Such an arc is called a type-1 arc. If A is contained in B, there is an arc from node A to node B, called a type-2 arc. Finally, if [A, C] is in the suspend list, there is an arc from node A to node C, called a type-3 arc. For example, the constraint graph for Figure 1 is given in Figure 3 below.
FIG. 3.
The constraint graphs of matches in Fig. 1a, b. Arcs of type 1, 2, and 3 are represented by dotted, solid, and dashed lines, respectively. In (a), matches m1 and m2 have been replaced with m1* according to the procedure for intraposed duplications discussed in Section 2.2, and node 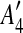 is omitted because it is identical to
is omitted because it is identical to 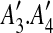 reappears in (b) after m3 has been eliminated.
reappears in (b) after m3 has been eliminated.
By Theorem 1, there must be at least one node with out-degree 0 in a constraint graph. In each iteration of the algorithm, we select a node v with out-degree 0 and remove the region corresponding to v from S. If there are several nodes of out-degree 0, the one with the highest similarity level in the self-alignment is selected as the latest duplicated region. By Theorem 2 below, the following algorithm identifies the true number of duplication events and a plausible sequence of such events in O(n2 log n) time.
Algorithm.
INFER-DUPS 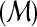
| 1 | Input: A set of matches 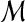 in a self-alignment in a self-alignment |
| 2 | Output: A set of duplication events |
| 3 | repeat |
| 4 | for all the pairs of matches 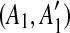 and and 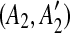 in in 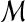
|
| 5 | do |
| 6 | ifA1 and A2 are adjacent but |
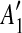 and and 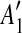 are separated by a region C of some match are separated by a region C of some match |
|
| 7 | then place [A1, C], 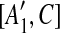 , [A2, C], and , [A2, C], and 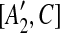 into the suspend list. into the suspend list. |
| 8 | G ← CONSTRUCT-CONSTRAINT-GRAPH 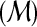
|
| 9 | Identify the regions of out-degree 0 in G |
| 10 | Remove the one with the highest similarity score from 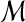 . . |
| 11 | if the removed region is an inserted region in the suspend list |
| 12 | then merge the corresponding suspended regions in 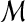 . . |
| 13 | 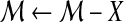 , where X is the set of matches that disappear with removal of the region , where X is the set of matches that disappear with removal of the region |
| 14 |
until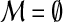
|
Algorithm.
CONSTRUCT-CONSTRAINT-GRAPH 
| 1 |
for all pairs of matches (A, A′) and (B, B′) in 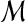
|
| 2 | do |
| 3 | ifA overlaps B |
| 4 | then type-1 arc of A → A′ and B → B′ |
| 5 | elseifA is contained in B (or vice versa) |
| 6 | then type-2 arc of A → B (or B → A) |
| 7 | elseifA (and/or B) is a suspended region depending on C |
| 8 | then type-3 arc of A → C (and/or B → C) |
Theorem 2
Suppose a sequence S evolves from a duplication-free sequence T in k duplication events. If the breakpoint uniqueness assumption holds, the algorithm identifies a series of k duplications and a duplication-free sequence T′ such that T′ transforms to S by the identified k duplications.
Proof
We prove this by induction on the number n duplications. The results are trivial when n = 1 or 2. Assume it is true for n ≤ k − 1, and that S evolves from a duplication-free sequence T by k duplications 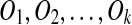 . Let A be the region first selected for removal by the algorithm, where A forms a match m = (A, A′) or m = (A′, A). Then A does not overlap with other matches and is not contained in any other matches, since the out-degree of A is 0 in the constraint graph. Let m be generated by duplication Oi. We consider the following cases.
. Let A be the region first selected for removal by the algorithm, where A forms a match m = (A, A′) or m = (A′, A). Then A does not overlap with other matches and is not contained in any other matches, since the out-degree of A is 0 in the constraint graph. Let m be generated by duplication Oi. We consider the following cases.
Case 1
If i = k, it means that m is generated by the latest duplication. Assume the resulting sequence is S″ when A is removed from S. If A is a target region of Ok, T transforms into S″ by 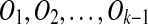 . By induction, the algorithm will reduce S″ to a duplication-free sequence T ″ such that T″ transforms into S″ by k − 1 duplications. Therefore, T ″ transforms into S by k duplications.
. By induction, the algorithm will reduce S″ to a duplication-free sequence T ″ such that T″ transforms into S″ by k − 1 duplications. Therefore, T ″ transforms into S by k duplications.
If A is instead a source region of Ok, then A′ is a target region. Since A does not overlap with any other matches and A is not contained in other matches, A cannot be involved in any other duplications. Thus T includes A, i.e., A is in the duplication-free sequence. Let S′ be the resulting sequence after removing A from S and let T ′ be the resulting sequence after removing A from T and inserting A′ in the corresponding position of S. By assumption, T ′ transforms into S′ by 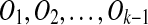 . By induction on S′, the algorithm outputs a duplication-free sequence T ″ that transforms into S′ by k − 1 duplications. Since S′ transforms into S by the duplication that creates m, the removal of A guarantees that we find a solution with the correct number of events.
. By induction on S′, the algorithm outputs a duplication-free sequence T ″ that transforms into S′ by k − 1 duplications. Since S′ transforms into S by the duplication that creates m, the removal of A guarantees that we find a solution with the correct number of events.
Case 2
If i < k, we consider the following sub-cases.
Sub-case 2.1
Suppose both of A and A′ in m have out-degree 0. If A is removed by the algorithm, none of the regions involved in duplications Oj, i < j ≤ k overlap A. Thus, the reordered events 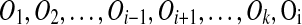 also transform T into S. This reduces to Case 1.
also transform T into S. This reduces to Case 1.
Sub-case 2.2
Suppose A is a target region of Oi with out-degree 0, but A′ does not have out-degree 0. Then since A is a target region, the resulting sequence S′ after the removal of A from S can be generated from T by k − 1 duplications 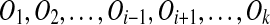 . Thus, by induction, the algorithm reduces S′ to a duplication-free sequence T″, and so T″ evolves into S in k duplications.
. Thus, by induction, the algorithm reduces S′ to a duplication-free sequence T″, and so T″ evolves into S in k duplications.
Sub-case 2.3
Suppose A is a source region of Oi with out-degree 0, but A′ does not have out-degree 0. Since A is not contained in any other match regions, A is a subsequence of the original duplication-free sequence T. In this case, if the breakpoint uniqueness assumption holds, then A is not inserted in any match region, and hence it must be in T. Let T ′ be the resulting sequence after removal of A and insertion of A′ in T. Then T ′ evolves into S by k − 1 duplications. By induction, the algorithm identifies a duplication-free sequence T ″ that evolves into S by k − 1 duplications. By modifying T ″ by inserting A′ and removing A, we can derive a duplication-free sequence that evolves into S in k duplications. ▪
2.4. Handling tandem duplication
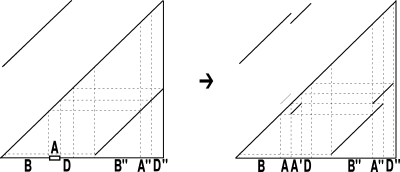
Our model assumption of breakpoint uniqueness may be violated by tandem duplication. Copy-and-paste transposons are an example of frequent reuse of duplication breakpoints. To infer duplication history more accurately, we need a way to model tandem duplication events. Suppose we have a tandem duplication that copies A into a location adjacent to its boundary. It produces a match (A, A′) where A′ is adjacent to A. If the target location A′ is not involved in any other matches, the tandem duplication does not affect the algorithm. But if it splits other matches resulting from earlier duplications, then the target region A′ appears in the split matches, which violates the conclusion of Theorem 1. For instance, let m be a match, where m = (BAD, B″A″D″). After the tandem duplication in A occurs, m is split into two matches m1 and m2, where m1 = (BA, B″A″) and m2 = (A′D, A″D″) (Fig. 2). This causes the algorithm to fail to detect the target region A′ because A′ is contained in a region of m1. Fortunately, we observe a property that one region of m1 has a boundary adjacent to a region of m2 while the other region of m1 overlaps the other region of m2. Also, the boundaries of the overlapped part correspond to region A″. Thus, the tandem duplication can be detected as follows. If there are two matches 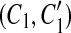 and
and 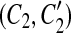 , where C1 and C2 are adjacent but
, where C1 and C2 are adjacent but 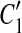 and
and 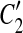 are overlapped (or vice versa), then the overlap is denoted as a temporary match (A, A″) where A″ is the overlapped part of
are overlapped (or vice versa), then the overlap is denoted as a temporary match (A, A″) where A″ is the overlapped part of 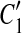 and
and 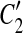 , and A is the corresponding part of C1. If there exists a match (A, A′) where A and A′ are adjacent, then [C1, A],
, and A is the corresponding part of C1. If there exists a match (A, A′) where A and A′ are adjacent, then [C1, A], 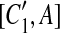 , [C2, A],
, [C2, A], 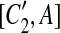 , [C1, A′],
, [C1, A′], 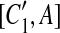 , [C2, A′], and
, [C2, A′], and 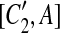 are all placed in the suspend list. In addition, while constructing the constraint graph, if A is contained in a suspended region whose inserted region is A, the drawing of a type-2 arc from A is skipped if A forms a match with a region adjacent to itself.
are all placed in the suspend list. In addition, while constructing the constraint graph, if A is contained in a suspended region whose inserted region is A, the drawing of a type-2 arc from A is skipped if A forms a match with a region adjacent to itself.
FIG. 2.
An example of the self-alignment change caused by a tandem duplication event.
One potential problem is whether the case we detect as tandem duplication can be generated by other scenarios. Suppose we have three matches m1, m2, and m3, where m1 = (BA, B″A″), m2 = (A′D, A″D″), m3 = (A, A′), and that A and A′ are adjacent. To simplify, we assume that the out-degree of m1, m2, and m3 in the constraint graph is 0. If we consider only parsimonious solutions for this case, the only other scenario is separate duplications corresponding to m1 and m2, with adjacent targets that violate the breakpoint uniqueness assumption. If tandem duplication is regarded as a special, common case of breakpoint reuse, inferring a tandem duplication of m3 and a prior duplication of a merged match of m1 and m2 makes more sense.
This modification can be extended for tandem duplications that copy a segment more than once into its adjacent location. These tandem duplications with more than one copy are detected as follows. Assume the same source region is used in all of the copies. If there are n(≥2) matches such that 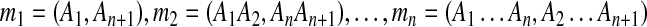 , then mi(2 ≤ i ≤ n) is converted into
, then mi(2 ≤ i ≤ n) is converted into 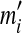 where
where 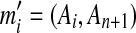 . Then, the latest region for this iteration can be identified by running the rest of the algorithm normally.
. Then, the latest region for this iteration can be identified by running the rest of the algorithm normally.
There is another event that may be confused with tandem duplication. This is a duplication that copies a source region into a location within itself. To handle these correctly, we replace the two matches formed by this type of duplication with one match. This step is motivated by the following. Let m1 and m2 be two matches, and suppose we observe AA′B′B or 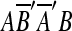 , where m1 = (A, A′), m2 = (B′, B) and
, where m1 = (A, A′), m2 = (B′, B) and 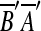 is the reverse complement of sequence A′B′. AA′B′B might arise from two duplication events: an event duplicating A and another duplicating B. It could also arise from a single duplication that copies AB within itself. The two-event explanation violates the breakpoint uniqueness hypothesis, and is also less parsimonious than a single event. Therefore, our algorithm infers that AA′B′B arose from a single event that copied and inserted AB within itself. In the same manner, we also infer that
is the reverse complement of sequence A′B′. AA′B′B might arise from two duplication events: an event duplicating A and another duplicating B. It could also arise from a single duplication that copies AB within itself. The two-event explanation violates the breakpoint uniqueness hypothesis, and is also less parsimonious than a single event. Therefore, our algorithm infers that AA′B′B arose from a single event that copied and inserted AB within itself. In the same manner, we also infer that  arose from a single event that copied and inserted AB within itself in the reverse orientation. In order to infer one event for two matches in AA′B′B, the two matches m1 and m2 are replaced with a new match m′ = (AB, A′B′). The two matches in
arose from a single event that copied and inserted AB within itself in the reverse orientation. In order to infer one event for two matches in AA′B′B, the two matches m1 and m2 are replaced with a new match m′ = (AB, A′B′). The two matches in 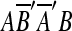 are also replaced in a similar fashion. We call this type of duplication intraposed duplication. The biological relevance of intraposed duplication remains unclear. However, we introduce this hypothetical event to apply the parsimony principle.
are also replaced in a similar fashion. We call this type of duplication intraposed duplication. The biological relevance of intraposed duplication remains unclear. However, we introduce this hypothetical event to apply the parsimony principle.
2.5. Illustration of the method
To demonstrate how the method works, we consider a genomic sequence S containing 10 matches mi, 1 ≤ i ≤ 10. The dot plot of the self-alignment of S is shown in Figure 1b.
First, we observe that the regions of m1 and m2 form a segment 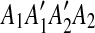 , where
, where 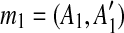 and
and 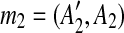 , so we infer that they were formed by an intraposed duplication event that inserted a copy of segment A1A2 within itself. We replace m1 and m2 with a new match m1*, whose regions are
, so we infer that they were formed by an intraposed duplication event that inserted a copy of segment A1A2 within itself. We replace m1 and m2 with a new match m1*, whose regions are 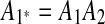 and
and 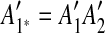 . Furthermore, the following two facts are true. Let
. Furthermore, the following two facts are true. Let 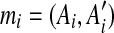 for 3 ≤ i ≤ 10.
for 3 ≤ i ≤ 10.
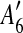 and
and 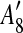 are adjacent, while A6 and A8 are separated by
are adjacent, while A6 and A8 are separated by 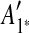 . Hence, we infer that
. Hence, we infer that 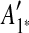 is an inserted region, and add
is an inserted region, and add 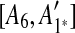 ,
, 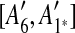 ,
, 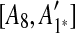 ,
, 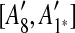 to the suspend list.
to the suspend list.Similarly,
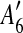 and
and  are adjacent, while
are adjacent, while 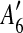 and
and 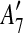 are separated by A10. Hence we add [A6, A10],
are separated by A10. Hence we add [A6, A10], 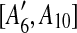 , [A7, A10],
, [A7, A10], 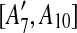 to the suspend list.
to the suspend list.
The constraint graph G for the 9 remaining matches is shown in Figure 3a. Note that there are no arcs leaving node 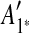 , so
, so 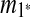 is selected as the latest duplication event. After
is selected as the latest duplication event. After 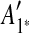 is removed from the sequence S, m6 and m8 are merged into a match
is removed from the sequence S, m6 and m8 are merged into a match 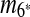 in the resulting sequence S′. In addition, since A3, A5 and A9 are contained in
in the resulting sequence S′. In addition, since A3, A5 and A9 are contained in 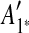 , the matches m3, m5, and m9 do not exist in S′. Overall, in the self-alignment of S′ shown in Figure 1b, only four matches remain, which are
, the matches m3, m5, and m9 do not exist in S′. Overall, in the self-alignment of S′ shown in Figure 1b, only four matches remain, which are 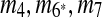 , and m10. The constraint graph for these four matches is shown in Figure 3b. Since there are no arcs leaving node A10, we select m10 as the latest duplication event. After removal of A10,
, and m10. The constraint graph for these four matches is shown in Figure 3b. Since there are no arcs leaving node A10, we select m10 as the latest duplication event. After removal of A10, 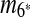 and m7 are merged into a match
and m7 are merged into a match 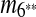 and m4 disappears in the resulting sequence S″. As a result, only
and m4 disappears in the resulting sequence S″. As a result, only 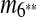 remains in the self-alignment of S″. In summary, we identify 3 duplication events that give rise to the matches in the given genomic sequence S.
remains in the self-alignment of S″. In summary, we identify 3 duplication events that give rise to the matches in the given genomic sequence S.
2.6. Identifying duplication events using two species
We extend the method to infer the duplication history using two species. The information obtained from a second species can help to identify duplication events more accurately. In order to determine the most recently duplicated regions in two species, we first construct a separate constraint graph for the gene cluster of each species. A node in the constraint graph indicates a match region in the self-alignment, and directed edges are drawn according to the rules of the previous illustration. In addition to the arcs obtained from the self-alignment, constraint information in the inter-species alignment is used to extend the constraint graph. The additional rule is as follows. For each match in the self-alignment, the boundaries of its two regions are compared to the boundaries of matches in the inter-species alignment. Let a match in a self-alignment be denoted m = (A, A′). If A overlaps or is contained in a match region in the inter-species alignment, then A has an outgoing arc toward A′, i.e., A cannot be the latest duplicated region. For A′, the same rule is applied. The correctness of the rule follows from the breakpoint uniqueness assumption and the geometric properties of a dot plot for inter-species alignment in Theorem 3.
Theorem 3
For a match that corresponds to the latest duplication after speciation in the self-alignment of one species, the target region is neither overlapped with nor contained in the regions of any other matches, and the source region must overlap or be contained in at least one match in the inter-species alignment.
Proof
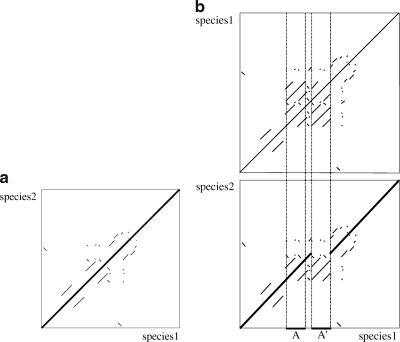
Suppose that a total of n duplication events occurred in the two sequences after speciation. We assume that the gene cluster's two sequences immediately after speciation are identical. Thus, the self-alignments for each species and the inter-species alignment between the two species are the same, i.e., there is a main diagonal in the dot plot of the inter-species alignment like Figure 4a. The diagonal line corresponds to the speciation event. We call the diagonal an orthologous match. The other matches formed before speciation in the inter-species alignment are called out-paralogous matches.
FIG. 4.
An example of an orthologous alignment: (a) Immediately after speciation. (b) After one duplication in species 1.
If one interval in a sequence is duplicated and the copy is inserted into a second location, the diagonal line in the inter-species alignment is split at the insertion location. If whole or partial regions of other matches that were generated by preceding duplications are involved in the current duplication, those regions form additional matches in the duplicated region. The regions of those newly formed matches are contained in the duplicated region. On the other hand, the source region overlaps with the diagonal line as shown in Figure 4b.
Thus, if n = 1, the target region is neither overlapped with nor contained in any other matches in the inter-species alignment. On the other hand, the source region overlaps the diagonal of the speciation event. Assume this is true for n = k − 1. There are k matches of speciation, because the diagonal has been split k − 1 times regardless of which lineage experienced each duplication event. Under the breakpoint uniqueness assumption, the boundaries of the source region of the kth duplication differ from the 2(k − 1) breakpoints of the orthologous alignments. Then, the source region overlaps or is contained in other matches in the inter-species alignment, but since the duplicated region is newly inserted, it is neither overlapped with nor contained in other matches. Hence, the theorem is proved by induction. ▪
Since the target region of the latest duplication after speciation is neither overlapped with nor contained in other matches in the inter-species alignment by Theorem 3, there must be at least one region of a match in the self-alignment which is neither overlapped with nor contained in any other matches in the inter-species alignment. The target region of the latest duplication after speciation does not have any out-going edges in the constraint graph constructed for the self-alignment. Thus, the out-degree of the region is still 0 in the extended constraint graph. Once the latest duplicated region after speciation is identified, the region can be removed from the inter-species alignment and self-alignments. The procedure is then repeated with the reduced alignments.
Theorem 4
For all the duplication events before speciation, neither the source nor target region can have out-degree 0 in the constraint graph, i.e., they either overlap or are contained in other matches in the inter-species alignment, or they are suspended regions.
Proof
If there is no duplication after speciation, the result is trivial since both the source and target region of every duplication before speciation are contained in the main diagonal corresponding to the speciation event in the inter-species alignment.
If a duplication occurs after speciation, its breakpoint changes the positional relationship of the match regions associated with duplications before speciation. Let O be a duplication event after speciation. Suppose O splits the diagonal of the speciation event at position s1 in sequence S1 and position s2 in sequence S2. If O occurs in S1, it splits out-paralogous matches containing s1 in the self-alignment of S1, with two cases depending on whether or not they are also split by other preceding duplications after speciation. If they are not, then two split matches are still contained in the orthologous alignments of the inter-species alignment, so the out-degree of these split regions in the constraint graph is not 0. In the second case, where the out-paralogous matches containing s1 have already been split by preceding duplications after speciation, the out-paralogous regions split by O are suspended regions, since the newly duplicated region is inserted in s1, Thus, the split out-paralogous regions still do not have out-degree 0. By the way, out-paralogous matches containing s2 in the self-alignment of S2 are not split by O. They overlap the split orthologous alignments in s2 of the inter-species alignment, and so their out-degree is not 0, either.▪
By Theorem 4, when there is no region which has out-degree 0 in the constraint graph, the algorithm already identifies all the duplication events after speciation. Thus, only diagonals due to orthologous matches and out-paralogous matches remain in the inter-species alignment. At that point the region of the original orthologous match is removed, i.e. the speciation event is reconstructed. Duplication events inferred from the matches that remain after removing the diagonal are the duplications before speciation.
The above procedure can be extended to reconstruct the duplication history for more than two species by iterating the reconstruction for two closest species in a bottom-up approach (Zhang et al., 2009).
2.7. Influence of deletion and inversion events
Deletion events can affect the inference of duplications, so it is important to consider them simultaneously. In order to infer deletions, we use the following procedure. Assume an input sequence S has two segments ABC and A′C′ for some non-empty segments A, B, C, A′, and C′ where (A, A′) and (C, C′) are matches. We may infer two duplication events that copy A and C respectively, or one duplication that copies ABC and one deletion event that deletes B′. Since our goal is to find a parsimonious duplication history for the cluster, we infer a duplication event and a deletion event when B is relatively short compared to the length of A and C. In our implementation, we detect all possible deletion events using a k-d tree data structure before entering each iteration of inferring duplication events.
In the case of inversions, if the inversion does not split any matches generated by duplication events (i.e., it contains the whole region of one or more other matches, or occurs in a region that does not have any matches), then it does not affect the inference of duplication events. If the inversion occurs within a match, it can be detected. If it splits other matches by involving source or target regions of duplication events, then two duplications are inferred rather than one, but since they will still be rolled back correctly, inference of other events will not be affected. However, if when using an inter-species alignment (as in Section 2.4), the inversion involves part of a source region of a match formed by a duplication, then the diagonal of orthologous matches is split. In this case, the algorithm may not be able to detect the orthologous match as one long diagonal. This is especially likely in fast-evolving regions with many substitutions.
When the orthologous matches are not completely merged into a single diagonal match even though there are no regions left for duplication after speciation, the orthologous matches are identified based on the similarity level and length of the remaining matches in the inter-species alignment. We assume that orthologous regions are more likely to be conserved, i.e., to have a higher similarity level, and the orthologous match also contains other out-paralogous matches. Then the common ancestor sequence for each orthologous match is obtained by taking the consensus of its two sequences, and the program continues to run for the identification of duplications before speciation.
3. Results
3.1. Human gene clusters
We first applied our method to 25 gene clusters in the human genome. For a genomic region containing each gene cluster, we constructed its self-alignment and identified matches using five different thresholds of similarity level: 98%, 93%, 89%, 85%, and 80%, in the same way as Zhang et al. (2008). These five levels correspond roughly to the sequence divergence between humans and great apes (GA), old-world monkeys (OWM), new-world monkeys (NWM), lemurs and galagos (LG), and dogs (DOG), respectively. These various levels allowed us to infer duplication and deletion events that occurred in different periods of the human lineage. The numbers of duplication and deletion events we obtained for these periods are summarized in Table 1.
Table 1.
Numbers of Large-Scale Duplications and Deletions Inferred in Human Gene Clusters Following Divergence from Various Mammalian Clades
| Cluster | Location | GA | OWM | NWM | LG | DOG |
|---|---|---|---|---|---|---|
| CYP4 | chr1:47048227–47411959 | 1, 0 | 4, 1 | 4, 1 | 5, 1 | 10, 1 |
| LCE | chr1:150776235–151067237 | 0, 0 | 0, 0 | 5, 1 | 6, 1 | 9, 2 |
| CR, DAP3 | chr1:153784948–154023311 | 0, 0 | 3, 2 | 12, 2 | 19, 5 | 21, 7 |
| FC | chr1:159742726–159915333 | 1, 2 | 1, 2 | 3, 2 | 4, 2 | 4, 2 |
| CR1 | chr1:205701588–205958677 | 1, 0 | 7, 0 | 8, 3 | 8, 3 | 10, 3 |
| CCDC, CFC1 | chr2:130461934–131153411 | 3, 0 | 5, 0 | 7, 5 | 7, 5 | 10, 5 |
| CXCL, IL8 | chr4:74781081–75209572 | 0, 0 | 0, 0 | 0, 0 | 2, 1 | 17, 8 |
| PCDH | chr5:140145736–140851366 | 0, 0 | 0, 0 | 0, 0 | 1, 0 | 36, 0 |
| HLA | chr6:29786467–30568761 | 0, 0 | 2, 0 | 27, 3 | 38, 5 | 50, 6 |
| HLA-D | chr6:33082752–33265289 | 0, 0 | 0, 0 | 0, 0 | 4, 3 | 6, 8 |
| OR2 | chr7:143005241–143760083 | 6, 1 | 8, 1 | 8, 1 | 10, 1 | 16, 1 |
| AKR1C | chr10:4907977–5322660 | 0, 0 | 3, 2 | 4, 3 | 9, 4 | 28, 4 |
| GAD2 | chr10:26458036–27007198 | 0, 0 | 4, 0 | 6, 1 | 15, 2 | 17, 2 |
| PNLIP | chr10:118205218–118387999 | 0, 0 | 0, 0 | 1, 0 | 2, 1 | 5, 2 |
| OR5, HB, TRIM | chr11:4124149–6177952 | 6, 0 | 7, 0 | 9, 0 | 9, 0 | 24, 2 |
| LST3, SLCO1B | chr12:20846959–21313050 | 0, 0 | 0, 0 | 0, 0 | 9, 2 | 21, 3 |
| C14orf | chr14:23177922–23591420 | 1, 0 | 4, 0 | 5, 2 | 6, 2 | 8, 3 |
| CYP1A1 | chr15:71687352–74071019 | 2, 0 | 12, 2 | 21, 3 | 23, 4 | 25, 4 |
| ACSM | chr16:20234773–20711192 | 2, 0 | 4, 2 | 4, 2 | 4, 2 | 5, 2 |
| LGALS9, NOS2A | chr17:22979762–23370074 | 0, 0 | 2, 0 | 2, 2 | 2, 2 | 3, 2 |
| OR, ZNF | chr19:8569586–9765797 | 4, 0 | 6, 0 | 14, 0 | 23, 0 | 33, 0 |
| NPHS1, ZNF | chr19:40976726–43450858 | 0, 0 | 6, 1 | 12, 1 | 16, 2 | 23, 4 |
| CYP2A | chr19:46016475–46404199 | 0, 0 | 5, 0 | 11, 3 | 14, 3 | 16, 3 |
| DGCR6L, ZNF74 | chr22:18594272–19312230 | 3, 0 | 4, 0 | 5, 1 | 5, 1 | 5, 1 |
| SLC5A, YWHAH | chr22:30379202–31096691 | 0, 0 | 3, 1 | 4, 1 | 6, 1 | 7, 1 |
GA, great apes (matches of at least 98% similarity); OWM, old world monkeys (93%); NWM, new world monkeys (89%); LG, lemurs and galagos (85%); DOG, dogs (80%). Cluster locations are indicated as coordinates in the March 2006 human genome sequence assembly.
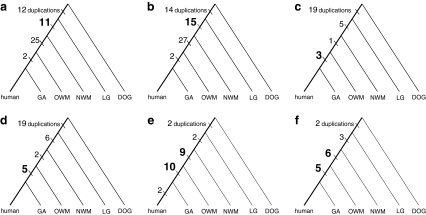
The human leukocyte antigen (HLA) gene cluster is known to be involved in narcolepsy (Nakayama et al., 2000) and celiac disease (Sollid et al., 2000). In addition, HLA has been observed in the association with prostate cancer (Haque et al., 2007) and breast cancer (Chaudhuri et al., 2000). For the HLA gene cluster, the MCMC method of Zhang et al. (2008) estimated 15 duplications in the lineage between NWM and LG, but our method inferred only 11 duplications (The numbers of the inferred events in the lineage are highlighted in bold in Figure 5a,b.
FIG. 5.
Duplication events inferred for (a) the HLA gene cluster by the combinatorial method, (b) the HLA gene cluster by the MCMC method, (c) the AKR1C gene cluster by the combinatorial method, (d) the AKR1C gene cluster by the MCMC method, and (e) the CYP1A1 gene cluster and (f) the CYP2A gene cluster by the combinatorial method.
The aldo-keto reductase (AKR) 1C gene cluster is involved in steroid hormone and nuclear receptors, and is associated with prostate disease, endometrial cancer, and mammary carcinoma (Penning et al., 2006). For this gene cluster, Figure 5c,d shows the inference results; our method identified 3 duplications between GA and OWM while the MCMC method inferred 5 duplications.
Another interesting observation is that several gene clusters were probably formed by recent gene duplications. For instance, we examined three Cytochrome P450 (CYP) gene clusters, which are associated with lung cancer (Crofts et al., 1994) and esophageal cancer (Sato et al., 1999). About 65% of the duplication events inferred for these clusters occurred in the evolutionary period between the divergence of humans from new-world monkeys and from great apes. Duplication events inferred for CYP1A1 and CYP2A are mapped onto the phylogeny in Figure 5e,f, respectively.
3.2. Validation test on simulated data
Starting from a 500-kb duplication-free sequence, we generated gene clusters by applying a series of duplication events based on the length and distance distributions for these events that we observed in the human genome. We generated 50 gene clusters formed from n duplications for 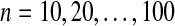 .
.
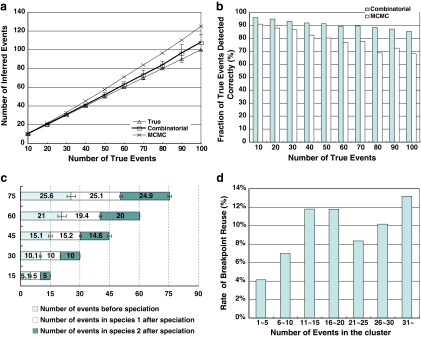
On these clusters, our method outperformed the MCMC method reported in Zhang et al. (2008) in terms of both the total number of inferred duplication events and the number of true duplications detected correctly, as indicated in Figure 6a,b. On average, our method estimated a number of events only 3% higher than the true number. A duplication event is expressed as a 3-tuple consisting of a source interval, a target location, and an orientation. If these values for an inferred event exactly match one of the true events, the event is defined to be correctly detected. The fraction of true events detected correctly by our method (91% on average) was much higher than for the MCMC method (80% on average).
FIG. 6.
Simulation results to evaluate detection of duplications. (a) Total numbers of reconstructed events and (b) fraction of true events detected correctly. (c) Simulation results of duplication detection for gene clusters in two species; each bar has three numbers: events before speciation, events in species 1 after speciation, and events in species 2 after speciation, for n true events of each type (i.e., 3n duplications in total) for n = 5, 10, 15, 20, 25. (d) Observed breakpoint reuse rate by the duplications in the human gene clusters.
It is worth noting that duplication breakpoints can be reused in the simulation dataset, since it was generated according to the observed distributions (Fig. 6d) without constraining the breakpoints to avoid reuse. However, the inferred events are still very close to the true events.
We also evaluated our method on simulated data sets in two species, which were generated as follows. Given a 500-kb duplication-free sequence, first, n duplication events before speciation are simulated for n = 5, 10, 15, 20, 25. Next, the entire gene cluster is copied, i.e., the sequence is treated as a common ancestral sequence of two species. Then, two different sets of n additional duplications are simulated, to represent duplications after speciation in each lineage, respectively. Finally, a self-alignment for each species and an inter-species alignment between the two species are obtained via BLASTZ (Schwartz et al., 2003).
For the simulation of two species, the performance of our method is better than its results for a single species (Fig. 6c). Since we have more constraint information for inferring duplications after speciation in the two species, the number of inferred events after speciation is almost exactly the same as the true number. The results for duplication before speciation are still similar to the single species case. For example, for n = 25 the method infers 2.4% more events before speciation than the true number, but only 0.8% more in total.
3.3. Defensin gene cluster
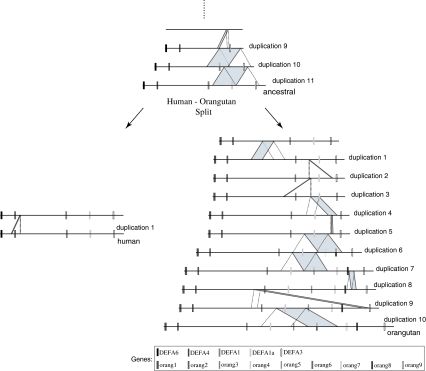
We reconstructed the ancestral sequence of the DEFA (defensin) gene cluster in the human (chr8:6769157-6869156) and orangutan (contig AC206038.3) genomes by applying our program with the extension for inferring duplications in two species. We inferred one duplication in the human lineage and 10 duplications in the orangutan lineage after the divergence of the two species. Before the divergence, 11 duplications were identified (Fig. 7).
FIG. 7.
Duplication reconstruction of the DEFA gene cluster in human and orangutan. The orangutan sequence gained 4 more genes from 10 duplications after the split of human and orangutan; the ancestral sequence of the two species had 5 genes. The dotted and shaded parallelograms represent the source and target regions of each duplication, respectively.
Currently, the orangutan DEFA gene cluster sequence is 1.86 times as long as the human one. This is explained by the fact that the orangutan cluster has 9 more duplications than the human one after the speciation. After rolling back all of the post-speciation duplications, the length of the cluster is almost the same in the two species. In addition to observing the number of events and the regions that are involved in each duplication, we investigated how genes are involved in the duplications. The gene annotations were obtained by using UCSC Genome Browser (http://genome.ucsc.edu) and GeneWise (Birney et al., 2004). The human DEFA cluster contains 5 genes, while the orangutan cluster has 9 genes. In the orangutan, 3 of the 10 duplications after the split (6th, 7th, and 10th in Fig. 7) involve genes. These duplications play a role in gaining 4 more genes in the orangutan. Interestingly, all three use the same source region containing the orang4 gene. Also, the orangutan sequence gained 2 more genes from the 6th duplication, although the source region contains only one gene. In this case, we suspect that there is a pseudo-gene in the source sequence. The 5th, 7th, and 8th events in the orangutan lineage and the 11th event in the ancestral one are tandem duplications.
Even though our method provides much useful information for genomic analysis in the DEFA gene cluster, it still has limitations. In general, we expect that two genomic regions which are involved in a duplication after the split of two species are likely to have higher similarity than the inter-species local alignments in those regions. Similarly, if the duplication occurs before speciation, the source and target regions are likely to have a lower similarity than their respective inter-species alignments. However, the 10th and 11th duplications in the ancestral lineage contradict this. These source and target regions have higher similarity levels with each other (99% in the human sequence and 97% in orangutan) than any of their corresponding inter-species alignments, but our algorithm, considering the genomic location of each alignment, nevertheless infers them as duplications before speciation, because this produces a more parsimonious solution. If they were assigned as events after speciation, we would have two duplications in each of the human and orangutan lineages respectively, i.e., 4 events in total, but our result has only two events in the ancestral lineage. Apparent discrepancies such as this may be explained by gene conversion events; thus the addition of a test for detecting gene conversions would improve accuracy and confidence in our solutions.
Another problem involves deletions. Suppose there are no inter-species alignments for two regions in one sequence due to a deletion in the other sequence, but the two regions in the first sequence form a self-alignment due to a duplication before speciation. Without an inter-species alignment in those regions to guide it, the algorithm may incorrectly detect the old duplication before speciation as a duplication after speciation in the first sequence, rather than a deletion in the other sequence. For example, the current orangutan DEFA contig is missing the 3′ end of the cluster because of incomplete sequencing, so incorrect duplications are reported there in the human lineage. In order to avoid this, we manually excluded the 3′ end of the human cluster which contains the DEFA5 gene for this analysis.
4. Conclusion
We have developed a combinatorial algorithm for reconstructing recent duplication and deletion operations in a gene cluster from a single present-day sequence or from two corresponding sequences in related species. The method in no way depends on the presence of protein-coding intervals, so for the purposes of our discussion a gene cluster can be understood to mean a region of the genome that contains recently duplicated segments. We have compared our combinatorial method with a probabilistic method for the same problem in Zhang et al. (2008) and shown that the relative performance of the combinatorial algorithm is quite good. In addition, a simulation study has demonstrated that our method is very effective for identifying the duplication history.
Our overarching goal is to find methods for analyzing large-scale evolutionary operations that integrate well with the specific needs of our current approach for producing whole-genome alignments (Miller et al., 2007). We are still in an exploratory stage where the aim is to investigate as many promising avenues as possible. This paper describes a new method whose accuracy, computational efficiency, and focus on an individual species make it a particularly strong contender.
It is appropriate to keep in mind that there are important limitations to the approach described here. A major limitation is that our methods depend heavily on the set of local alignments that they analyze, and it is widely appreciated that these alignments are highly sensitive to the particular programs and parameter settings used to produce them (Miller, 2001). The difficulty is exacerbated by the fact that, unlike an interspecies alignment where each pair of orthologous regions has been separated by the same amount of evolutionary time, with the intraspecies alignments that we require, each paralogous pair of regions can have a unique level of divergence. This makes selection of theoretically satisfying alignment scores (Chiaromonte et al., 2002) problematic. Another complication is that we are modeling a limited set of evolutionary operations, and other kinds of genomic recombination events can occasionally produce gene clusters that confuse methods that ignore the possibility of those events. Perhaps the most important of these confounding events are the so-called “gene conversion” events (Chen et al., 2007) (which again do not necessarily involve protein-coding regions). Such conversion events can make it difficult to determine the age of a duplication. These and other limitations are the subject of ongoing efforts in our lab and elsewhere to more accurately model the full complexity of evolutionary processes, and in particular to more precisely identify the orthology relationships within clusters of recently duplicated intervals.
Acknowledgments
We thank Yu Zhang, Cathy Riemer, and Bob Harris for helpful discussions. G.S. and W.M. were supported by NHGRI (grant HG02238), L.Z. was supported by NUS (ARF grant R-146-000-109-112), and T.V. was supported by the European Community (grant IRG-224885) and VEGA (grant 1/0210/10).
Disclosure Statement
No competing financial interests exist.
References
- Achaz G. Coissac E. Viari A., et al. Analysis of intrachromosomal duplications in yeast Saccharomyces cerevisiae: a possible model for their origin. Mol. Biol. Evol. 2000;17:1268–1275. doi: 10.1093/oxfordjournals.molbev.a026410. [DOI] [PubMed] [Google Scholar]
- Akhunov E. Akhunova A. Dvorak J. Mechanisms and rates of birth and death of dispersed duplicated genes during the evolution of a multigene family in diploid and tetraploid wheats. Mol. Biol. Evol. 2006;24:539–550. doi: 10.1093/molbev/msl183. [DOI] [PubMed] [Google Scholar]
- Bailey J. Liu G. Eichler E. An Alu transposition model for the origin and expansion of human segmental duplications. Am. J. Hum. Genet. 2006;73:823–834. doi: 10.1086/378594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bertrand D. Lajoie M. El-Mabrouk N., et al. Evolution of tandemly repeated sequences through duplication and inversion. Lect. Notes Comput. Sci. 2006;4205:129–140. [Google Scholar]
- Birney E. Clamp M. Durbin R. GeneWise and Genomewise. Genome Res. 2004;14:988–995. doi: 10.1101/gr.1865504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchette M. Kent W.J. Riemer C., et al. Aligning multiple genomic sequences with the threaded blockset aligner. Genome Res. 2004;14:708–715. doi: 10.1101/gr.1933104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chaudhuri S. Cariappa A. Tang M., et al. Genetic susceptibility to breast cancer: HLA DQB*03032 and HLA DRB1*11 may represent protective alleles. Proc. Natl. Acad. Sci. USA. 2000;97:11451–11454. doi: 10.1073/pnas.97.21.11451. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen J. Cooper D. Chuzhanova N., et al. Gene conversion: mechanisms, evolution and human disease. Nat. Rev. 2007;8:762–775. doi: 10.1038/nrg2193. [DOI] [PubMed] [Google Scholar]
- Chiaromonte F. Yap V. Miller W. Scoring pairwise genomic sequence alignments. Pac. Symp. Biocomput. 2002:115–126. doi: 10.1142/9789812799623_0012. [DOI] [PubMed] [Google Scholar]
- Crofts F. Taioli E. Trachman J., et al. Functional significance of different human CYP1A1 genotypes. Carcinogenesis. 1994;15:2961–2963. doi: 10.1093/carcin/15.12.2961. [DOI] [PubMed] [Google Scholar]
- Elemento O. Gascuel O. Lefranc M.P. Reconstructing the duplication history of tandemly repeated genes. Mol. Biol. Evol. 2002;19:278–278. doi: 10.1093/oxfordjournals.molbev.a004081. [DOI] [PubMed] [Google Scholar]
- Force A. Lynch M. Pickett F.B., et al. Preservation of duplicate genes by complementary, degenerative mutations. Genetics. 1999;151:1531–1545. doi: 10.1093/genetics/151.4.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green E.D. Strategies for the systematic sequencing of complex genomes. Nat. Rev. Genet. 2001;2:573–573. doi: 10.1038/35084503. [DOI] [PubMed] [Google Scholar]
- Haque A. Younger A.R. Amria S., et al. HLA class II protein expression in prostate cancer cells. J. Immunol. 2007;178:48.22. [Google Scholar]
- Hou M. Personal communication 2007.
- Hurles M. Gene duplication: the genomic trade in spare parts. PLoS Biol. 2004;2:e206. doi: 10.1371/journal.pbio.0020206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Z. Tang H. Ventura M., et al. Ancestral reconstruction of segmental duplications reveals punctuated cores of human genome evolution. Nat. Genet. 2007;39:1361–1368. doi: 10.1038/ng.2007.9. [DOI] [PubMed] [Google Scholar]
- Lander E.S. Linton L.M. Birren B., et al. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- Lupski J.R. Genomic rearrangements and sporadic disease. Nat. Genet. 2007;39:S43–S47. doi: 10.1038/ng2084. [DOI] [PubMed] [Google Scholar]
- Lynch M. Conery J.S. The evolutionary fate and consequences of duplicate genes. Science. 2000;290:1151–1155. doi: 10.1126/science.290.5494.1151. [DOI] [PubMed] [Google Scholar]
- Ma J. Ratan A. Raney B.J., et al. The infinite sites model of genome evolution. Proc. Natl. Acad. Sci. USA. 2008;105:14254–14261. doi: 10.1073/pnas.0805217105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Margulies E. Cooper G.M. Asimenos G., et al. Analyses of deep mammalian sequence alignments and constraint predictions for 1% of the human genome. Genome Res. 2007;17:760–764. doi: 10.1101/gr.6034307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller W. Comparison of genomic DNA sequences: solved and unsolved problems. Bioinformatics. 2001;17:391–397. doi: 10.1093/bioinformatics/17.5.391. [DOI] [PubMed] [Google Scholar]
- Miller W. Rosenbloom K. Hardison R.C., et al. 28-way vertebrate alignment and conservation track in the ucsc genome browser. Genome Res. 2007;17:1797–1808. doi: 10.1101/gr.6761107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nadeau J.H. Taylor B.A. Lengths of chromosomal segments conserved since divergence of man and mouse. Proc. Natl. Acad. Sci. USA. 1984;81:814–818. doi: 10.1073/pnas.81.3.814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakayama J. Miura M. Honda M., et al. Linkage of human narcolepsy with HLA association to chromosome 4p13-q21. Genomics. 2000;65:84–86. doi: 10.1006/geno.2000.6143. [DOI] [PubMed] [Google Scholar]
- Ohno S. Evolution by Gene Duplication. Springer; Berlin: 1970. [Google Scholar]
- Penning T. Steckelbroeck S. Bauman D.R., et al. Aldo-keto reductase (AKR) 1C3: role in prostate disease and the development of specific inhibitors. Mol. Cell. Endocrinol. 2006;248:182–191. doi: 10.1016/j.mce.2005.12.009. [DOI] [PubMed] [Google Scholar]
- Raphael B. Zhi D. Tang H., et al. A novel method for multiple alignment of sequences with repeated and shuffled elements. Genome Res. 2004;14:2336–2336. doi: 10.1101/gr.2657504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sammeth M. Stoye J. Comparing tandem repeats with duplications and excisions of variable degree. TCBB. 2006;3:395–407. doi: 10.1109/TCBB.2006.46. [DOI] [PubMed] [Google Scholar]
- Sato M. Sato T. Izumo T., et al. Genetic polymorphism of drug-metabolizing enzymes and susceptibility to oral cancer. Carcinogenesis. 1999;20:1927–1931. doi: 10.1093/carcin/20.10.1927. [DOI] [PubMed] [Google Scholar]
- Schwartz S. Kent W.J. Smit A., et al. Human-mouse alignments with BLASTZ. Genome Res. 2003;13:103–107. doi: 10.1101/gr.809403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sollid L. Markussen G. Ek J., et al. Evidence for a primary association of celiac disease to a particular HLA-DQ α∕β heterodimer. J. Exp. Med. 2000;169:345–350. doi: 10.1084/jem.169.1.345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wong K.K. deLeeuw R.J. Dosanjh N.S., et al. A comprehensive analysis of common copy-number variations in the human genome. Am. J. Hum. Genet. 2007;80:91–104. doi: 10.1086/510560. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang L. Ma B. Wang L., et al. Greedy method for inferring tandem duplication history. Bioinformatics. 2003;19:1497–1504. doi: 10.1093/bioinformatics/btg191. [DOI] [PubMed] [Google Scholar]
- Zhang Y. Song G. Hsu C., et al. Simultaneous history reconstruction for complex gene clusters in multiple species. In: Altman R.B., editor; Dunker A.K., editor; Hunter L., editor. Proc. Pac. Symp. Biocomput. 2009. 2009. pp. 162–173. [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. Song G. Vinar T., et al. Reconstructing the evolutionary history of complex human gene clusters. In: Vingron M., editor; Wong L., editor. Proc. 12th Annu. Int. Conf. Res. Comput. Mol. Biol. 2008. pp. 29–49. [Google Scholar]