Mosaic Graphs and Comparative Genomics in Phage Communities

Abstract

Comparing the genomes of two closely related viruses often produces mosaics where nearly identical sequences alternate with sequences that are unique to each genome. When several closely related genomes are compared, the unique sequences are likely to be shared with third genomes, leading to virus mosaic communities. Here we present comparative analysis of sets of Staphylococcus aureus phages that share large identical sequences with up to three other genomes, and with different partners along their genomes. We introduce mosaic graphs to represent these complex recombination events, and use them to illustrate the breath and depth of sequence sharing: some genomes are almost completely made up of shared sequences, while genomes that share very large identical sequences can adopt alternate functional modules. Mosaic graphs also allow us to identify breakpoints that could eventually be used for the construction of recombination networks. These findings have several implications on phage metagenomics assembly, on the horizontal gene transfer paradigm, and more generally on the understanding of the composition and evolutionary dynamics of virus communities.

1. Introduction

Viruses that infect bacteria, known as phages, evolve by accumulating mutations, but they also evolve through recombination events in which they exchange genetic material with other phages. These events have been suggested to explain the mosaic structure that arises when the genomes of two phages are compared: nearly identical sequences alternate with sequences that are merely similar or even completely divergent. The first evidence of such exchanges in bacteriophages dates back to the early 1990s and was obtained by heteroduplex mapping (Highton et al., 1990). Since then, numerous mosaics have been identified by sequence comparison, and the mosaic structure of bacteriophages is now a well-documented phenomenon, (Hatfull, 2008).

In this article, we study co-linear phages that infect a common host. These phages have small genomes—approximately 44,000 bp—that often have conserved order of gene function, called modules, such as:

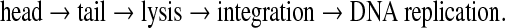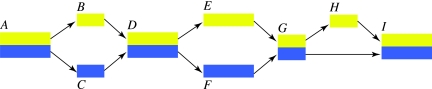
When two co-linear phages are compared along their genomes, the sequences coding for modules alternate between nearly identical sequences and more divergent ones. It may even be the case that two sequences coding for the same module do not have any recognizable homology. Graphs, such as the one in Figure 1, can be used to classify these events: nearly identical sequences are merged in a single block and arrows indicate transitions between consecutive intervals of the same genome.

FIG. 1.

Comparing two co-linear genomes with a directed graph. In this graph, the two colored bands represent the genomes. In block A both genomes are nearly identical, divergent in blocks B and C, identical in block D, and again divergent in blocks E and F. Block H does not appear in the second genome.

Although most studies still rely solely on two-by-two comparisons of phages, the first hints of mosaic communities began to appear a few years ago. For example, in Kwan et al. (2005), a total of 27 Staphylococcus aureus phage genomes are compared, showing genomic regions having more than 98% identity over more than 50 bp shared between one phage and as much as 16 other phages. A recent study of 50 mycobacteriophages that infect a common host also reveals pervasive mosaicism (Hatfull et al., 2008). Because only a tiny fraction of viruses are amenable to study using traditional cultivation methods, the wealth of genetic information is frequently accessed using metagenomic analysis. Viruses sampled in the same environment are in close contact, and recombination events observed in cultivated viruses are thus likely to happen in those communities. There is even evidence of long-range propagation of recombination events: nearly identical sequences of phages have already been detected in multiple environments, with varying geographical locations, both in fresh and saline waters (Breitbart et al., 2004; Short and Suttle, 2005; Bryan et al., 2008). Understanding the structure and evolution of phage communities is a major challenge. Due to the presence of many recombination events, traditional tools such as phylogenetic trees (Rohwer and Edwards, 2002) must be complemented by other methods. Gene phamilies (Hatfull et al., 2006), for example, compare the distinct evolutionary histories of genes that belong to a recombinant organism. Information on recombination events may also be incorporated in phylogenetic trees, such as in Glazko et al. (2007), or more general clustering approaches can be used to represent the evolutionary and functional relationships between phages in terms of shared genes (Lima-Mendez et al., 2008). Recombination networks have been extensively used in the context of population studies (Gusfield and Bansal, 2005; Huson and Bryant, 2006), modeling the evolution of fixed length sequences with point mutations and recombination events. Unfortunately, none of these approaches allows the representation and interpretation of the extensive recombination events observed in mosaic communities.

Even if numerous studies point out that recombination events are a major feature in phage evolution and organization, very little is known about the relationships between these events. Are sequences shared between more than two phages in closely related organisms? What types of transition may occur when similarity ends? Can all participating sequences become divergent from each other? Are the divergent sequences unique, or are they reused by third genomes? Do “parent” genomes survive along their recombinant descendants in a community? Are recombination breakpoints reused?

In this study, we report that sharing of large identical, or nearly identical, sequences (average 2723 base pairs with 99.98% identity) is a frequent phenomenon among groups of phages that infect Staphylococcus aureus. Recombinations occur almost anywhere along the typical genome of 44,000-bp phages, often involving more than two species, and phages that are identical along 75% of their genomes may diverge completely, gaining different partners in the divergent sequences. These interactions are complex, and we developed new concepts and representations in order to describe them: we introduce mosaic graphs as a complement to phylogenetic trees (Rohwer and Edwards, 2002) and reticulate representations (Hatfull et al., 2006; Glazko et al., 2007; Lima-Mendez et al., 2008; Huson and Bryant, 2006) in trying to understand phage communities.

2. Tiling ROSA

In order to assess the amount of “shared sequences” in phage communities, we conducted an exploratory experiment on the set of 27 phages described in Kwan et al. (2005), using a threshold of 98% identity over more than 500 bp (data not shown). These data turned out to be far more complex than we expected, but their analysis provided crucial observations.

A first unexpected finding was that the mismatches in alignments tended to be clustered in small regions, leaving between them large fragments that were identical. Using phage ROSA (AY954961) in BLAST (Altschul et al., 1990) queries, we identified 19 intervals of ROSA's genome of at least 400 bp that were 100% identical to sequences in five other S. aureus phages. These intervals cover 35,501 bp of ROSA's 43,155-bp genome (82.26%). Many pairs of intervals were at most one nucleotide apart, and we merged them to obtain 12 tiles of size ranging from 497 bp to 10390 bp, averaging 2958 bp. Table 1 shows the bounds of these intervals for ROSA and for the corresponding phages.

Table 1.

Covering Phage ROSA with Phages PhiNM4, 29, 53, 71, 80, and 88

		Start	End	Start	Size	Errors	Percentage identity
1	Rosa	1197	3212 Phage 71	1123	2016	1	99.95
2	Rosa	3271	6325 Phage 71	3197	3055	1	99.97
3	Rosa	6326	6863 PhiNM4	23734	538	0	100.00
4	Rosa	7874	18263 PhiNM4	24319	10390	0	100.00
5	Rosa	18265	22240 Phage 88	17226	3976	2	99.95
6	Rosa	22241	23491 Phage 53	22125	1251	0	100.00
7	Rosa	23492	28089 PhiNM4	39961	4598	1	99.98
8	Rosa	31047	36361 PhiNM4	4965	5314	1	99.98
9	Rosa	36462	36958 Phage 53	37544	497	0	100.00
10	Rosa	37062	39381 Phage 53	38144	2320	0	100.00
11	Rosa	39517	40064 Phage 53	40596	548	0	100.00
12	Rosa	42104	43101 Phage 29	41664	998	1	99.90

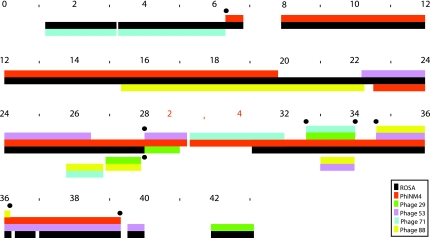
These data are perhaps best appreciated by looking at Figure 2, which shows how the five other genomes cover ROSA. Large identical, or nearly identical, sequences between phages are often attributed to recent recombination events (Nesbo et al., 2006). If this is the case, then ROSA must have participated in—or is the product of—many recent recombination events.

FIG. 2.

Tiling ROSA. Each solid band of a single color, or tile, represents a sequence that is shared between phage ROSA and another phage. These 12 tiles cover 35,501 bp of ROSA's genome (82.26%) with 7 errors, that is, 99.98% identity on average.

Except for phage PhiNM4 (DQ530362), the coordinates of all phages of Table 1, are comparable, reflecting the co-linearity of the genomes. The modules of PhiNM4 form a cyclic permutation of the order of the other five. When genomes are linear, such a cyclic permutation is due to a transposition in the genome. However, if the genomes are circular, a cyclic permutation merely accounts for a different start point in the assembly of the genome.

The fact that more than 80% of ROSA's genome could be covered by large identical sequences from already sequenced genomes was a surprise, and a good one. But it became quickly evident that we did not have the representation tools to understand the relations between these genomes. These are developed in the next sections.

3. From Alignments to Multiple Alignments

The prevalence of large identical sequences in a set of genomes offers a rather unique opportunity in comparative genomics, in the sense that it is easy to construct multiple alignments with pairs of alignments. In this section, we will study multiple alignments that can be constructed from the comparison of the set of phages of the preceding section: phages ROSA, PhiNM4, 29 (AY954964), 53 (AY954952), 71 (AY954962), and 88 (AY954966). First we have:

Definition 1

Let i ≤ k, and two alignments of genome A, one with interval A[i.j] with an interval of genome B, and one with interval A[k.l] with an interval of genome C. The two alignment overlap if k ≤ j. Two overlapping alignment induce a multiple alignment of genomes A, B and C in the interval A[k.min(j, l)].

In general, multiple alignments induced by pairs of alignments can be of poor quality. However, starting with alignments of identical sequences, or sequences that have occasional single mismatches separated by a few hundred nucleotides, the result is pretty good, as long as the overlapping intervals have significant lengths.

Since we now work with a fixed set of genomes, we used the software REPuter (Kurtz et al., 2001) in order to identify identical sequences of at least 400 bp. This software is based on a very efficient algorithm to find repetitions in a genome, or, in our case, the concatenation of two genomes. As in the preceding section, intervals that were at most one nucleotide apart were merged in a single alignment. Table 2 shows 23 alignments between nearly identical sequences, whose sizes range from 497 to 12,032 bp, averaging 2723 bp.

Table 2.

Shared Sequences between Phages Rosa, PhiNM4, 29, 53, 71, and 88

		Start	End	Start	End	Size	Errors	Percentage identity
1	Rosa	1197	3212 Phage 71	1123	3138	2016	1	99.95
2	Rosa	3271	6325 Phage 71	3197	6251	3055	1	99.97
3	Rosa	6319	6863 PhiNM4	23734	24271	545	0	100.00
4	Rosa	7874	19905 PhiNM4	24319	36350	12032	2	99.98
5	Rosa	15319	22240 Phage 88	14280	21201	6922	3	99.96
6	Rosa	22192	26454 Phage 53	22125	26387	4263	1	99.98
7	Rosa	22570	28089 PhiNM4	39038	1368	5520	1	99.98
8	Phage 71	25735	26922 Phage 88	25412	26599	1188	0	100.00
9	Phage 29	27408	28500 Phage 88	26777	27872	1096	0	100.00
10	PhiNM4	1370	2312 Phage 29	28596	29538	943	0	100.00
11	PhiNM4	1370	2521 Phage 53	29098	30249	1152	0	100.00
12	PhiNM4	2624	5291 Phage 71	29166	31833	2668	1	99.96
13	Rosa	31047	36361 PhiNM4	4965	10279	5315	1	99.98
14	Rosa	32642	34064 Phage 29	33988	35410	1423	0	100.00
15	Rosa	32642	34064 Phage 71	33671	35093	1423	3	99.79
16	Phage 53	33996	35065 Phage 88	32454	33523	1070	0	100.00
17	Rosa	34637	36238 Phage 88	34723	36322	1602	1	99.94
18	Rosa	34637	36361 Phage 53	35719	37443	1725	0	100.00
19	PhiNM4	8554	13285 Phage 53	35719	40450	4732	0	100.00
20	Rosa	36462	36958 Phage 53	37544	38040	497	0	100.00
21	Rosa	37062	39381 Phage 53	38144	40463	2320	0	100.00
22	Rosa	39517	40064 Phage 53	40596	41143	548	0	100.00
23	Rosa	42104	43101 Phage 29	41664	42661	998	1	99.90

In order to show the induced multiple alignements, Figure 3 displays them using ROSA coordinates (in 1000 bp) for most of the genomes, and phage PhiNM4 coordinates when ROSA is absent. In the first line, between positions 0 and 12,000, only pairs of genomes align well. On the second line, overlapping alignments start to appear: for example, the alignment of ROSA and PhiNM4 recruits phage 88 around position 15,000. On the third line, there are three examples of parallel alignments, meaning that two distinct alignments exist at approximately the same positions along the genomes. Line 3 contains two examples of multiple alignments of four sequences: phages ROSA, PhiNM4, 29, and 71 are equal on a length of 1423 bp except for 3 mismatches; and phages ROSA, PhiNM4, 53, and 88 are equal on a length of 1602 bp except for 1 mismatch.

FIG. 3.

Shared sequences between phages ROSA, PhiNM4, 29, 53, 71, and 88. The 23 alignments of Table 2 are drawn along phage ROSA coordinates (in 100 bp), except at marker 28 where coordinates are temporarily switched to phage PhiNM4 coordinates. Each solid line of color represents a phage genome. When two sequences are identical, the corresponding lines are stacked, creating multiple alignments when alignments overlap. Complex breakpoints, where at least two sequences are dropped and/or recruited simultaneously, are indicated by back dots.

We define breakpoints between multiple alignments when a new sequence is recruited into the alignment, or when a sequence is dropped from the alignment. A breakpoint is complex if at least two sequences are recruited and/or dropped almost simultaneously. Black dots in Figure 3 mark the 8 complex breakpoints in which sequences are dropped or recruited into an alignment within 15 bp. For example, phage ROSA recruits phage PhiNM4 at position 6319, and drops phage 71 at position 6325, a difference of 6 bp. A more complex example occurs around position 28,000: phage PhiNM4 drops phage ROSA at position 1368, and synchronously recruits phages 29 and 53 at position 1370. It is a striking feature of this dataset that 5 of the 8 complex breakpoints are synchronous. The positions of these synchronous events are bolded in Table 2.

4. Mosaic Graphs

The representation of Section 3 can give a quite accurate description of the relations between phages, as long as there is one genome—such as ROSA—that can be used almost always as a reference. In general, this will not be the case, and we need a more general representation that is independent from a particular genome.

In order to develop this representation, we must make a certain number of assumptions on the relations between compared genomes. In the preceding sections, we used the term “shared sequences” rather informally, but we were able to establish that there is ample evidence of sequence sharing in phage communities in the following sense:

Definition 2

A shared sequence between genomes A and B is a subsequence that appears exactly once in each genome, and that is of maximal length.

When a genome is compared to k other genomes, its sequence can be decomposed into alternating intervals of overlapping shared sequences and unique intervals. These unique intervals can be as short as one nucleotide. Using Definition 2, the multiple alignments induced by shared sequences are trivial: every column contains the same nucleotide. Such multiple alignments can thus be described by the bounds of the intervals of each of its participating genome. We next introduce the concept of mosaic graphs:

Definition 3

Given a set of genomes 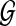, and a collection of shared sequences between pairs of genomes in S. A block is defined as a maximal induced multiple alignment, or as a unique interval of a genome. The mosaic graph of 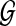is a directed graph whose vertices are blocks, and in which block S is connected to block T, represented as S → T, if S contains interval [i.j] of a genome in 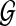, and T contains the interval [j + 1.k] of the same genome.

Mosaic graphs are meant to capture the relations between sequences that evolved by recombination events, but they have the advantage of being uniquely defined by the initial collection of shared sequence. In practice, two blocks separated by a single point mutation can be merged, and small blocks can be omitted from a graphical representation in order to yield a better visual representation. We next discuss one such example.

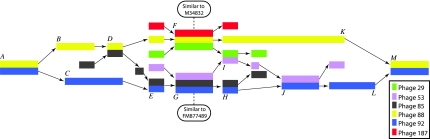
Our preliminary experiment showed that phages 88 and 92 (AY954967) shared their genomes along the initial half, but then each phage took a different path: on those parallel paths there was a pair of distinct multiple alignments of unusual depth. In these alignments, phage 88 associates with phages 29 and 187 (AY954950), and phage 92 with phages 53 and 85 (AY954953).

The mosaic graph of these 6 phages—with partial sequences³ for phages 29, 53, 85, and 187—uses the blocks of Table 3. There are 8 alignments of two sequences, and 2 multiple alignments of three sequences. The error count for the multiple alignments was obtained by counting the number of nucleotides that differ from the majority in a column of the alignment. The last column shows the percentage of correct nucleotides in the alignment. Figure 4 displays the resulting graph in the interval ranging from approximate positions 21,000 to 35,000 of phage 88.

Table 3.

Blocks of the Mosaic Graph of Phages 88, 92, 29 53, 85, and 187

		Start	End	Start	Size	Errors	Percentage matches
A	Phage 88	4	22484 Phage 92	1	22481	4	99.98
D	Phage 88	24403	25404 Phage 85	26417	1002	0	100.00
E	Phage 92	25305	26155 Phage 85	27658	851	1	99.88
F	Phage 88	26566	27946 Phage 29	27198	1381
	Phage 88	26566	27946 Phage 187	21618	1381	11	99.73
	Phage 29	27198	28577 Phage 187	21618	1380
G	Phage 92	26156	27688 Phage 85	28509	1533
	Phage 92	26156	27688 Phage 53	27552	1533	3	99.93
	Phage 53	27552	29084 Phage 85	28509	1533
I	Phage 53	29085	30256 Phage 29	28583	1172	1	99.91
H	Phage 92	27689	28534 Phage 85	30042	846	0	100.00
J	Phage 92	28547	29859 Phage 53	30597	1313	4	99.70
M	Phage 88	34186	39299 Phage 92	33383	5114	0	100.00
N	Phage 88	39790	43231 Phage 92	38987	3442	0	100.00

FIG. 4.

The partial mosaic graph of phages 29, 53, 85, 88, 92, and 187. The vertices of the graph are the multiple alignments of nearly identical sequences of Table 3, together with sequences that are unique to each genome. Two vertices S and T are connected if one of the genomes has consecutive intervals that belong to S and T. The two multiple alignments in the center have no recognizable homology between them but both contain sub-sequences highly similar to integrase genes. (Blocks are not necessarily to scale.)

The two blocks with multiple alignments of three sequences, F and G, have no recognizable homology between them. However both contain a sub-sequence highly similar to annotated integrase genes: phage Phi-11 (M34832) for sequences that clusters with phage 88, and phage Phi6390 (FM877489) for sequences that clusters with phage 92.

This region displayed also contains 3 complex breakpoints. One breakpoint is synchronous, G → I, and the two others occur within 12 bp: 5 extra bp in F → I, and 12 extra bp in H → J. Two of these complex breakpoints occur at the same ‘position’ in the genomes, begging the following question: is the transition F → H, missing for good reasons, or is there a phage out there waiting to be sequenced and that would make the required transition? In order to test the second possibility, we created a chimera composed of the last 495 bp of phage 88 in block F, followed by the 5 extra bp after block F, followed by the first 500 bp of phage 92 in block G. This composite sequence has an alignment with phage PhiMR25 (AB370205) with 996 identities over 1000 nucleotides. Thus we confirm that the desired transition is already sequenced.

4.1. From mosaic graphs to recombination networks

Mosaic graphs of related genomes and multiple alignments of similar sequences both give representations of evolutionary events, one focusing on recombination events and the other on point mutations. These representations do not specify the nature and order of the evolutionary events: this is done by phylogenetic inference, and the resulting constructions are subject to evaluation by parsimony or likelihood criteria.

Based on multiple alignments, phylogenetic trees are constructed under the assumption of point mutations modifying a common ancestral sequence, allowing for occasional horizontal gene transfers (Glazko et al., 2007). Recombination networks used in population studies (Gusfield and Bansal, 2005; Huson and Bryant, 2006) recognize recombination events and point mutations on an equal footing (Gusfield and Bansal, 2005; Huson and Bryant, 2006), but still rely on the common ancestor assumption.

Untangling the evolution history of phages that underwent frequent recent recombination events can certainly use the framework of recombination networks. In this case, they would be defined as networks that describe the nature and order of recombination events explaining a given mosaic graph. However, the construction of these networks cannot rest on the assumptions that held in population studies: gene sequences that code for analog functions often have no recognizable homology, ruling out the possibility of a fairly recent common ancestor; and breakpoints are given by the mosaic graph instead of being inferred. This opens up some exciting combinatorial problems:

Problem 1

Given a set of co-linear genomes that evolved by recombination events, and possible extinctions, from divergent ancestors, when is it possible to reconstruct its evolution history?

Problem 2

How can the phylogenetic information available by alignments of nearly identical sequences be used to guide the reconstruction?

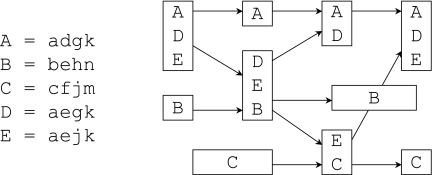
To the best of our knowledge, very few results seem to exist for Problem 1. In Figure 5, an instance of the problem is given with its mosaic graph. Each genome has four modules, and equal labels indicate shared sequences. We have the following two results that, unfortunately, are only sufficient conditions. The first one is immediate since any recombinant shares each part of its sequence with at least one parent.

FIG. 5.

An instance of the reconstruction problem and its mosaic graph.

Proposition 1

If there are no extinction events, then any genome that has a unique sequence in the graph is an ancestor.

The second one is almost as obvious, but can be used to resolve the example in Figure 5.

Proposition 2

If removing genome G disconnects the graph, then G has a parent in each remaining component.

In the example, genome E is the only genome that disconnects the graph. Of the two remaining components, one is trivial containing only genome C, and removing genome D from the other further disconnects the graph. Thus, there exists a reconstruction with two recombination events, with genomes A and B as parents of genome D, and genomes D and C as parents of genome E. Note that if, for example, B became extinct, either A or D could be ancestral in an optimal reconstruction.

5. A Survey of All Sequenced Viruses

In this section, we present results on shared sequences among the 2323 publicly available viral genomes, as of July 2009. The 3419 contigs—or chromosomes—representing these genomes were downloaded from the NCBI website and processed on a 64-nodes computer cluster. The computation took less than 8 hours and resulted in the discovery of 4610 shared segments of at least 400 bp in a total 810 pairwise sequence sharing.

To get a better understanding of the nature and the degree of interactions between the genomes, we introduce the genome interaction graph. This graph is defined by a set of vertices, each representing a distinct viral genome and a set of weighted edges. An edge connects two vertices if the corresponding genomes share at least one sequence of minimal fixed length (400 bp in the curent survey). The weight ω of an edge between genomes g₁ and g₂ reflects the amount of sequence sharing between these two genomes. It is equal to the percentage of shared sequences versus the total length of compared genomes, and is computed by the following formula, where genomes g₁ and g₂ share the sequences .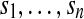

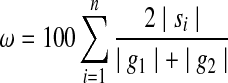We are interested in the connected components of the interaction graph. Isolated vertices, that is, genomes that share no sequence with any other, form the majority—1880 over 2323. The 343 remaining genomes are classified into 96 components whose five largest contain between 8 and 40 genomes. An important fraction of these components, 52 out of 96, are composed solely of phages genomes.

The partition induced by the connected components can be used as a simple tool to classify viral sequences, especially phage sequences. Indeed, the simple criteria of sharing a sequence of length at least 400 bp seems to be sufficient to discriminate between different hosts, and different genome sizes.

The largest component regroups 40 Staphylococcus aureus phages with lengths ranging from 39,620 bp to 47,432 bp. These phages show a remarkable degree of sequence sharing along their genome, represented by 417 genome-to-genome interactions. A total of 38 Staphylococcus phages share sequences with more than 14 other genomes and 25 share sequence with 20 or more other genomes. The rate of sequence sharing, as calculated by the above formula, was found to vary between 1%, found in 20 interactions, and 89%, between phage 53 and phage 77.

Two other components contained exclusively Staphylococcus aureus phages, one with three genomes with lengths ranging from 16,784 to 18,227 bp, and the other with two genomes with lengths, respectively, of 127,395 and 138,715 bp.

On the other hand, host and genome size are not the only factors promoting the exchange of sequences. For example, eight Mycobacterium phage genomes of circa 68k bp were divided in three different connected components. A pairwise comparison of any two genomes belonging to two distinct components revealed no more than 50 shared bp. This justifies the separation of these eight genomes and raises the question as to what other criteria promote the exchange of sequences amongst Mycobacterium phages of the same size.

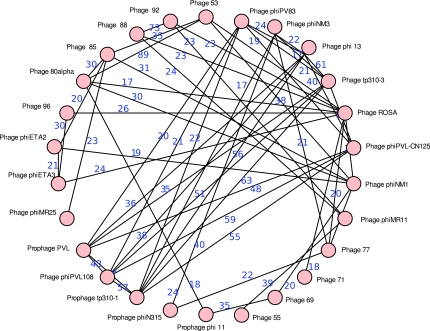
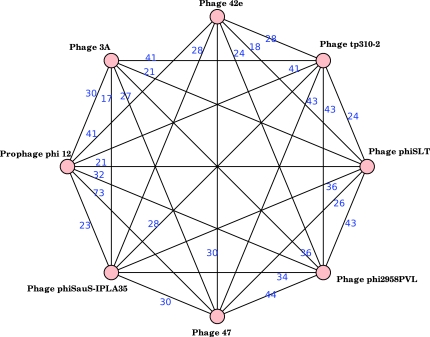
We studied further the impact of sequence sharing as a tool for clustering viral genomes by tightening the rules that define edges in the interaction graph. Imposing that two genomes share at least 15% of their combined lengths splits the largest component into two smaller components shown in Figures 6 and 7. The second figure is particularly remarkable in the sense that the component is almost complete, but two of the genomes, phages 3A and 42e, do not share any sequence. This component is thus an excellent starting point for the practical development of the concepts introduced in Section 4.

FIG. 6.

This graph is a sub-component of the interaction graph that clusters Staphylococcus phages. The numbers on the edges represent the percentage of the combined lengths that is comprised of shared sequences.

FIG. 7.

This graph is a sub-component of the interaction graph that clusters Staphylococcus phages. The graph is complete except for the missing edge between phages 3A and 42e that have no shared sequence of at least 400 bp.

This exploratory interaction graph is a good example as to the difficulties associated with classification of phages using a purely taxonomic system. Indeed, despite the inner natural segregation based on the host and the genome size, the intricate exchanges within the same interaction graph make it difficult to hierarchically represent phages in a natural and intuitive way. Mosaic graphs on the other hand are well suited for such task and are insightful abstractions underlying phages genomic mosaicism.

6. Conclusion

We showed that recombination events involving identical or nearly identical sequences are numerous in groups of phages that infect Staphylococcus aureus, and in many other families of phages that infect other bacteria. If this phenomenon is widespread, it has an immediate impact on the environmental metagenomics sequencing strategies. Next generation sequencing—such as 454 (Margulies et al., 2005) or Illumina (Bentley, 2006)—allows deeper sequencing of short reads, but these are often single reads. While such technologies are suitable for resequencing, mate-paired reads are necessary for de novo sequencing of genomes with long repeats. Even if phages seldom have long repeats, shared sequences introduce artificial repeats that can fool assembly software: when two genomes share a large sequence S such as in

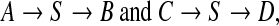an assembler working with single reads cannot distinguish between

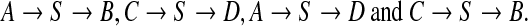The output of the assembler would thus be, at best, the mosaic graph itself.

A second consequence of our findings is that it sheds a new light on the concept of gene transfers between phages. Conventional wisdom recognizes transfers as from an organism to another, with recently transfered sequences more similar than sequences resulting from older transfers. In this context, what could be the meaning of long identical sequences in three or more different phages? Since phage ROSA is mostly made up of sequences identical to at least 5 other phages, how many events are necessary to construct ROSA, even assuming that transfers between two phages are not necessarily contiguous? Or is ROSA a donor?

Such questions are not easy to answer since the precise mechanisms that lead to mosaic structures are not entirely elucidated (Martinsohn et al., 2008). One interesting suggestion (Hendrix, 2002) is random recombination on a large scale followed by selection of the fittest. Clearly, some newly created genomes would lack vital parts, but if the recombinations happen at the junctions of the mosaic graph, then the resulting chimera could very well be able to reproduce itself. In this sense, a mosaic graph would be a better representation of a community of phages than a collection of individual genomes. We saw that junctions between blocks of the mosaic graph are complex and varied, and that many of the possible paths in the graph are indeed followed by particular phages. Are the paths that were unobserved in our datasets mostly non-existent, or just waiting to be sequenced?

Acknowledgments

A.B. was supported by NSERC (grant 121768). G.P. is supported by NSF (grant OCE 08-26650). M.B. and G.P. are supported by NIH (grant P20 RR-16467 from the National Center for Research Resources). The article's contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.

Disclosure Statement

No competing financial interests exist.