Abstract
Sequence alignment depends on the scoring function that defines similarity between pairs of letters. For local alignment, the computational algorithm searches for the most similar segments in the sequences according to the scoring function. The choice of this scoring function is important for correctly detecting segments of interest. We formulate sequence alignment as a hypothesis testing problem, and conduct extensive simulation experiments to study the relationship between the scoring function and the distribution of aligned pairs within the aligned segment under this framework. We cut through the many ways to construct scoring functions and showed that any scoring function with negative expectation used in local alignment corresponds to a hypothesis test between the background distribution of sequence letters and a statistical distribution of letter pairs determined by the scoring function. The results indicate that the log-likelihood ratio scoring function is statistically most powerful and has the highest accuracy for detecting the segments of interest that are defined by the statistical distribution of aligned letter pairs.
Key words: hypothesis testing, local alignment, power, scoring function, sequence alignment
1. Introduction
Sequence alignment is one of the most important problems in computational biology. Similar segments in gene or protein sequences often indicate evolutionary homology or functional relationships between the genes or proteins. Sequence alignment tasks are generally categorized into three different types: (1) global sequence alignment, which determines the best alignment of the sequences with their entire lengths by adjusting their relative positions and inserting gaps when necessary; (2) local sequence alignment, which determines segments in the sequences that are most similar with each other; and (3) semi-global or fit alignment, which searches for the occurrence of a short query sequence in a large sequence database (Waterman, 1995). In any case, a scoring function needs to be defined to evaluate the similarity of the sequences and a computational algorithm is employed to search for the best alignment. The classical algorithms are based on dynamic programming: the Smith-Waterman algorithm (Smith and Waterman, 1981) for local alignment and the Needleman-Wunsch algorithm (Needleman and Wunsch, 1970) for global alignment. Many heuristic algorithms have been proposed to speed up the search procedure, such as BLAST (Altschul et al., 1990), FASTA (Pearson, 1990), CLUSTAL W (Thompson et al., 1994), PSI-BLAST (Altschul et al., 1997), BLAT (Kent, 2002), BALSA (Zhu et al., 1998; Webb et al., 2002), ProbCons (Do et al., 2005), DIALIGN-T(X) (Subramanian et al., 2005, 2008), and Bowtie (Langmead et al., 2009). No matter what algorithm is used, the choice of a scoring function is the key to producing good alignments. Several scoring functions have been introduced, most of which are implicitly log-odds matrices (Altschul, 1991), i.e., log-likelihood ratio scoring functions. Dayhoff's PAM (Dayhoff et al., 1978) and Henikoff's BLOSUM (Henikoff and Henikoff, 1992) matrices are generally considered the standard in many applications. The PAM matrices were initially derived based on an explicit evolutionary model of closely related sequences and the observed mutations in these sequences. Dayhoff et al. (1978) separated proteins into families, constructed phylogenetic trees for each family, and examined every branch of the resulting trees for substitutions. The score for two letters is defined by the ratio of probability of substitution between the two letters over the expected probability. Some scoring functions—such as the JTT (Jones et al., 1992) and the GCB (Gonnet et al., 1992) matrices—were derived by extrapolation from closely related sequences based on PAM evolutionary model to increase accuracy of homology searches. The VTML matrix (Müler et al., 2002) was obtained by maximum likelihood estimation of Dayhoff's parameters. The BLOSUM matrices were derived based on known multiple aligned blocks of sequences with blocks being the aligned regions without gaps. The score between two amino acids was defined as 2 times log-ratio of the probability that the two amino acids are aligned in the blocks over the corresponding expected probability assuming the sequences are independent. The PMB matrix (Veerassamy et al., 2003) is based on the blocks which BLOSUM used, but added evolutionary distances to form an evolutionary model. Based on the fact that proteins have complicated three-dimensional (3-D) structures, some scoring functions make use of the structure information, such as the STR (Overington et al., 1992) and the STROMA (Qian and Goldstein, 2002) matrices. Some scoring functions like SDM (Prlić et al., 2000) were derived from protein pairs of similar structure instead of sequence similarity. The scoring functions used in Fugue (Shi et al., 2001) and Wurst (Torda et al., 2004) are based on sequence-structure homology. Bayesian methods have also been employed for constructing scoring functions for multiple sequence alignment, such as BILD (Altschul et al., 2010). Many scoring functions are designed for specific applications. Adachi and Hasegawa (1996) established a model of amino acid substitution matrix for mitochondrial DNA encoded protein sequences, estimating the score matrix by the maximum likelihood method from mtDNA data. Cao et al. (2009) developed scoring functions for DNA sequences based on information theory in the expectation maximization framework.
Among these scoring functions, determining which is most powerful to detect the truly related segments for a given sequence study is an important problem. Usually, the scoring function is empirically selected based on some assumptions about the sequences to be compared. Altschul (1991) argued that PAM120, among the PAM matrices, is probably most appropriate if only one matrix is used, based on information content of the score matrix measured in relative entropy. Henikoff and Henikoff (1993) evaluated the performance of some commonly used substitution matrices, and found that log-likelihood ratio based scoring functions derived directly from multiple alignment data are better for detecting distant relationships than matrices based on PAM evolutionary model and the STR matrix achieved similar performance to BLOSUM62. The performance was evaluated through the efficiency for detecting true amino acid sequences belonging to particular protein families.
Several investigators evaluated different scoring functions by comparing the alignments derived from the computer algorithm with the alignments generated by simulations through fidelity, confidence, and overall correctness (Polyanovsky et al., 2008; Holmes and Durbin, 1998). In our study, we also compare different scoring functions using these quantities, however with terms that are more commonly used in the field of classification studies (see Section 2.1 for details). These investigators studied global alignments. In our study, we consider local alignment and general scoring functions without gaps.
In this article, we consider sequence alignment as a statistical hypothesis testing problem and define scores using the log-likelihood ratio statistic based on the segments we intend to find. We focus on the relationship between the scoring function and the best aligned segment in the scenario of local sequence alignment. According to the Neyman-Pearson lemma (Neyman and Pearson, 1933), the likelihood-ratio statistic is most powerful to distinguish a given distribution of optimal alignment from the background distribution for fixed global alignments. The test statistic provides a form of a scoring function which can be used in the sequence alignment. We conjecture that this log-likelihood ratio scoring function is statistically the most powerful one to detect the best aligned segment. Under the assumption that the compared sequences are independent and identically distributed (i.i.d.) letters sampled from some background distributions, we can treat the sequence alignment problem as a hypothesis testing problem. The null hypothesis is that the sequences are independent, and the alternative hypothesis is that they are related due to some shared segments which have a given distribution of letter pairs. We choose the score of the best aligned segment, i.e., the highest score during local alignment, as the test statistic. We use the power of the statistic for the hypothesis test as a measurement of the performance of scoring functions. The higher the power, the better the scoring function is. We also take a classification perspective for detecting the aligned segments and use true positive rate (TPR), false discovery rate (FDR), and the f-statistic (a weighted average of TPR and FDR) as alternative criteria for evaluating the scoring functions. We show that the log-likelihood ratio scoring function is most powerful to detect aligned segments following the distribution derived from the scoring function. It applies to both DNA sequences and amino acid sequences.
The aim of this article is to cut through the many ways to construct scoring functions and show that any scoring function used in local alignment corresponds to a hypothesis test between the background distribution of sequence letters and a statistical distribution of letter pairs determined by the scoring function.
2. Methods
2.1. Theoretical motivation
In this section, we present the basis for the analysis we perform. The first result that motivated our work was the Neyman-Pearson Lemma (Neyman and Pearson, 1933). This remarkable result, which has an elegant proof, is central to statistical theory and practice. The setting is hypothesis testing and we present the most elementary form of the Neyman-Pearson Lemma. The data are 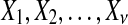 i.i.d. (independent and identically distributed) from model 0 with distribution P (the null hypothesis H0) or from model 1 with distribution Q (the alternate hypothesis H1). Do the data
i.i.d. (independent and identically distributed) from model 0 with distribution P (the null hypothesis H0) or from model 1 with distribution Q (the alternate hypothesis H1). Do the data 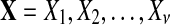 come from model 0 or 1? A test function φ satisfies φ(x) in {0, 1} where we say H0 is rejected if φ(x) = 1. The size of the test or level of significance is P(φ(X) = 1). Our ideal test function is one which has small size P(φ(X) = 1) = α and the largest possible power β = Q(φ(X) = 1). That is, we want a test statistic that has a small probability of rejecting a true null hypothesis, but the largest possible power or probability of rejecting H0 when H1 is true. The Neyman-Pearson Lemma states that the most powerful test statistic is
come from model 0 or 1? A test function φ satisfies φ(x) in {0, 1} where we say H0 is rejected if φ(x) = 1. The size of the test or level of significance is P(φ(X) = 1). Our ideal test function is one which has small size P(φ(X) = 1) = α and the largest possible power β = Q(φ(X) = 1). That is, we want a test statistic that has a small probability of rejecting a true null hypothesis, but the largest possible power or probability of rejecting H0 when H1 is true. The Neyman-Pearson Lemma states that the most powerful test statistic is
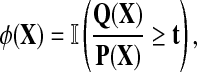 |
when
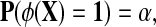 |
where 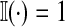 when the argument is true and 0 otherwise. This is one reason for the widespread use of likelihood ratio statistics.
when the argument is true and 0 otherwise. This is one reason for the widespread use of likelihood ratio statistics.
In sequence alignment, we are interested in pairs of aligned letters from finite alphabet 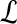 such as
such as  . An alignment
. An alignment 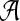 with length of ν of letters from sequences of random letters
with length of ν of letters from sequences of random letters 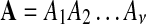 and
and 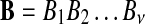 is represented as
is represented as
 |
The null hypothesis is that all the 2ν letters are i.i.d. P with P(A = a) = pa, and we call such an alignment P-distributed. The alternate hypothesis Q is a distribution over aligned pairs  with
with 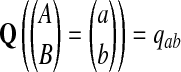 . In contrast
. In contrast 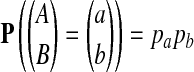 . Thus, we are testing the statistical distribution of letter pairs in the alignment: P-distributed alignments versus Q-distributed alignments.
. Thus, we are testing the statistical distribution of letter pairs in the alignment: P-distributed alignments versus Q-distributed alignments.
Following the Neyman-Pearson Lemma, to test the hypothesis that the alignment distribution is
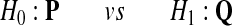 |
we should use the likelihood ratio
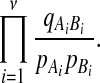 |
For convenience, we will use the logarithm of this statistic to form an equivalent test.
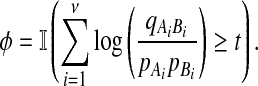 |
Thus, we have derived the log-likelihood scoring of alignments using alphabet scoring function
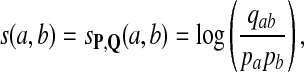 |
(1) |
which for sequence alignment goes back at least to Dayhoff et al. (1978) and was more recently employed by Henikoff and Henikoff (1992) and others. This article will explore the implications of this approach to scoring and its connection to hypothesis testing.
If we consider P as the background distribution and Q as the alternate distribution for the alignment, we should use the log-likelihood ratio scoring function s = sP,Q as the scoring function to best distinguish Q from P. However it is less evident what should be done for local alignment. We conjecture this scoring function is most powerful to detect Q distributed local alignments—aligned fragments with distribution Q. Now if there were one given, fixed-length alignment, our previous discussion would be the conclusion of the matter. Instead there are, for two random sequences of length n, O(n3) possible local alignments (we exclude indels where this number is much larger), and they are dependent in a subtle way. Is there any reason to be optimistic that log-likelihood scoring function is best for detecting local alignments of distribution Q from the background P? The mathematical result described next gives some hope for this.
The following result first appeared in Arratia et al. (1988) and was stated more generally in Karlin and Altschul (1990) with a form that was proven in Dembo et al. (1994). We give a version fitting our setup and do not completely repeat the notation we have defined above.
Let 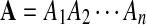 and
and 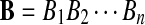 be i.i.d. random sequences with background distribution P. Assume s(a,b) is a scoring function that satisfies the conditions (i)
be i.i.d. random sequences with background distribution P. Assume s(a,b) is a scoring function that satisfies the conditions (i) 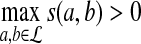 and (ii)
and (ii) 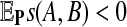 , where
, where
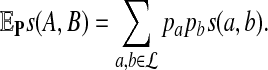 |
Let r > 0 be the largest real root of
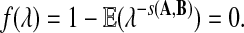 |
(2) |
Then the proportion of letter a from sequence A aligned with letter b from sequence B in the optimal alignment segment converges to 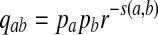 as sequence length n tends to infinity.
as sequence length n tends to infinity.
We now take the asymptotic distribution of the theorem and solve for s(a, b).
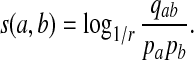 |
As positive multiples (cs(a,b) versus s(a,b) for any c > 0, for example) do not affect the results of local alignment, the numerical value of r > 0 is irrelevant. Therefore for any scoring function satisfying the hypotheses of the theorem, there is an asymptotic log-likelihood scoring function. It is easy to show (see Appendix A) that for any log-likelihood scoring function, the conditions of the theorem are satisfied so long as P and Q are not identical, that is for some (a,b), qab ≠ papb. Thus, we have a duality between scoring and likelihood ratio statistics.
The theorem assures us that in the i.i.d. case even with the complexity of O(n3) competing local alignments, with a given scoring function, a local alignment algorithm searches for Q distributed alignments. From this point of view, sequence alignment is hypothesis testing where
H0: The sequences 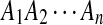 and
and 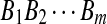 are from P i.i.d. letters.
are from P i.i.d. letters.
H1: The sequences 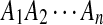 and
and 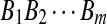 are mixture of P i.i.d. letters and a Q distributed local alignment at an unknown location.
are mixture of P i.i.d. letters and a Q distributed local alignment at an unknown location.
Because under either hypothesis the alignment algorithm is rewarding Q distributed local alignments, how do we determine signal from background? The answer is that this is not possible until the signal is significantly larger than the background. Fortunately, there is a well-studied basis for statistical significance in local alignments; the most famous is used in BLAST (Altschul et al., 1990) and is closely related to the theorem presented above, in addition to there being rigorous Poisson approximation methods which are equivalent (Waterman and Vingron, 1994). For our purposes, it will suffice to note that the growth of the alignment length of an optimal alignment, via an Erdös-Renyi law (Arratia et al., 1988), for two sequences of length n is
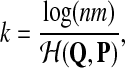 |
where
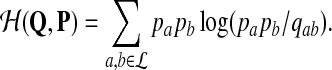 |
Let SP,Q(A, B), the maximum local alignment score under the scoring function sP,Q defined by P and Q, be the test statistic. For a given size α, we choose a threshold tα, so that
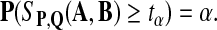 |
(3) |
We define the power of the alignment test statistic as
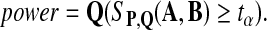 |
(4) |
A scoring function sP,Q yielding the highest power is preferred in local sequence alignment.
A natural way to evaluate the scoring function sP,Q is to see if the local aligned segment identified by the algorithm can find the signal of interest. A signal can be locally aligned segments. In our simulations, the signal is inserted at random positions of the two sequences. We treat the aligned position pairs of the signal as actual positives. However, the actual negatives are less easy to define because the other bases are not aligned. We denote the inserted signal by π* and let k* be the length of the signal π*. Similarly, the predicted positives are the aligned position pairs in the identified local aligned segment, which we refer to as π′. Let the length of identified alignment be k′. Table 1 shows the relationship among the terms. The predicted negatives are difficult to define though.
Table 1.
TP, FP, and FN by Comparing Algorithmic Alignment π′ with the Signal π*
| |
Signal π* |
|
|---|---|---|
| Positive | Negative | |
| Predicted alignment π′ | ||
| Positive | True positive = |π′ ∩ π*| | False positive = k1 − |π′ ∩ π*| |
| Negative | False negative = k* − |π′ ∩ π*| | True negative |
We use similar notation as in standard classification problems, and use TP, FP, and FN to represent true positive, false positive, and false negative, respectively. TPR (also referred to as sensitivity) is the fraction of true positives among the actual positives, i.e.,
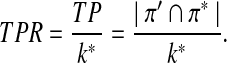 |
The positive predictive value (PPV) or precision is defined by
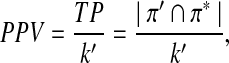 |
and FDR is defined as
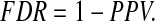 |
Scoring functions yielding high TPR and high PPV (and low FDR) are preferred. Another commonly used measure to evaluate the performance of a classification problem is the f-statistic defined as
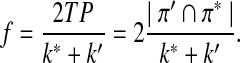 |
Note that the f-statistic is a weighted sum of TPR and PPV. In this study, we use TPR, FDR, and the f-statistic to evaluate the scoring function from the classification point of view.
2.2. Simulation studies
We carry out extensive simulations to show that when the scoring function used for sequence comparison is the log-likelihood ratio score defined in equation 1, the test statistic has the highest power, TPR, PPV, and the f-statistic. To achieve this objective, we carry out simulations as follows. First, we choose a set of P distributions as the background distribution of letters. Second, we define a set of Q-distributions which define how letter pairs align with each other in the simulated signal region.
For DNA sequences, we choose three “P”s and five “Q”s. The three “P” distributions are: uniform, “A” rich, and “GC” rich. The five “Q” distributions are: all matches have equal probability which is higher than the probability for mismatches, “AA” pair rich, “AA” pair poor, “GG”&“CC” rich, and “GG”&“CC” poor. For amino acid sequences, we choose two “P”s and three commonly used score matrices: BLOSUM45, BLOSUM62, and BLOSUM80. The “Q”s (Q1, Q2, Q3) corresponding to the three score matrices are derived by solving equation 2, and the corresponding Q-distribution is given by 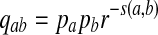 . The two “P”s are: equal probability for the 20 amino acids and the observed amino acid frequencies in vertebrates. For details about these choices, see Appendix B.
. The two “P”s are: equal probability for the 20 amino acids and the observed amino acid frequencies in vertebrates. For details about these choices, see Appendix B.
Third, for a given size α, we calculate a threshold tα(P, Q), as in equation 3, when a scoring function, sP,Q, defined by P and Q in equation 1, is used to align the two sequences as follows:
Generate i.i.d. random sequences A and B of length n with background distribution P.
Do local alignment of sequence A and sequence B with scoring function sP,Q using the Smith-Waterman algorithm (Smith and Waterman, 1981).
Repeat steps 1-2 for R1 = 10, 000 times and rank the resulting local sequence alignment scores in ascending order. Approximate the value of tα(P, Q) by the upper α percentile of the local alignment scores.
Fourth, we approximate the power of testing the hypotheses H0 versus H1 when a Q*-distributed alignment is inserted in the two random sequences as follows. The Q* distribution is referred to as the target distribution. We simultaneously calculate the approximate values of TPR, FDR, and the f-statitics with the procedure. The objective of this study is to identify an optimal scoring function to detect the relationship between sequences related through Q*-local alignment. The simulation steps are as follows:
Generate i.i.d. random sequences A and B of length n with background distribution P.
For a specific target distribution Q* from the group of “Q”s, generate a length k* aligned pairs with Q* distribution with
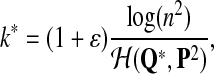 |
(5) |
where ɛ is a factor making the length of Q* segment somewhat larger than the expected length under the null model. To generate a Q* segment, we create a potential local alignment by independently drawing k* letter pairs from the Q* distribution. We refer to the generated aligned segment as a Q*-local alignment.
Let the generated Q*-local alignment be
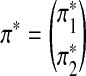 , where
, where 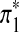 and
and 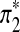 are sequences of length k*. Replace part of sequences A and B at random positions with
are sequences of length k*. Replace part of sequences A and B at random positions with 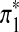 and
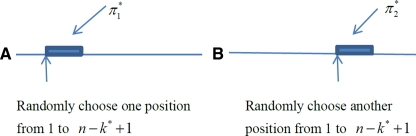
and 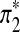 , respectively as shown in Figure 1. Define the resulting sequences as A* and B*.
, respectively as shown in Figure 1. Define the resulting sequences as A* and B*.Do local sequence alignment between sequence A* and sequence B* with scoring function sP,Q using the Smith-Waterman algorithm.
FIG. 1.
Insert Q*-local alignment into the sequences A and B.
We repeat the above four steps for R2 = 1,000 times, and the power of detecting the relationship between the two sequences with the Q*-local alignment inserted using score sP,Q is approximated by the fraction of times that the resulting local alignment score is at least tα(P, Q).
From the classification point of view, we are interested in the expectation of TPR, FDR and the f-statistic. Let TPr, 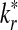 and
and 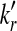 be the estimated corresponding values of TP, k* and k′ in the r-th experiments,
be the estimated corresponding values of TP, k* and k′ in the r-th experiments, 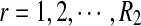 . Then TPRr, FDRr and fr,
. Then TPRr, FDRr and fr, 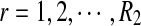 are estimated by
are estimated by
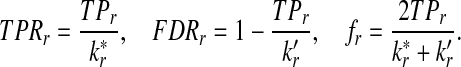 |
The expectation of TPR, FDR and f-statistic can be approximated by
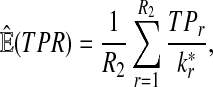 |
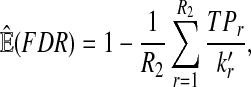 |
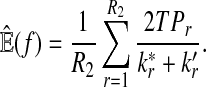 |
3. Results
In the simulations, we let the size α be 0.01 and 0.05 and ɛ in equation 5 be 0.03. The length n of sequences is 10,000. The simulation results are shown in Tables 2–7. In each table, the column direction represents a condition when one target Q*-local alignment is inserted, and the row direction represents the results using the log-likelihood scoring function derived from one P and one Q. From Table 2, by comparing the power among different Qs under the same P and Q*, it can be seen that the test has the largest power when Q equals to Q*. In other words, the highest power appears diagonally. For example, the power of the tests using log-likelihood ratio scoring functions corresponding to Q1 to Q5 when P = P2 and Q* = Q3 are 0.61, 0.51, 0.71, 0.68, and 0.55, respectively, for test size α = 0.01. The largest power among the five tests is 0.71 when Q = Q3. The other tables can be viewed similarly. Tables 2–4 are for DNA sequences. When Q = Q*, we obtain the highest power, TPR, the f-statistic, and the lowest FDR. That is, the scoring function derived from Q* is the most powerful scoring function to detect Q*-local alignment.
Table 2.
Power of the Tests Based on Different Scoring Functions when Different Target Q*-Local Alignments Are Inserted
| |
Target Q*, α = 0.01 |
Target Q*, α = 0.05 |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scoring function | Q1 | Q2 | Q3 | Q4 | Q5 | Q1 | Q2 | Q3 | Q4 | Q5 |
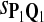 |
0.83 | 0.58 | 0.56 | 0.66 | 0.68 | 0.88 | 0.73 | 0.70 | 0.80 | 0.81 |
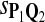 |
0.49 | 0.75 | 0.41 | 0.49 | 0.70 | 0.60 | 0.85 | 0.54 | 0.61 | 0.79 |
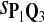 |
0.48 | 0.43 | 0.75 | 0.69 | 0.52 | 0.62 | 0.56 | 0.85 | 0.79 | 0.64 |
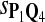 |
0.58 | 0.52 | 0.68 | 0.76 | 0.59 | 0.68 | 0.64 | 0.78 | 0.85 | 0.71 |
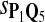 |
0.59 | 0.72 | 0.50 | 0.58 | 0.78 | 0.67 | 0.80 | 0.62 | 0.69 | 0.84 |
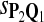 |
0.81 | 0.52 | 0.61 | 0.69 | 0.67 | 0.88 | 0.65 | 0.72 | 0.81 | 0.77 |
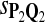 |
0.55 | 0.76 | 0.51 | 0.60 | 0.72 | 0.65 | 0.84 | 0.65 | 0.72 | 0.81 |
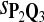 |
0.57 | 0.45 | 0.71 | 0.70 | 0.56 | 0.67 | 0.56 | 0.80 | 0.79 | 0.67 |
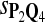 |
0.63 | 0.50 | 0.68 | 0.75 | 0.61 | 0.72 | 0.61 | 0.77 | 0.83 | 0.72 |
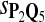 |
0.61 | 0.67 | 0.55 | 0.63 | 0.77 | 0.69 | 0.77 | 0.66 | 0.74 | 0.84 |
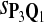 |
0.79 | 0.63 | 0.54 | 0.64 | 0.68 | 0.84 | 0.74 | 0.67 | 0.74 | 0.79 |
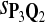 |
0.57 | 0.72 | 0.49 | 0.57 | 0.68 | 0.65 | 0.80 | 0.58 | 0.67 | 0.77 |
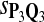 |
0.52 | 0.55 | 0.74 | 0.70 | 0.60 | 0.64 | 0.66 | 0.83 | 0.78 | 0.73 |
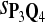 |
0.59 | 0.60 | 0.71 | 0.77 | 0.66 | 0.69 | 0.70 | 0.78 | 0.84 | 0.74 |
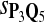 |
0.64 | 0.68 | 0.53 | 0.60 | 0.74 | 0.72 | 0.78 | 0.64 | 0.70 | 0.81 |
Test size α = 0.01 or 0.05 (DNA sequences).
Table 7.
f-Statistic of the Tests Based Different Scoring Functions when Different Target Q*-Local Alignments Are Inserted (Amino Acid Sequences)
| |
Target Q* |
||
|---|---|---|---|
| Scoring function | Q1 | Q2 | Q3 |
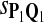 |
0.82 | 0.79 | 0.75 |
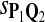 |
0.75 | 0.82 | 0.80 |
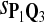 |
0.57 | 0.73 | 0.82 |
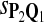 |
0.83 | 0.83 | 0.76 |
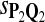 |
0.75 | 0.83 | 0.82 |
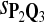 |
0.57 | 0.74 | 0.82 |
The target distributions Q1, Q2, and Q3 correspond to BLOSUM45, BLOSUM62, and BLOSUM80, respectively.
Table 4.
f-Statistic Using Different Scoring Functions when Different Target Q*-Local Alignments Are Inserted (DNA Sequences)
| |
Target distribution Q* |
||||
|---|---|---|---|---|---|
| Scoring function | Q1 | Q2 | Q3 | Q4 | Q5 |
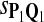 |
0.87 | 0.78 | 0.77 | 0.82 | 0.83 |
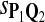 |
0.62 | 0.85 | 0.64 | 0.67 | 0.81 |
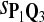 |
0.61 | 0.64 | 0.84 | 0.81 | 0.70 |
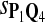 |
0.67 | 0.71 | 0.82 | 0.86 | 0.75 |
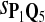 |
0.68 | 0.83 | 0.70 | 0.74 | 0.86 |
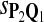 |
0.86 | 0.70 | 0.76 | 0.83 | 0.79 |
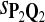 |
0.68 | 0.86 | 0.71 | 0.77 | 0.82 |
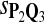 |
0.67 | 0.61 | 0.82 | 0.80 | 0.71 |
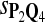 |
0.71 | 0.66 | 0.80 | 0.84 | 0.74 |
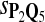 |
0.72 | 0.79 | 0.73 | 0.80 | 0.83 |
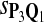 |
0.82 | 0.75 | 0.74 | 0.78 | 0.79 |
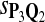 |
0.64 | 0.80 | 0.65 | 0.69 | 0.80 |
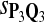 |
0.66 | 0.71 | 0.84 | 0.79 | 0.77 |
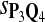 |
0.71 | 0.74 | 0.81 | 0.85 | 0.79 |
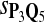 |
0.68 | 0.78 | 0.68 | 0.72 | 0.82 |
Table 3.
True Positive Rate (TPR) and False Discovery Rate (FDR) Using Different Scoring Functions when Different Target Q*-Local Alignments Are Inserted (DNA Sequences)
| |
Target Q*, TPR |
Target Q*, FDR |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Scoring function | Q1 | Q2 | Q3 | Q4 | Q5 | Q1 | Q2 | Q3 | Q4 | Q5 |
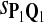 |
0.87 | 0.82 | 0.82 | 0.87 | 0.88 | 0.12 | 0.25 | 0.26 | 0.21 | 0.20 |
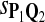 |
0.57 | 0.86 | 0.64 | 0.67 | 0.82 | 0.32 | 0.15 | 0.36 | 0.32 | 0.19 |
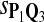 |
0.57 | 0.64 | 0.85 | 0.81 | 0.70 | 0.32 | 0.35 | 0.15 | 0.19 | 0.30 |
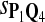 |
0.63 | 0.71 | 0.82 | 0.86 | 0.76 | 0.26 | 0.28 | 0.17 | 0.14 | 0.24 |
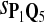 |
0.63 | 0.83 | 0.70 | 0.74 | 0.86 | 0.25 | 0.17 | 0.30 | 0.25 | 0.14 |
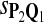 |
0.86 | 0.71 | 0.80 | 0.86 | 0.82 | 0.14 | 0.30 | 0.26 | 0.19 | 0.22 |
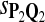 |
0.67 | 0.87 | 0.73 | 0.79 | 0.83 | 0.29 | 0.13 | 0.30 | 0.24 | 0.18 |
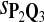 |
0.64 | 0.59 | 0.82 | 0.80 | 0.69 | 0.28 | 0.35 | 0.17 | 0.18 | 0.27 |
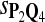 |
0.68 | 0.63 | 0.79 | 0.84 | 0.73 | 0.24 | 0.31 | 0.20 | 0.15 | 0.24 |
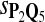 |
0.70 | 0.78 | 0.74 | 0.80 | 0.83 | 0.24 | 0.19 | 0.27 | 0.21 | 0.17 |
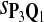 |
0.82 | 0.79 | 0.75 | 0.80 | 0.83 | 0.16 | 0.27 | 0.26 | 0.22 | 0.23 |
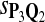 |
0.61 | 0.79 | 0.63 | 0.67 | 0.79 | 0.31 | 0.18 | 0.33 | 0.28 | 0.19 |
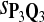 |
0.64 | 0.72 | 0.85 | 0.79 | 0.78 | 0.30 | 0.29 | 0.15 | 0.19 | 0.23 |
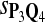 |
0.68 | 0.75 | 0.81 | 0.85 | 0.81 | 0.26 | 0.26 | 0.19 | 0.15 | 0.21 |
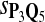 |
0.65 | 0.77 | 0.67 | 0.70 | 0.81 | 0.26 | 0.21 | 0.29 | 0.25 | 0.17 |
Tables 5–7 are for amino acid sequences. Similar conclusions as for DNA sequences are obtained. The power of the test based on scoring function derived from Q reach the highest when Q = Q*, no matter whether α = 0.01 or α = 0.05. It can also be seen from Table 5 that the power of the test based on sP,Q decreases as the distance between Q and Q* increases. For example, when Q* = Q1 corresponding to BLOSSOM45 and P = P2, the power of the tests based on BLOSUM45, BLOSSOM62, and BLOSSOM80 is 0.83, 0.75, and 0.56, respectively. Table 6 gives the TPR and FDR for the tests using different scoring functions. When the target distribution is Q3 corresponding to BLOSUM80, the TPR of the test using scoring functions 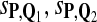 , and
, and 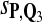 is close to 80%. On the other hand, Tables 6 and 7 show that the FDR is lowest and the f-statistic is the highest when the scoring function
is close to 80%. On the other hand, Tables 6 and 7 show that the FDR is lowest and the f-statistic is the highest when the scoring function 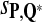 is used.
is used.
Table 5.
Power of Tests Based on Different Scoring Functions when Different Target Q*-Local Alignments Are Inserted
| |
Target Q*, α = 0.01 |
Target Q*, α = 0.05 |
||||
|---|---|---|---|---|---|---|
| Scoring function | Q1 | Q2 | Q3 | Q1 | Q2 | Q3 |
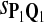 |
0.77 | 0.69 | 0.56 | 0.84 | 0.78 | 0.69 |
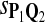 |
0.68 | 0.72 | 0.66 | 0.77 | 0.81 | 0.79 |
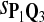 |
0.53 | 0.66 | 0.73 | 0.61 | 0.72 | 0.81 |
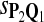 |
0.74 | 0.71 | 0.61 | 0.83 | 0.81 | 0.73 |
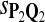 |
0.67 | 0.76 | 0.70 | 0.75 | 0.84 | 0.79 |
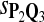 |
0.47 | 0.64 | 0.72 | 0.56 | 0.74 | 0.81 |
Test size α = 0.01 or 0.05 (amino acid sequences). The target distributions Q1, Q2, and Q3 correspond to BLOSUM45, BLOSUM62, and BLOSUM80, respectively.
Table 6.
True Positive Rate (TPR) and False Discovery Rate (FDR) of the Tests Based on Different Scoring Functions when Different Target Q*-Local Alignments Are Inserted (Amino Acid Sequences)
| |
Target Q*, TPR |
Target Q*, FDR |
||||
|---|---|---|---|---|---|---|
| Scoring function | Q1 | Q2 | Q3 | Q1 | Q2 | Q3 |
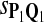 |
0.80 | 0.81 | 0.79 | 0.15 | 0.21 | 0.27 |
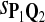 |
0.71 | 0.81 | 0.81 | 0.19 | 0.16 | 0.20 |
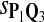 |
0.52 | 0.70 | 0.81 | 0.32 | 0.22 | 0.16 |
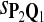 |
0.83 | 0.84 | 0.80 | 0.15 | 0.18 | 0.26 |
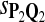 |
0.72 | 0.82 | 0.83 | 0.21 | 0.15 | 0.19 |
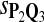 |
0.52 | 0.71 | 0.81 | 0.35 | 0.21 | 0.17 |
The target distributions Q1, Q2, and Q3 correspond to BLOSUM45, BLOSUM62, and BLOSUM80, respectively.
4. Discussion
Sequence alignments have been widely used to compare nucleotide and amino acid sequences. For a given scoring function, the local alignment score between two sequences is first obtained through a dynamic programming algorithm or a method such as BLAST (Altschul et al., 1990), and a p-value or E-value can be calculated. Log-likelihood ratio scoring functions based on known aligned sequences were derived for sequence comparisons by (Dayhoff et al., 1978) and (Henikoff and Henikoff, 1992). Previous studies showed the superiority of the log-likelihood ratio scoring function by evaluating whether it can successfully identify genes within the same family (Henikoff and Henikoff, 1993). It has also been argued that all reasonable substitution scoring functions are implicitly log-odds scoring functions (Karlin and Altschul, 1990; Karlin et al., 1990; Altschul, 1991), i.e., log-likelihood ratio scoring function. For a given scoring function s(·, ·), it has been shown that the probability that a is aligned to b in the best aligned segment is 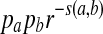 with r being the largest root of the equation 2. For a given distribution Q for the aligned segment, it is possible to define a scoring function by the log-likelihood ratio between the Q distribution and the P distribution. Thus, scoring functions and target Q-distributions are coupled. Suppose that two sequences are related through a target distribution Q* in an aligned segment. Intuitively, the scoring function defined by the log-likelihood ratio between Q* and P distributions should be used. However, to the best of our knowledge, no studies have been carried out to prove or dispute this claim.
with r being the largest root of the equation 2. For a given distribution Q for the aligned segment, it is possible to define a scoring function by the log-likelihood ratio between the Q distribution and the P distribution. Thus, scoring functions and target Q-distributions are coupled. Suppose that two sequences are related through a target distribution Q* in an aligned segment. Intuitively, the scoring function defined by the log-likelihood ratio between Q* and P distributions should be used. However, to the best of our knowledge, no studies have been carried out to prove or dispute this claim.
In this article, we regard sequence alignment as a hypothesis testing problem, and study the power of tests based on different scoring functions for detecting the relationship between two sequences. For our studies, aligned segments were randomly inserted into the two sequences. The results from our simulations indicate that the log-likelihood ratio scoring function is the most powerful scoring function to detect segments of Q distribution using the scoring function sP,Q, as it has the highest power, TPR, and f-statistic, and the lowest FDR. However, we cannot mathematically rigorously prove that the log-likelihood ratio scoring function is optimal. In our simulation studies, we tried to choose a set of Q distributions as representative as possible. As the Q can be sampled in a continuous space with 15 degrees of freedom for DNA sequences and 399 degrees of freedom for amino acid sequences, we cannot search over all possibilities for Q. We chose representative Qs from the sampling space, compared the scoring functions derived from these Qs, and used those values to provide evidence to show that the log-likelihood ratio scoring function is most powerful.
The field of sequence alignment lacks a proof of the claim we have conjectured. While for fixed length alignment the Neyman-Pearson Lemma holds, the distribution related to equation 2 is only true asymptotically. Thus we believe our result will only be proven as an asymptotic result. None the less it would be a significant advance for the general theory and practice of sequence alignment.
Our study has several limitations. First, we assume that the two sequences are i.i.d in the null model. In many situations, Markovian models fit the sequences much better than the i.i.d model. Under the Markovian model, the log-likelihood scoring function will become more complex and can depend on adjacent pairs. We are confident that our results hold in the more general setting, as for example the asymptotic distribution for local alignment holds here.
Second and more important, gaps should be considered in many alignment problems. Currently theoretical results are not available for local alignment on the length of gaps nor for aligned letter pairs for two random sequences. We conjecture that there is an asymptotic distribution for local alignment in this case as well, so long as
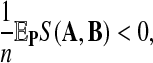 |
where S(A, B) is the global alignment of the sequences A and B of length n. The condition states that the per letter score accumulation is negative. The asymptotic distribution even in the i.i.d. case for gaps will depend on the letter composition aligned to the gaps. However summing over the composition will give a gap length distribution. The lack of theoretical results makes the design of simulation studies difficult. We hypothesize that the optimal scoring function is still the log-likelihood scoring function. Further studies are needed to prove or dispute this hypothesis. Such a result would be a significant extension of the results of Arratia et al. (1988) and Dembo et al. (1994). Similar results will hold for multiple local alignment.
5. Appendix
A: Duality between scoring functions and log-likelihood ratio scores
Claim
For any given P and Q distributions, the log-likelihood scoring function sP,Q defined in equation 1 by 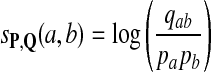 satisfies the conditions: (1)
satisfies the conditions: (1) 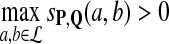 and (2)
and (2) 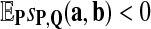 , unless
, unless 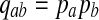 for all
for all  .
.
Proof
If 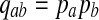 for all
for all 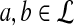 , then sP,Q(a, b) = 0 for all
, then sP,Q(a, b) = 0 for all 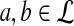 . Next assume that
. Next assume that 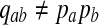 for some a, b. Then there must exist
for some a, b. Then there must exist 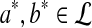 , such that
, such that 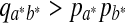 . Thus, sP,Q(a*, b*) > 0. By Jensen's inequality, if X is a random variable and X is not a constant with probability 1, and g(x) is a strictly concave function, then
. Thus, sP,Q(a*, b*) > 0. By Jensen's inequality, if X is a random variable and X is not a constant with probability 1, and g(x) is a strictly concave function, then 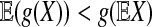 . Applying this inequality with g(x) = log(x), we have
. Applying this inequality with g(x) = log(x), we have
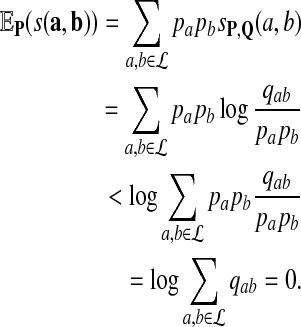 |
■
B: The choices of “P” and “Q” distributions
In our study, we choose several “P” and “Q” distributions to provide evidence that the log-likelihood scoring function yields the highest power, TPR, the f-statistic, and the lowest FDR. It is important to choose such distributions so that they cover as many possibilities as possible. In this study, we choose “P” and “Q” distributions for DNA sequences.
First, we consider equally likely distribution, i.e., 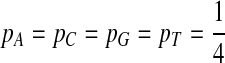 .
.
Second, we consider one-letter rich situation, e.g., “A”-rich. The background distribution pattern is set as 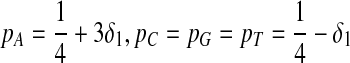 . If we let δ1 be
. If we let δ1 be 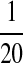 , then
, then 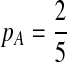 ,
, 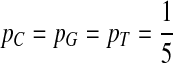 .
.
Third, we consider two-letter rich situation, e.g., “G” and “C.” 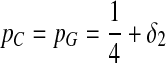 ,
, 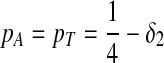 . When
. When 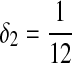 ,
, 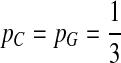 ,
, 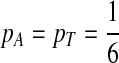 .
.
In summary, we set three types of “P”s: equally likely, “A” rich, and “G-C” rich, and denote them as P1, P2, and P3, respectively, as shown in Table 8.
Table 8.
Background Distribution P for DNA Sequences Used in the Simulations
| PA | PC | PG | PT | |
|---|---|---|---|---|
| P1 | 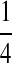 |
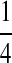 |
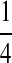 |
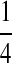 |
| P2 | 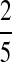 |
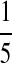 |
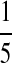 |
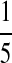 |
| P3 | 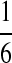 |
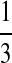 |
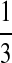 |
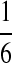 |
We choose the group of “Q” distributions for DNA sequences as follows.
First, we let the probability of matches be larger than that for the mismatches. We choose Q as
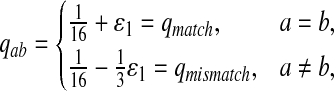 |
where 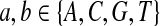 . When
. When 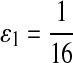 ,
, 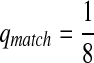 ,
, 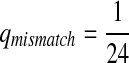 .
.
Second, we consider the situation that the match of one specific letter, e.g., “A”, is preferred than the match for other letters. We consider “AA” pair rich Q-local alignment. So we choose Q as follows.
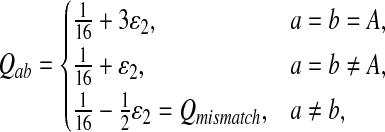 |
where 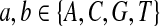 . When
. When 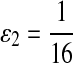 ,
, 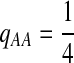 ,
, 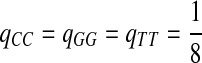 ,
, 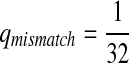 .
.
Third, instead of letting “AA” pair to be enriched in the aligned region, we let another match, e.g., “GG”, be enriched. We set Q as follows. The reason for choosing Q this way is to see what happens if the enriched matches in the aligned part is different from the most abundant nucleotide in the background sequences.
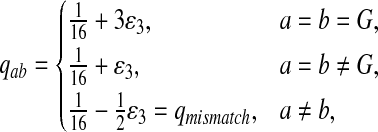 |
where 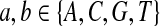 . When
. When 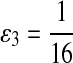 ,
, 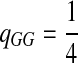 ,
, 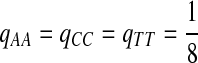 ,
, 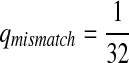 .
.
Fourth, we set Q so that matches for two letters are enriched, e.g., “CC” and “GG.” Note that “C” and “G” are the enriched nucleotides for P3 given above.
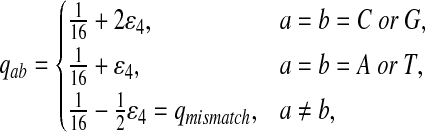 |
where 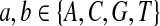 . When
. When 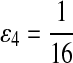 ,
, 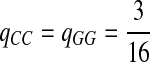 ,
, 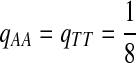 ,
, 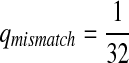 .
.
Fifth, we let “AA” and “TT” be enriched in Q. Note that the enriched matches in the Q-local alignments are different from the enriched nucleotides in P3.
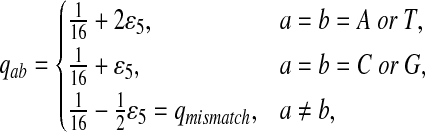 |
where 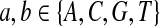 . When
. When 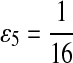 ,
, 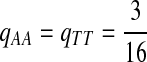 ,
, 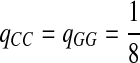 ,
, 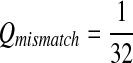 .
.
In summary, we have five “Q”s—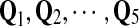 —as described above.
—as described above.
For P as the uniform distribution 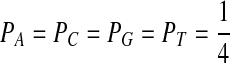 , Table 9 shows the “Q”s we choose and the corresponding scores as well as the expectations of the scores.
, Table 9 shows the “Q”s we choose and the corresponding scores as well as the expectations of the scores.
Table 9.
“Q” Distributions Used in the Simulations and the Corresponding Scores under the Equally Likely Background Distribution P1, as well as the Expectation of the Scores
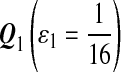 |
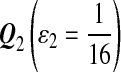 |
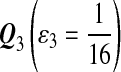 |
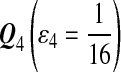 |
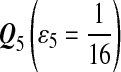 |
|
|---|---|---|---|---|---|
M: 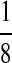
|
M(AA): 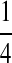
|
M(GG): 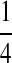
|
M(GG, CC): 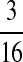
|
M(AA, TT): 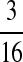
|
|
| Q | M(CC, GG, TT): 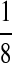
|
M(AA, CC, TT): 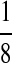
|
M(AA, TT): 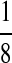
|
M(GG, CC): 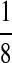
|
|
N: 
|
N: 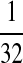
|
N: 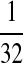
|
N: 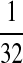
|
N: 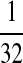
|
|
| M: 0.69 | M(AA): 1.39 | M(GG): 1.39 | M(GG, CC): 1.10 | M(AA, TT): 1.10 | |
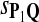 |
M(CC, GG, TT): 0.69 | M(AA, CC, TT): 0.69 | M(AA, TT): 0.69 | M(GG, CC): 0.69 | |
| N: − 0.41 | N: − 0.69 | N: − 0.69 | N: − 0.69 | N: − 0.69 | |
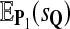 |
−0.135 | −0.30125 | −0.30125 | −0.29375 | −0.29375 |
M, match; N, mismatch.
Choices of “P”s and “Q”s for amino acid sequences. We choose the commonly used BLOSUM45, BLOSUM62 and BLOSUM80 as the group of scoring functions, and the corresponding “Q”s(Q1, Q2, Q3) are derived from the three scoring functions through solving equation 2 of λ, respectively.
We choose two P-distributions. The first gives equal probability to all the amino acids (P1) and the other one is the observed amino acid frequencies in vertebrates (P2) as shown in Table 10.
Table 10.
Observed Amino Acid Frequencies in Vertebrates (P2)
| A | Alanine | 7.4% |
| R | Arginine | 4.2% |
| N | Asparagine | 4.4% |
| D | Aspartic acid | 5.9% |
| C | Cysteine | 3.3% |
| Q | Glutamine | 3.7% |
| E | Glutamic acid | 5.8% |
| G | Glycine | 7.4% |
| H | Histidine | 2.9% |
| I | Isoleucine | 3.8% |
| L | Leucine | 7.6% |
| K | Lysine | 7.2% |
| M | Methionine | 1.8% |
| F | Phenylalanine | 4.0% |
| P | Proline | 5.0% |
| S | Serine | 8.1% |
| T | Threonine | 6.2% |
| W | Tryptophan | 1.3% |
| Y | Tyrosine | 3.3% |
| V | Valine | 6.8% |
C: The algorithm for simulation studies
Algorithm 1.
Procedure flow
Input: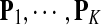 , , 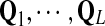 , n and ɛ , n and ɛ |
| Output:powerα = 0.01, powerα = 0.05, TPR, FDR, f |
| fork = 1; k ≤ K; k + + do |
| forj = 1; j ≤ L; j + + do |
| forr = 1; r ≤ R1; r + + do |
| generate sequence A and sequence B with background Pk; |
| local alignment between A and B using Qj; |
record 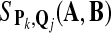 ; ; |
| end |
Rank 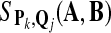 ; ; |
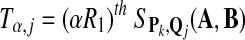 ; ; |
| end |
| fori = 1; i ≤ L; i + + do |
| Q* = Qi; |
| forr = 1; r ≤ R2; r + + do |
| generate sequence A and sequence B with background Pk; |
| plug in Q*-segment to generate new sequences A* and B*; |
| forj = 1; j ≤ L; j + + do |
| local alignment between A* and B* using Qj; |
record 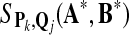 ; ; |
if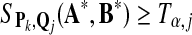 then then |
| Flagr(Pk, Q*, Qj) = 1; |
| else |
| Flagr(Pk, Q*, Qj) = 0; |
| end |
| calculate TPRr(Pk, Q*, Qj), FDRr(Pk, Q*, Qj), fr(Pk, Q*, Qj) |
| end |
| end |
| forj = 1; j ≤ L; j + + do |
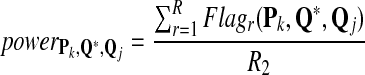 ; ; |
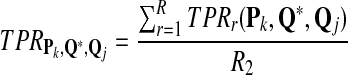 ; ; |
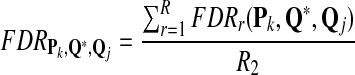 ; ; |
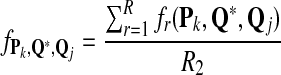 ; ; |
| end |
| end |
| end |
Acknowledgments
This work was supported by the NSFC (grant 30675012 to L.M., X.Z.; grant 60721003 to L.M.; grant 60928007 to F.S., X.Z.; grant 60805010 to F.S.) and the NIH (grant P50HG002790 to F.S., M.S.W.; grant R21AG032743 to F.S., M.S.W.).
Disclosure Statement
No competing financial interests exist.
References
- Adachi J. Hasegawa M. Model of amino acid substitution in proteins encoded by mitochondrial DNA. J. Mol. Evol. 1996;42:459–468. doi: 10.1007/BF02498640. [DOI] [PubMed] [Google Scholar]
- Altschul S. Wootton J. Zaslavsky E., et al. The construction and use of log-odds substitution scores for multiple sequence alignment. PLoS Comput. Biol. 2010;6:e1000852. doi: 10.1371/journal.pcbi.1000852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F. Amino acid substitution matrices from an information theoretic perspective. J. Mol. Biol. 1991;219:555–565. doi: 10.1016/0022-2836(91)90193-A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul S.F. Gish W. Miller W., et al. Basic local alignment search tool. J. Mol. Biol. 1990;215:403–410. doi: 10.1016/S0022-2836(05)80360-2. [DOI] [PubMed] [Google Scholar]
- Altschul S.F. Madden T.L. Schaffer A.A., et al. Gapped BLAST and PSI-BLAST: a new generation of protein database search programs. Nucleic Acids Res. 1997;25:3389–3402. doi: 10.1093/nar/25.17.3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arratia R. Morris P. Waterman M. Stochastic scrabble: large deviations for sequences with scores. J. Appl. Probab. 1988;25:106–119. [Google Scholar]
- Cao M.D. Dix T.I. Allison L. Computing substitution matrices for genomic comparative analysis. Proc. 13th Pacific-Asia Conf. Adv. Knowledge Discov. Data Mining. 2009:647–655. [Google Scholar]
- Dayhoff M.O. Schwartz R.M. Orcutt B.C. A model of evolutionary change in proteins. Atlas Protein Sequence Struct. 1978;5:345–351. [Google Scholar]
- Dembo A. Karlin S. Zeitouni O. Limit distribution of maximal non-aligned two-sequence segmental score. Ann. Appl. Probab. 1994;22:2022–2039. [Google Scholar]
- Do C.B. Mahabhashyam M.S. Brudno M., et al. Probcons: probabilistic consistency-based multiple sequence alignment. Genome Res. 2005;15:330–340. doi: 10.1101/gr.2821705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gonnet G.H. Cohen M.A. Benner S.A. Exhaustive matching of the entire protein sequence database. Science. 1992;256:1443–1445. doi: 10.1126/science.1604319. [DOI] [PubMed] [Google Scholar]
- Henikoff S. Henikoff J.G. Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. U.S.A. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henikoff S. Henikoff J.G. Performance evaluation of amino acid substitution matrices. Proteins. 1993;17:49–61. doi: 10.1002/prot.340170108. [DOI] [PubMed] [Google Scholar]
- Holmes I. Durbin R. Dynamic programming alignment accuracy. J. Comput. Biol. 1998;5:493–504. doi: 10.1089/cmb.1998.5.493. [DOI] [PubMed] [Google Scholar]
- Jones D.T. Taylor W.R. Thornton J.M. The rapid generation of mutation data matrices from protein sequences. Comput. Appl. Biosci. 1992;8:275–282. doi: 10.1093/bioinformatics/8.3.275. [DOI] [PubMed] [Google Scholar]
- Karlin S. Altschul S. Methods for assessing the statistical significance of molecular sequence features by using general scoring schemes. Proc. Natl. Acad. Sci. U.S.A. 1990;87:2264–2268. doi: 10.1073/pnas.87.6.2264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlin S. Dembo A. Kawabata T. Statistical composition of high-scoring segments from molecular sequences. Ann. Stat. 1990;18:571–581. [Google Scholar]
- Kent W.J. BLAT—the BLAST-like alignment tool. Genome Res. 2002;12:656–664. doi: 10.1101/gr.229202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B. Trapnell C. Pop M., et al. Ultrafast and memory-efficient alignment of short DNA sequences to the human genome. Genome Biol. 2009;10:R25. doi: 10.1186/gb-2009-10-3-r25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Müler T. Spang R. Vingron M. Estimating amino acid substitution models: a comparison of Dayhoff's estimator, the resolvent approach and a maximum likelihood method. Mol. Biol. Evol. 2002;19:8–13. doi: 10.1093/oxfordjournals.molbev.a003985. [DOI] [PubMed] [Google Scholar]
- Needleman S.B. Wunsch C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970;48:443–453. doi: 10.1016/0022-2836(70)90057-4. [DOI] [PubMed] [Google Scholar]
- Neyman J. Pearson E.S. On the problem of the most efficient tests of statistical hypotheses. Phil. Trans. R. Soc. A. 1933;231:289–337. [Google Scholar]
- Overington J. Donnelly D. Johnson M.S., et al. Environment-specific amino acid substitution tables: tertiary templates and prediction of protein folds. Protein Sci. 1992;1:216–226. doi: 10.1002/pro.5560010203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearson W.R. Rapid and sensitive sequence comparison with FASTP and FASTA. Methods Enzymol. 1990;183:63–98. doi: 10.1016/0076-6879(90)83007-v. [DOI] [PubMed] [Google Scholar]
- Polyanovsky V. Roytberg M.A. Tumanyan V.G. Reconstruction of genuine pairwise sequence alignment. J. Comput. Biol. 2008;15:379–391. doi: 10.1089/cmb.2007.0145. [DOI] [PubMed] [Google Scholar]
- Prlić A. Domingues F.S. Sippl M.J. Structure-derived substitution matrices for alignment of distantly related sequences. Protein Eng. 2000;13:545–550. doi: 10.1093/protein/13.8.545. [DOI] [PubMed] [Google Scholar]
- Qian B. Goldstein R.A. Optimization of a new score function for the generation of accurate alignments. Proteins. 2002;48:605–610. doi: 10.1002/prot.10132. [DOI] [PubMed] [Google Scholar]
- Shi J. Blundell T.L. Mizuguchi K. FUGUE: sequence-structure homology recognition using environment-specific substitution tables and structure-dependent gap penalties. J. Mol. Biol. 2001;310:243–257. doi: 10.1006/jmbi.2001.4762. [DOI] [PubMed] [Google Scholar]
- Smith T.F. Waterman M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981;147:195–197. doi: 10.1016/0022-2836(81)90087-5. [DOI] [PubMed] [Google Scholar]
- Subramanian A. Kaufmann M. Morgenstern B. DIALIGN-TX: greedy and progressive approaches for segment-based multiple sequence alignment. Algorithms Mol. Biol. 2008;3:6. doi: 10.1186/1748-7188-3-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Subramanian A. Weyer-Menkhoff J. Kaufmann M., et al. DIALIGN-T: an improved algorithm for segment-based multiple sequence alignment. BMC Bioinform. 2005;6:66. doi: 10.1186/1471-2105-6-66. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson J.D. Higgins D.G. Gibson T.J. CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994;22:4673–4680. doi: 10.1093/nar/22.22.4673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torda A.E. Procter J.B. Huber T. Wurst: a protein threading server with a structural scoring function, sequence profiles and optimized substitution matrices. Nucleic Acids Res. 2004;32:W532–W535. doi: 10.1093/nar/gkh357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veerassamy S. Smith A. Tillier E.R.M. A transition probability model for amino acid substitutions from blocks. J. Comput. Biol. 2003;10:997–1010. doi: 10.1089/106652703322756195. [DOI] [PubMed] [Google Scholar]
- Waterman M. Vingron M. Sequence comparison significance and Poisson approximation. Stat. Sci. 1994;9:367–381. [Google Scholar]
- Waterman M.S. Introduction to Computational Biology: Maps, Sequences and Genomes. Chapman & Hall; New York: 1995. [Google Scholar]
- Webb B.M. Liu J.S. Lawrence C.E. BALSA: Bayesian algorithm for local sequence alignment. Nucleic Acids Res. 2002;30:1268–1277. doi: 10.1093/nar/30.5.1268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J. Liu J.S. Lawrence C.E. Bayesian adaptive sequence alignment algorithms. Bioinformatics. 1998;14:25–39. doi: 10.1093/bioinformatics/14.1.25. [DOI] [PubMed] [Google Scholar]