Mechanical properties of hydroxyapatite single crystals from nanoindentation data

Abstract

In this paper we compute elasto-plastic properties of hydroxyapatite single crystals from nanindentation data using a two-step algorithm. In the first step the yield stress is obtained using hardness and Young’s modulus data, followed by the computation of the flow parameters. The computational approach is first validated with data from existing literature. It is observed that hydroxyapatite single crystals exhibit anisotropic mechanical response with a lower yield stress along the [1010] crystallographic direction compared to the [0001] direction. Both work hardening rate and work hardening exponent are found to be higher for indentation along the [0001] crystallographic direction. The stress-strain curves extracted here could be used for developing constitutive models for hydroxyapatite single crystals.

1. Introduction

Bone is a composite material with an organic matrix and inorganic minerals arranged in a hierarchy of structures spanning several length scales (Mann, 1993; Currey, 2005). At the nanometer length scale, e.g., the structure consists of self-assembled collagen fibrils and inorganic hydroxyapatite nano-crystals (Elliott, 1994 and 2002). The mechanical properties of the organic and inorganic phases together with their hierarchical arrangement impart bone its characteristic strength and toughness. There is therefore much interest in characterizing the mechanical properties of hydroxyapatite, not only for its importance in the overall mechanical behavior of bone in disease and in health but also for its wide-scale application in biomaterials, regenerated hard tissue, and in medicine (Rodrigues et al., 2003; Motskin et al. 2009). For instance, hydroxyapatite crystals act as an important reservoir for hosting different ions and cations and therefore play a key role in metabolic activity of bone (Bazin et al., 2009). Recent research has shown that hydroxyapatite crystals may induce cytotoxicity and apoptosis of certain cancer cells (Hou et al., 2009).

Defects such as dislocation and their density play an important role in the bioactivity of hydroxyapatite crystals. Dislocations have a major influence on the processes that leads to bone apposition on bioactive materials. Dislocations also have an important role in in vivo dissolution processes and in crystal maturation of biological apatites (Porter et al., 2004). Dislocations allow plastic deformation through slip. Early studies using microscale compression tests along different crystallographic directions have shown that the hexagonal lattice of hydroxyapatite crystal exhibits highly anisotropic plastic deformation at high temperatures (Nakano et al., 2000). Based on these experiments it is now recognized that the mechanical deformation of hydroxyapatite single crystals is based on crystallographic slip with {1010}<0001> type slip systems. In recent studies instrumented indentation experiments have been performed to investigate the mechanical properties of hydroxyapatite single crystals (Viswanath et al., 2007; Saber-Samandari et al., 2009). These studies exhibit interesting scale-dependent behavior. At the microscale, hydroxyapatite crystals are very brittle and crack during microindentation (Viswanath et al., 2007). However, nanoindentation reveals plastic response which is evidenced by pile-up of the material along the edges of the indenter and “pop-in” of the force-depth curves due to dislocation activity (Viswanath et al., 2007).

Nanoindentation of hydroxyapatite single crystals along the [0001] and [1010] crystallographic directions exhibits anisotropic deformation behavior with the crystal being softer and more ductile along the [1010] crystallographic direction. While the yield stress and hardness are lower along this direction, the fracture toughness is higher (Saber-Samandari et al., 2009). Other studies suggest that the mechanical properties of the hydroxyapatite crystals are a function of the crystal size (Gao et al., 2003). At the nanoscale, the crystal mechanical properties become insensitive to defects and reach their theoretical maximum values. A study of the mechanical response of hydroxyapatite single crystal using atomistic simulations shows that when the defects in the crystal do not contribute to the deformation, the yield stress and hardness of the crystal significantly increase (Ching et al., 2009). These simulations exhibit highly nonlinear anisotropic elastic-plastic deformation response with the crystal being softer along [1010] direction.

Although the instrumented indentation studies provide valuable qualitative information about the overall mechanical properties of hydroxyapatite single crystals, quantitative data on the mechanical properties especially in the nonlinear regime is missing. Number of studies have been focused to find the anisotropic elastic tensor of hydroxyapatite (Hearmon, 1961; Katz and Ukrainck, 1971; Lees, 1972; Gilmore, 1982; Lopez et al., 2000; Neih et al., 2001; Nelae et al., 2002; Guy et al., 2002; Synders et al., 2007). In a recent study, atomistic simulations have been performed to determine the elastic tensor of hydroxyapatite crystal (Ching et al., 2009). However, to develop a nonlinear mechanical model of the elastic-plastic response, more detailed analysis of the indentation data along multiple crystallographic directions must be performed.

Significant research has been performed to determine the stress-strain response of a material using indentation data (Cheng et al., 1998 and 2004; Dao et al., 2001). However, most of the algorithms that have been proposed make extensive use of finite element simulations to determine all the mechanical properties of the materials including Young’s modulus, hardness, yield stress, and flow properties simultaneously. In this paper, we build upon previous work and propose an algorithm which is straightforward and can be easily employed to uniquely identify the mechanical properties of a hard elastic-plastic material such as hydroxyapatite. In contrast to previous work, we first use the hardness and Young’s modulus obtained through indentation experiments to compute yield stress and the information to find flow properties.

We validate this method with existing data from various structural materials including ceramics and then use it to characterize the stress-strain response of hydroxyapatite single crystals from existing nanoindentation data. The significance of this model is that these nonlinear stress-strain data may be used to develop sophisticated constitutive models which can be used in a multiscale modeling framework to predict the mechanical response of artificial or natural hard tissue.

The paper is organized as follows. In section 2 a reverse analysis algorithm is introduced to identify the nonlinear elastic-plastic mechanical properties of hard materials. In Section 3 the model is validated with existing experimental data followed by elastic-plastic mechanical property identification of hydroxyapatite single crystal from nanoindentation data in Section 4.

2. Principle of indentation

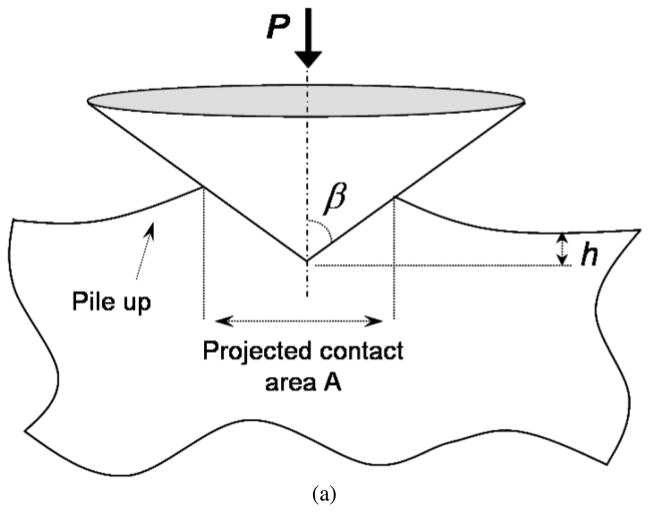
During instrumented indentation, the test specimen is indented with various indenter geometries and the force-depth response is measured during the loading and unloading cycle (Fig. 1(a)). The hardness (H) or the average contact pressure (P_ave) is the simplest data that can be extracted from such experiments as

Fig.1.

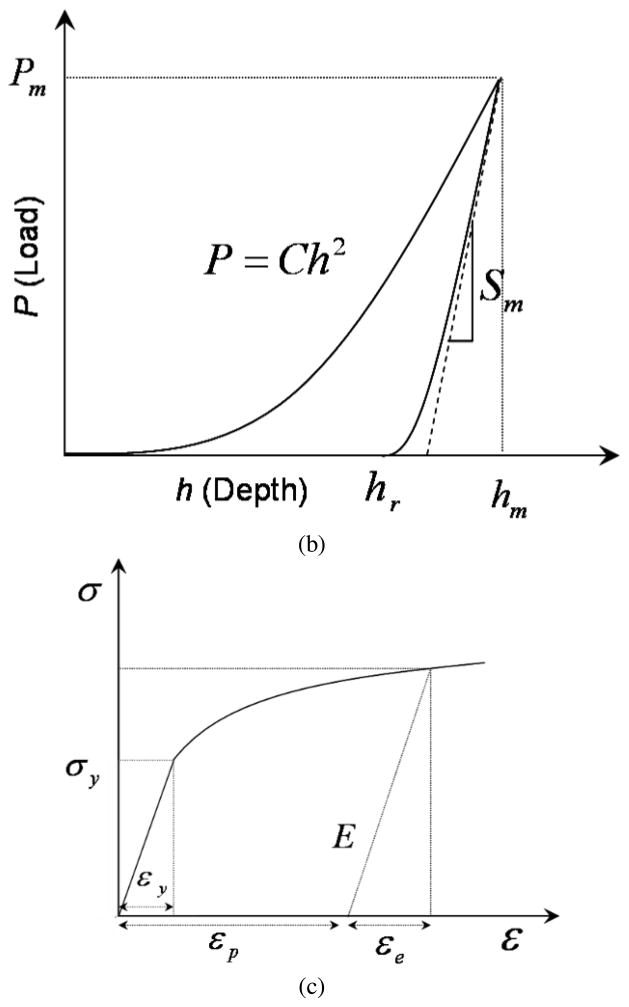
(a) Schematic illustration of instrumented indentation of a homogeneous, isotropic semi-infinite substrate with a sharp conical indenter. (b) Typical load–displacement curves obtained from an indentation experiment and (c) typical stress-strain curve

$$H=P_{\mathit{ave}}=\frac{P_m}{A_m}$$ (1)

where A_m is the projected contact area at maximum load P_m. For a sharp indenter, the loading curve is assumed to follow the following relationship

$$P={Ch}^2$$ (2)

where P is the force of indentation, h is the corresponding depth and C is the loading curvature. A more involved analysis is usually performed to process the indentation data to determine elastic-plastic properties including the loading curvature (C), unloading slope at maximum depth (S_m) and maximum (h_m) and residual indentation depths (h_r), respectively (Fig. 1(b)). The determination of these parameter is done in a two-step process. In the first step, we compute the yield stress from the hardness and Young’s modulus data (section 2.1) followed by determination of the hardening parameters in the second step (section 2.2). The overall analysis algorithm is presented in section 2.3.

2.1. Determination of the yield stress

In the earliest investigations according to the slip line field theory for rigid-perfectly plastic materials, the hardness of the material, obtained through indentation, is directly related to the yield stress H ≅ 3σ_y (Tabor, 1951). Subsequently, in the so-called expanding cavity models (ECMs), it was shown that the hardness related not only to the yield stress but also to the Young’s modulus of the indented material (Marsh, 1964). Further analyses showed that the hardness of elastic-plastic materials obtained through indentation is a function of the inclination of the face of the indenter (β) and the parameter E/σ_y where E is the Young’s modulus of the material and σ_y is the yield stress (Hirst and Howse, 1969; Johnson, 1969). Based on such observations, the overall relationship between the hardness and the yield stress of an elastoplastic material can be expressed as:

$$R_Y=\frac{H}{{\sigma }_y}={\mathrm{\Psi }}_1\left(\frac{E}{{\sigma }_y},\beta \right)$$ (3)

Using extensive analyses of the compression of materials using a wedge-type indenter, it was shown that for an incompressible material, the functional form of Eq. (3) may be chosen as (Johnson, 1969):

$$R_Y=\frac{H}{{\sigma }_y}=\frac{\xi }{\sqrt{3}}\left[1+ln\left(\frac{4{\sigma }_y}{3\pi E}tan\beta \right)\right]$$ (4)

where ξ is a parameter which depends on the ratio of the yield stress and Young’s modulus of the indented material. Based on our observations, for hard metallic alloys and ceramics, ξ may be chosen as $5\sqrt{2}/9$ and 1, respectively. Eq. (3) may therefore be used to compute the yield stress, if the hardness and Young’s modulus are known.

2.2. Determination of the hardening parameters

As the material plastically deforms it hardens and requires more energy for further plastic deformation. This behavior is usually mathematically expressed by a hardening law. For most materials the stress-strain response is usually represented by the following power law form (Fig. 1(c)):

$$\sigma =\{\begin{array}{cc}E\epsilon ,& (\sigma \le {\sigma }_y)\\ K{\epsilon }^n,& (\sigma \ge {\sigma }_y)\end{array}$$ (5)

where n and K are the work hardening exponent and rate, respectively. Hence, corresponding to an yield stress of σ_y, the yield strain (ε_y) is:

$${\sigma }_y=K{\epsilon }_y^n=E{\epsilon }_y$$ (6)

Based on dimensional analysis, several basic functional forms that relate the elastic-plastic properties of the material to the indentation data have been identified. It was proposed in (Cheng et al., 1998 and 2004) that the load curvature (C) in Eq. (1) has the following expression:

$$C=\frac{P}{h^2}=\overline{E}{\widehat{\mathrm{\Psi }}}_2\left(\frac{{\sigma }_y}{\overline{E}},n,\beta \right)$$ (7)

where Ē is the reduced Young’s modulus given by:

$$\overline{E}={\left(\frac{1-{\nu }^2}{E}+\frac{1-{\nu }_i^2}{E_i}\right)}^{-1}$$ (8)

where (ν, E) and (ν_i, E_i) are the Poisson’s ratio and Young’s modulus pairs of the indented specimen and the indenter, respectively. An alternative expression of the load curvature is proposed by (Dao et al., 2001):

$$C=\frac{P}{h^2}={\sigma }_r{\mathrm{\Psi }}_2\left(\frac{\overline{E}}{{\sigma }_r},n\right)$$ (9)

where σ_r is a representative stress corresponding to a characteristic strain of the indented material. As n, σ_r and Ē are unknown in Eq. (9), a more convenient expression is (Dao et al., 2001):

$$C=\frac{P}{h^2}={\sigma }_r{\mathrm{\Psi }}_3\left(\frac{\overline{E}}{{\sigma }_r},\frac{{\sigma }_y}{{\sigma }_r}\right)$$ (10)

in which onlyσ_r and Ē are unknown.

Through extensive FEM analysis (Giannakopoulos et al., 1994; Larsson et al., 1996; Giannakopoulos and Suresh, 1999; Venkatesh et al., 2000) it was proposed that Ψ₃ for most of materials may be expressed as:

$$C=\frac{P}{h^2}=A{\sigma }_{0.29}\left\{1+\frac{{\sigma }_y}{{\sigma }_{0.29}}\right\}\left\{B+ln\left(\frac{\overline{E}}{{\sigma }_y}\right)\right\}$$ (11)

where A and B are constants obtained from finite element computations (table 1) and depend on indenter geometry. σ_0.29 is a stress which corresponds to the characteristic strain ε_r = 0.29 for the indented material in uniaxial compression. The characteristic strain is an important parameter in such analysis and should be carefully selected. Previous FEM analyses for sharp indenters such as Berkovich and Vickers indenters suggest that ε_r = 0.29 (Giannakopoulos and Suresh, 1999), however other values have been chosen, see (Shim et al., 2008). In this work we use ε_r = 0.29.

Table 1.

Parameters A, B and c* for different indenter geometries

Indenter	A	B	c*
Vickers	6.5	−1	1.2105
Berkovich	6.02	−0.875	1.2370
Conical	The same as Vickers or Berkovich depending on the apex angle of the cone		1.1957

Computation of the reduced elastic constant (Ē) using Eq. (8) is not straightforward since finding the indenter elastic constant is challenging. A better way is to find another dimensional function from which the reduced elastic constant may be computed directly.

This is accomplished by using the unloading curve. If the unloading force is P_u, the slope of the unloading portion of the indentation curve is

$$S=\frac{{dP}_u}{dh}=\frac{{dP}_u}{dh}(h,h_m,\overline{E},{\sigma }_r,n)$$ (12)

Dimensional analysis gives (Dao et al., 2001):

$$S=\frac{{dP}_u}{dh}=\overline{E}h{\mathrm{\Psi }}_4\left(\frac{h_m}{h},\frac{{\sigma }_r}{\overline{E}},n\right)$$ (13)

At h = h_m

$$S_m=\frac{{dP}_u}{dh}{|}_{h=h_m}=\overline{E}{h}_m{\mathrm{\Psi }}_4\left(\frac{{\sigma }_r}{\overline{E}},n\right)$$ (14)

However, the function Ψ₄ has three unknowns (n, σ_r, and Ē). Based on previous analysis (King et al., 1987), we use a simpler dimensionless function:

$$S_m=\frac{{dP}_u}{dh}{|}_{h=h_m}=\overline{E}{h}_m{\mathrm{\Psi }}_5\left(\frac{\sqrt{A_m}}{h_m}\right)$$ (15)

where ψ₅ is expressed as:

$${\mathrm{\Psi }}_5=\frac{c\ast \sqrt{A_m}}{h_m}$$ (16)

Now a combination of Eqs. (15) and (16) gives:

$$\overline{E}=\frac{1}{c\ast \sqrt{A_m}}\frac{dP}{dh}{|}_{h=h_m}$$ (17)

where c* is a computationally driven parameter depend on the geometry of the indenter and its value for different indenter geometires is shown in table 1. Eq. (17) can be used to find the reduced elastic modulus Ē for indented material.

Now using σ_0.29 and σ_y, the work hardening exponent n can be computed as:

$$n=\frac{ln({\sigma }_{0.29})-ln({\sigma }_y)}{ln(0.29)-ln({\epsilon }_y)}$$ (18)

The work hardening rate K is obtained using Eq. (6).

2.3. The analysis algorithm

The following algorithm summarizes the procedure for computing the elastic-plastic parameters

1. Compute the yield stress σ_y from Eq. (4) using information regarding the geometry of the indenter (β), the hardness H and Young’s modulus E of the indenter.

2. Compute the actual projected contacted area (A_m) from the hardness value H and the maximum load of indentation P_m using Eq. (1).

3. Compute the slope of the unloading curve at $S_m=\frac{dP}{dh}{|}_{h=h_m}$.

4. Compute Ē from Eq. (17) based on A_m and S_m.

5. Compute $C=\frac{P}{h^2}$ by fitting to the indentation data during loading cycle.

6. Compute the characteristic stressσ_0.29 in Eq. (11) by using the computed values of C, Ē, and σ_y.

7. Compute the yield strain ε_y = σ_y/E.

8. Compute the work hardening exponent n in Eq. (18) using σ_0.29, σ_y, and ε_y.

9. Compute the work hardening rate parameter K using Eq. (6).

3. Validation

We perform validation studies before using the algorithm proposed in section 2.3 for the determination of the elastic-plastic properties of hydroxyapatite single crystals. In Table 2 we present the various parameters of the indentation curves for refractory alloy and steel (Venkatesh et al., 1999) and 6H-SiC ceramic crystal (Shim et al., 2008).

Table 2.

Indentation data for three different materials used for validation

Material	E (GPa)	H (GPa)	P (N)	C (GPa)	Am (M2)	Sm = dP/dh (N/M)
Refractory alloy	80	3.513	5.0	66.71	1.85e-9	3.97E6
Steel	210	1.538	5.0	42.26	3.25e-9	1.20E7
6H-SiC	300	21.98	0.1	386.24	4.56e-12	728.20E3

Our model predictions are compared with the results resented in literature in Table 3. For the 6H-SiC single crystal, results were provided based on finite element simulations considering two conditions – frictionless indenter and considering friction with coefficient μ = 0.2 (Shim et al., 2008). Our analysis provides flow values which are in-between these two cases. Analyses based on finite element simulations much more expensive compared to our method.

Table 3.

Comparison of the flow properties of three materials obtained by different methods with the source of experimental data noted within parentheses in the first column.

Material	Literature		This work
	σy (GPa)	n	σy (GPa)	n
Refractory alloy (Venkatesh et al., 1999)	1.5	0.05	1.60	0.047
Steel (Venkatesh et al., 1999)	0.5	0.10	0.49	0.120
6H-SiC (Shim et al., 2008)	7.0 (μ = 0) 8.3 (μ = 0.2)	0.214(μ = 0) 0.329 (μ = 0.2)	8.0	0.279

4. Flow properties of hydroxyapatite single crystals

Having validated our analysis algorithm we apply that to the extraction of the flow properties of single crystal hydroxyapatite based on nanoindentation data. Table 4 shows the nanoindentation data for hydroxyapatite single crystal corresponding to indentation on the prism (1010) and basal (0001) facets (Saber-Samandari and Gross, 2009) corresponding to the plots presented in Figure 2.

Table 4.

Indentation data for hydroxyapatite single crystal (Saber-Samandari and Gross, 2009)

Indented facet	E (GPa)	H (GPa)	P (N)	C (GPa)	Am (M2)	Sm = dP/dh (N/M)
(0001)	150.38	7.06	7.5E-3	2.32E11	7.08E-13	1.20E5
(1010)	143.56	6.41	5.0E-3	2.03E11	1.17E-12	1.65E5

Fig 2.

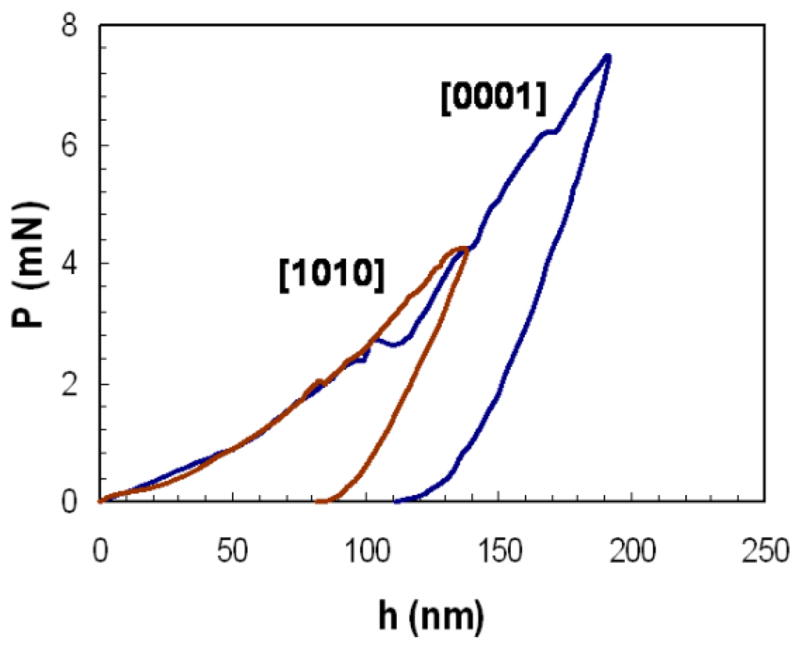
The P-h curves obtained from nanoindentation of hydroxyapatite single crystal on the (0001) and (1010) facets (experimental data from Saber-Samandari et al. 2009)

Table 5 presents the elastic-plastic properties obtained using our algorithm. Clearly, the yield stress is lower along the [1010] direction compared to [0001]. The work hardening rate coefficient and exponent are also higher along the [0001] direction. The corresponding stress-strain curves are plotted in Figure 3. The anisotropy of the flow properties may be related to the mechanisms responsible for plastic deformation in the crystal. It has been observed during compression loading that unlike other hcp crystals, only the {1010}<0001> slip systems get activated (Nakano et al. 2001) in hydroxyapatite, which explains its lower yield point along the [1010] direction. Such behavior is not surprising as hydroxyapatite is not an atomic crystal and experiences more constraints to dislocation motion along certain crystallographic directions than atomic crystals.

Table 5.

Flow properties of hydroxyapatite single crystal

Facet	σy (GPa)	K (GPa)	n
(0001)	2.42	18.82	0.49
(1010)	2.17	14.47	0.45

Fig. 3.

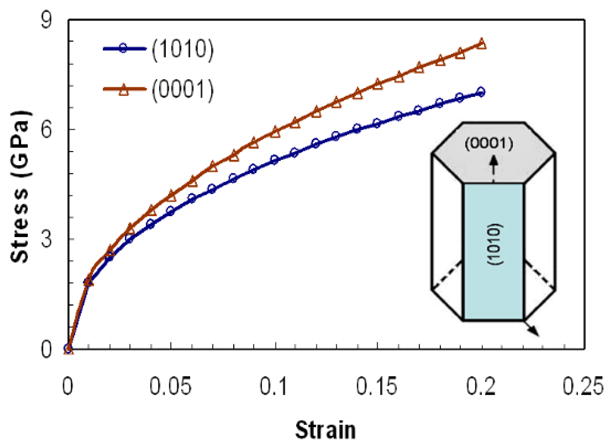
Stress strain response of the hydroxyapatite single crystal extracted from nanoindentation data.

5. Conclusions

A computational approach has been presented to extract the elastic-plastic properties of hydroxyapatite single crystals from nanoindentation data. The method was validated by comparing its predictions to data obtained from literature. The flow properties of hydroxyapatite single crystal, obtained using this method, exhibits anisotropy. The crystal has a lower yield stress along the [1010] crystallographic direction compared to the [0001] direction. The predicted stress-strain curves show a lower rate of work hardening and work hardening exponent along the [1010] direction, which confirms that hydroxyapatite single crystals are more ductile along this direction.

While we have considered the effect of dislocation induced plastic flow in characterizing the anisotropic nonlinear behavior of hydroxyapatite single crystals, changes in molecular orientation and debonding are also important factors. Based on ab initio simulations of defect-free hydroxyapatite single crystals it has been shown in (Ching et al., 2009) that uniaxial loading along the [0001] direction exhibits a more brittle response compared to the [1010] direction. It was observed that during tensile straining, the deformation behavior of defect free hydroxyapatite single crystal is mainly due to the rotation of the PO4 tetrahedra with associated motion of both columnar and axial Ca⁺⁺ ions. However, the ab initio simulations were unable to consider the effects of dislocation. For a complete description of the anistropic mechanical response of hydroxyapatite crystals, it is important to consider the elastic anisotropy arising out of molecular flexibility together with slip activities and damage evolution.

The results presented here are valuable not only for the analysis and modeling of hydroxyapatite based biomaterials and scaffolds but also for other hard biocrystals and ceramics.