Computational ligand-based rational design: Role of conformational sampling and force fields in model development

Abstract

A significant number of drug discovery efforts are based on natural products or high throughput screens from which compounds showing potential therapeutic effects are identified without knowledge of the target molecule or its 3D structure. In such cases computational ligand-based drug design (LBDD) can accelerate the drug discovery processes. LBDD is a general approach to elucidate the relationship of a compound's structure and physicochemical attributes to its biological activity. The resulting structure-activity relationship (SAR) may then act as the basis for the prediction of compounds with improved biological attributes. LBDD methods range from pharmacophore models identifying essential features of ligands responsible for their activity, quantitative structure-activity relationships (QSAR) yielding quantitative estimates of activities based on physiochemical properties, and to similarity searching, which explores compounds with similar properties as well as various combinations of the above. A number of recent LBDD approaches involve the use of multiple conformations of the ligands being studied. One of the basic components to generate multiple conformations in LBDD is molecular mechanics (MM), which apply an empirical energy function to relate conformation to energies and forces. The collection of conformations for ligands is then combined with functional data using methods ranging from regression analysis to neural networks, from which the SAR is determined. Accordingly, for effective application of LBDD for SAR determinations it is important that the compounds be accurately modelled such that the appropriate range of conformations accessible to the ligands is identified. Such accurate modelling is largely based on use of the appropriate empirical force field for the molecules being investigated and the approaches used to generate the conformations. The present chapter includes a brief overview of currently used SAR methods in LBDD followed by a more detailed presentation of issues and limitations associated with empirical energy functions and conformational sampling methods.

1. Introduction

When ligands and data on the biological activities of those ligands are the only information available for drug development, computer-aided ligand based drug design (LBDD)^1-6 is an effective method to extend the knowledge of the known ligands to design compounds with improved biological activity. The importance of LBDD is emphasized by more than 50 % of current FDA-approved drugs targeting membrane proteins such as G protein coupled receptors (GPCRs), nuclear receptors, and transporters⁷, for which three-dimensional (3D) structures are often not available, a necessary prerequisite for target based drug design approaches^8-10. Considering the difficulties in determining 3D structures of membrane-associated proteins, LBDD methodologies are anticipated to continue to have a significant impact on drug development into the foreseeable future^{11, 12}.

Drugs typically exert their pharmacological effects by specific interactions with their target proteins. Such unique interactions have been understood as “lock-and-key”¹³, “induced-fit”¹⁴, “conformational selection” or “population shift” hypotheses,^15-19 which are based on the inherent chemical structure of molecules, their dynamic conformational properties and how those two influence the receptor. Therefore, identifying any causation or correlation between structures and activities, referred to as a structure-activity relationship (SAR)^20-22, can be of utility for ligand design. LBDD based SAR identifies similarities and/or differences in structural or physicochemical properties of compounds and relates them to activity, including efficacy (e.g. activation or stimulation of receptors, V_max of enzymes), affinity (e.g. K_i), selectivity (e.g. K_{i, isoform1}/K_{i, isoform 2}), pharmacokinetics (ADME)^{23, 24}, drug-drug interactions, or any biological properties of interest. Various descriptors of the ligands are related to biological activities through various statistical methods, for instance, regression, classification, dimension reduction, variable selection, etc. from which important features of the ligands responsible for activity are identified and used to develop new leads or to optimize known ligands.

Three major categories of LBDD are quantitative structure activity relationship (QSAR)^25-27, pharmacophore modeling^28-32, and similarity searching^33-36. Over several decades, statistics, computational algorithms, and descriptors comprising the three categories and their pipelining have led to significant improvements both in efficiency and accuracy. Programs can deal with 100∼1000s of molecules to build models or search molecular properties against databases of millions compounds in a short period of time. Overall improvements have been achieved by sophisticated data mining techniques and by more accurate mathematical descriptions of molecules through molecular mechanics (MM)³⁷ and quantum mechanics (QM) methods³⁸.

Recent advances in statistical, algorithmic and chemoinformatics in relation to LBDD have been discussed elsewhere in depth^39-42. This chapter will briefly overview LBDD followed by a detailed presentation of new developments in the areas of conformational sampling and force fields (FF) with respect to LBDD.

2. Basic components of computer-aided LBDD

2.1. Representation of molecules

Molecules may be described in different ways ranging from one- to three dimensional (3D) and higher methods. For simple counting of molecular constitutions or fragments in 1D, one can use line notation such as SMILES (Simplified molecular input line entry specification)⁴³ and SLN (SYBYL line notation)⁴⁴ or chemical fingerprints, such as the MACCS representation⁴⁵. 1D representations are used for fast lookup and comparison and in some cases do not yield a unique description of the molecules, as in the MACCS fingerprints. When molecules are represented as a graph⁴⁶, atoms are nodes and bonds are edges connecting the nodes, yielding a 2D description of a molecule. Information on bond or atom types, atom size, or stereochemistry and so on can be stored in the form of matrix and readily accessed. Along with the graph representation, a simple connection table may be used to calculate 2D molecular properties, for example, molecular weight, molar refractivity, number of rotatable bonds, branching, number of hydrogen bond acceptors and donors, and sum of atomic polarizabilities. Such descriptors are widely used in QSAR analysis. For a more detailed and realistic representation of molecules, a 3D representation, typically in the form of atomic Cartesian coordinates, is required. Such 3D descriptions also allow for the calculations of various descriptors and, more importantly, can represent the bio-active conformations of a molecule. This is particularly important when comparing compounds with different chemical structures that may show similar biological properties by having similar 3D placement of biologically important functional groups. 3D descriptors, such as the spatial relationship between functional groups, may be calculated using semi-empirical or ab initio QM methods for small size ligands (number of atoms ≤ 100) and MM for most ligands. With growing computational power, the use of QM & MM is significantly increasing in the field of LBDD^{1, 38}. Beyond 3D methods are 4D and higher representations. For example, the different possible conformations of the 3D structure of a molecule may be considered a 4D representation. The remainder of section 2 will present different nD representations of molecules and their utilization in LBDD.

2.2. 2D-QSAR

A large number of 1D or 2D molecular descriptors have been developed^{47, 48}. Most software packages that include a QSAR module calculate a range of descriptors such as physicochemical, electronic, topological, and shape properties. Lipinski's rule of five⁴⁹ is a classical example of a straightforward application of QSAR where bioavailability is related to descriptors including octanol/water partition coefficient (logP), molecular weight, number of hydrogen bond donors and acceptors, and number of rotatable bonds.

Development of SAR models often requires pre-processing of the descriptors prior to model development. Values are often normalized such that coefficients obtained from fitted models represent the significance of the individual descriptors. Importantly, given the large number of possible 1D/2D descriptors it is necessary that the number of descriptors used during model development be limited by selection methodologies^{50, 51}. In simple terms highly correlated descriptors are typically removed from model development. Descriptor selection is then often linked to model development itself. Those descriptors most predictive of a target property are selected by iterative analysis (stepwise multiple linear regression (MLR)⁵², replacement method⁵³) or by learning algorithms (Genetic algorithm⁵⁴, adaptive fuzzy partition algorithm⁵⁵, Gaussian processes⁵⁶, or Genetic function approximation (GFA)⁵⁷). Correlated or redundant descriptors may also be eliminated by partial least square (PLS)^58-61 or principle component analysis (PCA)^{62, 63}.

Given a suitable training set (i.e. set of compounds with known biological activities) and descriptors, one applies statistical methods according to the characteristics of the data set. When linearity is present MLR and PLS are good choices. Nonlinearity^{64, 65} occurs when one handles a large number of non-homologous data sets, for example in pharmacokinetic (PK) studies where multiple biological phenomena such as absorption and metabolism can impact the biological data, or when activities are influenced by many factors such as receptor dimerization, existence of receptor isoforms, and conformational changes. Selection (or design) of the experimental data for model development can minimize nonlinearity, thereby reducing possible ambiguities in the developed QSAR but users need to keep in mind the inherent complexity of biological phenomena. Selection of the appropriate statistical methods also depends on whether the goal of the study is interpretation or predictability. Classical methods such as MLR produce explicit physical meaning but predictability is not as good as using modern statistical tools that improve predictability. However, interpretability is often compromised with improved predictability. While the MLR method, which maximizes interpretability, was the most used method in 2008, it was followed by PLS & support vector machine (SVM) approaches that yield improved predictability. Newly developed statistical methods³⁹ include Gene Expression Programming (GEP) ⁶⁶, Project Pursuit Regression (PPR)⁶⁷, Local Lazy Regression (LLR)⁶⁸ while recent variations in QSAR approaches are hologram-QSAR⁶⁹, auto-QSAR⁷⁰, and inverse-QSAR⁷¹ among others. Hologram-QSAR⁶⁹ partitions molecules into smaller fragments and uses size, length, and as well as additional information on those fragments as descriptors. It is usually combined with PLS to derive a QSAR. Auto-QSAR⁷⁰ is an automated QSAR where the best descriptors, the best statistical methods, and validations are chosen for given set of molecules and updated as the number of molecules in training set increases. In Inverse-QSAR⁷¹ after a QSAR model is built, distributions of descriptors yielding optimal activity are estimated and structures are generated or searched that match those distributions.

As a last step in QSAR model development, the models require validation^{72, 73}. Approaches to do this include cross-validation, y-randomization, or external test set. It is generally perceived that leave-one-out or leave-n-out cross-validations do not necessarily indicate predictability directly and external validation using compounds not included in model development is recommended to verify predictability of the developed models. An overview of statistical methods used in QSAR analysis is given in Table S1 of the supporting information.

2.3. nD-QSAR (3 ≤ n ≤ 7)

QSAR methods based on 3D descriptors (Table 1) such as molecular volume, surface area, ΔG_solvation, dipole moments, HOMO, and LUMO, depend on the chemical and spatial features of molecules. Alternatively, 3D-QSAR^74-76 may be based on the molecular interaction field mapped onto a 3D grid surrounding the molecules of interest. The descriptors are the magnitudes of the fields at the grid points, an approach used in CoMFA (comparative molecular field analysis)⁷⁷ and CoMSIA (comparative molecular similarity indices)⁷⁸. For example, in CoMFA polar or hydrophobic probes are placed on grid points and non-bonded interaction energies with the ligands are calculated, with the resulting values used as descriptors for each molecule, such that each molecule has, in essence, a number of descriptors that correspond to the number of grid points. The grid point values are subjected to statistical methods such as PLS or PCA and related to biological activities. Notably, these approaches require alignment of the different ligands being studied. When flexibility is added to the shape information by using multiple conformations, it is classified as 4D-QSAR^{79, 80}. Although 3D-QSAR can use multiple conformers it means multiple model evaluations, with the input into each model being one static conformer for each ligand in the training set. 4D-QSAR, in one embodiment, overcomes this limitation by using grid cell occupancy descriptors calculated based on multiple conformers. 5D-QSAR^{81, 82} attempts to construct a pseudo-receptor based on ligand information in combination with a GA to vary the grid point locations to produce a favorable induced-fit state. Beyond this, 6D-QSAR⁸³ incorporates solvation energy terms. Finally, the inclusion of 3D structure of the target from X-ray crystallography or NMR in the models represents the highest dimension, 7D, applied to date, though the approach is no longer formally LBDD.

Table 1. Overview of nD-QSAR approaches (3 ≤ n ≤ 7).

method	description
CoMFA	Probes placed on grid points in the 3D field around a molecule experience an interaction energy with the ligands that defines the molecular shape and electrostatic properties in the surrounding environment.
CoMSIA	It expands CoMFA by including hydrophobic and hydrogen bonding contributions and calculates how these contributions are similar between molecules.
GRIND	It eliminates alignment-dependency by using distances between 3D grid points. Highly relevant regions among a set of molecules are selected as nodes and the intensity of molecular interaction field at those nodes are used as descriptors. The program ALMOND provides tools to compute, analyze, and interpret the GRIND.
VolSurf	Information on 3D grid voxels (shape, electrostatic, volume) are compressed into 2D numerical descriptors by image analysis tools.
4D-QSAR	Multiple conformations in a grid box generate the occupancies at grid points, with those occupancies used as the descriptors.
5D-QSAR	Multiple hypothetical binding pockets are generated around ligands based on a 3D grid and the receptor models are evolved by GA with the most favorable binding pocket model evaluated by relative free energy of ligand binding.
6D-QSAR	It includes optimization of structures in aqueous solution and calculates solvation energy and charges by semi-empirical QM method, AMSOL86. Ligands' arrangement in pseudo-binding pocket is determined by MC simulation.

Of the methods in Table 1, CoMFA and CoMSIA are the most widely used. Their main limitations are their dependency and sensitivity to conformations and alignments of the molecules under study. Different occupancies by different conformations or changes in molecular alignments can cause different interaction fields yielding different QSAR models. To overcome the limitations, alignment-independent 3D-QSAR was developed by transforming 3D-grid data into 2D descriptors such as GRIND (Grid independent descriptors)^{84, 85} and VolSurf⁸⁴. The approaches are listed and summarized in Table 1.

2.4. Pharmacophore modelling

The IUPAC definition⁸⁷ of a pharmacophore is “the ensemble of steric and electronic features that is necessary to ensure the optimal supramolecular interaction with a specific biological target structure and to trigger (or block) its biological response.” Pharmacophore modelling is closely related to 3D or 4D-QSAR and commonly used pharmacophoric keys include hydrogen bond donors and acceptors, ionizable groups, aromatic rings, aliphatic hydrophobic groups, among others. In many cases superimposed compounds based on pharmacophore models are the starting point for 3D-QSAR analysis. Alternatively, pharmacophore features may be identified by building 3D-QSAR iteratively with different conformations or alignment attempted to increase activity prediction²⁸. As with 3D-QSAR methods, critical steps in pharmacophore modelling are selection of bio-active conformations and structure alignments. Conformations can be pre-calculated and saved in a database or be generated on-the-fly during alignments. Various sampling methods used to generate multiple conformations will be discussed below. Using a collection of pharmacophoric keys or points (i.e. functional groups that may contribute to biological activity) and a conformational ensemble which is expected to include the active conformation, molecular alignment (or superposition)^{1, 28, 31, 32, 88} is carried out by mapping fragments of the compounds with a target function being minimized. In the clique detection algorithm⁸⁹ distances between features are stored in a matrix and the differences between two matrices become the target function. Another way is using GA,⁹⁰ where a chromosome describes a molecule and genes encoded in it represent the ligand fragments to be matched to the features of the reference compound. The target function or fitness function in GA can include a range of information such as the similarities between features and volumes of aligned structures. The GA is often extended for on-the-fly conformational sampling by including geometric information of a molecule into the chromosomes. FlexS algorithm⁹¹ is also used in pharmacophore feature mapping. It decomposes a molecule and grows it on top of the reference compound beginning from an anchor fragment. In all cases, it is important to select a reference structure that has high experimental activity, a known 3D binding conformation or a favorable docking score to facilitate interpretation of the obtained model. Details of methods used by the major pharmacophore modelling programs and recent research on alignment methods were reviewed in Leach et al.³¹ and Lemmen and Lengauer⁸⁸. Such alignment methods are also of general utility for pharmacophore-based similarity searching.

2.5. Ligand based similarity searching

Similarity searching is an effective, computationally accessible method to identify compounds with qualities similar to that of an active, lead compound. For example, if the number of ligands for which biological activity is known are too few to build a QSAR model, similarity searching may be effective. Similarity searching can be based on a number of features including chemical fingerprints, physiochemical properties as well as 2D and 3D features selected by QSAR or pharmacophore models. If compounds structurally similar to active compounds are desired, searches based on chemical fingerprints are appropriate. However, if the goal of the study is the identification of ligands that have a new scaffold/chemical structure but maintain the desired biological activity (i.e. scaffold hopping⁹²), searching based on physiochemical properties may be of utility. The most widely used descriptors in similarity searching are chemical fingerprints or large numbers of physiochemical properties. Fingerprints can have diverse properties and combinatorial or compressed fingerprints are emerging and efforts are being made to improve the fingerprint representations. To quantify the extent of similarity between compounds, different similarity measures are used alone or in combinations; these include the Tanimoto, Cosine, Hamming, Russel-Rao, and Forbes indices. Finally, it should be noted that it is useful to perform successive searches using the nearest neighbors of a query compound. A number of software packages, including MOE (Molecular Operating Environment, Chemical Computing Group⁹³) and Discovery Studio (Acclerys Inc⁹⁴) allow for similarity searching. Public small molecule databases such as PubChem⁹⁵ ZINC⁹⁶ and ChEMBL⁹⁷ or open source software⁹⁸ using those databases provide similarity searching and clustering tools. Notable are clustering techniques⁹⁹ where output structures from a similarity search are further grouped into subsets to reduce redundancy and to check diversity in compounds selected, for example, for a target-based database screen¹⁰⁰. Results of clustering vary based on classification algorithms, descriptors, and similarity measures^101-103 and there is no gold standard to obtain the best clustering. Therefore it is desirable to perform clustering with a combination of methods, descriptors, and similarity coefficients followed by manual evaluation of the results to achieve the desired outcome.

3. Conformational sampling

For the 3D and higher order methods it is essential that the appropriate, biologically relevant conformations be identified. Considering that drug-like molecules can have 10 or more rotatable bonds and each such bond may have 3 accessible rotamers a compound may have 3¹⁰ conformations that must be considered. The need to access a large number of these conformations is further emphasized by studies showing that bioactive conformations of compounds in X-ray crystal structures of ligand-protein complexes can have energies 15∼20 kcal/mol higher than the global minimum^104-107. While the value of 3¹⁰ is likely an overestimation due to steric clashes, it is evident that a major concern in modern LBDD methods is securing bioactive conformations given that model assessment includes multiple conformations in a large number of studies^{105, 106, 108-112}. Furthermore, taking all conformations into account during model development can account for the dynamic nature of molecules; 4D-QSAR^{79, 80} and the Conformationally sampled pharmacophore (CSP)^113-115 are representative methods that use this information.

Various methods are employed to generate multiple conformations of a ligand. Systematic search approaches^116-118 formally perform an exhaustive sampling of conformational space, thereby covering the whole energy surface. However, as the degrees of freedom increases the number of possible conformations becomes enormous and often includes non-physical structures. Systematic search procedures therefore often limit the number of conformations accessed and select conformations within a user-defined energy difference range. For example, MOE supports a maximum of up to 10000 conformers and each one is subjected to trial model buildup. An alternative to systematic sampling is Monte Carlo based approaches^119-121 where random changes in structures (i.e. trial moves) are attempted by rotation about a dihedral angle or other geometric change with the new conformations associated with the trial moves accepted or rejected according to the Metropolis criterion^{120, 121}. In the Metropolis method a conformation with an energy, ΔE, lower than that of the previous conformation is accepted while conformations with higher, less favorable energies are kept based on the acceptance probability, p=e^-ΔE/kT where k is the Boltzmann constant, T is the temperature and p is compared to a random number. If p is greater than the random number the conformation is accepted, allowing higher energy conformations to be sampled. In this method energy barriers are easily overcome by increasing the effective temperature but random elements still exist during sampling leading to inefficiencies due to similar conformations being accessed. The Poling method¹²² adds a penalty function (poling function) to the energy during the conformational search that is inversely proportional to the root mean square distance between conformations so sampling of similar conformation is avoided while accessing new conformation is maximized. With the same goal as the Poling method, Tabu search¹²³ keeps a record of previous sampled states thereby maximizing the exploration of previously unsampled conformations. When GA^{124, 125} is applied for conformational sampling, each chromosome is a conformer and contains genes corresponding to structural degrees of freedom in the molecule. Chromosomes undergo mutations and crossover resulting in the sampling of diverse conformations in the descendant conformations. Molecular dynamics (MD) simulations sample conformations deterministically according to Newton's equations of motion and overcome trapping in local minima due to the inclusion of kinetic energy in the system, as described below. All of the methods mentioned in this paragraph have advantages and disadvantages. For small molecules systematic search algorithms in combination with an accurate force field, as discussed below, can assure that all relevant conformations are taken into account. With larger molecules, exhaustive sampling of all accessible conformations is not feasible, MC or MD methods allow for extensive sampling of accessible conformations, though care must be taken to assure that all the relevant conformations are being sampled. One outstanding advantage of both MD and MC methods is that a variety of methods that allow for detailed representation of the biological environment of a molecule by, for example, the explicit treatment of waters and ions have been developed for these approaches. Given the wide use of MD methods for conformational sampling as well as for studies of the dynamics of molecules ranging from small ligands to large macromolecular complexes containing 1 million or more atoms, the remainder of the discussion of conformational sampling will focus on MD based approaches^126-130.

MD simulations ^{127, 131, 132} are based on Newton's equations of motions. The second law F=ma states that from position r_i(t), velocity v_i(t), and mass m_i for an atom i at time t, force F_i(t) can be calculated. In MD simulations, forces are usually obtained from analytical derivatives of the potential energy function and integration methods are used to obtain new positions r_i(t+δt) and velocities v_i(t +δt) from the previous states, r_i(t), v_i(t), and a_i(t). For example, the original Verlet integrator¹³³ uses a Taylor series expansion of position. Summing equation 1a and 1b yields 1c which determines the new position. This integration minimizes memory requirements as it is not necessary to store velocities, although they can readily be calculated using equation 1d if required.

$$r(t+\delta t)=r(t)+v(t)\delta t+\frac{1}{2}a(t)\delta t^2$$ Equation 1a

$$r(t-\delta t)=r(t)-v(t)\delta t+\frac{1}{2}a(t)\delta t^2$$ Equation 1b

$$r(t+\delta t)=2r(t)-r(t-\delta t)+a(t)\delta t^2$$ Equation 1c

$$v(t)=\frac{r(t+\delta t)-r(t-\delta t)}{2\delta t}$$ Equation 1d

Leapfrog Verlet integration^{134, 135} uses an expansion of positions and velocities to the second order and an interval 1/2δt instead of δt. Subtraction of equation 2b from 2a yields 2c. New positions may then be obtained by substituting v(t) from rearrangement of 2a into v(t) of 1a and truncating the expansion at the velocity term yielding equation 2d.

$$v(t+\frac{1}{2}\delta t)=v(t)+\frac{1}{2}a(t)\delta t$$ Equation 2a

$$v(t-\frac{1}{2}\delta t)=v(t)-\frac{1}{2}a(t)\delta t$$ Equation 2b

$$v(t+\frac{1}{2}\delta t)=v(t-\frac{1}{2}\delta t)+a(t)\delta t$$ Equation 2c

$$r(t+\delta t)=r(t)+v(t+\frac{1}{2}\delta t)\delta t$$ Equation 2d

Extended integration methods have been developed to enhance accuracy and provide special features for the simulation system of interest¹³⁶. For example, for simulations of aqueous solutions it may be desirable to reproduce constant pressure, temperature, or volume in accord with the specific ensemble being targeted. For example, simulations in the constant pressure, temperature and number of particles ensemble (NPT) may be used to calculate Gibbs free energies while a constant volume, temperature and number of particles ensemble (NVT) yields Helmholtz free energies. However, such simulations require the appropriate boundary conditions, such as periodic boundaries¹³⁶. While these are necessary for sampling the conformations of ligands in the presence of explicit solvent, for LBDD MD simulations are typically performed in the absence of explicit solvent. Such simulations may be performed in the “gas phase” or using implicit solvent models to treat the solvent environment, as detailed below.

High temperature MD has long been used to facilitate the crossing of high energy barriers to assure a broad sampling of conformational space. In high temperature MD, the probability of particles having the necessary velocity (or kinetic energy) to cross energy barriers is increased over room temperature simulations. While sampling in MD is driven by information on the molecular forces thereby guiding conformational sampling to physically meaningful regions, unwanted sampling may occur in high temperature MD. This is due to the high temperature leading to sampling of conformations that are inaccessible at room temperature thereby causing inefficient use of computational effort. However, care to avoid excessively high temperatures can minimize this problem and a number of protocols, referred to as simulated annealing¹³⁷, perform high temperature MD followed by room temperature MD to assure that conformations relevant to the latter are being sampled.

A simple way to improve sampling via MD simulations is to perform multiple simulations of the system starting with different initial random number seeds to assign the velocities to the particles in the system. Typically, a Gaussian distribution of velocities are randomly generated and assigned to each particle with those initial velocities satisfying a Maxwell-Boltzmann distribution defining a selected temperature. While the overall velocity distribution is approximately reproduced with the different random number seeds yielding the same macroscopic temperature, the individual atoms have different velocities, thereby directing the molecule to sample different conformations. However, this approach does not always avoid kinetic trapping for larger molecules due to large barriers often associated with large conformational changes.

Methods that go beyond the use of high temperature and multiple MD runs are referred to as generalized ensemble (GE) algorithms.^138-140 These include replica exchange MD (REXMD)¹⁴¹, meta-dynamics^{142, 143}, accelerated MD (AMD)¹⁴⁴ and λ-dynamics¹⁴⁵ among others. In GE algorithms energy barriers are overcome by adding an external biasing potential(s) to the system. This may be performed by accessing additional conformations from additional simulations, as in REXMD, or by approaches that directly modify the free energy landscape of the system. Many GE MD simulation approaches sample the free energy landscape efficiently and may be used to calculate accurate free energy differences. The free energies are often calculated by thermodynamic integration (TI) ¹⁴⁶ or the weighted histogram analysis method (WHAM).¹⁴⁷

Standard REXMD involves parallel independent simulations (replicas) at a range of temperatures and exchanges conformations between replicas according to an exchange probability (Equation 3).

$$P(\mathit{\text{exchange}})=\{\begin{array}{l}{e}^{-\Delta },\mathit{\text{for}}\Delta >0\\ 1,\mathit{\text{for}}\Delta \le 0\end{array}$$ Equation 3a

$$\begin{array}{l}\text{where}\Delta =\left(\frac{1}{k{T}_i}-\frac{1}{k{T}_j}\right)\left(E(q_j)-E(q_i)\right)\\ \text{in REXMD}\end{array}$$ Equation 3b

$$\begin{array}{l}\text{or}\Delta =\frac{1}{kT}\left[\left(E^j(q_j)-E^j(q_i)\right)-\left(E^i(q_j)-E^i(q_i)\right)\right]\\ \text{in HREXMD}\end{array}$$ Equation 3c

In equation 3 T_i indicates the temperature of replica i, q_i is the configuration of replica i at the point of exchange, and Eⁱ represents Hamiltonian energy of replica i. The main idea behind REXMD is that one MD trajectory in a local minima can take conformational information from another replica which may be found in another region of conformational space (e.g. across an energy barrier) but have similar energies. The probability of exchange between replicas is such that it enforces sampling of a Boltzmann distribution of conformations, thereby satisfying a proper thermodynamic ensemble as defined by the simulation conditions. Implementation of REXMD is not straightforward, with issues including how to set up the proper temperature spacing, the number of replicas, and the exchange frequency. For large systems with explicit solvent, REXMD requires a large number of replicas and small temperature difference between adjacent replicas to achieve an acceptable exchange ratio. To overcome this implicit solvent models, as discussed below, may be used thereby allowing for a significant increase in the difference in temperature between adjacent replicas. For example, in the presence of explicit solvent replicas may have temperature differences of 10 K while when implicit solvent is used 30 K may be used. In addition, hybrid methods have been developed¹⁴⁸. Concerning, exchange frequency, higher exchange frequencies typically lead to enhanced sampling¹⁴⁹. However, care must be taken as although high temperature enhances barrier crossing, it may shift the equilibrium between two states and make high temperature states more favorable throughout all replicas.

Hamiltonian replica exchange molecular dynamics (HREXMD)^150-152 overcomes drawbacks of REXMD by scaling the potential energy function (i.e. Hamiltonian) rather than the temperature (Equation 3c). Perturbation of the Hamiltonian can involve almost any term in a force field such as the peptide backbone conformational energies, dielectric constant or ligand-solvent interactions. HREXMD needs a lower number of replicas than REXMD since the perturbation is applied locally on selected components of the system. Generally the perturbation is expressed as a function of an order parameter λ in

$$H({\lambda }_i)={\lambda }_i{H}_1+(1-{\lambda }_{\mathrm{i}})H_0$$ Equation 4

where 0 ≤ λ_i ≤ 1, such that the Hamiltonian is the reference state H₀ (i.e. the ground state) when λ is zero and target state H₁ (i.e. fully perturbed) when λ is one. In HREXMD, simulations are carried on each replica with H(λ_i) and conformations exchanged between adjacent H(λ_i) replicas thereby facilitating the crossing of energy barriers.

There are single MD approaches using dynamic variations of λ. Lambda-dynamics^{145, 153} implements λ as an artificial particle that is propagated during the MD simulations thereby sampling various λ values as dictated by the free energies of the system without the need of using pre-defined λ values. The Hamiltonian is expressed by adding two more terms for dynamic λ variables to H(λ_i), as shown below, and {λ_i} is used since multiple λs can be used to perturb different components of the Hamiltonian such as electrostatic or dihedral energies. In the approach the extended Hamiltonian, comprised of the standard, ground state Hamiltonian and the perturbations associated with the λ terms is defined as

$$H_{\mathit{\text{extended}}}(\{{\lambda }_i\})=H(\{{\lambda }_i\})+\sum _{i=1}^n\frac{1}{2}{m}_i{\lambda }_{\mathrm{i}}^2+U^{\ast }(\{{\lambda }_i\})$$ Equation 5

where m_i and λ_i are dynamic variables which overcome the limitation of using discrete λ values and U*({λ_i}) is a λ_i-dependent biasing potential which can take various forms to sample as many states as possible.

Another single dynamics GE method, Metadynamics^{142, 143, 154} uses a history-dependent biasing potential to force selected degrees of freedom (e.g. collective variables, CV) of the system being sampled away from conformations visited frequently. This is performed by “lifting” low energy regions with a biasing potential as those regions are being sampled, thereby facilitating conformational changes away from the low energy regions. The biasing potential is the sum of Gaussian functions, V_G, that are used to fill valleys of the free energy surface as defined as follows

$$V_G(U(q),t)=h\sum _t{e}^{-\left(\frac{{(U(q)-CV(t))}^2}{2w^2}\right)}$$ Equation 6

where U(q) is the potential energy of coordinates q at time t, h is Gaussian height, w is Gaussian width, and CV(t) is the value of the CV at time t. The simulation remembers information about the added biasing potentials and the final V_G is a negative image of the free energy surface thereby allowing reconstruction of the original free energy surface. Metadynamics is able to run with multiple CVs such as distance between two atoms, angles, or torsion angles; the choice of CVs, and optimal h and w for each CV are user selected and optimization of these parameters for the system of interest is often required.

Taking a similar strategy, the orthogonal space random walk (OSRW) algorithm^{155, 156} is another efficient way of conformational sampling. This strategy simultaneously perturbs the order parameter space (general term for λ or CV above) and generalized free energy space to overcome not only local minima trapping but also lagging of changes in the environment surrounding the CV or λ required for conformational changes to occur. OSRW uses 2D Gaussian-shaped repulsive potentials to flatten the free energy surface and avoid often-visited states. After searching the whole conformational space it is possible to select accessible conformations by order parameters associated with the conformational change.

Another approach is accelerated MD (AMD).¹⁴⁴ AMD is a simple but efficient sampling method that has shown good performance for biomolecules. Compared to metadynamics and OSRW, it uses a simpler form of the biasing potential (equation 7). When applying the method, the boost energy E and α, which is a tuning factor for the biasing potential's well-depth, need to be pre-defined and the biasing potential is applied when the potential energy is less than E.

$$V^{\ast }(r)=\{\begin{array}{ll}V(r),& V(r)\ge E\\ V(r)+\frac{{(E-V(r))}^2}{\alpha +(E-V(r))},& V(r)<E\end{array}$$ Equation 7

REXMD and HREXMD have been successfully used for conformational sampling of flexible ligands^{114, 157-159}, while the other GE algorithms have been used mainly in biomolecules to date. However, considering their success in conformational sampling, problems involved in flexible protein loops and ligand passage in receptors^{160, 161}, it is anticipated that they will be of utility to conformational sampling in LBDD.

In addition to the sampling algorithms, an important consideration is the role of solvent in conformational sampling. Conformational changes and sampling are dependent on the surrounding environment of all molecules such that energetically favorable conformations in gas phase may not be favorable in solution (or a receptor binding site) and vice versa. This occurs due to water competing for favorable intramolecular interactions, for example, by disrupting intramolecular hydrogen bonds or reduced intramolecular dipole-dipole interactions. Alternatively, water can impact the orientation of hydrophobic groups, which may remain “accessible” in the gas phase, but cluster together in the presence of solvent. Therefore sampling conformations in the presence of explicit water molecules is ideal when studying biological systems but such calculations are computationally expensive due to the presence of additional particles in the system. In addition, the viscosity of the water surrounding a molecule can slow conformational sampling during MD simulations, thereby further increasing the computational costs. An effective alternative to explicit solvent are continuum solvent models that allow for distributions of conformations to be obtained that approximate an explicit solvent environment while allowing for efficient sampling by avoiding the increased number of particles and the viscosity issues with water. A large number of implicit solvent models are available and recent reviews on the topic have been presented^162-164. Simple implicit solvent models use constant or distance-dependent dielectric constants. Another approach is using solvation parameters for each atom based on their solvent accessibility so that particles in the system have varying responses to environments. More accurate solutions to solvation effects are obtained by the Poisson-Boltzmann (PB)^{165, 166} or Generalized Born (GB)¹⁶⁷ models. In MD, the most widely used methods are GB models due to the high efficiency of their analytical solution and comparable accuracy with respect to PB models that typically require numerical solutions. GB models calculate the electrostatic component of the solvation free energy as shown in Equation 8, with that term added to the total energy.

$$\Delta G_{\mathit{\text{elec}}}\approx -\frac{1}{2}\left(1-\frac{1}{\mathit{\varepsilon }}\right){\sum }_{i,j}\frac{q_i{q}_j}{\sqrt{r_{ij}^2+R_i{R}_{j}exp\left(\frac{r_{ij}^2}{4R_i{R}_j}\right)}}$$ Equation 8

In equation 8 ε is the dielectric constant of solvent, q_i is the partial atomic charge of atom i, r_ij is the interatomic distance between atom i and j, and R_i, which is the most important parameter in GB models, is the effective Born radii of atom i. The effective Born radii can be understood as an atom's degree of burial within the solute or radius exposed to the solvent environment. A number of GB models have been developed such as GBMV¹⁶⁸ and GBSW¹⁶⁹ in CHARMM^{170, 171} and GB^{OBC 163} in AMBER^{172, 173} which differ primarily in the way that the effective Born radii are calculated.

The final portion of this section presents a simple example of sampling the conformational space of a peptide using three MD-based sampling approaches based on the CHARMM22/CMAP protein force field¹⁷⁴. Figure 1 shows the extent of sampling attained by MD in both vacuum and explicit solvent (Fig. 1a and 1b) and by two sampling methods (single MD vs. HREXMD using explicit solvent, Fig. 1b and 1c) for the flexible opioid pentapeptide, Leu-enkephalin. For the explicit solvent HREXMD, λ=0, 0.14, 0.19, 0.27, 0.37, 0.52, 0.72, and 1.0 where 1.0 represents a CHARMM phi, psi energy surface that is flat for non-glycine residues, as implemented using the CMAP tool¹⁷⁴. Simulations were performed using the REPDSTR module in CHARMM for 10 ns, attempting exchanges every 0.5 ps for the HREXMD. The range of conformational sampling was measured by the 2D probability distribution of the distance between two aromatic rings (A and B) and the angle between two aromatic rings and N-terminal nitrogen (N). Additional details of the simulation methodology are included in the supporting information. Comparison of figures 1a and 1b show that the sampling of conformational space by MD differs in gas phase vs explicit solvent. In explicit solvent, structures with longer AB distances and larger ANB angles are being sampled. These represent more extended structures due to the presence of solvent; in the gas phase the peptide folds back on itself leading to more compact structures as no solvent is available to compete for intramolecular interactions. As expected, HREXMD (1c) samples a similar range of conformations as the standard explict solvent MD (1b), but the extent of sampling is more complete using the same amount of simulation time. The more complete sampling by HREXMD is due to the simulation overcoming an energy barrier in the vicinity of 10∼12 Å for the AB distance and 60∼100° for the ANB angle. Although this example is not a rigorous test from which better performance can be proved based on more efficient sampling, it points out the importance of the simulation method and solvent environment when performing conformational sampling.

Figure 1.

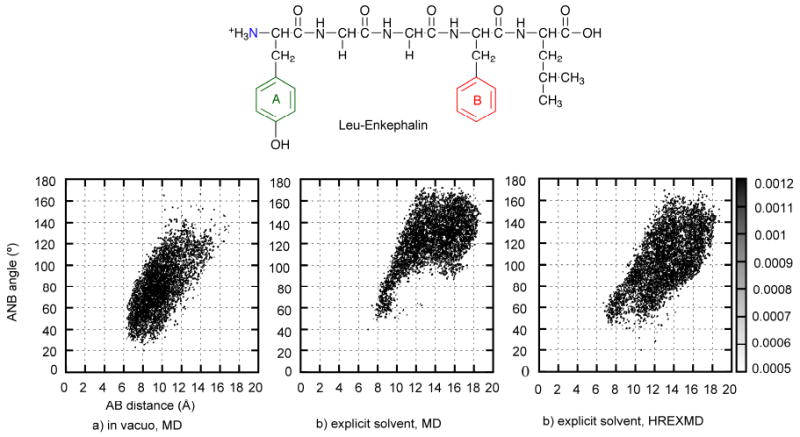
2D-probability distribution of AB distance-ANB angle pair of Leu-Enkephalin. Pharmacophoric point A represents the centroid of the aromatic ring of tyrosine, B is the centroid of the aromatic ring of phenylalanine, and N is the basic nitrogen. a) through c) compares different sampling of conformational space by a) gas phase MD, b) explicit solvent MD and c) explicit solvent HREMD. Simulation details are in the supporting information.

An important consideration when performing conformational sampling is the extent of convergence; have all the accessible conformations of the molecule been sampled? When conformational sampling is done by MD, convergence of sampling may be checked by continuing the simulation time and testing if additional conformations are being sampled. If additional conformations are not being sampled the sampling may be considered converged. For conventional MD, root mean square deviations of overall structure, distance between atoms or functional groups (as in Figure 1), or torsions may be used for simple evaluation of convergence. Alternatively, differences in probability distributions between two intervals of a trajectory (e.g. the first and second half) can also indicate if the simulation has reached convergence. For GE methods, convergence of the calculated free energy surface indicates adequate sampling. However, it should be emphasized that the appearance of convergence does not necessarily mean that true convergence has been attained. There is always the possibility that a molecule, especially more complex molecules such as polypeptides, may have access to significantly different conformations than those accessed in the performed simulations.

4. Force fields (FF)

While the appropriate sampling approaches can assure that the required range of conformations is being accessed it is the underlying energy function that largely determines the probability of the conformations being sampled. While QM methods can supply this information their computational demand limits their utility for sampling large numbers of conformations for even small molecules. Accordingly, it is necessary to use molecular mechanics energy functions. While such functions are computationally efficient, they are based on simple terms that require a set of parameters to allow for the energy and forces on a molecule to be accurately calculated, as described below. These parameters, therefore, dictate the applicability and quality of the force field and a number of force fields are available for drug-like molecules. In the remainder of this article an overview of the force fields most commonly used for ligands will be presented, including examples of the ability of selected force fields to reproduce QM conformational energies of two example ligands.

A force field consists of a potential energy function and the associated parameters that allow the energy and forces to be calculated as a function of the molecular structure and conformation. Potential energy functions used in molecular mechanics typically include terms for bond stretching, angle bending, rotation around bonds (dihedral or torsion angles), out of plane motions (improper angles), and non-bonded interactions (electrostatic and van der Waal energies). Such force fields are referred to as Class I models. In Class II force fields crossterms to treat correlation between bonds and angles, angles and torsions, and so on are included and different variations of the nonbond terms may be used. Equations 9 and 10 show examples of potential energy functions in the two classes, which are classified by their simplicity and potential transferability. Detailed descriptions of the example functional forms are found in Brooks et al.¹⁷⁰ for the class I force field in CHARMM and in Plimpton^{175, 176} for a class II FF. Class I FFs include those specialized for biomolecules (see below). The simple functional form shown in Equation 9 is computationally efficient allowing them to handle macromolecules in aqueous or other condensed phase environments. Equation 10 is a typical energy function used in a Class II FF and employs more complex form which facilitates (but doesn't necessarily dictate) transferability across a wider range of molecules.

$$\mathit{\text{ClassI}}:U(\overrightarrow{R})=\sum _{\mathit{\text{bonds}}}{K}_b{(b-b_0)}^2+\sum _{\mathit{\text{angles}}}{K}_{\theta }{(\theta -{\theta }_0)}^2+\sum _{\mathit{\text{Urey}}-\mathit{\text{Bradley}}}{K}_{UB}{(S-S_0)}^2+\sum _{\mathit{\text{dihedrals}}}{K}_{\varphi }(1+cos(n\varphi -\delta ))+\sum _{\mathit{\text{impropers}}}{K}_{\omega }{(\omega -{\omega }_0)}^2+\sum _{\mathit{\text{residues}}}{U}_{\mathit{\text{CMAP}}}(\varphi ,\phi )+\sum _{\begin{array}{l}\mathit{\text{nonbonded pairs}}\end{array}}\left\{{\mathit{\varepsilon }}_{ij}\left[{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^6\right]+\frac{q_i{q}_j}{4\pi \mathit{\varepsilon }{r}_{ij}}\right\}$$ Equation 9

In equation 9 b, θ, S, n, φ, δ, and ω represent the bond length, angle, distance between 1-3 atoms, multiplicity, torsion, phase, and improper angle, respectively, and the subscript zero indicates the equilibrium geometry parameter. K_x are the associated force constants. The Lennard-Jones 6-12 equation is commonly used to model the van der Waals energy between atom i and j, where ε_ij, r_ij, and R_min,ij are the well-depth, interatomic distance, and interaction distance at minimum of the energy between atoms i and j, respectively. In the electrostatic or Coulombic term, q_i and q_j are partial atomic charges and ε is the dielectric constant.

For equation 10 the same symbols are used as in Equation 9 and additionally b′ and θ ′ used in the crossterms represent the second bond or angle associated with the cross interaction.

$$\mathit{\text{ClassII}}:U(\overrightarrow{R})=\sum _{\mathit{\text{bonds}}}[K_{b2}{(b-b_0)}^2+K_{b3}{(b-b_0)}^3+K_{b4}{(b-b_0)}^4]+\sum _{\mathit{\text{angles}}}[K_{\theta 2}{(\theta -{\theta }_0)}^2+K_{\theta 3}{(\theta -{\theta }_0)}^3+K_{\theta 4}{(\theta -{\theta }_0)}^4]+\sum _{\mathit{\text{dihedrals}}}[K_{\varphi 1}(1+cos\varphi )+K_{\varphi 2}(1+cos2\varphi )+K_{\varphi 3}(1+cos3\varphi )]+\sum _{\mathit{\text{impropers}}}{K}_{\omega }{(\omega )}^2+\sum _{\begin{array}{l}\mathit{\text{nonbonded pairs}}\end{array}}\left\{{\mathit{\varepsilon }}_{ij}\left[2{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^9-3{\left(\frac{R_{min,ij}}{r_{ij}}\right)}^6\right]+\frac{q_i{q}_j}{4\pi \mathit{\varepsilon }{r}_{ij}}\right\}+\sum _{\mathit{\text{bonds}}}\sum _{\mathit{\text{bonds}}\prime }{K}_{bb\prime }(b-b_0)(b\prime -{b\prime }_0)+\sum _{\mathit{\text{angles}}}\sum _{\mathit{\text{angles}}\prime }{K}_{\theta \theta \prime }(\theta -{\theta }_0)(\theta \prime -{\theta \prime }_0)+\sum _{\mathit{\text{bonds}}}\sum _{\mathit{\text{angles}}}{K}_{b\theta }(b-b_0)(\theta -{\theta }_0)+\sum _{\mathit{\text{bonds}}}\sum _{\mathit{\text{dihedrals}}}(b-b_0)[K_{b,\varphi 1}cos\varphi +K_{b,\varphi 2}cos2\varphi +K_{b,\varphi 3}cos3\varphi ]+\sum _{\mathit{\text{bonds}}\prime }\sum _{\mathit{\text{dihedrals}}}(b\prime -{b\prime }_0)[K_{b\prime ,\varphi 1}cos\varphi +K_{b\prime ,\varphi 2}cos2\varphi +K_{b\prime ,\varphi 3}cos3\varphi ]+\sum _{\mathit{\text{angles}}}\sum _{\mathit{\text{dihedrals}}}(\theta -{\theta }_0)[K_{\theta ,\varphi 1}cos\varphi +K_{\theta ,\varphi 2}cos2\varphi +K_{\theta ,\varphi 3}cos3\varphi ]+\sum _{\mathit{\text{angles}}}\sum _{\mathit{\text{angles}}\prime }\sum _{\mathit{\text{dihedrals}}}{K}_{\theta \theta \text{'}\varphi }(\theta -{\theta }_0)(\theta \prime -{\theta \prime }_0)cos\varphi$$ Equation 10

To move from a potential energy function to a FF requires determination of the values of the parameters, a process referred to a parameter optimization or parametrization. Parameters to be optimized in equations 9 and 10 include force constants, equilibrium geometries, partial atomic charges, well depth and interaction distance at minimum energy (R_min,ij) and so on. The goal of parameter optimization is reproducing a collection of quantum mechanical and/or experimental observables for the ligands of interest.

Parameters for macromolecules such as proteins, nucleic acids, lipids and carbohydrates have been paid special attention and optimized extensively in Class I FFs such as AMBER(Assisted Model Building with Energy Refinement)^{172, 173}, CHARMM(Chemistry at Harvard Molecular Mechanics)^{170, 171}, GROMACS¹⁷⁷ and OPLS(Optimized Potential for Liquid Simulations)^{178, 179}. Subsequently, parameters for drug-like molecules were added to be compatible with the individual biomolecular FFs while maintaining the accuracy of the “parent” biomolecular FF. To achieve this, the parent and related small molecule parameters use the same form of the potential energy function and strategy used for optimization of the FF. This is necessary to provide consistent and balanced energy and force evaluations during simulations of small molecule-biomolecular complexes. For example, the CHARMM General FF (CGenFF) ¹⁸⁰ follows the standard optimization procedure of the CHARMM additive biomolecular FF¹⁸¹.

As an example of parameter optimization the approach used in the CHARMM additive force field for small molecules, with which we are intimately familiar, will be used. Typically, optimization of CGenFF parameters is performed as follows. Force constants, equilibrium bond lengths and valence angles are parametrized to reproduce experimental or QM vibrational frequencies and geometries. Dihedral angle force constants, phases, and multiplicities are optimized targeting QM potential energy scans or spectroscopic data such as NMR J coupling constants. Charges are optimized by evaluating optimal distances and interaction energies of water interaction with the drug-like molecule based on QM calculations as well as dipole moments and optimization of LJ parameters is guided by the reproduction of pure solvent or crystal experimental data. To date, CGenFF includes approximately 150 atom types, 400 bond, 1200 angle, 3000 torsion parameters explicitly optimized based on 500 model compounds. When extending the force field to new chemical entities, parameters for the new molecules not already available in the CGenFF may be assigned by analogy for the bond/angle/dihedral and LJ terms, while determination of the partial atomic charges is based on a bond-charge increment algorithm extended to included angle- and dihedrals increments that have been trained to reproduce CGenFF charges for over 500 model compounds (K. Vanommeslaeghe and A.D. MacKerell, Jr., work in progress). A web-based utility in the context of the ParamChem project is available to perform these functions. An important feature of CGenFF when automatically assigning parameters is information about the quality of the assigned parameter based on a penalty score. This is important as the ability of parameters to be transferred between molecules in the context of empirical force fields is limited, as shown below, and it allows users to know which parameters require validation and further optimization to obtain the required level of accuracy. However, as with conformational sampling, even in cases where the parameters are directly transferred to a new molecule, the possibility that those parameters may not perform with adequate accuracy exists, such that the aware user is advised to perform validation tests of the transferred parameters, as previously described.¹⁸⁰

Beyond CGenFF there are a number of other small molecule FFs designed to be compatible with biomolecular FFs. GAFF (General AMBER FF)¹⁸² was developed for the simulation of pharmaceutical compounds with the AMBER biomolecular FF. It is based on QM optimization of about 3000 model compounds and geometric information from the Cambridge structure database (CSD)¹⁸³. It has 57 atom types, 700 bond length parameters, 3000 angle parameters, and 500 dihedral angle parameters. Beyond these available parameters, the Antechamber toolkit¹⁸⁴ is used to assign parameters for novel molecules. SwissParam is a web-based utility used to generate CHARMM consistent parameters for ligands. It takes internal energy parameters and charges from MMFF (Merck Molecular FF)^{185, 186} while cubic and quadratic terms for bond, angle, and improper energies that are present in the Class II force field are truncated as required for use with the Class I CHARMM additive FF. In addition, van der Waals energy parameters are from the CHARMM additive FF based on atom type similarity. However, it should be noted that the nonbond parameters being derived in a different manner than that of the parent biomolecular FF make them formally incompatible with the CHARMM biomolecular FF. OPLS-AA (All Atom) emphasizes parameters to reproduce the conformational energetic and condensed phase properties of small molecules for use in biological environments. Initial parameters were adopted from the OPLS-UA (united atom), AMBER, and CHARMM FFs and 50 model compounds were optimized focusing on torsion and non-bonded parameters¹⁷⁸. OPLS-AA uses experimental liquid properties as target data during parameter optimization. Thus, Class I biomolecular FFs have been extended to include parameters for a range of small molecules though the extent of chemical space covered and the quality of the parameters for those molecules vary significantly.

Class II FFs were initially designed to treat a wide range of small molecules. Examples include CFF/CVFF (consistent valence FF)¹⁸⁷, MM2 (molecular mechanics)¹⁸⁸, MM3¹⁸⁹, MM4¹⁹⁰, MMFF94¹⁸⁵, and Tripos 5.2 FF¹⁹¹. These FFs are typically not optimized with respect to interactions with the environment, with the exception of MMFF, limiting their applicability. In general, Class II force fields were optimized to reproduce geometries, vibrational spectra and conformational energies in the gas phase, with the various cross and higher order terms in the energy functions (Equation 10) included to allow for both better reproduction of those properties as well as facilitate transferability of the parameters to a wider range of compounds. MMFF94 is currently one of the most widely used FFs for small molecules and is available in numerous LBDD software packages for small molecule simulations. Its goal is broad applicability and QM data for over 3000 molecules and condensed phase data for 2800 CSD compounds were used to optimize and validate the parameters. Allinger and coworkers have developed the MM1-4 FF series achieving high accuracy for organic molecules with respect to geometries, conformational properties and heats of formation. Upon going from MM1 to MM2, the MMx series shifted to a simpler form of Class II FF and MM3 lead to further improvements by including more model compounds, additional experimental data, and higher energy conformations during parameter optimization. MM4 represents a further extension of a Class II FF due to the inclusion of four-fold torsional energy terms, torsion-improper-torsion cross terms, bond-torsion-bond cross terms, two torsion-bond cross terms for central and terminal bonds each and so on. MM4 was optimized targeting thermodynamic quantities ΔH, ΔS, ΔG, and geometries from QM calculations or experimental spectroscopic data. All of these class II FFs are primarily utilized for organic compounds in the gas phase, though MMFF94 has shown limited use in macromolecular condensed phase simulations.

Use of a FF for energy evaluation, energy minimization, MD simulation or other sampling approach represents a significant, important step forward in most modern LBDD studies and the quality of the FF plays an important role in the outcomes of such studies. As emphasized in the preceding paragraph, the various FFs were optimized targeting a training set of molecules. Accordingly, each FF may be anticipated to reproduce the energies and forces of the molecules in the respective training sets with reasonable accuracy. However, the question of transferability remains such that how accurate is the treatment of a molecule not in the training set originally used to optimize the FF. While a full investigation to address this issue represents a significant challenge, two examples of the transferability of selected FFs will be given targeting QM dihedral potential energy scans of dimethyltryptamine and dimethylamino[1,4]diazepine which are analogues of serotonin and clozapine.

Figure 2 shows dihedral potential energy surface generated by MMFF, SwissParam, CGenFF, and, in 2b, CGenFF after additional parameter optimization along with QM data obtained at the MP2/6-31G* level using the Gaussian03 program¹⁹². Dihedral angles, shown as curved arrows in the figure, were rotated in 15° increments and the geometries were optimized at each step. MMFF, SwissParam and CGenFF parameters were input into CHARMM and geometries were minimized to an RMS force of < 10^-6 kcal/mol/Å. With dimethyltryptamine, MMFF and SwissParam underestimated the height of energy barriers and CGenFF had a different peak shape at 45° and 330°. Since SwissParam adopted parameters from MMFF, its energy surfaces were similar to that of MMFF, though not identical. This is due to the different representations of the nonbond terms, which contribute to the energy surfaces and emphasize the problem with mixing parameters from different force fields. Overall, the shape of the surfaces for dimethyltryptamine are acceptable for all three FFs. However, results for dimethylamino[1,4]diazepine emphasize that caution needs to be taken as when transferring parameters to new compounds (Figure 2b and Table 2). The MMFF energy surface has local minima around 150° and 270° which will lead to errors in conformational sampling; similar problems are present with the parameters generated by SwissParam. When energies as a function of conformation are incorrectly represented the conformations selected from the sampling approach will typically be incorrect or the probabilities of those conformations improperly represented. Initial parameters from CGenFF showed poor agreement with the QM PES, but the FF is in significantly better agreement following optimization of selected dihedral angle parameters. The results with all the tested FFs indicate the limited ability to transfer parameters to new molecules. An advantage of CGenFF is that penalty values are provided for each parameter assignment. This alerts the user to possible limitations in the FF, such as occur in dimethylamino[1,4]diazepine's conformational energy. In such cases validation of the parameters and additional optimization should be performed as required. Efforts to extend the ParamChem web server to include an automated interface for parameter validation and optimization are ongoing (K. Vanommeslaghe, S. Pamidighantam, M. Sheetz and A.D. MacKerell, Jr. Work in progress).

Figure 2.

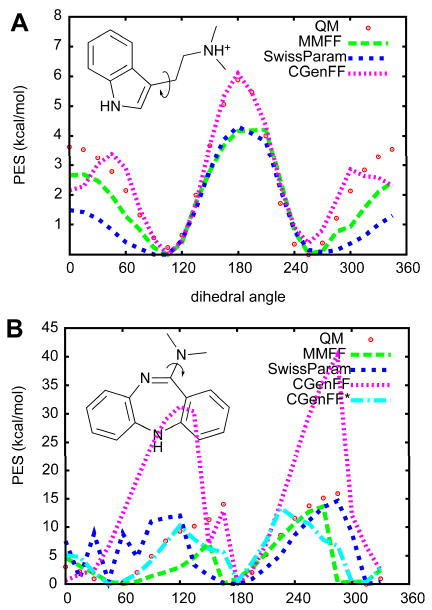
Comparison of conformational energy surface. A) is potential energy surface (PES) of dimethyltryptamine and B) shows that of dimethylamino-dibenzo[1,4]diazepine.

Table 2. Root mean square deviation from QM potential energy surface.

	RMSD
FF	dimethyltryptamine	dimethylamino-dibenzo[1,4]diazepine
MMFF	0.87	5.04
SwissParam	1.42	5.42
CGenFF	0.62	12.84
CGenFF*	n.d.	3.59

5. Conformationally sampled pharmacophore (CSP)

Leveraging the ability to perform extensive conformational sampling of small molecules using a properly optimized FF for the ligands of interest facilitated the development of a novel approach in our laboratory, the conformationally sampled pharmacophore (CSP)^{113-115, 159, 193, 194}. CSP is a LBDD approach based on extensive sampling of conformational space, under the assumption that such sampling will lead to inclusion of the bioactive conformation being sampled despite that conformation not being known. The use of all accessible conformations in the CSP approach allows for probability distributions of different geometric features and/or physical properties to be determined, as shown in Figure 1 for Leu-Enkephalin. As 4D-QSAR uses occupancy of lattice points on a 3D grid by conformations of the ligands being studied as descriptors, CSP uses probability distributions of pharmacophoric features (e.g. distances, angles and dihedrals) as descriptors for model development. The use of all accessible conformations in CSP has allowed it to be applied successfully to highly flexible molecules such as peptidic opioids^113-115 and bile acids^{159, 193, 194}. A strength of the method is the ability to connect the pharmacophore models to molecular details of the ligands being studied thereby facilitating physical interpretation of the models and applying the knowledge for ligand optimization, including rational drug design. By including all conformations, CSP can often recognize subtle differences among structurally similar compounds as well common pharmacophore features among diverse compounds. By using the quantitative overlap of pharmacophoric feature probability distributions of different ligands rather than conformations of the ligands themselves during model fitting, the molecular alignment problem is eliminated. However, once a suitable model is developed the conformational distributions from the MD simulations used in CSP model development may be used to guide possible superposition thereby identifying the biologically relevant conformations of the ligands. For example, CSP model for δ-opioid receptor ligands demonstrated how flexible peptidic opioids can be superimposed with non-peptidic opioids¹¹⁴.

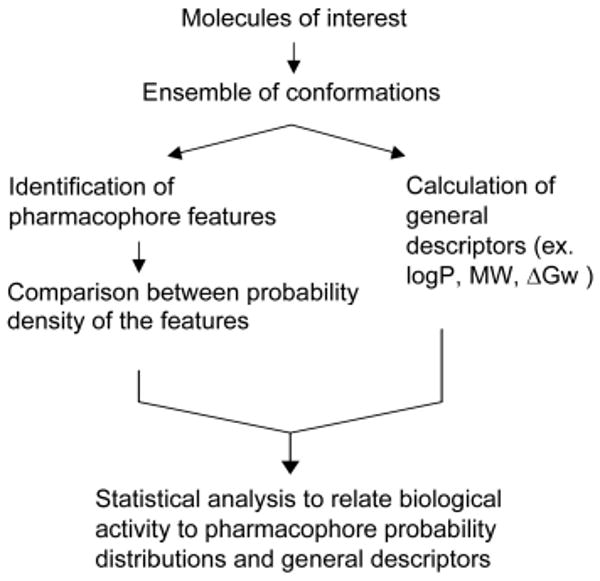
For proper CSP modelling, accurate FF and efficient conformation searching are needed. To date, MMFF and CGenFF have been used successfully. Conformational sampling has used extended MD simulations alone at both room and high temperatures^113-115 and temperature REXMD simulations in implicit solvent^{114, 159, 194}. Figure 3 shows the general procedure used in CSP modelling. Once conformations are pre-enumerated for the training set of compounds, which may be performed using any of the above sampling methods, pharmacophore development is performed in an automated, computationally feasible fashion. As for identification of pharmacophore features, aromatic ring, ionizable groups, or hydrogen bond donors and acceptors can be identified, the associated probability distributions between the features calculated and, based on the extent of overlap of those distributions, the various combination of overlaps iteratively regressed against biological data, with those features yielding the best correlation with experimental data used for further model development. Notably, the CSP method can be readily combined with physicochemical descriptors to further facilitate model development^{159, 194}.

Figure 3. Schematic diagram of CSP procedures.

6. Conclusions

Presented is an overview of computational ligand-based drug design approaches currently in use in rational drug design. Over the last 2-3 decades, a large number of methods have been developed and many of these have been implemented in readily accessible software packages. While this convenience is important for utilization of these methods, it is essential that users understand the assumptions and limitations in those methods allowing for decision on the suitability of the methods for a given project, what kind of knowledge one can obtain through the study, and which aspect is the limiting factor with respect to producing accurate SAR models. As many LBDD approaches require extensive sampling of conformational space emphasis in this article was placed on recent FF development and the use of MD simulations and related techniques for conformational sampling.