Recently, polymeric nanoparticles (NPs) have attracted enormous attention as targeted drug delivery vehicles.[1-4] Especially, biodegradable and biocompatible polymeric NPs comprised of poly(lactide-co-glycolide)-b-polyethyleneglycol (PLGA-PEG) block copolymers exhibit optimal physicochemical characteristics such as the ability to incorporate various targeting agents, enhanced immune evasion, controlled drug release, and high payload of drug molecules.[5-6] Targeted PLGA-PEG NPs have shown very promising in vivo results for treatment of cancer[7-9] and they are now poised to enter clinical trials. Preparation of such targeted NPs in a robust and reproducible manner has thus become very important for therapeutic applications where precise control of the physicochemical properties of NPs is required to achieve optimal biodistribution and therapeutic efficacy.[10]
While the conventional approach to synthesize polymeric NPs relies on ‘bulk’ nanoprecipitation by solvent exchange,[11-12] our group recently reported a new reproducible synthesis of highly uniform PLGA-PEG NPs using 2D hydrodynamic flow focusing (HFF) in microfluidic channels.[13-14] In this method, the polymer stream in acetonitrile (ACN) horizontally focused only by water sheath streams experiences rapid mixing with water with a characteristic mixing time faster than the NP assembly time, resulting in homogeneous NPs.[13,15] However, one of the challenges for optimal NP synthesis by 2D HFF is that NPs made from polymers with a PLGA block of high molecular weight (MW) (> 45 kDa) tend to aggregate on the channel walls, resulting in clogging of the channels. Aggregation is caused by the adsorption of the hydrophobic PLGA onto the hydrophobic walls of PDMS, which depends both on concentration and molecular weight.[16-17] This substantially reduces the robustness of operation – the ability to synthesize NPs without device failure – and is a nontrivial drawback of the 2D HFF technique because NPs made from high MW PLGA blocks tend to exhibit higher drug loading and tunable drug release profile as the polymer MW is varied.[12,18-19] Furthermore, aggregation of the polymer on the channel walls frequently causes the device to irreversibly fail due to increased internal pressure.[20] Such channel fouling may be circumvented by modification of the channel surface with Teflon-like materials.[21] However, efficient surface modification requires laborious silicon/glass fabrication or a separate deposition/curing step that is extremely demanding, and the coating tends to degrade over time. For this application and many others, a preferred solution would be to isolate the precipitating polymer from the channel walls by 3D focusing in both the horizontal and the vertical dimensions, thereby preventing aggregation and clogging. Over the past few years, several unique 3D HFF systems have been reported,[22-31] including intrinsic 3D structures such as horizontal nozzles[22-23] and vertical chimneys[24]. Other 3D HFF systems with 3D channel network either with a single two-level layer[27-28] or with two individual layers[29-31] have been also proposed. However, their construction requires high-level expertise of fabrication, considerably high costs and limited reproducibility. More recently, ‘microfluidic drifting,’ a methodology of 3D fluid manipulation in a single layer, has been also introduced.[25-26] Despite its fabrication simplicity, this method functions only at high Re numbers and a relatively low sample flow rate, which may cause substantial dilution of the sample flow and low throughput. Because of the complications with the previously proposed 3D HFF systems, there is demand for a platform that is sufficiently versatile and simple for both fabrication and operation.
In this paper we present a simple design for 3D HFF composed of a monolithic single layer with three sequential inlets for vertical focusing followed by a conventional cross junction for horizontal focusing. We use this device for the synthesis of polymeric NPs at various polymer concentrations and MWs —the assembly of some of them being significantly difficult by 2D HFF or bulk nanoprecipitation. Optimal ranges of operational parameters are predicted by mathematical modeling and geometric dimensions of channels and inlet holes are fine-tuned by finite element simulations to ensure that the polymer stream is sufficiently exposed to the anti-solvent (water) stream but is not in touch with channel walls. Using confocal microscopy, we further confirm the presence, the position and the shape of the 3D focused polymer stream, which is important for optimal nanoprecipitation of polymeric NPs.
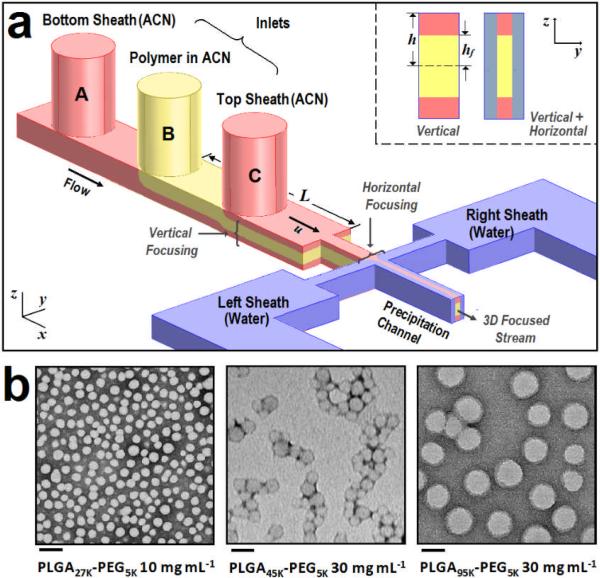
Figure 1a shows a schematic of our 3D focusing channel design for polymeric NP synthesis. The polymer flow (Inlet B) containing polymer precursors dissolved in ACN is first vertically focused by two vertical ACN sheath flows (Inlet A and C). The vertically arranged stream is subsequently focused horizontally by the water sheath streams and the resulting solvent exchange induces self-assembly of the nanoparticles. Thus, 3D focusing enables isolation of the precipitating polymer from the channel walls. Using this microfluidic device, we synthesized various PLGA-PEG NPs at different polymer precursor concentrations and MWs to investigate the robustness of nanoprecipitation by 3D HFF. In Figure 1b, TEM images of PLGA-PEG NPs made from polymers with various MW and concentrations by 3D HFF show that this method yields fairly monodisperse NPs with a range of sizes.
Figure 1.
(a) Concept of device for 3D hydrodynamic focusing (not to scale) consisting of three sequential inlets for vertical focusing and a separate inlet for side sheath flows (not shown). The cross-sectional views in the inset show the vertically focused stream profile (left) and the heterogeneous 3D hydrodynamic focusing where the sample flow is isolated both horizontally and vertically (right). (b) TEM images of PLGA-PEG NPs obtained from PLGA27K-PEG5K at 10 mg mL-1 in ACN (scale bar 100 nm), PLGA45K-PEG5K at 30 mg mL-1 in ACN (scale bar 100 nm) and PLGA95K-PEG5K at 30 mg mL-1 in ACN (scale bar 200 nm) using 3D HFF with the flow ratio of Polymer:ACN = 3:7 and organic:water = 1:5. Average NP sizes are 33.8, 55.0, and 200 nm, respectively.
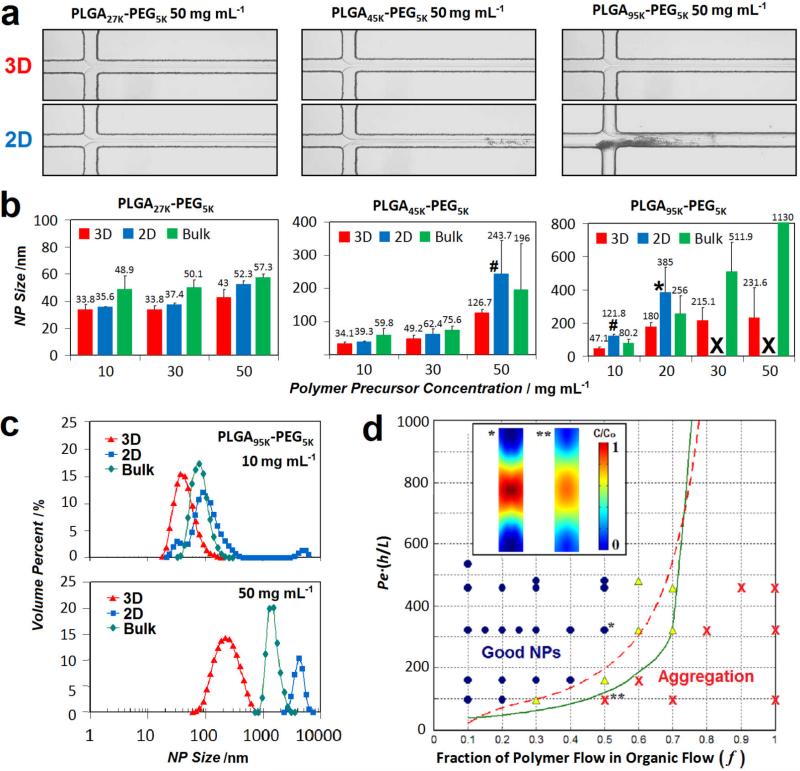
For comparison between the conventional 2D HFF and 3D HFF, we also constructed 2D HFF channel with identical geometry except for the absence of the two ACN sheath inlets in Figure 1a and we maintained all flow parameters such as net organic stream and water stream flow rates, ensuring similar focused stream geometry and molecular residence time the same for 2D and 3D. When comparing nanoprecipitation using 2D versus 3D HFF (Figure 2a), we found that only the 3D HFF method could successfully produce NPs with long-term operation (>10 min) without channel fouling. Polymers with high MWs or high concentrations are usually more susceptible to aggregation in microchannels. Such aggregation during 2D HFF occurred unpredictably at random locations along the channel and thus resulted in poor reproducibility. We also compared the size and monodispersity of NPs synthesized by 3D HFF to 2D HFF and conventional bulk nanoprecipitation for various concentrations (10-50 mg mL-1) and PLGA-PEG MWs (27, 45, and 95 kDa) to verify the quality of NPs prepared by this method (Figure 2b). 3D HFF consistently yielded NPs with the smallest size and lowest polydispersity while 2D HFF and bulk method sometimes produced distinctly larger NPs, or failed to produce NPs at all. NP synthesis by 2D HFF was impossible for high MW and high concentration cases due to device failure caused by aggregation. Figure 2c shows a comparison of the size distributions of NPs made from PLGA95K-PEG5K precursors at low and high concentrations (10 mg mL-1 and 50 mg mL-1, respectively) using the three different methods. At high concentrations, NPs obtained by 2D HFF and bulk method yielded highly polydisperse particles of extremely large size (>1000 nm), while 3D HFF consistently resulted in smaller NPs with relatively low polydispersity regardless of polymer concentrations. These observations indicate that 2D HFF is comparable with 3D HFF only for small MW polymers or very low polymer concentrations where the channels are less susceptible to fouling. Consequently, 3D HFF is the only method that enables the reproducible synthesis of monodisperse NPs made from different PLGA MWs and at different concentrations with average NP sizes ranging from 30 to 230 nm.
Figure 2.
Comparison of 3D HFF (f = 0.3), 2D HFF, and bulk nanoprecipitation of PLGA-PEG NPs under different conditions with the flow ratio of organic:water = 1:10. (a) Representative channel images of the device during synthesis of PLGA-PEG NPS by 3D HFF and 2D HFF for various MW precursors, showing aggregation in the case of 2D HFF. All micrographs were captured after ~500 s of operation (channel width 20 μm). (b) Effect of the PLGA-PEG precursor concentration on the final NP sizes depending on the MW of the precursors and the choice of a synthesis method. X = Clogging of channel within 3 minutes of operation. * = Aggregation of polymer in channel observed after 5-10 minutes of operation. # = Aggregation of polymer in channel observed after >10 minutes of operation. (c) Size distributions by volume fraction of PLGA95K-PEG5K NPs prepared by microfluidic 3D HFF, 2D, and bulk mixing methods for the precursor concentrations of 10 and 50 mg/mL, respectively. Aggregated particles are found in the 1,000-10,000 nm range. (d) Phase space of 3D HFF operation parameters (Pe* and f) for synthesis of PLGA NPs from pure PLGA70K precursors (10 mg mL-1). Solid green line represents condisitons where Pef*=10 and dashed red line represents conditions under which the PLGA70K precursor reaches a critical wall concentration (1 mg mL-1) that results in aggregation. Both lines delineate conditions that result good synthesis of NPs (Phase I) from those that are susceptible to aggregation (Phase II). Symbols indicate experimental data for the synthesis of PLGA70K NPs. (O: reproducible, successful NP synthesis, X: aggregation with microparticle formation, Δ: mild or occasional aggregation). Inset shows simulated concentration profiles at the starting poirnt of nanoprecipitation under the conditions where flow rates (umax) are different but f is the same for Phase I (*) and Phase II (**), respectively.
To identify conditions that enable robust nanoprecipitation in our 3D HFF device, we assembled pure poly(lactic-co-glycolic acid) (PLGA) NPs that are especially prone to aggregation due to the absence of the protective hydrophilic PEG chain as an extreme case model of PLGA-PEG NPs without the PEG shell. Since the flow velocity is slow before horizontal focusing by the water streams, diffusion of the vertically focused polymer stream to the walls must be minimized to prevent isolation. We used a mathematical model to predict optimal parameter ranges for reproducible synthesis of PLGA NPs without aggregation. These parameters collectively define two phases to which the synthesis conditions correspond; the conditions where good and predictable NPs are synthesized in the microfluidic rapid mixing environment without aggregation (Phase I, Good NPs) and the conditions where aggregation occurs (Phase II, Aggregation) (Figure 2d). We expressed the phase space in terms of two parameters: i) the fraction of polymer flow rate and ii) the modified Péclet number (Pe*). First, as the fraction of polymer flow rate in total organic (polymer + ACN) flow rate (f) increases, the vertical sheath layer becomes thinner, and eventually the focusing profile approaches to 2D HFF (f=1 for 2D HFF), where the system is more susceptible to aggregation . Second, Pe*, defined as a product of the Péclet number (umax·h/D, where umax is the maximal flow velocity and D is the diffusion coefficient of polymer precursors in ACN) and the ratio of channel height to focusing length (h/L), takes into account the relative importance of convection to diffusion of the polymer precursor. The solid green line in Figure 2d represents conditions where the focusing Péclet number, Pef=(1/3)*Pe*·(1-f)2, is 10, which indicates that axial convection effectively dominates over lateral diffusion. This dimensionless number not only describes the ratio of diffusive and convective timescales but accounts for thickness of the sheath layer during flow focusing. For low Pe*, precursor molecules in the focused stream rapidly diffuse from the center to the channel wall. We then expect significant concentration of polymer at the wall, invalidating vertical focusing. The condition where Pef=10 thus serves as a suggested boundary line between Phasse I and II. The polymer precursor concentration near the walls acts as a critical determinant of aggregation. Based on the empirical observations that aggregation occurred only when the polymer concentration exceeded a certain threshold (in case of 2D HFF), we defined a critical wall concentration (1 mg/mL for PLGA70K) for 3D HFF, above which aggregation may be expected. Conditions under which a wall concentration of 1 mg/mL is obtained from mathematical modeling (dashed red line in Figure 2d) agree qualitatively with the line corresponding to Pef=10, as is expected for the polymer concentration used in experiments. Consequently, Figure 2d shows good agreement between experimental data and the calculated phase diagram. These results suggest that diffusion of polymers into the vertical sheath flows, governed by the polymer flow ratio (f) and the modified Péclet number can explain regimes where the 3D HFF device can successfully isolate the precipitating polymers from the channel walls and operate without aggregation. Thus, we can mathematically predict optimal operating conditions in our system that result in robust nanoprecipitation of NPs and prevent fouling of the microchannel (For detailed discussion about mathematical modeling and analysis, see the supporting information).
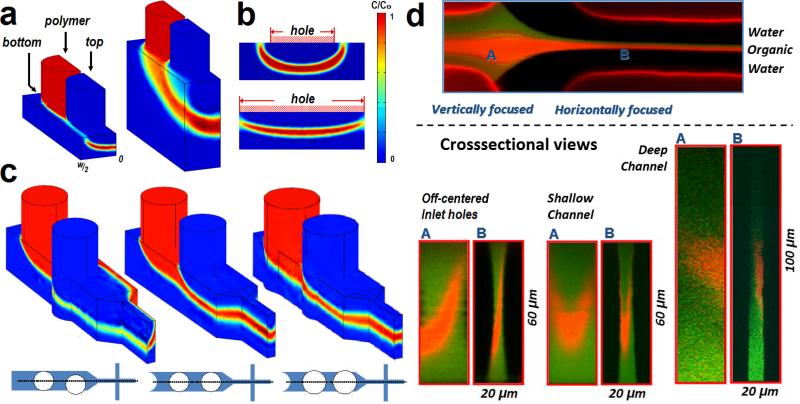
To elucidate the effect of inlet hole geometry on device performance, we performed finite element simulations using COMSOL. The aspect ratio (width to height, w/h) of the channel where vertical focusing occurs and the size and position of inlet holes are particularly important design factors since they determine the shape of 3D focusing in the channel. The simulations showed a strong influence of the aspect ratio (w/h) on the distribution of the polymer after vertical focusing (Figure 3a). For the deep channel with w/h < 2, vertical lamination successfully occurred with a flat concentration profile, whereas the channel with w/h > 2 resulted in a ‘banana-like’ profile with long tails extending to the top wall, making this configuration more susceptible to aggregation. The inlet hole diameter was also found to significantly influence the concentration profile (Figure 3b) and the most uniform vertical focusing was obtained for hole sizes slightly larger than the channel width. Smaller holes significantly compromised vertical focusing, again resulting in a ‘banana-like’ polymer stream profile. Likewise, the lateral position of inlet holes affected the shape of vertically focused polymer stream. Off-centered inlets resulted in a tilted polymer stream (Figure 3c), which invalidates vertical focusing since precipitating polymer would touch the channel wall. These simulations show that the best 3D focusing is obtained using deep, high aspect ratio channels with well-centered holes of diameters slightly larger than the channel width. Finally, we used confocal microscopy to verify the performance of 3D HFF by three sequential inlets. We used a FITC (green) labeled stream as the focused stream, and a rhodamine (red) labeled stream as the vertical sheath streams. The results in Figure 3d showed vertical and horizontal hydrodynamic focusing with the three-sequential-inlet system. In accordance with simulation results, we observed a biased distribution of the focused flow for off-center holes. Similarly, with an inlet hole size smaller (~150 μm) than the width (~200 μm) of the shallow channel, ‘banana-like’ concentration profiles were observed as predicted with simulations. However, such distortion in polymer distributions was avoided and successful 3D focusing was obtained with a deep channel (low w/h). These observations by confocal microscopy, collectively, are in good agreement with the previous simulations. In summary, we presented a new yet simple method to isolate precipitating precursors in microfluidic channels using 3D hydrodynamic focusing enabled by sequential inlets. This approach was used to synthesize PLGA-PEG and PLGA NPs by nanoprecipitation under conditions where monodisperse NPs could neither be synthesized by 2D HFF nor by bulk mixing in a controlled manner. NPs synthesized by 3D HFF exhibited smaller sizes and improved monodispersity compared to 2D HFF or bulk synthesis, keeping the NP size small enough for optimal uptake (i.e. < 100 nm), which is desired in applications where a high MW PLGA block is needed to obtain a specific release profile or where different hydrophobic polymers are mixed.[32-34] More importantly, the monodispersity of the 3D HFF enables the fine-tuning of NP size by carefully choosing PLGA block size of the polymer and the concentration in ACN. Mathematical modeling, together with simulations and confocal microscopy verified the design validity for the performance of the device and defined optimal device geometry and operating conditions for robust 3D HFF. This simple yet versatile design can be easily adapted to microfluidic reactors for synthesis of various materials where isolation of precipitating or reacting flow streams is desirable to prevent fouling and increase robustness during operation.[31, 35-37]
Figure 3.
(a) 3D simulations with different channel aspect ratios (w/h); 3.33 (left) and 0.83 (right), respectively. Perspective views of the channel with the width of 200 μm and the inlet of 150 μm. Only the left halves about the symmetry plane are shown. (b) Simulated cross-sectional views for two different inlet hole diameters at a fixed channel aspect ratio (w/h = 3.33). (c) 3D simulations for a channel of w = 100 μm and h = 100 μm, showing off–centered inlet (left), well aligned inlet (center), and slightly larger inlet (right). (d) Confocal micrographs showing cross-sectional views of vertical focusing before (A) and after (B) horizontal focusing. The top panel shows a top-view of the system near the lateral squeezing cross juction. In the bottom left panel, off-centered holes directly compare with the left panel in (c). The bottom center panel shows vertical focusing occurred in the channel of w/h = 3.33 while the sequential inlet hole size was slightly smaller. The bottom right panel shows vertical focusing occurred in the channel of w/h = 1.0.
Experimental
Experimental Subheading
Experimental Details. 12 point, double-spaced. References are not superscripted and appear before punctuation [6].
[CCDC nnnnnn contains the supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.] ((delete if not applicable))
[Further details of the crystal structure investigation(s) may be obtained from the Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen (Germany), on quoting the depository number CSD-...] ((delete if not applicable))
((Physical data should be quoted with decimal points and negative exponents (e.g. 25.8 J K−1 mol−1), and arranged as follows where possible: mp/bp 20 °C; [α]D20 = −13.5 (c = 0.2 in acetone) (please also give units for [α] and c, usually deg cm3 g−1 dm−1 and gcm−3, respectively); 1H NMR (400 MHz, DMSO-d6, δ): 7.15 (s, 2H, Ar H), 1.3 (q, J = 8 Hz, 2H; CH2), 0.9 (t, J = 8 Hz, 3H; CH3); 13C NMR (100 MHz, CDCl3, δ): 175.4 (C=O), 156.5 (C4); IR (KBr): ν = 2972 (w), 2907 (w), ..., 1026 (s; νas(SiOSi)), 971 (vs), ..., 666 (w; νs(SiOSi)), ..., 439 (m), 401 cm−1 (m); UV-vis (n-hexane): λmax (ε) = 320 (5000), 270 nm (12000); EIMS (m/z (%)): 108 (20) [M+], 107 (60) [M+ − H], 91 (100) [C7H7+]; HRMS (ESI, m/z): [M + H]+ calcd for C21H38N4O6S, 475.2591; found, 475.2593. Anal. calcd for C45H28N4O7: C 62.47, H 3.41, N 6.78; found: C 62.27, H 3.46, N 6.80.))
Supplementary Material
Supporting Information
Synthesis of Size-tunable Polymeric Nanoparticles Enabled by 3D Hydrodynamic Flow Focusing in Single-Layer Microchannels
By Minsoung Rhee1,2,3, †, Pedro M. Valencia4, †, Maria I. Rodriguez5, Robert Langer3,4,6, Omid C. Farokhzad,2,6,*, Rohit Karnik,1,*
1Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139. 2Laboratory of Nanomedicine and Biomaterials and Department of Anesthesiology, Brigham and Women's Hospital, Harvard Medical School, Boston, MA 02115. 3David H. Koch Institute for Integrative Cancer Research, Massachusetts Institute of Technology, Cambridge, MA 02139. 4Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139. 5Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139. 6MIT-Harvard Center for Cancer Nanotechnology Excellence, Massachusetts Institute of Technology, Cambridge, MA 02139.
Contents
1. Mathematical Analysis for flat-profile flow
2. Convective length scale as an indicator of aggregation
3. Simulations with 2D geometry
4. SEM images of the device
5. Visualizations of aggregation occurring during 2D HFF
6. Synthesis of PLGA and PLGA-PEG NPs
7. Experimental
1. Mathematical Analysis for flat-profile flow
Here, we describe a mathematical model of the vertical focusing section of the 3D HFF device. Since flow in the channel prior to horizontal focusing by the water streams is more than an order of magnitude slower than that following focusing by the water sheath streams, diffusion in the channel prior to focusing determines the polymer wall concentrations when the organic stream is focused by the water sheath streams. Furthermore, in our design, the channel width decreases from 100 μm to 20 μm just prior to focusing by the water sheath streams. Since the flow velocity is much higher in the 20 μm channel just prior to focusing, we do not consider diffusion in this section (see focusing length L in Figure 1).
The governing transport equation for the vertical single-phase hydrodynamic focusing system is given by
| (1) |
where c is the sample concentration, u, v, and w are velocity components in x, y and z directions, and D is the diffusion coefficient of the sample in the solvent. The time dependency in Eq. (1) is neglected since the hydrodynamic focusing occurs in continuous systems. Diffusion in the x-direction is negligible compared to high convection in the same direction. We also assumed constant concentrations in the y-direction as in the case of two infinite parallel plates since channel aspect ratio (w/h >> 1) , which subsequently removes the y-dependency in Eq. (1). The simplified governing equation is then given by
| (2) |
A further simplification by assuming a flat uniform velocity, umax, across the channel is valid when the channel aspect ratio (w/h) is high enough (>>1) and gives the mass transport equation as
| (3) |
with initial and boundary conditions as follows.
| (4) |
| (5) |
| (6) |
| (7) |
Substituting Eq. (3) with its dimensionless forms gives a non-dimensionalized governing equation as
| (8) |
where
| (9) |
By separation of variables, the solution to Eq. (8) is found to be
| (10) |
resulting in a thicker focused stream than the real focused stream, but the effect of axial convection near the wall will be increased, making solutes near the wall move faster along the channel. These two different effects will compensate for each other, and thus assumption of a flat velocity profile gives much simpler and quicker mathematical analysis with sufficiently accurate estimations than the more accurate solution for the parabolic velocity profile model.
Figure S-1 shows the variation of dimensionless wall concentrations along the vertical focusing channel at various sample flow rate fractions (f), when the flow velocity is assumedly flat. When the velocity of a flow becomes flat across the channel, the focused stream will be less squeezed,
Figure S-1. Mathematical predictions on the variations of the dimensionless wall concentration along the vertical focusing channel at various sample/sheath flow rate ratios (f) with the solute concentration and the total flow rate fixed, when the velocity profile is assumed flat with a constant velocity.
2. Modified Péclet number as an indicator of aggregation
The modified Péclet number is defined as a product of the Péclet number and the ratio of channel height to focusing length (h/L), which takes into account the relative importance of convection to diffusion of the polymer precursor. The focusing length (L) in Figure 1 starts from the position where focused stream enters and ends where the channel becomes narrow. This is because the narrowed channel makes Pe significantly higher, which, in turn, imples that there will be almost no change in polymer concentration in the narrowed channel. When the hydrodynamic flow focusing occurs in microchannels, it will change the diffusion timescale due to the squeezed center stream. The focusing Péclet number (Pef), a ratio of diffusive timescale for the sheath layer to convective timescale along the channel length, can be then defined as
| (11) |
The focusing Péclet number may determine how efficiently the polymer precursors will be retained out of the channel wall during the course of travel. As Pef increases, the distance diffused by the polymer decreases for a given precipitation time, thereby diminishing the chance of aggregation. When Pef approaches to 1, the diffusive timescale becomes comparable to the convective timescale, which implies a significant increase in wall concentrations for the same time course, resulting in more susceptibility to aggregation. Similarly, a larger channel height or smaller polymer flow ratio increases the distance between the polymer stream and the channel top and bottom, again decreasing the susceptibility to aggregation. However, higher flow rates will generate larger pressure drops along the channel and thus increase the chance of device failure. In addition, microfabrication of the device always imposes a technical limitation on the channel aspect ratio (width to height) that constrains the channel height for a given width.
3. Simulations with 2D geometry
To reduce the computational demand, most of the simulations can be done in 2D geometry without significant loss of accuracy compared to 3D simulations that requires substantially more resources. In Figure S-2, the vertical focusing progress in a straight channel for various flow rate ratios was simulated. The vertically focused stream remains for an extended time around the centerline and gradually diffuses into both sheath streams, eventually reaching at the top and bottom walls. Note that the sample stream will be lifted upward by the bottom sheath stream first and then will be pushed downward by the top sheath stream. This difference in the contact order makes the sample diffuse out to the bottom slightly faster than to the top (Figure S-3a). Figure S-3b shows a good agreement between the simulated wall concentration change along the channel and the corresponding results calculated by mathematical modeling.
Figure S-2. Two-dimensional simulations showing the vertical focusing progress in a straight channel for various flow rate fractions (f).
Figure S-3. 2D simulations showing the development and fade-out of vertical focusing in a straight channel for various flow rate ratios. (a) Polymer solute distributions depending on the flow rate ratio and the distance that the combined flow travels in the x-direction. (b) Bottom wall concentration changes along the channel depending on the flow rate ratio. Solid lines represent simulated results from 2D simulations while markers are shown based on mathematical predictions.
For higher sample flow rate fractions (f), the wall concentration increases more rapidly. Therefore, sample solutes can be vertically isolated for longer time when its flow rate ratio to sheath flows is low. However, for low sample flow rate ratios, the solute concentration of the focused stream decreases faster as can be seen in Figure S-4. In other words, the focused stream with a low flow rate ratio tends to lose its precursor molecules more quickly by diffusion and become diluted rapidly.
Figure S-4. Two-dimensional simulations showing the change in the centerline concentration depending on the flow rate ratio during the vertical focusing progress in a straight channel.
4. SEM images of the device
The size and position of inlet holes play a critical role in determining the shape of hydrodynamic focusing in the channel. Figure S-5 shows typical inlet holes constructed within vertical focusing channels by a mechanical drill capable of positioning x and y locations precisely.
Figure S-5. SEM images of inlet holes and a cross junction of the sequential hole 3D HFF device.
5. Visualizations of aggregation occurring during 2D HFF
In Figure S-6, the PLGA precursor solution with molecular weight of ~ 70,000 was prepared in acetonitrile at a concentration of 10 mg mL-1. Wall adsorption and aggregation began only a few seconds after the stream was introduced. By the time of a few minutes, the PLGA precipitate becomes large enough to block the channel. However, 3D hydrodynamic focusing with three sequential holes provided a robust and consistent means to successfully synthesize PLGA nanoparticles from the equivalent condition without any complications such as channel block or wall adsorption. Movie clips showing how aggregation blocks the channel during 2D HFF are also available online from Wiley InterScience or from the author.
Figure S-6. Growth of PLGA particles and its effects on the channel. During 2D hydrodynamic focusing, vigorous aggregation of PLGA particles occurs within a minute. Agglomerated PLGA microparticles stick to the walls and block the entire channel after a few minutes (Top panel). During 3D hydrodynamic focusing with the equivalent conditions, successful synthesis of PLGA nanoparticles was observed without channel block or wall adsorption (Bottom panel).
6. Synthesis of PLGA and PLGA-PEG NPs
Figure S-7 shows how PLGA particles easily grow and aggregate on the channel wall when they encounter the anti-solvent (water) under the Phase II conditions (similar aggregation also occurs in 2D HFF). 3D HFF under Phase I conditions, however, provided a robust and predictable means to successfully synthesize PLGA nanoparticles at the equivalent condition without any aggregation.
Figure S-7. Synthesis of PLGA NPs from pure PLGA70K precursors (10 mg mL-1) by 3D HFF for varying operation parameters. (a) Channel image at the conditions that result good synthesis of NPs and (b) that are susceptible to aggregation. (c) Channel fouling due to long-term aggregation of PLGA microparticles (bottom) (scale bars 20 μm).
Figure S-8. Comparison of size distributions by volume fraction of PLGA-PEG NPs prepared by microfluidic 3D HFF, 2D, and bulk mixing methods for the precursor concentrations of 10 (low) and 50 mg mL-1 (high), respectively. Aggregated particles are found in the 1000-10,000 nm range.
Figure S-8 shows the size distributions of NPs made from various MW polymer precursors at low and high concentrations (10mg/mL and 50mg/mL, respectively) using the three different methods. At high concentrations, NPs obtained by 2D HFF and bulk methods yielded highly polydisperse particles of extremely large size (>1000 nm), while the implementation of 3D HFF consistently resulted in smaller NPs with relatively low polydispersity regardless of polymer concentrations. These observations indicate that 2D HFF is comparable with 3D HFF only for small MW polymers or very low polymer concentrations where the channels are less susceptible to fouling.
Aggregated particles are larger and thus reflect more light so that the solution with aggregated particles can look opaque. Figure S-9 shows direct visualization of collected sample solutions that contain synthesized PLGA-PEG particles with various sizes.
Figure S-9. Synthesis of various PLGA-PEG NPs. (a) Photos of NP solutions prapared by 3D HFF, 2D HFF, and bulk synthesis. Opacity of the solution roughly indicates the average size of NPs in the solution. Clear solutions contain small NPs (< ~50 nm) and opaque solutions have large particles up to several microns. (b) Calculated light intensity along the red dashed line in (a) to estimate the opacity of the solutions.
7. Experimental
Polymer Precursors. For PLGA NPs, a solution of PLGA (inherent viscosity 0.82 dL g-1, molecular weight ~ 70,000; Lactel, Pelham, AL) was dissolved in ACN at varying concentrations from 0.5 to 10 mg mL-1). For PLGA-PEG NPs, solutions of PLGA-PEG (Boehringer Ingelheim GmbH, Germany) at molecular weights of PLGA27K-PEG5K, PLGA45K-PEG5K, and PLGA95K-PEG5K were dissolved in ACN at concentrations of 10-50 mg mL-1.
Device Fabrication. The prototypical device was manufactured using the standard soft-lithographic technique. The SU-8 (MicroChem) resist was spun on a bare 4” silicon wafer and prebaked on a hot plate for 3 min at 65 °C and for 9 min subsequently at 95 °C. After exposure to 365 nm UV light, the coated wafer was postbaked for 1 min at 65 °C and for 7 min subsequently at 95 °C. The successive 4 min development resulted in the 60 μm thick mold. PDMS (Sylgard 184, Dow Corning) monomer and curing agent were mixed in a ratio of 10:1 by weight, poured over the silicon wafer mold, and degassed. After curing at 100 °C for 60 min, the cured PDMS cast was carefully removed from the mold and diced into individual dies. For each die, inlet/outlet holes were drilled by a 150 μm diameter drill bit. To prevent holes drilled at off-center positions, a manual travel translation stage was used with a mechanical drill to define the position precisely. The PDMS component was then bonded to a 1 in. × 2 in. glass slide using air plasma. Typical channel dimensions used in the NP synthesis experiments had a width of 100 μm and a height of 60 μm for the vertical focusing part and had a width of 20 μm for the horizontal focusing part, or precipitation channel.
Fluid Control and NP synthesis. For 3D HFF, A 2.500 mL syringe for water injection was mounted on a syringe pump (SP101I, World Precision Instruments), two 500 μL syringes for ACN injection were mounted on a different syringe pump (PHD 2000, Harvard Apparatus), and finally a 250 μL syringe for polymer solution injection was mounted on a syringe pump (PHD ULTRA, Harvard Apparatus). Water and organic flow rates were maintained at 50 μL min-1 and 10 μL min-1, respectively (60 μL min-1 in total), while the fraction of polymer flow rates in the organic flow were varied from 0.1 to 1. To prepare NPs by 2D HFF we used a channel design previously published [5] and ran a polymer stream at different concentrations at an organic to aqueous flow ratio of 1:10. For 3D and 2D, we used devices with the exactly same dimensions, and all flow rates were also identical. The water flow rate was always 50 μL min-1 for both 3D and 2D, and the organic flow rate was always 10 μL min-1 for both 3D and 2D. For example, for 3D HFF with polymeric stream 3 μL min-1 and total ACN sheath 7 μL min-1 (f = 0.3) for a net organic flow rate of10 μL min-1, the corresponding 2D HFF polymeric stream flow rate was 10 μL min-1. Consequently, the width of the organic stream focused by the water sheath streams, fluid velocities, and residence times were the same for 3D and 2D. The average fluid velocity for the vertical focusing region was approximately 0.028 m s-1. The corresponding residence time for this 1.5 mm vertical focusing region was about 54 ms. The average fluid velocity in the following precipitation channel was 0.83 m s-1 and the residence time for 4 mm long precipitation channel was about 4.8 ms. The total residence time for polymeric molecules in the microfluidic channel was ~58.8 ms. Reynolds numbers for precipitation and vertical focusing channels were 16.6 and 3.5, respectively. In bulk, we mixed 200 μL of polymer precursor solution drop-wise with 2mL of water during 1-2 hrs. NPs were measured immediately after. It was also noticed that NPs size did not varied significantly after washing NPs with water several times.
Particle Sizing. Particle sizing was performed using dynamic light scattering with Zetasizer Nano ZS (Malvern Instruments Ltd., U.K.). For each measurement, 100 μL or more volume of the sample was loaded in a disposable low-volume cuvette. More than three measurements were performed on each sample. All measurements were performed at ACN concentrations of less than 10% ACN to ensure that any observed variation in particle size was not due to the solvent.
Transmission Electron Microscopy (TEM). TEM experiments were carried out on a JEOL JEM-2011 instrument at an acceleration voltage of 200 kV. The TEM sample was prepared by depositing 10 μL of the NP suspension (1.0 mg mL-1) onto a 300-mesh carbon-coated copper grid. Samples were blotted away after 30 min incubation and grids were negatively stained for 20 min at the room temperature with sterile-filtered 3% (w/v) uranyl acetate aqueous solution. The grids were then washed twice with distilled water and air dried prior to imaging.
Image Acquisition. For confocal imaging, a Zeiss LSM 510 Laser Scanning Confocal microscope (Carl Zeiss MicroImaging, Inc., Thornwood, NY) was used. Microfluidic device was mounted on a thin cover slip and with corresponding tubing for inlets and outlets. A FITC solution was used for the focused stream at flow rates of 1-5 μL min-1 and a rhodamine solution was used for the vertical sheath streams at flow rates of 5-9 μL min-1. Water stream was not labeled. For each combination of flow rates a z-stack of 165 images was taken at 0.76 μm per z-sectioning step at different regions of the channel. Lasers at 488 nm and 543 nm wavelengths were used together with 25x objective. For nanoparticle synthesis the experiments were performed on the device oriented on a stage of a stereomicroscope (Nikon Eclipse TE 2000U).
Simulation Methods. Two-dimensional and three-dimensional simulations were performed using COMSOL Multiphysics software, a commercial finite element package (COMSOL Inc., Burlington, MA). The flow rates at the bottom, polymer, and top inlets were 3.5, 3, and 3.5 μL/min, respectively, as were used in the experiments. After flow profiles in the channel were obtained by solving the incompressible Navier-Stokes equation, concentration profiles were separately calculated by solving the Convection and Diffusion equation. The diffusion coefficient of the polymeric solute (PLGA70K) in ACN used in the simulations (D ~ 1.95 × 10-10 m2 s-1) was based on the value estimated from the Einstein-Stokes equation (ACN viscosity ~ 0.38 cp, radius of gyration of PLGA precursors ~ 4-5 nm) and further comparison with the data for similar molecules.
Acknowledgements
This research was supported by the Koch-Prostate Cancer Foundation Award in Nanotherapeutics (R.L. and O.C.F.), by the Concept Development Grant 5P50CA090381-09 from the Dana Farber Cancer Institute Prostate SPORE (O.C.F.), and by NIH Grants CA119349 (R.L. and O.C.F.) and EB003647 (O.C.F.). We thank Jongho Lee (MIT), Mikhail Hanewich-Hollatz (MIT) and Fawziya Z. Karim (MIT) for their assistance in experiments. We also appreciate valuable discussions on mathematical analysis with Soyeon Lee (Indiana University).
Footnotes
Supporting Information Supporting Information is available online from Wiley InterScience or from the author.
Contributor Information
Minsoung Rhee, Department of Mechanical Engineering Massachusetts Institute of Technology, Cambridge, MA 02139; David H. Koch Institute for Integrative Cancer Research Massachusetts Institute of Technology, Cambridge, MA 02139.
Pedro M. Valencia, Department of Chemical Engineering Massachusetts Institute of Technology, Cambridge, MA 02139.
Maria I. Rodriguez, Department of Electrical Engineering and Computer Science Massachusetts Institute of Technology, Cambridge, MA 02139
Robert Langer, David H. Koch Institute for Integrative Cancer Research Massachusetts Institute of Technology, Cambridge, MA 02139; Department of Chemical Engineering Massachusetts Institute of Technology, Cambridge, MA 02139.
Omid C. Farokhzad, Laboratory of Nanomedicine and Biomaterials Department of Anesthesiology, Brigham and Women's Hospital Harvard Medical School, Boston, MA 02115
Rohit Karnik, Department of Mechanical Engineering Massachusetts Institute of Technology, Cambridge, MA 02139; Laboratory of Nanomedicine and Biomaterials Department of Anesthesiology, Brigham and Women's Hospital Harvard Medical School, Boston, MA 02115.
References
- 1.Soppimatha KS, Aminabhavi TM, Kulkarnia AR, Rudzinski WE. J. Controlled Release. 2001;70:1. doi: 10.1016/s0168-3659(00)00339-4. [DOI] [PubMed] [Google Scholar]
- 2.Peer D, Karp JM, Hong S, Farokhzad OC, Margalit R, Langer R. Nat. Nanotechnol. 2007;2:751. doi: 10.1038/nnano.2007.387. [DOI] [PubMed] [Google Scholar]
- 3.Davis ME, Chen ZG, Shin DM. Nat. Rev. Drug. Discov. 2008;7:771. doi: 10.1038/nrd2614. [DOI] [PubMed] [Google Scholar]
- 4.Riehemann K, Schneider SW, Luger TA, Godin B, Ferrari M, Fuchs H. Angew Chem Int. Ed. Engl. 2009;48:872. doi: 10.1002/anie.200802585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gref R, Minamitake Y, Peracchia MT, Trubetskoy V, Torchilin V, Langer R. Science. 1994;263:1600. doi: 10.1126/science.8128245. [DOI] [PubMed] [Google Scholar]
- 6.Farokhzad OC, Langer R. ACS Nano. 2009;3:16. doi: 10.1021/nn900002m. [DOI] [PubMed] [Google Scholar]
- 7.Farokhzad OC, Cheng J, Teply BA, Sherifi I I, Jon S, Kantoff PW, Richie JP, Langer R. Proc. Natl. Acad. Sci. USA. 2006;103:6315. doi: 10.1073/pnas.0601755103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Farokhzad OC, Jon S, Khademhosseini A, Tran TN, Lavan DA, Langer R. Cancer Res. 2004;64:7668. doi: 10.1158/0008-5472.CAN-04-2550. [DOI] [PubMed] [Google Scholar]
- 9.Gu F, Zhang L, Teply BA, Mann N, Wang A, Radovic-Moreno AF, Langer R, Farokhzad OC. Proc. Natl. Acad. Sci. U S A. 2008;105:2586. doi: 10.1073/pnas.0711714105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Murday JS, Siegel RW, Stein J, Wright JF. Nanomedicine. 2009;5:251. doi: 10.1016/j.nano.2009.06.001. [DOI] [PubMed] [Google Scholar]
- 11.Cheng J, Teply BA, Sherifi I, Sung J, Luther G, Gu FX, Levy-Nissenbaum E, Radovic-Moreno AF, Langer R, Farokhzad OC. Biomaterials. 2007;28:869. doi: 10.1016/j.biomaterials.2006.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Avgoustakis K. Curr. Drug Deliv. 2004;1:321. doi: 10.2174/1567201043334605. [DOI] [PubMed] [Google Scholar]
- 13.Karnik R, Gu F, Basto P, Cannizzaro C, Dean L, Kyei-Manu W, Langer R, Farokhzad OC. Nano Lett. 2008;8:2906. doi: 10.1021/nl801736q. [DOI] [PubMed] [Google Scholar]
- 14.Valencia PM, Basto PA, Zhang L, Rhee M, Langer R, Farokhzad OC, Karnik R. ACS Nano. 2010;4:1671. doi: 10.1021/nn901433u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Johnson BK, Prud'homme RK. Phys. Rev. Lett. 2003;91:118302. doi: 10.1103/PhysRevLett.91.118302. [DOI] [PubMed] [Google Scholar]
- 16.Wong I, Ho CM. Microfluid Nanofluid. 2009;7:291. doi: 10.1007/s10404-009-0443-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wu D, Luo Y, Zhou X, Dai Z, Lin B. Electrophoresis. 2005;26:211. doi: 10.1002/elps.200406157. [DOI] [PubMed] [Google Scholar]
- 18.Govender T, Riley T, Ehtezazi T, Garnett MC, Stolnik S, Illum L, Davis SS. Int. J. Pharm. 2000;199:95. doi: 10.1016/s0378-5173(00)00375-6. [DOI] [PubMed] [Google Scholar]
- 19.Riley T, Stolnik S, Heald CR, Xiong CD, Garnett MC, Illum L, Davis SS, Purkiss SC, Barlow RJ, Gellert PR. Langmuir. 2001;17:3168. [Google Scholar]
- 20.Chan EM, Alivisatos AP, Mathies RA. J. Am. Chem.Soc. 2005;127:13854. doi: 10.1021/ja051381p. [DOI] [PubMed] [Google Scholar]
- 21.Rolland JP, Van Dam RM, Schorzman DA, Quake SR, DeSimone JM. J. Am. Chem. Soc. 2004;126:2322. doi: 10.1021/ja031657y. [DOI] [PubMed] [Google Scholar]
- 22.Yanga R, Feeback DL, Wanga W. Sensor Actuat. A. 2005;118:259. [Google Scholar]
- 23.Huang S, Tan W, Tseng F, Takeuchi S. J. Micromech. Microeng. 2006;16:2336. [Google Scholar]
- 24.Wolff A, Perch-Nielsen IR, Larsen UD, Friis P, Goranovic G, Poulsen CR, Kuttera JP, Telleman P. Lab Chip. 2003;3:22. doi: 10.1039/b209333b. [DOI] [PubMed] [Google Scholar]
- 25.Mao X, Waldeisen JR, Huang TJ. Lab Chip. 2007;7:1260. doi: 10.1039/b711155j. [DOI] [PubMed] [Google Scholar]
- 26.Lim J-M, Kim S-H, Yang S-M. Microfluid. Nanofluid. 2010 DOI 10.1007/s10404-010-0649-5. [Google Scholar]
- 27.Simonnet C, Groisman A. Appl. Phys. Lett. 2005;87:114104. [Google Scholar]
- 28.Scott R, Sethu P, Harnett CK. Rev. Sci. Instrum. 2008;79:046104. doi: 10.1063/1.2900010. [DOI] [PubMed] [Google Scholar]
- 29.Kim DS, Kim DS, Han K, Yang W. Microelectron. Eng. 2009;86:1343. [Google Scholar]
- 30.Chang C-C, Huang Z-X, Yang R-J. J. Micromech. Microeng. 2007;17:1479. [Google Scholar]
- 31.Bong KW, Bong KT, Pregibon DC, Doyle PS. Angew. Chem. Int. Ed. 2010;49:87. doi: 10.1002/anie.200905229. [DOI] [PubMed] [Google Scholar]
- 32.Jiang W, Kim BY, Rutka JT, Chan WC. Nat. Nanotechnol. 2008;3:145. doi: 10.1038/nnano.2008.30. [DOI] [PubMed] [Google Scholar]
- 33.Beletsi A, Panagi Z, Avgoustakis K. Int. J. Pharm. 2005;298:233. doi: 10.1016/j.ijpharm.2005.03.024. [DOI] [PubMed] [Google Scholar]
- 34.Cho H-K, Cheong I-W, Lee J-M, Kim J-H. Korean J. Chem. Eng. 2010;27:731. [Google Scholar]
- 35.Takayama S, Ostuni E, LeDuc PR, Naruse K, Ingber DE, Whitesides GM. Nature. 2001;411:1016. doi: 10.1038/35082637. [DOI] [PubMed] [Google Scholar]
- 36.Dittrich PS, Schwille P. Anal. Chem. 2003;75:5767. doi: 10.1021/ac034568c. [DOI] [PubMed] [Google Scholar]
- 37.de Mello AJ, Edel JB. J. Appl. Phys. 2007;101:084903. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information
Synthesis of Size-tunable Polymeric Nanoparticles Enabled by 3D Hydrodynamic Flow Focusing in Single-Layer Microchannels
By Minsoung Rhee1,2,3, †, Pedro M. Valencia4, †, Maria I. Rodriguez5, Robert Langer3,4,6, Omid C. Farokhzad,2,6,*, Rohit Karnik,1,*
1Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139. 2Laboratory of Nanomedicine and Biomaterials and Department of Anesthesiology, Brigham and Women's Hospital, Harvard Medical School, Boston, MA 02115. 3David H. Koch Institute for Integrative Cancer Research, Massachusetts Institute of Technology, Cambridge, MA 02139. 4Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139. 5Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA 02139. 6MIT-Harvard Center for Cancer Nanotechnology Excellence, Massachusetts Institute of Technology, Cambridge, MA 02139.
Contents
1. Mathematical Analysis for flat-profile flow
2. Convective length scale as an indicator of aggregation
3. Simulations with 2D geometry
4. SEM images of the device
5. Visualizations of aggregation occurring during 2D HFF
6. Synthesis of PLGA and PLGA-PEG NPs
7. Experimental
1. Mathematical Analysis for flat-profile flow
Here, we describe a mathematical model of the vertical focusing section of the 3D HFF device. Since flow in the channel prior to horizontal focusing by the water streams is more than an order of magnitude slower than that following focusing by the water sheath streams, diffusion in the channel prior to focusing determines the polymer wall concentrations when the organic stream is focused by the water sheath streams. Furthermore, in our design, the channel width decreases from 100 μm to 20 μm just prior to focusing by the water sheath streams. Since the flow velocity is much higher in the 20 μm channel just prior to focusing, we do not consider diffusion in this section (see focusing length L in Figure 1).
The governing transport equation for the vertical single-phase hydrodynamic focusing system is given by
| (1) |
where c is the sample concentration, u, v, and w are velocity components in x, y and z directions, and D is the diffusion coefficient of the sample in the solvent. The time dependency in Eq. (1) is neglected since the hydrodynamic focusing occurs in continuous systems. Diffusion in the x-direction is negligible compared to high convection in the same direction. We also assumed constant concentrations in the y-direction as in the case of two infinite parallel plates since channel aspect ratio (w/h >> 1) , which subsequently removes the y-dependency in Eq. (1). The simplified governing equation is then given by
| (2) |
A further simplification by assuming a flat uniform velocity, umax, across the channel is valid when the channel aspect ratio (w/h) is high enough (>>1) and gives the mass transport equation as
| (3) |
with initial and boundary conditions as follows.
| (4) |
| (5) |
| (6) |
| (7) |
Substituting Eq. (3) with its dimensionless forms gives a non-dimensionalized governing equation as
| (8) |
where
| (9) |
By separation of variables, the solution to Eq. (8) is found to be
| (10) |
resulting in a thicker focused stream than the real focused stream, but the effect of axial convection near the wall will be increased, making solutes near the wall move faster along the channel. These two different effects will compensate for each other, and thus assumption of a flat velocity profile gives much simpler and quicker mathematical analysis with sufficiently accurate estimations than the more accurate solution for the parabolic velocity profile model.
Figure S-1 shows the variation of dimensionless wall concentrations along the vertical focusing channel at various sample flow rate fractions (f), when the flow velocity is assumedly flat. When the velocity of a flow becomes flat across the channel, the focused stream will be less squeezed,
Figure S-1. Mathematical predictions on the variations of the dimensionless wall concentration along the vertical focusing channel at various sample/sheath flow rate ratios (f) with the solute concentration and the total flow rate fixed, when the velocity profile is assumed flat with a constant velocity.
2. Modified Péclet number as an indicator of aggregation
The modified Péclet number is defined as a product of the Péclet number and the ratio of channel height to focusing length (h/L), which takes into account the relative importance of convection to diffusion of the polymer precursor. The focusing length (L) in Figure 1 starts from the position where focused stream enters and ends where the channel becomes narrow. This is because the narrowed channel makes Pe significantly higher, which, in turn, imples that there will be almost no change in polymer concentration in the narrowed channel. When the hydrodynamic flow focusing occurs in microchannels, it will change the diffusion timescale due to the squeezed center stream. The focusing Péclet number (Pef), a ratio of diffusive timescale for the sheath layer to convective timescale along the channel length, can be then defined as
| (11) |
The focusing Péclet number may determine how efficiently the polymer precursors will be retained out of the channel wall during the course of travel. As Pef increases, the distance diffused by the polymer decreases for a given precipitation time, thereby diminishing the chance of aggregation. When Pef approaches to 1, the diffusive timescale becomes comparable to the convective timescale, which implies a significant increase in wall concentrations for the same time course, resulting in more susceptibility to aggregation. Similarly, a larger channel height or smaller polymer flow ratio increases the distance between the polymer stream and the channel top and bottom, again decreasing the susceptibility to aggregation. However, higher flow rates will generate larger pressure drops along the channel and thus increase the chance of device failure. In addition, microfabrication of the device always imposes a technical limitation on the channel aspect ratio (width to height) that constrains the channel height for a given width.
3. Simulations with 2D geometry
To reduce the computational demand, most of the simulations can be done in 2D geometry without significant loss of accuracy compared to 3D simulations that requires substantially more resources. In Figure S-2, the vertical focusing progress in a straight channel for various flow rate ratios was simulated. The vertically focused stream remains for an extended time around the centerline and gradually diffuses into both sheath streams, eventually reaching at the top and bottom walls. Note that the sample stream will be lifted upward by the bottom sheath stream first and then will be pushed downward by the top sheath stream. This difference in the contact order makes the sample diffuse out to the bottom slightly faster than to the top (Figure S-3a). Figure S-3b shows a good agreement between the simulated wall concentration change along the channel and the corresponding results calculated by mathematical modeling.
Figure S-2. Two-dimensional simulations showing the vertical focusing progress in a straight channel for various flow rate fractions (f).
Figure S-3. 2D simulations showing the development and fade-out of vertical focusing in a straight channel for various flow rate ratios. (a) Polymer solute distributions depending on the flow rate ratio and the distance that the combined flow travels in the x-direction. (b) Bottom wall concentration changes along the channel depending on the flow rate ratio. Solid lines represent simulated results from 2D simulations while markers are shown based on mathematical predictions.
For higher sample flow rate fractions (f), the wall concentration increases more rapidly. Therefore, sample solutes can be vertically isolated for longer time when its flow rate ratio to sheath flows is low. However, for low sample flow rate ratios, the solute concentration of the focused stream decreases faster as can be seen in Figure S-4. In other words, the focused stream with a low flow rate ratio tends to lose its precursor molecules more quickly by diffusion and become diluted rapidly.
Figure S-4. Two-dimensional simulations showing the change in the centerline concentration depending on the flow rate ratio during the vertical focusing progress in a straight channel.
4. SEM images of the device
The size and position of inlet holes play a critical role in determining the shape of hydrodynamic focusing in the channel. Figure S-5 shows typical inlet holes constructed within vertical focusing channels by a mechanical drill capable of positioning x and y locations precisely.
Figure S-5. SEM images of inlet holes and a cross junction of the sequential hole 3D HFF device.
5. Visualizations of aggregation occurring during 2D HFF
In Figure S-6, the PLGA precursor solution with molecular weight of ~ 70,000 was prepared in acetonitrile at a concentration of 10 mg mL-1. Wall adsorption and aggregation began only a few seconds after the stream was introduced. By the time of a few minutes, the PLGA precipitate becomes large enough to block the channel. However, 3D hydrodynamic focusing with three sequential holes provided a robust and consistent means to successfully synthesize PLGA nanoparticles from the equivalent condition without any complications such as channel block or wall adsorption. Movie clips showing how aggregation blocks the channel during 2D HFF are also available online from Wiley InterScience or from the author.
Figure S-6. Growth of PLGA particles and its effects on the channel. During 2D hydrodynamic focusing, vigorous aggregation of PLGA particles occurs within a minute. Agglomerated PLGA microparticles stick to the walls and block the entire channel after a few minutes (Top panel). During 3D hydrodynamic focusing with the equivalent conditions, successful synthesis of PLGA nanoparticles was observed without channel block or wall adsorption (Bottom panel).
6. Synthesis of PLGA and PLGA-PEG NPs
Figure S-7 shows how PLGA particles easily grow and aggregate on the channel wall when they encounter the anti-solvent (water) under the Phase II conditions (similar aggregation also occurs in 2D HFF). 3D HFF under Phase I conditions, however, provided a robust and predictable means to successfully synthesize PLGA nanoparticles at the equivalent condition without any aggregation.
Figure S-7. Synthesis of PLGA NPs from pure PLGA70K precursors (10 mg mL-1) by 3D HFF for varying operation parameters. (a) Channel image at the conditions that result good synthesis of NPs and (b) that are susceptible to aggregation. (c) Channel fouling due to long-term aggregation of PLGA microparticles (bottom) (scale bars 20 μm).
Figure S-8. Comparison of size distributions by volume fraction of PLGA-PEG NPs prepared by microfluidic 3D HFF, 2D, and bulk mixing methods for the precursor concentrations of 10 (low) and 50 mg mL-1 (high), respectively. Aggregated particles are found in the 1000-10,000 nm range.
Figure S-8 shows the size distributions of NPs made from various MW polymer precursors at low and high concentrations (10mg/mL and 50mg/mL, respectively) using the three different methods. At high concentrations, NPs obtained by 2D HFF and bulk methods yielded highly polydisperse particles of extremely large size (>1000 nm), while the implementation of 3D HFF consistently resulted in smaller NPs with relatively low polydispersity regardless of polymer concentrations. These observations indicate that 2D HFF is comparable with 3D HFF only for small MW polymers or very low polymer concentrations where the channels are less susceptible to fouling.
Aggregated particles are larger and thus reflect more light so that the solution with aggregated particles can look opaque. Figure S-9 shows direct visualization of collected sample solutions that contain synthesized PLGA-PEG particles with various sizes.
Figure S-9. Synthesis of various PLGA-PEG NPs. (a) Photos of NP solutions prapared by 3D HFF, 2D HFF, and bulk synthesis. Opacity of the solution roughly indicates the average size of NPs in the solution. Clear solutions contain small NPs (< ~50 nm) and opaque solutions have large particles up to several microns. (b) Calculated light intensity along the red dashed line in (a) to estimate the opacity of the solutions.
7. Experimental
Polymer Precursors. For PLGA NPs, a solution of PLGA (inherent viscosity 0.82 dL g-1, molecular weight ~ 70,000; Lactel, Pelham, AL) was dissolved in ACN at varying concentrations from 0.5 to 10 mg mL-1). For PLGA-PEG NPs, solutions of PLGA-PEG (Boehringer Ingelheim GmbH, Germany) at molecular weights of PLGA27K-PEG5K, PLGA45K-PEG5K, and PLGA95K-PEG5K were dissolved in ACN at concentrations of 10-50 mg mL-1.
Device Fabrication. The prototypical device was manufactured using the standard soft-lithographic technique. The SU-8 (MicroChem) resist was spun on a bare 4” silicon wafer and prebaked on a hot plate for 3 min at 65 °C and for 9 min subsequently at 95 °C. After exposure to 365 nm UV light, the coated wafer was postbaked for 1 min at 65 °C and for 7 min subsequently at 95 °C. The successive 4 min development resulted in the 60 μm thick mold. PDMS (Sylgard 184, Dow Corning) monomer and curing agent were mixed in a ratio of 10:1 by weight, poured over the silicon wafer mold, and degassed. After curing at 100 °C for 60 min, the cured PDMS cast was carefully removed from the mold and diced into individual dies. For each die, inlet/outlet holes were drilled by a 150 μm diameter drill bit. To prevent holes drilled at off-center positions, a manual travel translation stage was used with a mechanical drill to define the position precisely. The PDMS component was then bonded to a 1 in. × 2 in. glass slide using air plasma. Typical channel dimensions used in the NP synthesis experiments had a width of 100 μm and a height of 60 μm for the vertical focusing part and had a width of 20 μm for the horizontal focusing part, or precipitation channel.
Fluid Control and NP synthesis. For 3D HFF, A 2.500 mL syringe for water injection was mounted on a syringe pump (SP101I, World Precision Instruments), two 500 μL syringes for ACN injection were mounted on a different syringe pump (PHD 2000, Harvard Apparatus), and finally a 250 μL syringe for polymer solution injection was mounted on a syringe pump (PHD ULTRA, Harvard Apparatus). Water and organic flow rates were maintained at 50 μL min-1 and 10 μL min-1, respectively (60 μL min-1 in total), while the fraction of polymer flow rates in the organic flow were varied from 0.1 to 1. To prepare NPs by 2D HFF we used a channel design previously published [5] and ran a polymer stream at different concentrations at an organic to aqueous flow ratio of 1:10. For 3D and 2D, we used devices with the exactly same dimensions, and all flow rates were also identical. The water flow rate was always 50 μL min-1 for both 3D and 2D, and the organic flow rate was always 10 μL min-1 for both 3D and 2D. For example, for 3D HFF with polymeric stream 3 μL min-1 and total ACN sheath 7 μL min-1 (f = 0.3) for a net organic flow rate of10 μL min-1, the corresponding 2D HFF polymeric stream flow rate was 10 μL min-1. Consequently, the width of the organic stream focused by the water sheath streams, fluid velocities, and residence times were the same for 3D and 2D. The average fluid velocity for the vertical focusing region was approximately 0.028 m s-1. The corresponding residence time for this 1.5 mm vertical focusing region was about 54 ms. The average fluid velocity in the following precipitation channel was 0.83 m s-1 and the residence time for 4 mm long precipitation channel was about 4.8 ms. The total residence time for polymeric molecules in the microfluidic channel was ~58.8 ms. Reynolds numbers for precipitation and vertical focusing channels were 16.6 and 3.5, respectively. In bulk, we mixed 200 μL of polymer precursor solution drop-wise with 2mL of water during 1-2 hrs. NPs were measured immediately after. It was also noticed that NPs size did not varied significantly after washing NPs with water several times.
Particle Sizing. Particle sizing was performed using dynamic light scattering with Zetasizer Nano ZS (Malvern Instruments Ltd., U.K.). For each measurement, 100 μL or more volume of the sample was loaded in a disposable low-volume cuvette. More than three measurements were performed on each sample. All measurements were performed at ACN concentrations of less than 10% ACN to ensure that any observed variation in particle size was not due to the solvent.
Transmission Electron Microscopy (TEM). TEM experiments were carried out on a JEOL JEM-2011 instrument at an acceleration voltage of 200 kV. The TEM sample was prepared by depositing 10 μL of the NP suspension (1.0 mg mL-1) onto a 300-mesh carbon-coated copper grid. Samples were blotted away after 30 min incubation and grids were negatively stained for 20 min at the room temperature with sterile-filtered 3% (w/v) uranyl acetate aqueous solution. The grids were then washed twice with distilled water and air dried prior to imaging.
Image Acquisition. For confocal imaging, a Zeiss LSM 510 Laser Scanning Confocal microscope (Carl Zeiss MicroImaging, Inc., Thornwood, NY) was used. Microfluidic device was mounted on a thin cover slip and with corresponding tubing for inlets and outlets. A FITC solution was used for the focused stream at flow rates of 1-5 μL min-1 and a rhodamine solution was used for the vertical sheath streams at flow rates of 5-9 μL min-1. Water stream was not labeled. For each combination of flow rates a z-stack of 165 images was taken at 0.76 μm per z-sectioning step at different regions of the channel. Lasers at 488 nm and 543 nm wavelengths were used together with 25x objective. For nanoparticle synthesis the experiments were performed on the device oriented on a stage of a stereomicroscope (Nikon Eclipse TE 2000U).
Simulation Methods. Two-dimensional and three-dimensional simulations were performed using COMSOL Multiphysics software, a commercial finite element package (COMSOL Inc., Burlington, MA). The flow rates at the bottom, polymer, and top inlets were 3.5, 3, and 3.5 μL/min, respectively, as were used in the experiments. After flow profiles in the channel were obtained by solving the incompressible Navier-Stokes equation, concentration profiles were separately calculated by solving the Convection and Diffusion equation. The diffusion coefficient of the polymeric solute (PLGA70K) in ACN used in the simulations (D ~ 1.95 × 10-10 m2 s-1) was based on the value estimated from the Einstein-Stokes equation (ACN viscosity ~ 0.38 cp, radius of gyration of PLGA precursors ~ 4-5 nm) and further comparison with the data for similar molecules.