Compressing Genomic Sequence Fragments Using SlimGene

Abstract

With the advent of next generation sequencing technologies, the cost of sequencing whole genomes is poised to go below $1000 per human individual in a few years. As more and more genomes are sequenced, analysis methods are undergoing rapid development, making it tempting to store sequencing data for long periods of time so that the data can be re-analyzed with the latest techniques. The challenging open research problems, huge influx of data, and rapidly improving analysis techniques have created the need to store and transfer very large volumes of data. Compression can be achieved at many levels, including trace level (compressing image data), sequence level (compressing a genomic sequence), and fragment-level (compressing a set of short, redundant fragment reads, along with quality-values on the base-calls). We focus on fragment-level compression, which is the pressing need today. Our article makes two contributions, implemented in a tool, SlimGene. First, we introduce a set of domain specific loss-less compression schemes that achieve over 40× compression of fragments, outperforming bzip2 by over 6×. Including quality values, we show a 5× compression using less running time than bzip2. Second, given the discrepancy between the compression factor obtained with and without quality values, we initiate the study of using “lossy” quality values. Specifically, we show that a lossy quality value quantization results in 14× compression but has minimal impact on downstream applications like SNP calling that use the quality values. Discrepancies between SNP calls made between the lossy and loss-less versions of the data are limited to low coverage areas where even the SNP calls made by the loss-less version are marginal.

1. Introduction

With the advent of next generation sequencing technologies, such as Helicos Biosciences, Pacific Biosciences, 454, and Illumina, the cost of sequencing whole genomes has decreased dramatically in the past several years, and is poised to go below $1000 per human individual in a few years. As more and more genomes are sequenced, researchers are faced with the daunting challenge of interpreting all of the data. At the same time, analysis methods are undergoing rapid development making it tempting to store sequencing data for long periods of time so that the data can be re-analyzed with the latest techniques. The challenging open research problems, huge influx of data, and rapidly improving analysis techniques have created the need to store and transfer very large volumes of data.

The study of human variation and genome-wide association (GWA) was traditionally accomplished using micro arrays, for which the data is smaller by over three orders of magnitude. However, these GWA studies have been able to explain only a very small fraction of heritable variation present in complex diseases. Many researchers believe that whole genome sequencing may overcome some of the limitation of micro arrays. The incomplete picture formed by micro arrays, the many applications of sequencing (e.g., structural variations), and the expected improvement in cost and throughput of sequencing technology ensure that sequencing studies will continue to expand rapidly. The question of data handling must therefore be addressed.

Even with the limited amount of genetic information available today, many genome centers already spend millions of dollars on storage (Dublin, 2009). Beyond research laboratories, the fastest growing market for sequencing studies is big pharmaceutical companies (Dublin, 2009). Further, population studies on hundreds of thousands of individuals in the future will be extremely slow if individual disks have to be shipped to an analysis center. The single genome data set we use for our experiments takes 285 GB in uncompressed form. At a network download rate of 10 Mb/s, this data set would take 63.3 hours to transfer over the Internet. In summary, reducing storage costs and improving interactivity for genomic analysis makes it imperative to look for ways to compress genomic data.

While agnostic compression schemes like Lempel-Ziv (Ziv and Lempel, 1978) can certainly be used, we ask if we can exploit the specific domain to achieve better compression. As an example, domain-specific compression schemes like MPEG-2 exploit the use of a dictionary or reference specific to the domain. Here, we exploit the fact that the existing human assembly can be used as a reference for encoding. We mostly consider loss-less compression algorithms. Specifically, given a set of genomic data S, we define a compression algorithm by a pair of functions (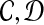) such that 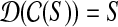. The compression factor c.f., defined by 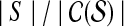describes the amount of compression achieved.

The genomic data S itself can have multiple forms and depends upon the technology used. Therefore, the notion of “loss-less” must be clarified in context. In the Illumina Genome Analyzer, each cycle produces four images, one for each of the nucleotides; consequently, the set S consists of the set of all images in all cycles. By contrast, the ABI technology maps adjacent pairs of nucleotides to a “color-space” in the unprocessed stage. We refer to compression at this raw level as a. Trace Compression. The raw, trace data is processed into base-calls creating a set of fragments (or, reads). This processing may have errors, and a quality value (typically a Phred-like score given by −⌊10 log(P_error)⌋) is used to encode the confidence in the base-call. In b. Fragment Compression, we define the genomic data S by the set of reads, along with quality values of each base-call. Note that the set of reads all come from the genomic sequence of an individual. In c. Sequence Level Compression, we define the set S simply as the diploid genome of the individual.

There has been some recent work on compressing at the sequence level (Brandon et al., 2009; Chen et al., 2002; Christley et al., 2009; Li et al., 2001). Brandon and colleagues introduce the important notion of maintaining differences against a genomic reference and integer codes for storing offsets (Brandon et al., 2009). However, such sequence compression relies on having the fragments reconciled into a single (or diploid) sequence. While populations of entire genomes are available for mitochondria and other microbial strains sequenced using Sanger reads, current technologies provide the data as small genomic fragments. The analysis of this data is evolving, and researchers demand access to the fragments and use proprietary methods to identify variation, not only small mutations, but also large structural variations (Iafrate et al., 2004; Feuk et al., 2006; Sharp et al., 2006; Newman et al., 2005). Further, there are several applications (e.g., identifying SNPs, structural variation) of fragment data that do not require the intermediate step of constructing a complete sequence.

Clearly, trace data are the lowest level data and the most difficult to compress. However, it is typically accessed only by a few expert researchers (if at all), focusing on a smaller subset of fragments. Once the base-calls are made (along with quality values), the trace data is usually discarded.

For these reasons, we focus here on fragment level compression. Note that we share the common idea of compressing with respect to a reference sequence. However, our input data are a collection of potentially overlapping fragments (each, say 100 bps long) annotated with quality values. These lead to compression needs and algorithms different from those of Brandon et al. (2009) and Christley et al. (2009), because fragment compression must address the additional redundancy caused by high coverage and quality values. Further, the compression must efficiently encode differences due to normal variation and sequencing errors, for the downstream researcher.

Our article makes two contributions, implemented in a tool, SlimGene. First, we introduce a set of domain specific loss-less compression schemes that achieve over 40× compression of fragments, outperforming bzip2 by over 6×. Including quality values, we show a 5× compression. Unoptimized versions of SlimGene run at comparable speeds to bzip2. Second, given the discrepancy between the compression factor obtained with and without quality values, we initiate the study of using “lossy” quality values and investigate its effect on downstream applications. Specifically, we show that using a lossy quality value quantization results in 14× compression but has minimal impact on SNP calls using the CASAVA software. Less than 1% of the calls are discrepant, and we show that the discrepant SNPs are so close to the threshold of detection that no miscalls can be attributed to lossy compression. While there are dozens of downstream applications and much work needs to be done to ensure that coarsely quantized quality values will be acceptable for users, our article suggests this is a promising direction for investigation.

2. Data Sets and Generic Compression Techniques

Generic compression techniques: Consider the data as a string over an alphabet Σ. We consider some generic techniques. First, we use a reference string so that we only need to encode the differences from the reference. As each fragment is very small, it is critical to encode the differences carefully. Second, suppose that the letters of σ ∈ ∑ are distributed according to probability P(σ). Then, known compression schemes (e.g., Huffman codes, Arithmetic codes) encode each symbol σ using 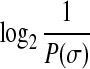bits, giving an average of 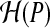(entropy of the distribution) bits per symbol, which is optimal for the distribution, and degrades to log(|Σ|) bits in the worst case.

Our goal is to devise an encoding (based on domain specific knowledge) that minimizes the entropy. In the following, we will often use this scheme, describing the suitability of the encoding by providing the entropy values. Also, while it is asymptotically perfect, the exact reduction is achievable only if the probabilities are powers of 2. Therefore, we often resort to techniques that mimic the effect of Huffman codes. Finally, if there are inherent redundancies in data, we can compress by maintaining pointers to the first occurrence of a repeated string. This is efficiently done by tools such as bzip2, and we reuse the tools.

Data formats: Many formats have been proposed for packaging and exporting genomic fragments, including the SAM/BAM format (Li et al., 2009) and the Illumina Export format. Here, we work with the Illumina Export format, which provides a standard representation of Illumina data. It is a tab delimited format, in which every row corresponds to a read, and different columns provide qualifiers for the read. These include ReadID, CloneID, fragment sequence, and a collection of quality values. In addition, the format also encodes information obtained from aligning the read to a reference, including the chromosome strand, and position of the match. The key thing to note is that the fragment sequences, the quality values, and the match to the chromosomes represent about 80% of the data, and we will focus on compressing these. In SlimGene, each column is compressed independently, and the resulting data is concatenated.

2.1. Data sets: experimental, and simulated

We consider a data-set of human fragments, obtained using the Illumina Genome Analyzer, and mapped to the reference (NCBI 36.1, Mar. 2006). A total of 1.1B reads of length 100 were mapped, representing 35× base-coverage of the haploid genome. We refer to this data-set as GAhum. The fragments differ from the reference either due to sequencing errors or genetic variation, but we refer to all changes as errors. The number of errors per fragment is distributed roughly exponentially, with a heavy tail and a mean of 2.3 errors per fragment (Table 1). Because of the heavy tail, we did not attempt to fit the experimental data to a standard distribution.

Table 1.

Distribution of the Number of Errors per Read

#Errors(k)	0	1	2	3	4	5	6	7	8	9	≥10
Pr(k errors)	0.43	0.2	0.09	0.06	0.04	0.03	0.02	0.02	0.01	0.01	0.09

The first row shows a number of errors with which a read aligns with the reference. The second row shows the probability with which an alignment occurs with the respective number of errors.

Simulating coverage: While we show all compression results on GAhum, the results could vary on other data-sets depending upon the quality of the reads, and the coverage. To examine this dependence, we simulated data-sets with different error-rates, and coverage values. We choose fragments of length 100 at random locations from Chr 20, with a read coverage given by parameter c. To simulate errors, we use a single parameter P₀ as the probability of 0 errors in the fragment. For all k > 0, the probability of a fragment having exactly k errors is given by P_k = λPr(k errors) from the distribution of Table 1. The parameter λ is adjusted to balance the distribution (Σ_i P_i = 1). The simulated data-set with parameters c, P₀ is denoted as GAsim(c, P₀).

3. Compressing Fragment Sequences

Consider an experiment with sequence coverage c(∼30×), which describes the expected number of times each nucleotide is sequenced. Each fragment is a string of characters of length L(≃100) over the nucleotide alphabet Σ (Σ = {A, C, G, T, N}). The naive requirement is 8c bits per nucleotide, which could be reduced to c log(|Σ|) ≃ 2.32c bits with a more efficient encoding. We describe an encoding based on comparison to a reference that all fragments have been mapped to.

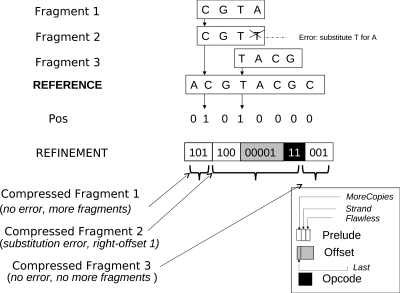
The position vector: Assume a Position bit vector Pos with one position for every possible location of the human genome. We set Pos[i] = 1 if at least one fragment maps to position i (Pos[i] = 0 otherwise). For illustration, imagine an eight-character reference sequence, ACGTACGC, as depicted in Figure 1. We consider two 4bp fragments, CGTA and TACG, aligned to positions 2 and 4, respectively, with no error. Then, Pos = [0, 1, 0, 1, 0, 0, 0, 0]. The bit vector Pos would suffice if (a) each fragment matched perfectly (no errors), (b) matches to the forward strand, and (c) at most one fragment aligns to a single position (possible if L > c). The space needed reduces to 1 bit per nucleotide (possibly smaller with a compression of Pos), independent of coverage c.

FIG. 1.

A simple proposal for fragment compression starts by mapping fragments to a reference sequence. The fragments are encoded by a position vector and a refinement vector consisting of variable size records representing each compressed fragment. The compressed fragments are encoded on a “pay as needed” basis in which more bits are used to encode fragments that map with more errors.

In reality, these assumptions are not true. For example, two Fragments 1 and 2 match at position 2, and Fragment 2 matches with a substitution (Fig. 1). We use a Refinement vector that adds count and error information. However, the Refinement vector is designed on a “pay as needed basis”—in other words, fragments that align with fewer errors and fewer repeats need fewer bits to encode.

The refinement vector: The Refinement Vector is a vector of records, one for each fragment, each entry of which consists of a static Prelude (3 bits) and an ErrorInstruction record, with a variable number of bits for each error in the alignment.

The 3-bit Prelude consists of a MoreCopies, a Strand, and a Flawless bit. All fragments that align with the same location of the reference genome are placed consecutively in the Refinement Vector, and their MoreCopies bits share the same value, while the respective bits of consecutive fragments that align to different locations differ. Thus, in a set of fragments, the MoreCopies bit changes value when the chromosome location varies. The Strand bit is set to 0 if the fragment aligns with the forward strand and 1 otherwise, while the Flawless bit indicates whether the fragment aligns perfectly with the reference, in which case there is no following ErrorInstruction.

When indicated by the Flawless bit, the Prelude is followed by an ErrorInstruction, one for every error in the alignment. The ErrorInstruction consists of an Offset code (number of bp from the last erroneous location), followed by a variable length Operation Code or OpCode field describing the type of error.

Opcode: As sequencing errors are mostly nucleotide substitutions, the latter are encoded by using 2 bits, while the overhead of allocating more space to other types of error is negligible. Opcode 00 is reserved for other errors. To describe all substitutions using only three possibilities, we use the circular chain A → C → G → T → A. The opcode specifies the distance in chain between the original and substituted nucleotide. For example, an A to C substitution is encoded as 01. Insertions, deletions, and counts of N are encoded using a Huffman-like code, to get an average of T = 3 bits for Opcode.

Offset: Clearly, no more than O = log ₂ L bits are needed to encode the offset. To improve upon the log₂(100) ≃ 7 bits per error, note that the quality of base calling worsens in the later cycles of a run. Therefore, we use a back-to-front error ordering to exploit this fact, and a Huffman-like code to decrease O.

The record for Fragment 2 (CGTT, Fig. 1) provides an example for the error encoding, with a prelude equal to 100 (last fragment that maps to this location and error instructions follow) followed by a single ErrorInstruction. The next 5 bits (00001) indicate the relative offset of the error from the end of the fragment. The first bit of the offset is a “Last” bit that indicates that there are no more errors. The offset field is followed by an opcode (11) which describes a substitution of T for A, a circular shift of 3. Further improvement is possible.

Compact offset encoding: We now describe a method of encoding errors that exploits the locality of errors to create a more efficient encoding than if errors were formally distributed. Let 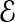denote the expected number of errors per fragment, implying an offset of 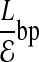. Instead, we use a single bitmap, Error, to mark the positions of all errors from all fragments. Second, we specify the error location for a given fragment as the number of bits we need to skip in Error from the start offset of the fragment to reach the error. We expect to see a “1” after 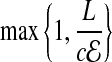bits in Error. Thus, instead of encoding the error offset as 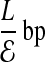, we encode it as the count using

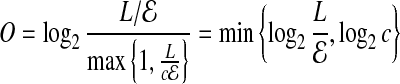bits. For smaller coverage 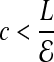, we can gain a few bits in computing O. Overall, the back-to-front ordering, and compact offset encoding leads to O ≃ 4 bits.

Compression analysis: Here, we do a back-of-the-envelope calculation of compression gains, mainly to understand bottlenecks. Compression results on real data, and simulations will be shown in Section 3.2. To encode Refinement, each fragment contributes a Prelude (3 bits), followed by a collection of Opcodes (T bits each), and Offsets (O bits each). Let 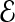denote the expected number of errors per fragment, implying a refinement vector length of

per fragment. Also, encoding Pos, and Error requires 1 bit each, per nucleotide of the reference. The total number of bits needed per nucleotide of the reference is given by

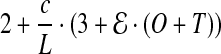(1)

Substituting T = 3, O = 4, L = 100, we have

(2)

Equation 2 provides a basic calculation of the impact of error-rate and coverage on compressibility using SlimGene. For GAhum, 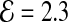(see Section 2.1). For high coverages, the c.f. is ≃ 8/0.19 ≃ 42. For lower coverages, the fixed costs are more important, but the Pos and Error bitmaps are very sparse and can be compressed well, by (say) bzip2.

3.1. Encoding offsets and opcodes

The reader may wonder how our seemingly ad hoc encoding technique compares to information theoretic bounds. We first did an experiment to evaluate the effectiveness of OpCode assignment. We tabulated the probability of each type of error (all possible substitutions, deletions, and insertions) on our data set and used these probabilities to compute the expected OpCode length using our encoding scheme. We found that the expected OpCode length using our encoding was 2.2, which compares favorably with the entropy, which was 1.97.

Opcodes: Table 2 summarizes the probability with which each type of error appears while aligning fragments against GAhum. Note that we can encode the 12 possible substitutions using three symbols by using the reference. Insertions and deletions create an additional five symbols. To encode runs of Ns, we use distinct symbols up to 10, and a single symbol for 10 or more Ns. Any true encoding must additionally store the number of N's. Therefore, the entropy of distribution implied by Table 2 is a lower bound on the number of bits needed for Opcodes.

Table 2.

Probabilities of Alignment Errors

	Operation	Probability
Substitute	A → C	0.31
	C → G
	G → T
	T → A
Substitute	A → T	0.31
	C → T
	G → A
	T → C
Substitute	A → G	0.31
	C → A
	G → C
	T → G
Insert	1 N	0.056
Insert	2 N's	0.0041
Insert	3 N's	0.0016
Insert	4 N's	0.00069
Insert	5 N's	0.00038
Insert	6 N's	0.00041
Insert	7 N's	0.00030
Insert	8 N's	0.00027
Insert	9 N's	0.00056
Insert	≥ 10 N's	0.0019
Insert	A	0.001225
Insert	C	0.001225
Insert	G	0.001225
Insert	T	0.001225
Delete		0.0049

The probabilities are empirically estimated by aligning Chromosome 1 fragments from GAhum against the human reference (hg18). We encode the 12 possible substitutions using three symbols by using the reference. Insertions and deletions create an additional five symbols. To encode runs of Ns, we use distinct symbols up to 10. Here we use a single symbol for 10 or more Ns to get a lower bound on the entropy of the distribution.

In our implementation, 2 bits encode the three substitution cases between nucleotide letters A, C, G, and T, while 5 bits encode all four cases of insertion, deletions, and single substitution between a nucleotide and a N. We use 12 bits to encode runs of N's. Empirically, the number of bits needed for the Opcode is computed to be 2.2, which is close to the entropy of 1.97.

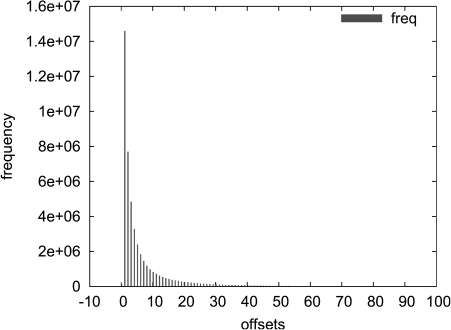
Offsets: The width of the error location O depends on the number of bits that we need to skip in Error to reach the error location for a given fragment. According to the histogram of Figure 2, which has been obtained from the error distribution of chromosome 20 of GAhum, the majority of cases involves the skipping of up to 10 bits in Error. Indeed, the entropy of the distribution of Figure 2 is 3.69. Thus, the allocation of 3 or 4 bits for the offset encoding is compatible with the theoretical limits.

FIG. 2.

Distribution of offsets to the next Error bit. The data have been obtained from the error distribution of chromosome 20 of GAhum and represent the number of bits that we need to skip in Error to reach the error location for a given fragment. The entropy of the distribution is 3.69, which agrees with the observation that the majority of cases involves the skipping of up to 10 bits in that vector.

3.2. Experimental results on GAsim(c, P₀)

We tested SlimGene on GAsim(c, P₀) to investigate the effect of coverage and errors on compressibility. Recall that for GAhum, P₀ = 0.43, c = 30, 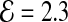. As P₀ is varied, is approximately .

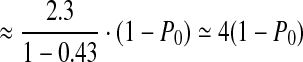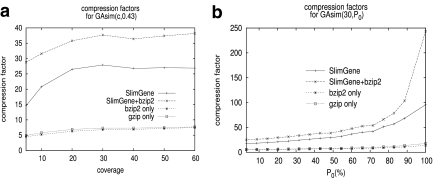
In Figure 3a, we fix P₀ = 0.43, and test compressibility of GAsim(c, 0.43). As suggested by Eq. 2, the compressibility of SlimGene stabilizes once the coverage is sufficient. Also, using SlimGene+bzip2, the compressibility for lower coverage is enhanced due to better compression of Pos and Error. Figure 3b explores the dependency on the error rates using GAsim(30, P₀). Again, the experimental results follow the calculations in Eq. 2, which can be rewritten as

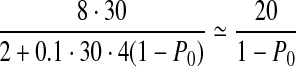FIG. 3.

Compressibility of GAsim(c, P₀). (a) The compression factors achieved with change in coverage. c.f. is lower for lower coverage due to the fixed costs of Pos, and Error, and stabilizes subsequently. (b) Compressibility as a function of errors. With high values of P₀ (low error), up to two orders of magnitude compression is possible. Note that the values of P₀ are multiplied by 100.

At high values of P₀, SlimGene produces two orders of magnitude compression. However, it outperforms bzip2 and gzip even for lower values of P₀.

4. Compressing Quality Values

For the Genome analyzer, as well as other technologies, the Quality values are often described as ≈ −log(P_err). Specifically, the Phred score is given to be ⌊−10 · log(P_err)⌋. The default encoding for GAhum require 8 bits to encode each Q-value. We started by testing empirically if there was a non-uniform distribution on these values (see Section 2). The entropy of the Q-values is 4.01. A bzip2 compression of the data-set resulted in 3.8 bits per Q-value. For further compression, we need to use some characteristics of common sequencers.

Position-dependent quality: Base calling is highly accurate in the early cycles, while it gradually loses its accuracy in subsequent cycles. Thus, earlier cycles are populated by higher quality values and later cycles by lower values. To exploit this, consider a matrix in which each row corresponds to the Q-values of a single read in order. Each column therefore corresponds (approximately) to the Q-values of all reads in a single cycle. In Figure 4a, we plot the entropy of Q-value distribution at each columns. Not surprisingly, the entropy is low at the beginning (all values are high), and at the end (all values are low), but increases in the middle, with an average entropy of 3.85.

FIG. 4.

Distribution of quality, and Δ values, and Markov encoding. (a) A distribution of Q-values at each position. The entropy is low at the beginning (all values are high) and at the end (all values are low), but increases in the middle. (b) A histogram of Δ-values. (c) Markov encoding: Each string of Q-values is described by a unique path in the automaton starting from q = 0, and is encoded by concatenating the code for each transition. Huffman encoding bounds the number of required bits by the entropy of the distribution. Edge labels describe the required number of bits for each transition.

Encoding Δ values: The gradual degradation of the Q-values leads to the observation that Q-values that belong to neighboring positions differ slightly. Thus, if instead of encoding the quality values, one encodes their differences between adjacent values (Δ), it is expected that such a representation would be populated by smaller differences. For instance, Figure 4b shows a histogram of the distribution of Δ-values. However, the entropy of the distribution is 4.26 bits per Δ-value.

Markov encoding: We can combine the two ideas above by noting that the Δ-values also have a Markovian property. As a simple example, assume that all Q-values from 2 to 41 are equally abundant in the empirical data. Then, a straightforward encoding would need ⌈ log ₂(41 − 2 + 1) ⌉  = 6 bits. However, suppose when we are at quality value (say) 34 (Fig. 4c), the next quality value is always one of 33, 32, 31, 30. Therefore, instead of encoding Q′ using 6 bits, we can encode it using 2 bits, conditioning on the previous Q-value of 34.

We formalize this using a Markov model. Consider an automaton M in which there is a distinct node q for each quality value, and an additional start state q = 0. To start with, there is a transition from 0 to q with probability P₁(q). In each subsequent step, M transitions from q to q′ with probability Pr(q → q′). Using an empirical data-set D of quality values, we can estimate the transition probabilities as

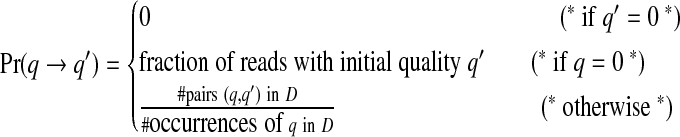(3)

Assuming a fixed length L for fragments, the entropy of the Markov distribution is given by

(4)

Empirical calculations show the entropy to be 3.3 bits. To match this, we use a custom encoding scheme (denoted as Markov-encoding) in which every transition q → q′ is encoded using a Huffman code of − log (Pr(q → q′)) bits. Table 3 summarizes the results of Q-value compression. The Markov-encoding scheme provides a 2.32× compression, requiring 3.45 bits per character. Further compression using bzip2 does not improve on this.

Table 3.

Quality Value Compression Results

	Raw file	bzip2	Δ (Huffman)	Markov (Huffman)
Bits per character	8	3.8	4.25	3.45
c.f.	1	2.11	1.88	2.32

In the uncompressed form, a quality value required 8 bits for its representation. Using bzip2 and delta encoding, it needs 3.8 and 4.25 bits, respectively. Finally, Markov encoding assigns 3.45 bits per quality value, which results in a 2.32× compression.

5. Lossy Compression Of Quality Values

Certainly, further compression of Quality (Q) values remains an intriguing research question. However, even with increasing sophistication, it is likely that Q-value compression will be the bottleneck in fragment-level compression. So we ask the sacrilegious question: can the quality values be discarded? Possibly in the future, base-calling will improve to the point that Q-values become largely irrelevant. Unfortunately, the answer today seems to be “no.” Many downstream applications such as variant calling, and many others consider Q-values as a critical part of inference, and indeed, would not accept fragment data without Q-values. Here, we ask a different question: is the downstream application robust to small changes in Q-values? If so, a “lossy encoding” could be immaterial to the downstream application.

Denote the number of distinct quality values produced as |Q| = Q_max − Q_min, which is encoded using log₂(|Q|) bits. Note that a Q-score computation such as ⌊ − 10 · log ₂(P_err) ⌋ already involves a loss of precision. The error here can be reduced by rounding.

We test the impact of the lossy scheme on Illumina's downstream application called CASAVA (see http://www.illumina.com/pages.ilmn?ID=314) that calls alleles based on fragments and associated Q-scores. CASAVA was run over a 50 M wide portion of the Chr 2 of GAhum using the original Q-values, and it returned a set S of |S| = 17, 021 variants that matched an internal threshold (the allele quality must exceed 10; in heterozygous cases the respective threshold for the weak allele is 6). For each choice of parameter 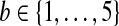, we reran CASAVA after replacing the original score Q with Q_min + |Q| · LQ-score_b(Q). Denote each of the resulting variant sets as S_b. A variant 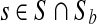is concordant. It is considered discrepant if .

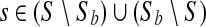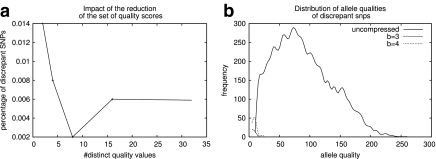
The results in Figure 5 are surprising. Even with b = 1 (using 1 bit to encode Q values), 98.6% of the variant calls in S are concordant. This improves to 99.4% using b = 3. Moreover, we observe (Fig. 5b) that the discrepant SNPs are close to the threshold. Specifically, 85% of the discrepant SNPs have allele qualities of ≤10.

FIG. 5.

Impact of lossy compression on CASAVA. CASAVA was run on a 50 M wide region of Chr 2 of GAhum using lossless and lossy compression schemes. (a) The y-axis plots the fraction of discrepant SNPs as a function of lossy compression. The x-axis shows the number of bits used to encode Q-scores. (b) The allele quality distribution of all lossless SNPs and the discrepant SNPs for 3- and 4-bit quantization. The plot indicates that the discrepant variants are close to the threshold of detection (allele quality of 6 for weak alleles in the heterozygous case, 10 for the homozygous case).

5.1. Is the loss-less scheme always better?

We consider the 38 positions in Chr 2 where the lossy (3-bits) compression is discrepant from the loss-less case. On the face of it, this implies a 0.2% error in SNP calling, clearly unacceptable when scaled to the size of the human genome. However, this assumes that the loss-less call is always correct. We show that this is clearly not true by comparing the SNP calls based on lossy and loss-less data in these 38 positions with the corresponding entries, if any, in dbSNP (version 29). We show that most discrepancies come from marginal decisions between homozygote and heterozygote calls.

For simplicity, we only describe the 26/38 SNPs with single nucleotide substitution in dbSNP. In all discrepant cases, the coverage is no more than five reads (despite the fact that the mean coverage is 30×). Further, in all but two cases, both lossy and lossless agree with dbSNP, and the main discrepancy is in calling heterozygote versus homozygotes. Specifically, lossy calls 14/10 homozygotes and heterozygotes, against lossless (12/12). With coverage of ≤5, the distinction between homozygote and heterozygotes is hard to make. Close to 50% of the differences were due to consideration of extra alleles due to lossy compression, while in the remaining, alleles are discarded. Given those numbers, it is totally unclear that our lossy compression scheme yields worse results than the lossless set, not to mention that in some cases it can lead to better results.

We next consider the two positions where the discrepant SNPs produced by the lossy scheme completely disagree with the dbSNP call. Table 4 shows that at position 43150343 dbSNP reports C/T. The loss-less Q-values and allele calls were respectively 39 G, 28 G, 20 G, 30 G; CASAVA did not make a call. On the other hand, the lossy reconstruction led to values 41 G, 27 G, 22 G, 32 G, which pushed the overall allele quality marginally over the threshold, and led to the CASAVA call of “G.” In this case, the lossy reconstruction is quite reasonable, and there is no way to conclude that an error was made. The second discrepant case tells an identical story.

Table 4.

Analysis of Discrepant Alleles

Position	dbSNP entry	Scheme		Q-values			Allele quality	Decision
43150343	C/T	lossy-8	41G	27G	22G	32G	10.2	G
		lossless	39G	28G	20G	30G	9.9	—
46014280	A/G	lossy-8	27C	37C	37C		10.1	C
		lossless	27C	36C	36C		9.9	—

In both cases, the lossy quality values result in a score that marginally exceeds the threshold of 10 used to call the allele. Thus, CASAVA would make a SNP call only in the lossy scheme of both cases.

Given the inherent errors in SNP calling (lossy or lossless), we suggest that the applications of these SNP calls are inherently robust to errors. The downstream applications are usually one of two types. In the first case, the genotype of the individual is important in determining correlations with a phenotype. In such cases, small coverage of an important SNP must always be validated by targeted sequencing. In the second case, the SNP calls are used to determine allelic frequencies and SNP discovery in a population. In such cases, marginally increasing the population size will correct errors in individual SNP calls (especially ones due to low coverage). Our results suggest that we can tremendously reduce storage while not impacting downstream applications by coarsely quantizing quality values.

6. Putting It All Together: Compression Results

We used SlimGene to compress the GAhum data-set with 1.1B reads, which are sorted according to the alignment location; their total size is 285 GB. We focus on the columns containing the reads, their chromosome locations and match descriptors (124.7 GB), and the column containing Q-values (103.4 GB), for a total size of 228.1 GB. The results are presented in Table 5 and show a 40× compression of fragments. Using a lossy 1-bit encoding of Q-values results in a net compression of 14× (8× with a 3-bit encoding).

Table 5.

Compression of GAhum Using SlimGene

	Fragments+ alignment (GB)	Q-values (GB)	total (GB)	Execution time (hr)
Uncompressed	124.7	103.4	228.1	N/A
gzip (in isolation)	15.83	49.92	65.75	N/A
bzip2 (in isolation)	17.9	46.49	64.39	10.79
SlimGene	3.2	42.23	45.43	7.38
SlimGene+bzip2	3.04	42.34	45.38	7.38
SlimGene+lossy Q-values (b = 3)	3.2	26	29.8	7.38
SlimGene+lossy Q-values (b = 1)	3.2	13.5	16.7	7.38

Using a loss-less Q-value compression, we reduce the size by 5×. A lossy Q-value quantization results in a further 3× compression, with minimal effect on downstream applications.

7. Comparison With Samtools

Table 6 compares the performance of the SlimGene with SAMtools. The input of SlimGene is the set of export files that comprise the GAhum, while the SAMtools compress the GAhum files after their conversion into the SAM format. Note that not only does the input dataset include the columns of Table 5, but also read names, alignment scores, mate pointers, and unmapped reads, which are compressed by SlimGeneusing gzip. As we can see, SlimGene provides higher compression rates in a lower execution time.

Table 6.

Compression of GAhum Using SlimGene and SAMtools

	Quality values		No quality values
	Size (GB)	c.f	Size (GB)	c.f	Time (hr)
Uncompressed	294	1	294	1
SlimGene	57.0	5.16	16.2	18.15	7.39
SAMtools	89.5	3.28	32.8	8.96	10.79

The size of the entire uncompressed dataset is 294 GB. SlimGene compresses GAhum in 7.39 hours for a compression factor of 5.15×. On the other hand, SAMtools provide a compression factor of 3.28× in 10.79 hours. In the absence of quality values (all bases have an identical quality), the advantage of SlimGene is magnified.

In the absence of the quality scores, SlimGene would have achieved higher compression rates as compared to SAMtools. Although SAMtools cannot compress SAM files without quality scores, we substituted all quality scores of GAhum with the same string. In this way, we make sure that any general purpose tool can recognize the repetition and minimize the impact of the size of the quality scores on the compressed files. As Table 6 shows, we get an 18× compression with SlimGene, versus 9× for SAMtools.

8. Conclusion

The SlimGene toolkit described here is available on request from the authors. While we have obtained compression factors of 35 or more for fragment compression, we believe that in the future we will do somewhat better and get closer to information theoretic limits. Currently, error-encoding is the bottleneck, and we do not distinguish between sequencing errors and genetic variation. By storing multiple (even synthetic) references, common genetic variation can be captured by exact matches instead of error-encoding. To do this, we only have to increase the Pos vector while greatly reducing the number of ErrorInstructions. This trade-off between extra storage at the compressor/decompressor versus reduced transmission will be explored further in the future.

While this article has focused on fragment compression as opposed to sequence compression (Brandon et al., 2009), we believe both forms of compression are important and, in fact, complementary. In the future, if individuals have complete diploid genome sequences available as part of their personal health records, the focus will shift to sequence-level compression. It seems likely that fragment level compression will continue to be important to advance knowledge of human genetic variation and is the pressing problem faced by researchers today. We note that Brandon et al. (2009) also mention fragment compression briefly, but describe no techniques.

While we have shown 2–3× compression of quality values, we believe it is unlikely this can be improved further. It is barely conceivable that unsuspected relations exist, which allow us to predict Q-values at some positions using Q-values from other positions; this can then be exploited for additional compression. However, there is nothing in the physics of the sequencing process that suggests such complicated correlations exist. Further, it would be computationally hard to search for such relations.

If compressing quality values beyond 3× is indeed infeasible, then lossy compression is the only alternative for order of magnitude reductions. Our results suggest that the loss is not significant for interpretation. However, we have only scratched the surface. Using companding, from Pulse Code Modulation (Bellamy, 2000), we plan to deviate from uniform quantization, and focus on wider quantization spacings for the middle quality values and smaller spacing for very high and very low quantization values. Further, we need to investigate the effect of quantization on other analysis programs for say de novo assembly, structural variation, and CNV detection. The number of quantization values in SlimGene is parameterized, and so different application programs can choose the level of quantization for their needs. A more intriguing idea is to use multi-level encoding as has been suggested for video (Steven et al., 1996); initially, coarsely quantized quality values are transmitted, and the analysis program only requests finely quantized values if needed.

As sequencing of individuals becomes commoditized, its production will shift from large sequencing centers to small, distributed laboratories. Further, analysis is also likely to be distributed among specialists who focus on specific aspects of human biology. Our article initiates a study of fragment compression, both loss-less and lossy, which should reduce the effort of distributing and synthesizing this vast genomic resource.

Acknowledgments

C.K. and V.B. acknowledge partial support from the National Science Foundation (grant IIS0810905) and the National Institutes of Health (RO1-HG004962), as well as a U54 center grant (5U54HL108460).

Disclosure Statement

No competing financial interests exist.