Modelling of Lysozyme Binding to a Cation Exchange Surface at Atomic Detail: The Role of Flexibility

Abstract

Different approaches were made to predict the adsorbed orientation based on rigid, flexible, or a mixture of both models. To determine the role of flexibility during adsorption, the orientation of lysozyme adsorbed to a negatively charged ligand surface was predicted by a rigid and a flexible model based on two differing protein structures at atomic resolution. For the rigid model, the protein structures were placed at different distances from the ligand surface and the electrostatic interaction energy was calculated for all possible orientations. The results were compared to a flexible model where the binding to the ligand surface was modeled by multiple molecular dynamics simulations starting with 14 initial orientations. Different aspects of the adsorption process were not covered by the rigid model and only detectable by the flexible model. Whereas the results of the rigid model depended sensitively on the protein-surface distance and the protein structure, the preferred orientation obtained by the flexible model was closer to a previous experimental determined orientation, robust toward the initial orientation and independent of the initial protein structure. Additionally, it was possible to obtain insights into the preferred binding process of lysozyme on a negatively charged surface by the flexible model.

Introduction

Interactions of proteins with charged surfaces are important in many applications such as chromatographic separation of proteins (1), immobilization (2), biosensors (3), and design of biocompatible materials for medical applications (4). To model the contribution of structure, flexibility, and physiochemical properties of the protein and the surface to the free energy of binding and the preferred orientation of the protein bound to the surface, a wide variety of methods at different levels of detail have been applied. In experimental studies, the effects of protein concentration, pH, ionic strength, and the protein surface to the binding properties were investigated (5). It has been shown that the interactions between proteins and adsorbers are complex, and that properties of the protein such as charge distribution, hydrophobicity, molecular geometry, and flexibility significantly influence the adsorption process (5). Although the crystal structure of many proteins has been solved by x-ray diffraction (6), the protein structure bound to an adsorber has not yet been determined at atomic detail. Therefore, the interactions between a bound protein and the adsorber were investigated by computational techniques such as protein surface analysis (7), Brownian dynamics (8,9), and molecular dynamics (MD) simulations (10–18).

By representing the protein as a rigid sphere, the effect of charge, protein dipole moment, protein size, and ionic strength to the kinetics and thermodynamics of binding were studied (19). It has been suggested that a more realistic description of protein binding should be achieved by more complex models that take into account the distribution of positive and negative charges on the protein surface (20). However, refining the charge distribution does not necessarily improve the quality of model, as it has been shown by comparison of three different models of lysozyme and chymotrypsinogen (21).

In most approaches to model the interaction of a protein with an adsorber, binding properties such as protein orientation and binding affinity were evaluated by systematically calculating the interaction energies of a rigid protein for different orientations and distances to a surface (7,9,22–24). To study protein binding, different approaches were done by comparing modeling results to experimentally measured retention factors. Although the absolute values of four cytochrome c variants were underestimated by the model, differences between the variants were quantitatively reproduced (25). Similar results were obtained for fibroblast growth factors FGF-1 and FGF-2. However, the experimentally determined relative binding affinities of cytochrome c and lysozyme could not be reproduced by the model (26).

Although generally only indirect experimental data on the orientation of a protein bound to an adsorber are available, direct experimental data on the orientation of lysozyme bound to a negatively charged surface were obtained by labeling the accessible residues in the bound state, allowing a direct comparison (27). A preferred binding orientation was approximated and in agreement with the experimentally determined orientation by averaging electrostatic binding energies of MD simulations in implicit solvent with fixed backbone but flexible side chains (16). Additionally, it was possible to predict experimentally derived retention factors and conductivities of lysozyme and ribonuclease A at different ligand densities and pH values. Because a binding pathway was not observable the process of binding still remained unclear.

It is generally agreed that electrostatic interactions dominate the ion-exchange chromatography binding process, but it has been suggested that molecular flexibility might also play an important role (13). MD simulations and steered molecular dynamics (SMD) simulations with proteins on different surfaces have been carried out to treat the protein and the adsorber as flexible molecules. A fibrinogen γ-chain was simulated by MD simulation at charged, hydrophobic, or neutral surfaces with a starting distance of 7 Å at one specific starting orientation (10). It could be shown that the adsorption behavior was different on the varying surfaces. The dominant role of electrostatic energies was demonstrated by MD and SMD simulations of the 10th type III module of fibronectin (12) and of amelogenin (11) at a hydroxyapatite surface where the protein was initially placed close to the surface, equilibrated by MD simulations, and then pulled off the surface by SMD simulations. Simulations of fibronectin and albumin initially placed close to a graphite surface demonstrated that conformational changes in backbone structure of the protein at the binding interface can occur (17,18).

Recently, computationally intensive MD simulations in explicit solvent of lysozyme adsorption initially placed at a maximum of 9 Å and 2–4 different orientations from a negatively charged solid SiO₂ surface showed a preferential adsorption site at the N- and C-terminal protein face and detected the crucial role of the C-terminal Arg-128 (13–15).

Although the influence of the direct interactions between surface and protein were analyzed in detail, and general trends of the binding process could be observed by previous publications, a detailed analysis of the binding process is still missing. Major drawbacks of previous simulation studies with complete flexibility were that the proteins have initially been placed near the surface, which might restrict the reorientation of the proteins, and that the amount of MD simulations with different starting orientations were insufficient for comparison and detection of a common binding pathway.

We compared two different approaches, a rigid model calculating the binding energies of a rigid protein in different orientations, and simulations of a flexible model of a protein placed at a distance from a cation exchanger ligand surface in implicit solvent. For the rigid model the electrostatic binding energies of 312 orientations of lysozyme at five different distances over the cation exchanger surface were considered. For the flexible model MD simulations of lysozyme initially placed at a high distance of 25 Å from a cation exchanger surface with 14 different starting orientations were carried out, allowing reorientation and binding to the ligand surface at atomic detail. Two different protein structures were used for both methods. The results were compared quantitatively to the available experimentally derived orientation. As a result, we were able to show the necessity of including flexibility into adsorption models and describe the statistically preferred molecular mechanism of the binding process as well as the included structural changes in detail.

Methods

Protein models

Hen egg white lysozyme atomic coordinates of an NMR structure (28) and an x-ray crystal structure (29), further referred to as structure I and structure II, respectively, were taken from the Protein Data Bank (6). Crystal waters were removed and methylated lysines of structure II were demethylated. The protonation states were assigned according to experimentally derived data at pH 7 (30). Lysozyme is a protein with a size of ∼14.3 kDa consisting of 129 residues. It has a pI of 11 (31) and is positively charged (+8) at pH 7.

Protein orientation

Determination of lysozyme orientations was achieved by measuring two angles: 1), the angle Ψ between the normal vector of the ligand surface and the vector (COM, C_α^Ala-90) from the mass weighted center of mass (COM) to Ala-90, and 2), the angle Φ between the two planes spanned by the normal and vector (COM, C_α^Ala-90), and by vector (COM, C_α^Ala-90), and vector (C_α^Ala-90, C_α^Gly-22) (Fig. 1). Orientations for the calculated electrostatic binding energies and simulation pathways were displayed by a Mollweide projection (32). By this display method the calculated orientation-dependent binding energy of the protein is displayed as a map, where the angle Φ corresponds to the degree of longitude and the angle Ψ to the degree of latitude. The previously published experimentally determined orientation of lysozyme bound to Source 15S (GE Healthcare Life Sciences) at low surface coverage (27) resulted in the orientation (Φ, Ψ) = (−85°,−37°).

Figure 1.

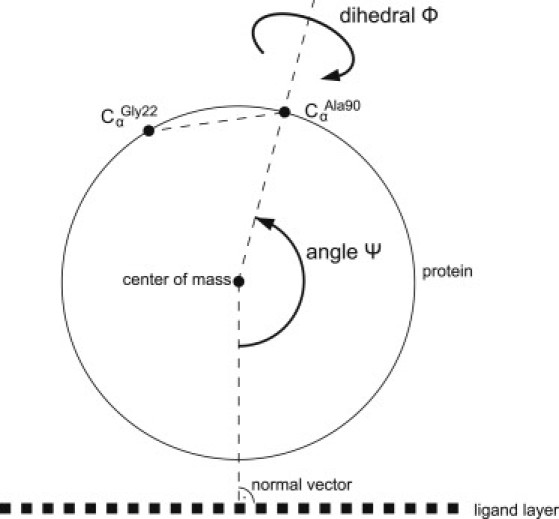
Orientation detection of the protein during simulations.

Rigid model to determine orientation

Electrostatic binding energies of different lysozyme orientations near a planar surface were computed to evaluate the preferred orientation of lysozyme. First, lysozyme was rotated about its horizontal axis from 0° to 180° by steps of 15°. Then it was rotated by 15° about the vertical axis, and the rotation from 0° to 180° about the horizontal axis was performed again. This procedure was continued until rotation about the vertical axis reached 360°. For each orientation the distance between the ligand surface and the protein was adjusted to a minimal distance of 1, 5, 10, 15, or 20 Å. Thus, in total 312 orientations at five different distances were evaluated. As a model of the adsorber, a negatively charged ligand surface was constructed by placing 11 × 11 charged spheres (radius 1.7 Å, charge −1) on a lattice with a spacing of 7 Å, resulting in a surface charge density of 3.4 μmol/m² and a side length of the lattice of 77 Å, which is 50% larger than the diameter of the protein. The chosen ligand distance is very dense compared to the usual ion-exchange materials and leads to a high surface charge density, which was still in the field of strong ion exchangers (33). However, it was necessary to keep the ligand distance as dense as possible: 1), for minimizing the fluctuations in electrostatic binding energies with respect to translation of the protein parallel to the adsorber surface for the rigid model and 2), to prevent the protein from moving in between the ligands and tilting at single ligands for the flexible model. A previous comparison of experimental retention data using a different ion exchanger SP Sepharose Fast Flow (GE Healthcare Life Sciences) showed that the results were most reliable at small ligand distances (16), although a large spacing of the ligands results in a high sensitivity of the calculated binding energy on translation of the protein parallel to the ligand surface. The small ligand distance of 7 Å also prevented the protein from moving into the space between two ligand molecules.

Binding energy calculation

The approach used to calculate electrostatic interaction energies assumes the electrostatic interactions between the protein and ligand surface to be dominating and makes use of the Poisson-Boltzmann equation. For computing the electrostatic potential, the DELPHI program was used, and resulting binding energies were calculated by the energy partitioning method (34,35):

$$\Delta G_{\text{b}}=\Delta G_{\text{coul}}+\Delta G_{\text{rxn}}+\Delta G_{\text{ion}},$$ (1)

where ΔG_b is the electrostatic binding energy and is a sum of ΔG_coul, the coulombic energy, ΔG_rxn, the reaction field energy (solvation energy), and ΔG_ion, the ionic energy. The calculations were performed for a salt concentration of 0.1 M for 25,000 iteration steps that led to energy convergence. Boundary conditions at the edge of the lattice were set to coulombic: approximated by the sum of Debye-Huckel potentials of all the charges. Parameters for atom types and particle charges of the protein were taken from the Amber force field (36). It turned out that the computation of binding energies was sensitive for close distances of the boundary box to the modeled ligand surface. For that reason a grid size of 351 × 351 × 351 and grid spacing of 0.5 Å were used, resulting in a box side length of 175.5 Å.

To evaluate the preferred orientation, two methods were used:

• 1.The global energy minimum orientation was detected by selecting the orientation with the lowest electrostatic binding energy.
• 2.The energy-weighted average orientation was defined by the vector $\overrightarrow{{\mathbf{o}}_{Bw}}$, which was calculated by the vector sum of all orientation vectors ${\overrightarrow{o}}_i$ from COM to C_α^Ala-90, Boltzmann-weighted by their electrostatic binding energies ΔG_b:

$$\overrightarrow{{\mathbf{o}}_{Bw}}=\frac{\sum _i{\overrightarrow{\mathbf{o}}}_i\cdot e^{\frac{-\Delta G_{\text{bi}}}{kT}}}{\sum _i{e}^{\frac{-\Delta G_{\text{bi}}}{kT}}}.$$ (2)

Ligand parameterization

The Source 15S ligand structure was constructed using ArgusLab (37) and the geometry was optimized by Gaussian (38) using a Hartree-Fock approach and 6-31G^∗. After convergence, the RESP method (39) was applied for fitting the partial charges (Table S1 in the Supporting Material). Bond parameters for S–O and bond angle parameters for O–S–O and C–S–O were taken from the Amber force field of the phosphate group (Fig. S1 in the Supporting Material).

Ligand surface construction

A planar model of Source 15S was constructed by placing 11 × 11 ligands with a spacing of 7 Å. Therefore, the total system charge was −113 (−121 for the ligand surface and +8 for lysozyme). During the simulations, the terminal carbon atoms C1 and C2 of the ligands (Fig. S1) were constrained (10 kcal/mol × Å²) whereas all other atoms were allowed to move freely.

Flexible model to determine orientation

MD simulations were carried out using Amber 8.0 (36) with the f99 force field and an implicit solvent (generalized Born model). The 14 different starting orientations of the protein were generated using the same procedure as the rigid model. However, a larger rotation angle of 45° was chosen for the rotation step size. No boundary conditions, explicit ions, or box definitions were used as the implicit solvent continuum model corresponds to solvation in an infinite volume of solvent. The initial protein orientations were placed at a distance of 25 Å to the ligand layer at the beginning of the simulations. During and after minimization of the system without periodic boundary conditions the backbone of lysozyme was constrained (5 kcal/mol × Å²) to keep the protein in position. A cutoff of 12 Å for electrostatic interactions was applied while heating to 300 K for 10 ps. During the following production MD simulations of 2 ns all lysozyme atoms were allowed to move freely and a cutoff of 100 Å for electrostatic interactions was applied. The integration step of 2 fs and SHAKE algorithm was used.

The distance of lysozyme to the ligand surface was quantified by measuring the closest distance of any atom on the ligand surface to any atom of the protein on the vertical axis. Measured negative distances were caused by the movement of amino acid side chains between the ligand molecules.

For testing convergence, each of the 14 simulations was continued by shifting the protein perpendicular to the ligand surface without changing its orientation, and binding of the protein was again simulated. This process was repeated three times, by shifting the protein by 20, 15, and 10 Å, resulting in a total of three 500 ps simulations for each of the 14 initial orientations.

To analyze the overall binding behavior of amino acids that are involved in binding at the ligand surface of structure I and II, the results of the 14 MD simulations were summed up. For each amino acid and each time step, the numbers of simulations were counted, in which a contact of the respective amino acid with the ligand surface occurred. All amino acids were selected that had ligand surface contacts in more then 10 simulations. For these amino acids, the order of binding was determined by identifying the first time the residue was in contact with the ligand surface in >7 simulations.

Results

At pH 7 the total charge of lysozyme is +8. Eleven positively charged arginines and 6 lysines form 5 positive patches on the protein surface. The two largest patches patch 1 and patch 2, are located on opposite sides of the protein. Patch 1 is located near the N- and C-terminus and consists of Arg-5, Lys-13, Arg-14, Lys-33, Arg-125, and Arg-128, patch 2 consists of Arg-45, Arg-61, Arg-68, and Arg-73. The medium-sized patch 3 consists of residues Arg-112, Arg-114, and Lys-116, patch 4 of Arg-21, Lys-96, and Lys-97. The smallest patch 5 is formed by the N-terminal Lys-1. The experimentally determined binding orientation is facing the ligand surface in the region of patch 1.

Two experimentally determined structures of lysozyme were compared to study the effect of local structure on binding. The backbone root mean-square deviation (RMSD) between structure I and II was 1.6 Å. Major differences between the structures were the orientation of the C-terminus (near patch 1) and the conformation of a loop (near patch 2). Specifically, the orientation of the C-terminal amino acid residues Arg-128 and Leu-129 differ as they point into opposite directions. None of the other 252 lysozyme structures in the Protein Data Bank showed a local structure of the C-terminus similar to structure II.

Rigid model

To model the preferred orientation, electrostatic binding energies for each of the different orientations (Φ, Ψ) were calculated. The energy landscapes on a (Φ, Ψ) map were compared for the two structures at different distances from the ligand surface.

For structure I at a distance of 1 Å orientations with patches 2, 3, and 4 facing the ligand surface resulted into positive repellent binding energies (Fig. 2). Only a small number of orientations with patches 1 and 5 facing the ligand surface resulted in negative attractive binding energies. At a distance of 5 Å the area of negative binding energies became larger and included patches 1, 3, 4, and 5. Patch 2 facing the ligand surface resulted in positive binding energies. For higher distances of 10 Å, 15 Å, and 20 Å the binding energies of the entire (Φ, Ψ) maps were negative. The values of the binding energies were decreased by increasing the distance between protein and adsorber.

Figure 2.

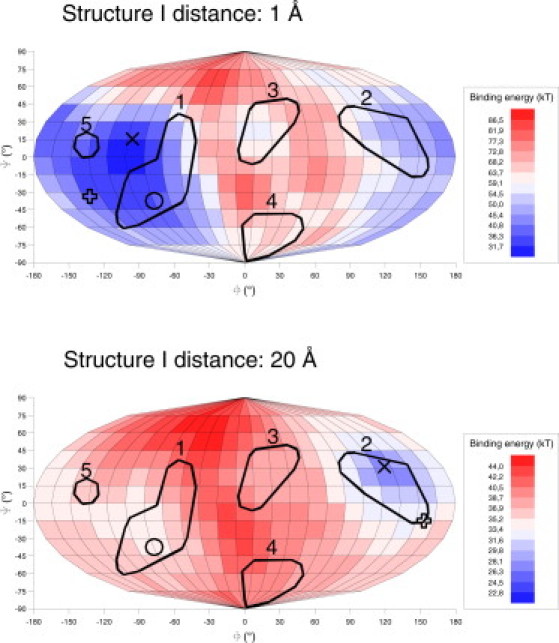
Computed binding energies of structure I at 1 Å and 20 Å distance in Mollweide projection. ○: experimental result, ×: global energy minimum orientation, and +: energy-weighted average orientation.

The global energy minimum orientation, which shows the orientation of the protein with the lowest binding energy on the (Φ, Ψ) map, was facing the ligand surface with patch 1 for all distances. It changed within patch 1 from the orientation (Φ, Ψ) = (−67°, 14°) at 1 Å distance to the orientation (Φ, Ψ) = (−113°,−22° ± 8°) at all other distances between the protein and the adsorber. Furthermore, the energy-weighted average orientation, showing the orientation of the resulting moment of the sum of all binding energies on the (Φ, Ψ) map, was facing the ligand surface with patch 1 for all distances and changed from the orientation (Φ, Ψ) = (−72°, 15°) at 1 Å distance to (Φ, Ψ) = (−111°,−18° ± 6°) at all other distances. The orientation of the global energy minimum orientation and the energy-weighted average orientation of structure I was similar for similar distances between the protein and the adsorber.

For structure II at a distance of 1 Å orientations with patches 2, 4, and 5 facing the ligand surface resulted in positive binding energies (Fig. S2). Only a small number of orientations located between patches 1 and 3 facing the ligand surface resulted in negative binding energies. At a distance of 5 Å the area of negative binding energies facing the ligand surface became larger and included patches 1, 3, and 4. The orientations facing the ligand surface with an area between patch 2 and 5 resulted in positive binding energies. For higher distances of 10, 15, and 20 Å the binding energies of the entire (Φ, Ψ) maps became negative. The values of the binding energies decreased with increasing distance of protein and adsorber.

The global energy minimum orientation for structure II was facing the ligand surface with patch 3 (Φ, Ψ) = (8°, 44° ± 14°) for all distances, whereas the energy-weighted average orientation was facing the ligand surface with patch 3 (Φ, Ψ) = (−2°, 24°) for the distance of 1 Å and changed gradually by increasing the distance to an orientation (Φ, Ψ) = (−41°, 14°) facing the ligand surface with patch 1 for the distance of 20 Å. In contrast to structure I the global energy minimum orientation and the energy-weighted average orientation of structure II were not similar for similar distances between the protein and the adsorber.

The deviation from the experimental orientation (Φ, Ψ) = (−85°,−37°) of the global energy minimum orientation and the energy-weighted average orientation were generally smaller with structure I and decreased with increasing distance from 54° and 53°, respectively at 1 Å distance to 25° and 28°, respectively, at 20 Å distance (Fig. S3). Similarly, the deviations for the energy-weighted average orientations of structure II decreased with increasing distance from 101° to 1 Å and 66° at 20 Å. The deviation of the global energy minimum orientation was about constant for all distances by 115° ± 7°. Generally more accurate predictions were obtained by increasing the distance between the protein and the ligand surface, except for the global energy minimum orientation of structure II.

The results demonstrated that the preferred orientation as predicted by the rigid model sensitively depends on the protein structure and the distance between the protein and the ligand surface. In particular, the predictions of the orientation for structure II varied considerably with distance and the method used to evaluate the preferred orientation.

Flexible model

To explore the binding of a flexible model of lysozyme to a flexible ligand surface in atomic detail, the system was simulated by multiple MD simulations, starting with two structures of lysozyme in 14 different orientations, each at a distance of 25 Å. The orientations were generated by 45° stepwise rotation around two perpendicular axes. During the MD simulations, the protein reoriented under the influence of the negatively charged ligand surface and approached the ligand surface within 400 ps of simulation time (Figs. S4 and S5). The average RMSD of the backbone between the simulated protein structure after 500 ps and the starting structure was 2.7 Å for structure I and 1.7 Å for structure II. Although the pathways of the reorienting protein structures depended on the initial orientations and differed between structure I or II (Fig. 3), the protein structures finally bound to the ligand surface with patch 1 or the interspace between patch 1 and patch 3, 4, and 5 facing the ligand surface. All possible remaining orientations were avoided. The orientations facing the ligand surface with the interspace between patch 1 and 4 occurred only in simulations with structure I, whereas orientations facing the ligand surface with the interspace between patch 1 and 3 only occurred in simulations with structure II. After binding to the ligand surface, the simulations were continued for a total of 2 ns and the orientations did not further change.

Figure 3.

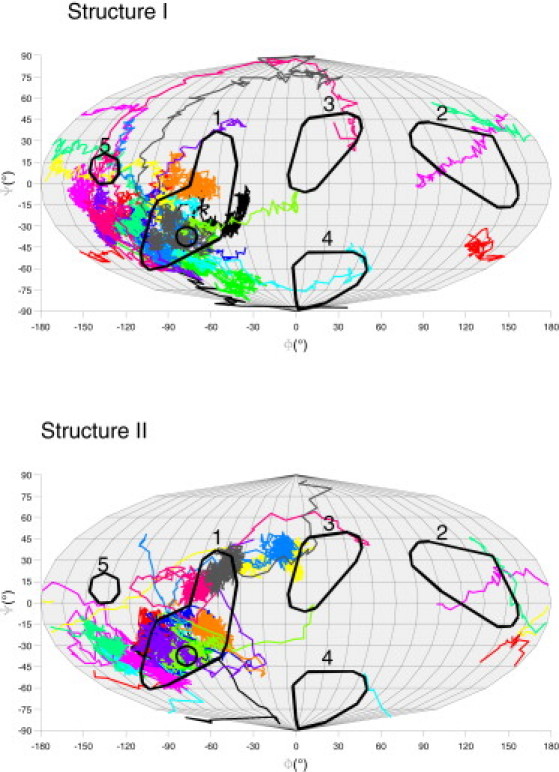
Orientation pathways of MD simulations in Mollweide projection. Starting orientations were equally distributed. ○: experimental result.

To compare the binding energy of the flexible and the rigid model, electrostatic binding energies for the flexible model were calculated using the same procedure as the rigid model (Fig. 4). In contrast to the rigid model all binding energies of the protein bound to the adsorber were negative. The energy-weighted average orientations of the flexible model differed from the experimental value by only 23° and 20° for structure I and II, respectively. The energy-weighted average orientation therefore was independent of the starting structure, in contrast to the rigid model.

Figure 4.

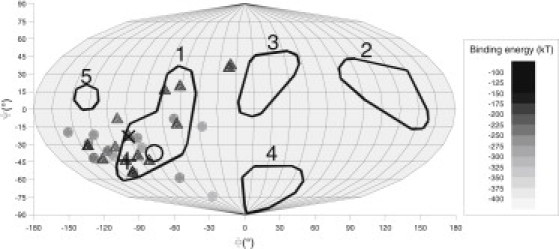
Energy of simulations at bound state in Mollweide projection. ○: experimental result, +: energy-weighted average orientation of structure I, ×: energy-weighted average orientation of structure II, ●: final binding orientations of structure I, and ▴: final binding orientations of structure II.

Because the bound orientations differed, it was tested to determine if the observed pattern of bound orientations can be refined. The protein (structure II) was shifted into steps by 20, 15, and 10 Å perpendiculars to the ligand surface while maintaining the respective orientation. After each shift of the protein, MD simulations of binding to the ligand surface were performed. In comparison to the initial simulations, starting at a distance of 25 Å, the energy-weighted average orientations changed by <5°, and the total area covered by the different orientations did not change. Thus, a refinement of the observed pattern by iterative shifting and rebinding was not observed.

As an example, we describe a typical binding pathway using structure II (Fig. 3, cyan): Starting at an orientation where the surface is faced by patch 4, the protein rotated to an orientation facing the surface by patch 1. At the same time conformational changes of two loops, one at patch 5 and one between patch 3 and 4, by 5 and 4 Å, respectively, were observed. Upon further approach to the surface, a first contact was established by the side chain of Arg-128. The protein then tilted by 35° and the side chains of Arg-125 and Arg-5 contacted the surface. Subsequently, a kink was formed between residues Val-2 and Phe-3, and the N-terminus contacted the surface. After a further slight tilt of the protein by 8°, Lys-33 and Arg-114 formed a contact with the surface. Thus, after an initial contact to the surface by Arg-128 a cascade of rearrangements followed, including tilting of the whole protein and local conformational changes. After this cascade of binding events, the structure and orientation of the protein was stable until the end of the simulation.

Because the orientation pathways were different for each simulation, the molecular details of the binding process also differed. For a description of a preferred binding process, the simulations were analyzed by observation of amino acids predominantly contacting the ligand surface (Fig. S6). Six amino acids played a prominent role (Lys-1, Val-2, Arg-5, Arg-125, Gly-126, Arg-128) by having ligand surface contacts in >10 simulations for each of both structures (Table 1). For those amino acids a preferred order of ligand surface contacts was identified (Fig. 5): Upon approach to the ligand surface (Fig. 6 A) the C-terminal Arg-128 initially contacted the ligand surface (Fig. 6 B). The N-terminal Arg-5, and the C-terminal Arg-125 and Gly-126 followed, however in variable order for each structure (Fig. 6 C and D). Finally, the ligand surface was contacted by N-terminal Lys-1 and Val-2 (Fig. 6 E). During the final N-terminal binding process a conformational change was observed by forming a kink between residues Val-2 and Phe-3. Consequently, the complete protein structure tilted in the direction of the N-terminus. Afterward the orientations did not further change.

Table 1.

Amino acids with >10 summed up surface contacts sorted by their order of binding

Structure	Structure I	Structure II	Structure II	Structure II	Structure II
Starting distance	25 Å	25 Å	20 Å	15 Å	10 Å
Simulation time ↓	Arg-128	Arg-128	Arg-128	Arg-128	Arg-128
	Gly-126	Arg-125	Arg-125	Arg-125	Arg-125
	Arg-125	Arg-5	Arg-5	Arg-5	Gly-126
	Arg-5	Gly-126	Gly-126		Arg-5
	Lys-1	Lys-1
	Val-2	Val-2
	Gln-121	Lys-33
		Asn-37
		Arg-114

Figure 5.

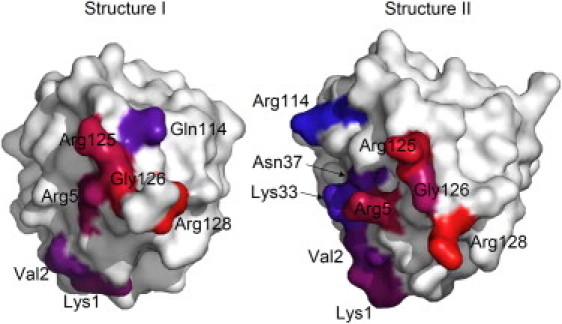
Molecular surface of structure I and II. Amino acids contacting the adsorber ligand surface in >10 simulations are colored from red to blue in the order of the occurrence of 7 simultaneous contacts.

Figure 6.

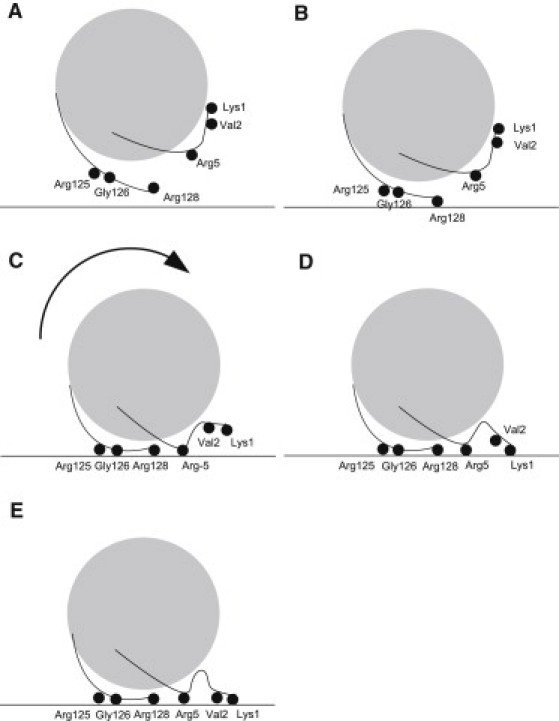
Binding of lysozyme to the ligand surface. The MD simulation started with the protein facing the ligand surface by the area at patch 3 (A). Afterward the protein rotated while approaching the ligand surface. The first contact to the ligand surface was established by the C-terminal Arg-128 (B) followed by Arg-125 (C). A tilting of the protein on the ligand surface then occurred and Arg-5 contacted the ligand surface (D). By binding of the N-terminal Lys-1, a conformational change of the N-terminus occurred (E) and the protein stayed in this orientation during the remaining time of the MD simulation.

Discussion

Two methods to model the preferred binding orientation of lysozyme at a negatively charged ligand surface were compared: a flexible model using MD simulations at full flexibility of protein and ligand surface with implicit solvent starting in 14 different orientations at a distance of 25 Å, and a rigid model using rigid protein structures and a rigid ligand surface for scanning the electrostatic interaction energies of 312 different orientations at five different distances. To determine the sensitivity of the predicted orientation to the structure of the protein, two lysozyme structures (backbone RMSD: 1.6 Å) differing by the conformation of the C-terminus and a loop were compared. The energy-weighted average binding orientations of both structures using the flexible model were in accordance with a previous experimentally determined orientation of lysozyme bound to a cation-exchange chromatographic material (27).

The results derived by the rigid model showed a sensitive dependence on subtle details of protein structure and on the distance between protein and ligand surface. Because structure I and structure II are highly similar, the deviations of the predicted binding orientations were most likely caused by the local structural differences in the orientation of the C-terminus (near patch 1) and the conformation of a loop (near patch 2). Predictions using the rigid model led to better results with higher distance than with lower distance between the protein and the ligand surface by trend, demonstrating that errors introduced by local structural differences on the predicted orientation decrease with increasing the distance between the protein and the ligand surface. However, the differences between both structures were still strong enough to result in different predicted orientations at higher distances. In contrast, the flexible model resulted in similar predicted average binding orientations with both structures. The error introducing local lysozyme structures of the rigid model changed in the flexible model under the influence of the ligand surface leading to better predictions. Therefore, flexibility can play a considerable role on the binding orientation of the protein to a ligand surface. In the case of lysozyme on a negatively charged surface, it is most likely the flexibility and structure of the C-terminal region near patch 1 as it is the major difference between both protein structures and located at the preferred contact site facing the ligand surface (14,15).

Comparison of the calculated electrostatic binding energies between the structures derived by the rigid and the flexible model showed differences. Although the protein and the ligand surface had opposite charges, repulsive electrostatic binding energies were calculated for some orientations by the rigid model for close distances of protein and ligand surface. In contrast, the flexible model resulted in binding of the protein at the ligand surface and attractive electrostatic binding energies were calculated for similar orientations. We suppose that using the flexible model, the structures of the protein and of the ligand surface adapt to each other upon binding, positively charged amino acid side chains reorient toward the negatively charged ligands and are able to move between two negatively charged ligand molecules, whereas negatively charged side chains point away from the ligand surface. This process was neglected by the rigid model and therefore resulted in repellent binding energies for most orientations at close distances, because the negative charges at the protein surface are interacting with negatively charged surface ligands, and the high charge density of the ligand surface amplifies this effect. For higher distances the reorientation of side chains and ligands become less relevant, whereas the influences of the total charges of protein and ligand surface become dominant, and binding energies become attractive for all orientations of the protein. Thus, the flexibility of amino acid side chains and of the ligand surface can have a major effect on the orientation and energetics of proteins.

The calculated interaction energies using the Poisson-Boltzmann calculations were remarkably high, but comparable to interaction energies calculated previously (16). Although the interaction energies only account for the enthalpy contribution to the free energy, the experimentally measured free energy of binding also includes an entropy contribution due to the release of water from the ligand surface and a loss of flexibility of the protein upon binding. In this work, we put the main focus on the orientation of the protein on the ligand surface. Our simulation cannot be used to analyze the entropy contribution directly. Simulations using umbrella sampling or steered MD simulations with an explicit water model, considering different salt and protein concentrations, and incorporation of the hydrophobic backbone material of the adsorber are indispensable to the evaluation of interaction energies.

In addition to finding that flexibility of amino acid side chain structures is necessary for detection of the lysozyme binding pathway; the flexible model showed that the backbone structure also plays an important role. At the initial binding step the flexibility of C-terminus influenced the variety of preferred binding orientations and multiple MD simulations were necessary to predict an averaged preferred binding orientation. Later on, the bound orientation was changed by the influence of the N-terminus, which formed a kink in backbone structure to contact the surface. The formation of the kink is also visible in a figure of a previous publication (15).

Neglect of protein flexibility can cause errors and might be the explanation why rigid models sometimes failed to predict retention (26), and simple sphere models were superior to rigid models at atomic resolution (21).

Keeping the starting distance of protein and ligand low may restrict reorientation of the protein. In some of the MD simulations, the flexible model lysozyme structures rotated >180° while approaching the surface, proving that 25 Å distance allowed enough time for free reorientation under the electrostatic influence of the ligand surface before binding. The MD simulations resulted in diverse binding orientations deviating from the experimental value by up to 84° with an accumulation near the experimentally determined orientation. Hence, the previous statement that a variety of binding sites exist, some with higher probability than others, is supported by our results (16). The energy-weighted average orientation, which should conform to the experimentally measurable value, was close to a previously experimentally determined orientation (deviation of <23°) (27). The evaluation of energy-weighted average binding orientations after MD simulations of structure I in comparison to structure II resulted in more reliable and reproducible results than those of the rigid model. The improvement of the result with structure II using a flexible model in comparison to the rigid model demonstrates the independence of the flexible model to small changes in structure. This recommends the application of the flexible model for structures that have structural ambiguities; for example, homology models or x-ray-derived protein structures that may contain structural changes due to crystal contacts.

Our results support the finding of previous MD simulations using an explicit solvent model that a negatively charged surface is preferably initially contacted by the C-terminal residue Arg-128 and that the final preferential adsorption site is at the region of the N- and C-terminus (13–15). By using an implicit solvent model, friction is neglected and the role of explicit water interactions and dielectric shielding can not be analyzed. The advantage of the implicit solvent model is a shorter computing time and therefore the possibility to use multiple MD simulations with different starting orientations, as shown previously (16).

Although this model allows for full flexibility and molecular detail of the interactions between protein and surface, there are still several limitations. The partial charges of all atoms are assumed to be constant; however, upon approach of a titratable group to the negatively charged surface, a shift in its pKa and thus its protonation state can be expected. The good agreement of the orientation evaluated by the flexible method with the experimental orientation indicates that the effect of pKa shift seems to be neglectable for lysozyme. However, other proteins might undergo stronger electrostatic changes due to induced pKa shifts.

The polystyrene backbone material of Source 15S was not included in the study. It has been discussed that hydrophobic interactions of the backbone material with the protein are possible but there was no clear evidence (40). Although hydrophobic effects cannot be excluded, the good agreement of our results with experimental data indicates that the adsorbed orientation of lysozyme on the ion exchanger surface of Source 15S at lower salt concentrations is mainly influenced by the electrostatic interactions.

The conclusion that the structure of the C-terminal region plays an important role in the binding orientation by the rigid model was also supported by the results of the flexible model. Though detailed analysis of the structural changes showed that binding was initiated by the C-terminal patch 1, there was no preferred structure of the C-terminus during the binding process. Instead, we suppose that the flexibility of the C-terminus led to a larger variety of different binding orientations as compared to a protein with less flexibility at the initial contact site. Only the energy-weighted average binding orientation of multiple MD simulations was able to quantitatively reproduce the experimentally determined orientation with lysozyme. Apart from the changes in the structure of the C-terminus at the initial binding, the N-terminus was subjected to a structural change due to its flexibility at a later point in time. It performed a kink to contact the ligand surface. This behavior has not been described before, but is observable on already published figures of MD simulations with bound lysozyme to a negatively charged surface (15). Consequently, the protein tilted toward patch 5. Hence, the flexibility of the N-terminus has an additional influence on the final orientations of the protein on the ligand surface.

Conclusions

Multiple MD simulations of lysozyme starting with several initial orientations at a distance of 25 Å provided insights into the binding process and reproduced the preferred orientation of lysozyme bound to a negatively charged ligand surface. The result showed that not one optimal binding orientation, but a variety of preferred binding orientations exist. We found that flexibility has influence on different aspects during binding: 1), It influenced the diversity of binding orientations due to the flexible C-terminus. 2), Flexibility of the protein leads to a preferred order of amino acids contacting the surface. 3), Flexibility at the N-terminus enables a conformational change for contacting the surface and inducing a tilt of the protein at the ligand surface. 4), Flexibility of the amino acid side chains increases the binding energies compared to a rigid model by reorienting under electrostatic influence and movement between ligand molecules. Thus, a detailed molecular model with flexible protein and ligand can be a prerequisite to interpret experimentally determined properties such as orientation and binding affinity, and to predict the effect of mutations or a change in pH or salt concentration.