Model of Aquaporin-4 Supramolecular Assembly in Orthogonal Arrays Based on Heterotetrameric Association of M1-M23 Isoforms

Abstract

Tetramers of aquaporin-4 (AQP4) water channels form supramolecular assemblies in cell membranes called orthogonal arrays of particles (OAPs). We previously reported evidence that a short (M23) AQP4 isoform produced by alternative splicing forms OAPs by an intermolecular N-terminus interaction, whereas the full-length (M1) AQP4 isoform does not by itself form OAPs but can coassemble with M23 in OAPs as heterotetramers. Here, we developed a model to predict number distributions of OAP size, shape, and composition as a function M23:M1 molar ratio. Model specifications included: random tetrameric assembly of M1 with M23; intertetramer associations between M23 and M23, but not between M1 and M23 or M1; and a free energy constraint limiting OAP size. Model predictions were tested by total internal reflection fluorescence microscopy of AQP4-green-fluorescent protein chimeras and native gel electrophoresis of cells expressing different M23:M1 ratios. Experimentally validated model predictions included: 1), greatly increased OAP size with increasing M23:M1 ratio; 2), marked heterogeneity in OAP size at fixed M23:M1, with increased M23 fraction in larger OAPs; and 3), preferential M1 localization at the periphery of OAPs. The model was also applied to test predictions about binding to AQP4 OAPs of a pathogenic AQP4 autoantibody found in the neuroinflammatory demyelinating disease neuromyelitis optica. Our model of AQP4 OAPs links a molecular-level interaction of AQP4 with its supramolecular assembly in cell membranes.

Introduction

Aquaporin-4 (AQP4) is a water channel expressed at the plasma membrane in astrocytes throughout the central nervous system, as well as in peripheral organs including kidney tubules, airway epithelium, skeletal muscle, and gastric parietal cells (1,2). In brain, AQP4 is involved in water balance, neuroexcitation, astrocyte migration, and neuroinflammation (3–7). AQP4 is also implicated in the multiple sclerosis-like disease neuromyelitis optica (NMO), where pathogenic autoantibodies against AQP4 (NMO-IgG) cause neuroinflammation and demyelination, leading to paralysis and blindness (8–10).

Human AQP4 protein is expressed as two isoforms, a full-length, long (M1) isoform with translation initiation at Met-1, and a shorter (M23) isoform produced by alternative splicing with translation initiation at Met-23 (11–13). We discovered that M23 AQP4 forms supramolecular assemblies called orthogonal arrays of particles (OAPs) (14), which are square arrays of particles visualized by freeze-fracture electron microscopy (FFEM) in brain, kidney, skeletal muscle, and other tissues (15–18). Though the M1 isoform by itself does not form OAPs, M1 can coassemble with M23 in arrays, producing smaller OAPs than those formed by M23 alone (19,20). We reported evidence, by quantum dot single particle tracking, single molecule photobleaching, and blue-native gel electrophoresis, that M1 and M23 can associate in heterotetramers (21,22), which could explain the observation that M1 incorporates into M23-containing OAPs, but does not by itself form OAPs (19). At the molecular level, we found by truncation and mutagenesis analysis that OAP formation by M23 involves an intermolecular N-terminus interaction between two M23 molecules by residues just downstream of Met-23, and that the inability of M1 by itself to form OAPs is due to blocking of the N-terminal interaction by residues just upstream of Met-23 (23).

Here, we developed a mathematical model of AQP4 OAP assembly to test our experimental evidence-based ideas about M23 association and M1/M23 heterotetramer formation. The model provides quantitative insight into the role of M1/M23 composition in OAP assembly, and made predictions about OAP topography and composition that were tested experimentally by biophysical and biochemical measurements on M1/M23-transfected cells. The model inputs included M1:M23 molar ratio, association rules, and free energy constraints, and the model outputs included number distributions of OAP size and shape, and total/perimeter M1/M23 composition. The association rules for the initial model included random M1/M23 association in heterotetramers and monovalent M23-M23 intermolecular association.

Fig. 1 illustrates the idea. Individual AQP4 tetramers contain zero, one, two, three, or four M1 monomers, in six possible independent configurations (with rotation possible) (Fig. 1 A). If tetramer-tetramer association requires at least one intertetrameric M23-M23 interaction, then many OAP configurations are possible of different size, shape, and composition. Conceptually, more M1 at fixed M23 is predicted to reduce OAP size because M1 blocks tetramer associations by coating the outer surface of OAPs (Fig. 1 B). The modeling here involved the serial generation of AQP4 tetramers whose M1/M23 composition was determined using random numbers (for each monomer) and the specified M1:M23 ratio. Newly generated AQP4 tetramers were then appended to an existing OAP until no more tetramers could be added, at which point mature OAPs were analyzed for size, shape, and M1/M23 composition for number histogram generation (Movie S1, Supporting Material). Specified association rules and free energy constraints were applied at the step of appending newly generated tetramers.

Figure 1.

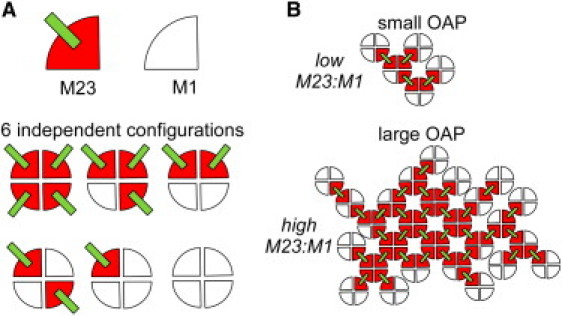
Schematic of OAP assembly from AQP4 M1/M23 heterotetramers. (A) (top) M23 and M1 AQP4 monomers. Projection from M23 monomer denotes potential site of M23-M23 intertetrameric interaction. (bottom) Six possible independent AQP4 M1/M23 heterotetramers. Four-way rotational variants of each are possible as well. (B) Examples of OAPs at low and high M23:M1 ratios.

Experimental Procedures

Constructs and cell transfections

The cDNA constructs encoding human M1 and M23 AQP4 were polymerase chain reaction-amplified using human brain cDNA as template. M1 and M23 AQP4-green-fluorescent protein (GFP) chimeras, with GFP appended to the AQP4 C terminus, were generated as described (22). Polymerase chain reaction fragments were ligated into mammalian expression vector pcDNA3.1 (Invitrogen, Carlsbad, CA). Constructs were fully sequenced. U87MG cells (human glioblastoma-astrocytoma, ATCC HTB-14) were cultured at 37°C in 5% CO₂, 95% air in appropriate medium containing 10% fetal bovine serum, 100 units/ml penicillin, and 100 μg/ml streptomycin. Cells were transfected in antibiotic-free medium 12–24 h before the experiments using FuGene HD (Roche, Basel, Switzerland) at a 3:1 ratio (μl/μg DNA, 0.18 μg DNA/cm² culture). In various experiments different ratios of plasmids encoding the untagged or GFP-tagged M1 and M23 AQP4 constructs were used.

Electrophoresis and immunoblot analysis

Imidazole, γ-aminocaproic acid, Triton X-100, Tricine, and ferritin were purchased from Sigma (St. Louis, MO), and acrylamide/bisacrylamide and Coomassie Blue G-250 from Serva (Heidelberg, Germany). Large pore polyacrylamide native gradient gels (2–9%) were prepared as described (24). Cell cultures were lysed with Blue Native buffer (25) containing Triton X-100 (detergent/protein ratio of 4.0 g/g). Lysates were centrifuged at 20,000 × g for 20 min at 4°C and the pellet discarded. Samples (10 μg protein) were mixed with 5% Coomassie Blue G-250 and loaded into each lane. Ferritin was used as the molecular mass standard (440 and 880 kDa). The running buffers were 25 mM imidazole, pH 7 (anode buffer), and 50 mM Tricine, 7.5 mM imidazole, 0.02% Coomassie Blue G-250, pH 7 (cathode buffer). Proteins were blotted onto polyvinylidene difluoride membranes (Millipore, Bedford, MA) for immunoblot analysis using a native transfer buffer (50 mM Tricine, 7.5 mM imidazole). For the second dimension, lanes from the first dimension were cut into individual strips and equilibrated in denaturation buffer (1% sodium dodecyl sulfate (SDS), 1% β-mercaptoethanol) for 1–2 h at room temperature. A single strip was then placed into a second dimension gel of the same thickness and subjected to Tricine SDS-polyacrylamide gel electrophoresis (PAGE) using standard protocol (25).

For one-dimensional Laemmli SDS-PAGE, gels consisted of a 12% running gel and 3% stacking gel. Samples were not heated before loading. SeeBlue Plus2 Pre-Stained Standard (Invitrogen, Carlsbad, CA) was used as molecular weight markers. Proteins were blotted onto polyvinylidene -difluoride membranes at 160 mA for 1.5 h using a TGE-SDS buffer: 1.92 M glycine, 0.25 M Tris base, 10 mM EDTA, 1% SDS. For immunoblot analysis, membranes were blocked with 3% bovine serum albumin and incubated with rabbit anti-AQP4 (Santa Cruz Biotech, Santa Cruz, CA) at room temperature for 2 h. Membranes were then rinsed, incubated for 1 h with horseradish peroxidase-conjugated goat anti-rabbit IgG (Jackson ImmunoResearch Laboratories, West Grove, PA), rinsed extensively, and labeled proteins were detected using the ECL Plus enzymatic chemiluminescence kit (Amersham Biosciences, Pittsburgh, PA).

Total internal reflection fluorescence microscopy

Total internal reflection fluorescence (TIRF) microscopy was done on a Nikon Eclipse TE2000E microscope equipped with infrared autofocus, ×100, 1.49 numerical aperture Apo TIRF objective, Nikon TIRF attachment, Photometrics QuantEM 512SC charge-coupled device (CCD) camera, and Spectra-Physics Advantage 161C 10 milliwatt argon ion laser (coupled to fiber optic via a quarter wave plate). Filters included a Z488/10× excitation filter, Z488RDC dichroic mirror, and ET525/50 m emission filter (Chroma, Bellows Falls, VT). For imaging, cells were grown on 18-mm-diameter coverglasses, mounted in a custom chamber with phosphate buffered saline containing 6 mM glucose and 1.1 mM sodium pyruvate, and maintained at 37°C by a Harvard Apparatus microincubator. Images were acquired using identical CCD settings in the central region (∼20 × 20 μm) of the CCD chip. Image processing, as described (22,26), was done to generate number histograms of background-subtracted, area-integrated fluorescence intensities from fluorescent spots. Intensities were referenced to monomeric recombinant GFP.

NMO-IgG binding to AQP4

Binding of a monoclonal recombinant antibody (rAb-53, (21,27)) was measured to U87MG cells expressing M1 and M23 AQP4 at specified molar ratios using a quantitative ratio imaging method as described (28,29). Briefly, cells were incubated for 60 min with rAb-53 at 50 μg/ml, washed, permeabilized, and then incubated with an antibody against the common (to M1 and M23) AQP4 C-terminus. Using secondary antibodies r53-Ab was stained green and total AQP4 red. Measured green/red fluorescence ratio (background-subtracted) was taken as a quantitative measure of NMO-IgG binding to AQP4.

Mathematical Model

The mathematical model as diagrammed in Fig. 2 contains three components: tetramer generation; OAP generation; and OAP characterization. The model was programmed using MATLAB 7.0 (The MathWorks, Natick, MA), which facilitated matrix manipulations and image processing. For tetramer generation, the M1 versus M23 identities of each of the four monomers/tetramer were determined randomly from specified M23:M1 molar ratio, using a random number from 0 to 1 with threshold specified from the M23:M1 ratio. AQP4 tetramers were generated serially, generally >10,000/computation, to give robust predictions that were insensitive to a generation of more tetramers (typical error <1%).

Figure 2.

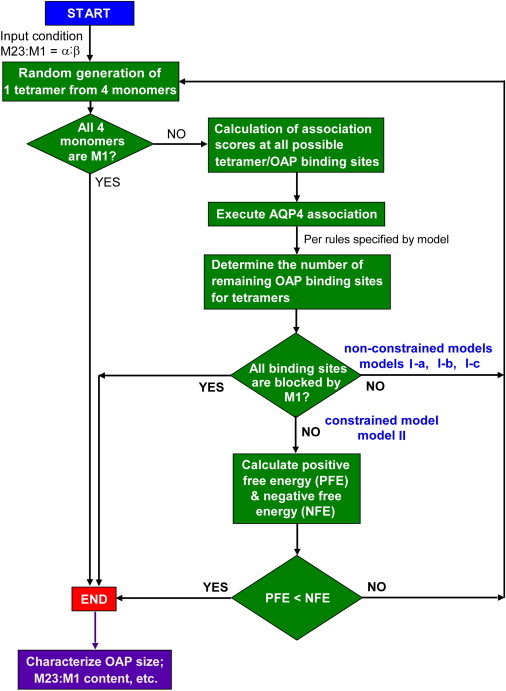
Schematic of modeling approach. See Mathematical Model section for description.

Matrix operations were done for OAP generation to associate newly generated tetramers to a nascent OAP. M23 and M1 are represented by numbers 1 and 0, respectively, according to the association rule that only M23-M23 interaction can occur. Each tetramer is represented by a 2 × 2 matrix (for example, tetramer with three M23 and one M1 is described by the 2 × 2 matrix, T = [1 1; 1 0]. The tetramer can be rotated at the binding site, with tetramer rotation expressed by rot90(T, k) (k = 0, 1, 2, and 3, respectively, for 0, 90, 180, and 270 degree rotations). If a newly generated tetramer is composed of pure M1, then the tetramer is counted as an OAP of unity size and another tetramer is generated. A nascent OAP, containing many AQP4 tetramers is represented by an N × N matrix, with each potential binding site at the periphery of the OAP by a 2 × 2 matrix. At each tetramer-OAP association step, an association score at each binding site was computed by multiplication of the tetramer and binding site matrices. Additional details are provided in the Supporting Material.

In the first-generation nonconstrained models, tetramer generation and tetramer-OAP association was repeated until all OAP binding sites were occupied. In model I-a (optimal-association model), the site of tetramer association was determined by maximum association score (valency). In model I-b (random-association model), the binding site was selected randomly without regard to (nonzero) association score. In model I-c (self-association model), association was allowed only when tetramers contained one or three M23 monomers. In the second-generation constrained model OAP growth and completion was determined both by M1 blocking (as in the first-generation models) but also by a free energy constraint. Positive free energy (PSE) was computed as the total number of M23-M23 associations, and negative free energy (NFE) was computed semiempirically to reproduce experimentally measured OAP sizes (described below, see Fig. 5 A). The free energy constraint was applied at each tetramer addition step, allowing tetramer-OAP association when PFE < NFE. OAP completion occurs when all the binding sites are blocked by M1 or when PFE < NFE, even if all binding sites are not blocked by M1.

Figure 5.

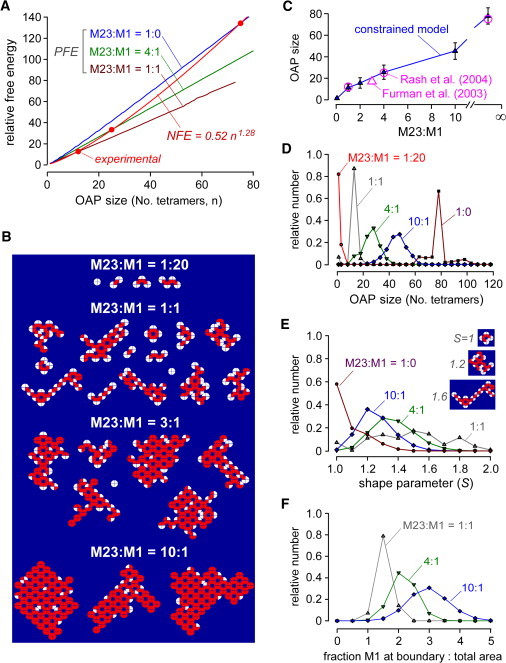
Second-generation, free energy-constrained OAP model. (A) Free energy versus OAP size relation. Positive free energy (M23-M23 interactions/OAP) as a function of OAP size computed for indicated M23:M1. Empirically determined negative free energy (red), which constrains OAP size. (B) Gallery of OAPs generated by the model at indicated M23:M1 ratio. (C) Computed average OAP size (mean ± SD) as a function of M23:M1 ratio for the second-generation model (solid triangles), shown with experimental data (open circles and triangle). (D–F) Number histograms of the distribution of OAP size (D), shape (E), and boundary composition (F) at indicated M23:M1 ratios. OAP size quantified as number of tetramers; OAP shape as the ratio of monomers at the periphery to the square root of the total number of monomers (examples of OAPs with different shaped parameters shown in panel E, right); and content as the fraction M1 at the boundary to the fraction M1 throughout the OAP.

Results

Our model assumes random association of M1 and M23 AQP4 monomers in homotetramers or heterotetramers (Fig. 1 A) and that intermolecular M23-M23 associations promote OAP formation, whereas intermolecular M1-M23 and M1-M1 interactions are insignificant. As such, increased M1 relative to M23 reduces mean OAP size as depicted in Fig. 1 B. As summarized in Fig. 2, the modeling computation involved serial generation of a large number of AQP4 tetramers whose composition was determined by random numbers in which the specified molar M23:M1 ratio was applied using threshold conditions. Newly generated tetramers were rotated and translated to select a suitable site for binding to a nascent OAP (Movie S1). If the OAP is unable to accommodate additional AQP4 tetramers it was considered completed, and analyzed for size, shape, and total/peripheral M23:M1 content. The AQP4 tetramers/OAP generation process was continued to specified statistical endpoints.

General features of the model were explored from initial computations done with the minimal assumptions of random heterotetrameric M1 and M23 AQP4 association and energetically optimal AQP4 tetramer binding to nascent OAPs (binding prioritization dictated by valency) (model I-a). Fig. 3 A shows a gallery of generated OAPs at an M23:M1 ratio of 1:1. Generally, OAPs consisted of a M23-rich core with M1 monomers decorating the periphery, which limits OAP size by preventing further binding of AQP4 tetramers. Individual AQP4 tetramers containing four M1 monomers (OAP size = 1) were generated as well. There was considerable heterogeneity in OAP size and shape at fixed M23:M1, which has been seen for OAPs in cell membrane by freeze-fracture electron microscopy (FFEM) (19,20). OAPs with internal defects (holes) were also occasionally generated by the model (Fig. 3 A, bottom right), resembling those seen in published freeze-fracture electron micrographs (19,20,30,31). Increased M23:M1 ratio predicts OAPs of larger size, with one example of a very large OAP shown in Fig. 3 A (bottom right). Fig. 3 B shows number histograms of OAP size, as quantified by the number of tetramers per OAP, at different M23:M1 ratios. Increased M23:M1 ratio produced OAPs of greater average size, with considerable size heterogeneity seen at intermediate M23:M1 ratios. Fig. 3 C shows number histograms of OAP composition, quantified as the fraction of M23 monomers (to total AQP4 monomers) in each OAP. Increased M23:M1 produced OAPs with increased average M23 content, as expected, and with considerable heterogeneity in M23 content, particularly at a low M23:M1 ratio. As reported below, these general features of the model were robust, insensitive to model details, and verified experimentally.

Figure 3.

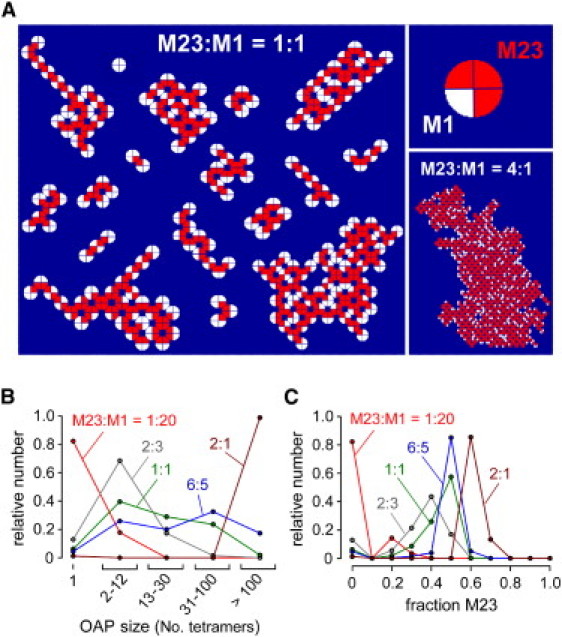
Predictions of first-generation OAP model. The model assumes random M1 and M23 association in heterotetramers, and monovalent intertetrameric M23-M23 interactions. (A) Gallery of OAPs generated for 1:1 M23:M1 molar ratio (left). Example of heterotetramer (top right), and of very large OAP for 4:1 M23:M1 ratio (bottom right). (B and C) Number histograms of the distribution of OAP size (B) and content (fraction M23) (C) at indicated M23:M1. There were>10,000 tetramers generated/condition.

Fig. 4 A summarizes the average OAP size as predicted for the first-generation model above (solid circles). OAP size increased remarkably with an increasing M23:M1 ratio. Some OAPs grow without bound at M23:M1 > 1:1, and >90% of OAPs grow without bound at M23:M1 > 2:1. Unrestricted OAP growth at high M23:M1 is not the case in reality, with experimentally measured average OAP sizes deduced from FFEM (19,30) shown in Fig. 4 A.

Figure 4.

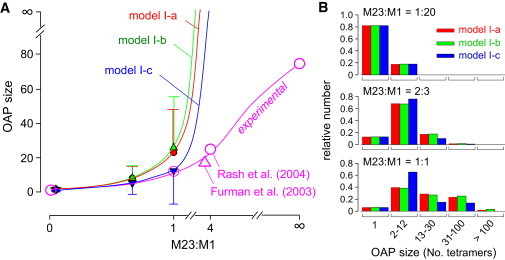
OAP size predictions of first-generation non-constrained models. (A) Average OAP size (number of AQP4 tetramers/OAP) as a function of the M23:M1 ratio for three variations (a-c) of nonconstrained first-generation models (mean ± SD). Open circles and triangle are from published freeze-fracture electron micrographs (19,30). (B) Number histograms of the distribution of OAP size for models I-a, I-b, and I-c at M23:M1 ratios of 1:20, 2:3, and 1:1.

Several variations of the first-generation model were implemented to investigate the sensitivity of model predictions to the rules of tetramer association and to attempt to reproduce experimentally measured OAP size at high M23:M1. In one variation of the first-generation model (model I-b, random-association model), the assumption of energetically optimal AQP4 tetramer binding to nascent OAPs was relaxed so that generated AQP4 tetramers bind at random on the OAP (nonenergetically optimized). Predictions of model I-b for M23:M1-dependent average OAP size (Fig. 4 A) and size distribution (Fig. 4 B) were very similar to those of model I-a (optimal-association model). In another model variation (model I-c, self-association model), AQP4 tetramer association was allowed only when tetramers contained one or three M23 monomers, reasoning that intertetrameric M23-M23 associations might be prevented for two M23 monomers in a tetramer if an intratetrameric association occurs. Though model I-c mildly reduced OAP size (Fig. 4, A and B), it was also unable to reproduce experimentally measured OAP sizes. In each of the three variations of the nonconstrained model, the general model predictions, including greatly increased OAP size with increasing M23:M1 ratio and preferential localization of M1 to the OAP periphery, were insensitive to the details of model assumptions. Similar findings were obtained with other model I variations, including inclusion of repulsive M1-M1 and/or M1-M23 interactions (not shown).

A second-generation model was developed in which a free energy constraint was applied to reproduce experimentally measured M23:M1-dependent OAP sizes. There are multiple determinants of OAP free energy that are not considered in the first-generation models, which are likely to be involved in limiting OAP size at a fixed M23:M1 ratio. For example, though the addition of one AQP4 tetramer to a nascent OAP is energetically favorable because of M23-M23 interaction(s), it is entropically unfavorable because of reduced translational and rotational freedom of the enlarged OAP compared to the original OAP and the free AQP4 tetramer. In addition, there are energetic barriers, such as membrane curvature, that limit OAPs size, as well as membrane crowding effects, and AQP4-lipid and AQP4-(non-AQP4) protein interactions. Because these factors cannot be quantified, we lump them together as a single negative free energy parameter.

A semiempirical approach was used to apply free energy constraints in the second-generation OAP model. As shown in Fig. 5 A, PFE was computed as the number of M23-M23 interactions/OAP, which increases with OAP size and M23:M1 ratio. NFE was taken as a curvilinear (2-parameter power law) function of OAP size as constrained by experimentally measured OAP sizes. The free energy constraint was applied as a decision point after each AQP4 tetramer binding event in a growing OAP, in which further OAP growth was allowed only for PFE > NFE (Fig. 2). Fig. 5 B shows representative OAPs generated using the second-generation model. The OAPs were smaller than those in first-generation models, but preserved the general features of M23:M1 ratio-dependent OAP size, composition, and peripheral M1 localization. Fig. 5 C shows that the predicted average OAP sizes determined using the empirically derived NFE function agreed with experimental data.

Fig. 5, D–F shows number histograms of OAP size, shape, and peripheral OAP composition for different M23:M1 ratios. Average OAP size, as well as OAP size heterogeneity, increased with M23:M1 ratio (Fig. 5 D). OAP shape was quantified by a shape parameter that was computed as the ratio of monomers at the periphery to the square root of the total number of monomers in total area. An S-value of unity indicates a square array, with S > 1 signifying more elongated and complex arrays as depicted in Fig. 5 E (right). OAPs were generally more elongated with a reduced M23:M1 ratio. Peripheral OAP composition, expressed as the fraction M1 at the boundary to that in the total OAP, shows reduced M1 fraction at the boundary with greater M23:M1 ratio, which is a consequence of the NFE constraint that limits OAP size independent of peripheral M1 accumulation.

Key predictions of the model were tested experimentally by biophysical and biochemical measurements on cells expressing AQP4 at defined M23:M1 ratios. The size of AQP4 aggregates, representing OAPs, and the M1/M23 spatial distribution were determined by total internal reflection fluorescence microscopy in cells expressing GFP-AQP4 chimeras. In one set of experiments cells were transfected with GFP-M1 and GFP-M23 AQP4 at different ratios under conditions of low expression to enable visualization of individual fluorescent spots, each representing a single AQP4 aggregate or tetramer. AQP4 aggregate size was deduced from spot-integrated fluorescence intensities referenced to GFP standards, as done previously (22,26). Fig. 6 A shows total internal reflection fluorescence microscopy images (top) and number histograms (bottom) of (background-subtracted) single spot fluorescence in U87MG cells expressing GFP-M23 and GFP-M1 at specified ratios. The number histogram showed ∼4-fold greater intensity of individual M1 tetramers than monomeric GFP, as expected. Higher spot fluorescence intensities, corresponding to larger AQP4 aggregates (OAPs), were seen at greater M23:M1 ratios, with considerable heterogeneity seen at all ratios.

Figure 6.

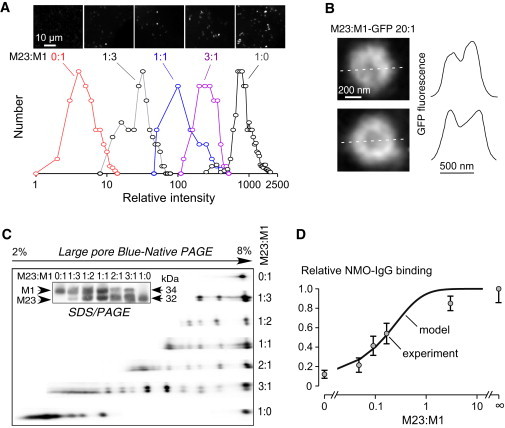
Experimental measurements of OAP properties and NMO-IgG/AQP4 binding. (A) U87MG cells were transfected with GFP-M23 and GFP-M1 AQP4 at indicated ratios. Representative TIRF micrographs show fluorescent spot (top). Deduced number histograms of single spot fluorescence (background-subtracted, area-integrated intensities), proportional to AQP4 aggregate (OAP) size, shown at the bottom. Unity represents the intensity of monomeric GFP. (B) U87MG cells were transfected with (untagged) M23 AQP4 and GFP-M1 AQP4 and at a ratio of 20:1. Representative TIFR micrographs of large AQP4 aggregate (left) show relative concentration of fluorescence at the periphery. Line profiles (dashed white lines at the left) shown at the right. (C) AQP4 immunoblot after SDS/PAGE (inset) and BN-SDS/PAGE of lysates from U87MG cells expressing (untagged) M1 and M23 AQP4 at indicated ratios. (D) NMO-IgG binding to AQP4 OAPs. U87MG cells expressing M1 and M23 AQP4 (both untagged) were stained with NMO-IgG (recombinant monoclonal antibody rAb-53(28)) and anti-AQP4 antibody as described under Experimental Procedures section. Relative binding (normalized to unity at M23:M1 = ∞) measured by quantitative ratio imaging (SE n = 4) shown along with model-predicted curve: relative binding = 0.14 + 0.86 [1-(1+α)^-4], where α is the M23:M1 ratio; [1-(1+α)^-4] is the probability that an AQP4 monomer is OAP-associated.

In a second set of experiments cells were transfected with GFP-M1 and (untagged) M23 AQP4 to visualize the spatial distribution of M1 AQP4. Experiments were done at high M23:M1 to generate large OAPs of size greater than the TIRF x,y-resolution (diffraction limit). Fig. 6 B (left) shows high magnification TIRF micrographs of two large AQP4 aggregates in which GFP-M1 fluorescence was greater at the periphery than at the center, as confirmed by line scans (Fig. 6 B, right).

The composition of AQP4 aggregates was assessed by 2-dimensional blue native (BN)-SDS/PAGE and immunoblot analysis in which M23 and M1 AQP4 in aggregates of increasing relative sizes were visualized in the nondenaturing direction (from right to left), exploiting differences in molecular mass (in the denaturing direction) to identify M23 versus M1 AQP4 (Fig. 6 C). BN-PAGE is a semiquantitative biochemical method to infer the presence of AQP4 aggregates/OAPs (21,29,32). Because the membrane is solubilized and the details of the banding pattern depend on detergent conditions and dye binding properties, it is not possible to assign distinct aggregate sizes to the various bands or to make quantitative inferences about absolute M23:M1 content (24). Notwithstanding this limitation, however, the large pore BN-SDS/PAGE in Fig. 6 C shows that M1 did not form aggregates on its own, as evidenced by a single spot, and that coexpression of M23 with M1 produced multiple bands in the nondenaturing direction in which the number and relative molecular size of the spots increased with a greater M23:M1 ratio. The relative M23-to-M1 amount was greater in the bands corresponding to larger aggregates, as seen in the denaturing direction. SDS/PAGE (Fig. 6 C, inset) confirmed relative M23-to-M1 expression in cells transfected with different amounts of the M23 versus M1 plasmids.

The model was also applied to investigate the binding mechanism of a NMO autoantibody that recognizes 3-dimensional extracellular epitopes on AQP4. For these measurements we used a recombinant monoclonal antibody, rAb-53, that binds with greater affinity to OAP-assembled AQP4 than to AQP4 in individual tetramers, which is typical of NMO autoantibodies (28). The rAb-53 binding to AQP4 was measured by quantitative ratio imaging in cells expressing AQP4 at different M23:M1 ratios, in which antibody binding was normalized to total membrane AQP4 by ratio imaging fluorescence microscopy. Fig. 6 D shows increased rAb-53 binding to AQP4 with an increasing M23:M1 ratio, with 50% maximal effect at M23:M1 ∼ 0.2. The experimental data fitted well to the model curve based on the simple assumption that rAb-53 binds to (non-OAP-associated) M1 AQP4 tetramers with low affinity, and to OAPs with relatively high (OAP-size-independent) affinity.

Discussion

Our model of AQP4 OAP assembly served several purposes. First, as constrained by experimental data on OAP size as a function of AQP4 M23:M1 ratio, it established a minimum set of rules required to reproduce the major topographic and compositional features of OAPs in cell membranes. As such, the model provided insight into how the AQP4 N-terminus M23-M23 intermolecular interaction translates to assembly of OAPs, whose size, shape, and composition, and heterogeneity thereof, depend strongly on the relative proportion of M1 versus M23 AQP4. The model predicted key features of AQP4 OAPs with minimal inputs on heterotetramer composition, M23-M23 interaction, and OAP free energy. Notably, the model did not require the inclusion of AQP4 interactions with other components, such as membrane lipids or proteins, or soluble proteins, nor did it require ascribing an active role to M1 AQP4 in limiting OAP size. In addition to establishing AQP4 association rules and providing an explanation for experimental observations on OAPs, the model has clinical relevance to the human disease NMO, where anti-AQP4 autoantibodies produce neuroinflammation and neurological impairment by binding to AQP4-expressing astrocytes in spinal cord and optic nerve, and, to a lesser extent, in brain (8,10,33,34). The model was applied to investigate the mechanism by which NMO autoantibodies bind preferentially to M23 AQP4.

Our modeling approach involved the serial generation of random AQP4 tetramers that were appended to a nascent OAP by a matrix multiplication method in which all possible binding locations and tetramer rotational orientations were probed. AQP4 tetramers composed of four M1 monomers were considered as unable to associate into OAPs and were counted separately. An OAP was allowed to grow by serial tetramer acquisitions until all possible tetramer binding sites were occupied, or, in the constrained model, if further OAP growth caused negative free energy to exceed positive free energy. A completed OAP was then analyzed for size, shape, and compositional parameters, which were stored for subsequent number histogram generation and averaging. This serial tetramer/OAP generation approach required minimal memory, with computation time determined primarily by the random number generation and matrix multiplication operations. An alternative modeling approach would involve the generation of a large number of random tetramers and their parallel assembly into a minimum free energy state. Though such free-energy-based models could be useful for OAP modeling, they would be computationally prohibitive and require difficult-to-justify assumptions about parameters describing the energy and entropy of all possible M1 and M23 interactions.

With a minimal set of input rules, the major model predictions agreed with reported experimental data on OAPs and with new experimental data generated in this study. The inputs of the nonconstrained models included random M1/M23 association in heterotetramers and intertetrameric M23-M23 interaction but not M1-M23 or M1-M1 interaction. Though the nonconstrained models allowed unrestricted OAP growth at high M23:M1 ratios and thus could not quantitatively predict OAP size, the model accurately predicted the observations of increased OAP size with M23:M1 ratio, marked OAP size heterogeneity, OAP size-dependent M1/M23 composition, and preferential localization of M1 AQP4 at the periphery of OAPs. These predictions were insensitive to the details of the association rules in the nonconstrained models (optimal-association versus random-association versus self-association variations). The predictions were also insensitive to the application of a free energy constraint in the constrained model, which was required to prevent unrestricted OAP growth. TIRF microscopy of GFP-AQP4 chimeras and native gel electrophoresis were done on cells expressing different M23:M1 ratios to test key predictions of the model. In agreement with model predictions, the experimental data showed increased OAP size with increasing M23:M1 ratio, considerable OAP size heterogeneity at a fixed M23:M1 ratio, increased M23 versus M1 in larger OAPs, and preferential peripheral localization of M1 AQP4. The model also predicted occasional defects in OAPs, in agreement with freeze-fracture electron micrographs.

Notwithstanding the simplicity of the model and its demonstrated predictive value, there are a number of caveats and potential limitations. i), As described below, an empirically deduced negative free energy term was required to limit OAP size. ii), As a non-energy-based thermodynamic model, as mentioned above, the model does not allow for rearrangements in OAP geometry, as could occur spontaneously (22) or in response to regulatory factors (21) or changes in M23 versus M1 expression (31). However, if such changes are slow on the time-scale of AQP4 cellular turnover then the present model would be applicable. iii), The model does not account for the possibility of small M1-only arrays, which have been occasionally seen by FFEM in M1 AQP4-transfected cells (19,30,31). Such incipient arrays are small in number compared to non-OAP-associated M1 tetramers, and hence would be difficult to model without inclusion of many additional assumptions. Furthermore, experimental evidence is lacking that these apparent small arrays are composed exclusively of M1 AQP4. iv), The model assumes heterotetrameric M1 and M23 association, which is supported by experimental data from our laboratory (21,22). An alternative possibility is that separate M1 and M23 homotetramers associate as hetero-hexadecimers. It is noted that the model here, up to a size-scale factor, is formally equivalent for M1/M23 heterotetramers and homotetramer hetero-hexadecimers.

The constrained model required the generation of an empirical negative free energy function to recapitulate experimentally measured OAP sizes at different M23:M1 ratios. The idea is based on the second law of thermodynamics, in which tetramer-OAP association results in entropy loss, which must be balanced by a gain in free energy to favor association. The positive (association) free energy was determined by counting the number of N-terminus interactions. However, theoretical quantification of the negative free energy is not feasible. The entropy of assembly contains translational, rotational, vibrational, and conformational components (35). In previous reports on entropy loss during macromolecular assembly, entropy loss depends on multiple parameters, including its root mean-squared amplitude (36), molecular weight (37), and free volume (35,38), producing a total entropy loss that increases in an approximately linear manner with the number of molecules in an aggregate. For OAPs in biological membranes, in addition to entropic contributions, the negative free energy contains contributions of membrane curvature, which is unfavorable to assembly of large OAPs, as well as membrane crowding and AQP4 interactions with various other cellular proteins and lipids. Our modeling approach lumped together these ill-defined factors into an empirically derived negative free energy function.

The model was also applied to investigate the differential binding of NMO-IgG to M1 versus M23 AQP4. Several labs have shown increased binding of NMO-IgG in NMO patient serum to M23 versus M1 AQP4 (21,39,40). We recently reported that introduction of an OAP-disrupting mutation in M23 AQP4, which prevented OAP assembly, abolished the enhanced NMO-IgG binding to M23 versus M1 AQP4 (28). Taken together with data showing that Fab fragments generated from recombinant purified NMO-IgG retained the difference in M23 versus M1 binding, we proposed that OAP assembly by AQP4 alters the NMO-IgG binding epitope(s) so as to increase binding affinity. Here, we compared model predictions to quantitative measurements of NMO-IgG binding to cells expressing AQP4 at a wide range of M23:M1 ratios. Fifty percent enhancement of NMO-IgG binding was found at M23:M1 ∼ 0.2, with maximal enhancement of ∼6-fold at M23:M1 of 1:0. Model predictions were in excellent agreement with experimental data, providing quantitative support for our conclusion about the AQP4 isoform-specific determinants of NMO-IgG binding (28).

In conclusion, the relatively simple model of AQP4 association reported here recapitulated the major experimental observations on OAP assembly. As more refined experimental data become available on OAP size, shape, and composition in live cells, perhaps by super-resolution imaging methods, additional predictions of the model can be tested and the model further refined. In addition to its value in understanding the rules and determinants of AQP4 OAP assembly, the model has utility, as demonstrated in the one example here, in quantitative analysis of NMO-IgG binding to AQP4 OAPs in the human neurological disease, NMO.