Abstract
The effect of an inert small molecule osmolyte, trimethyl amine N-oxide (TMAO), upon the conformational equilibria of Escherichia coli adenylate kinase was studied using time-resolved FRET. The relative populations of open and closed clefts between the LID and the CORE domains were measured as functions of the concentrations of the substrate ATP over the concentration range 0–18 mM and TMAO over the concentration range 0–4 M. A model was constructed according to which the enzyme exists in equilibrium among four conformational states, corresponding to combinations of open and closed conformations of the LID-CORE and AMP-CORE clefts. ATP is assumed to bind only to those conformations with the closed LID-CORE cleft, and TMAO is assumed to be differentially excluded as a hard spherical particle from each of the four conformations in accordance with calculations based upon x-ray crystallographic structures. This model was found to describe quantitatively the dependence of the fraction of the closed LID-CORE cleft upon the concentrations of both ATP and TMAO over the entire range of concentrations with just five undetermined parameters.
Introduction
In recent years, it has become increasingly appreciated that nonspecific interactions between macromolecules in solution mixtures containing a high total concentration of macromolecules (macromolecularly crowded solutions) can significantly modulate the stability, conformation, and tendency to self- and/or hetero-associate for dilute as well as concentrated macromolecules in such solutions (1–4). In general, the most significant of these nonspecific interactions is steric repulsion or volume exclusion, which, in crowded solutions, has been described as being as ubiquitous as gravity (5). Volume exclusion leads to a size- and shape-dependent reduction in the configurational entropy, and hence an increase in the chemical potential of all species present that can be quite substantial at high total macrosolute concentration (1,6). One prediction of excluded volume theory is that high concentrations of inert macromolecules should stabilize the compact native state of a globular protein with respect to denaturation by heat or chaotropes (7), and such stabilization has been observed experimentally (8–11).
Concurrently, it has been observed that high concentrations of trimethylamine oxide (TMAO), a relatively small (MW 75), highly soluble, and nominally inert cosolute, can greatly stabilize the native conformation of a variety of proteins with respect to unfolding (12,13). Exhaustive thermodynamic analysis of this phenomenon has led to the conclusion that this stabilization may be primarily attributed to an unfavorable interaction between TMAO and the protein backbone (12,14). The parallelism between the results of this analysis and the analysis of protein stabilization resulting from macromolecular crowding suggests that stabilization of proteins by TMAO and by inert macromolecules may be due to the same type of nonspecific interaction, namely volume exclusion.
Many years ago, it was predicted based on simplified statistical-thermodynamic models for volume exclusion that high concentrations of space-filling cosolutes could alter the equilibrium between alternate conformations of a dilute macromolecule (1). This prediction has been recently quantified through atomistic Brownian dynamics simulations (11,15), and experimental observation of significant modulation of functionally significant native-state conformational equilibria of two proteins upon addition of high concentrations of nominally inert polymers has likewise been recently reported (11,16). It was therefore decided to test the hypothesis that functionally significant native-state conformational equilibria of a protein could be modulated by the addition of high concentrations of TMAO, and that such modulation could be accounted for in the context of excluded volume theory.
This prediction may be tested by studying the crowding effect on the distributions of conformational characteristics of ensembles of flexible protein molecules such as phosphotransferase molecules in solution (17). The structural flexibility of enzymes and its role in their function (18,19), which is most evident in the case of transferases, is well documented. To avoid abortive hydrolysis and to facilitate transfer of charged groups, transferases must undergo structural changes to screen the active center from water in the substrate-bound state (20–25). The observed structural changes involve domain displacements and result in the closure (or partial closure) of the enzyme interdomain cleft. Convincing supporting evidence for substrate-induced domain closure in solution was obtained from studies of substrate-induced structural changes of several enzymes by diffuse x-ray scattering (26,27).
Escherichia coli adenylate kinase (AK), catalyzing the phosphoryl transfer reaction MgATP + AMP ⇆ MgADP + ADP (28), is a suitable model for studying the effect of crowding on ensembles of flexible protein molecules in solution. The transition from apo-AK to the ternary complex is associated with a stepwise closure of the enzyme interdomain clefts. This interpretation was strongly supported by a series of crystal structure analyses of enzyme-substrate complexes (Fig. 1) (23,29,30). The stepwise closure of the interdomain clefts in AK associated with substrate binding in solution was shown using time-resolved resonance excitation energy transfer (trFRET)-based methods (31,32). The means of the distributions of the labeled AK both in the ligand free state and in the ternary complex were found to be close to the distances predicted from the corresponding crystal structures (30,33) but there is a significant overlap of the distributions of the interdomain distance observed for the two states of the protein. Single-molecule-detected FRET experiments confirmed the existence of this equilibrium and gave an upper-limit estimation for the rates of exchange between conformations (34–36). The intrinsic dynamics of the ligand free AK revealed by single-molecule detection experiments (37), the width of the distributions, and the low angle x-ray scattering results, led to the hypothesis that the crowding effect might shift the equilibrium toward the closed conformers.
Figure 1.
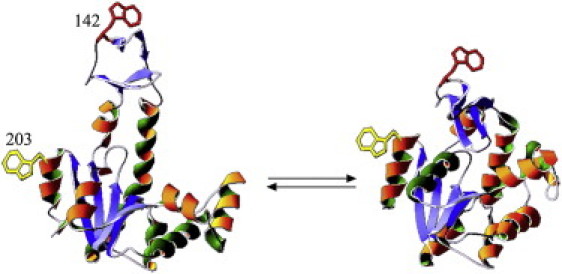
Crystal structures of E. coli AK in the ligand free state (PDB 4AKE) (left) and when bound to the two substrate mimicking inhibitor Ap5A (PDB 1AKE). The labeled sites are indicated both in 203 and in 142 by an indole side chain.
trFRET experiments (38–40), in either the ensemble or the single-molecule approach, can resolve subpopulations whose exchange rate is slower than the nanosecond regime. The mean and width of the distance distributions that characterize conformational subpopulations can be resolved (41–43). We have measured the distribution of distances between residue 142 on the LID domain and residue 203 on the CORE domain over a wide range of concentrations of both the substrate ATP and the crowding agent TMAO. Our results indicate that the binding of ATP and the volume excluded by high concentrations of TMAO act synergistically to shift conformational equilibria toward more compact conformers.
Materials and Methods
Preparation and characterization of labeled AK mutants
Selection of labeling sites was based on the crystal structures of apo- and holo-AK (Fig. 1), which show a large change of mean distance between the two end states. The LID domain was labeled with a donor probe at residue 142, a tryptophan residue, and the CORE domain was labeled at residue 203 by replacement with a Cys residue and reaction with iodo-acetamidocoumarin-4-carboxylic acid (44). Positions of these labels are indicated in Fig. 1. A mutant labeled by the donor without the acceptor was prepared by reaction of the cysteine residue with iodoacetamide. This formed a pair of labeled proteins, i.e., the donor-acceptor (DA) and the donor-only (DO) mutants, respectively. Each mutant and preparation was purified by chromatography (see Fig. S1 in the Supporting Material). The absorption and emission parameters of the probes attached to the protein are reported in Table S1 in the Supporting Material. The two modified residues are solvent-exposed, and several control experiments (Table S2) demonstrated that the genetic and chemical modifications had only a minor effect on the structural characteristics of the protein and its enzymatic activity (Table S1).
Control experiments
The far-ultraviolet circular-dichroism spectra and thermal stability of each mutant were monitored (Fig. S2). The enzymatic activity of a series of labeled mutants was determined (Table S2) and these tests showed that the labeling treatment of the AK molecule at this pair of exposed residues did not cause any significant change of the structural characteristics tested. Spectroscopic experiments were repeated using the reverse labeled mutant, where the Trp residue was inserted at position 203 and the Cys residue inserted at position 142 to exclude possible effects of local interactions of the probes with the backbone of neighboring side chains (Table S2). The distance distribution parameters obtained by analysis of the fluorescence decay curves of the reverse mutant (donor at residue 203) were within the uncertainty range of the results obtained by analysis of the decay curves obtained for the mutant with the donor labeled at residue 142.
Steady-state anisotropy values measured for single-labeled mutants (Table S2) support FRET data analysis based on the assumption of fast averaging of probe orientation (39,45).
Results and Analysis
Time-resolved FRET experiments
The data collected in typical trFRET experiments are shown in Fig. 2. The reduction of donor fluorescence lifetime in the presence of acceptor is much more pronounced when substrate is bound (closed conformation, Fig. 2 B) than when substrate is absent (open conformation, Fig. 2 A), due to more efficient energy transfer associated with a shorter donor-acceptor distance. Joint analysis of the decay curves of the donor-acceptor (DA) mutant, AK(203W, 142Cca) and the donor-only (DO) mutant, AK(203W, 142IAA) using the skewed Gaussian distance distribution model (38) yielded results shown in Fig. 3. In this figure are plotted the distributions of the distance between residues 142 and 203 in double-labeled apoAK (open conformation), and AK saturated with ATP and bis(adenosine)-5-pentaphosphate (Ap5A) (closed conformations). In apoAK, the mean of the distance distribution was 31.7 ± 1 Ǻ and its full width at half-maximum (FWHM) was 11.5 ± 2 Ǻ. The width of the distance distributions is a measure of the conformational variability of the AK molecule with respect to the interdomain distance.
Figure 2.
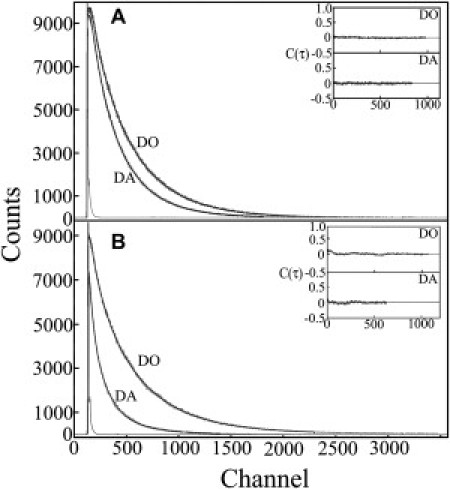
Typical experimental decay curves of the donor in the presence (DA) and absence (DO) of an acceptor in apoAK [no ligand = open conformation] (A) and in holoAK [saturating concentration of Ap5A = closed conformation] (B), measured at 25°C in 50 mM Tris buffer pH 7.8. Each pair of decay curves was fit in a joint analysis to a distance distribution model. (Insets) Autocorrelation of the residuals from each model fit.
Figure 3.
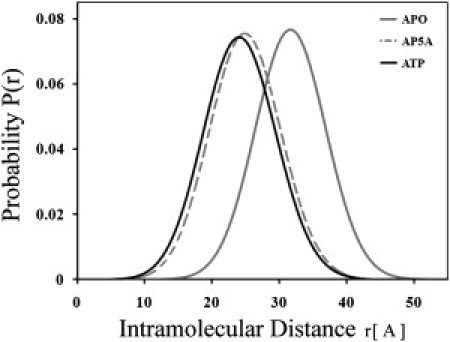
Distribution of donor-acceptor distances obtained by global modeling of fluorescence decay curves. The interprobe distance distribution in AK(142W, 203Cca) in the absence of TMAO at room temperature was determined under saturating concentrations of the inhibitor Ap5A and ATP as well as in the ligand free, apoAK. The shift of distribution toward smaller distances accompanying ligand binding, reflecting domain closure, and partial overlap of the distributions is shown.
Both ATP and the two-substrate mimicking inhibitor, Ap5A, induce a tighter closure of the gap between the domains. The domain closure involves a reduction of the mean interprobe distance from 31.7 ± 1 Ǻ to 24.8 ± 1 Ǻ. A significant overlap of the interdomain distance distributions of the AK molecule in the ligand free state (apoAK) and when saturated with high affinity inhibitor Ap5A (holoAK) (black and the gray-broken traces in Fig. 3) was observed. It is interesting to note that even under saturation of the enzyme molecules with the high affinity inhibitor, we did not find a significantly narrower distance distribution between the labeled sites. The observed FWHM is significantly larger than can be accounted for by the uncertainty in the position and orientation of the two probes. That means that the ensemble of the bound AK molecules maintains a degree of conformational variability. Using the present trFRET method, we did not detect nanosecond-domain closure motions in either the apo- or the holoAK ensembles.
The analysis of the decay curves obtained for the pair of mutants (DO and DA) under subsaturation concentrations of either ATP or Ap5A yielded distributions with intermediate (between apo and holoAK) mean distance and increased FWHM. That is a strong indication for the coexistence of the two ensembles, the apo- and the holoAK. The width of both the holo and apoAK was smaller than the width found for the partially saturating ATP concentrations and hence it was reasonable to assume that under those conditions two subpopulations coexist. Therefore, we reanalyzed the titration experiments by the global analysis approach using a model of two subpopulations of the distributions of the distance between the probes.
In this mode of analysis, the parameters of the distance distributions of the two subpopulations were globally bound (using the values obtained in the absence of TMAO with and without saturating concentrations, 20 mM, of ATP) and fixed for all experiments done under the series of TMAO and ATP concentrations. The parameter determining the populations' ratio was left free. The gradual transition between the open and closed ensembles during titration with ATP is shown in Fig. 4. The fraction of closed conformations exhibits a dependence upon the concentration of ATP resembling a simple binding isotherm, as will be discussed subsequently. In this analysis, the uncertainty in the values of the population ratio parameter depends on the uncertainty in the parameters of the distance distributions of the two subpopulations and in the global analysis described above. This uncertainty, which was evaluated by the procedure of rigorous analysis, was 5% or less.
Figure 4.
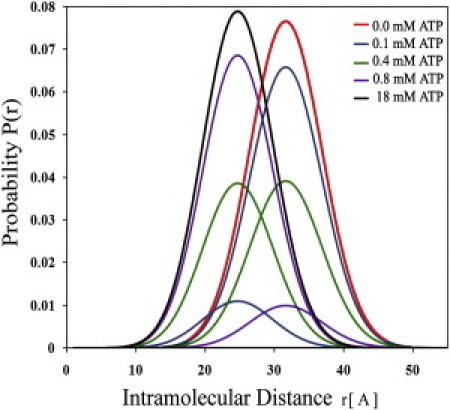
Distributions of donor-acceptor distance between residues 142 and 203 in AK in the presence of increasing concentrations of ATP. Analysis based on a two-subpopulation model is consistent with the hypothesis that in the absence of TMAO, ATP binding is both sufficient and necessary for domain closure.
Modulation of the conformational equilibrium by the crowding effect
We next turned to determination of the effect of high concentrations of TMAO on the ratio of the two populations representing the ensembles of the closed and the open conformers. The prediction based on a preliminary hard-sphere excluded-volume model was that only a small effect could be expected in the absence of ATP, and this prediction was subsequently verified (see below). However, in the presence of a subsaturating concentration of ATP (0.1 mM), the addition of TMAO resulted in a substantial shift from open to closed conformations (Fig. 5).
Figure 5.
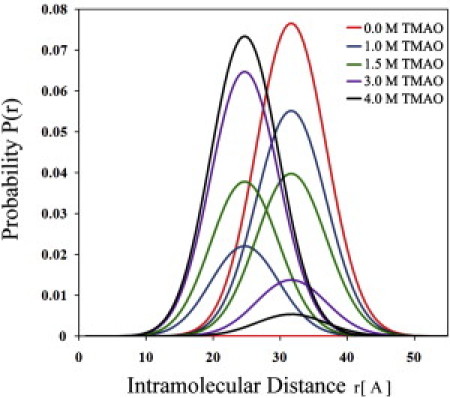
Distributions of donor-acceptor distance between residues 142 and 203 in AK in the presence of a fixed low concentration of ATP (0.1 mM) and varying TMAO concentrations. The population of closed conformations is seen to increase substantially with increasing TMAO concentration.
Therefore, a series of experiments was conducted in which the ratio of the two subpopulations of conformers of AK was determined as a function of the concentrations of both ATP (0–18 mM) and TMAO (0–4 M). The results of these experiments are summarized in Fig. 6 A, where the symbols indicate the fraction of states with closed LID-CORE cleft in the presence of various combinations of the concentrations of ligand L (ATP) and TMAO. Visual inspection of these results clearly indicates that at subsaturating concentrations of ATP, high concentrations of TMAO shift the conformational equilibrium toward closed conformations. These results were globally analyzed in the context of the four-conformational-state model described below.
Figure 6.
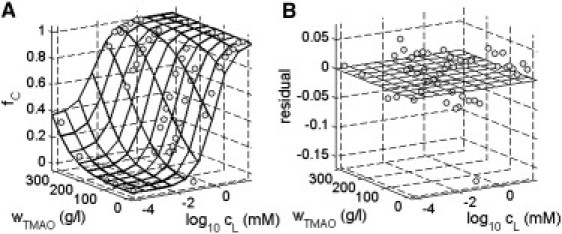
(A) Fraction of closed LID domain as a function of ATP and TMAO concentrations. (Symbols) Fraction derived from analysis of experimental data as described in text. (Surface) Calculated using Eqs. 4–11 with log K012 = −3.0, log K013 = −2.4, log K014 = −40, log KCL (M−1) = 5.6, and r = 3.0 Å. (B) fC (experimental) − fC (calculated) as a function of ATP and TMAO concentrations.
Analysis of the conformational shift using a four-state model
Although it is likely that AK exists in a large manifold of conformational states, for the sake of simplicity we group these into four conformational states that are expected to be most abundant under specified conditions:
-
1.
The fully open (apo) state.
-
2.
The fully closed (holo) state.
-
3.
A state with the LID domain closed and the AMP domain open.
-
4.
A state with the LID domain open and the AMP domain closed.
These four states are indicated schematically in Fig. 7. We assume that state 1 has the structure of the molecule with no ligand bound, state 2 has a structure similar or identical to the structure of AK with Ap5A bound, state 3 has a structure similar or identical to that of AK with ATP-only bound, and state 4 has a structure similar or identical to that of AK with AMP-only bound. It is further assumed, as suggested by the results shown in Fig. 3, that states 2 and 3 have essentially the same structure at the ATP binding site and therefore equal affinity for binding of ATP (here denoted by L for ligand). State 4, which has an open LID domain, is assumed not to bind ATP.
Figure 7.
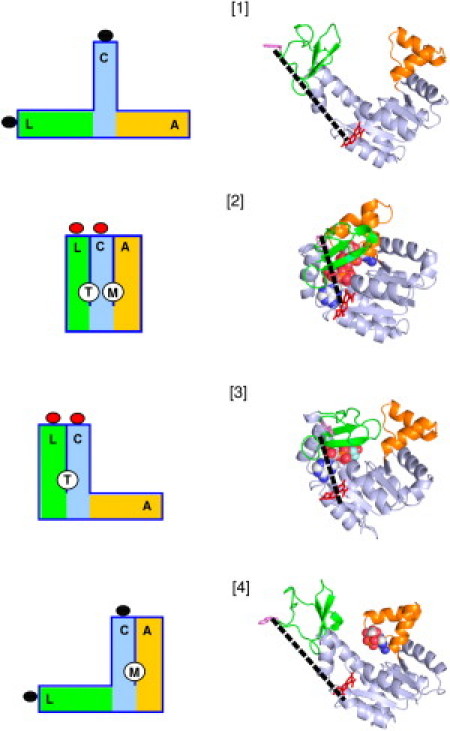
Schematic diagrams and structural cartoons of the four conformational states specified in the model described in the text. In the schematic diagrams, L (green), C (cyan), and A (orange), respectively, designate the LID, CORE, and AMP domains. T and M designate the ATP and AMP binding sites created upon closure of the LID and AMP domains, respectively. The lobes attached to the ends of the L and C domains represent donor and acceptor fluorophores attached to residues 142 and 203, respectively, and the change in color represents the presence of FRET upon closure of the LID domain. For the structural cartoons, the individual domains are colored as in the diagrams. (Dashed lines) Distance between donor and acceptor fluorophores in each structure.
Conformational and ligand binding equilibria within this scheme are defined as
| (1) |
| (2) |
| (3) |
where the conformational states indicated in curly brackets are those with a closed LID domain (closed states), Kij denotes the equilibrium constant for isomerization between conformational states i and j, cL the molar concentration of ligand L, and KCL the equilibrium constant for binding of ligand L to a closed state.
According to the model specified above, the equilibrium fraction of states with closed LID domain is given by
| (4) |
where
TMAO is assumed to influence the conformational equilibria between state 1 and the other three states (unliganded and/or unliganded) by virtue of differential volume exclusion,
| (5) |
where K01i denotes the value of the equilibrium constant K1i in the absence of added TMAO, and γi the TMAO-dependent activity coefficient of conformational state i. According to first-order excluded volume theory (46),
| (6) |
where Vi,TMAO denotes the volume excluded by a molecule of conformational state i to a molecule of TMAO, and ρTMAO denotes the number density of TMAO molecules, in units of inverse volume. It follows from Eqs. 5 and 6 that
| (7) |
where
The volume excluded by each conformational state to a spherical cosolute is estimated as follows. Crystal structures of all four of the presumed conformations have been published, but a full set of structures from the same species is not available. For conformational states 1 and 2, crystal structures of the E. coli AK in the open apo conformation (Protein DataBank entry 4AKE) and with bis(adenosine)-5-pentaphosphate bound (1AKE) were used for excluded volume calculations. For the other two states, homology models of the E. coli enzyme were built using structures of enzymes from other species. Protein Data Bank (PDB) entry 1DVR (a crystal structure of yeast AK with an ATP analog bound) was used as the template for the model of conformational state 3, and 2AK3 (bovine mitochondrial AK with AMP bound) was used as the template for conformational state 4.
For each model, the three-dimensional structure of the E. coli apo-enzyme (4AKE) was superimposed on the template structure using the align function of the program PyMOL (47), which implements a simultaneous sequence alignment and structural superposition. The resulting sequence alignments were then used in building homology models, which included the nucleotides bound to the template structures, with the program MODELER (48) using the standard parameter and topology files.
The volume excluded to a spherical molecule by a protein structure, the covolume, was calculated using a grid search algorithm. An evenly-spaced cubic grid was first constructed around the protein atomic coordinates. A probe sphere with radius rp was placed at each grid position, and the atomic coordinates were searched to identify any atoms lying within distance rp − ratom, where ratom is the atomic radius. The volume occupied by protein hydrogen atoms was accounted for implicitly by using the group atomic radii of Chothia (49).
Grid points for which any atom lay within this distance from the probe were counted as occupied, and the total excluded volume was calculated by multiplying the number of occupied points by the volume of a single grid element. Trial calculations demonstrated that the calculated volumes were independent of the grid spacing (to <∼1%), provided that the spacing was no more than one-half of the probe radius. Accordingly, a grid spacing of 1 Å was used for probe radii from 2–5 Å, and the spacing was 5 Å for probe radii from 10–50 Å. Results of this calculation are presented in Table S1.
Values of ΔV12, ΔV13, and ΔV14 in units of Å3, calculated from values given in Table S1, are plotted in Fig. S3 as functions of r ≤ 5 Å together with the respective best-fit quadratic fitting functions given below, assuming that ΔV1i goes to zero as r goes to zero (i.e., actual volume of protein in vacuo independent of conformational state),
| (8) |
| (9) |
| (10) |
Because ΔV1i is specified in units of Å3, it follows that the number density of TMAO molecules (MW = 75) is given by
| (11) |
where denotes the w/v concentration of TMAO in g/L.
It follows from the model specified above that fC, the fraction of conformational states with closed LID domain, may be calculated as a function of the molar concentration of ATP (denoted by cL) and the w/v concentration of TMAO (wTMAO) using Eqs. 4–11 together with specified values of and r. We have utilized the method of nonlinear least-squares minimization to globally fit this set of equations to the results of our entire collection of measurements of fC in the presence of varying concentrations of ATP and TMAO, representing a total of 48 independently conducted experiments. In Fig. 6 A, the dependence of fC upon the concentrations of ATP (L) and TMAO calculated according to Eqs. 4–11 using the best-fit parameter values given in the figure caption are plotted together with the combined data. The agreement between data and calculated best fit may be best observed by rotating the figure around the z axis (see Fig. S6).
The residuals, or difference between observed and best-fit calculated values of fC, are plotted as a function of ATP and TMAO concentration in Fig. 6 B. It may be seen that the four-state model described above, with a single set of parameters, can describe the dependence of fC upon both the ATP concentration over a range of 0–18 mM and the TMAO concentration over a range of 0–300 g/L with an average accuracy of or better than ±3%. According to this model, the abundance of conformational state 4, with open LID domain and closed AMP domain, is negligible under the conditions of the present experiments, in which the ligand ATP binds only to a site in the closed LID domain. The four-conformational-state model therefore reduces to a three-conformational state model in the present instance. However, conformation 4 would be expected to occur in significant abundance in the presence of AMP, Ap5A, or any other ligand that can bind to the second nucleotide binding site created upon closure of the AMP domain. This prediction may be tested directly using appropriately labeled mutants.
Given the best-fit parameters of the model, the fractional saturation of the enzyme with ATP may be calculated as a function of the concentrations of ATP and TMAO according to
| (12) |
In Fig. 8, fsat is plotted as a function of log [ATP] for four concentrations of TMAO. The affinity of AK for ATP is observed to increase by a factor of ∼4 upon addition of each increment of 100 g/L TMAO, amounting to an ∼60-fold increase in affinity at the highest concentrations of TMAO utilized in this study.
Figure 8.
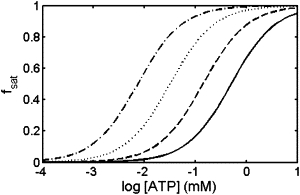
Fractional saturation of AK with ATP calculated using Eq. 12, plotted as a function of ATP concentration in the presence of the following concentrations of TMAO: 0 g/L (solid curve), 100 g/L (dashed curve), 200 g/L (dotted curve), and 300 g/L (dot-dashed curve).
Discussion
AK was chosen as the model system for this study for two main reasons:
First, the known crystal structures and spectroscopic experiments showed that significant detectable conformational changes are associated with the ligand binding reaction.
Second, the AK molecule is very stable and large enough to be robust under chemical and genetic manipulation. Several control experiments were performed to confirm that the preparative and labeling procedures did not cause significant conformational change of the molecule. The far-ultraviolet circular-dichroism spectra, the thermal stability, and the enzymatic activity were determined and found to be similar to those of the wt protein.
The mean of the interprobe distance distribution in the holoAK is separated from that of the apoAK by only 7 Ǻ. The width of these two distributions was significantly larger than that difference. Each set of fluorescence decay curves of the donor in the DA mutant obtained when both the holo- and apo-AK were present in the solution (e.g., in the presence of 0.1 mM ATP and 4 M TMAO) could be modeled both using a single-component, skewed end-to-end distance distribution and two skewed distributions representing the closed and the open ensembles of conformers. The difference in the quality of fit of the experimental data between these two modes of analysis was not statistically significant. However, the two-population model permits us to describe the entire set of data obtained at all concentrations of ATP and TMAO using parameters obtained from just two distributions (the open and closed populations) and one additional number for each experiment (the fraction of closed conformations).
Single-molecule-detected intramolecular FRET experiments are frequently used for resolution of subpopulations in ensembles of labeled biopolymers (50). In another project, we are studying the dynamics of the domain closure in AK by means of single-molecule detection of the FRET between residues 142 and 214, in parallel with the experiments described in this report. Indeed, it is possible to show that two subpopulations can be resolved in the distance distribution between the LID and the CORE domains by single-molecule-detected FRET experiments. However, the shot-noise expansion of the width of each subpopulation makes the quantitative determination of the subpopulations' ratio very difficult. We therefore preferred the use of the ensemble trFRET mode of measurements.
The sensitivity of the predicted dependence of fC upon cL and wTMAO to changes in the values of the best-fit parameters of our model determines the precision with which each of these values can be determined via least-squares fitting of the model to the data. The extent to which a parameter value can vary without significantly degrading the quality of fit, as judged by a Fisher F-test, was estimated via parameter scanning (51), as described in Fig. S5. The data do not enable us to determine lower limits of and with >50% confidence. KCL is subject to an uncertainty of ∼10-fold, and the best-fit value r is relatively well defined (3 ± ∼0.5 Å).
To test the assumption that TMAO may be represented by an equivalent hard sphere, the covolumes of a molecular model of TMAO and a selection of hard spheres of varying size were calculated, as described in the Supporting Material. The calculated set of covolumes was quantitatively described by an expression for the covolume of each hard sphere with a second hard sphere of radius 2.74 Å. The agreement between this value and that of the spherical cosolute best accounting for the observed dependence of fC upon the concentrations of ATP and TMAO (3 ± 0.5 Å) provides strong support for our conclusion that the interaction between TMAO and AK is due primarily to volume exclusion or steric repulsion.
Given the best-fit values of the parameters, one can calculate the fractional abundance of each conformational state as a function of the concentrations of ATP and TMAO. We define
| (13) |
and
| (14) |
The calculated fractional abundances of the two closed states 2 and 3 are plotted in Fig. 9. This plot shows the vivid effect of TMAO upon conformational equilibria of AK. In the absence of TMAO, state 3—the state with LID domain closed and AMP domain open—becomes highly populated (up to 90% of total protein) and state 2 becomes only modestly populated (up to ∼10%) as the concentration of ATP increases. This is a clear indication that the motions of the LID and AMP domains relative to the core domain are largely but not entirely independent, as suggested previously by Sinev et al. (32) However, in the presence of 300 g/L TMAO, state 2—the state with both domains closed—is significantly populated (∼25% of total protein) even in the absence of ATP and increases to a maximum of ∼80% with increasing ATP. The shift in conformations from 3 to 2 with increasing TMAO is attributed to the associated reduction in covolume of protein and TMAO.
Figure 9.
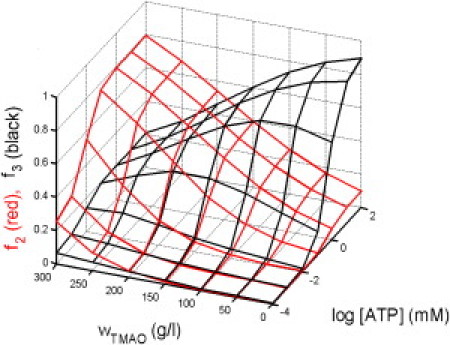
Fractional abundance of conformational states 2 and 3 as functions of ATP and TMAO concentration.
Many enzymes, including AK, undergo a conformational change upon ligand binding (20,27,52). In many cases, ligand binding is accompanied by a shift from a less compact open to a more compact closed conformation (53,54). Dhar et al. (16) have very recently demonstrated by means of FRET that the average distance between two domains of a molecule of phosphoglycerokinase connected by a flexible linker region is substantially reduced in the presence of high concentrations of Ficoll 70, an inert polysaccharide, and that the catalytic activity of the enzyme simultaneously increases severalfold.
Accompanying atomistic simulations suggest that these effects are caused by a reduction of steric exclusion between the protein and polymer upon domain closure. The experiments reported here indicate the presence of a qualitatively similar phenomenon occurring in the presence of high concentrations of an inert small molecule. The major difference between the two studies, besides the different proteins and crowders studied, is that we have been able to quantify structural changes taking place in the presence of ligand as well as crowder, and derive a relatively simple quantitative model that accounts globally for the dependence of structural change on both ligand and crowder concentrations.
According to our model, volume exclusion arising from addition of a significant volume fraction of the inert cosolute TMAO shifts conformational equilibria toward more compact closed or partially closed states, thus substantially enhancing the affinity of the AK molecule for binding the ligand ATP, even though the difference between the covolumes of apo-AK and holo-AK with TMAO is small (∼5%). The experiments reported here further demonstrate that it may be qualitatively incorrect to estimate the ligand binding affinities of enzymes or other proteins in the crowded intracellular environment based on measurements made in the absence of substantial concentrations of volume-occupying cosolutes.
Acknowledgments
We thank Dr. M. A. Sinev and Dr. L. Sineva for contributions to the preliminary work of this project.
This work was supported by research and equipment grants from the Israel Science Foundation (ISF 1102/06), the United States-Israel Binational foundation (BSF 2005270), the U.S. National Science Foundation (MCB-0749464), by the Marie Curie Transfer of Knowledge grant from the European Union (29936), and by the Damadian Center for Magnetic Resonance Research, Bar-Ilan University. A.P.M.'s research is supported by the Intramural Research Division of the National Institute of Diabetes and Digestive and Kidney Diseases.
Footnotes
Asaf Grupi's present address is Section on Physical Biochemistry, Laboratory of Biochemistry and Genetics, National Institute of Diabetes and Digestive and Kidney Diseases, National Institutes of Health, Bethesda, MD.
Sureshbabu Nagarajan's present address is Chemistry Division, MS J567, Los Alamos National Laboratory, Los Alamos, NM.
Supporting Material
References
- 1.Minton A.P. Excluded volume as a determinant of macromolecular structure and reactivity. Biopolymers. 1981;20:2093–2120. [Google Scholar]
- 2.Zhou H.-X., Rivas G., Minton A.P. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Hall D., Minton A.P. Macromolecular crowding: qualitative and semiquantitative successes, quantitative challenges. Biochim. Biophys. Acta. 2003;1649:127–139. doi: 10.1016/s1570-9639(03)00167-5. [DOI] [PubMed] [Google Scholar]
- 4.Zimmerman S.B., Minton A.P. Macromolecular crowding: biochemical, biophysical, and physiological consequences. Annu. Rev. Biophys. Biomol. Struct. 1993;22:27–65. doi: 10.1146/annurev.bb.22.060193.000331. [DOI] [PubMed] [Google Scholar]
- 5.Ellis R.J. Macromolecular crowding: obvious but underappreciated. Trends Biochem. Sci. 2001;26:597–604. doi: 10.1016/s0968-0004(01)01938-7. [DOI] [PubMed] [Google Scholar]
- 6.Minton A.P. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol. Cell. Biochem. 1983;55:119–140. doi: 10.1007/BF00673707. [DOI] [PubMed] [Google Scholar]
- 7.Minton A.P. Effect of a concentrated inert macromolecular cosolute on the stability of a globular protein with respect to denaturation by heat and by chaotropes: a statistical-thermodynamic model. Biophys. J. 2000;78:101–109. doi: 10.1016/S0006-3495(00)76576-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sasahara K., McPhie P., Minton A.P. Effect of dextran on protein stability and conformation attributed to macromolecular crowding. J. Mol. Biol. 2003;326:1227–1237. doi: 10.1016/s0022-2836(02)01443-2. [DOI] [PubMed] [Google Scholar]
- 9.Tokuriki N., Kinjo M., Yomo T. Protein folding by the effects of macromolecular crowding. Protein Sci. 2004;13:125–133. doi: 10.1110/ps.03288104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Christiansen A., Wang Q., Wittung-Stafshede P. Factors defining effects of macromolecular crowding on protein stability: an in vitro/in silico case study using cytochrome c. Biochemistry. 2010;49:6519–6530. doi: 10.1021/bi100578x. [DOI] [PubMed] [Google Scholar]
- 11.Samiotakis A., Wittung-Stafshede P., Cheung M.S. Folding, stability and shape of proteins in crowded environments: experimental and computational approaches. Int. J. Mol. Sci. 2009;10:572–588. doi: 10.3390/ijms10020572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bolen D.W. Protein stabilization by naturally occurring osmolytes. In: Murphy K.P., editor. Protein Structure, Stability and Folding. Humana Press; Totowa, NJ: 2001. pp. 17–36. [Google Scholar]
- 13.Wang A., Bolen D.W. A naturally occurring protective system in urea-rich cells: mechanism of osmolyte protection of proteins against urea denaturation. Biochemistry. 1997;36:9101–9108. doi: 10.1021/bi970247h. [DOI] [PubMed] [Google Scholar]
- 14.Bolen D.W., Baskakov I.V. The osmophobic effect: natural selection of a thermodynamic force in protein folding. J. Mol. Biol. 2001;310:955–963. doi: 10.1006/jmbi.2001.4819. [DOI] [PubMed] [Google Scholar]
- 15.Dong H., Qin S., Zhou H.-X. Effects of macromolecular crowding on protein conformational changes. PLOS Comput. Biol. 2010;6:e1000833. doi: 10.1371/journal.pcbi.1000833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dhar A., Samiotakis A., Cheung M.S. Structure, function, and folding of phosphoglycerate kinase are strongly perturbed by macromolecular crowding. Proc. Natl. Acad. Sci. USA. 2010;107:17586–17591. doi: 10.1073/pnas.1006760107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bennett W.S., Jr., Steitz T.A. Glucose-induced conformational change in yeast hexokinase. Proc. Natl. Acad. Sci. USA. 1978;75:4848–4852. doi: 10.1073/pnas.75.10.4848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ptitsyn O.B. Inter-domain mobility in proteins and its probable functional role. FEBS Lett. 1978;93:1–4. doi: 10.1016/0014-5793(78)80791-1. [DOI] [PubMed] [Google Scholar]
- 19.Bennett W.S., Huber R. Structural and functional aspects of domain motions in proteins. CRC Crit. Rev. Biochem. 1984;15:291–384. doi: 10.3109/10409238409117796. [DOI] [PubMed] [Google Scholar]
- 20.Koshland D.E., Jr. Enzyme flexibility and enzyme action. J. Cell. Comp. Physiol. 1959;54:245–258. doi: 10.1002/jcp.1030540420. [DOI] [PubMed] [Google Scholar]
- 21.Jencks W.P. Binding energy, specificity, and enzymic catalysis: the Circe effect. Adv. Enzymol. Relat. Areas Mol. Biol. 1975;43:219–410. doi: 10.1002/9780470122884.ch4. [DOI] [PubMed] [Google Scholar]
- 22.Eklund H., Samma J.P., Jones T.A. Structure of a triclinic ternary complex of horse liver alcohol dehydrogenase at 2.9 Å resolution. J. Mol. Biol. 1981;146:561–587. doi: 10.1016/0022-2836(81)90047-4. [DOI] [PubMed] [Google Scholar]
- 23.Schulz G.E., Schiltz E., Schirmer R.H. Structural relationships in the adenylate kinase family. Eur. J. Biochem. 1986;161:127–132. doi: 10.1111/j.1432-1033.1986.tb10132.x. [DOI] [PubMed] [Google Scholar]
- 24.Harlos K., Vas M., Blake C.F. Crystal structure of the binary complex of pig muscle phosphoglycerate kinase and its substrate 3-phospho-D-glycerate. Proteins. 1992;12:133–144. doi: 10.1002/prot.340120207. [DOI] [PubMed] [Google Scholar]
- 25.Remington S., Wiegand G., Huber R. Crystallographic refinement and atomic models of two different forms of citrate synthase at 2.7 and 1.7 Å resolution. J. Mol. Biol. 1982;158:111–152. doi: 10.1016/0022-2836(82)90452-1. [DOI] [PubMed] [Google Scholar]
- 26.Pickover C.A., McKay D.B., Steitz T.A. Substrate binding closes the cleft between the domains of yeast phosphoglycerate kinase. J. Biol. Chem. 1979;254:11323–11329. [PubMed] [Google Scholar]
- 27.McDonald R.C., Steitz T.A., Engelman D.M. Yeast hexokinase in solution exhibits a large conformational change upon binding glucose or glucose 6-phosphate. Biochemistry. 1979;18:338–342. doi: 10.1021/bi00569a017. [DOI] [PubMed] [Google Scholar]
- 28.Noda L. Adenylate kinase. In: Boyer P.D., editor. The Enzymes. Academic Press; New York: 1973. pp. 279–305. [Google Scholar]
- 29.Muller Y.A., Schumacher G., Schulz G.E. The refined structures of a stabilized mutant and of wild-type pyruvate oxidase from Lactobacillus plantarum. J. Mol. Biol. 1994;237:315–335. doi: 10.1006/jmbi.1994.1233. [DOI] [PubMed] [Google Scholar]
- 30.Berry M.B., Meador B., Phillips G.N., Jr. The closed conformation of a highly flexible protein: the structure of E. coli adenylate kinase with bound AMP and AMPPNP. Proteins. 1994;19:183–198. doi: 10.1002/prot.340190304. [DOI] [PubMed] [Google Scholar]
- 31.Sinev M.A., Sineva E.V., Haas E. Towards a mechanism of AMP-substrate inhibition in adenylate kinase from Escherichia coli. FEBS Lett. 1996;397:273–276. doi: 10.1016/s0014-5793(96)01195-7. [DOI] [PubMed] [Google Scholar]
- 32.Sinev M.A., Sineva E.V., Haas E. Domain closure in adenylate kinase. Biochemistry. 1996;35:6425–6437. doi: 10.1021/bi952687j. [DOI] [PubMed] [Google Scholar]
- 33.Schulz G.E. Mechanisms of enzyme catalysis from crystal structure analyses. Ciba Found. Symp. 1991;161:8–27.. doi: 10.1002/9780470514146.ch2. [DOI] [PubMed] [Google Scholar]
- 34.Hanson J.A., Duderstadt K., Yang H. Illuminating the mechanistic roles of enzyme conformational dynamics. Proc. Natl. Acad. Sci. USA. 2007;104:18055–18060. doi: 10.1073/pnas.0708600104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Henzler-Wildman K.A., Thai V., Kern D. Intrinsic motions along an enzymatic reaction trajectory. Nature. 2007;450:838–844. doi: 10.1038/nature06410. [DOI] [PubMed] [Google Scholar]
- 36.Wolf-Watz M., Thai V., Kern D. Linkage between dynamics and catalysis in a thermophilic-mesophilic enzyme pair. Nat. Struct. Mol. Biol. 2004;11:945–949. doi: 10.1038/nsmb821. [DOI] [PubMed] [Google Scholar]
- 37.Henzler-Wildman K.A., Lei M., Kern D. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
- 38.Haas E. Fluorescence resonance energy transfer (FRET) and single molecule fluorescence detection studies of the mechanism of protein folding and unfolding. In: Kiefhaber J.B.a.T., editor. Protein Folding Handbook, Part I. Wiley-VCH Verlag; Weinheim, Germany: 2004. pp. 573–633. [Google Scholar]
- 39.Haas E., Katchalski-Katzir E., Steinberg I.Z. Effect of the orientation of donor and acceptor on the probability of energy transfer involving electronic transitions of mixed polarization. Biochemistry. 1978;17:5064–5070. doi: 10.1021/bi00616a032. [DOI] [PubMed] [Google Scholar]
- 40.Lakowicz J.R., Gryczynski I., Joshi N. Distance distributions in proteins recovered by using frequency-domain fluorometry. Applications to troponin I and its complex with troponin C. Biochemistry. 1988;27:9149–9160. doi: 10.1021/bi00426a012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Chung H.S., Gopich I.V., Eaton W.A. Extracting rate coefficients from single-molecule photon trajectories and FRET efficiency histograms for a fast-folding protein. J. Phys. Chem. A. 2010 doi: 10.1021/jp1009669. (E-pub ahead of print) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Huang F., Lerner E., Fersht A.R. Time-resolved fluorescence resonance energy transfer study shows a compact denatured state of the B domain of protein A. Biochemistry. 2009;48:3468–3476. doi: 10.1021/bi801890w. [DOI] [PubMed] [Google Scholar]
- 43.Okamoto K., Terazima M. Distribution analysis for single molecule FRET measurement. J. Phys. Chem. B. 2008;112:7308–7314. doi: 10.1021/jp712104h. [DOI] [PubMed] [Google Scholar]
- 44.Sinev M., Landsmann P., Haas E. Design consideration and probes for fluorescence resonance energy transfer studies. Bioconjug. Chem. 2000;11:352–362. doi: 10.1021/bc990132l. [DOI] [PubMed] [Google Scholar]
- 45.Valeur B. Wiley-VCH Verlag; Weinheim, Germany: 2002. Molecular Fluorescence Principles and Applications. [Google Scholar]
- 46.Minton A.P. Molecular crowding: analysis of effects of high concentrations of inert cosolutes on biochemical equilibria and rates in terms of volume exclusion. Methods Enzymol. 1998;295:127–149. doi: 10.1016/s0076-6879(98)95038-8. [DOI] [PubMed] [Google Scholar]
- 47.DeLano W.L. Schrödinger; Portland, OR: 2010. The PyMOL Molecular Graphics System, Ver. 1.3. [Google Scholar]
- 48.Sali A., Blundell T.L. Comparative protein modeling by satisfaction of spatial restraints. J. Mol. Biol. 1993;234:779–815. doi: 10.1006/jmbi.1993.1626. [DOI] [PubMed] [Google Scholar]
- 49.Chothia C. Structural invariants in protein folding. Nature. 1975;254:304–308. doi: 10.1038/254304a0. [DOI] [PubMed] [Google Scholar]
- 50.Michalet X., Weiss S., Jäger M. Single-molecule fluorescence studies of protein folding and conformational dynamics. Chem. Rev. 2006;106:1785–1813. doi: 10.1021/cr0404343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Saroff H.A. Evaluation of uncertainties for parameters in binding studies: the sum-of-squares profile and Monte Carlo estimation. Anal. Biochem. 1989;176:161–169. doi: 10.1016/0003-2697(89)90287-x. [DOI] [PubMed] [Google Scholar]
- 52.Huber R., Bennett W.S., Jr. Functional significance of flexibility in proteins. Biopolymers. 1983;22:261–279. doi: 10.1002/bip.360220136. [DOI] [PubMed] [Google Scholar]
- 53.Banks R.D., Blake C.C., Phillips A.W. Sequence, structure and activity of phosphoglycerate kinase: a possible hinge-bending enzyme. Nature. 1979;279:773–777. doi: 10.1038/279773a0. [DOI] [PubMed] [Google Scholar]
- 54.Sinev M.A., Razgulyaev O.I., Ptitsyn O.B. Correlation between enzyme activity and hinge-bending domain displacement in 3-phosphoglycerate kinase. Eur. J. Biochem. 1989;180:61–66. doi: 10.1111/j.1432-1033.1989.tb14615.x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


