Abstract
Clinicians need to predict the number of involved nodes in breast cancer patients in order to ascertain severity, prognosis, and design subsequent treatment. The distribution of involved nodes often displays over-dispersion—a larger variability than expected. Until now, the negative binomial model has been used to describe this distribution assuming that over-dispersion is only due to unobserved heterogeneity. The distribution of involved nodes contains a large proportion of excess zeros (negative nodes), which can lead to over-dispersion. In this situation, alternative models may better account for over-dispersion due to excess zeros. This study examines data from 1152 patients who underwent axillary dissections in a tertiary hospital in India during January 1993-January 2005. We fit and compare various count models to test model abilities to predict the number of involved nodes. We also argue for using zero inflated models in such populations where all the excess zeros come from those who have at some risk of the outcome of interest. The negative binomial regression model fits the data better than the Poisson, zero hurdle/inflated Poisson regression models. However, zero hurdle/inflated negative binomial regression models predicted the number of involved nodes much more accurately than the negative binomial model. This suggests that the number of involved nodes displays excess variability not only due to unobserved heterogeneity but also due to excess negative nodes in the data set. In this analysis, only skin changes and primary site were associated with negative nodes whereas parity, skin changes, primary site and size of tumor were associated with a greater number of involved nodes. In case of near equal performances, the zero inflated negative binomial model should be preferred over the hurdle model in describing the nodal frequency because it provides an estimate of negative nodes that are at “high-risk” of nodal involvement.
Keywords: Nodal Involvement, Count Models, Breast Cancer
1. INTRODUCTION
Accurate prediction of the number of involved nodes in breast cancer patients helps in grading severity of disease, avoid extensive axillary surgery dissections and assists with treatment decisions such as the use of neoadjuvant chemotherapy [1,2]. Many studies have been performed to predict nodal status in breast cancer patients. Most of them merely predict the presence/absence of involved nodes rather than the number of involved nodes [3]. Until now, only two studies have tried to predict the number of involved nodes in breast cancer patients. Guern and Vinh-Hung [3] found that a negative binomial model describes the number of nodal involvement better than the Poisson model due to excess variability, a condition called over-dispersion. Another study showed that the negative binomial model provides a better fit as compared to the Poisson model for the total number of involved nodes in breast cancer patients in a meta-analysis [4]. These studies used a negative binomial model, which posited that the over-dispersion occurred entirely due to unobserved heterogeneity and/or nodal clustering. However, count data often involve over-dispersion not only due to unobserved heterogeneity and/or clustering but also due to the preponderance of zero frequency (negative node in the case of cancer) [5]. Consequently, the nominal Poisson or the negative binomial distributions may not satisfactorily account for excess variability if this variability is indeed due to excess zeros. In such situations, use of these models may likely underestimate the probability of negative node status, and may provide misleading results. Zero hurdle or zero inflated regression models can be used to increase predictability in situations with excess zeros.
In count data, the observed zeros can be either structural zeros (e.g., the subject is at no risk of the event of interest) or sampling zeros (e.g., the subject is indeed at some risk of the event of interest). It has been suggested that zero hurdle models are more appropriate in case of excessive sampling zeros while zero inflated models should be preferred in cases of mixtures of zeros i.e., involvement of both types of zeros [6]. In breast cancer, all the patients are indeed at some risk of having nodal involvement and thus all zeros are strictly sampling zeros. Thus, according to the prevailing wisdom, zero hurdle models could be employed to predict the nodal frequency among breast cancer patients.
In epidemiologic studies, generally count data involves zeros at some risk of outcome of interest. In such circumstances, there exists alternative ways to conceptualize the so-called structural zeros and sampling zeros. Using the epidemiological parlance, we can conceptualize zeros in terms of disease on-set and disease progression. In breast cancer patients, a lack of nodal involvement (observed zero) may be because the cancer is detected early enough in the disease progression (closer to the time of disease onset) or the cancer itself is of slow progression and/or absence of risk factors for high rate of disease progression. These kinds of zeros may be identified as true or structural zeros. The rest of the zeros may be observed in the presence of various risk factors leading up to a high rate of disease progression. These latter types of zeros can be identified as false or sampling zeros. Thus, within the framework of zero inflated models, excess zeros can be modeled as a mixture of true zeros and false zeros. Note that the false zeros can also arise either due to chance, false recording and/or due to false observation. It has been reported that some of the involved (positive) nodes may be recorded as negative due to misclassification by the pathologist (referred to as reporting error) [7]. One study reported that non-dissection of complete axillary lymph nodes might provide false negative nodes [8]. These false negative nodes may be more likely to be found among patients with a high risk of nodal involvement. This indicates a need of estimation of false negative nodes so that they can follow up or be reassessed for diagnostic accuracy. In these situations, we suggest use of the zero inflated models, not only to account for excess zeros, but also to estimate the proportion of false zeros or patients with zeros at high risk of nodal positivity.
Significant applications of zero hurdle and zero inflated models have been made in various fields of research [9–11]. In recent years, the application of these models and their comparisons with other count models has also increased in medical and health fields [12–19]. A review of the application of such models in health research is also reported [20]. Extensions of these models for describing correlated data have also been reported [21–24]. These studies illustrate that zero hurdle/inflated models should be used if over-dispersion in the data is due to excess zeros. Results also indicate that zero hurdle models should be preferred if only at-risk zeros are present in the population. However, to our knowledge, the relative performance of zero hurdle and inflated models in predicting the number of involved nodes has not been addressed. In this paper, prediction of the number of involved nodes is made using Poisson regression (PR), negative binomial (NB), zero hurdle Poisson (ZHP), zero inflated Poisson (ZIP), zero hurdle negative binomial (ZHNB) and zero inflated negative binomial (ZINB) models. Zero hurdle models in many epidemiologic studies like the present one may satisfactorily account for excess zeros, perhaps even as good as zero inflated models. We arguably demonstrate that the zero inflated models have an added advantage over the former in describing the event of interest in relation to the disease process itself, including identification of the factors involved in predicting the disease onset and disease progression.
2. MATERIALS AND METHODS
2.1. Subjects
We utilized one of the largest breast cancer datasets available in India to assess the number of involved nodes distribution. The data were extracted from the computerized database of breast cancer patients maintained at the Department of Surgical Oncology, Institute Rotary Cancer Hospital (IRCH), All India Institute of Medical Sciences (AIIMS), New Delhi, India, a tertiary care center, during the period from January 1993 to January 2005. The dataset was updated using the original records kept in the record section of IRCH. Data from all patients who underwent surgery for breast cancer, including axillary lymph node dissections, were included in this study. Patients with recurrent breast cancer, bilateral breast carcinoma, any evidence of metastasis, unknown primary site and male breast carcinoma were excluded from the study.
Covariates and their forms were chosen based on breast cancer literature and an exploratory analysis of this dataset. Patients’ age at presentation was stratified as younger (below 35 years) and elder (more than or equal to 35 years). Duration from onset of symptoms until presentation was classified as less than or equal to 2, 2–4, 4–8 and more than 8 months. Parity was categorized as nulliparous, single/doubleparous, and multiparous. Other covariates included menopausal status (post/pre); family history of breast cancer (absent/present); primary side (left/right); skin changes (no/yes); neoadjuvant chemotherapy (no/yes); primary site {medial (lower inner quadrant and upper inner quadrant)/lateral (lower outer quadrant and upper outer quadrant)/central (multiple, central and others)}; tumor type (infiltrating ductal carcinoma/infiltrating lobular carcinoma and others); and pathological tumor size was according to TNM classification (< = 2/2–5/> 5cm). The neoadjuvant chemotherapy and total number of dissected nodes were only used in the model for adjustment, because these variables are highly associated with involved nodes. The study population consisted of all cases of breast cancer and the outcome in question was the number of involved nodes in a patient. Patients with negative nodes (zeros) were divided into two groups-those with “at low risk” of nodal involvement and those with “at high risk” of nodal involvement. A patient with negative nodes and having a relatively low risk of nodal involvement was defined as “at low risk” zero and labeled, in the context of modeling, as a “true or structural” zero. The remaining patients with negative nodes and a relatively high risk of nodal involvement due to the presence of various risk factors were defined as “at high risk” zeros. In the context of modeling, we label them as “false or sampling” zeros.
2.2. Statistical Models
The Poisson regression model (PR) describes count outcomes or proportion/rates. Generally, the PR model explains less variability of counts than the observed variability. As a result, this often gives misleading relationships between covariates and outcomes. Excess variability can be adjusted within the PR framework using inflation approaches of standard errors of the regression coefficients [25]. As such, it may be the appropriate model to use for drawing correct inferences in the case of over-dispersion due to unobserved heterogeneity and/or clustering/temporal dependency. However, it may not be the most appropriate in the case of excess zeros, as expected in assessing the distribution of number of involved nodes. In the PR model, yi is the number of involved nodes for the ith patient, and λi is the mean number of involved nodes. If the number of involved nodes follows a Poisson distribution, its probability mass function can be expressed as:
| (1) |
If βi’s are regression coefficients corresponding to the set of considered covariates xi’s, and k is the number of considered covariates, then the PR model can be expressed using Eq.1 as:
| (2) |
As an alternative to the PR model, the negative binomial (NB) model has an inbuilt provision to account for over-dispersion due to unobserved heterogeneity and/or temporal dependency [26]. As a result, this model helps not only in adjusting the standard errors of the regression coefficients but also provides a more flexible approach for prediction of the count outcome. Under the assumption of over-dispersion being merely due to unobserved heterogeneity and/or temporal dependency, the NB model was used. The unobserved heterogeneity may be due to unobserved predictors and/or too much variation in some of the clinical and pathological cofactors. Temporal dependency in nodes may be occurring due to clustering of nodal involvement within patients. The NB model is expressed as:
| (3) |
In this model, α is the over-dispersion parameter due to unobserved heterogeneity and λi is the mean number of involved nodes. The NB regression model can be obtained similar to Eq.2 by using Eq.3.
The NB model may not be appropriate if the over-dispersion is due to excess zeros because it underestimates the probability of zeros and consequently underestimates the variability present in the outcome. In such situations, alternative models such as zero inflated/hurdle models that account for over-dispersion due to excess zeros are useful.
Zero hurdle models are typically used when the excess zeros arise from an “at risk” population. Under the assumption that over-dispersion results from excess zeros arising from an “at risk” group, zero hurdle Poisson (ZHP) was used. In this model, all zeros are considered to be observed from a non-counting process, as opposed to a counting process. Within this model, all zeros are typically described through logistic regression, whereas positive counts are described through a zero truncated Poisson model. In the ZHP model, pi is “at risk” negative nodes under logistic model. Assuming the mean number of involved nodes (λi) under zero truncated Poisson model, the ZHP distribution may be expressed [27] as:
If γi’s and βi’s are respective regression coefficients under logistic and zero truncated Poisson models corresponding to considered covariates (xi’s), and the number of considered covariates is k in each of the models, then using Eq.4 regression models can be expressed as:
| (4) |
| (5) |
The ZHP model provides two sets of results. These results can also be obtained separately by fitting both a logistic regression and zero truncated Poisson model. This is why hurdle models are referred to as two-part models. The binary process model identifies factors associated with the presence/absence of nodal involvement, whereas modeling count process yields factors associated with an increase in the number of involved nodes given that the patient has involved nodes. Note that the ZHP model accounts for over-dispersion due to excess zeros but not due to unobserved heterogeneity and/or temporal dependency in nodal involvement. In the latter case, one may use the zero hurdle negative binomial (ZHNB) model by considering count process as zero truncated negative binomial distribution. Substituting a zero truncated negative binomial distribution in Eq.4 yields the ZHNB distribution, and it can be expressed as Eq.6.
| (6) |
Zero inflated models are typically used when the excess zeros are a mixture of two types of zeros-true (structural zeros) and false (sampling zeros). We propose to categorize the negative nodes in our population as a mixture of two types, those with very low/no risk of nodal involvement (true zeros) and those with high risk of nodal involvement (false zeros). In this way, use of the zero inflated model framework not only accounts for the extra variability due to excess zeros but also estimates the relative proportion of these at “low risk” and at “high risk” zeros. Further, this can be used to identify subjects with a high likelihood of being in one or the other type of zero classification using the risk factors. In zero inflated models, occurrence of zeros is considered as a result of two distinct processes. Some of the zeros (zeros at “high risk”) are considered to be observed from counting process and others (zeros at “low risk”) from non-counting process. As an inbuilt mechanism within these models, true zeros are typically described through logistic regression, whereas false zeros are described through simple count model. Like hurdle models, the zero inflated models also provide two sets of results. However, the interpretation of regression coefficients under inflated models is different from the hurdle models. Modeling binary process provides factors associated with negative nodes in a “low risk” population as compared to a “high risk” population, whereas modeling count process provides factors associated with the extent of the number of involved nodes, including false negative nodes given that patients are in a high risk population. Here, the probability of observing negative nodes is the sum of observing negative nodes (true) under the logistic model plus the probability that a individual is not in the binary process, and the probability that negative nodes (false) under the considered count model. If the count process follows the Poisson distribution then it is called a zero inflated Poisson (ZIP) model. To understand the ZIP model, consider the occurrence of at “low risk” negative nodes with probability pi under a logistic model, whereas that of involved nodes (including at “high risk” false negative nodes) with probability (1-pi) under the Poisson model, having a mean number of involved nodes (λi,), the ZIP distribution can be expressed [28] as:
| (7) |
If γi’s and βi’s are respective regression coefficients under logistic and Poisson models corresponding to considered covariates (xi’s), and the number of considered covariates is k in each of the models, then using Eq.7, regression models can be expressed as:
| (8) |
| (9) |
If the count process does not follow the Poisson model then one may use the zero inflated negative binomial (ZINB) model by considering count process as a negative binomial distribution. In contrast to ZIP, the ZINB model accounts for the over-dispersion due to both types of zeros as well as due to unobserved heterogeneity and/or temporal dependency. Substituting negative binomial distribution in Eq.7, the ZINB distribution can be expressed as:
2.3. Model Comparisons
The PR, NB, ZIP, ZHP, ZHNB and ZINB models were used to describe the number of involved nodes in breast cancer patients. The covariates found to be significant in univariate analysis with any of the regressions were included into all the regression models to maintain the comparative findings. The nested models (e.g., PR versus NB and ZIP, NB versus ZINB, and ZHP versus ZHNB) were compared using a likelihood ratio. Significant result of the likelihood ratio test of comparison (PR versus NB, NB versus ZINB, and ZHP versus ZHNB) indicates the presence of over-dispersion due to heterogeneity and/or temporal dependency. The non-nested models (PR with ZHP, PR with ZHNB, PR with ZINB, NB with ZHP, NB with ZIP, NB with ZHNB, ZHP with ZIP, ZHP with ZINB and ZHNB with ZINB) as well as nested models were also compared using the Vuong test [29]. Significant and better fit of comparisons (PR with ZHP/ZIP, and NB with ZHNB/ZINB) explores whether or not the over-dispersion is due to excess zeros.
To compare the predictive performance of the models, various indices such as log likelihood, Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC), mean squared prediction error (MSPE) and mean absolute prediction error (MAPE) were also obtained. A probability plot (observed probability minus predicted probability of positive nodes versus number of positive nodes) was constructed for each model. The probability plot was constructed after truncation at 10 positive nodes for ease of visual comparison. The best-fitted model was also validated using the leave-one-out cross validation method [30]. The p-values less than 5% were considered as significant results. STATA 9.0 package was used for all statistical analyses.
3. RESULTS
A total of 1152 patients were found to be eligible for this study. Of those in the study, the presence of involved nodes was found in 705 (61.2%) patients. The mean and standard deviation of the number of involved nodes per patient were 3.9 and 5.6 respectively (median 1 and range: 0–33). Median number of total dissected nodes per patient was 14 (range: 1–46). The mean age was 47.7 (standard deviation, 11.1) years and range 20–86 years. The distributions of covariates considered in the analysis are shown in Table 1.
Table 1.
Zero inflated negative binomial model for number of involved nodes.
| Variables | N | Logistic Portion* Odds Ratio (95% CI) |
NB Portion Risk Ratio (95% CI) |
|---|---|---|---|
| Age (year) | |||
| > 35 | 977 | 1.00 | 1.00 |
| < = 35 | 175 | 0.98 (0.54, 1.80) | 1.12 (0.90, 1.38) |
| Symptom duration (month) | |||
| < = 2 | 376 | 1.00 | 1.00 |
| 3–4 | 263 | 0.74 (0.43, 1.26) | 1.00 (0.82, 1.23) |
| 5–8 | 266 | 1.13 (0.71, 1.81) | 1.17 (0.95, 1.43) |
| > = 9 | 247 | 0.73 (0.43, 1.24) | 1.08 (0.88, 1.33) |
| Parity | |||
| Nulliparous | 47 | 1.00 | 1.00 |
| P1/P2 | 445 | 1.18 (0.26, 5.31) | 1.82 (1.20, 2.77) |
| Multiparous | 660 | 1.67 (0.38, 7.44) | 1.95 (1.29, 2.95) |
| Menopausal | |||
| Post Menopausal | 587 | 1.00 | 1.00 |
| Pre Menopausal | 565 | 0.69 (0.45, 1.04) | 1.01 (0.85, 1.18) |
| Primary side | |||
| Left | 583 | 1.00 | 1.00 |
| Right | 569 | 0.87 (0.60, 1.26) | 0.91 (0.79, 1.06) |
| Primary site | |||
| Medial (UIQ + LIQ) | 235 | 1.00 | 1.00 |
| Lateral (LOQ + UOQ) | 681 | 0.62 (0.40, 0.96) | 1.29 (1.05, 1.60) |
| Central/Multiple/Other | 236 | 0.38 (0.19, 0.74) | 1.24 (0.97, 1.58) |
| Skin changes | |||
| No | 746 | 1.00 | 1.00 |
| Yes | 406 | 0.38 (0.23, 0.62) | 1.40 (1.19, 1.66) |
| Tumor type | |||
| Other/ILC | 78 | 1.00 | 1.00 |
| IDC | 1074 | 0.62 (0.31, 1.22) | 1.14 (0.82, 1.57) |
| Tumor size (centimeter) | |||
| < = 2 | 236 | 1.00 | 1.00 |
| 2–5 | 666 | 0.63 (0.40, 1.01) | 1.28 (1.03, 1.59) |
| > 5 | 250 | 0.61 (0.34, 1.09) | 1.49 (1.17, 1.91) |
The odds ratio of negative nodes in low risk group
All the results are adjusted in relation to neoadjuvant chemotherapy as well as total number of dissected nodes
A descriptive comparison reveals that the cofactors parity, skin changes, primary site and pathological tumor size were consistently associated with outcome across all models. Three additional covariates, age, menopausal status and tumor type, were statistically significant only in the PR model. There was good concordance in the assessment of statistical significance in all aspects among ZHP, ZIP and NB models. A similar relation could also be seen between the ZINB and ZHNB models in providing factors associated with the extent of nodal involvement. In other words, parity, skin changes, primary site and tumor size were found associated with a greater number of involved nodes in both models. However, the ZHNB model provided primary site, skin changes and pathological tumor size associated with presence of positive nodes whereas ZINB model provided only primary site and skin changes associated with presence of positive nodes in at high-risk population.
The significant Pearson chi square goodness of fit (gof) test (p < 0.001) along with other characteristics of model fit indicated that the PR model produced a poor fit for nodal involvement data. In the NB model, the estimated dispersion statistic (α) was 1.73 (95% CI: 1.54, 1.95). A significant likelihood ratio test (p < 0.001) of dispersion statistic from zero favored the NB model over the PR model. Recall that more than one third of the patients had negative nodes, indicating an excess of negative nodes. Intuitively, this suggests that over-dispersion is most likely due to excess negative nodes. Firstly, all negative nodes were considered to arise from an at-risk group, justifying use of the ZHP model. Further, to estimate false negative nodes, it was considered that some of these negative nodes might be observed among patients who had a “low risk” of nodal positivity (true zeros) and some proportion might be observed among patients who had “high risk” of nodal involvement (false zeros). With this more natural consideration, the ZIP model was used. Both the Vuong test (V = 12.60 and p < = 0.001) and the significant likelihood ratio test favored the ZHP model over the PR model. However, the comparison of ZHP and ZIP using Vuong test (V = 2.01 and p = 0.04) slightly favored the ZIP model. The results of Vuong tests also favored the NB model over the ZHP model (8.86, p = < 0.001) and the ZIP model (8.84, p < 0.001). As observed through improved fit of the NB model over PR and ZHP/ZIP models, it clearly indicates that over-dispersion is involved due to unobserved heterogeneity and/or clustering. In addition, ZHP/ZIP provided evidence of over-dispersion due to excess negative nodes, in comparison to the PR model. Hence, a model incorporating over-dispersion due to excess negative nodes as well as unobserved heterogeneity simultaneously was expected to provide improved predictability of number of involved nodes. Accordingly, ZHNB and ZINB models were used to predict number of involved nodes. Under ZHNB and ZINB models, the estimated dispersion parameters of zero truncated negative binomial and NB models were observed different than zero as [(α = 0.70; 95% CI: (0.56, 0.87)] and [(α = 0.71; 95% CI: (0.57, 0.89)] respectively. This suggests that ZHNB/ ZINB models are more appropriate than ZHP/ZIP models in describing the number of involved nodes. The better fit of ZHNB/ZINB models over the NB model suggests that over-dispersion is not only due to excessive negative nodes but also due to unobserved heterogeneity and/or clustering. The result of the Vuong test showed no difference between ZHNB and ZINB models in predicting nodal frequency (1.53, p = 0.13).
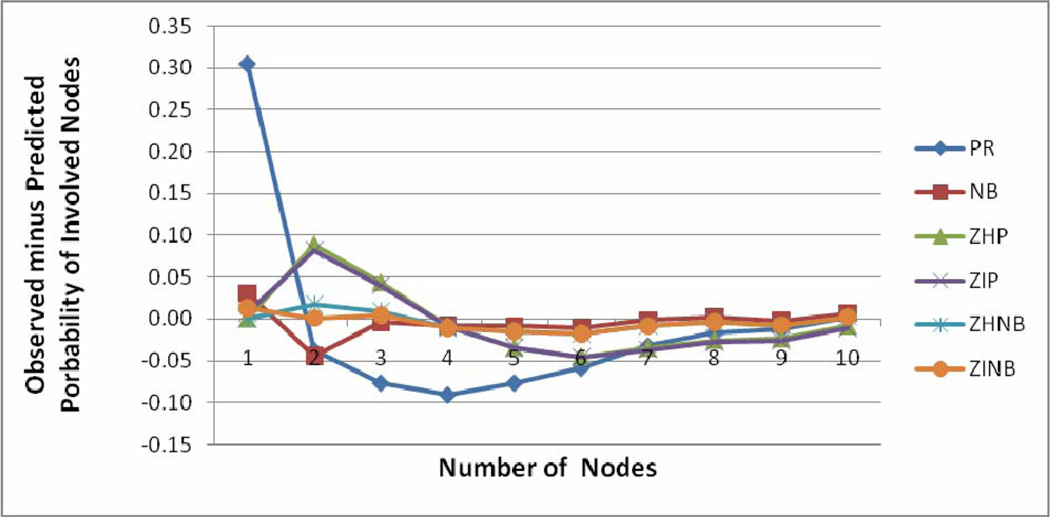
The model fit characteristics are shown in Table 2. The minimum BIC was observed for the NB model, followed by ZHNB/ZINB models. However, other validity indices of the model (maximum log likelihood, minimum AIC, MSPE and MAPE) favored ZHNB/ZINB models over all other models. The plot of observed minus predicted probability of involved nodes at each count is shown in Figure 1. The PR model underestimates probability of occurrence of negative node and overestimates occurrence of one positive node. The line of difference between observed minus predicted probability of positive nodes was close to the reference zero line, showing better fit of ZHNB/ZINB models than the other models. There is virtually no difference between ZHNB and ZINB models in all aspects of describing the number of involved nodes. The ZINB model provides slightly smaller validity indices as compared to ZHNB. Finally, the ZINB model was assessed by the leave one out cross validation method. The MSPE in cross validation of the ZINB model was the lowest of all the models (0.0007), indicating that the ZINB model performs well for predicting nodal involvement in future patients. The ZINB model predicts that 70.6% all negative nodes are at “low risk” zeros, and the remaining 29.4% are at “high risk” for negative nodes. This indicates that almost 30% of the patients observed as negative for nodal involvement are at “high risk” of nodal involvement based on cofactors.
Table 2.
Comparison of model fit characteristics.
| PR | NB | ZHP | ZIP | ZHNB | ZINB | |
|---|---|---|---|---|---|---|
| Log Likelihood | −4093.9 | −2598.6 | −3019.7 | −3018.4 | −2553.7 | −2551.1 |
| AIC | 8221.8 | 5233.1 | 6107.4 | 6104.8 | 5185.4 | 5172.2 |
| BIC | 8307.6 | 5324.0 | 6279.0 | 6276.5 | 5382.3 | 5348.9 |
| MSPE | 4764.0 | 139.1 | 632.5 | 627.62 | 52.9 | 49.2 |
| MAPE | 27.5 | 6.2 | 13.1 | 13.0 | 4.8 | 4.7 |
Figure 1.
Plots of observed minus predicted probability of positive nodes versus number of positive nodes for six models.
Table 1 displays the estimates of regression coefficients for various cofactors of both portions of the ZINB model. For ZINB, the results of both parts of the models together help in understanding the role of the factors on nodal distribution. The logistic portion showed that medial primary site and absence of skin changes significantly increased the chance of negative nodes in breast cancer patients. Negative binomial portion reveals that the risk of a greater number of involved nodes was 82 percent higher in single/doubleparous patients versus nulliparous patients, given that the patients are in a high-risk group. Further, this was 95 percent higher among multiparous patients. The patients with lateral site involvement had 1.29 times higher likelihood for having a larger number of positive nodes than patients with the medial site. Women with skin changes had 1.39 times more involvement of higher positive nodes as compared to their counterparts. The chance of increased positive nodes was 28 percent higher among patients with 2–5 cm tumor size, in comparison to patients with less than 2 cm tumor size. It was again 1.49 times more likely among patients with more than 5 cm tumor size as compared to less than 2 cm tumor size.
4. DISCUSSION
The number of involved nodes is one of the most important therapeutic and prognostic factors for breast cancer [1]. Clinicians need to predict the number of involved nodes in breast cancer patients in order to improve health outcomes. To the best of our knowledge, few studies have described the number of involved nodes in breast cancer patients, and tested statistical models to accurately predict involved node number. As for most of the count data, studies also found excess variability in nodal distribution than that expected by a Poisson model. They also generally assume the cause of over-dispersion to be solely due to unobserved heterogeneity, and therefore used the NB model to fit and describe nodal frequency [3,4]. However, data with nodal involvement often involve excess zeros, which also cause over-dispersion. This indicates a need to explore fitting zero hurdle and zero inflated models, which can also account for variability due to excessive zeros. In the current paper, we fitted various count models to identify putative causes of over-dispersion, and to assess the predictive performance of these models with regard to the nodal status in a population of patients with breast cancer. We also illustrated the significance of using zero inflated models in count data involving zeros that emanate from the subjects that are all “at-risk” of the event of interest.
The ZHNB/ZINB regression models provide the best fit when predicting the number of involved nodes in breast cancer patients. This confirms that the distribution of the involved nodes contained over-dispersion not only due to unobserved heterogeneity but also due to excessive negative nodes (zeros). As expected, the PR model had the worst prediction ability for nodal frequency. Accounting only one source of over-dispersion, either due to excessive zeros or due to unobserved heterogeneity, the prediction ability of nodal frequency improved as indicated by NB, ZHP, ZIP models. However, use of ZHNB/ZINB models, which assumes involvement of more than just one source of over-dispersion, provided smaller prediction error.
The ZHNB and ZINB models were consistent and similar for factor-identification in the extent of nodal involvement as well as for prediction of number of positive (involved) nodes. In the current study, we focused on predicting nodal frequency. On that basis, either model can be used to predict number of involved nodes. Due to ease of interpreting the results of ZHNB model, it can be preferred over ZINB model. These findings are supported by Rose et al. [6], who also found good concordance between the ZHNB and ZINB models on vaccine adverse data—a case of only “at risk” zeros similar to the data used in our study. They suggested that the model selection should be determined based on study objectives and the data generating process. They recommend using the ZHNB model due to involvement of only “at risk” zeros. However, Baughman [31] suggested that model choice should be based on the rationale behind the consideration of data generating mechanism. Gilthorpe et al. [32] suggested that the zero inflated models should be used according to the underlying disease process i.e., considerations of disease onset and disease progression. In our opinion, zero hurdle models should be preferred if data consist of zeros which are all coming from the subjects at “no-risk” of the outcome of interest, and over-dispersion is due to excess zeros. In such cases, zeros from the “no-risk” population arise from a non-counting process. However, zeros coming from an “at risk” population belong to the count process, thus influencing model choice based on the rationale behind the data generation of the “at risk” population. In the present study, if diagnosis is close to or at disease onset, the risk of finding the event of interest (nodal involvement) would be minimal, whereas if the diagnosis is late and during disease progression, the risk of the event of interest would be relatively high. Previous studies note that the distribution of involved nodes often consists of some proportion of false negative nodes, which may often arise in the “high-risk” group [7,8]. There is ample evidence to consider “at risk” zeros, at least in breast cancer, as a mixture of “low-risk” and “high-risk” zeros, thus, suggesting the use of zero inflated models. Use of the ZINB model not only gives estimate of the false negative nodes i.e., zero at “high risk” of nodal involvement, but also provides slightly better predictive performance than the ZHNB model.
The ZINB model estimated about 30 percent of the zeros that can be considered false/at “high risk” negative nodes, suggesting that these patients are at high risk of nodal involvement. Among these, some patients might have been observed or reported falsely as having negative nodes. If so, then those patients might have been under-treated and/or misclassified, resulting in an inaccurate predicted prognosis. This model will help to identify such patients, and reduce misclassification. There is a need to develop a sound strategy to classify patients at “high risk” zeros and “low risk” zeros. This issue is under investigation by us, and is the subject of a future publication.
The mean square prediction error was found to be 35.4% less using ZINB as compared to the NB regression model. In addition, the predictive performance of the ZINB model was significantly better than the NB regression model, indicating that the NB model may not always be appropriate for describing nodal distribution. The leave-one-out cross-validation assessment of the developed ZINB model provided the minimum mean square prediction error compared to the other developed models, indicating that the model performs well, even for future patients, in comparison to other models.
This study is the first report to analyze patterns of nodal involvement in breast cancer, using a large dataset collected in India. In our study, 61.2% of the patients had the presence of involved nodes. Sandhu et al., using a different Indian dataset, also reported a 61.6% nodal involvement [33]. A different study, also using a population from India, reported an even higher nodal positivity rate of 80.2% [34]. In our study, both presence of other than medial primary site and skin changes among patients are associated with high risk of nodal involvement and with a greater number of involved nodes. In addition to these two factors, higher parity and larger tumor size are also associated with an increased risk of a higher number of involved nodes, given that the patients are in high risk population. These factors are consistently found to be associated with the presence of involved nodes in other studies [35–41], and are directly or indirectly consequences of late diagnosis. Overall, these findings confirm the need for ongoing efforts to minimize diagnostic delay in patients suspected of having breast cancer.
One limitation to our study is that it uses a dataset not designed for our analysis. Important covariates, such as lymphatic vascular invasion and S-phase function, were not included in this database. These covariates could be significantly associated with involved nodes, as reported in various studies [42–45]. In addition, instead of adjustment of these results in relation to dissected number of nodes, an attempt could be made to model the proportion of positive nodes in patients through count data models or binomial models.
5. CONCLUSIONS
The ZHNB/ZINB regression models can be used to describe nodal distribution more appropriately than the NB model. However, the ability of the ZINB model to more accurately estimate at “high-risk” zeros while having a comparatively lower prediction error, as compared to the ZHNB model, suggests that it is the best model for predicting and describing the number of involved nodes. Many of the factors associated with nodal involvement may be a result of diagnostic delay of breast cancer patients, indicating the need to minimize delay in diagnosis of breast cancer patients. There is also a need to further investigate the consequences of using zero inflated models, as an alternative to zero hurdle models, in at- risk populations.
6. ACKNOWLEDGEMENTS
The authors would like to express their thanks to Dr. V. Sreenivas, Department of Biostatistics, All India Institute of Medical Sciences, New Delhi; Dr. Arvind Pandey, National Institute of Medical Statistics, New Delhi; and also Dr. Kishore Chaudhry and Dr. D. K. Shukla, Division of Non-Communicable Diseases, Indian Council of Medical Research, New Delhi, for their critical comments throughout this study.
REFERENCES
- 1.Hernandez-Avila CA, Song C, Kuo L, Tennen H, Armeli S, Kranzler HR. Targeted versus daily naltrexone: Secondary analysis of effects on average daily drinking. Alcoholism, Clinical and Experimental Research. 2006;30(5):860–865. doi: 10.1111/j.1530-0277.2006.00101.x. [DOI] [PubMed] [Google Scholar]
- 2.Slymen DJ, Ayala GX, Arredondo EM, Elder JP. A demonstration of modeling count data with an application to physical activity. Epidemiologic Perspectives & Innovations. 2006;3(3):1–9. doi: 10.1186/1742-5573-3-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Horton NJ, Kim E, Saitz R. A cautionary note regarding count models of alcohol consumption in randomized controlled trials. BioMed Central Medical Research Methodology. 2007;7(9):1–9. doi: 10.1186/1471-2288-7-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Salinas-Rodriguez A, Manrique-Espinoza B, Sosa-Rubi SG. Statistical analysis for count data: Use of health services applications. Salud Publica Mex. 2009;51(5):397–406. doi: 10.1590/s0036-36342009000500007. [DOI] [PubMed] [Google Scholar]
- 5.Asada Y, Kephart G. Equity in health services use and intensity of use in Canada. Biomed Central Health Services Research. 2007;7(41):1–12. doi: 10.1186/1472-6963-7-41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Grootendorst PV. A comparison of alternative models of prescription drug utilization. Health Economics. 1995;4(3):183–198. doi: 10.1002/hec.4730040304. [DOI] [PubMed] [Google Scholar]
- 7.Afifi AA, Kotlerman JB, Ettner SL, Cowan M. Methods for improving regression analysis for skewed continuous or counted responses. Annual Review of Public Health. 2007;28:95–111. doi: 10.1146/annurev.publhealth.28.082206.094100. [DOI] [PubMed] [Google Scholar]
- 8.Hur K, Hedeker D, Henderson W, Khuri S, Daley J. Modeling clustered count data with excess zeros in health care outcomes research. Health Services and Outcomes Research Methodology. 2002;3:5–20. 2002. [Google Scholar]
- 9.Lee AH, Wang K, Scott JA, Yau KK, McLachlan GJ. Multi-level zero-inflated Poisson regression modeling of correlated count data with excess zeros. Statistical Methods in Medical Research. 2006;15(1):47–61. doi: 10.1191/0962280206sm429oa. [DOI] [PubMed] [Google Scholar]
- 10.Yau KK, Lee AH. Zero-inflated Poisson regression with random effects to evaluate an occupational injury prevention programme. Statistics in Medicine. 2001;20(19):2907–2920. doi: 10.1002/sim.860. [DOI] [PubMed] [Google Scholar]
- 11.Min Y, Agresti A. Random effect models for repeated measures of zero-inflated count data. Statistical Modelling. 2005;5(1):1–19. [Google Scholar]
- 12.Gardner W, Mulvey EP, Shaw EC. Regression analyses of counts and rates: Poisson, overdispersed Poisson, and negative binomial models. Psychological Bulletin. 1995;118(3):392–404. doi: 10.1037/0033-2909.118.3.392. [DOI] [PubMed] [Google Scholar]
- 13.Hardin JW, Hilbe JM. Generalized Linear Models and Extensions. Stat-Corp LP, Texas: A Stata Press Publication; 2007. [Google Scholar]
- 14.Mullay J. Specifications and testing of some modified count data model. Journal of Econometrics. 1986;33(3):341–365. [Google Scholar]
- 15.Lambert D. Zero-inflated Poisson regression, with application to defects in manufacturing. Technometrics. 1992;34(1):1–14. [Google Scholar]
- 16.Vuong QH. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica. 1989;57(2):307–333. [Google Scholar]
- 17.Picard R, Cook D. Cross-Validation of Regression Models. Journal of the American Statistical Association. 1984;79(387):575–583. [Google Scholar]
- 18.Baughman LA. Mixture model framework facilitates understanding of zero-inflated and hurdle models for count data. Journal of Biopharmaceutical Statistics. 2007;17(5):943–946. doi: 10.1080/10543400701514098. [DOI] [PubMed] [Google Scholar]
- 19.Gilthorpe MS, Frydenberg M, Cheng Y, Baelum V. Modelling count data with excessive zeros: The need for class prediction in zero-inflated models and the issue of data generation in choosing between zero-inflated and generic mixture models for dental caries data. Statistics in Medicine. 2009;28(28):3539–3553. doi: 10.1002/sim.3699. [DOI] [PubMed] [Google Scholar]
- 20.Sandhu DS, Sandhu S, Karwasra RK, Marwah S. Profile of breast cancer patients at a tertiary care hospital in north India. Indian Journal of Cancer. 2010;47(1):16–22. doi: 10.4103/0019-509X.58853. [DOI] [PubMed] [Google Scholar]
- 21.Saxena S, Rekhi B, Bansal A, Bagga A, Chintamani, Murthy NS. Clinico-morphological patterns of breast cancer including family history in a New Delhi hospital, India-A cross-sectional study. World Journal of Surgical Oncology. 2005;3:67–75. doi: 10.1186/1477-7819-3-67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nouh MA, Ismail H, Ali El-Din NH, El-Bolkainy MN. Lymph node metastasis in breast carcinoma: Clinicopathologic correlations in 3747 patients. Journal of Egyptian National Cancer Institute. 2004;16(1):50–56. [PubMed] [Google Scholar]
- 23.Gann PH, Colilla SA, Gapstur SM, Winchester DJ, Winchester DP. Factors associated with axillary lymph node metastasis from breast carcinoma descriptive and predictive analyses. Cancer. 1999;86(8):1511–1518. doi: 10.1002/(sici)1097-0142(19991015)86:8<1511::aid-cncr18>3.0.co;2-d. [DOI] [PubMed] [Google Scholar]
- 24.Olivotto IA, Jackson JSH, Mates D, Andersen S, Davidson W, Bryce CJ, Ragaz J. Prediction of axillary lymph node involvement of women with invasive breast carcinoma a multivariate analysis. Cancer. 1998;83(5):948–955. [PubMed] [Google Scholar]
- 25.Ravdin PM, De Laurentiis M, Vendely T, Clark GM. Prediction of axillary lymph node status in breast cancer patients by use of prognostic indicators. Journal of National Cancer Institute. 1994;86(23):1771–1775. doi: 10.1093/jnci/86.23.1771. [DOI] [PubMed] [Google Scholar]
- 26.Chua B, Ung O, Taylor R, Boyages J. Frequency and predictors of axillary lymph node metastases in invasive breast cancer. Australian and New Zealand Journal of Surgery. 2001;71(12):723–728. doi: 10.1046/j.1445-1433.2001.02266.x. [DOI] [PubMed] [Google Scholar]
- 27.Manjer J, Balldina G, Garne JP. Tumour location and axillary lymph node involvement in breast cancer: A series of 3472 cases from Sweden. European Journal of Surgical Oncology. 2004;30(6):610–617. doi: 10.1016/j.ejso.2004.04.008. [DOI] [PubMed] [Google Scholar]
- 28.Manjer J, Balldin G, Zackrisson S, Garne JP. Parity in relation to risk of axillary lymph node involvement in women with breast cancer. European Surgical Research. 2005;37(3):179–184. doi: 10.1159/000085966. [DOI] [PubMed] [Google Scholar]
- 29.Olivotto IA, Jackson JSH, Mates D, Andersen S, Davidson W, Bryce CJ, Ragaz J. Prediction of axillary lymph node involvement of women with invasive breast carcinoma a multivariate analysis. Cancer. 1998;83(5):948–955. [PubMed] [Google Scholar]
- 30.Ravdin PM, De Laurentiis M, Vendely T, Clark GM. Prediction of axillary lymph node status in breast cancer patients by use of prognostic indicators. Journal of National Cancer Institute. 1994;86(23):1771–1775. doi: 10.1093/jnci/86.23.1771. [DOI] [PubMed] [Google Scholar]
- 31.Chua B, Ung O, Taylor R, Boyages J. Frequency and predictors of axillary lymph node metastases in invasive breast cancer. Australian and New Zealand Journal of Surgery. 2001;71(12):723–728. doi: 10.1046/j.1445-1433.2001.02266.x. [DOI] [PubMed] [Google Scholar]
- 32.Cetintas SK, Kurt M, Ozkan L, Engin K, Gokgoz S, Tasdelen I. Factors influencing axillary node metastasis in breast cancer. Tumori. 2006;92(5):416–422. doi: 10.1177/030089160609200509. [DOI] [PubMed] [Google Scholar]
- 33.Fisher B, Bauer M, Wickerham DL, Redmond CLK, Fisher ER. Relation of number of positive axillary nodes to the prognosis of patients with primary breast cancer. Cancer. 1983;52(9):1551–1557. doi: 10.1002/1097-0142(19831101)52:9<1551::aid-cncr2820520902>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 34.Harden SP, Neal AJ, Al-Nasiri N, Ashley S, Quercidella RG. Predicting axillary lymph node metastases in patients with T1 infiltrating ductal carcinoma of the breast. The Breast. 2001;10(2):155–159. doi: 10.1054/brst.2000.0220. [DOI] [PubMed] [Google Scholar]
- 35.Guern AS, Vinh-Hung V. Statistical distribution of involved axillary lymph nodes in breast cancer. Bull Cancer. 2008;95(4):449–455. doi: 10.1684/bdc.2008.0620. [DOI] [PubMed] [Google Scholar]
- 36.Kendal WS. Statistical kinematics of axillary nodal metastases in breast carcinoma. Clinical & Experimental Metastasis. 2005;22(2):177–183. doi: 10.1007/s10585-005-7211-y. [DOI] [PubMed] [Google Scholar]
- 37.Cameron AC, Trivedi PK. Econometric Society Monograph. New York: Cambridge University Press; 1998. Regression Analysis of Count Data. [Google Scholar]
- 38.Rose CE, Martin SW, Wannemuehler KA, Plikaytis BD. On the use of zero-inflated and hurdle models for modeling vaccine adverse event count data. Journal of Biopharmaceutical Statistics. 2006;16(4):463–481. doi: 10.1080/10543400600719384. [DOI] [PubMed] [Google Scholar]
- 39.Rampaul RS, Miremadi A, Pinder SE, Lee A, Ellis IO. Pathological validation and significance of micrometastasis in sentinel nodes in primary breast cancer. Breast Cancer Research. 2001;3(2):113–116. doi: 10.1186/bcr282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Schaapveld M, Otter R, de Vries EG, Fidler V, Grond JA, van der Graaf WT, de Vogel PL, Willemse PH. Variability in axillary lymph node dissection for breast cancer. Journal of Surgical Oncology. 2004;87(1):4–12. doi: 10.1002/jso.20061. [DOI] [PubMed] [Google Scholar]
- 41.Martin TG, Wintle BA, Rhodes JR, Kuhnert PM, Field SA, Low-Choy SJ, Tyre AJ, Possingham HP. Zero tolerance ecology: Improving ecological inference by modeling the source of zero observations. Ecology Letters. 2005;8(11):1235–1246. doi: 10.1111/j.1461-0248.2005.00826.x. [DOI] [PubMed] [Google Scholar]
- 42.Zorn CJW. Midwest Political Science Association. San Diego: 1996. Evaluating zero-inflated and hurdle Poisson specifications. [Google Scholar]
- 43.Boucher JP, Denuit M, Guillen M. Risk classification for claim counts: A comparative analysis of various zero inflated mixed Poisson and hurdle models. North American Actuarial Journal. 2007;11(4):110–131. [Google Scholar]
- 44.Bohning D, Dietz E, Schlattmann P, Mendonca L, Kirchner U. The zero inflated Poisson model and the decayed, missing and filled teeth index in dental epidemiology. Journal of the Royal Statistical Society (Series A) 1999;162(2):195–209. [Google Scholar]
- 45.Cheung YB. Zero-inflated models for regression analysis of count data: A study of growth and development. Statistics in Medicine. 2002;21(10):1461–1469. doi: 10.1002/sim.1088. [DOI] [PubMed] [Google Scholar]