Characterization of Patient Specific Signaling via Augmentation of Bayesian Networks with Disease and Patient State Nodes

Abstract

Characterization of patient-specific disease features at a molecular level is an important emerging field. Patients may be characterized by differences in the level and activity of relevant biomolecules in diseased cells. When high throughput, high dimensional data is available, it becomes possible to characterize differences not only in the level of the biomolecules, but also in the molecular interactions among them. We propose here a novel approach to characterize patient specific signaling, which augments high throughput single cell data with state nodes corresponding to patient and disease states, and learns a Bayesian network based on this data. Features distinguishing individual patients emerge as downstream nodes in the network. We illustrate this approach with a six phospho-protein, 30,000 cell-per-patient dataset characterizing three comparably diagnosed follicular lymphoma, and show that our approach elucidates signaling differences among them.

I. INTRODUCTION

Cells respond to their environment via signaling pathways, in which extracellular cues trigger a cascade of information flow, causing signaling molecules to become chemically, physically or locationally modified, gain new functional capabilities, and affect subsequent molecules in the cascade, culminating in a phenotypic cellular response. The disregulation of signaling pathways has been implicated in numerous disease states, such as autoimmune disease and cancer [8], [9]. Characterization of disease state via signaling profiling of patient samples has been previously successful, identifying prognostic indicators and segregating patients based on disease outcome [2]. However, these studies have focused on signaling proteins in isolation, neglecting the multivariate interactions among the signaling proteins, that result from the highly intertwined signaling network that they compose. Additional information is contained in this multivariate data which is not utilized by the univariate analyses performed in these studies. This additional information may help to further characterize patient profiles, leading to a potential for better and earlier diagnostic tests and improved prognostic indicators. Here, we propose a novel approach to characterize patient signaling profiles, based on analysis of high throughput, multidimensional single cell measurements performed using an approach called flow cytometry. Single cell measurements of signaling proteins of interest are obtained in high throughput for each patient, yielding thousands of cells per patient. The large sample size provides an opportunity to examine not only the distribution of individual phospho-proteins but also - because the molecules are measured simultaneously - enables the elucidation of statistical relationships among them.

Cancer is a heterogeneous disease, thought to arise from a culmination of multiple random mutations [8]. Because of this, patients bearing identical diagnoses may behave quite differently on a molecular level [9]. We present an approach to characterize patients based on patient-specific signaling and elucidate inter-patient signaling variability. This approach distinguishes patients based on what nodes in the interconnected phospho-protein network are dependent on the identity of each patient, in a sense, which nodes are influenced by each patient. The approach is based on Bayesian network structure learning, in which the data, consisting of single cell measurements of signaling proteins, is augmented by ‘state nodes’, indicator variables reflecting the origin of each cell in the data matrix. These state nodes, one per patient, are included in the Bayesian network structure learning step, and the resulting graph automatically indicates which nodes and interactions in the network contain variability specific to each patient, providing a high level characterization of patient signaling profiles.

In this proof of principle study, we apply our approach to a dataset of 3 equivalently diagnosed follicular lymphoma patients. We show that our approach is able to distinguish molecular level heterogeneity among these patients.

Flow cytometric patient data

The data we employ comes from flow cytometry, a unique proteomic tool which allows high throughput profiling of the protein content of individual cells, measuring thousands of cells per second [9]. It is possible to specifically measure the abundance of the phosphorylated form of proteins of interest, a crucial feature, since the phosphorylated form is typically the active form. Phosphorylated signaling proteins of interest are labeled with fluorescent-tagged antibodies, and fluorescence is quantified on a cell by cell basis. In prior studies, B cells from follicular lymphoma patients were stimulated through the B-cell antigen receptor (BCR) and, at several time points following stimulation, the cells were fixed, permeabilized, and stained to measure the activation state of six signaling proteins, SYK, Src family kinases (SFK, e.g. Lyn), ERK, p38, and CBL [3]. Here we focused on the time point eight minutes following activation of BCR signaling in order to compare differences in initiation and amplification of signaling. Data studied were from tumor biopsy specimens taken prior to any therapy from patients newly diagnosed with follicular lymphoma [3]. Tumor specimens were obtained with informed consent in accordance with the Declaration of Helsinki and this study was approved by Stanford University's Administrative Panels on Human Subjects in Medical Research.

Bayesian networks

We employ a graphical model technique called Bayesian network (BN) structure learning to learn statistical dependencies among variables. Bayesian networks [4], represent probabilistic dependence relationships among multiple interacting components, illustrating the effects of pathway components upon each other in the form of an influence diagram - a graph (G) - and a joint probability distribution. In the graph, the nodes represent variables (the biomolecules) and the (lack of) edges represent (conditional in)dependencies [4]. For each variable, a conditional probability distribution (CPD) quantitatively describes the form and magnitude of its dependence on its parent(s) [5]. These models can be automatically derived from experimental data through a statistically founded computational procedure termed network inference or structure learning.

A. Overview of approach

Our goal in this work is to provide a high-level characterization of patient signaling. We approach this by building a multivariate model of statistical interactions among random variables (the measured phospho-proteins), into which we incorporate nonrandom 'state variables’, representing each patient. We build a graphical model to learn the statistical dependencies among the variables, in which the state variables are allowed to participate as root nodes. For each patient, points of distinction in the network emerge as targets of the patient node. These targets (known as ”children”) of each patient node provide an indication of which phospho-proteins and interactions are distinct in a particular patient, as compared to other patients or to a background distribution from healthy samples, yielding a characterization of patient-specific signaling.

To learn the model structure, we start with the measured phospho-protein levels in each cell. In this dataset, over 30,000 cells were available for each patient, providing a statistically robust dataset size for probabilistic analysis. Each dataset consists of a matrix with 6 columns, one for each phospho-protein, and 10,000 (or more) rows, one for each cell. We first concatenate the data matrices from each patient, producing one large matrix with 6 columns and 10,000 * n rows, assuming n patients and 10,000 cells per patient. Next, the data matrix is augmented with additional columns of binary indicator variables, one for each patient, labeling the source of each cell in the data matrix. For instance, if cells 10,001-20,000 came from patient 2, those rows will contain a 1 for the patient 2 state node, and a zero in the other state nodes. When healthy samples are included in the analysis, the rows corresponding to cells from healthy samples will contain zeros in the columns for all the patient nodes. A ‘disease state’ node can also be incorporated, by augmenting the data matrix with an additional column bearing a 1 for each patient derived cell (regardless of patient identity) and a zero for each cell originating in a healthy sample. Note than in general, the state nodes need not be binary (for instance, they can indicate degree of severity of disease sample, if known). Finally, Bayesian network structure learning is performed, with state nodes constrained to be root nodes (i.e. have an in-degree of zero).

We are aware of two earlier studies in which data were similarly augmented by state nodes, in a Bayesian network learning context. Eaton and Murphy [1] included state variables for drug activities and Lee et al. [6] utilized state variables to represent yeast genotype. In each of these earlier efforts, the focus was on learning the structure of the random variables; the state variables served to help in the structure learning effort. In the approach proffered here, we focused less on the inferred structure among the phospho-protein variables and aimed instead to characterize the state (patient) nodes themselves. To our knowledge, this is the first time such an approach has been employed.

B. Model justification and interpretation

Learning the Bayesian network model augmented with state nodes allows us to find the points of influence of the state nodes, providing a characterization of these nodes. How does this work, and how should the results be interpreted? In the structure learning algorithm, an edge may be added from node i (either a state node or a regular node representing a random variable) to node j if i is predictive of j, in the context of j's other parents (if any). There is a tradeoff between simple models and those that accurately capture the empirical distribution observed in the data. The employed Bayesian scoring metric captures this trade-off, thus, an edge will be added only if sufficient evidence exists to support it [5]. When sufficient data exists, an edge will appear even if it is only evident in a subset of the data. Thus, with our approach employing a concatenated matrix of all patient data, edges can appear if they are supported by any of the data subsets, originating from individual patients. The patient specificity of these edges will be indicated by outgoing edges from each patient node. For example, if phospho-protein Y is well predicted by phospho-protein X in the dataset, the learned structure between them may be X → Y. If, for patient i, X is no longer predictive of Y, or if it is predictive but the conditional distribution P(Y|X) is altered, then the structure learning algorithm may also add the edge i → Y.

In general, an edge from a state node to a phospho-protein indicates that the distribution of the phosphorylated form of that protein (conditioned on its other parents in the network) is different when conditioned also on the patient, in other words, that phospho-protein's distribution is different for the patient than it is in the background distribution (i.e. the distribution observed in the other patients or in the healthy samples). This may appear as a simple change in abundance of the phosphorylated form of a particular protein. However, it can also be true even if the phospho-protein abundance has not changed. To envision this, consider phospho-proteins A and B, with the relationship A → B, where A is an activator of B. In patient i, the level of A is particularly low, so we anticipate the relationship i → A. In this case, the arrow corresponds to a change in the level of A. However, the patient may also have an altered A → B relationship, in which the activation of B by A is much stronger than usual. Since the conditional distribution of B is different for patient i, the edge i → B will emerge, however, B's level may be imperceptibly different from the background distribution. This kind of patient specific alteration, in which the overall value of a phospho-protein is unchanged, but its conditional distribution is affected, is very difficult to discern by inspection of two and three dimensional plots, especially if the relationship itself is complex and involves multiple variables. However, it is straightforward to elucidate this change using the Bayesian network approach.

Our approach characterizes patient-specific signaling alterations, leading naturally to the possibility of comparing these alterations across patients. In particular, the patients in this study all have equivalent diagnoses: does this translate into similar signaling profiles? In fact it does not, as specific differences are clearly elucidated, a fact that can be seen at a glance when inspecting the resulting models. Detailed interpretation of the graphs requires more care. Patients with different downstream targets indicate differences in alterations, as anticipated. However, patients pointing to the same phospho-protein target may in fact have unique alterations with respect to that phospho-protein; each Patient→Phospho-Protein edge indicates a difference of the patient specific distribution as compared to the background distribution, but does not tell us how each patient's imposed distribution compares to the other patients’ altered distributions. This further level of details can be extracted from the model CPDs, a useful extension that we leave for future study.

II. RESULTS

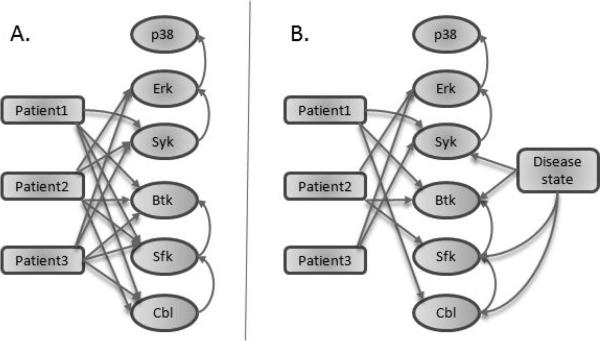
In this proof of principle study, we applied our approach to data from three patients and from healthy controls. Samples were stimulated as described and fixed at 8 minutes after stimulating BCR signaling [3]. Six phospho-proteins were profiled, three at a time, with SYK, ERK and p38 measured in one stain set panel, and CBL, SFK and BTK in a second panel. Two stain sets were used because measuring phosphorylated forms of all 6 proteins together, along with the necessary surface markers for identification of the relevant cell types, would have caused logistical and technical difficulties. Additionally, the data were not originally generated for multivariate analysis, and so no attempt was made to increase the dimensionality of each experiment. We augmented the data matrix as described above, adding a state node for each patient. Because both stimulated and unstimulated data were included, a stimulation state node was included as well, to avoid confounding the distributions. This state node was fully connected as anticipated, so it has been eliminated from the results graphs for visual convenience. Data were discretized to 6 levels, and structure learning was performed as previously described [7], with all state nodes constrained to be root nodes. The resulting model (figure 1A) shows very high, nearly full, connectivity, with nearly all patients pointing to nearly all phospho-proteins. None of the patients pointed to p38, in spite of the fact that p38 is higher in these patient samples than in the normal controls (see [3]). Although the abundance of phosphorylated p38 changed in the disease state, this difference was explained by the influence of ERK on p38. Thus, the absolute amount of phosphorylated p38 was altered, but the conditional distribution P(p38|ERK) remained the same. Patient 1 alone did not point to ERK. Consistent with this, the correlation between ERK and SYK in the Patient 1 sample was similar to that in the healthy samples (R ≈ 0.8, data not shown), while the correlation in the Patient 2 and Patient 3 samples was distinct.

Fig. 1.

Model results. Structure learning was performed on the phospho-protein variables augmented with A. patient nodes only or B. patient nodes in addition to a disease state node. All state nodes are constrained to be roots.

The disease state results in general changes, making the patients as a group distinct from the healthy samples. These differences obscure individual patient to patient variation in the model results. We addressed this by including a disease state node, which indicated for each cell in the data whether it was from a healthy sample or a disease sample in a patient nonspecific manner. The resulting model (figure 1B) is significantly more sparse than the original model, with general disease differences indicated by the disease state node. From stain set 1, the disease state node points to SYK, but not to ERK or p38. Irish et al. [3] reported a difference in activation of all three of these phospho-proteins, but our model was able to discern that the difference was due to the difference in SYK; their conditional distributions remain unchanged from the healthy to disease state. Additionally, the original study did not explore the role of CBL or SFK, but our model discerned a change in these phospho-proteins. Examination of the data revealed a change in the distributions of these molecules (figure 3), however, because the data are non-normal and nonunimodal, the summary statistics employed in [3] missed these changes. Thus, our approach successfully identifies differences between healthy and disease states.

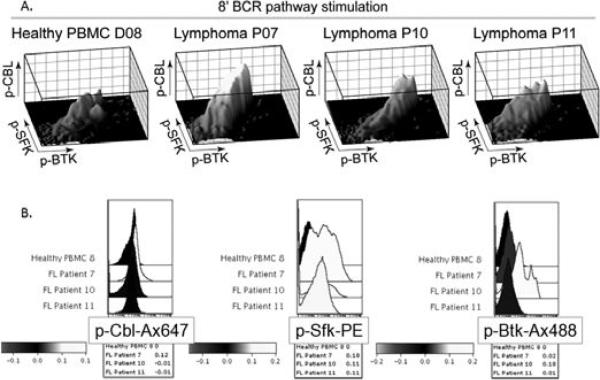
Fig. 3.

Raw data. A. 3-dimensional and B. Histogram plots of stain set 2 phospho-proteins. Patient 7 corresponds to patient 1, patient 10 to patient 2 and patient 11 to patient 3. A healthy control is included for comparison.

Differences among the patients could be seen more clearly once the major disease/healthy alterations were represented separately (by the disease state node). As before, Patient 1 did not point to ERK because the SYK, ERK correlation was similar to healthy samples. Note that the disease state node did not change this, because it itself did not point to ERK. Patient 2 did not point to SYK, which is consistent with the data – the SYK distribution was about average among the patient samples. However, the SYK, ERK correlation for Patient 2 was different from the other patients, explaining the presence of an edge from Patient 2 to ERK. (See figure 2)

Fig. 2.

Raw data. 2 dimensional plot of SYK versus ERK. Patient 7 corresponds to patient 1, patient 10 to patient 2 and patient 11 to patient 3. A healthy control is included for comparison.

Prominently, for the stain set 2 phospho-proteins, Patient 3 pointed to no phospho-proteins. This is unsurprising, as the values of three phospho-proteins were about average for the disease state for this patient. Patient 2 had a level of CBL that was about average for the disease state, but a drastically altered distribution of SFK and BTK, as discerned by the model. A visual inspection of the data demonstrates that the joint distributions of the stain set 2 phospho-proteins were different among the three patients, though it does not clearly demonstrate the specific points of difference for each patient, aside from those mentioned above (figure 3). In general, the technique was more sensitive to changes, as compared to what can be discerned by visual inspection. As the dimensionality of our data increases to 4 dimensions and beyond, a thorough visual inspection of the complex interactions becomes impossible, necessitating a computational examination of patient differences.

III. Discussion and Conclusions

In this work, we presented a new modeling scheme for the characterization of patient and disease state from multivariable data-sets. We did this by augmenting the Bayesian Networks model of the phospho-protein signaling pathway by nodes pertaining to the patients and the disease states. This modeling scheme is extremely effective in terms of characterizing the relationship between the patient state and phospho-protein concentrations. In particular, very complex relationships can be detected and reported. This is obvious in our results, especially in the cases where the causal relationships between the patient nodes and phospho-proteins were reported, even in the cases where the average concentration of the proteins wasn't affected by the patient (but the distribution was affected). Additionally, our modeling scheme distinguished between phospho-proteins that had different concentrations purely because of patient properties, and those that had different concentrations because of the difference in other proteins.

Similar advantages of our scheme are evident in the characterization of the disease state. Our scheme detects very complex changes in per-cell phospho-protein concentrations, when there are enough data to support the validity of those changes. Additionally, phospho-proteins affected by the disease state were well distinguished from those that were affected purely by changes in other phospho-proteins’ concentrations.

Our ability to characterize disease state and patient signaling, indicating differences in comparably diagnosed patients, may lead to the development of improved and more detailed diagnostic tools, which, if assessed for prognostic indications, may enable more specific, more personalized and more effective therapies.