Skip to main content
NCBI home page
Biophysical Reviews logoLink to Biophysical Reviews
. 2010 Aug 5;2(3):137–145. doi: 10.1007/s12551-010-0036-1

A short survey on protein blocks

Agnel Praveen Joseph 1,2,3, Garima Agarwal 4, Swapnil Mahajan 4,5, Jean-Christophe Gelly 1,2,3, Lakshmipuram S Swapna 4, Bernard Offmann 6,7, Frédéric Cadet 6,7, Aurélie Bornot 1,2,3, Manoj Tyagi 8, Hélène Valadié 9, Bohdan Schneider 10, Catherine Etchebest 1,2,3, Narayanaswamy Srinivasan 4, Alexandre G de Brevern 1,2,3,✉
PMCID: PMC3124139  PMID: 21731588

Abstract

Protein structures are classically described in terms of secondary structures. However, even if the regular secondary structures have relevant physical meaning, their recognition based on atomic coordinates has a number of important limitations, such as uncertainties in the assignment of the boundaries of the helical and β-strand regions. In addition, an average of about 50% of all residues are assigned to an irregular state, i.e., the coil. These limitations have led different research teams to focus on abstracting the conformation of the protein backbone in the localized short stretches. To this end, different geometric measures are being used to cluster local stretches in protein structures in a chosen number of states. A prototype representative of the local structures in each cluster is then generally defined. These libraries of local structure prototypes are named "structural alphabets". We have developed a structural alphabet, denoted protein blocks, not only to approximate the protein structure but also to predict them from the sequence. Since its development, we and others have explored numerous new research fields using this structural alphabet. Here, we review some of the most interesting applications of this structural alphabet.

Keywords: Protein structures, Secondary structures, Structural alphabet, Structure prediction, Structural superimposition, Mutation, Binding site

Introduction

Protein structures have been classically described in two regular states, the α-helix and β-strand, with the remaining unassigned regions described as an irregular state (coil) that corresponds to a large number of diverse conformations. However, the use of only three states oversimplifies the description of protein structures. A detailed description for 50% of the residues classified as coils is lacking even when they encompass a repeating local structure. To date, the description of local protein structures has focused on the elaboration of complete sets of small prototypes or "structural alphabets" (SAs), that help to approximate each part of the protein backbone (Offmann et al. 2007). Designing an SA requires the identification of a set of average recurrent local protein structures that (efficiently) approximates each part of the known structures. As each residue is associated to one of these prototypes, the whole three-dimensional (3D) protein structure can be translated into a series of prototypes (letters) in one dimension (1D) as the sequence of prototypes.

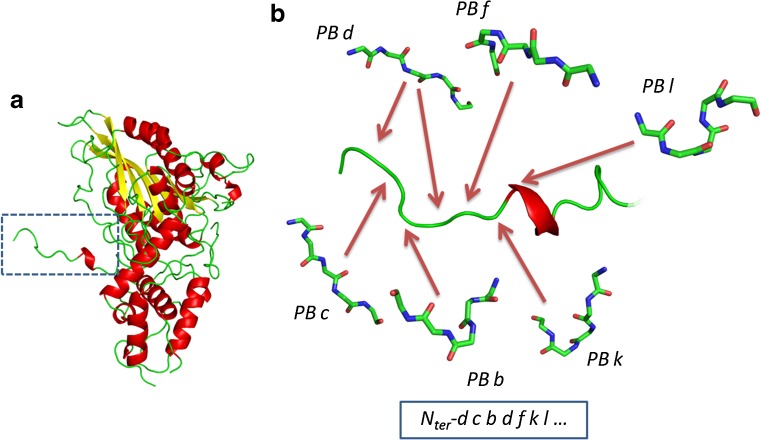
Figure 1 shows an example of the encoding of a protein structure with an SA. The N-terminal extremity of Aspergillus niger acid phosphatase (Kostrewa et al. 1999) chain B is shown. A local protein structure prototype was associated to each residue, thereby enabling the precise description of the coil region as a succession of small protein prototypes instead of as a succession of identical states.

Fig. 1.

Fig. 1

Open in a new tab

Principle of encoding of protein structures using a “structural alphabet”. The N-terminal extremity of chain B of Aspergillus niger acid phosphatase (Kostrewa et al. 1999) (a) is encoded in terms of a structural alphabet (b). Each residue is approximated by a specific prototype—here a protein block (PB). Hence, the crude description as a coil region (determined by any secondary structure assignment method) is replaced by a more precise series of PBs dcbdfkl

Protein blocks

Secondary structure assignments are widely used to analyze protein structures. However, such an approach often results in a coarse description of 3D protein structures, with about half of the residues being assigned to an undefined state (Bornot and de Brevern 2006). Moreover, the structural diversity observed in α-helices and β-strands is hidden. Indeed, α-helices are frequently not linear; rather, they are either curved (58%) or kinked (17%) (Martin et al. 2005). The absence of a secondary structure assignment for a significant proportion of the residues has led to the development of local protein structure libraries that are able to approximate all (or almost all) of the local protein structures without the need for classical secondary structures. These libraries have yielded prototypes that are representative of local folds found in proteins. The complete set of local structure prototypes defines an SA (Offmann et al. 2007).

Ten years ago, Serge Hazout developed a novel SA with two specific goals (de Brevern et al. 2000): (1) to obtain a good local structure approximation and (2) to predict local structures from the sequence. Fragments five residues in length were first coded in terms of the φ/ϕ dihedral angles, and then a root mean square deviation on angle (RMSDA) score was used to quantify the structural difference among the fragments (Schuchhardt et al. 1996). Using an unsupervised cluster analyzer related to self-organizing maps (SOM; Kohonen 1982, 2001), a three-step training process was carried out. The first step involved identifying the structural difference between fragments in terms of RMSDA; the second step took the transition probability (probability of transition from one fragment to another in a sequence) into consideration along with the RMSDA, i.e., in a similar way to the Markov model (Rabiner 1989). In the third step, the constraint based on transition probability was removed. Optimal prototypes were identified by considering both the structural approximation and the prediction rate. A set of 16 prototypes called protein blocks (PBs), represented as average dihedral vectors, was obtained at the end of this process (de Brevern et al. 2000).

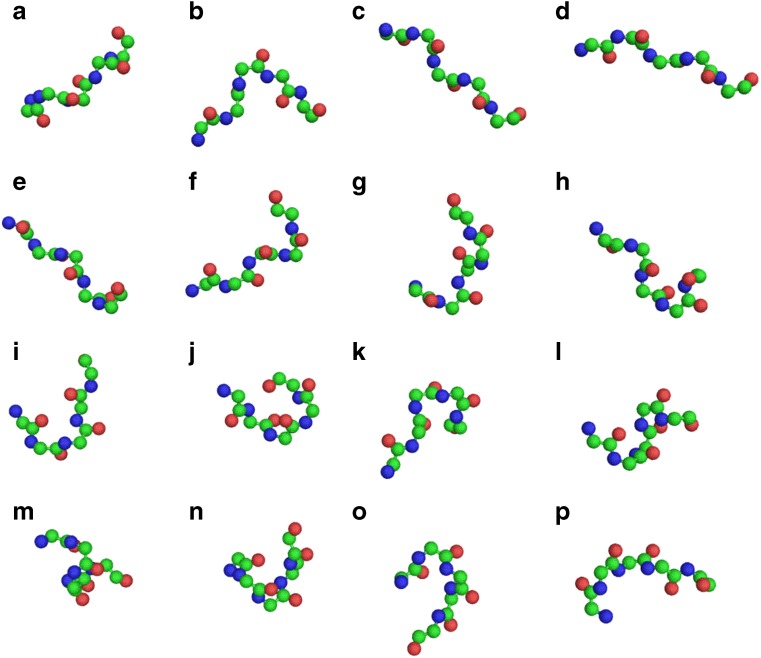
These PBs are displayed represented in Fig. 2. PBs m and d can be described roughly as prototypes of the central α-helix and central β-strand, respectively. PBs a through c primarily represent β-strand N-caps and PBs e and f, β-strand C-caps; PBs g through j are specific to coils, PBs k and l to α-helix N-caps, and PBs n through p to α-helix C-caps. This SA allows a good approximation of local protein 3D structures, with an average RMSD now evaluated at 0.42 Å (de Brevern 2005). PBs have been assigned using in-house software (available at http://www.dsimb.inserm.fr/DOWN/LECT/) or using PBE web server (http://bioinformatics.univ-reunion.fr/PBE/) (Tyagi et al. 2006b).

Fig. 2.

Fig. 2

Open in a new tab

The protein blocks. PBs from a to p are shown using PyMol software (DeLano 2002).. For each PB, the N -ap extremity is shown on the left and the C-cap on the right. Each prototype is five residues in length and corresponds to eight dihedral angles (φ,ψ). The PBs m and d are mainly associated to the central region of α-helix and the central region of β-strand, respectively (de Brevern 2005; de Brevern et al. 2000)

PBs (de Brevern et al. 2000) have been used both to describe the 3D protein backbones (de Brevern 2005) and to perform local structure prediction (de Brevern et al. 2000, 2007, 2002; Etchebest et al. 2005). Our earlier work on PBs revealed that PBs are effective in describing and predicting conformations of long fragments (Benros et al. 2006, 2009; Bornot et al. 2009; de Brevern and Hazout 2001, 2003; de Brevern et al. 2002, 2007; ) and short loops (Fourrier et al. 2004; Tyagi et al. 2009a,b), analyzing protein contacts (Faure et al. 2008), in building a transmembrane protein (de Brevern 2005; de Brevern et al. 2009), and in defining a reduced amino acid alphabet to aid the design of mutations (Etchebest et al. 2007). This reduced amino acid alphabet was recently proved suitable for predicting protein families or sub-families and secretory proteins of Plasmodium falciparum (Zuo and Li 2009, 2010). We have also used PBs to superimpose and to compare protein structures (Tyagi et al. 2006a, b, 2008).

Other laboratories have taken advantage of PBs to reconstruct globular protein structures (Dong et al. 2007), design peptides (Thomas et al. 2006), and define binding site signatures (Dudev and Lim 2007). Novel prediction methodologies (Li et al. 2009; Rangwala et al. 2009; Zimmermann and Hansmann 2008) and fragment-based local statistical potentials (Li et al. 2009) have also been developed. The features of this alphabet have been compared by Karchin et al. (2003) with those of eight other SAs, revealing that our PB alphabet is highly informative, with the best predictive ability of those tested. Among the currently available SAs, it is the most widely at the present time.

Applications

Binding site signature

Protein blocks enable the detection of structural similarity between proteins with excellent efficiency. Dudev, Lim and co-workers (Dudev and Lim 2001; Yang et al. 2008) used this concept to locate structural motifs of metal/ligand-binding sites in proteins (Dudev and Lim 2007). These researchers encoded a protein structure databank in terms of PBs and subsequently located PBs encompassing specific metal-binding sites. They then defined a discontinuous PB pattern, similar to a PROSITE pattern. First, the structural motifs of the Cys4 Zn-finger domains, which are known to adopt a specific structure, were analyzed. They then focused on structural motifs of the Mg2+-binding sites in a set of non-redundant Mg2+-binding proteins. Four Mg2+-structural motifs were identified that showed important binding site relationships were identified, and then other features of the proteins were defined (Dudev and Lim 2007). This strategy can be easily extended to other cases. These researchers have recently extended the approach to DNA and RNA binding sites, highlighting a novel non-specific motif enabling diverse interactions with DNA and RNA as with proteins (Wu et al. 2010).

Definition of a reduced amino acid alphabet

The reduced amino acid alphabet is a popular concept that has been explored by many research teams. Indeed, the appropriate selection of an amino acid type in a reliable set is a particularly helpful approach to limit the number of experiments. Most of such approaches are mainly based on sequence properties (Akanuma et al. 2002; Clarke 1995; Kamtekar et al. 1993).

In this area, PBs not only help in describing protein structures, but they are also useful in extracting sequence–structure relationships. Based on this relation, we have proposed an association of amino acids in a limited number of clusters. This approach permits an exchange of amino acids that are equivalent in terms of sequence–structure relationship, while still maintaining local protein structure conformation (Etchebest et al. 2007). Zuo and Li used this reduced amino acid alphabet to predict different properties through a learning approach (Zuo and Li 2009, 2010).

Long structural fragments

Protein blocks are 5-residue-long fragments. To assess the structural stability of these short fragments, we identified the most frequent series of five consecutive PBs which are nine residues long. We then selected the 72 most frequent series and named them structural words (SWs). Interestingly, SWs encompass 92% of the residues (nearly 100% of the repetitive structures and 80% of secondary structure coil). By using most of the SWs, we were able to create a simple network describing most of the transitions between the SWs in proteins (de Brevern et al. 2002). The study of SWs yields a pertinent description of a large part of 3D structures, but as they constitute a sub-set of all five PBs combinations, they do not allow for a description of every part of the protein structure. We therefore have developed a novel approach named the Hybrid Protein Model (HPM; de Brevern and Hazout 2000). This innovative approach allowed us to create longer prototypes comprising 10–13 residues Benros et al. 2002, 2003, 2006, 2009; de Brevern and Hazout 2001, 2003). This resulted in a higher structural variability for the longer fragments through a significant increase in the number of prototypes, e.g., 100–130 prototypes (Benros et al. 2006, 2009; de Brevern and Hazout 2001, 2003). These longer fragments were used to perform structural superimposition (de Brevern and Hazout 2001), methodological optimization (Benros et al. 2003; de Brevern and Hazout 2003), and analyses of the sequence–structure relationship (Benros et al. 2006, 2009; Bornot et al. 2009; de Brevern and Hazout 2001). A modified version of HPM proposed by Serge Hazout has led to the construction of networks of local protein structures (Hazout 2005).

Structural alignment

The SA allows 3D protein structures to be translated into a series of letters (see Fig. 1a). Consequently, it is possible to use classical sequence alignment methodology to perform structure-based alignment (see Fig. 1b). The main difficulty lies in obtaining a pertinent substitution matrix in order to find the similarity score between PBs for alignments. Using the homologs of known 3-D structures in the PALI database (Gowri et al. 2003) encoded in terms of PBs, it has been possible to compute a PB substitution matrix (Tyagi et al. 2006b). A dedicated webserver has been developed (http://bioinformatics.univ-reunion.fr/PBE/) that performs optimal alignments of a query protein structure with entries of 3-D structures in a database by using PBs and the substitution matrix (Tyagi et al. 2006a). A recent benchmark has proved that this method is most efficient in mining PDB and identifying proteins of a similar 3-D structure (Tyagi et al. 2008).

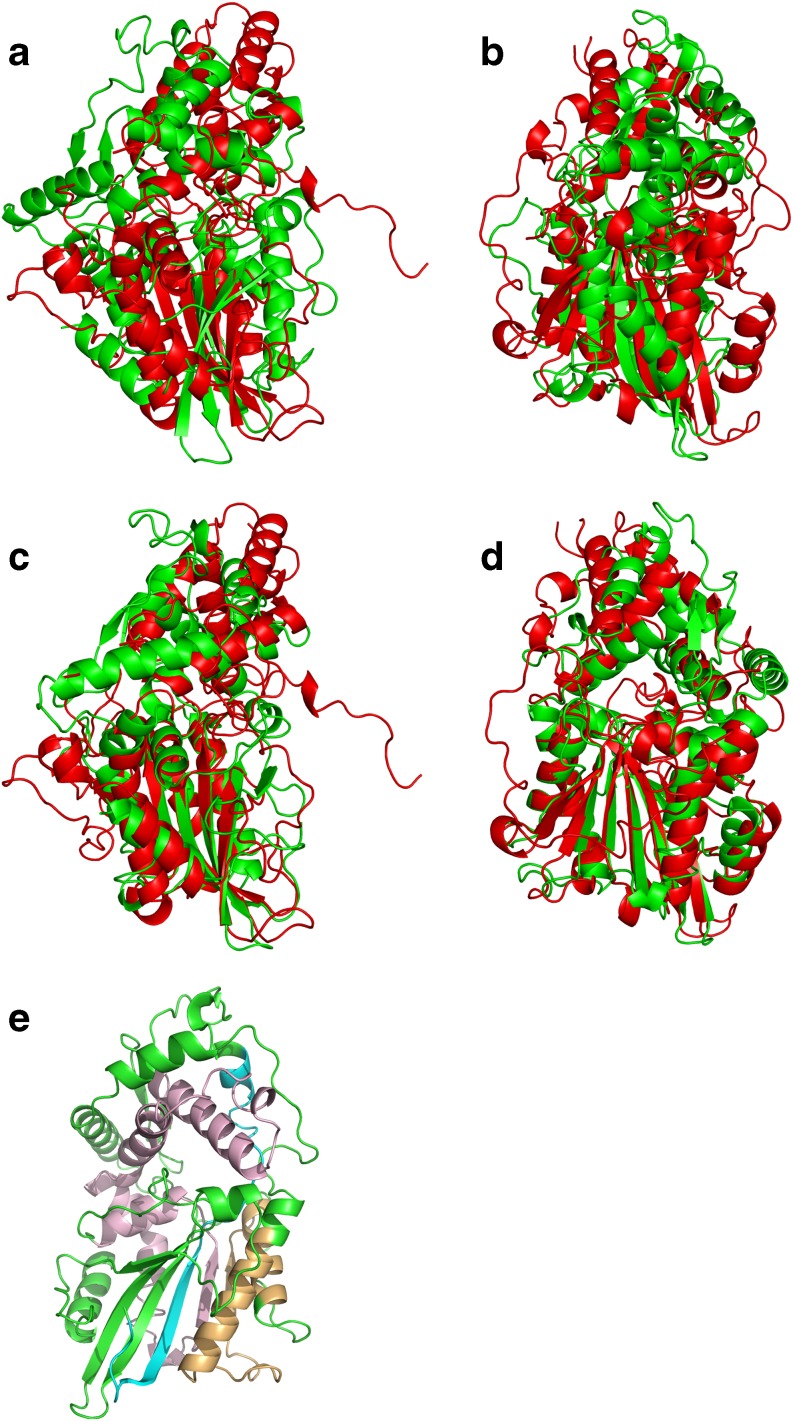
New developments in the field of protein structure have originated from this work. One of these relates directly to the use of the substitution matrix and concerns the characterization of conformational patterns in active and inactive forms of kinases. A comparison of closely related kinases revealed a higher global similarity between the active state kinases compared to the inactive states (as reflected from their PB scores) (Agarwal et al. 2010). The second axis focuses on the database, which is the basis for generating the substitution matrix, namely, the PALI database. The superimposed structures of PALI show regions with the correct alignments linked with regions more difficult to align (named variable regions). A novel optimization of the superposition based on PBs shows a global improvement in the variable regions. Hence, PBs improve PALI database alignments (Agarwal et al. in preparation). The last axis concerns the alignment approach. Even though the recent benchmark has demonstrated the quality of the methodology (Tyagi et al. 2008), some structural alignments still show poor consistency. Optimization of the substitution matrix and a novel alignment methodology have improved both the mining and the superimposition of protein structures (Joseph et al. in preparation). Figure 3 illustrates a very difficult case of superimposition of the 3D structures of Aspergillus niger acid phosphatase (Kostrewa et al. 1999) and Escherichia coli periplasmic glucose-1-phosphatase (Lee et al. 2003). In comparison, the superimposition obtained with our previous approach (Tyagi et al. 2006b) is quite poor. Our novel procedure allows the recognition of highly similar regions (shown on Fig. 3e) and provides a spectacular improvement in the superimposition. Figure 3c, d show that the bottom part of the protein structures can truly be superimposed. Figure 4 gives the alignment in terms of PBs.

Fig. 3.

Fig. 3

Open in a new tab

An example of difficult superimposition of three-dimension (3D) protein structures using PBs. The 3D structure of the Aspergillus niger acid phosphatase (Kostrewa et al. 1999) chain B has been superimposed on the 3D structure of Escherichia coli periplasmic glucose-1-phosphatase chain A (Lee et al. 2003). a, b Superimposition using a previous approach (Tyagi et al. 2006b), c, d superimposition with the novel approach. Using regions of high similarity as seeds (blue, gold and pink), as shown in e, the root mean square deviation is 17 Å lower than the value previously computed

Fig. 4.

Fig. 4

Open in a new tab

An example of a hard case of superimposition of 3D protein structures using PBs. The 3D superimposition shown in Fig. 3 is presented here as the PB alignment. Repetitive PBs and direct N-cap and C-cap are shown in color

Prediction

As with secondary structure prediction, it is possible to predict local structures in terms of the SA (see Table 1 for a summary of all prediction approaches). Indeed, concomitant to an accurate description of the local 3D structure, the definition of PBs is driven by prediction capabilities (de Brevern et al. 2000). The prediction principle is based on Bayes’ theorem. First, a set of protein chains used in training were encoded in terms of PBs using the minimal RMSDA criterion. Then, sequence windows of 15 residues length were considered for calculating the propensities associated with each PB. For each PB, the probability of occurrence of an amino acid at each position in the sequence window was calculated and an occurrence matrix generated, i.e., 16 for the 16 PBs. Bayes theorem was applied to predict the structure of the new sequences. A prediction rate of 34.4% was achieved (de Brevern et al. 2000, 2004). Nonetheless, as only one amino acid occurrence matrix is associated to each PB, the sequence information is averaged. A clustering approach related to SOM (Kohonen 1982, 2001) performed on PBs sequences revealed well-defined sequence families for some PBs; an amino acid occurrence matrix was then computed for each sequence family. This strategy increased sequence specificities for some PBs and permitted an improved prediction rate of 40.7% to be achieved (de Brevern et al. 2000, 2004). Finally, a simulated annealing approach in the process of sequence family generation helped to improve the overall prediction to 48.7% (Etchebest et al. 2005). Importantly, this approach did not bring any biased or unbalanced improvements between the PBs. Combining the secondary structure information with the Bayesian prediction did not result in any significant improvement in the prediction rate. A website, LocPred (http://www.dsimb.inserm.fr/∼debrevern/LOCPRED/), which includes most of the tools developed to date, is available to facilitate researchers in performing these predictions (de Brevern et al. 2004). Predictions were also performed with the SWs (de Brevern et al. 2002, 2007) and specifically for short loops (Fourrier et al. 2004; Tyagi et al. 2009a, b).

Table 1.

Summary of prediction methods in terms of approaches, year of publication, prediction rate, and remarks

Approach Year Information Prediction rate (%) Reference Web server Remarks
Bayesian prediction 2000 One sequence 34.4 de Brevern et al. [10] LocPred First method
Sequence families 2000 One sequence 40.7 de Brevern et al. [10] LocPred Based on Bayesian prediction
Bayesian prediction 2002 One sequence 34.4 de Brevern et al. [16] None Prediction of structural words
Hidden Markov Model 2003 One sequence None Karchin et al. [34] None Fold recognition
Sequence families 2005 One sequence 48.7 Etchebest et al. [20] LocPred Improved sequence families
Pinning strategy 2007 One sequence 43.6 de Brevern et al. [18] None Prediction of structural words
knowledge-based prediction 2007 One sequence 62.0 Offmann et al. [42] pb_prediction Pentapeptide match/SCOP class
Two-layer support vector machine 2008 Evolutionnary 61.0 Zimmermann and Hansmann [57] LOCUSTRA First use of evolutionary information
Database-matching approach 2009 One sequence 45.3 Li et al. [40] LSSRAP Use also accessibility and secondary structure
svmPRAT 2009 Evolutionnary 68.9 Rangwala et al. [44] svmPRAT Protein residue annotation toolkit
Open in a new tab

A knowledge-based approach for predicting local backbone structure was also developed. In this case, overlapping fragments of five residues from a query sequence are extracted and queried against a pentapeptide database. In this database, which was built from the SCOP database culled at 95% identity, each pentapeptide is mapped to a PB. In absence of any “hit” in the database, pentapeptides in which constraint of identity in the central position (position 3) is relaxed are considered. Overall performance of the approach was about 62%.

Recent developments have been made by other teams. Li and co-workers proposed an innovative approach for PB prediction that takes into account information from secondary structure and solvent accessibility (Li et al. 2009). Prediction rates were significantly improved (http://sg.ustc.edu.cn/lssrap/). Interestingly, this approach was found to be useful for fragment threading, pseudo-sequence design, and local structure predictions.

Support vector machine (SVM) methodology coupled with evolutionary information greatly improved the prediction rates. Hence, Zimmermann and Hansmann were able to develop a method for PB prediction using SVMs with a radial basis function kernel, leading to an improvement of the prediction rate to 60–61% (Zimmermann and Hansmann 2008). This method, called Locustra, is available online at http://www.fz-juelich.de/nic/cbb/service/service.php. In a very recent work, Rangwala, Kauffman, and Karypis developed a novel tool named svmPRAT (Rangwala, et al. 2009) that involves formulating the annotation problem as a classification or regression problem using SVMs (http://www.cs.gmu.edu/∼mlbio/prosat/). An impressive increase in prediction rate of about 69% is achieved using such an approach. PB prediction is part of MONSTER (Minnesota prOteiN Sequence annoTation servER, http://bio.dtc.umn.edu/monster/). Thus, in less than a decade, the prediction rate of PBs has doubled in a very efficient way.

As emphasized by Li and co-workers (Li et al. 2009), it is often difficult to accurately compare the different studies because of the different definitions considered for local structures or different dataset and/or different criteria used for evaluating success predictions.

HPM strategy was used to construct a new library of local structures in order to extend the analyses to long structural fragments. As a result, 120 structural clusters (named local structure prototypes, LSPs) were then proposed to describe fragments that are 11 residues long (Benros et al. 2006). An original prediction method based on logistic regressions was first developed for predicting local structures from a single sequence. This method proposed a short list of the best structural candidates among the 120 LSPs of the library. A prediction rate of 51.2% was reached within the framework of a geometrical assessment. This result was quite significant, given the fragment length and the high number of classes (Benros et al. 2006). An improved prediction method based on SVMs and evolutionary information has recently been proposed. A global prediction rate of 63.1% was achieved and the prediction for 85% of the proteins was improved. This method has been shown to be among the most efficient of cutting-edge local structure prediction strategies (Bornot et al. 2009).

Conclusions and perspectives

Since 1989, nearly 12 different SAs have been developed (see, for example, Fetrow et al. 1997; Ku and Hu 2008; Sander et al. 2006; Unger et al. 1989; Unger and Sussman 1993; for dedicated reviews, see Joseph et al. 2010; Offmann et al. 2007). However, almost none of these have been used outside their the laboratories where they were developed. The PB alphabet is the only exception, and the reason for this rests with the ease with which protein 3D structures can be encoded as PBs. The PB alphabet can be considered as the classical standard of the SA, similar to DSSP being the classical standard for secondary structure assignment (Kabsch and Sander 1983).

PBs have been utilized in numerous different applications, such as the modeling of a transmembrane protein implicated in malarial infection (de Brevern 2005, 2009; de Brevern et al. 2009). It has also led to the development of an excellent superimposition method (Tyagi et al. 2008) and is now used by various research teams (Joseph et al. 2010). We have also developed confidence indexes associated to prediction accuracy (Bornot et al. 2009; de Brevern et al. 2000; Etchebest et al. 2005). We now link the uncertainties with the prediction of protein flexibility, looking at data from X-ray analysis, molecular dynamics (Bornot et al. submitted) and nuclear magnetic resonance. In the same way, superimposition approaches are constantly being improved. We have also examined protein–protein interactions from the standpoint of PBs (Swapna et al. in preparation).

Acknowledgments

The authors would like to thank the reviewers for their comments that help improve the manuscript. The research was supported by grants from the French Ministry of Research, University of Paris Diderot–Paris 7, University of Saint-Denis de la Réunion, French National Institute for Blood Transfusion (INTS), French Institute for Health and Medical Research (INSERM), and Indian Department of Biotechnology. APJ and GA are supported by CEFIPRA number 3903-E and Council of Scientific and Industrial Research, respectively. AB had a grant from the French Ministry of Research, MT has a post-doctoral fellowship from NIH, and HV had a post-doctoral fellowship from CEA. NS and AdB acknowledge CEFIPRA for collaborative grant (number 3903-E). BS and AdB acknowledge Partenariat Hubert Curien Barrande (2010–2011). BS is supported by grant AV0Z50520701.

Footnotes

Agnel Praveen Joseph and Garima Agarwal contributed equally to this article.

References

  1. Agarwal G, Dinesh D, Srinivasan N and de Brevern AG (2010) Characterization of conformational patterns in active and inactive forms of kinases using Protein Blocks approach. In: Maulik U, Bandyopadhyay S, Wang J (eds) Computational Intelligence and Pattern Analysis in Biological Informatics. Wiley, in press
  2. Akanuma S, Kigawa T, Yokoyama S. Combinatorial mutagenesis to restrict amino acid usage in an enzyme to a reduced set. Proc Natl Acad Sci USA. 2002;99:13549–13553. doi: 10.1073/pnas.222243999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Benros C, Hazout S, de Brevern AG (2002) Extension of a local backbone description using a structural alphabet. "Hybrid Protein Model": a new clustering approach for 3D local structures. In: International Workshop on Bioinformatics ISMIS. Lyon, pp 36-45
  4. Benros C, de Brevern AG, Hazout S (2003) Hybrid Protein Model (HPM): A method for building a library of overlapping local structural prototypes. Sensitivity study and improvements of the training. In: IEEE Workshop on Neural Networks for Signal Processing. IEEE Int Work 1:53–72
  5. Benros C, de Brevern AG, Etchebest C, Hazout S. Assessing a novel approach for predicting local 3D protein structures from sequence. Proteins. 2006;62:865–880. doi: 10.1002/prot.20815. [DOI] [PubMed] [Google Scholar]
  6. Benros C, de Brevern AG, Hazout S. Analyzing the sequence-structure relationship of a library of local structural prototypes. J Theor Biol. 2009;256:215–226. doi: 10.1016/j.jtbi.2008.08.032. [DOI] [PubMed] [Google Scholar]
  7. Bornot A, de Brevern AG. Protein beta-turn assignments. Bioinformation. 2006;1:153–155. doi: 10.1093/bioinformatics/1.3.153. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bornot A, Etchebest C, de Brevern AG. A new prediction strategy for long local protein structures using an original description. Proteins. 2009;76:570–587. doi: 10.1002/prot.22370. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Clarke ND. Sequence 'minimization': exploring the sequence landscape with simplified sequences. Curr Opin Biotechnol. 1995;6:467–472. doi: 10.1016/0958-1669(95)80077-8. [DOI] [PubMed] [Google Scholar]
  10. de Brevern AG. New assessment of a structural alphabet. In Silico Biol. 2005;5:283–289. [PMC free article] [PubMed] [Google Scholar]
  11. de Brevern AG. New opportunities to fight against infectious diseases and to identify pertinent drug targets with novel methodologies. Infect Disord Drug Targets. 2009;9:246–247. doi: 10.2174/1871526510909030246. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. de Brevern AG, Hazout S. Hybrid Protein Model (HPM): a method to compact protein 3D-structures information and physicochemical properties. IEEE–Computer Society. 2000;S1:49–54. [Google Scholar]
  13. de Brevern AG, Hazout S. Compacting local protein folds with a "hybrid protein model". Theor Chem Acc. 2001;106:36–47. [Google Scholar]
  14. de Brevern AG, Hazout S. 'Hybrid protein model' for optimally defining 3D protein structure fragments. Bioinformatics. 2003;19:345–353. doi: 10.1093/bioinformatics/btf859. [DOI] [PubMed] [Google Scholar]
  15. de Brevern AG, Etchebest C, Hazout S. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins. 2000;41:271–287. doi: 10.1002/1097-0134(20001115)41:3<271::AID-PROT10>3.0.CO;2-Z. [DOI] [PubMed] [Google Scholar]
  16. de Brevern AG, Valadie H, Hazout S, Etchebest C. Extension of a local backbone description using a structural alphabet: a new approach to the sequence-structure relationship. Protein Sci. 2002;11:2871–2886. doi: 10.1110/ps.0220502. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. de Brevern AG, Benros C, Gautier R, Valadie H, Hazout S, Etchebest C. Local backbone structure prediction of proteins. In Silico Biol. 2004;4:381–386. [PMC free article] [PubMed] [Google Scholar]
  18. de Brevern AG, Etchebest C, Benros C, Hazout S. "Pinning strategy": a novel approach for predicting the backbone structure in terms of protein blocks from sequence. J Biosci. 2007;32:51–70. doi: 10.1007/s12038-007-0006-3. [DOI] [PubMed] [Google Scholar]
  19. de Brevern AG, Autin L, Colin Y, Bertrand O, Etchebest C. In silico studies on DARC. Infect Disord Drug Targets. 2009;9:289–303. doi: 10.2174/1871526510909030289. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. DeLano WLT (2002) The PyMOL Molecular Graphics System. DeLano Scientific, San Carlos. Available at: http://www.pymol.org.
  21. Dong QW, Wang XL, Lin L. Methods for optimizing the structure alphabet sequences of proteins. Comput Biol Med. 2007;37:1610–1616. doi: 10.1016/j.compbiomed.2007.03.002. [DOI] [PubMed] [Google Scholar]
  22. Dudev T, Lim C. Modeling Zn2+-cysteinate complexes in proteins. J Phys Chem. 2001;105:10709–10714. [Google Scholar]
  23. Dudev M, Lim C. Discovering structural motifs using a structural alphabet: application to magnesium-binding sites. BMC Bioinform. 2007;8:106. doi: 10.1186/1471-2105-8-106. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Etchebest C, Benros C, Hazout S, de Brevern AG. A structural alphabet for local protein structures: improved prediction methods. Proteins. 2005;59:810–827. doi: 10.1002/prot.20458. [DOI] [PubMed] [Google Scholar]
  25. Etchebest C, Benros C, Bornot A, Camproux AC, de Brevern AG. A reduced amino acid alphabet for understanding and designing protein adaptation to mutation. Eur Biophys J. 2007;36:1059–1069. doi: 10.1007/s00249-007-0188-5. [DOI] [PubMed] [Google Scholar]
  26. Faure G, Bornot A, de Brevern AG. Protein contacts, inter-residue interactions and side-chain modelling. Biochimie. 2008;90:626–639. doi: 10.1016/j.biochi.2007.11.007. [DOI] [PubMed] [Google Scholar]
  27. Fetrow JS, Palumbo MJ, Berg G. Patterns, structures, and amino acid frequencies in structural building blocks, a protein secondary structure classification scheme. Proteins. 1997;27:249–271. doi: 10.1002/(SICI)1097-0134(199702)27:2<249::AID-PROT11>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
  28. Fourrier L, Benros C, de Brevern AG. Use of a structural alphabet for analysis of short loops connecting repetitive structures. BMC Bioinform. 2004;5:58. doi: 10.1186/1471-2105-5-58. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Gowri VS, Pandit SB, Karthik PS, Srinivasan N, Balaji S. Integration of related sequences with protein three-dimensional structural families in an updated version of PALI database. Nucleic Acids Res. 2003;31:486–488. doi: 10.1093/nar/gkg063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hazout S (2005) Une nouvelle méthode d’apprentissage: “Self-Learning by Information Share-Out” (SLISO). Sixièmes Journées Ouvertes de Biologie, Informatique et Mathématiques (JOBIM) pour la génomique Lyon, pp 483-488
  31. Joseph AP, Bornot A, de Brevern AG (2010) Local Structure Alphabets. In: Rangwala H, Karypis G. (eds), Protein Structure Prediction. Wiley, in press
  32. Kabsch W, Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
  33. Kamtekar S, Schiffer JM, Xiong H, Babik JM, Hecht MH. Protein design by binary patterning of polar and nonpolar amino acids. Science. 1993;262:1680–1685. doi: 10.1126/science.8259512. [DOI] [PubMed] [Google Scholar]
  34. Karchin R, Cline M, Mandel-Gutfreund Y, Karplus K. Hidden Markov models that use predicted local structure for fold recognition: alphabets of backbone geometry. Proteins. 2003;51:504–514. doi: 10.1002/prot.10369. [DOI] [PubMed] [Google Scholar]
  35. Kohonen T. Self-organized formation of topologically correct feature maps. Biol Cybern. 1982;43:59–69. doi: 10.1007/BF00337288. [DOI] [Google Scholar]
  36. Kohonen T (2001) Self-organizing maps, 3rd edn. Springer, Berlin Heidelberg New York
  37. Kostrewa D, Wyss M, D'Arcy A, van Loon AP. Crystal structure of Aspergillus niger pH 2.5 acid phosphatase at 2. 4 A resolution. J Mol Biol. 1999;288:965–974. doi: 10.1006/jmbi.1999.2736. [DOI] [PubMed] [Google Scholar]
  38. Ku SY, Hu YJ. Protein structure search and local structure characterization. BMC Bioinform. 2008;9:349. doi: 10.1186/1471-2105-9-349. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Lee DC, Cottrill MA, Forsberg CW, Jia Z. Functional insights revealed by the crystal structures of Escherichia coli glucose-1-phosphatase. J Biol Chem. 2003;278:31412–31418. doi: 10.1074/jbc.M213154200. [DOI] [PubMed] [Google Scholar]
  40. Li Q, Zhou C, Liu H. Fragment-based local statistical potentials derived by combining an alphabet of protein local structures with secondary structures and solvent accessibilities. Proteins. 2009;74:820–836. doi: 10.1002/prot.22191. [DOI] [PubMed] [Google Scholar]
  41. Martin J, Letellier G, Marin A, Taly JF, de Brevern AG, Gibrat JF. Protein secondary structure assignment revisited: a detailed analysis of different assignment methods. BMC Struct Biol. 2005;5:17. doi: 10.1186/1472-6807-5-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Offmann B, Tyagi M, de Brevern AG. Local protein structures. Curr Bioinf. 2007;3:165–202. doi: 10.2174/157489307781662105. [DOI] [Google Scholar]
  43. Rabiner LR. A tutorial on hidden Markov models and selected application in speech recognition. Proc IEEE. 1989;77:257–286. doi: 10.1109/5.18626. [DOI] [Google Scholar]
  44. Rangwala H, Kauffman C, Karypis G. svmPRAT: SVM-based protein residue annotation toolkit. BMC Bioinf. 2009;10:439. doi: 10.1186/1471-2105-10-439. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Sander O, Sommer I, Lengauer T. Local protein structure prediction using discriminative models. BMC Bioinform. 2006;7:14. doi: 10.1186/1471-2105-7-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Schuchhardt J, Schneider G, Reichelt J, Schomburg D, Wrede P. Local structural motifs of protein backbones are classified by self-organizing neural networks. Protein Eng. 1996;9:833–842. doi: 10.1093/protein/9.10.833. [DOI] [PubMed] [Google Scholar]
  47. Thomas A, Deshayes S, Decaffmeyer M, Van Eyck MH, Charloteaux B, Brasseur R. Prediction of peptide structure: how far are we? Proteins. 2006;65:889–897. doi: 10.1002/prot.21151. [DOI] [PubMed] [Google Scholar]
  48. Tyagi M, Gowri VS, Srinivasan N, de Brevern AG, Offmann B. A substitution matrix for structural alphabet based on structural alignment of homologous proteins and its applications. Proteins. 2006;65:32–39. doi: 10.1002/prot.21087. [DOI] [PubMed] [Google Scholar]
  49. Tyagi M, Sharma P, Swamy CS, Cadet F, Srinivasan N, de Brevern AG, Offmann B. Protein Block Expert (PBE): a web-based protein structure analysis server using a structural alphabet. Nucleic Acids Res. 2006;34:W119–W123. doi: 10.1093/nar/gkl199. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Tyagi M, de Brevern AG, Srinivasan N, Offmann B. Protein structure mining using a structural alphabet. Proteins. 2008;71:920–937. doi: 10.1002/prot.21776. [DOI] [PubMed] [Google Scholar]
  51. Tyagi M, Bornot A, Offmann B, de Brevern AG. Analysis of loop boundaries using different local structure assignment methods. Protein Sci. 2009;18:1869–1881. doi: 10.1002/pro.198. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Tyagi M, Bornot A, Offmann B, de Brevern AG. Protein short loop prediction in terms of a structural alphabet. Comput Biol Chem. 2009;33:329–333. doi: 10.1016/j.compbiolchem.2009.06.002. [DOI] [PubMed] [Google Scholar]
  53. Unger R, Sussman JL. The importance of short structural motifs in protein structure analysis. J Comput Aided Mol Des. 1993;7:457–472. doi: 10.1007/BF02337561. [DOI] [PubMed] [Google Scholar]
  54. Unger R, Harel D, Wherland S, Sussman JL. A 3D building blocks approach to analyzing and predicting structure of proteins. Proteins. 1989;5:355–373. doi: 10.1002/prot.340050410. [DOI] [PubMed] [Google Scholar]
  55. Wu CY, Chen YC and Lim C (2010) A structural-alphabet-based strategy for finding structural motifs across protein families, Nucleic Acids Res. doi: 10.1093/nar/gkq478 [DOI] [PMC free article] [PubMed]
  56. Yang TY, Dudev T, Lim C. Mononuclear versus binuclear metal-binding sites: metal-binding affinity and selectivity from PDB survey and DFT/CDM calculations. J Am Chem Soc. 2008;130:3844–3852. doi: 10.1021/ja076277h. [DOI] [PubMed] [Google Scholar]
  57. Zimmermann O, Hansmann UH. LOCUSTRA: accurate prediction of local protein structure using a two-layer support vector machine approach. J Chem Inf Model. 2008;48:1903–1908. doi: 10.1021/ci800178a. [DOI] [PubMed] [Google Scholar]
  58. Zuo YC, Li QZ. Using reduced amino acid composition to predict defensin family and subfamily: Integrating similarity measure and structural alphabet. Peptides. 2009;30:1788–1793. doi: 10.1016/j.peptides.2009.06.032. [DOI] [PubMed] [Google Scholar]
  59. Zuo YC, Li QZ. Using K-minimum increment of diversity to predict secretory proteins of malaria parasite based on groupings of amino acids. Amino Acids. 2010;38:859–67. doi: 10.1007/s00726-009-0292-1. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Reviews are provided here courtesy of Springer

RESOURCES