Tests of homoscedasticity, normality, and missing completely at random for incomplete multivariate data

Abstract

Test of homogeneity of covariances (or homoscedasticity) among several groups has many applications in statistical analysis. In the context of incomplete data analysis, tests of homoscedasticity among groups of cases with identical missing data patterns have been proposed to test whether data are missing completely at random (MCAR). These tests of MCAR require large sample sizes n and/or large group sample sizes n_i, and they usually fail when applied to non-normal data. Hawkins (1981) proposed a test of multivariate normality and homoscedasticity that is an exact test for complete data when n_i are small. This paper proposes a modification of this test for complete data to improve its performance, and extends its application to test of homoscedasticity and MCAR when data are multivariate normal and incomplete. Moreover, it is shown that the statistic used in the Hawkins test in conjunction with a nonparametric k-sample test can be used to obtain a nonparametric test of homoscedasticity that works well for both normal and non-normal data. It is explained how a combination of the proposed normal-theory Hawkins test and the nonparametric test can be employed to test for homoscedasticity, MCAR, and multivariate normality. Simulation studies show that the newly proposed tests generally outperform their existing competitors in terms of Type I error rejection rates. Also, a power study of the proposed tests indicates good power. The proposed methods use appropriate missing data imputations to impute missing data. Methods of multiple imputation are described and one of the methods is employed to confirm the result of our single imputation methods. Examples are provided where multiple imputation enables one to identify a group or groups whose covariance matrices differ from the majority of other groups.

1 Introduction

In almost all areas of empirical research, incomplete data sets are more of a rule than exception. In an analysis of incomplete data, ignoring the cases that have missing values can result in biased and/or inefficient inference. Statistical methods that include incomplete cases in the analysis have been proposed in various contexts (see e.g., Little & Rubin, 2002, and references therein). Validity of inference resulting from such methods depends on the missing data mechanism; that is the process that leads to missing data. Missing completely at random (MCAR) and missing at random (MAR) are two popular missing data mechanisms coined by Rubin (1976) and further described by Little and Rubin (1987). Briefly, MCAR is a process in which the missing-ness of the data is completely independent of both the observed and the missing values, and MAR is a process in which the missing-ness of the data depends on the observed values, but is independent of the missing values. When the missing data mechanism is neither MCAR nor MAR and, in particular, the missing-ness depends on the missing values themselves, the process is called missing not at random (MNAR).

This paper considers statistical tests of MCAR. Little (1988) lists a number of important instances where it is important to verify that data are MCAR. Essentially, if the missing data mechanism is MCAR, then the results from many missing data procedures would be valid. On the other hand, if data are not MCAR, care must be exercised in employing routine missing data procedures (see, e.g., Little, 1988). Thus, statistical tests of MCAR are important and of interest.

The methods considered here for testing MCAR are based on testing homogeneity of covariances (or test of homoscedasticity), and one of the methods considered can also be used as a test of multivariate normality. Let Y denote a set of n observations on p variables, where some of the cases are incompletely observed. Suppose that there are g different missing (observed) data patterns among the cases, including the completely observed pattern. Moreover, let n_i and p_i(≤ p) respectively denote the number of cases and the number of observed variables in the ith missing data pattern for i = 1, ⋯, g; thus $n={\Sigma }_{i=1}^g{n}_i$. An approach that has been employed to test for MCAR is to test homogeneity of means and covariances amongst the g groups of data, distinguished by their missing data patterns (see, e.g., Little, 1988, and Kim & Bentler, 2002). Assuming that data are from a multivariate normal distribution, Little (1988) developed a likelihood ratio test to test equality of the variable means amongst the g groups. He argued that rejection of this test provides evidence that data are not MCAR. Little (1988) also mentioned a likelihood ratio test of MCAR based on testing homogeneity of combined mean and covariances of the g groups, but casted doubt on its success unless the sample size is very large.

Using the same approach to test for MCAR, Kim and Bentler (2002) studied tests of homogeneity of means (HM), homogeneity of covariances or homoscedasticity (HC), and homogeneity of means and covariances (HMC) amongst the g groups consisting of cases with identical missing data patterns. They studied the HM and HMC likelihood ratio tests of Little (1988) in addition to a likelihood ratio test of HC. Little’s HM test performed well in Kim and Bentler’s study. Motivated by applications in structural equation models where often covariances are modeled, Kim and Bentler (2002) expressed importance of examining homogeneity of covariances. Their study confirmed Little’s doubt that the likelihood ratio tests of HC and HMC fail in that the observed significance levels of these tests far exceed their corresponding nominal significance levels.

To improve on the performance of the likelihood ratio test, and at the same time to overcome a restriction n_i ≥ p_i of the likelihood ratio tests of HC and HMC, Kim and Bentler (2002) developed three tests of HM, HC, and HMC based on generalized least squares. Hereafter we refer to these tests as “KB tests”. They conducted a simulation study to make a comparison of the performance of the likelihood ratio test to their proposed generalized least squares test. Their study included values of n ranging from 100 to 1500, values of p ranging from 5 to 30, percent of missing ranging from 10 to 50, and missing data patterns were restricted to at most 32 patterns. This study revealed that the KB tests perform better than the likelihood ratio tests under these settings in terms of achieving the nominal significance level, when data are MCAR.

Bentler, Kim, and Yuan (2004) pointed out that the KB tests can have large degrees of freedom and can fail in cases where data consist of patterns with small n_i’s and a large number of data patterns. For example, missing data patterns with n_i = 1 have zero contribution to the KB’s HC and HMC test statistics, while at the same time they inflate the degrees of freedom of the test. Referring to the KB test statistics, Bentler, Kim, and Yuan (2004) state:

“As with the distribution of MLE, these homogeneity test statistics require that n_i go to infinity, and that the proportion c_i[= n_i/n] → γ_i and k_i[= (n_i − 1)/n] → γ_i [for some constants γ_i, i = 1, ⋯, g]. Neither of these conditions could reasonably be assumed to hold for any sample missing data pattern that exhibits n_i = 1. Even with very small n_i the asymptotic assumptions underlying the tests are not met.”

In Section 5 of this paper we will shed some light on the effect of n_i on the performance of the KB test of HC and the other tests that are proposed in this paper. Bentler, Kim, and Yuan (2004) recommended dropping cases with small n_i when using the KB tests. While this recommendation goes a long way to improve the performance of the KB tests, it does not provide a satisfactory solution to the problem, as evidenced by their simulation studies.

Our goal in this paper is to make an advance in testing of MCAR, by proposing new tests of homoscedasticity between groups of identical missing data patterns. In practice, testing for MCAR may entail testing for homogeneity of means, covariances, and possibly other parameters between various missing data patterns. As noted above, the Kim and Bentler (2002) test of MCAR includes tests of mean and covariances between identical missing data patterns. Since many tests of homogeneity of means, including the likelihood ratio test of Little (1988) and the generalized least squares test of Kim and Bentler (2002), perform well, hereafter we will mainly focus on the tests of homoscedasticity.

Let Y_i denote the n_i by p matrix of values for the ith missing data pattern, with Y_obs,i and Y_mis,i respectively denoting the observed and the missing part of Y_i, and let Y_ij = (Y_obs,ij, Y_mis,ij) denote the j-th case in the i-th group. Furthermore, let r_ij denote a p by 1 vector of indicator variables with elements of 1 corresponding to the observed values of Y_ij and elements 0 corresponding to missing values of Y_ij. In this paper we assume that given r_ij, Y_ij has the density f(Y_ij; Σ_i, θ) parameterized by the covariance matrix Σ_i = cov(Y_ij) (depending on the missing data pattern i), and other parameters θ which are homogenous across missing data patterns. θ may include mean parameters or other types of parameters. In the Appendix we have shown that under the above setting, homogeneity of covariances implies MCAR. This is the premise underlying our test of MCAR as well as the tests of Little (1988) and Kim and Bentler (2002).

Little (1988) assumed normality, an assumption that is done away with by the KB tests as well as one of the tests proposed here. We will propose a test of homoscedasticity, based on the work of Hawkins (1981), for the case where f(Y_ij; Σ_i, θ) is multivariate normal; for this case θ is the mean of the population. Moreover, we will propose a nonparametric test of homoscedasticity where f(Y_ij; Σ_i, θ) is not necessarily normal.

The remaining sections of the paper are organized as follows: In Section 2, we give background needed to develop our tests of homoscedasticity. In Section 3, we give details of our tests of homoscedasticity under normal and non-normal data. In Section 4, we report on the result of a simulation study where we compare the performance of the KB test of HC and our proposed tests under various scenarios of n, p, percentages of missing, and data distributions. Based on this simulation study, our nonparametric test overall outperforms the other tests, especially when data are non-normal. In Section 5, we examine the effect of n_i on the performance of the KB tests as well as our newly proposed test. Since our proposed tests rely on imputation of missing data, in Section 6 we assess the variability due to imputation for our proposed tests using a multiple imputation method. As we will see, in some cases the multiple imputation method introduced enables us to identify group(s) whose covariances differ from the majority of the other groups. Finally, we give a summary and a discussion in Section 7, including a guideline as to how the proposed tests can be employed to test for multivariate normality, homoscedasticity, and MCAR.

2 Preliminaries and Background

Our approach in constructing the proposed tests of MCAR and homoscedasticity is to impute the missing data for each group (missing data pattern), and then apply a complete data method to the completed data. Hence, selection of an appropriate test of homoscedasticity for complete data is important. In particular, it is of interest to employ methods that handle small group sample sizes n_i well. Many tests of homoscedasticity for complete data rely on asymptotic theory that requires large n_i (for a list of references to such tests see, e.g., Jamshidian & Schott, 2007). Hawkins (1981) proposed a test statistic to test homoscedasticity for multivariate normal data based on a statistic whose distribution is known exactly, even if the n_i’s are small. Because it works well for small n_i’s, we utilize Hawkins test to construct both a normal theory based and a nonparametric test of homoscedasticity here. Moreover, Hawkins test is a test of homogeneity of covariances as well as a test of multivariate normality. As we will explain, by using the Hawkins test in conjunction with the proposed nonparametric test we will be able to make inference about homoscedasticity, MCAR, and multivariate normality of a set of data; the latter is important in its own right as many statistical procedures are valid only under the multivariate normality assumption. In what follows we describe Hawkins test of homoscedasticity and a modification of it that we have used for the proposed tests here.

Let X be an n × p matrix of completely observed cases on g groups, with X_ij denoting the j-th case from the i-th group; j = 1, ⋯, n_i and i = 1, ⋯, g. Assume that

$${\mathbf{X}}_{\mathit{\text{ij}}}~{𝒩}_p({\mathit{\mu }}_i,{\mathbf{\Sigma }}_i),$$ (1)

where 𝒩_p(μ_i, Σ_i) denotes the p-variate normal distribution with mean μ_i and covariance Σ_i. Let

$${\overline{\mathbf{X}}}_i=\frac{1}{n_i}{\displaystyle \sum _{j=1}^{n_i}}{\mathbf{X}}_{\mathit{\text{ij}}},S_i=\frac{1}{n_i-1}{\displaystyle \sum _{j=1}^{n_i}}({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i){({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i)}^T\text{ and }S={\displaystyle \sum _{i=1}^g}\left(\frac{n_i-1}{n-g}\right)S_i$$

respectively denote group i sample mean, sample covariance, and the overall pooled covariance. Moreover, let ${\mathbf{X}}_{(\mathit{\text{ij}})}^{*}\text{ and }{S}_{(\mathit{\text{ij}})}^{*}$ denote the mean vector of group i and the pooled covariance matrix obtained after removal of X_ij from the sample. Consider the statistic

$$T_{\mathit{\text{ij}}}^2=\left(\frac{n_i-1}{n_i}\right){({\mathbf{X}}_{\mathit{\text{ij}}}-{\mathbf{X}}_{(\mathit{\text{ij}})}^{*})}^T{(S_{(\mathit{\text{ij}})}^{*})}^{-1}({\mathbf{X}}_{\mathit{\text{ij}}}-{\mathbf{X}}_{(\mathit{\text{ij}})}^{*}).$$

Hawkins (1981) showed that under the null hypothesis

$$H_0:{\mathbf{\Sigma }}_1=\cdots ={\mathbf{\Sigma }}_g\equiv \mathbf{\Sigma },$$ (2)

where Σ denotes the common covariance matrix, $T_{\mathit{\text{ij}}}^2$ has a Hotelling’s T² distribution, and thus $F_{\mathit{\text{ij}}}=(n-g-p)T_{\mathit{\text{ij}}}^2/((n-g-1)p)$ follows an ℱ distribution with p and n − g − p degrees of freedom. A more computationally tractable form of F_ij is given by

$$F_{\mathit{\text{ij}}}=\frac{(n-g-p)n_i{V}_{\mathit{\text{ij}}}}{p\{(n_i-1)(n-g)-n_i{V}_{\mathit{\text{ij}}}\}},\text{where }{V}_{\mathit{\text{ij}}}={({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i)}^T{S}^{-1}({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i).$$

Now, let

$$A_{\mathit{\text{ij}}}=\mathit{\text{Pr}}[ℱ>F_{\mathit{\text{ij}}}]$$ (3)

denote the probability that an ℱ-distributed random variable with degrees of freedom p and n − g − p exceeds F_ij. If the model of homoscedastic normal distribution holds, then A_ij is distributed as a uniform random variate over the range (0, 1). Hawkins proposed testing A_ij for uniformity as a test of homoscedasticity. Specifically, if A_ij are deemed not to be uniform on (0,1), then the null hypothesis (2) or the normality assumption (1) are rejected.

Various tests have been proposed for testing uniformity of a sequence of independent observed variates (see, e.g., Marhueda, Morales, & Pardo, 2005, for a review and a comparison of tests of uniformity). Hawkins (1981) suggested using the Anderson and Darling (1954) test to test uniformity of A_ij’s for each group or by combining all the A_ij into one group and testing the uniformity of the n combined values. He followed the former procedure, and proposed rejecting H₀ if the p-value for at least one of the groups is smaller than a threshold, corrected for simultaneity. A caveat here is that A_ij are not in general independent. However, Hawkins argued that for large n_i the interdependence among the A_ij is sufficiently weak so that the A_ij’s behave like a set of independent uniform variates. He tested this in a simulation study and concluded that if n_i ≥ 4, the independence assumption holds quite well. In a fairly comprehensive simulation study that we don’t report here we have also confirmed that independence holds when n_i ≥ 4, both for the complete data and the incomplete data cases that we will consider in the next section. We give a discussion of this issue in Section 5.

In a modification to the Hawkins test, and in order to attain better power, we suggest using the Neyman (1937) test of uniformity in place of the Anderson and Darling (1954) test. This choice is supported by our own simulation studies as well as other studies reported in the literature (see, e.g., Rayner & Best, 1990; Ledwina, 1994; and Marhueda, Morales, & Pardo, 2005). In our setting, the Neyman test for testing uniformity on (0, 1) rejects the null hypothesis of uniformity for large values of

$$N_{\mathit{\text{ik}}}={\displaystyle \sum _{\ell =1}^k}{\{n_i^{-1/2}{\displaystyle \sum _{j=1}^{n_i}}{\pi }_{\ell }(A_{\mathit{\text{ij}}})\}}^2,i=1,\cdots ,g,$$

where π₁, π₂, ⋯, π_k are normalized Legendre polynomials on (0, 1). Ledwina (1994) gives a method to determine the choice of k adaptively, based on the data. However, it turns out that k = 4 works very well for most practical purposes (see, e.g., David, 1939; Ledwina, 1994; and Marhueda, Morales, & Pardo, 2005), and this is what we have used in our simulation studies. The first four Legendre polynomials π₁, ⋯, π₄ are given in David (1939). It can be shown that if the null hypothesis of uniformity holds, as n_i → ∞, the distribution of N_ik approaches to the central chi-squared distribution with k degrees of freedom (see, e.g., David, 1939). Because our applications can involve small n_i’s, we avoid methods that rely asymptotically on n_i and compute p-values for our test based on an empirical distribution of N_ik obtained by simulating a large number (1,000,000 in our simulation study) of N_ik’s.

In yet another modification to the Hawkins test, we combine the p-values from each group to obtain a single p-value for the overall test. Specifically, let P₁, ⋯, P_g denote the p-values obtained from the Neyman test. Again, if the null hypothesis of equality of covariances is true, then the P_i’s would have a uniform distribution on (0, 1). We propose to apply the procedure proposed by Fisher (1932) for combining p-values. Namely, we use the statistic

$$P_T={\displaystyle \sum _{i=1}^g}(-2\text{ log }{P}_i)~{\chi }_{2g}^2,$$ (4)

which under the null is distributed as ${\chi }_{2g}^2$, the central chi-squared distribution with 2g degrees of freedom.

Our examination of the modified version of the Hawkins test with complete data, where we use the combined statistics (4) and the Neyman test of uniformity in place of the Anderson and Darling test, showed that this test is more powerful than the original version of the test proposed by Hawkins (1981). Since our main concern in this paper is dealing with incomplete data, we will not report our simulation studies of the modified Hawkins test for the complete data. In the next section we extend the Hawkins method to construct tests of homoscedasticity between groups with identically missing data patterns for incomplete data.

3 Tests of Homoscedasticity and Normality

In this section we give an extension of the modified Hawkins test of homoscedasticity, described in Section 2, to the case where data are not completely observed. When data come from a normally distributed population, rejection of the Hawkins test implies non-homogeneity of covariances. However, if the population distribution is not known, then rejection of the Hawkins test can be due to either non-normality or non-homogeneity of covariances. In general one does not know whether the data are normally distributed; and, if this is the case, we propose the following sequence of actions. First apply the Hawkins test. If the test is not rejected, then there is no ground to suspect non-normality or heterogeneity of covariances. On the other hand, if the Hawkins test is rejected, then apply a nonparametric test of homoscedasticity. If the nonparametric test is not rejected, then we may conclude that the data are non-normal; and if the nonparametric test is rejected, then non-homogeneity of covariances will be concluded. In the following two subsections we will describe our extension of the Hawkins (1981) test to incomplete data as well as a nonparametric test of homoscedasticity.

3.1 Test of homoscedasticity under the normality assumption

Following notation of Section 1, assume that Y_ij is independent of Y_ik for all i and j ≠ k, and

$${\mathbf{Y}}_{\mathit{\text{ij}}}~{𝒩}_p({\mathit{\mu }}_i,{\mathbf{\Sigma }}_i),i=1.\cdots ,g,j=1,\cdots ,n_i.$$ (5)

We propose to impute the missing data and apply the method of Section 2 with each group comprising of the cases that had identical missing data patterns prior to the imputation. In the outset we note that the result of the proposed test depends on the imputed data and does not take into account the variation in the imputation. However, our simulation studies in Section 4 show promise for our single imputation method. To assess the effect of variability of the results due to imputation, we will present the use of multiple imputation in Section 6.

Let μ_i and Σ_i be partitioned according to their missing and observed values as

$${\mathit{\mu }}_i=\left(\begin{array}{c}\hfill {\mathit{\mu }}_{o,i}\hfill \\ \hfill {\mathit{\mu }}_{m,i}\hfill \end{array}\right),{\mathbf{\Sigma }}_i=\left(\begin{array}{cc}\hfill {\mathbf{\Sigma }}_{\mathit{\text{oo}},i}\hfill & \hfill {\mathbf{\Sigma }}_{\mathit{\text{om}},i}\hfill \\ \hfill {\mathbf{\Sigma }}_{\mathit{\text{mo}},i}\hfill & \hfill {\mathbf{\Sigma }}_{\mathit{\text{mm}},i}\hfill \end{array}\right).$$

Then, the conditional distribution of Y_mis,ij given Y_obs,ij, μ_i, and Σ_i is

$${\mathbf{Y}}_{\text{mis},\mathit{\text{ij}}}|{\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}},{\mathit{\mu }}_i,{\mathbf{\Sigma }}_i~{𝒩}_{p-p_i}({\mathit{\mu }}_{m,i}+{\mathbf{\Sigma }}_{\mathit{\text{mo}},i}{\mathbf{\Sigma }}_{\mathit{\text{oo}},i}^{-1}({\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}}-{\mathit{\mu }}_{o,i}),{\mathbf{\Sigma }}_{\mathit{\text{mm}},i}-{\mathbf{\Sigma }}_{\mathit{\text{mo}},i}{\mathbf{\Sigma }}_{\mathit{\text{oo}},i}^{-1}{\mathbf{\Sigma }}_{\mathit{\text{om}},i}).$$ (6)

For known μ_i, and Σ_i, Equation (6) suggests a method to impute the missing values Y_mis,ij, namely we can generate a random variate from the distribution in (6) to fill Y_mis,ij, the missing data for the i-th case of the j-th group.

In most applications μ_i, and Σ_i are not known. Since our main aim is to test the null hypothesis (2), we assume μ₁ = ⋯ = μ_g = μ and Σ₁ = ⋯ = Σ_g = Σ and estimate the common mean μ and the common covariance Σ using the method of maximum likelihood (see, e.g., Jamshidian & Bentler, 1999). If the means are not equal, then ML estimates of μ_i can be used for each group. Let μ̂ and Σ̂ be the maximum likelihood estimates of μ and Σ, respectively. In an imputation step, we use these quantities in place of μ_i and Σ_i in (6) to impute the Y_mis,i for all i by generating random variates from a multivariate normal with mean and covariance specified in (6).

If μ_i and Σ_i were known, then the above imputation would produce a set of complete data that satisfies assumption (1) and thus, under the null hypothesis (2), uniformity of A_ij in (3) would hold. Hence, employment of the Hawkins test to test the null hypothesis (2) based on the imputed data set is justified. In the more realistic event that μ_i and Σ_i are unknown, under the null hypothesis (2), μ̂ and Σ̂ converge in probability to μ and Σ, respectively, and thus employment of the new method can be justified for large n. Note that the convergence in probability, mentioned above, depends on the overall sample size n, and not on the groups sample sizes n_i. As we show in the Appendix, the distribution of F_ij used in (3) is independent of n_i under the normality and homoscedasticity assumptions.

3.2 A nonparametric test of homoscedasticity

In this section we propose a test of homoscedasticity for the case, described in Section 1, where data come from a population with a density of the form f(Y_ij; Σ_i, θ), where we test equality of the covariances Σ_i. Our test will utilize the F_ij statistic given in Section 2. We have argued in the Appendix that if the distribution of X_ij, the complete case version of Y_ij, is distinguished only by their covariances, and if the null hypothesis (2) holds, then the distribution of F_ij will be identical for all i and j provided that all the n_i are equal, or if n_i are not equal this result holds asymptotically provided that n_i are sufficiently large. Hence, we reject the null hypothesis (2) if the distributions of the F_ij between the i = 1, ⋯, g groups are not the same. When X_ij are normal, the distribution of F_ij is known. However, when the distribution of X_ij is not known a nonparametric test should be utilized to test whether the distribution of F_ij differs between groups i = 1, ⋯, g. Again, because we are faced with incomplete data, we propose to use imputation.

Since we are under the assumption that the distribution of the data is unknown, an imputation method such as that described in Section 3.1 will not be appropriate. In this section we consider an imputation method that only assumes independence of the observations from case to case and the continuity of their cumulative distribution function; no specific distributional assumptions are required. This method is in the spirit of a method given by Srivastava and Dolatabadi (2009) and described in Srivastava (2002). To obtain appropriate imputation values, the best linear predictors of the missing observations are obtained first, and then random errors are added to them to obtain imputation values. This method of imputation implicitly assumes that variables are linearly related. Yuan (2009) gives examples of families of distributions where variables are linearly related.

Without loss of generality, assume that the first group is completely observed with n₁ observations. Moreover, assume that n₁ is of reasonable size with n₁ > p. Let Ȳ₁ and S₁, respectively denote the sample mean and covariance obtained from the n₁ complete cases. If n₁ is small, one can use the ML estimates μ̂ and Σ̂ in place of Ȳ₁ and S₁. This is what we have used in our simulation study. As in the previous subsection, let Y_obs,ij and Y_mis,ij denote respectively the observed and the missing observations for the j-th case in the i-th group, and partition Ȳ₁ and S₁ according to these missing and observed cases as follows:

$${\overline{\mathbf{Y}}}_1=\left(\begin{array}{c}\hfill {\overline{\mathbf{Y}}}_{o,1}\hfill \\ \hfill {\overline{\mathbf{Y}}}_{m,1}\hfill \end{array}\right),{\mathit{S}}_1=\left(\begin{array}{cc}\hfill {\mathit{S}}_{\mathit{\text{oo}},1}\hfill & \hfill {\mathit{S}}_{\mathit{\text{om}},1}\hfill \\ \hfill {\mathit{S}}_{\mathit{\text{mo}},1}\hfill & \hfill {\mathit{S}}_{\mathit{\text{mm}},1}\hfill \end{array}\right).$$

Then the best linear predictor for Y_mis,ij is given by

$${\widehat{\mathbf{Z}}}_{\text{mis},\mathit{\text{ij}}}={\overline{\mathbf{Y}}}_{m,1}+{\mathit{S}}_{\mathit{\text{mo}},1}{\mathit{S}}_{\mathit{\text{oo}},1}^{-1}({\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}}-{\overline{\mathbf{Y}}}_{o,1}).$$

As Srivastava (2002) notes, the conditional covariance of Ẑ_mis,ij given Σ is approximately

$$\frac{1}{n_1}({\mathbf{\Sigma }}_{\mathit{\text{mm}},i}-{\mathbf{\Sigma }}_{\mathit{\text{mo}},i}{\mathbf{\Sigma }}_{\mathit{\text{oo}},i}^{-1}{\mathbf{\Sigma }}_{\mathit{\text{om}},i}),$$

which is smaller, by a factor of 1/n₁, from the conditional variance of Y_mis,ij. Thus, Ẑ_mis,ij will have less variability than Y_mis,ij, and would not be appropriate to use as an imputation for Y_mis,ij. To remedy this problem, Srivastava (2002, Chapter 18) proposes computing the following residuals from the complete cases:

$${\mathit{e}}_j={\left(\frac{n_1}{n_1-1}\right)}^{\frac{1}{2}}({\mathbf{Y}}_{1j}-{\overline{\mathbf{Y}}}_1),j=1,\cdots ,n_1.$$

Then, a sample of size n − n₁ is drawn with replacement from the above residuals. Denote elements of this sample by ${\mathit{e}}_{\mathit{\text{ij}}}^{*}$, i = 2, ⋯, g, and j = 1, ⋯, n_i. The conditional mean and covariance of ${\mathit{e}}_{\mathit{\text{ij}}}^{*}$, given the complete cases Y₁, are 0 and S₁, respectively. Using these residuals compute

$${\mathit{\eta }}_{\mathit{\text{ij}}}^{*}={\mathit{e}}_{m,\mathit{\text{ij}}}^{*}-{\mathit{S}}_{\mathit{\text{mo}},1}{\mathit{S}}_{\mathit{\text{oo}},1}^{-1}{\mathit{e}}_{o,\mathit{\text{ij}}}^{*},$$

where ${\mathit{e}}_{\mathit{\text{ij}}}^{*}=({\mathit{e}}_{o,\mathit{\text{ij}}}^{*},{\mathit{e}}_{m,\mathit{\text{ij}}}^{*})$ is partitioned according to the observed and missing parts of Y_ij = (Y_obs,ij, Y_mis,ij). Then an appropriate imputed value for Y_mis,ij is given by

$${\widehat{\mathbf{Y}}}_{\text{mis},\mathit{\text{ij}}}={\widehat{\mathbf{Z}}}_{\text{mis},\mathit{\text{ij}}}+{\mathit{\eta }}_{\mathit{\text{ij}}}^{*}.$$ (7)

As Srivastava (2002) argues, the covariance of the imputed observations Ŷ_mis,ij will be close to the covariance of Y_mis,ij, if they were observed, with this approximation getting better for larger n_i. Hence, inference can be made about the covariances Σ_i by using the completed data set.

Once we impute the missing values, using (7), then we need to test equality of distribution of F_ij between the groups i = 1, ⋯, g, computed based on the completed data. Specifically, we consider the g samples F_ij for i = 1, ⋯, g and j = 1, ⋯, n_i and test whether they come from the same distribution. When the density f is unknown, this will require a nonparametric (so called) k-sample test. We have considered various k-sample tests for our problem. Based on our numerical experiments, k-sample tests of Thas and Ottoy (2004) and Scholz and Stephens (1987) were most successful. These tests exhibited a better power as compared to other tests that we tried, such as the Kruskal-Wallis test (Kruskal & Wallis, 1952) and the k-sample Kolmogorov-Smirnov test. In the simulation studies reported in the next section we have used the Scholz and Stephens (1987), also known as the Anderson-Darling k-sample test, because it is more computationally efficient than the Thas and Ottoy (2004) test. This test uses a rank statistic of the form $T=\frac{1}{N}{\Sigma }_{i=1}^g{T}_i$ with

$$T_i=\frac{1}{n_i}{\displaystyle \sum _{j=1}^{N-1}}\frac{{(N{M}_{\mathit{\text{ij}}}-{\mathit{\text{jn}}}_i)}^2}{j(N-j)},$$ (8)

where $N={\Sigma }_{i=1}^g{n}_i$ is the size of the pooled sample of F_ij’s, and M_ij is the number of observations in the ith sample that are not greater than the j-th order statistic in the pooled sample of F_ij’s.

To summarize, in the nonparametric test (referred to as the NP test hereafter) we impute the missing data using (7), compute F_ij as defined in Section 2, and apply the Anderson-Darling k-sample test to test equality of distribution of F_ij’s amongst groups i = 1, ⋯, g. If this test is rejected, we conclude that the covariances are non-homogeneous, and in the context of the incomplete data problem data are not MCAR.

4 Simulation Studies

4.1 A comparison of Type I error rates for the KB, Hawkins, and the NP tests

In this section we report on a simulation study that we conducted to compare the observed significance levels of the KB test, our proposed test in Section 3.1 (referred to as the Hawkins test hereafter), and the nonparametric test given in Section 3.2. Tables 1–3 contain the result of our simulation study for this section. We have considered sample sizes n = 200, 500, and 1000, and number of variables p = 4, 7, and 10. Additionally, data were generated according to eight different (population) distributions: (i) The standard multivariate normal 𝒩_p(0, I) (denoted by N); (ii) a correlated multivariate normal 𝒩_p(0, Σ) (denoted by Corr-N); (iii) a multivariate t distribution with mean 0, covariance I, and degrees of freedom 4 (denoted by t); (iv) a multivariate t distribution with mean 0, covariance Σ, and degrees of freedom 4 (denoted by Corr-t); (v) a multivariate uniform obtained by generating independent uniform (0,1) random variates (denoted by U); (vi) a correlated multivariate uniform obtained by generating independent uniform (0,1) random variates and multiplying by Σ^1/2 to have a covariance Σ (denoted by Corr-U); (vii) a random variate W = N + 0.1N³, where N is the standard multivariate normal (denoted by W); (viii) a multivariate Weibull distribution obtained by generating independent Weibull random variates with scale parameter 1, and shape parameter 2 (denoted by Weibull). The distributions (v) and (vii) were used in Hawkins (1981) simulation study as two examples of light-tailed and heavy-tailed distributions, respectively. Here t and Corr-t are also heavy-tailed, and Corr-U is a light-tailed distribution. Finally, the Weibull distribution is an example of a skewed to the right distribution.

Table 1.

Type I rejection rates when 10% of data are MCAR.

		n = 200			n = 500			n = 1000
	n*	195	177	141	483	435	367	987	894	799
	#ni	5	8	8	6	8	11	9	11	19
Dist.	Method	p = 4	p = 7	p = 10	p = 4	p = 7	p = 10	p = 4	p = 7	p = 10
N	KB	8.2	13.3	17.4	5.6	8.1	10.5	8.5	7.2	13.3
	Hawkins	4.4	4.9	5.0	4.5	5.3	4.2	5.5	4.9	5.8
	NP	4.6	7.2	7.6	5.8	6.7	6.3	8.1	5.3	8.5
Corr-N	KB	8.1	13.4	16.8	6.8	8.1	9.9	9.4	7.7	12.9
	Hawkins	4.0	5.2	4.7	4.3	5.5	5.4	5.1	5.3	5.6
	NP	5.6	7.9	7.8	5.6	6.8	7.6	7.4	5.3	7.6
t	KB	68.8	91.4	93.4	85.1	99.6	100	93.9	99.9	100
	Hawkins	100	100	100	100	100	100	100	100	100
	NP	8.6	10.1	10.5	7.8	8.9	9.6	13.7	12.9	16.6
Corr-t	KB	62.9	88.9	92.5	82.7	99.5	100	93.3	100	100
	Hawkins	100	100	100	100	100	100	100	100	100
	NP	8.2	11.5	10.5	9.1	9.4	9.7	15.5	13.6	15.8
U	KB	0.9	0.6	1.1	0.2	0.3	0.1	0.2	0.2	0.0
	Hawkins	99.5	80.0	41.0	100	100	99.9	100	100	100
	NP	7.0	9.5	7.1	7.1	5.4	7.8	11.1	8.6	10.3
Corr-U	KB	0.6	0.5	1.5	0.2	0.3	0.1	0.2	0.2	0.0
	Hawkins	99.1	80.9	40.8	100	100	100	100	100	100
	NP	8.4	10.3	8.4	10	6.4	9.0	12.9	9.7	12.2
W	KB	45.9	62.6	63	55.8	76.3	87.7	66.7	87	93.7
	Hawkins	95.2	95.1	93.9	100	100	100	100	100	100
	NP	5.5	7.9	6.9	6.3	6.4	6.8	8.8	6.2	7.9
Weibull	KB	10.3	17.2	17.7	10.6	12.9	17.6	12.1	17.3	21.2
	Hawkins	5.9	7.0	5.8	13.5	11.4	8.2	27.8	21.4	14.0
	NP	6.8	8.6	8.8	9.1	7.7	9.3	9.9	8.4	9.3

Table 3.

Type I rejection rates when 30% of data are MCAR.

		n = 200			n = 500			n = 1000
	n*	173	74	8	489	289	42	989	821	280
	#ni	9	7	1	14	22	5	15	51	29
	Method	p= 4	p= 7	p= 10	p= 4	p= 7	p= 10	p= 4	p= 7	p= 10
N	KB	6.5	NED	NED	7.2	8.0	NED	4.2	9.2	NED
	Hawkins	5.7	NED	NED	7.1	6.0	NED	6.4	9.5	NED
	NP	6.0	NED	NED	8.6	11.5	NED	6.8	14.5	NED
Corr-N	KB	6.5	NED	NED	5.6	8.8	NED	5.4	8.7	NED
	Hawkins	6.0	NED	NED	6.3	7.1	NED	6.6	9.2	NED
	NP	6.8	NED	NED	9.2	10.5	NED	8.0	13.8	NED
t	KB	85.9	NED	NED	98.3	100	NED	99.5	100	NED
	Hawkins	95.6	NED	NED	100	100	NED	100	100	NED
	NP	9.5	NED	NED	10.3	19.5	NED	10.9	33.0	NED
Corr-t	KB	84.9	NED	NED	97.8	100	NED	99.6	100	NED
	Hawkins	96.7	NED	NED	100	100	NED	100	100	NED
	NP	10.1	NED	NED	13.8	19.5	NED	12.0	28.2	NED
U	KB	0.1	NED	NED	0.1	0.1	NED	0.0	0.0	NED
	Hawkins	59.7	NED	NED	100	34.1	NED	100	99.1	NED
	NP	10.2	NED	NED	8.6	10.2	NED	7.9	15.2	NED
Corr-U	KB	0.1	NED	NED	0.0	0.1	NED	0.1	0.0	NED
	Hawkins	57.0	NED	NED	100	29.5	NED	100	96.8	NED
	NP	9.2	NED	NED	10.1	11.1	NED	9.2	16.3	NED
W	KB	62.1	NED	NED	82.3	97.5	NED	90.4	100	NED
	Hawkins	82.5	NED	NED	99.5	98.1	NED	100	100	NED
	NP	8.0	NED	NED	9.1	14.6	NED	7.7	20.2	NED
Weibull	KB	12.5	NED	NED	12.3	16.8	NED	11.1	21.2	NED
	Hawkins	8.0	NED	NED	11.2	10.6	NED	21.2	14.2	NED
	NP	11.2	NED	NED	12.9	16.8	NED	11.4	20.4	NED

The population distributions (ii), (iv), and (vi) require a population covariance Σ. In every case we generated data using the factor analysis covariance structure Σ = ΛΦΛ^T + Ψ, where Λ is a p by k matrix of factor loadings, Φ is the factor correlation (with diagonal elements fixed to 1), and Ψ is a diagonal matrix with unique variances on its diagonal. For p = 4 we used a two-factor model (k = 2) with Λ_i1 = 0.8 for i = 1, 2, Λ_i2 = 0.8 for i = 3, 4, and all other elements fixed to 0. For p = 7 we used a two-factor model (k = 2) with Λ_i1 = 0.8 for i = 1, 2, 3, Λ_i2 = 0.8 for i = 4, 5, 6, 7, and all other elements fixed to 0. For p = 10 we used a three-factor model (k = 3) with Λ_i1 = 0.8 for i = 1, 2, 3, Λ_i2 = 0.8 for i = 4, 5, 6, Λ_i3 = 0.8 for i = 7, 8, 9, 10, and all other elements fixed to 0. All factor correlations were set to 0.3, and unique variances were set to 1.

For each combination of n and p, data Y_ij were generated according to each of the above distributions. When a fraction q of missing data was desired, independent u_ij ~ uniform (0, 1) were generated and if u_ij < q, then Y_ij was set as a missing value. This led to incomplete data with MCAR missing data mechanism. We have used q = 0.1, 0.2, and 0.3, in Tables 1–3 respectively. Moreover, we have removed missing data patterns that included 6 or less cases. In cases where this removal resulted in deletion of more than half of the cases, we did not carry out the simulation; we mark these instances in the tables by “NED” (not enough data). The number of remaining cases, after deletion of missing data patterns with small number of observations, is indicated in the rows labeled n^*. We kept the patterns of missing data constant under each condition. The rows labeled #n_i indicate the number of missing data patterns in each case. The values within the body of the table are the percentage of rejections over 1000 repetitions of each test under a given circumstance. All the test were carried out at 5% significance level, thus ideally the observed significance levels (or the rejection rates) should be close to 5%.

4.1.1 Type I error rates for the KB test

As shown in Tables 1–3, when data are normally distributed, the observed significance levels for the KB test are acceptable, but slightly inflated. In each case, as the number of variables p increases the observed significance levels of the KB test increase. The smaller the n_i’s relative to p, the more inflated the observed significance levels are for the KB test. In a simulation study, not reported here, in which we retained missing data patterns with n_i > 3, the KB test’s observed Type I error rates were more inflated than those shown in Tables 1–3. In Section 5, we will discuss the effect of small n_i’s on the performance of the tests that we have considered and we will see why the KB test is especially sensitive to small n_i’s.

For the Weibull distribution, the KB test’s observed significance levels are consistently above 10%, and go as high as 23%. The rejection rates increase significantly for the heavy-tailed distributions t, Corr-t, and W. On the other hand, the observed rejection rates are far below the 5% nominal level for the short-tailed distributions U and Corr-U. This can be explained as follows: The KB test statistic is a weighted sum of quantities of the form

$$\text{trace}{[({\mathit{S}}_{\mathit{\text{oo}},i}-{\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}){\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}]}^2={[\text{vec}({\mathit{S}}_{\mathit{\text{oo}},i}-{\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i})]}^T[{\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}\otimes {\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}][\text{vec}({\mathit{S}}_{\mathit{\text{oo}},i}-{\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i})],$$

where S_oo,i is the sample covariance based on the observed data for the i-th pattern, Σ̂_oo,i is the sub-matrix of Σ̂ corresponding to the observed variables in the i-th missing data pattern, Σ̂ is the normal theory ML estimate of Σ obtained under the null hypothesis (2), and finally trace and vec are the usual matrix operators. In this test statistic, the quantity S_oo,i − Σ̂_oo,i is a measure of the deviance of the observed covariance for each group and the corresponding covariance obtained under the null hypothesis. This quantity is normalized (Studentized) by an estimate of its covariance, namely ${\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}\otimes {\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}$. Yuan, Bentler, and Zhang (2005) argue that the estimate ${\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}\otimes {\widehat{\mathbf{\Sigma }}}_{\mathit{\text{oo}},i}^{-1}$ is negatively biased for heavy-tailed distributions and it is positively biased for light-tailed distributions. Using this result, the KB test statistics will be too small for light-tailed distributions and too large for heavy-tailed distributions, which explains the significance levels obtained in Tables 1–3 for KB. Therefore we conclude that the KB test is not appropriate to use for testing homogeneity of covariances when the population distribution is not known or normality cannot be assumed.

4.1.2 Type I error rates for the Hawkins test

When data are normally distributed, the Hawkins test rejection rates are very close to their nominal level of 5% and in almost all cases they are less than their KB test counter part. The largest deviation from the ideal 5% level for the normal case occurs when n = 1000, p = 7, and q = 0.3. In this case there are 51 missing data patterns, after deletion of patterns with n_i ≤ 6, and these include a large number of patterns with small n_i’s. Again, as we will explain in Section 5, small n_i can affect the performance of the Hawkins test, but this test is fairly robust to small n_i’s. In a simulation study of this test, where we deleted patterns with n_i ≤ 3, the performance of the test was quite acceptable.

When data are not normal, Hawkins test rejection rates are very high. This is expected, since the Hawkins test, as mentioned earlier, is a test of multivariate normality as well as homogeneity of covariance. When data are non-normal, then the F_ij no longer follow an F distribution. Interestingly, however, the power of the Hawkins test as a test of normality against the alternative of Weibull distribution is not as high as the other distributions that we have considered. Overall, like the KB test, this test would not be appropriate to use as a test of homoscedasticity for non-normal populations.

4.1.3 Type I error rates for the NP test

When data are normally distributed, the Type I rejection rates for the NP test are somewhat larger than the Hawkins rejection rates, but in almost all of these cases they are acceptable. When data are non-normal, the performance of the NP test is far superior than the Hawkins and the KB tests, having acceptable Type I error rates in most cases. The NP test’s observed significance levels deviate more from the nominal 5% level as n, p, and q get large. The increase in these values results in more patterns of missing, smaller n_i’s, and more unbalanced n_i’s, all of which contribute to this inflation. Overall, however, the NP test performs well both for normal and non-normal data.

4.2 A study of the power of the Hawkins, and the NP tests

In this section we report on simulation studies that we have performed to test the power of the Hawkins and the NP tests. We consider two types of alternatives, one where we test the power of these tests when data are MAR, and another where we generate data with non-homogeneous covariances within each pattern of missing. We refer to the former as the MAR alternative and the latter as the non-HC alternative.

We have used the same distributions described in the previous section to generate data. To generate data according to the MAR alternative, we have used the following scheme: For each datum Y_ij, i = 1, ⋯, n; j = 2, ⋯, p, we have set a value as missing if the value of the corresponding datum Y_i,j−1 is larger than a given threshold. The threshold was set to achieve a desired percentage of missing-ness. To generate data according to the non-HC alternative, we considered the pairs of distributions (N, Corr-N), (t, Corr-t), and (U, Corr-U). For each pair we generated the data according to one of the distributions in the pair, imposed the MCAR missing data mechanism, identified the missing data pattern with the largest number of cases, and replaced the data for this pattern with data from the distribution of the other pair. For example, when considering the pair (N, Corr-N), we generated n cases according to 𝒩(0, I), then imposed MCAR missing data as in Section 4.1, and identified the group with the largest number of cases (excluding the group with all complete data) and replaced the data for that missing data pattern by data generated from 𝒩(0, Σ); this is denoted by N/Corr-N in our tables. In another scenario, denoted by Corr-N/N, we generate data according to 𝒩(0, Σ) and then we replace the missing data pattern with the largest number of cases with 𝒩(0, I) data. Other pairs of distributions were simulated similarly. In each scenario we have considered n = 200, 500 and 1000 and fractions of missing q = 0.1, 0.2, and 0.3.

4.2.1 Power of the Hawkins test

In our power studies of the Hawkins test we only consider the normal and correlated normal distributions, as the Hawkins test Type-I error rates for non-normal data are large, and therefore a power study for the non-normal cases is meaningless. Table 4 shows the rejection rates of the Hawkins test under both the MAR alternative and the non-HC alternative. The rows labeled as N/MAR and Corr-N/MAR indicate power under the MAR alternative, and the rows labeled N/Corr-N and Corr-N/N indicate power of the test under two non-HC alternatives, described earlier. As expected, as the number of cases increase the power of the Hawkins test increases. When the sample size is 200, the power of the Hawkins test is fairly low, especially in the cases where p is large. Note that since we remove patterns with n_i ≤ 6, as p gets large more patterns with n_i ≤ 6 are generated and thus more cases are removed. As before, table entries “NED” indicate situations where, after removal of cases with n_i ≤ 6, less than half of the cases remain. Overall, the power of the Hawkins test for n = 500 is reasonable, and it is quite respectable when n = 1000.

Table 4.

Power of the Hawkins test

	q	n = 200			n = 500			n = 1000
Dist.		p = 4	p = 7	p = 10	p = 4	p = 7	p = 10	p = 4	p = 7	p = 10
N/MAR	0.1	18.0	8.0	5.7	50.2	19.6	11.4	90.5	58.5	27.0
	0.2	16.7	8.5	NED	45.5	23.6	NED	86.9	50.7	27.5
	0.3	19.7	NED	NED	42.9	29.1	NED	82.8	53.6	NED
Corr-N/MAR	0.1	17.2	9.6	5.6	49.5	20.3	10.6	89.6	58.5	26.6
	0.2	18.7	9.0	NED	43.5	23.4	NED	83.9	46.1	27.3
	0.3	18.6	NED	NED	39.5	27.5	NED	76.7	49.5	NED
N/Corr-N	0.1	31.7	39.2	45.2	66.2	85.0	84.4	83.9	97.3	99.8
	0.2	23.0	22.6	NED	42.8	50.0	NED	80.9	84.1	84.3
	0.3	17.9	NED	NED	40.5	35.1	NED	79.0	70.6	NED
Corr-N/N	0.1	12.4	11.9	13.5	28.1	25.8	24.8	38.3	37.3	40.3
	0.2	12.5	8.3	NED	19.8	14.2	NED	42.4	23.3	25.2
	0.3	9.3	NED	NED	18.5	13.5	NED	41.9	20.1	NED

4.2.2 Power of the NP test

Table 5 gives the rejection rates of the NP test when data were generated according to the eight distributions considered in Section 4.1, and the missing data were generated according to the MAR alternative. As expected, as the sample size increases the power of the NP test increases. The power of the test is especially good for the light-tailed distributions U and Corr-U. On the other hand we observe the least power for the W and Weibull distributions. Overall the power is quite good for large sample sizes n = 500 and 1000. For the MAR alternative case, there is not much difference between the N and Corr-N cases. However, when comparing the power for N/Corr-N to Corr-N/N, the power for the latter case is noticeably larger.

Table 5.

Power of the NP test with MAR alternative

	q	n = 200			n = 500			n = 1000
Dist.		p = 4	p = 7	p = 10	p = 4	p = 7	p = 10	p = 4	p = 7	p = 10
N	0.1	39.8	19.1	12.5	78.2	40.8	24.4	98.8	83.3	54.5
	0.2	28.4	12.6	NED	56.2	33.4	NED	88.2	63.5	35.0
	0.3	18.2	NED	NED	20.2	29.7	NED	29.6	42.5	NED
Corr-N	0.1	39.2	19.6	12.4	78.2	41.6	24.4	99.0	83.7	53.5
	0.2	28.4	12.6	NED	56.2	33.4	NED	88.2	63.5	35.0
	0.3	17.7	NED	NED	20.4	27.3	NED	27.8	36.4	NED
t	0.1	30.5	51.2	49.0	64.8	91.2	91.3	86.8	100	100
	0.2	29.9	31.4	NED	46.1	83.7	NED	59.7	99.1	97.8
	0.3	30.0	NED	NED	36.2	84.2	NED	43.1	98.6	NED
Corr-t	0.1	31.1	48.9	47.8	62.5	91.5	91.2	87.0	100	100
	0.2	30.4	31.2	NED	46.6	83.1	NED	62.5	99.4	98.0
	0.3	29.7	NED	NED	36.2	82.7	NED	45.1	97.8	NED
U	0.1	88.9	48.5	32.2	100	95.9	62.2	100	100	98.7
	0.2	91.7	37.3	NED	99.9	94.6	NED	100	100	90.3
	0.3	38.8	NED	NED	90.2	59.9	NED	100	98.7	NED
Corr-U	0.1	89.5	48.5	34.3	100	95.9	63.2	100	100	99.2
	0.2	90.4	36.5	NED	99.9	94.3	NED	100	100	89.7
	0.3	38.9	NED	NED	87.6	56.9	NED	99.9	97.1	NED
W	0.1	14.4	12.2	11.7	20.8	12.8	13.4	28.4	25.2	19.5
	0.2	20.5	15.9	NED	21.5	27.4	NED	27.6	35.4	34.7
	0.3	26.5	NED	NED	25.0	48.5	NED	26.5	61.7	NED
Weibull	0.1	23.9	17.6	13.1	51.9	29.3	17.8	81.8	61.0	38.2
	0.2	14.4	11.0	NED	16.5	20.1	NED	20.4	26.0	23.6
	0.3	24.1	NED	NED	41.2	30.9	NED	71.3	47.0	NED

Table 6 gives the rejection rates of the NP test when data were generated according to the non-HC alternative. Again, the power of the test increases as the sample size increases. Also, the power is quite good for the light-tailed uniform distributions. Overall the power is good for n = 500, and quite good when the sample size is 1000.

Table 6.

Power of the NP test with non-HC alternative

	q	n = 200			n = 500			n = 1000
Dist.		p = 4	p = 7	p = 10	p = 4	p = 7	p = 10	p = 4	p = 7	p = 10
N/Corr-N	0.1	42.0	50.1	55.1	79.9	92.0	91.3	92.4	99.1	100
	0.2	34.5	30.3	NED	56.5	59.8	NED	90.7	89.9	91.4
	0.3	27.0	NED	NED	51.4	44.6	NED	87.5	79.3	NED
Corr-N/N	0.1	24.4	26.0	26.6	54.1	50.0	43.1	67.1	63.8	65.7
	0.2	25.5	14.1	NED	37.3	25.6	NED	71.8	43.7	45.0
	0.3	16.6	NED	NED	32.0	22.3	NED	64.9	36.9	NED
t/Corr-t	0.1	31.0	28.8	29.2	67.4	56.9	45.0	79.7	83.6	79.6
	0.2	24.0	19.8	NED	37.9	31.9	NED	70.5	58.4	59.3
	0.3	20.0	NED	NED	34.5	29.8	NED	58.7	59.2	NED
Corr-t/t	0.1	12.1	13.1	13.6	16.5	17.4	18.2	29.1	19.2	25.8
	0.2	13.2	13.0	NED	22.9	18.3	NED	42.4	29.4	34.4
	0.3	15.0	NED	NED	28.1	26.0	NED	44.0	43.7	NED
U/Corr-U	0.1	80.2	81.3	81.2	99.5	100	99.9	100	100	100
	0.2	65.2	47.2	NED	93.0	90.6	NED	99.8	100	99.8
	0.3	46.7	NED	NED	87.8	64.9	NED	99.8	97.8	NED
Corr-U/U	0.1	57.8	46.5	46.5	94.1	88.4	81.1	98.7	97.7	98.2
	0.2	52.6	22.2	NED	77.0	52.7	NED	99.2	82.3	75.0
	0.3	31.0	NED	NED	66.4	34.9	NED	97.0	65.5	NED

5 The Effect of n_i on the Performance of the Tests

As we have seen, the performance of each of the KB, Hawkins, and NP tests depends on the sample size n_i for each of the groups. Also, as noted in the Introduction, the generalized least squares statistic used in the KB test has a χ² distribution provided that n_i go to infinity and n_i/n → γ_i, for some constant γ_i. In Section 2 we pointed out that independence of F_ij plays a role in testing the uniformity of A_ij in the Hawkins test, and Hawkins (1981) argued that for large n_i, as small as 4, the independence amongst F_ij holds. As for the NP test, application of the Anderson-Darling k-sample test requires that the F_ij be independent, and again it can be argued as in Hawkins (1981), that for large n_i this independence holds. So a common denominator here is that all of these tests perform well when n_i are large. But the question is how large is sufficiently large. In this section we report on our search to answer this question.

We have compared the theoretical distribution of the test statistics used for each of the tests to their observed distribution on several examples. We report on a typical example, where 1000 data sets are generated from the standard multivariate normal with n = 500, p = 7, and a fixed MCAR missing data pattern with 20% missing data. Furthermore, we consider four versions of each data set obtained by deleting groups with n_i = 1, n_i ≤ 3, n_i ≤ 6, and n_i ≤ 9; we refer to each of these cases respectively as D₁, D₃, D₆ and D₉. Finally for each instance of D₁, D₃, D₆ and D₉, using the generated data, we compute 1000 copies of the generalized least squares test statistic for the KB test, the P_T statistics given in (4) for the Hawkins test, and the T statistic given in Section 3.2 for the nonparametric test. Figures 1–3 give the Q-Q plot of the quantiles of these observed statistics against each of their theoretical quantiles.

Figure 1.

Q-Q plots of 1000 KB test statistics when H₀ is true.

Figure 3.

Q-Q plots of 1000 NP T test statistics when H₀ is true.

Figure 1 includes the Q-Q plots related to the KB test. Plots for D₁ and D₃ indicate that the observed distribution of the KB statistic has a heavier tail than its theoretically assumed (asymptotic) distribution. This pattern continues on the plots corresponding to D₆ and D₉, but the deviance from the assumed theoretical distribution decreases as the minimum n_i increases. The observed significance level corresponding to each case is given on the caption of each plot. For the KB test these values exceed their nominal level of 5%, but approach it as n_i gets larger. This suggests that if a data set consists of missing data patterns with a few observations, then it would not be appropriate to use the KB test.

Figure 2 shows the Q-Q plots related to the Hawkins test. The Q-Q plots for the cases D₃, D₆ and D₉ look quite good, confirming that our assumed distribution in (4) holds for n_i as low as 4. As shown on the figure, the observed significance level for D₃ is reasonably close to its nominal level of 5%, and that for D₆ and D₉ are very close to their nominal level of 5%, respectively being 4.8% and 4.3%. It’s interesting that the Q-Q plot for the case D₁ is parallel, but above the “y = x” line. Our investigation of this led us to note that in this case P_i’s are dependent for very small n_i’s, which violates an assumption required for (4) to hold. When P_i’s are dependent, Hou (2005) shows that the distribution of the Fisher’s test statistic is a multiple of chi-square with an adjusted degrees of freedom. Thus, if we adjust the degrees of freedom appropriately, we expect the Hawkins test to work well for cases with minimum n_i as small as 2. It turns out that the degrees of freedom adjustment proposed by Hou (2005) requires an estimate of Cov(−2 log P_i, −2 log P_j) which is not easily computable. We opted not to pursue this further because our test performs well for cases with n_i as low as 4, and thus the effort may not practically be warranted.

Figure 2.

Q-Q plots of 1000 Hawkins P_T test statistics when H₀ is true.

Finally, Figure 3 shows the Q-Q plots related to the T statistics for the NP test. This statistic does not have a closed form distribution, and so we approximated its theoretical quantiles by simulating 10,000 copies of T. Again, due to dependency of the F_ij, the observed significance level is quite inflated for the D₁ case, and the Q-Q plot shows a distinct difference between the theoretical and the observed distributions. However, this difference closes gap quickly for the cases with n_i as low as 4. In the best scenario case of D₉, the observed significance level is 7.4%, reasonably close to its nominal value of 5%, and that for the case D₆ is 8.6%. The observed significance levels for D₃ is 14.2%, which is somewhat inflated. Of course the main advantage of the NP test is that it works well for data that are not normally distributed. We performed a same exercise using multivariate t, and we observed a similar pattern to that in Figure 3 with slightly larger observed significance levels; for example the observed significance level for D₉ was 9%. The inflated rejection rates for the NP test can be attributed to the fact that the k-sample test used requires data within each group to be uncorrelated, but for our setting F_ij are not uncorrelated, but their correlation decreases with larger n_i.

6 Multiple Imputation

The tests proposed in this paper impute the missing data and apply a complete-data method to the completed data. A problem with single imputation methods is that the variance due to the imputed values is not accounted for. A way to account for this variance is to multiply impute the data (see Rubin, 1987). In parameter estimation, various methods exist that combine parameter estimates and variances from each single imputation of the data to obtain parameter estimates and variances that account for imputation variation. When testing hypotheses, however, combining the p-values obtained from each single imputation to get a single overall p-value is not simple. For example, the Fisher (1932) method, described in Section 2, cannot be applied since the p-values obtained from each of the imputed data sets are not independent. In order to assess the variability of imputations, we propose multiply imputing data and examining the variability in the p-values obtained using exploratory methods. Various methods of multiple imputation are available (see, e.g., Little & Rubin, 2002, Chapter 10). Here we discuss two methods and employ one.

Recall that in the Hawkins method we imputed a missing datum Y_mis,ij by replacing μ and Σ in (6) by their respective ML estimates μ̂ and Σ̂. Equation (6) can also be used to produce multiple imputations, by generating multiple estimates of μ and Σ via the asymptotic distribution of their ML estimates. Let θ denote a p+p(p+1)/2 vector containing the parameters in μ and Σ and let θ̂ denote an ML estimate of θ. If data are normally distributed and MCAR, it is well-known that θ̂ ~ 𝒩(θ, Ω), where Ω can be estimated by Ω̂, the negative of the inverse of the observed information matrix evaluated at θ̂. Thus, in this case multiple estimates of μ and Σ can be obtained by multiply generating from the distribution 𝒩(θ̂, Ω̂). Each estimate then can be used in (6) to generate a set of imputed values. This approach can be used with non-normal data as well, given consistency results under certain conditions (Yuan, 2009) and availability of sandwich type estimators to replace for Ω̂. Our experiments with this method of multiple imputation has been successful with normal data. The method just described is one of several methods described by Little and Rubin (2002, Chapter 10). Alternatively, Bayesian-based methods can be used for obtaining imputation values. For our problem, our limited experience with the Bayesian methods shows little advantage over the method that we just described. Indeed an advantage of the method that we just described, as compared to many Bayesian methods, is that it is computationally simpler and, for example, does not require assessing convergence of iterative simulations (see Little & Rubin, 2002, Chapter 10).

An alternative method is to employ the nonparametric method of imputation of Section 3.2 for multiple imputation for both normal and non-normal data. Recall that in the method of Section 3.2, we obtain the best linear estimator for Y_mis,ij based on the completely observed data and add a random component e_j that is a function of a sample from the residuals e_j. To extend this method for multiple imputation, Srivastava (2002) and Srivastava and Dolatabadi (2009) recommend re-sampling the e_j, computing ${\mathit{\eta }}_{\mathit{\text{ij}}}^{*}$ for each instance of multiple imputation, and using (7) to form the imputations. Variations to this method are discussed in Srivastava and Dolatabadi (2009). We have experimented with some of these variations, and because the method that we just described works well and is simple we have adopted it. In all of the examples that follow, we have used this method of multiple imputation.

6.1 Examples of applications of multiple imputation

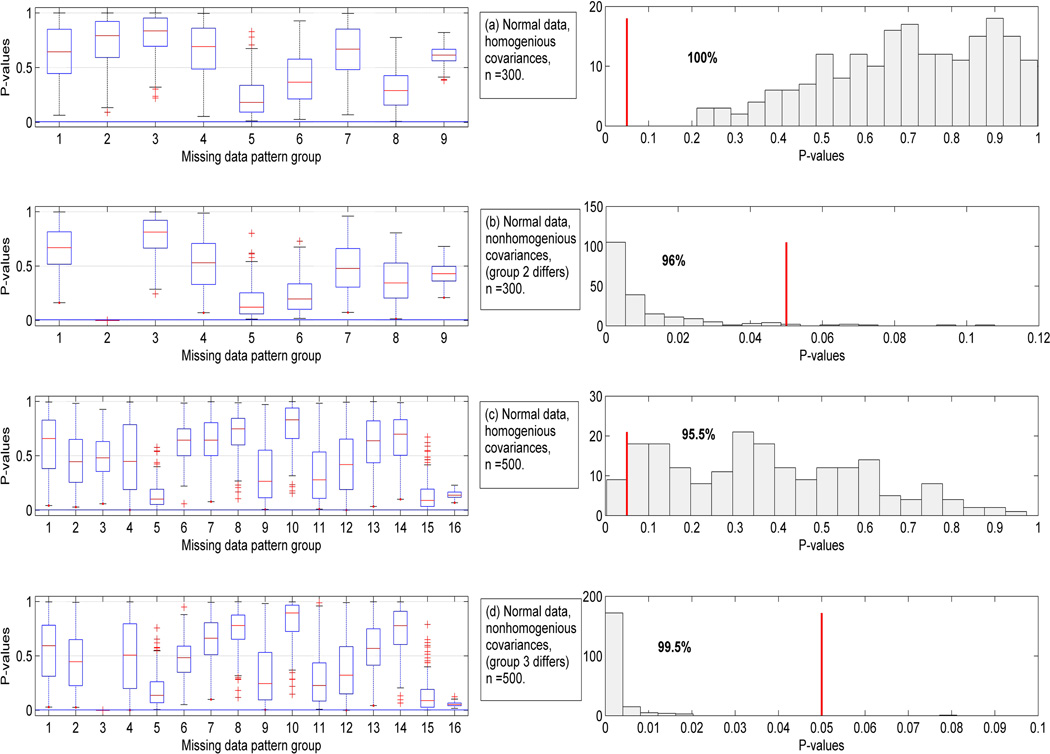
In this section we discuss applications of multiple imputation using examples. We start with normally distributed data. Figure 4 shows boxplots and frequency histograms of the p-values obtained from 200 imputations of two data sets consisting of 20% MCAR data and generated from a standard multivariate normal. Figure 4(a) corresponds to a data set consisting of n = 300 cases generated from 𝒩(0, I). For this example, there were 9 missing data patterns. Each boxplot corresponds to a missing data pattern, and is a summary boxplot of the 200 p-values P_i, described in Section 2, obtained for each of the imputed data sets. Since the null-hypothesis (2) holds here, as expected these p-values range almost uniformly in the interval (0,1). The last boxplot in this figure corresponds to the group which was completely observed. This boxplot indicates the least variation in the corresponding p-values with over 75% of the p-values being larger than 0.5. The graphs shown on the right column are the frequency histograms of the overall p-values, P_T, for the 200 imputations. While the p-values vary from imputation to imputation, they are all above the 5% mark, indicated by the vertical line on the plot.

Figure 4.

Boxplots of p-values for each set of missing data patterns and the frequency histogram of the overall p-values, when missing data were imputed 200 times; p = 7. The vertical bar indicates the location of the 5% significance level.

A similar scenario as in Figure 4(a) is used in Figure 4(b), except that in the latter we have used the population covariance matrix 2I for the second group, and have kept the covariances for the remaining groups equal to I. It is interesting that the boxplot corresponding to group 2 is clearly below the horizontal 5% line shown on the figure, thus this plot identifies the group that is responsible for non-homogeneity. Also, the frequency histogram of the p-values in panel 4(b) shows the variation due to imputation, but in 96% of the cases the p-values are smaller than the 5% significant level and the null hypothesis is correctly rejected.

Figures 4(c) and 4(d) are analogs of Figures 4(a) and 4(b), respectively, with a sample size of n = 500. For this case we have 16 data patterns. Most of the boxplots in 4(c) span the entire (0,1) range. The frequency histogram of P_T shows that 95.5% of the p-values are above the 5%-level thus correctly not rejecting H₀. The data for Figure 4(d) has been set so that the covariance for the second missing data pattern equals to 2I. The boxplot for group 2 is well below the 5% line, thus again enabling us to identify the group with a different covariance matrix, as compared to the remaining groups. In this example the frequency histogram shows that the null hypothesis is correctly rejected for 99.5% of the imputed data sets.

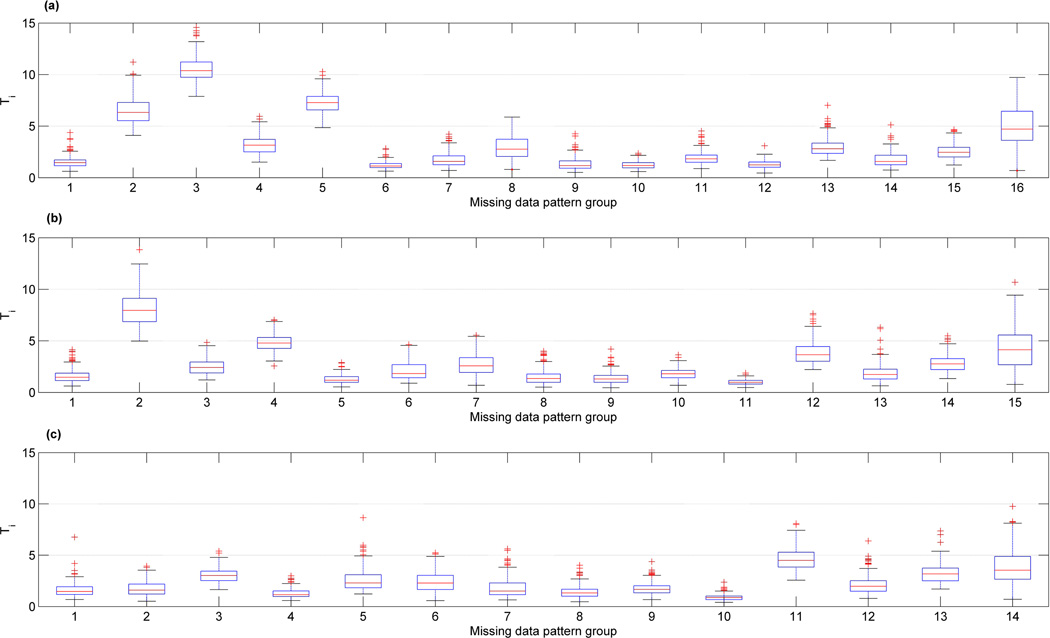
Figure 5 is analogous to Figure 4, except that here we have used the standard multivariate t distribution with 4 degrees of freedom to generate data. For this example, in place of the boxplot of p-values for each group we have shown the boxplot of the T_i values given in (8). The T_i values indicate the contribution of each group to the overall T statistic, and thus a group with unusually high T_i value is perhaps a good candidate, responsible for non-homogeneity of covariances. Figures 5(a) and 5(c) correspond to examples with homogeneous population covariances. In both of these cases while the frequency histograms of the p-values show variation due to multiple imputation, in over 98.5% of the cases the NP test of HC is not rejected at 5% level. Figures 5(b) and 5(d) correspond to cases where data for groups 5 and 13 were respectively generated from a covariance matrix of 2I, as opposed to I for other groups. These figures clearly identify the groups with a different covariance matrix than others. The p-values for 61% of the cases in Figure 5(b) are below the 5% level, and that for Figure 5(d) is 100%.

Figure 5.

Boxplots of T_i-values for each set of missing data patterns and the frequency histogram of the overall p-values, when missing data were imputed 200 times; p = 7. The vertical bar indicates the location of the 5% significance level.

The above examples suggest that if one group’s covariance differs from others, then using the boxplots, we are able to identify that group. We have tried this on several similar examples and have been able to identify the single group with a different covariance than the remaining groups. Now, as the number of groups with different covariances than the majority of groups increases, identification of such groups becomes more difficult. Nonetheless, one may be able to get some information by examining the distribution of T_i’s. Figure 6(a) shows an example where data are generated similar to those in Figure 5(c), except that the covariances for the second and third groups are 2I and different from the other groups. In Figure 6(a), the boxplot for group 3 clearly stands above, but that for groups 2 and 5 are also higher than others, although group 5 does not have a different covariance matrix from the majority. We eliminated group 3, the group with the highest boxplot, and reexamine the boxplots for the newly formed data. The result of this experiment is shown in Figure 6(b). Now group 2 (our original group 3) is the only one with a boxplot standing above others. Eliminating group 2 from Figure 6(b) gives rise to a set of homogeneous data and for this no boxplot seems to standout clearly, as depicted in Figure 6(c). This shows an example of a sequence of elimination and testing to identify groups with different covariances from the majority of groups. In general, we recommend that conclusions from such analyses be substantiated by using the knowledge about the data.

Figure 6.

A sequence of boxplots of T_i-values obtained by each time eliminating the group with significantly higher T_i values.

To summarize this section, we recommend that multiple imputation be conducted in each case and the histogram of the p-values be examined. If this histogram indicates a large percentage of rejections, then we should declare non-homogeneity of covariances. If homoscedasticity is rejected, then this analysis can be followed by examining the box plots of T_i’s for each group in the hope of identifying a group or groups whose covariances are different from the majority of the groups.

7 Summary and Discussion

Tests of homoscedasticity have a number of applications and, in particular in the context of incomplete data analysis, have been suggested as a test of MCAR by Little (1988) and Kim and Bentler (2002). These authors have proposed that if a test of homogeneity of covariances between groups with identical missing data patterns is rejected, then data are deemed not to be MCAR; a premise that we further explored in this paper. Little (1988) proposed a likelihood ratio test of MCAR for normally distributed data. His test requires that n_i, the number of observations in a missing data pattern, be greater than the number of variables p_i for that missing data pattern. Moreover, it is well-known that the normal theory likelihood ratio test in testing homoscedasticity requires a large n and is sensitive to deviation from normality (see, e.g., Jamshidian & Schott, 2007). To do away with the requirement of n_i ≥ p_i and normality, Kim and Bentler (2002) proposed a generalized least squares test (KB) to test for MCAR. In this paper we have argued why the KB test may not perform well when n_i are small. Moreover, we have demonstrated, both in a simulation study and based on an argument, that the Type I rejection rates for the KB test are too high for heavy-tailed distributions, and too low for light-tailed distributions.

In this paper we proposed two tests of homoscedasticity that work well for reasonably small n_i, one for normal data, and another for normal or non-normal data. In the context of complete data, Hawkins (1988) proposed a test of homoscedasticity that works well when n_i are small. We have proposed an improved version of this test for complete data and have extended its use for test of homoscedasticity for incomplete data. Furthermore, we have employed the Hawkins (1988) statistic in conjunction with a nonparametric k-sample test to construct a nonparametric test of homoscedasticity (NP) that works well when data are non-normal.

Our simulation studies show that when data are normally distributed our proposed Hawkins test performs well in the sense that its observed significance levels are close to the nominal significance level. The KB test works well when p is small (say, p ≤ 4) and the n_i are large. In our simulations with p = 4, the KB test had generally a higher power than the Hawkins test with the gap closing as the sample size and percentage of missing increased. However, for p = 7 and p = 10 the KB test had somewhat inflated observed significance levels; because as the values of p increased in our simulations, the number of groups with smaller n_i also increased, and this mainly was the reason for poorer performance of the KB test. Both the Hawkins test and the KB test fail as a test of homoscedasticity for non-normal data.

Our simulations show that the proposed NP test works well for normal and non-normal data, both in the sense of achieving observed significance levels close to the nominal level and in terms of power. For normally distributed data, however, overall the Hawkins test performs best in terms of the observed significant level followed by NP and KB in that order.

Since Hawkins test is a test of homoscedasticity as well as multivariate normality, interestingly the combination of the Hawkins test and the NP test will afford us testing for both homoscedasticity and multivariate normality when the following sequence of tests is applied. Begin by applying the Hawkins test. If this test is not rejected, then there is no evidence against either normality or homoscedasticity. On the other hand, if the Hawkins test is rejected and normality cannot be assumed, then apply the NP test. At this stage, if the NP test is rejected, then we conclude non-homogeneity of covariances (reject MCAR); and if the NP test is not rejected, then we conclude non-normality, but homoscedasticity of the data. This is our recommended procedure, and it is depicted in the flowchart given in Figure 7.

Figure 7.

Flowchart of sequence of tests to test normality and MCAR using the Hawkins and NP tests.

Our proposed Hawkins and NP tests rely on imputing the missing values. We propose that multiple imputation be performed in order to assess the uncertainty due to imputing values. As we explained, in addition to confirmation of our single imputation test result, in some cases the multiple imputation enables us to identify a group or groups whose covariance significantly differs from the other groups.

The problems that we have considered here assume a saturated model for the covariance. Our methods can easily be extended to test homoscedasticity when a structure is imposed on the covariances, as in structural equations models. In an extension of our method to such problems the estimate of the covariance matrix under the saturated model should be replaced by the estimate of the covariance under a given structure Σ(θ).

An important note is that in testing MCAR we have assumed that the complete data come from a single population, and homoscedasticity in the incomplete data would result because of a non-MCAR missing data mechanism. There can be situations where the original data come from multiple groups with distinct covariance matrices, and we have missing data. For such cases, the tests proposed here would be inconclusive. For example, we may have a situation where missing data mechanism is MCAR; but due to multiple group nature of data, including groups with non-homogeneous covariances, our tests of homoscedasticity would be rejected. For such cases, one may employ the tests considered in Jamshidian and Schott (2004), provided that the groups are known a’priori.

In general, in the absence of any information about missing data, tests of MCAR can be quite valuable. If a test of MCAR is rejected, a flag should be raised to a researcher to look into the missing data mechanism carefully and perhaps use the substantive knowledge from the data to deal with the missing data problem and perhaps incorporate a model for the missingness in the analysis. On the other hand, not rejecting a test of MCAR should provide some degree of comfort in employing many analyses, such as ML, that incorporate missing cases in the analysis.

Table 2.

Type I rejection rates when 20% of data are MCAR.

		n = 200			n = 500			n = 1000
	n*	175	105	43	489	369	207	982	855	557
	#ni	6	7	4	11	16	13	12	30	33
	Method	p= 4	p= 7	p= 10	p= 4	p= 7	p= 10	p= 4	p= 7	p= 10
N	KB	6.2	10.2	NED	7	10.4	NED	6.1	8.6	11.1
	Hawkins	3.8	4.0	NED	4.9	4.5	NED	3.6	5.9	6.1
	NP	5.9	7.1	NED	7.0	8.6	NED	5.1	9.6	11.2
Corr-N	KB	6.1	11.1	NED	6.9	9.8	NED	7.0	9.2	10.8
	Hawkins	3.2	5.8	NED	4.8	5.3	NED	5.0	6.3	7.2
	NP	5.3	7.0	NED	6.7	9.1	NED	5.6	9.4	11.6
t	KB	76.8	92.2	NED	96.4	100	NED	99.1	100	100
	Hawkins	99.2	99.1	NED	100	100	NED	100	100	100
	NP	6.9	7.9	NED	9.9	13.1	NED	14.0	15.4	25.6
Corr-t	KB	77.5	94.4	NED	95.1	99.9	NED	99.0	100	100
	Hawkins	99.4	100	NED	100	100	NED	100	100	100
	NP	7.9	9.6	NED	9.9	11.9	NED	12.0	18.2	25.0
U	KB	0.2	0.7	NED	0.0	0.1	NED	0.0	0.0	0.0
	Hawkins	90.5	17.9	NED	100	97.9	NED	100	100	96.3
	NP	8.2	8.3	NED	6.4	10.5	NED	9.4	11.4	11.1
Corr-U	KB	0.2	0.4	NED	0.0	0.0	NED	0.0	0.0	0.0
	Hawkins	87.8	20.3	NED	100	96.7	NED	100	100	94.6
	NP	8.2	9.0	NED	10.2	11.8	NED	10.7	13.2	13.4
W	KB	51.7	60.2	NED	76.8	90.9	NED	81.8	99.1	99.1
	Hawkins	84.9	75.4	NED	99.9	99.8	NED	100	100	100
	NP	6.7	9.0	NED	6.6	8.5	NED	5.4	10.6	14.5
Weibull	KB	9.2	14.5	NED	13.3	15.5	NED	11.6	18.7	23.5
	Hawkins	6.9	6.3	NED	10.7	8.5	NED	23.1	12.5	12.6
	NP	9.8	10.5	NED	9.9	11.9	NED	10.2	14.3	14.9

A Appendix

A.1 Distribution of F_ij and its dependence on n_i

The quantity F_ij is a constant multiple of $T_{\mathit{\text{ij}}}^2$, with the multiplicative constant (n − g − p)/((n − g − 1)p) independent of n_i. In this section we discuss the distribution of $T_{\mathit{\text{ij}}}^2$ when X_ij are either normal or non-normal. It can be shown that

$$S_{(\mathit{\text{ij}})}^{*}=\frac{n-g}{n-g-1}[S-\frac{n_i-1}{n_i(n-g)}({\mathbf{X}}_{\mathit{\text{ij}}}-{\mathbf{X}}_{(\mathit{\text{ij}})}^{*}){({\mathbf{X}}_{\mathit{\text{ij}}}-{\mathbf{X}}_{(\mathit{\text{ij}})}^{*})}^T].$$

We note that the relationship between S and $S_{(\mathit{\text{ij}})}^{*}$ given on page 106 of Hawkins (1981) is incorrect. Now define

$${\mathit{u}}_{\mathit{\text{ij}}}\equiv {\left(\frac{n_i-1}{n_i}\right)}^{1/2}({\mathbf{X}}_{\mathit{\text{ij}}}-{\mathbf{X}}_{(\mathit{\text{ij}})}^{*})={\left(\frac{n_i}{n_i-1}\right)}^{1/2}({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i),$$ (9)

where the second equality can be shown to hold using some algebraic manipulations. Rewriting $S_{(\mathit{\text{ij}})}^{*}$ in terms of u_ij, we have $S_{(\mathit{\text{ij}})}^{*}=[(n-g)S-{\mathit{u}}_{\mathit{\text{ij}}}{\mathit{u}}_{\mathit{\text{ij}}}^T]/(n-g-1)$, and by applying the Sherman-Morrison formula we obtain

$${(S_{(\mathit{\text{ij}})}^{*})}^{-1}=\frac{n-g-1}{n-g}[S^{-1}-\frac{S^{-1}{\mathit{u}}_{\mathit{\text{ij}}}{\mathit{u}}_{\mathit{\text{ij}}}^T{S}^{-1}}{{\mathit{u}}_{\mathit{\text{ij}}}^T{S}^{-1}{\mathit{u}}_{\mathit{\text{ij}}}-(n-g)}].$$

Thus,

$$T_{\mathit{\text{ij}}}^2={\mathit{u}}_{\mathit{\text{ij}}}^T{(S_{(\mathit{\text{ij}})}^{*})}^{-1}{\mathit{u}}_{\mathit{\text{ij}}}=\frac{(n-g-1){\mathit{u}}_{\mathit{\text{ij}}}^T{S}^{-1}{\mathit{u}}_{\mathit{\text{ij}}}}{n-g-{\mathit{u}}_{\mathit{\text{ij}}}^T{S}^{-1}{\mathit{u}}_{\mathit{\text{ij}}}}.$$ (10)

Equation (10) indicates that the distribution of $T_{\mathit{\text{ij}}}^2$ depends on n_i only through the u_ij given in Equation (9). Note that $S=\frac{1}{n-g}{\Sigma }_{i=1}^g{\Sigma }_{j=1}^{n_i}({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i){({\mathbf{X}}_{\mathit{\text{ij}}}-{\overline{\mathbf{X}}}_i)}^T$, and is the same for all i and j. Now, if X_ij’s satisfy the normality assumption given in (1) and the null hypothesis (2) holds, then u_ij ~ 𝒩(0, 03A3), independent of i and j, and in fact $T_{\mathit{\text{ij}}}^2$ has a Hotelling’s T² distribution with $F_{\mathit{\text{ij}}}=(n-g-p)T_{\mathit{\text{ij}}}^2/((n-g-1)p)$ following an F distribution with degrees of freedom p and n − g − p independent of n_i.

If X_ij’s are not normally distributed, but we have a balanced case where n₁ = n₂ = ⋯ = n_k and all X_ij are identically distributed, then in this case the distribution of u_ij will be the same for all i and j. In particular, if the distribution of X_ij has a pmf or pdf of the form f(X_ij, Σ_i, θ) whose second central moment Σ_i can vary across groups, and other distribution parameters θ (e.g., means) are equal for all groups, then if the null hypothesis (2) holds, the distribution of F_ij will be the same for all i and j.

Finally, if X_ij are not normally distributed and we are in the unbalanced case where not all n_i are equal, then obviously the distribution of u_ij will in general depend on n_i. However, again if all X_ij are identically distributed, and n_i are sufficiently large, then n_i/(n_i − 1) will be close to 1 and by the central limit theorem, under some regularity conditions on the distribution of X_ij, the distribution of X̄_i tends to normal and the dependency of the distribution of u_ij on n_i weakens as n_i increases.

A.2 HC Implies MCAR

In using the test of homogeneity of covariances amongst groups consisting of identical missing data patterns to test for MCAR, we are effectively under the premise that HC implies MCAR. In this section we discuss the assumptions under which this holds. Following the notation of Section 3.2, let Y_i be the n_i by p matrix of values for the ith missing data pattern, with Y_obs,i and Y_mis,i respectively denoting the observed and the missing part of Y_i, and Y_ij = (Y_obs,ij, Y_mis,ij) denoting the j-th case in the i-th group. Moreover, let r_i denote a p by 1 vector of indicator variables corresponding to the observed and missing values of Y_i with a 1 and 0 respectively indicating that the corresponding component is observed or missing. Let Σ_i = cov(Y_ij), and f(Y_ij; Σ_i, θ) be the density of Y_ij parametrized by Σ_i (depending on i) and θ. Here we assume that θ are all equal across the missing data patterns i = 1, ⋯, g. For example, f can be the multivariate normal density that depends on the mean and covariance, and we assume that the means are equal across groups. Another example is the multivariate t which is parameterized by a mean vector, a covariance matrix, and a degrees of freedom parameter; in this case we assume that the mean and the degrees of freedom parameter are equal over the g groups. We then test the hypothesis

$$H_0:{\mathbf{\Sigma }}_1=\cdots ={\mathbf{\Sigma }}_g\equiv \mathbf{\Sigma },$$ (11)

where Σ denotes a common value. We assume that given r_i, the distribution of of Y_ij depends on Σ_i and is f(Y_ij; Σ_i, θ). Moreover, if the hypothesis of homoscedasticity (11) holds, then

$$f({\mathbf{Y}}_{\mathit{\text{ij}}};{\mathbf{\Sigma }}_i,\mathit{\theta }|{\mathbf{r}}_i)=f({\mathbf{Y}}_{\mathit{\text{ij}}};{\mathbf{\Sigma }}_i,\mathit{\theta })=f({\mathbf{Y}}_{\mathit{\text{ij}}};\mathbf{\Sigma },\mathit{\theta }).$$ (12)

The first equality essentially states that if we know that we are under r_i, or have the i-th missing data pattern, then our distribution is given by f(Y_ij; Σ_i, θ). That is, the data come from a single population, and the distinction is only based on missing data patterns and through Σ_i. The second equality obviously holds, if (11) holds.

Theorem: Under the above setting, if the null hypothesis (11) holds, then data are MCAR.

Proof: We need to show that the missing data mechanism r_i is independent of the observed or missing values. Let f(r_i|Y_ij) = f(r_i; ψ_i|Y_obs,ij, Y_mis,ij) denote the conditional density (or probability mass function) of r_i given Y_ij = (Y_obs,ij, Y_mis,ij), where ψ_i is a vector of parameters related to r_i and is disjoint from θ and Σ_i. Note that in this section we use f generically to denote a pdf or pmf.

$$\begin{array}{cc}f({\mathbf{r}}_i;{\psi }_i|{\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}},{\mathbf{Y}}_{\text{mis},\mathit{\text{ij}}})\hfill & =\frac{f({\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}},{\mathbf{Y}}_{\text{mis},\mathit{\text{ij}}};{\mathbf{\Sigma }}_i,\mathit{\theta }|{\mathbf{r}}_i)f({\mathbf{r}}_i;{\psi }_i)}{f({\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}},{\mathbf{Y}}_{\text{mis},\mathit{\text{ij}}};{\mathbf{\Sigma }}_i,\mathit{\theta })}\hfill \\ \hfill & =\frac{f({\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}},{\mathbf{Y}}_{\text{mis},\mathit{\text{ij}}};\mathbf{\Sigma },\mathit{\theta })f({\mathbf{r}}_i;{\psi }_i)}{f({\mathbf{Y}}_{\text{obs},\mathit{\text{ij}}},{\mathbf{Y}}_{\text{mis},\mathit{\text{ij}}};\mathbf{\Sigma },\mathit{\theta })}[\text{since }(11)\text{ holds}]\hfill \\ \hfill & =f({\mathbf{r}}_i;{\psi }_i)\hfill \end{array}$$

Thus, the missing data mechanism is MCAR.

Yuan (2009) considers a class of distributions characterized as y = μ + Az, where y = (y₁, ⋯, y_p) and z = (z₁, ⋯, z_p) are random vectors with z₁, ⋯, z_p independent and E(z_i) = 0 and V ar(z_i) = 1. Furthermore, μ is a p by 1 vector, consisting of the mean of y, and A is a lower diagonal matrix such that the cov(y) = Σ = AA′. The theorem above can apply to this class of distributions, provided that the distribution of z_i does not depend on any parameters (e.g., z_i ~ N(0, 1), or z_i ~ Unif(0, 1)), or if it does these parameters are equal across all the g groups.