Abstract
The focus of this paper is to examine whether conformational search using constrained molecular dynamics (MD) method is more enhanced and enriched towards “native-like” structures compared to all-atom MD for the protein folding as a model problem. Constrained MD methods provide an alternate MD tool for protein structure prediction and structure refinement. It is computationally expensive to perform all-atom simulations of protein folding because the processes occur on a timescale of microseconds. Compared to the all-atom MD simulation, constrained MD methods have the advantage that stable dynamics can be achieved for larger time steps and the number of degrees of freedom is an order of magnitude smaller, leading to a decrease in computational cost. We have developed a generalized constrained MD method that allows the user to “freeze and thaw” torsional degrees of freedom as fit for the problem studied. We have used this method to perform all-torsion constrained MD in implicit solvent coupled with the replica exchange method to study folding of small proteins with various secondary structural motifs such as, α-helix (polyalanine, WALP16), β-turn (1E0Q), and a mixed motif protein (Trp-cage). We demonstrate that constrained MD replica exchange method exhibits a wider conformational search than all-atom MD with increased enrichment of near native structures. “Hierarchical” constrained MD simulations, where the partially formed helical regions in the initial stretch of the all-torsion folding simulation trajectory of Trp-cage were frozen, showed a better sampling of near native structures than all-torsion constrained MD simulations. This is in agreement with the zipping-and-assembly folding model put forth by Dill and coworkers for folding proteins. The use of hierarchical “freeze and thaw” clustering schemes in constrained MD simulation can be used to sample conformations that contribute significantly to folding of proteins.
Keywords: constrained MD, GNEIMO, hierarchical clustering, protein folding, Trp-cage
Introduction
One of the bottlenecks of all-atom Cartesian molecular dynamics (MD) simulations for large proteins, is its long computational time. Recently, there has been tremendous progress in speed up stemming from software optimization for graphics processing units1 as well as from using special purpose machines dedicated to performing fast MD simulations.2 Another approach to increasing the simulation time scale is to increase the integration time step size by imposing explicit bond length constraints that eliminate high frequency modes. MD techniques that impose such bond length constraints as soft constraints include the SHAKE3 and RATTLE4 algorithms available in widely used software packages such as CHARMM, AMBER, and NAMD. However these algorithms provide only a modest increase to about two femtoseconds in time step size. An alternative approach is to incorporate holonomic bond length and bond angle constraints directly into the molecular model and thereby reduce the number of degrees of freedom (dofs). Here the molecule is modeled as a collection of rigid bodies known as ‘clusters’ connected by flexible hinges. Each rigid cluster is a collection of atoms within which all bond lengths and bond angles are fixed using hard holonomic constraints, with torsional hinges connecting the rigid clusters. This approach uses torsional angle coordinates (and more generally other modes such as bond angles if needed) as dofs instead of the atomic Cartesian coordinates. MD simulations using such models are referred to as internal coordinate MD, constrained MD, or torsion angle MD.
The number of dofs in constrained MD models is approximately one order of magnitude smaller than that in the all-atom Cartesian MD models. The elimination of high frequency modes allows over an order of magnitude increase in integration time step, and hence enables longer time scale simulations.5–12 However, the equations of motion in internal coordinates become coupled, and solving them for accelerations requires inverting a dense
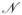 ×
×
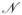 mass matrix, where
mass matrix, where
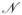 denotes the number of dofs in the constrained model. The computational time taken by these methods scale as the third power of the number of dofs5,6,9 making the algorithms impractical for large proteins where the number of torsions is large. To enable an increase in time step size for larger proteins, we adapted algorithms from the Spatial Operator Algebra (SOA) mathematical framework for multibody dynamics,13,14 and developed the Newton-Euler Inverse Mass Operator (NEIMO) method for torsional MD.7 In contrast with the conventional O(
denotes the number of dofs in the constrained model. The computational time taken by these methods scale as the third power of the number of dofs5,6,9 making the algorithms impractical for large proteins where the number of torsions is large. To enable an increase in time step size for larger proteins, we adapted algorithms from the Spatial Operator Algebra (SOA) mathematical framework for multibody dynamics,13,14 and developed the Newton-Euler Inverse Mass Operator (NEIMO) method for torsional MD.7 In contrast with the conventional O(
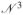 ) techniques for solving the equations of motion,5 the NEIMO algorithm (exactly) solves the same equations of motion with O(
) techniques for solving the equations of motion,5 the NEIMO algorithm (exactly) solves the same equations of motion with O(
 ) computational cost.
) computational cost.
Due to the reduced dofs and the efficient NEIMO algorithm for solving the coupled equations of motion in internal coordinates, the constrained MD approach can be a very efficient tool for enhancing conformational sampling. Constrained dynamics has been used in various applications such as studying the folding kinetics of poly-alanine15 and domain motions of phosphoglycerate kinase.11 Schwieters et al. have used minimization and dynamics in internal coordinates for protein structure refinement.12 Chen et al.8 have shown that the torsional dynamics expands the conformational search. They have also shown that the torsional potential barrier in constrained MD method is higher than in Cartesian dynamics owing to fixed covalent geometry and the correction to the torsional potential leads to enhanced conformational sampling.
All-atom Cartesian MD has been successfully used in recent times with both explicit and implicit solvation to study folding of various small proteins.16–21 Here we explore the use of constrained MD along with replica exchange method and implicit Generalized-Born Surface Area (GB/SA) solvation method to fold short α helical and β turn peptides and mixed motif small peptides and proteins. We have developed a hierarchical framework for performing coarse grain constrained MD, that allows a wide range of dynamic models of the protein, ranging from all-torsion to “freezing and thawing” parts of the protein as rigid and sampling just the torsional dofs connecting these rigid bodies. We call this method as the “Generalized NEIMO” (GNEIMO) method. We have implemented the replica exchange protocol22–24 in constrained MD to further enhance the conformational search of constrained MD methods, as was first demonstrated by Chen et al.8
In this paper, we have studied the folding of polyalanine 20-mer, WALP peptide in membrane environment, a beta hairpin peptide derived from ubiquitin, and Trp-cage protein using constrained MD along with replica exchange method and implicit Generalized-Born Surface Area (GB/SA) solvation to fold the proteins to native or near-native states. Use of constrained MD allows us to study the impact of various clustering (or freeze and thaw) schemes in the dynamic model of the proteins. The dynamic model with secondary structure motifs (such a backbone of helices) treated as clusters while sampling only the torsions connecting these clusters is termed as “hierarchical clustering”. This hierarchical clustering scheme in the constrained MD simulations leads to faster convergence in sampling the native state of the protein. We demonstrate that constrained MD is a viable tool for folding studies, and elucidate the advantages of hierarchical clustering in conformational sampling.
Experimental Methods
All folding simulations were started from an extended conformation of the peptide/protein sequence, unless otherwise stated. The structure was subjected to conjugate gradient minimization with a convergence factor of 10−2 Kcal/mol/Å in force gradient. The constrained MD GNEIMO simulations were carried out using parm99 forcefield part of AMBER99 forcefield25 and implicit solvation GB/SA OBC model26 with a GB/SA interior dielectric value of 1.75 for the solute and GB/SA exterior dielectric constant of 78.3 for the solvent.27 We used a solvent probe radius of 1.4Å for the nonpolar solvation energy component of GB/SA. The non-bond forces were smoothly switched off at a cutoff radius of 20Å. Constrained MD simulations were done using all torsional degrees of freedom except for Trp-cage simulations where various other hierarchical clustering schemes were also examined. The dynamics was done using a Lobatto integrator, and an integration step size of 5 f s. The conformational sampling was improved by using the replica exchange simulation method.22–24 The number of replicas required for efficient conformational sampling is proportional to the square root of the number of dofs.28 Since a constrained dynamics model has approximately a tenth of the dofs of all-atom models, the number of replicas required in constrained MD replica exchange simulations is cut down by approximately a factor of three. We have used eight replicas in the temperature range of 325K to 500K (in steps of 25K) and these were sufficient to fold these systems. Poly-alanine was folded with just six replicas. The temperatures between the replicas were exchanged every 2ps, and the total time duration of all replica exchange simulations were up to 20ns per replica.
Principal Component Analysis (PCA) and Clustering
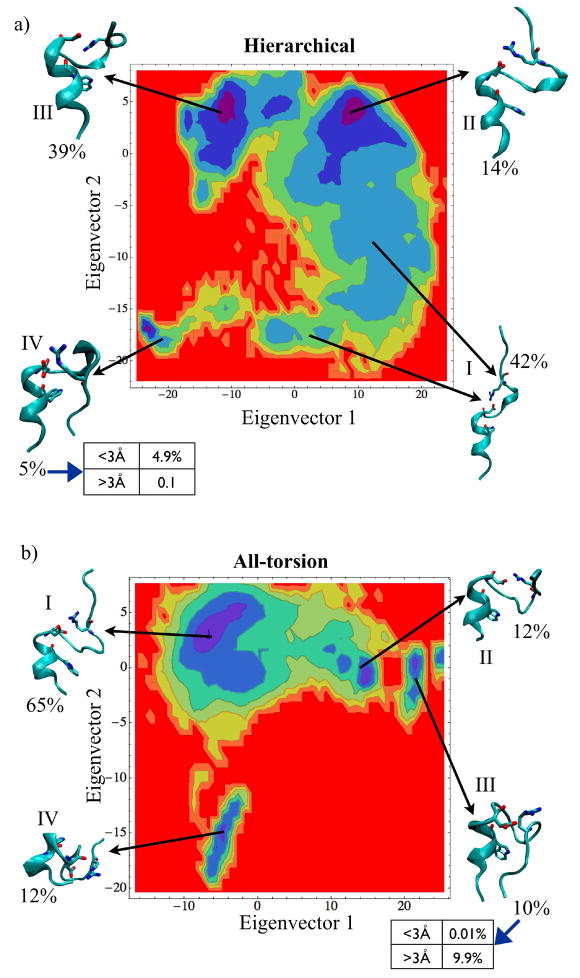
To compare the similarities and differences between the conformations sampled during folding for hierarchical and torsional constrained MD simulations, we examined the conformation population density distribution in a 2D plane spanned by the first two principal components of the simulation trajectories (Figure 7A and B). The principal components (PC) were calculated by constructing covariance matrices of the Ca atom coordinates from each snapshot of the entire GNEIMO simulation trajectories. The density maps shown in Figure 7 is a projection of the simulation trajectories onto the two most significant principal components. Color-coding is used to differentiate the highly dense (blue end of the spectrum) from the sparsely populated (red end of the spectrum). K-means clustering algorithm was used to cluster simulation trajectories into structurally similar subsets. A structure representative of each cluster group was generated by averaging 1000 snapshots from each cluster. The population percentage of each cluster was computed as the fraction of conformations belonging to each cluster.
Figure 7.
The population density calculated from simulation trajectories as a function of the first and second principal component axis for (A) hierarchical and (B) all-torsion simulation. The representative snapshots shown here for the different high density basins have been found by averaging thousand trajectories belonging to each cluster. The proximity to native state is illustrated in the table adjacent to the folded clusters for hierarchical and all torsion simulations.
Results
Poly-alanine and WALP16 – α helical peptides
Poly-alanine (Ala20) and WALP16, a transmembrane peptide, (sequence: Ace-GWW(LA)5WWA-Nme) are the simplest peptides that fold into an α-helical structure in water and membrane environment respectively. Constrained MD simulation study of poly-alanine was done previously using Dreiding forcefield without explicit solvation, but with distance dependent dielectric.15 Chen et al. have also performed folding of a shorter Ala20 and WALP16 peptide using constrained all-torsion dynamics with CHARMM FF and GBSW solvation method.8
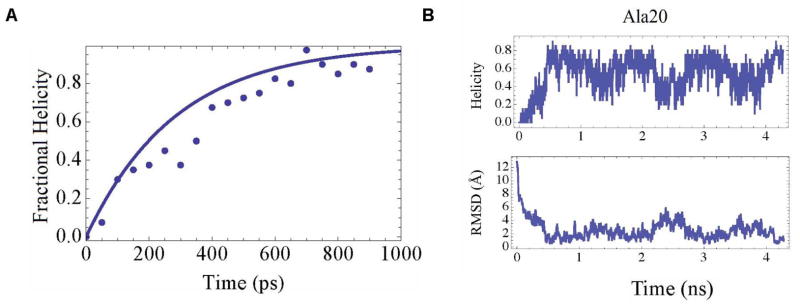
In the present folding simulations we have used an external dielectric constant of 78.3 and 40.0 for Ala20 and WALP peptide respectively to represent water and membrane environments. Our simulations with GB/SA solvation forces were performed at 300K and did not require the elevated temperatures for folding Ala20, as required in the simulations by Bertsch et al.15 Figure 1A shows the variation of the fraction of residues in helical conformation with time averaged over 40 all-torsion MD simulations at 300K. A residue is considered to be in helical conformation if the backbone torsional angles were within 20° of the ideal α-helical angles φ = −57° and ψ = −47°. The helicity for a structure was defined as the fraction of total residues in the helical conformation. It is observed that Ala20 folds into a α helix with 80% helicity (Figure 1B). The deviation from 100% helicity is due to the four residues at the carboxy and amino termini, thus reducing the helicity to 80%. We have calculated the rate constant for helix formation k = 0.0035ps−1, from fitting to the rate equation [1 – exp(−kt)]. This rate constant is in good agreement with the values calculated in the previous work.15 We also performed replica exchange torsional MD simulations with six replicas for Ala20 folding. With replica exchange constrained MD simulations polyalanine folded within 0.5ns which is twice as fast as the torsional MD simulations without replica exchange.
Figure 1.
(A) Plot of fractional helicity formed for poly-alanine as a function of time averaged over 40 trajectories simulated using constrained MD for 1ns (points). (B) Plot of helicity and backbone RMSD from canonical helix for Ala20.
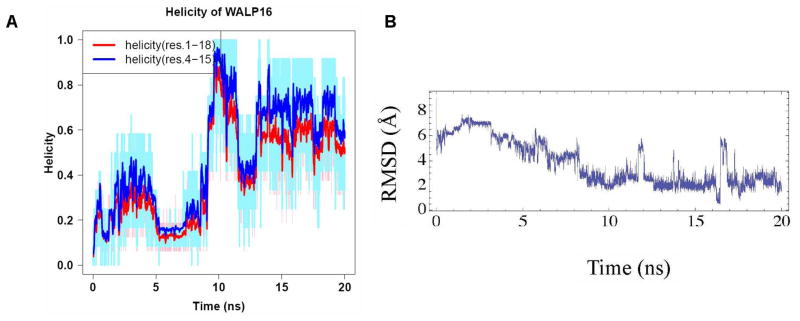
Replica exchange torsional MD simulations with eight replicas were performed on the trans-membrane peptide WALP16, in a low dielectric environment to mimic the membrane. WALP16 folded to a helix with an average backbone RMSD (in coordinates) of 2Å to a canonical helix, and the structure with best backbone RMSD was 0.5Å. The RMSD for all atoms excluding the hydrogens is 3.2Å. Figure 2 shows the RMSD in coordinates from a canonical helix versus time for the eight replicas. Chen et al. showed that the sampling of near native structures decreases with increase in time step. For a time step of 5 f s we find that the near native structures ranging from 0.5 Å to 2 Å in RMSD are sampled in these simulations.
Figure 2.
(A) Plot of helicity of WALP16 peptide calculated for the full length of the peptide shown in red, and for the residues 4 to 15 omitting the terminal residues shown in blue. The red and blue lines are the moving average calculated from the raw data shown in pale blue and pink. (B) Moving average of the RMSD in coordinates calculated for WALP16 from the experimental structure.
The helicity of the WALP16 peptide alternates between 0.6 to 0.8 (shown in red in Figure 2), due to fluctuations of the terminal residues as well as insufficient description of the solvation effects. The helicity goes up when the terminal residues are not included in the calculation of helicity as shown in blue line in Figure 2. Figure S1 in the Supporting Information shows the helicity calculated using φ = −62 ° and ψ = −41 °. These backbone angles are based on analysis of the protein structures from the Protein Data Bank. However as seen in Figure S1, the trend in helicity remains the same for both sets of φ and ψ values. In this study we have used a uniform low dielectric constant instead of a membrane potential. However the RMSD in coordinates shows tight native like structure.
Folding of a β-hairpin peptide
In this section we describe folding torsional MD simulations of a β-hairpin peptide (PDB code: 1E0Q) derived from the N-terminal segment of globular protein ubiquitin, with a point mutation T9D.29 The structure with pdb ID 1E0Q is 17 residues long, with the sequence MQIFVKTLDGK-TITLEV. The NMR measurements have shown that 1E0Q forms a type-I β-turn with Gly10 at the fourth position in the turn sequence Thr-Leu-Asp-Gly.29 The Gly10 also has a preference to be at the third position in a β-turn, and an alternate structure for the peptide has been suggested with a type-II β-turn.30 In this type-II turn structure the opposing chains are displaced by one residue. The conformation with type-II β-turn was not observed in the NMR study.29
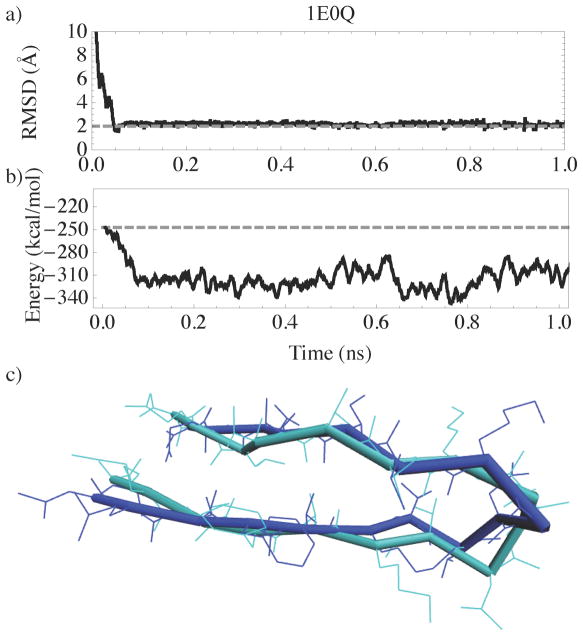
We performed torsional MD replica exchange simulations with eight replicas and a simulation time of 20ns per replica, starting from an extended conformation. The best folded structure of this peptide has a backbone RMSD of 1.5Å (2.8Å is the RMSD for all atoms) to the NMR structure,29 while the average backbone RMSD for the folded phase of the simulations was 2.2Å. Torsional Monte Carlo folding simulations performed by Ulmschneider et al.31 showed a minimum RMSD structure with 1.2 Å from NMR structure, though the average RMSD in their folded trajectory was 2.5 Å. All-atom MD simulations by Jang et al.21 showed a structure with backbone RMSD of 1.36 Å from the NMR structure. Our results are comparable to these prior results. Most of the conformations in the trajectory ranges from 2Å to 6Å in backbone RMSD. The good agreement between the NMR structure and a representative folded structure from our simulations is illustrated in Figure 3C.
Figure 3.
Plot of (A) RMSD as a function of time and (B) potential energy versus time for 1E0Q. The gray dashed line in (B) shows the initial potential energy. (C) Figure comparing the NMR structure (cyan) with a representative structure(blue) from the simulation.
The β strand region exhibited lower fluctuations than the turn region (residues 7 to 11) with an average backbone RMSD of 2Å compared with 2.6Å for the turn. Figure 3 shows a RMSD vs. the potential energy from the replica that folded to the native structure. Comparing Figure 3A and Figure 3B, we observe that the potential energy reduces as the conformation gets closer to the native state. This shows that the energy function is adequate for folding simple peptides using constrained MD.
A stable type-I turn, similar to the NMR structure, was observed in our simulations. Five out of the six backbone hydrogen bonds present in the NMR structure were highly populated. A comparison of the backbone hydrogen bond lengths from the simulations and NMR measurements is shown in Table 1. The hydrogen bond length from the simulation is the average length over the last 19ns of the simulation. Except for the hydrogen bond between Leu15(O)-Ile3(N), the other five backbone hydrogen bond measurements were in good agreement with the NMR measurements. The large deviation in the Leu15(O)-Ile3(N) hydrogen bond length is due to the twisting of the residues close to the termini.
Table 1.
Comparison of backbone hydrogen bond distances of NMR data with simulations for the β-turn peptide
| H-bond | NMR-data [Å] | Simulation [Å] |
|---|---|---|
| Met1(O)-Val17(N) | 4.0 ± 0.4 | 4.4 ± 1.2 |
| Leu15(O)-Ile3(N) | 3.4 ± 0.2 | 6.8 ± 0.4 |
| Ile3(O)-Leu15(N) | 3.13 ± 0.08 | 2.7 ± 0.2 |
| Ile13(O)-Val5(N) | 3.7 ± 0.4 | 3.0 ± 0.1 |
| Val5(O)-Ile13(N) | 3.8 ± 0.3 | 3.0 ± 0.2 |
| Lys11(O)-Thr7(N) | 3.6 ± 0.2 | 3.4 ± 0.3 |
The NMR structure of 1E0Q (the mutant with T9D mutation) showed a marked pH dependence compared to the wild type, in the pH range 2.0 to 3.8. Significant differences in chemical shifts and coupling constants from those anticipated for an unstructured state, were observed consistently at pH 3.8 compared to pH 2.0. This is in contrast to that of the wild type peptide, for which no significant pH dependence was observed over this pH range. This suggests that Asp9 in the 1E0Q mutant could get deprotonated and the salt bridge between Asp9 and Lys11 stabilizes the turn. Analysis of the torsional MD trajectory showed that the average N-O distance between the side chains of Lys11 and Asp9 was about 2.8Å supporting the formation of a salt-bridge between of Lys11 and COO− of Asp9.
Folding simulations of a fast-folding protein, Trp-cage
Trp-cage, a 20 residue protein is a mixed alpha helical and loop protein which serves as a good model test system for folding using torsional MD simulations. Trp-cage is thought to be the fastest folding protein known so far.32 Residues one through nine forms an α-helix while residues eleven through thirteen form a 310 helix. The two hydrophobic cores in Trp-cage, namely the residues one through nine that form a helix, and the residues sixteen through twenty that form a loop, pack against each other stabilized by a salt bridge between Asp9 and Arg16. There are various all-atom MD folding studies of Trp-cage using explicit17 as well as implicit solvent models.16,33
Dill and coworkers proposed the “zipping and assembly” (ZA) model as possible mechanism that proteins use to fold efficiently. ZA model is a “mechanism based search” of conformational space that makes the conformational search efficient thus allowing for fast folding.34 We have developed a torsional MD simulation platform that allows testing of freezing various sections of the protein that contain or form secondary structures, for example helical regions, and perform torsional MD for torsions connecting these rigid sections. This will allow us to test the ZA model and the hierarchical assembly mechanism of folding proposed by Dill and coworkers. This hierarchical constrained MD simulation platform can be used for other simulation applications as well.
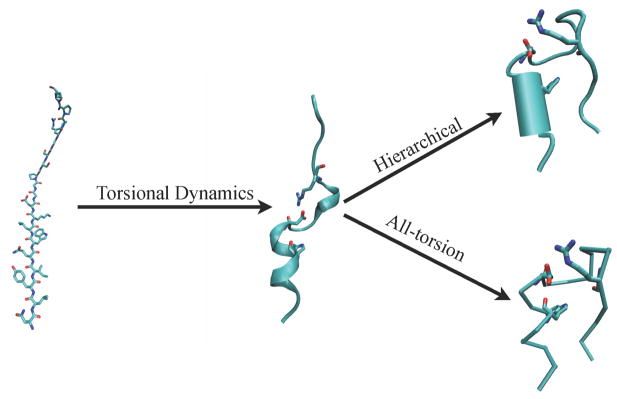
The goals of this section are multifold: a) showing constrained MD as a viable tool for folding Trp-cage, b) examining the folding landscape traversed by constrained MD simulations, and c) to demonstrate the advantages of hierarchical clustering schemes in folding studies using constrained MD. We performed Trp-cage folding in two stages, as illustrated in Figure 4. In the first stage, the extended conformation is allowed to fold into an intermediate state using all-torsion dynamics. At this intermediate state the helix formation is nearly complete and has the two partially formed hydrophobic cores correctly folded, and is stabilized by a salt-bridge connecting Asp9 and Arg16. Such an intermediate conformation has also been observed previously in the pathway of the all-atom folding simulations.17 The folding of extended state to the intermediate state took less than 6ns each of replica exchange simulation with eight replicas. In the second stage of simulations, a snapshot from the intermediate folded state was taken to perform hierarchical and all-torsion simulations in order to compare the different approaches. The hierarchical simulation was performed with the backbone of residues one through eight treated as a rigid body while the rest of the torsions were allowed to move (Figure 4). Eight replicas were used in the replica exchange simulations, with 20ns of simulation time for each replica. Two sets of REXMD simulations were performed for both hierarchical as well as all-torsion simulations. This totals to two sets of 160ns (8 replicas × 20ns) for each of hierarchical and all-torsion simulations.
Figure 4.
The two stages of Trp-cage simulation followed in order to highlight the differences between hierarchical and all-torsion method. Torsional dynamics is done in the first stage until the intermediate state is formed. In the hierarchical simulation of the second stage, the backbone of residues 1 to 8, part of the helix, is treated as a rigid body keeping all other torsions flexible. In the all-torsion simulations of the second stage, torsional MD is continued.
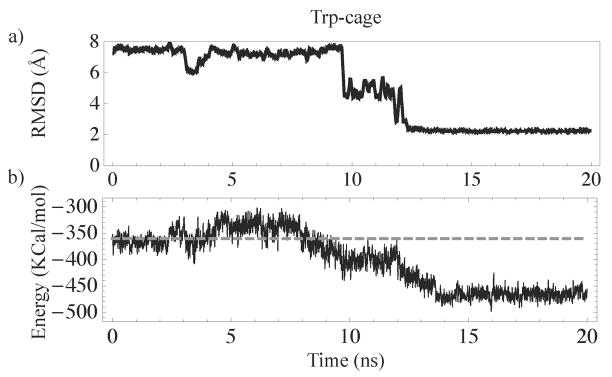
The variation in the backbone RMSD difference (excluding the two terminal residues) between the NMR structure of Trp-cage and folded conformations from the hierarchical and all-torsion simulations were between 2Å and 3Å. The best structure from the hierarchical simulations had a backbone RMSD difference of 1.5Å excluding the termini and 1.9Å for the full length, from the NMR structure.32 The all-atom RMSD excluding the hydrogens of the best structure is 3.4Å. Comparison of the NMR structure with a representative structure from the hierarchical constrained MD simulation is shown in Figure 5. The sidechain in Tyr3 is closely packed with Trp6 as seen in the NMR structure. The salt-bridge between Asp9 and Arg16 stabilizes the folded structure. The 310-helix comprising of the residues eleven through fourteen is partially formed, similar to the NMR structure. The potential energy of the folded structure is lower than the non-native like structures as shown in Figure 6.
Figure 5.
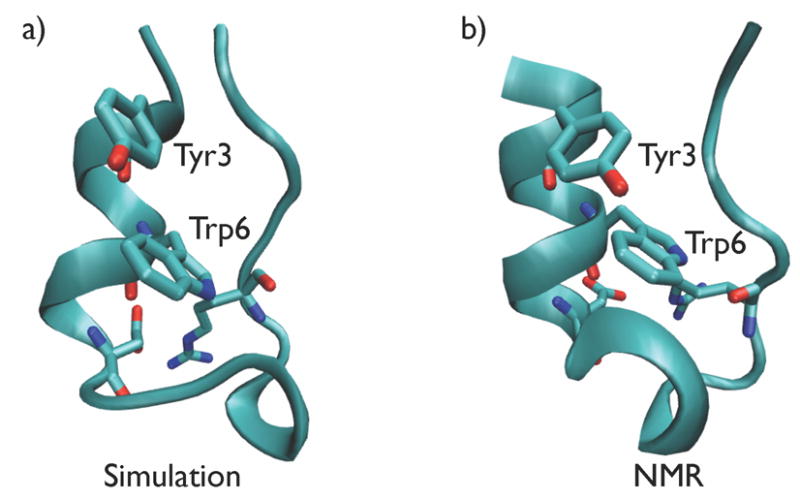
Representative snapshot from (A) Trp-cage folding hierarchical MD simulation, and (B) NMR structure.
Figure 6.
Plot of (A) backbone RMSD as a function of time and (B) potential energy versus time for Trp-cage. The gray dashed lined in (B) shows the initial potential energy of the system.
To compare the similarities and differences between folding space of hierarchical and torsional constrained MD simulations, we examined the conformation population density distribution in a 2D plane spanned by the first two principal components of the simulation trajectories (Figure 7A and B). The average conformation for each cluster (obtained from K-means clustering algorithm) was obtained by averaging all the snapshots contained in each cluster. In this foregoing and the following sentences the word cluster refers to the clusters obtained from the K-means clustering algorithm and not the rigid bodies used in the dynamic model. The structural conformations of the protein corresponding to various clusters were analyzed. Figure 7 shows the 2D landscape of the population density of various clusters plotted with respect to the two principal components. The highly populated regions are colored blue, and the sparsely populated regions colored red, with the average structures corresponding to the different high density basins are shown on the side.
Hierarchical MD simulations
Cluster-I shown in Figure 7A is close to the intermediate structure shown in Figure 4. Clusters-II and III in hierarchical simulation shown in Figure 7A, are the various intermediates with the two hydrophobic cores packed to different degrees. These intermediate structures are well populated during the simulations before the structure folds into the native state, that is represented by cluster-IV in the Figure 7A. Similar intermediate states were also observed in the all-torsion simulations shown as cluster-II in Figure 7B. One key difference is that the population of cluster-III corresponding to an intermediate state (Figure 7A) is 39% of the total conformations in the hierarchical simulations.
All-torsion MD simulations
The population of cluster-II in the all-torsion simulations corresponds to a conformation similar to that of cluster-III in the hierarchical simulations, and is only 12% of the total conformations. There is an equal population (12%) of a cluster (cluster-IV in Figure 7B) of conformations with an unraveled helix in the all-torsion simulations. This is absent in the hierarchical simulations obviously since the helix is kept rigid.
Comparison of the trajectories of the two simulations
Freezing the backbone of the helix into a rigid body, completely avoided sampling this unraveled state in the hierarchical simulations shown in Figure 7A, and this facilitates the enriched sampling of native like structures compared to all-torsion simulations. Even all-atom MD simulations are known to have unfolding events during the folding of a protein.35 The population of native like structures is higher in the all-torsion simulations (10% for cluster-III in Figure 7B compared to 5% for cluster-IV in Figure 7A) compared to the hierarchical simulations, though the hierarchical simulations had on an average lower RMSD from native compared to all-torsion simulations. Out of this 5%, 4.9% of the population in the heirarchical simulations, was in the CRMSD range of < 3Å which is close to the experimental structure and the rest 0.1% falling in the > 3Å CRMSD. For all-torsion simulations, the cluster containing the folded state had a population of 10%, twice as much as the same state in hierarchical simulations. The majority of the population (9.9%) had an CRMSD > 3Å with about 0.01% of the conformations having CRMSD < 3Å. However it is possible that a longer all-torsion simulation time could enrich structures closer to the native state (< 3 Å). The fact that hierarchical simulations, in a stipulated simulation time, enriched the near-native states more than the all-torsion simulation, holds good for repeated simulations. Thus using knowledge about possible secondary structure regions in a protein sequence, or of motifs/regions that fold faster one can use hierarchical simulation techniques in constrained MD and avoid sampling states that are not of significance in protein folding. This technique could also be used for the refinement of low resolution protein structures or for studying the domain motion in proteins.
Effect of clustering schemes on folding Trp-cage
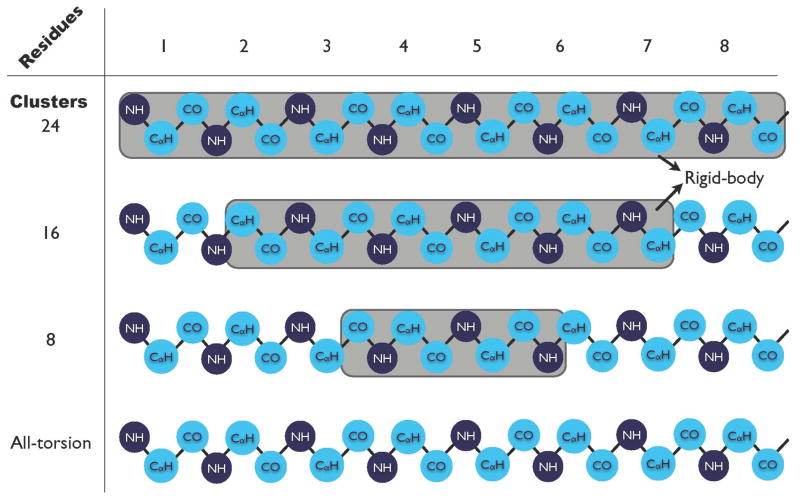
In this section, we have studied the effect of various clustering schemes on the dynamics of folding of Trp-cage protein. The regions of secondary structure such as helical lengths are not precisely predictable and also the termini of helices are normally more flexible than their core. We performed hierarchical constrained MD simulations with varied lengths of helices kept fixed as rigid bodies to analyze the effect of different clustering schemes. There were 24 clusters of atoms in the backbone of the helical region (residues 1 to 8) of Trp-cage as shown in Figure 8. In the first hierarchical simulations described so far all the 24 clusters were frozen and treated as a rigid body – the clustering scheme 1 in Figure 8. We have performed simulations with the 16 and 8 clusters in the center of the helix frozen as rigid bodies; these two clustering schemes are termed as 2 and 3 respectively in Figure 8.
Figure 8.
Schematic of the clusters involved in various hierarchical schemes in Trp-cage. The cyan and dark blue circles show the “basic clustering” scheme used in all-torsion MD simulations. The shaded area in each scheme shows the number of basic clusters frozen as one rigid body.
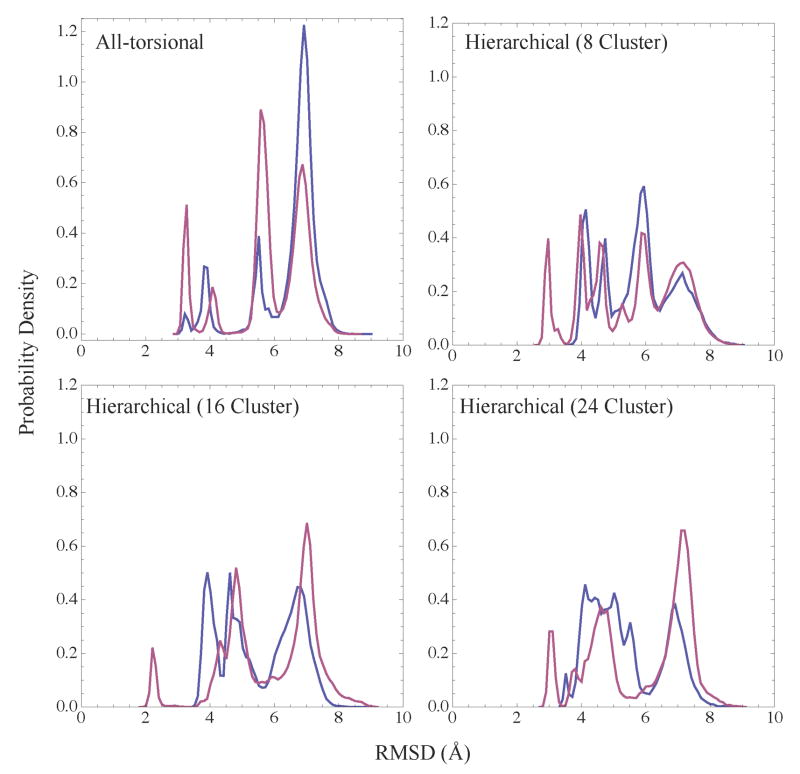
Two replica exchange simulations (with eight replicas and 20ns for each replica) were performed for each of the clustering schemes 1, 2 and 3. The conformations from each of these trajectories were arranged into bins depending on how close they are to the native structure. Figure 9 shows the probability density versus the RMSD in coordinates to the native structure, for simulations with various clustering schemes and all-torsion simulations. The all-torsion simulations show a greater probability (> 87%) of non-native (> 5Å in RMSD from the native structure) like conformations compared to simulations from all the three hierarchical schemes 1 to 3. Structures with smaller RMSD for the hierarchical simulations could arise from fixing the helix. It should be noted that the helix obtained from the intermediate structure during simulations (which was not the same as the helix in the native structure) was kept fixed in the various hierarchical schemes. On the other hand, we observe that in simulations from all the three hierarchical schemes, the replicas span the RMSD space more uniformly than the all-torsion simulations. By treating the helix as a rigid body, we avoid sampling conformations where the helix unravels, and on an average only 60% of the conformations sampled, had a backbone RMSD greater than 5Å. The conformations that are between the native like (< 3Å ) and non-native structures (> 5Å) could serve as intermediates to folding in the hierarchical simulations. Thus we observe that the hierarchical simulations lead to more efficient and native like conformational search compared to all-torsion simulations.
Figure 9.
Plot of the probability distribution of conformations from all replicas occupying various RMSD from the native state. Shown here for all the replicas from two replica exchange simulations (blue, purple) for all-torsion and hierarchical cases with 8, 16 and 24 clusters in the helical backbone frozen as a rigid body.
Conclusions
Use of MD methods to study protein folding is a computationally challenging problem. Typically, proteins fold on a timescale of microseconds to milliseconds, and performing all-atom simulations is computationally expensive. In the current work, we have demonstrated the use of constrained MD approach coupled with replica exchange method for improved conformational sampling and as a viable tool for ab initio folding studies. In this paper we have established the following advantages of using constrained MD:
Typically for a system with N atoms, an all-atom replica exchange simulation will require number of replicas for efficient sampling. Since the number of dofs in constrained MD of an N atom system is approximately N/3, the number of replicas required for replica exchange simulation using constrained MD is proportional to – a factor of three smaller in number of replicas than that for the all-atom MD simulations. To illustrate this, in all-atom Trp-cage folding studies by Pitera et al.,16 23 replicas were used between temperatures of 250K to 630K. We have shown here in our constrained MD replica exchange simulations, only eight replicas (a factor three lower than all-atom case) were used in the temperature range of 325K to 600K.
Since the higher frequency (and not so significant) modes such as bond and angle vibration are not sampled, one can use a higher timestep for integration and still get stable dynamics. We have demonstrated stable dynamics using a 5 f s timestep for a second-order integrator involving only one force calculation per integration step. This is a factor of five times in speed up compared to the 1 f s timestep required in all-atom MD simulations.
We have demonstrated a clustering method that enables the user to treat parts of the molecule as rigid body, allowing sampling of torsions connecting the rigid parts. This method known as the hierarchical constrained MD method allows the user to use a multiscale dynamic model of the protein ranging from all-atom, to all-torsion, to making parts of the protein rigid. Such hierarchical modeling of the protein also enhances the conformational sampling closer to the native state as demonstrated in the folding studies of Trp-cage protein (Figure 9).
This study sets the stage for future work where we will explore the importance of constrained MD as a tool for other applications such as studying long timescale protein dynamics and refinement of low resolution protein structures.
Supplementary Material
Acknowledgments
This project has been supported by Grant Number RO1GM082896-01A2 from the National Institute of Health. We thank Dr. Jerry Li and Dr. Karin Remington for their support and encouragement. Part of the research described in this paper was performed at the Jet Propulsion Laboratory (JPL), California Institute of Technology, under contract with the National Aeronautics and Space Administration. We thank Simbios for providing us with the GB/SA solvation module, Mark Friedrichs for his help with validating our GB/SA module, Michael Sherman and Christopher Bruns for helping us with running Simbody. The Simbios software was made freely available on https://simtk.org/home/openmm by the Simbios NIH National Center for Biomedical Computing.
Footnotes
Supporting Information Available
References
- 1.Stone JE, Hardy DJ, Ufimtsev IS, Schulten K. J Mol Graph Model. 2010;29:116–25. doi: 10.1016/j.jmgm.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Shaw DE, et al. Anton, a special-purpose machine for molecular dynamics simulation. 2007. [Google Scholar]
- 3.Ryckaert J, Ciccotti G, Berendsen HJC. J Comput Phys. 1977;23:327–341. [Google Scholar]
- 4.Andersen HC. J Comput Phys. 1983;52:24–34. [Google Scholar]
- 5.Mazur AK, Abagyan RA. J Biomol Struct Dyn. 1989;6:815–832. doi: 10.1080/07391102.1989.10507739. [DOI] [PubMed] [Google Scholar]
- 6.Mazur AK, Dorofeev VE, Abagyan RA. J Comput Phys. 1991;92:261–272. [Google Scholar]
- 7.Jain A, Vaidehi N, Rodriguez G. J Comput Phys. 1993;106:258–268. [Google Scholar]
- 8.Chen J, Im W, Brooks CL. J Comput Chem. 2005;26:1565–1578. doi: 10.1002/jcc.20293. [DOI] [PubMed] [Google Scholar]
- 9.Gibson KD, Scheraga HA. J Comput Chem. 1990;11:468–486. [Google Scholar]
- 10.Vaidehi N, Jain A, Goddard W. J Phys Chem. 1996;100:10508–10517. [Google Scholar]
- 11.Vaidehi N, Goddard WA. J Phys Chem A. 2000;104:2375–2383. [Google Scholar]
- 12.Schwieters CD, Clore GM. J Mag Res. 2001;152:288–302. doi: 10.1006/jmre.2001.2413. [DOI] [PubMed] [Google Scholar]
- 13.Jain A. J Guid Control Dynam. 1991;14:531–542. [Google Scholar]
- 14.Rodriguez G, Kreutz-Delgado K, Jain A. Int J Robot Res. 1991;10:371–381. [Google Scholar]
- 15.Bertsch R, Vaidehi N, Chan S, Goddard W. Protein Struct Funct Genet. 1998;33:343–357. doi: 10.1002/(sici)1097-0134(19981115)33:3<343::aid-prot4>3.0.co;2-b. [DOI] [PubMed] [Google Scholar]
- 16.Pitera J, Swope W. P Natl Acad Sci USA. 2003;100:7587–7592. doi: 10.1073/pnas.1330954100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhou R. P Natl Acad Sci USA. 2003;100:13280–5. doi: 10.1073/pnas.2233312100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kannan S, Zacharias M. Proteins. 2009;76:448–460. doi: 10.1002/prot.22359. [DOI] [PubMed] [Google Scholar]
- 19.Jang S, Kim E, Shin S, Pak Y. J Am Chem Soc. 2003;125:14841–14846. doi: 10.1021/ja034701i. [DOI] [PubMed] [Google Scholar]
- 20.Snow CD, Qiu L, Du D, Gai F, Hagen SJ, Pande VS. P Natl Acad Sci USA. 2004;101:4077–82. doi: 10.1073/pnas.0305260101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jang S, Shin S, Pak Y. J Am Chem Soc. 2002;124:4976–7. doi: 10.1021/ja025675b. [DOI] [PubMed] [Google Scholar]
- 22.Swendsen RH, Wang JS. Phys Rev Lett. 1986;57:2607–2609. doi: 10.1103/PhysRevLett.57.2607. [DOI] [PubMed] [Google Scholar]
- 23.Hansmann UH. Chem Phys Lett. 1997;281:140 – 150. [Google Scholar]
- 24.Sugita Y, Okamoto Y. Chem Phys Lett. 1999;314:141–151. [Google Scholar]
- 25.Wang J, Cieplak P, Kollman P. J Comput Chem. 2000;21:1049–1074. [Google Scholar]
- 26.Onufriev A, Bashford D, Case DA. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 27.This code was made freely available on https://simtk.org/home/openmm by the Simbios NIH National Center for Biomedical Computing. Simbios is supported by the National Institutes of Health through the NIH Roadmap for Medical Research Grant U54 GM072970. (2007).
- 28.Fukunishi H, Watanabe O, Takada S. J Chem Phys. 2002;116:9058–9067. [Google Scholar]
- 29.Zerella R, Chen PY, Evans PA, Raine A, Williams DH. Protein Sci. 2000;9:2142–50. doi: 10.1110/ps.9.11.2142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Searle MS, Williams DH, Packman LC. Nat Struct Mol Biol. 1995;2:999–1006. doi: 10.1038/nsb1195-999. [DOI] [PubMed] [Google Scholar]
- 31.Ulmschneider J, Jorgensen W. J Am Chem Soc. 2004;126:1849–1857. doi: 10.1021/ja0378862. [DOI] [PubMed] [Google Scholar]
- 32.Neidigh JW, Fesinmeyer RM, Andersen NH. Nat Struct Biol. 2002;9:425–30. doi: 10.1038/nsb798. [DOI] [PubMed] [Google Scholar]
- 33.Simmerling C, Strockbine B, Roitberg AE. J Am Chem Soc. 2002;124:11258–9. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 34.Ozkan SB, Wu GA, Chodera JD, Dill KA. P Natl Acad Sci. 2007;104:11987–11992. doi: 10.1073/pnas.0703700104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Shaw DE, Maragakis P, Lindorff-Larsen K, Piana S, Dror RO, Eastwood MP, Bank JA, Jumper JM, Salmon JK, Shan Y, Wriggers W. Science. 2010;330:341–346. doi: 10.1126/science.1187409. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.