Abstract
The significance of conical intersections in photophysics, photochemistry, and photodissociation of polyatomic molecules in gas phase has been demonstrated by numerous experimental and theoretical studies. Optimization of conical intersections of small- and medium-size molecules in gas phase has currently become a routine optimization process, as it has been implemented in many electronic structure packages. However, optimization of conical intersections of small- and medium-size molecules in solution or macromolecules remains inefficient, even poorly defined, due to large number of degrees of freedom and costly evaluations of gradient difference and nonadiabatic coupling vectors. In this work, based on the sequential quantum mechanics and molecular mechanics (QM∕MM) and QM∕MM-minimum free energy path methods, we have designed two conical intersection optimization methods for small- and medium-size molecules in solution or macromolecules. The first one is sequential QM conical intersection optimization and MM minimization for potential energy surfaces; the second one is sequential QM conical intersection optimization and MM sampling for potential of mean force surfaces, i.e., free energy surfaces. In such methods, the region where electronic structures change remarkably is placed into the QM subsystem, while the rest of the system is placed into the MM subsystem; thus, dimensionalities of gradient difference and nonadiabatic coupling vectors are decreased due to the relatively small QM subsystem. Furthermore, in comparison with the concurrent optimization scheme, sequential QM conical intersection optimization and MM minimization or sampling reduce the number of evaluations of gradient difference and nonadiabatic coupling vectors because these vectors need to be calculated only when the QM subsystem moves, independent of the MM minimization or sampling. Taken together, costly evaluations of gradient difference and nonadiabatic coupling vectors in solution or macromolecules can be reduced significantly. Test optimizations of conical intersections of cyclopropanone and acetaldehyde in aqueous solution have been carried out successfully.
INTRODUCTION
Conical intersections of potential energy surfaces have been recognized as a key concept in understanding mechanisms of photochemical reactions and photophysical processes.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 Conical intersections are not a single point but a multidimensional seam of 3N −8 degrees of freedom where N is the number of atoms in a system. These conical intersections are usually formed between electronic states with same spatial symmetries and spins, which are defined as seams of the true degeneracy between electronic states.1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 19, 20, 21, 22, 23, 24, 25, 26 The manifold of ground and excited electronic states for almost all molecular systems is rife with conical intersections. These intersections provide an efficient and effective pathway for nonradiative decays.1, 5, 7, 9, 10, 21 As conical intersections are prevalent over many-dimensional manifold of states, accurate treatments of conical intersections are very crucial. Nonadiabatic transition between different electronic states occurs efficiently near conical intersections, and thereby ultrafast photophysical processes and photochemical reactions have been frequently related to the existence of conical intersections. For example, ultrafast internal conversion processes have been believed to be responsible for protecting DNA from photodamage.27, 28, 29, 30 Due to the substantial development of efficient optimization techniques of conical intersections, such as the projected gradient method of Robb et al.,19 the Lagrange multiplier constrained procedure of Yarkony,31 and the penalty function method of Martinez et al.,23 the understanding of ultrafast processes related to conical intersections has progressed rapidly.1, 4, 6, 7, 8, 14, 15, 17, 19, 22, 23, 25, 31, 32, 33, 34, 35, 36, 37, 38, 39
Combined quantum mechanics and molecular mechanics (QM∕MM) method, first developed by Warshel and Levitt, provides an accurate and efficient energetic description of complex chemical, biological systems, and materials.7, 26, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61 It is a multi-scale and multi-resolution method: The chemically active part of a system, such as the active site in macromolecules or the solute in solution, is described at the electronic level with the QM methods, whereas the rest of macromolecules or solvents are described at the atomistic level with the MM methods. This combined QM∕MM method allows reliable electronic-structure calculations for chemical reactions, with a realistic and atomistic description of macromolecular or solvent environments.41, 42, 47, 49, 50, 62 Such a method takes advantage of the accuracy of the QM methods for chemical reactions and the computational efficiency of the MM methods for macromolecular or solvent environments, which normally consist of many thousands of atoms. The development of the QM∕MM method has enabled simulations of complex chemical and biological processes, leading to significant advances in our understanding of chemical reaction mechanisms in solution or macromolecules.13, 26, 44, 45, 46, 63, 64, 65, 66, 67
In order to make the QM∕MM minimization in solution or macromolecules efficient, we have developed a sequential optimization method where the QM and MM optimizations are sequentially, not concurrently, carried out.44, 64, 65, 66, 68, 69, 70 In this method, expensive but accurate optimization methods, such as Newton–Raphson and rational functional optimization methods, are used for optimizations of the QM subsystem, while efficient optimization methods, such as steepest descent and conjugated gradient methods, are used for minimizations of the MM subsystem.44 As chemical reactions mainly proceed in the QM subsystem, transition state optimizations mainly depend on degrees of freedom of the QM subsystem. In general, Hessian-matrix-based optimization methods are needed to locate efficiently transition states of chemical reactions. Hence, in comparison with the concurrent optimization scheme, this sequential QM and MM optimization method is more efficient for locating transition states of chemical reactions in solution or macromolecules because transition state optimizations are mainly dependent on degrees of freedom of the QM subsystem.44, 64, 71
This strategy of sequential optimizations has recently been extended to free energy calculations in solution or macromolecules. To compute reaction free energies directly and overcome difficulties associated with optimizations on potential energy surfaces and bias stemming from a single initial conformation, we have recently developed the QM∕MM-minimum free energy path (QM∕MM-MFEP) method for simulations of reactions both in macromolecules and in solution. In this method, the QM subsystem is full optimized in the MM environment. A finite ensemble generated via molecular dynamics simulations is used to calculate the potential of mean force surface; then, the QM conformations are optimized on this calculated potential of mean force surface. The QM optimization and the MM sampling are sequentially performed until convergence.42, 62, 68, 70, 72, 73 This improvement obviates the QM∕MM-FE requirement of defining a minimum energy reaction path prior to free energy calculations.65, 66, 68, 69
Recently, conical intersections of potential energy surfaces for reactions in solution or macromolecules have received much attention.27, 28, 29, 74, 75, 76, 77 However, conical intersection optimizations in solution or macromolecules is more difficult than those in gas phase due to the large dimensionality of potential energy surfaces. Conical intersection optimization techniques used for small- and medium-size systems in gas phase could be inefficient for macromolecules or solution. Therefore, developing efficient optimization techniques for conical intersections in macromolecules or solution is significant.
Conical intersections on potential energy surfaces in macromolecules or solution, in the framework of the QM∕MM method, have been explored before. For example, Martinez et al. employed the floating occupation semi-empirical configuration interaction method to study conical intersections in solution and macromolecules,26, 37, 78 whereas Bearpark et al. studied conical intersection optimizations with the ONIOM method.79 Furthermore, conical intersection optimizations in solution or macromolecules with the QM∕MM method have also been explored by several groups.7, 12, 13, 80, 81 However, these studies mainly focus on potential energy surfaces, not potential of mean force surfaces, and conical intersection optimizations are carried out concurrently, not sequentially, which means that conical intersection optimizations of the QM subsystem and minimizations of the MM subsystem are performed simultaneously.
It is difficult to locate conical intersections in solution or macromolecules in terms of potential energy surface due to its large dimensionality. Conical intersections of potential of mean force surfaces are considered as an alternative to describe photochemical reactions and photophysical processes in solution or macromolecules. In 2004, Burghardt et al. employed the dielectric continuum model to derive formulations of conical intersection optimizations on potential of mean force surfaces and studied cis-trans isomerizations of the retinal protonated Schiff base.82, 83 Kato et al., by using the linear response theory and Gaussian fluctuation model, developed a conical intersection optimization procedure of potential of mean force surfaces in solution, which employs the reference interaction site model with the complete active space self-consistent field method.84, 85, 86, 87, 88 Recently, Mori et al. extended this method to use the multi-state complete active space second order perturbation theory.87 Furthermore, Aguilar et al. used the averaged solvent electrostatic potential from molecular dynamics simulations of solvents, as a perturbation potential embedded into Hamiltonian of solute, to optimize conical intersections in solution.89, 90, 91
Conical intersections of free energy surfaces, i.e., potential of mean force surfaces, are useful for understanding photophysical and photochemical processes in condensed phase.82, 83, 84, 85, 86 First, it is usually expensive, even impossible, to search each local QM conical intersection structure related to each MM configuration. The MM subsystem mainly acts as a perturbation on the QM subsystem; thus, the structure and the energetics of the QM conical intersection change subtly as a result of a small position displacement of the MM subsystem. Using conical intersections of potential of mean force surfaces, we do not need to focus on each local QM conical intersection corresponding to each MM configuration, but on the averaged QM conical intersection corresponding to an ensemble of MM configurations. Second, although “on the fly” ab initio nonadiabatic dynamics simulations can provide more dynamical information for internal conversion processes via conical intersections, the time scale of ab initio nonadiabatic dynamics is rather limited, always within or near picoseconds, because of expensive evaluations of gradient difference and nonadiabatic coupling vectors and small time steps. Thus, they are mainly used to simulate ultrafast, nonequilibrium nonadiabatic processes in small- and medium-size polyatomic molecules.7, 12, 13, 26, 37, 80, 81, 92 However, relatively slow reactions, more than hundreds of picoseconds, remain ubiquitous in solution photochemistry and biophotochemistry, where topological structures, such as conical intersections of potential of mean force surfaces, could be more useful and can provide valuable insights into mechanisms.27, 28, 74, 75, 76, 77
In this work, we have combined our sequential optimization technique with the QM∕MM and QM∕MM-MFEP methods and developed two conical intersection optimization methods for small- and medium-size molecules in solution or macromolecules on potential energy surfaces and potential of mean force surfaces, respectively. The theoretical background, fundamental formulations, algorithms, and implementations are given in detail. Conical intersection optimizations of cyclopropanone and acetaldehyde in aqueous solution, as a pilot test, show the feasibility of our methods.
THEORETICAL BACKGROUND
QM∕MM method
To form a self-contained work, we briefly present basic formulations of the QM∕MM method.40, 41, 42, 43, 44, 45, 46, 49, 50, 56, 59, 72, 80 In this work, differences between ground and excited states in formulations will be emphasized when needed. To discuss conical intersections, we use subscripts, I and J, to represent lower and upper electronic states, respectively. Subscript I can be electronically ground or excited states.
The total QM∕MM potential energy for electronic state I is expressed as
| (1) |
where EI,qm(rqm), EI,mm(rmm), and EI,qm∕mm(rqm,rmm) are quantum mechanical energy of the QM subsystem for electronic state I, molecular mechanical interactions of the MM subsystem when the QM subsystem is at electronic state I, and QM∕MM interactions between the QM subsystem at electronic state I and the MM subsystem, respectively; rqm and rmm are atomic coordinates of the QM and MM subsystems. In practical applications, we usually use standard force fields for EI,mm(rmm) calculations, although these force-field parameters are fitted for ground state applications. This approximation, EI,mm(rmm)≃Emm(rmm), is usually valid because relevant processes involved electronic structure changes in a chemical reaction mainly occur in the QM subsystem. For QM∕MM interactions, there are mainly three components, as in the following equation:
| (2) |
where the MM bonded interaction, EI,MM−bonded(rqm,rmm), refers to the MM bond, angle, and dihedral energy terms, which involve at least one atom of the MM subsystem and one of the QM subsystem, EI,vdw(rqm,rmm) represents van der Waals interaction between the QM and MM subsystems, and EI,ele(rqm,rmm) is the electrostatic interaction between the QM and MM subsystems. As done for the above EI,mm(rmm), ground-state force field parameters are adequate for the former two QM∕MM interactions, EI,MM−bonded(rqm,rmm)≃EMM−bonded(rqm,rmm) and EI,vdw(rqm,rmm)≃Evdw(rqm,rmm).
However, for EI,ele(rqm,rmm) we must explicitly calculate it by means of electronic structure methods. Usually the sum of EI,qm(rqm) and EI,ele(rqm,rmm) can be calculated together as eigenenergies of an effective Hamiltonian Heff(rqm,rmm), namely,
| (3) |
This effective calculation can be performed by using density functional theory, configuration interaction methods, and even multi-reference methods. If covalent bonds are broken when we separate the QM and MM subsystems, an appropriate scheme is needed to mimic the boundary condition, such as, the link atom scheme, the generalized hybrid orbital scheme, and the pseudobond scheme developed in our group.43, 51, 59 With these approximations, the total energy of a system at the QM∕MM level becomes
| (4) |
Electrostatic potential fitting
For sequential optimizations of the QM and MM subsystems, the electrostatic potential fitting (ESP) scheme is more feasible, as have been done in our group.42, 44, 62, 68, 71, 72 In such scheme, the QM∕MM electrostatic interaction at electronic state I can be expressed as
| (5) |
where QI,α(rqm,rmm) is the electrostatic potential fitted charge on the αth QM atom when the QM subsystem is at electronic state I. These charges are different from one electronic state to another. With this ESP scheme, we can define the internal energy of the QM subsystem as below42, 44, 62, 68, 72
| (6) |
This definition of the QM internal energy in the QM∕MM method, which is dependent on atomic coordinates of the QM and MM subsystems, is different from the regular QM internal energy of a system in gas phase, which is only dependent on the QM atomic coordinates. This modified QM internal energy has also been used to study the reaction path potential.93, 94
This ESP treatment can be used to reduce computational effort drastically in conjunction with the sequential optimization method, especially with the QM∕MM-MFEP method.42, 44, 62, 68, 72 In the QM∕MM total energy expression, Eq. 1, molecular mechanics energy of the MM subsystem, MM-bonded QM∕MM interaction, and van der Waals QM∕MM interaction can be calculated with the fixed QM subsystem. Only two interaction terms involve the QM degrees of freedom: electrostatic interactions between the QM electrons and the MM point charges and between the QM nuclei and the MM point charges. In our sequential optimization scheme, this electrostatic interaction can be approximated with fitted ESP charges, as shown in Eq. 5. Thus, we only use one approximation that ESP charges of the QM atoms do not change during one cycle of minimizations of the MM subsystem. After one cycle of MM minimizations, the QM optimizations start. At the end of the QM optimizations when it converges, new ESP charges of the QM atoms are re-calculated. This algorithm has been described in detail before.44 The similar scheme is also used in the QM∕MM-MFEP method, except that the MM minimizations are replaced by statistical samplings in molecular dynamics simulations.68, 72 However, further improvements of these ESP charges are still available.68, 95
Potential of mean force
Here we briefly review formulations used to calculate the free energy profile of a chemical reaction.41, 42, 44, 62, 68, 72, 96 The free energy as a function of atomic coordinates of the QM subsystem, also known as potential of mean force, can be expressed as
| (7) |
where the configurational partition function is defined as below
| (8) |
In principle, the absolute free energy can be calculated using Eq. 7; however, the relative free energy change is more useful in practical applications, which can be calculated with free energy perturbation and thermodynamics integration methods.42, 44, 62, 68, 72
Free energy gradient
The recently developed QM∕MM-MFEP method can efficiently optimize stationary structures on potential of mean force surfaces both for electronically ground and excited states.42, 62, 66, 68, 70, 72 According to Eqs. 7, 8, the potential of mean force of the QM subsystem at electronic state I with the QM∕MM-MFEP method is expressed
| (9) |
where EI(rqm,rmm) is the total QM∕MM energy of a system at electronic state I with the QM subsystem is fixed at rqm. To perform optimizations efficiently in available procedures, gradients of the QM subsystem on the potential of mean force surface are usually required.72 Gradients of the QM subsystem can be expressed as
| (10) |
where the brackets indicate an ensemble average of the QM gradients over the MM degrees of freedom
| (11) |
METHODS
Conical intersections of potential energy surface
Here we also give a brief discussion on conical intersection optimizations of potential energy surfaces, which is helpful to understand conical intersection optimizations of potential of mean forces below. Conical intersections of two potential energy surfaces are the nuclear coordinate space where these two electronic states are truly degenerate.1, 2, 3, 6, 9 Conical intersections can be efficiently located by using optimization techniques.14, 19, 21, 22, 23, 25, 31, 78, 97 In this work we only focus on formulations of conical intersection optimizations in the framework of the QM∕MM method, where only electronic degrees of freedom in the QM subsystem are explicitly considered. This means that conical intersection optimizations proceed in the QM subsystem, while the MM subsystem only represents a perturbative environment.
Conical intersection optimizations with the QM∕MM method require gradient difference and nonadiabatic coupling vectors between lower and upper electronic states I and J:
| (12) |
| (13) |
where g IJ and h IJ vectors are gradient difference and nonadiabatic coupling vectors between potential energy surfaces, which are dependent on atomic coordinates of the QM and MM subsystems, rqm and rmm are atomic coordinates of the QM and MM subsystems, and ΨI and ΨJ are electronic wave functions of lower and upper electronic states I and J, calculated from Eq. 3. These two vectors define the branching plane of a conical intersection. Near a conical intersection, the degeneracy of two potential energy surfaces is lifted rapidly along gradient difference and nonadiabatic coupling vectors, while the degeneracy is preserved along all other 3N −8 dimensions. Hence, an efficient algorithm used for locating conical intersections equals minimizing the potential energy of the upper electronic state J along the seam of the 3N −8 subspace that are orthogonal to the vectors, g IJ (rqm,rmm) and h IJ (rqm,rmm).14, 19, 23, 25, 31 Finally, one should note that only QM components of gradient difference and nonadiabatic coupling vectors are used in our sequential optimizations of the QM conical intersections, making the MM components zeros. This approximation is usually feasible in the framework of the QM∕MM method, as done in many groups.13, 26
Here we focus on the projection gradient method of Bearpark et al.19, 91, 97 The gradients projected to the 3Nqm−8 subspace can be written as a transformation:
| (14) |
where gqm is the atomic gradients of the QM subsystem that have been projected to the seam subspace. The specific transformation form in Eq. 14 can be found in literature.19, 78, 97 By using these projected gradients to minimize the potential energy of the upper electronic state J, we can obtain minimum energy conical intersections.
Other methods for conical intersection optimizations should also work, but different formulations are needed.6, 14, 19, 22, 31, 78, 97 For example, in the penalty function method of Martinez et al., it does not need nonadiabatic coupling vector whose evaluation is expensive, instead it only needs the energies and gradients of both lower and upper electronic states.23 Since the implementation of our QM∕MM and QM∕MM-MFEP methods is based on GAUSSIAN03 and SIGMAX2.2 packages, using the projected gradient method of Bearpark et al. for conical intersection optimizations is our preference in this work.19
On the other hand, the gradients of the MM subsystem can be approximated as
This approximation is reasonable and acceptable because electronic structure changes dominantly take place in the QM subsystem. With the derived QM and MM gradients, concurrent and sequential optimizations can be carried out. In this work, we only focus on the latter as concurrent scheme has been explored by many groups with the same approximations.7, 26, 37, 78, 79
Sequential QM conical intersection optimization and MM minimization
In general, conical intersection optimizations of potential energy surfaces for small- and medium-size molecules in solution is carried out with concurrent optimization techniques, which require to calculate gradient difference and nonadiabatic coupling vectors of the QM subsystem and gradients of the MM subsystem simultaneously. However, as stated by Zhang et al., efficiency of concurrent algorithms is highly dependent on the size of a system and the cost to calculate potential energies.44 Algorithms developed for the QM optimizations, such as quasi-Newton minimizer, are still inefficient to deal with thousands of atoms in a system due to the need of second-order derivatives of the system, which is rather expensive, even impossible in certain cases. On the other hand, powerful minimization methods have been developed for the molecular mechanical potential energy surface of the MM subsystem. Nevertheless, the requirement for second-order derivatives or for large number of energy and gradient evaluations makes concurrent optimization methods impractical for ab initio QM∕MM studies in solution or macromolecules.
In contrast, iterative QM and MM optimizations, namely, sequential QM and MM optimizations can use advantages of both QM and MM optimizers.44 Accurate but expensive quasi-Newton optimizers, due to second-order derivatives, are employed to optimize minima and transition states of the QM subsystem, while powerful minimization methods, designed for the molecular mechanics, are employed to minimize the MM subsystem. Eventually, the QM and MM optimizations form an iterative, sequential process. This sequential optimization technique has been successfully used for the QM∕MM potential energy minimizations and for free energy calculations in the recent QM∕MM-MFEP method, demonstrating its efficiency.44, 68 Details of the sequential optimizations and their applications can be found in recent papers.42, 44, 65, 66, 68, 69, 70
In general the region that is relevant to electronic-structure change is placed into the QM subsystem; thereby, decoupling the QM conical intersection optimizations from the MM minimizations is reasonable.
The sequential optimization algorithm used for our QM conical intersection optimizations and MM minimizations can be summarized below:
Initiate the QM and MM subsystems, and , and set n = 1.
- (2) Carry out the QM conical intersection optimizations using the projected gradients of the QM atoms with the fixed MM subsystem, , until a converged energy gap between the lower and upper electronic state I and J is reached; Actually, this is a constrained minimization process, namely, optimizing the conical intersections in the 3Nqm−8 intersection space.19, 26, 78, 97 By projecting the gradients of the QM atoms into the 3Nqm−8 subspace as done in Eq. 14, the constrained minimization of the upper electronic state J is satisfied.
where the g IJ and h IJ vectors are gradient difference and nonadiabatic coupling vectors between the lower and upper electronic states I and J, as shown in Eq. 14.(15) - Carry out the MM minimizations with the fixed QM subsystem, , until convergence
(16) Go to step (2) until both QM and MM subsystems are converged.
Conical intersections of potential of mean force surface
On potential of mean force surfaces, however, gradient difference and nonadiabatic coupling vectors are a little different from those on potential energy surfaces. Considering that conical intersections can efficiently “funnel” the electronic population transfer from the upper electronic state J to the lower electronic state I, and the MM subsystem is in equilibrium with the upper electronic state J before the J → I nonadiabatic transition via conical intersections, it is hence rational to expect that when the electronic population transfers from the upper electronic state J to the lower electronic state I, the nuclei in the system do not respond immediately to set up a new equilibrium with the electrons at the lower electronic state I. This is consistent with the physical picture of photophysical process via a conical intersection occurred in solution or macromolecules. In other words, at conical intersections, the MM subsystem is in equilibrium with the upper electronic state J and is not in equilibrium with the lower electronic state I. Therefore, we can similarly define gradient difference and nonadiabatic coupling vectors of potential of mean force surfaces using the MM sampling of the upper electronic state J:
| (17) |
| (18) |
where and are the vectors of the corresponding gradient difference and nonadiabatic coupling on potential of mean force surfaces, which are only dependent on the coordinates of the QM subsystem. The MM degrees of freedom have been integrated out. Based on the gradient difference and nonadiabatic coupling vectors of potential of mean force surfaces, the projected gradients of the QM subsystem orthogonal to the above gradient difference and nonadiabatic coupling vectors can be calculated with the same transformation used for the potential energy surfaces:
| (19) |
This transformation process is the same as that used in Eq. 14. After minimizing the free energy of the upper electronic state J with the projected gradients of potential of mean force surfaces, we can optimize conical intersection of potential of mean force surfaces.19
In principle, the absolute free energy of the upper electronic state J can be calculated with Eq. 7; however, the relative free energy change is more useful in practical applications, which can be calculated with the free energy perturbation method. With such a method, the relative free energy of the upper electronic state J can be expressed as
| (20) |
where AJ, ref is the reference free energy of the upper electronic state J, and EJ, ref (rmm) is the total reference QM∕MM energy of the system with the QM subsystem fixed at the reference QM configuration.42, 68, 72 The projected gradients of potential of mean force surface for conical intersection optimizations are
| (21) |
Finally, conical intersections on potential of mean force surfaces can be optimized with available optimization procedures when the corresponding relative free energy and projected gradients are input. This process is expressed as
| (22) |
Sequential QM conical intersection optimization and MM sampling
A straightforward optimization algorithm for Eq. 22 requires each step in the QM conical intersection optimization to be associated with a new and converged MM sampling.72 Each QM conical intersection optimization step to a new conformation on the potential of mean force surface is followed by a MM sampling of the upper electronic state J, which is rather expensive for ab initio QM∕MM-MFEP method, even unaffordable in solution or macromolecules due to time scale and expensive evaluations of gradient difference and nonadiabatic coupling vectors. To enhance the efficiency of the QM∕MM-MFEP method, especially for macromolecules, one of the authors of this paper reformulated the concurrent QM optimization and the MM sampling into an iterative step of the MM sampling with a fixed QM conformation and the subsequent QM optimization within the fixed MM conformational ensemble.68 Its remarkably enhanced efficiency is recently demonstrated by several successful simulations of enzyme catalysis.65, 66, 69, 70 In our QM conical intersection optimization and MM sampling scheme, we use this sequential optimization algorithm with some modifications below:
(1) Initiate the QM and MM subsystems, and , and set n=1.
(2) Carry out a MM sampling with the QM atoms fixed at , obtain an ensemble of the MM subsystem, where i is the step of the MD simulation and N is the number of the total steps. This sampling is generated by the reference energy as follows:
| (23) |
The QM structure is obtained from the previous .
(3) Carry out a QM conical intersection optimization using the projected gradients of the QM atoms on potential of mean force surface with the MM ensemble fixed at ; Similar to the above QM conical intersection optimization of potential energy surface, by projecting the gradients of the QM atoms into the 3Nqm−8 intersection subspace as done in Eq. 19, the constrained minimization of the upper electronic state J is satisfied.
| (24) |
where is the projected gradient vector of the QM subsystem orthogonal to the gradient difference and nonadiabatic coupling vectors, discussed in Eq. 21.
(4) Go to step (2) until the QM conical intersection optimizations are converged.
COMPUTATIONAL DETAILS
To test our sequential QM conical intersection optimizations on potential energy surfaces or potential of mean force surfaces, we use cyclopropanone and acetaldehyde as our testing systems, as shown in Fig. 1. Here we focus on optimizations of conical intersections of these two systems in aqueous solution. Specifically, the S1∕S0 conical intersections of potential energy surfaces or potential of mean force surfaces of cyclopropanone and acetaldehyde in aqueous solution will be optimized. The cc-pVDZ basis set is employed to expand electronic wave functions of the systems in electronic structure calculations. In order to provide a comparison, the corresponding conical intersections in gas phase are also determined. Finally, one should note that these solvated molecules, not representing real systems, are only used here to test our proposed sequential QM conical intersection optimization and MM minimization or sampling methods.
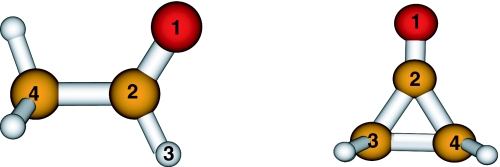
Figure 1.
Testing systems used in this work: acetaldehyde (left) and cyclopropanone (right). Index 1 is used for oxygen atom in both molecules; indexes 2, 3, and 4 are for carbon atoms in cyclopropanone; in acetaldehyde, indexes 2 and 4 are for carbon atoms, while index 3 is for hydrogen atom.
Conical intersection optimizations in gas phase
All conical intersection optimizations are carried out with the state-averaged complete active space self-consistent field (SA-CASSCF) method. In the SA-CASSCF calculations, selection of active space is rather crucial. For cyclopropanone molecule, we place eight electrons (seven orbitals) into the active space, denoted as CASSCF(8,7), which includes one pair of π electrons (π and π* orbitals) of the C2=O1 group, one pair of n electrons (n orbital) of the O1 atom, and two pairs of σ electrons (σ and σ* orbitals) of the C2–C3 and C2–C4 bonds. For acetaldehyde molecule, six electrons distributed in five orbitals, referred to as CASSCF(6,5) hereinafter, are used in the SA-CASSCF calculations. The six electrons (five orbitals) are one pair of π electrons (π and π* orbitals) of the C2=O1 group, one pair of n electrons (n orbital) of the O1 atom, and one pair of σ electrons (σ and σ* orbitals) of the C2–C4 bond. Furthermore, in the SA-CASSCF calculations, equally average state weights over the involved two states are used whenever possible. All the CASSCF calculations are performed with Gaussian03 packages.98
Conical intersection optimizations in solution
All methodologies presented in this work have been implemented in our locally modified SIGMAX2.2 packages, which can seamlessly interface to GAUSSIAN03.68, 72 It can calculate ground and excited state electronic structure properties in the framework of the QM∕MM method.
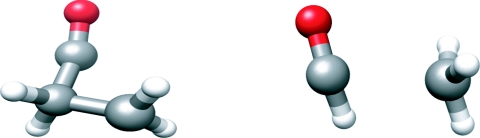
To optimize the QM conical intersections in aqueous solution with the sequential QM conical intersection optimization and MM minimization or sampling method, we first need to set up the solvated systems. A water box of 40 × 40 × 40 Å is used for cyclopropanone and acetaldehyde systems, respectively. Specifically, there are 8 atoms in the QM subsystem and 2106 water molecules in the MM subsystem for cyclopropanone; there are 7 atoms in the QM subsystem and 2105 water molecules in the MM subsystem for acetaldehyde. The solvated systems are illustrated in Fig. 2. The corresponding ground and excited state properties of the QM subsystem are calculated by means of the SA-CASSCF method, which is the same as that used in gas-phase calculations, while for the MM subsystem, the TIP3P water model is used.99 The equilibrium structures are chosen as the initial ones for conical intersection optimizations in aqueous solution.
Figure 2.
Solvated cyclopropanone (left) and acetaldehyde (right) used in the sequential QM conical intersection optimization and MM minimization or sampling.
In MD simulations for the sequential QM conical intersection optimization and MM sampling, step size of integrating Newton equation is 1 fs for short-range interactions, 4 fs for medium-range ones, and 8 fs for long-range ones.100, 101 The particle mesh Ewald (PME) method is employed to accelerate calculations of long-range electrostatic interactions.102 Nine and fifteen dual cutoffs are employed to generate pair lists of nonbonded interactions, which are updated every 16 fs. Temperature is controlled at 300 K with Berendsen thermostat scheme.103 Eighty picosecond MD sampling on the MM subsystem with the frozen QM subsystem is used to calculate projected gradients of the QM atoms.19 All calculations here are performed with the locally, latest modified SIGMAX2.2 and GAUSSIAN03 packages.98
RESULTS
Conical intersections in gas phase
Although conical intersection optimizations of cyclopropanone and acetaldehyde in gas phase are not our purpose in this work, to compare with the counterparts in aqueous solution, a brief discussion is given here. The CASSCF(8,7)∕cc-pVDZ and CASSCF(6,5)∕cc-pVDZ calculated S1∕S0 conical intersections for cyclopropanone and acetaldehyde are illustrated in Fig. 3 with the main structural parameters tabulated in Tables 1, 2. In these two conical intersections, the S1 state is originated from the n → π* transition of the C=O group. This characteristic of electronic structure does not change in aqueous solution, as discussed below. Moreover, both conical intersections are located on the pathways of the alpha C–C bond fissions in the S1 states, which can be illustrated from the corresponding structural parameters. For example, the C2–C4 bond length in the conical intersection of cyclopropanone is 2.178 Å; the C2–C4 bond length in the conical intersection of acetaldehyde is 2.441 Å. The energy gap between the S1 and S0 states is predicted to 0.0 kcal∕mol for both conical intersections, which are perfectly degenerate. Finally, one should note that these conical intersections are very different from their equilibrium structures in the S0 and S1 states, where the corresponding C2–C4 bonds are not broken. Nonetheless, in both conical intersections, the C2–C4 bonds are broken. These structural characteristics have recently been discussed.15, 104, 105
Figure 3.
Schematic S1∕S0 conical intersections of cyclopropanone (left) and acetaldehyde (right). Detailed structural parameters are in Tables 1, 2.
Table 1.
Main structural parameters and energy gap (kcal∕mol) of the S1∕S0 conical intersection of cyclopropanone in gas phase and water solution. GAS-PES: gas phase potential energy surface; 〈SOL-PES〉5: CI averaged by five samples for solution potential energy surface; SOL-FES: solution potential of mean force surface.
| O1–C2 (Å) | C2–C3 | C2–C4 | O1–C2-C4 (°) | O1–C2–C3–C4 | Energy gap | |
|---|---|---|---|---|---|---|
| GAS-PES | 1.181 | 1.502 | 2.178 | 131.7 | −96.6 | 0.0 |
| 〈SOL-PES〉5 | 1.187 | 1.527 | 2.295 | 136.5 | −100.7 | 0.6 |
| SOL-FES | 1.220 | 1.555 | 2.423 | 144.6 | −111.4 | 0.6 |
Table 2.
Main structural parameters and energy gap (kcal∕mol) of the S1∕S0 conical intersection of acetaldehyde in gas phase and water solution. GAS-PES: CI for gas phase potential energy surface; 〈SOL-PES〉5: CI averaged by five samples for solution potential energy surface; SOL-FES: CI for solution potential of mean force surface.
| O1–C2 (Å) | C2–H3 | C2–C4 | O1–C2–C4 (°) | O1–C2–H3–C4 | Energy gap | |
|---|---|---|---|---|---|---|
| GAS-PES | 1.185 | 1.071 | 2.441 | 106.5 | 87.3 | 0.0 |
| 〈SOL-PES〉5 | 1.212 | 1.064 | 2.463 | 107.4 | 86.2 | 0.7 |
| SOL-FES | 1.244 | 1.036 | 2.427 | 104.7 | 83.8 | 0.6 |
Conical intersections in aqueous solution
With our sequential QM conical intersection optimization and MM minimization or sampling method, the corresponding S1∕S0 conical intersections on potential energy surfaces and potential of mean force surfaces, respectively, for cyclopropanone and acetaldehyde in aqueous solution, have been optimized. Their key structural parameters are tabulated in Tables 1, 2. These sequential optimization processes are efficient; in this research, several cycles of the QM conical intersection optimizations are adequate to make the energy gap between the S1 and S0 states less than 1 kcal∕mol from their initial equilibrium structures. For example, the S1∕S0 energy gap in the conical intersection of cyclopropanone is 0.6 kcal∕mol for potential energy surfaces and 0.6 kcal∕mol for potential of mean force surfaces; and the S1∕S0 energy gap in the conical intersection of acetaldehyde is 0.7 kcal∕mol for potential energy surfaces and 0.6 kcal∕mol for potential of mean force surfaces. Finally, for clarity, it should be noticed that our QM∕MM optimization is converged in several cycles. The QM CI optimizations and MM minimizations or samplings are sequentially conducted, not concurrently. In each cycle of QM CI optimizations, about 15–20 steps are needed with the fixed MM structure or ensemble.
Structural differences between gas phase and aqueous solution
The S1∕S0 conical intersections in aqueous solution are similar to the counterparts in gas phase, as shown in Fig. 3; nevertheless, the specific structural parameters are evidently different from gas phase to aqueous solution, as shown in Tables 1, 2. In order to compare with the conical intersections of potential of mean force surfaces (SOL-FES) in aqueous solution, several conical intersections of potential energy surfaces in aqueous solution are optimized, where the MM subsystem is randomly selected from the MM ensemble generated in molecular dynamics simulations associated with the QM∕MM-MFEP conical intersection optimizations and is fixed during the QM conical intersection optimizations. Then, their structural parameters are averaged for comparison, referred to as 〈SOL-PES〉5 in Tables 1, 2. The O1–C2–C4 angle in the conical intersection of cyclopropanone is 131.7° in gas phase, 136.5° on potential energy surfaces in aqueous solution, and 144.6° on potential of mean force surfaces in aqueous solution; its O1–C2–C3–C4 angle is −96.6° in gas phase, −100.7° on potential energy surfaces in aqueous solution, and −111.4° on potential of mean force surfaces in aqueous solution. The O1–C2–C4 angle in the conical intersection of acetaldehyde is 106.5° in gas phase, 107.4° on potential energy surfaces in aqueous solution, and 104.7° on potential of mean force surfaces in aqueous solution; its O1–C2–H3–C4 angle is 87.3° in gas phase, 86.2° on potential energy surfaces in aqueous solution, and 83.8° on potential of mean force surfaces in aqueous solution. The other changes of the structural parameters can be also found. This illustrates that solvent or environment effect is very important for understanding mechanisms of photochemical reactions and photophysical processes because this effect can considerably change structures of critical points on potential energy surfaces or potential of mean force surfaces, thereby altering energetics and eventually changing mechanisms. The structural parameters between 〈SOL-PES〉5 and SOL-FES are similar to each other; thus, conical intersections on potential of mean force surfaces, as averaged conical intersections on potential energy surfaces, are meaningful. The small differences between them are ascribed to the fact that the five MM configurations for the QM conical intersection optimizations on potential energy surfaces represent very small sample size.
Gradient difference and nonadiabatic coupling vectors
The branching plane near a conical intersection, expanded by gradient difference and nonadiabatic coupling vectors, is very important for understanding internal conversion processes via conical intersections.1, 2, 3, 4, 9, 10 We have tabulated the values of these vectors from the S1∕S0 conical intersections of cyclopropanone and acetaldehyde both in aqueous solution and in gas phase (see tables in the supplementary material).106 After analyzing these data, it can be found that nonadiabatic coupling vector changes subtly from potential energy surfaces in gas phase to potential energy surfaces or potential of mean force surfaces in aqueous solution. As electronic structure calculations for conical intersection optimizations mainly use the QM subsystem, the MM subsystem plays a perturbation role; electronic wave functions of the system vary little from gas phase to aqueous solution. In contrast, solvent environment affects gradient difference vector remarkably. This can be ascribed to the fact that topologies of potential energy surfaces or potential of mean force surfaces change from gas phase to aqueous solution.
DISCUSSION
Sequential is better than concurrent
The proposed two sequential conical intersection optimization methods in the framework of the QM∕MM method, one for potential energy surfaces and another for potential of mean force surfaces, are more efficient than the concurrent ones. In the concurrent optimization methods, gradient difference and nonadiabatic coupling vectors need to be calculated for each movement of the QM or MM subsystem. This drastically increases computational effort because dimensionalities of gradient difference and nonadiabatic coupling vectors are huge. However, in the sequential ones, these vectors need to be calculated only when the QM subsystem moves. Furthermore, as evaluations of gradient difference and nonadiabatic coupling vectors are expensive, large number of evaluations of these vectors are unaffordable; thus, we should reduce these evaluations as much as possible. This is achieved with the sequential optimization methods, developed in this work, within the framework of the QM∕MM and QM∕MM-MFEP methods.42, 44, 62, 68, 72 Conical intersection optimizations with ab initio electronic structure methods are performed only for the QM subsystem; for the MM subsystem, regular energy minimizations or MD samplings are carried out. This partition is rational because the region, where electronic structure changes remarkably in a chemical reaction, is placed into the QM subsystem. With this improvement, dimensionalities of gradient difference and nonadiabatic coupling vectors are significantly decreased since the QM subsystem is relatively small, about tens of atoms. Also the number of evaluations of these vectors is also decreased because we only need to calculate them as the QM subsystem moves, independent of the MM minimizations or samplings. Finally, by decoupling the QM optimizations and MM minimizations or samplings, we can make maximum use of accuracy of Hessian-matrix-based optimization methods for the QM conical intersections and of efficiency of minimizers, which are designed for the MM potential energy surfaces.
Averaged conical intersections on potential of mean force surfaces
Conical intersection in a molecular system is not an isolated point in the coordinate space, but a 3N−8 dimensional hyperspace where N is the number of atoms in this molecular system. Like the case in the 3N−6 coordinate space, there are many local minima in this 3N−8 hyperspace, which are known as minimum energy conical intersections.1, 2, 3, 6, 9, 10, 19, 31, 107 Moreover, it is also reasonable to expect that the number of local minima in the 3N−8 hyperspace increases with the increasing number of atoms in a system. Specifically, in the framework of the QM∕MM method, a small position displacement of the MM subsystem, even only one coordinate of one atom in the MM subsystem, will change the conical intersection structure of the QM subsystem, albeit the resultant changes both in structure and in energetics for the QM conical intersection are small. Usually, there are tens of thousands of atoms in the MM subsystem in a regular QM∕MM simulation; hence, it is expensive, even impossible, to search each local QM conical intersection structure related to one MM configuration. Additionally, searching each QM conical intersection for each MM configuration is not necessary. Since the MM subsystem only plays as a perturbation on the QM subsystem, and the structure and the energetics of the QM conical intersection change subtly due to a small displacement of the MM subsystem, one thereby expects that conical intersections of potential of mean force surfaces are more useful. In such case, we need not focus on each local QM conical intersection corresponding to each MM configuration, instead focus on an averaged QM conical intersection corresponding to an ensemble of MM configurations sampled by MD simulations. This is one reason why we need averaged conical intersections of potential of mean force surfaces.
Another issue we need to address is about the validation of conical intersections of potential of mean force surfaces in solution or macromolecules. Conical intersections of potential of mean force surfaces could be meaningless for ultrafast (less than 1 ps) excited state processes because in such case, solvent or macromolecular environment cannot response so fast to adopt a new equilibrium with the excited state electron population. For such ultrafast excited state processes, “on the fly” ab initio nonadiabatic dynamics simulations in combination with the QM∕MM method should be more useful.7, 12, 13, 26, 37, 80, 81, 92 However, time scale of “on the fly” ab initio nonadiabatic dynamics is rather limited, always within or near picoseconds, due to expensive evaluations of gradient difference and nonadiabatic coupling vectors and small time steps. However, relatively slow reactions, more than hundreds of picoseconds, remain ubiquitous in solution photochemistry and biophotochemistry.27, 28, 74, 75, 76, 77 For such situations, it is impractical to perform an “on the fly” ab initio nonadiabatic dynamics simulations to study photochemical reactions. More importantly, one trajectory is statistically meaningless; hundreds even thousands of trajectories are in general required to gain statistical information to certain extent. In contrast to “on the fly” ab initio nonadiabatic dynamics, topological structures, such as conical intersections of potential of mean force surfaces, could be more useful and provide us invaluable insights into mechanisms of photophysical processes and photochemical reactions in solution or macromolecules. This is another reason why we need averaged conical intersections of potential of mean force surfaces.
CONCLUSION
On the basis of the previous sequential QM∕MM and QM∕MM-MFEP methods, we have designed two sequential conical intersection optimization methods for small- and medium-size molecules in solution or macromolecules: one for potential energy surfaces and the other for potential of mean force surfaces. Detailed theoretical background, formulations, algorithms, and implementations are given. In such methods, conical intersection optimizations are carried out only in the QM subsystem, which includes the region where electronic structure remarkably changes in photochemical reactions or photophysical processes. With this QM∕MM partition and sequential optimization scheme (not concurrent one), two advantages are accessible.
First, dimensionalities of gradient difference and nonadiabatic coupling vectors, required for conical intersection optimizations, are decreased due to the relatively small QM subsystem, always about tens of atoms. This advantage is accessible for both concurrent and sequential optimization schemes in the framework of the QM∕MM method.
Second, the number of evaluations of gradient difference and nonadiabatic coupling vectors is reduced, because the QM conical intersection optimizations and MM minimizations or samplings are sequentially, not concurrently, performed. In sequential scheme, these vectors need to be calculated only when the QM subsystem moves, independent of the MM minimizations or samplings. However, for concurrent one, they must be calculated when the QM or MM subsystem moves. This advantage is accessible only for sequential optimization scheme, as proposed in this work.
Test optimizations of conical intersections of cyclopropanone and acetaldehyde in aqueous solution have also been carried out. Further development of these methods is in progress.
ACKNOWLEDGMENTS
This work has been supported by the National Science Foundation (CHE-09-11119) and the National Institute of Health (5R01-GM-061870-09). We also thank Dr. Todd Martinez for helpful discussions and Dr. Aaron Virshup for discussions and assistance in reading and proofing the manuscript.
References
- Domcke W., Yarkony D. R., and Koppel H., in Conical Intersections: Electronic Structure, Dynamics & Spectroscopy (World Scientific, River Edge, NJ, 2004). [Google Scholar]
- Yarkony D. R., Rev. Mod. Phys. 68, 985 (1996). 10.1103/RevModPhys.68.985 [DOI] [Google Scholar]
- Yarkony D. R., Acc. Chem. Res. 31, 511 (1998). 10.1021/ar970113w [DOI] [Google Scholar]
- Robb M. A., Garavelli M., Olivucci M., and Bernardi F., Rev. Comp. Chem. 15, 87 (2000). 10.1002/9780470125922.ch2 [DOI] [Google Scholar]
- Levine B. G. and Martinez T. J., Annu. Rev. Phys. Chem. 58, 613 (2007). 10.1146/annurev.physchem.57.032905.104612 [DOI] [PubMed] [Google Scholar]
- Robb M. A., Bernardi F., and Olivucci M., Pure Appl. Chem. 67, 783 (1995). 10.1351/pac199567050783 [DOI] [Google Scholar]
- Groenhof G., Boggio-Pasqua M., Schafer L. V., and Robb M. A., Adv. Quantum Chem. 59, 181 (2010). 10.1016/S0065-3276(10)59006-3 [DOI] [Google Scholar]
- Fang W. H., Acc. Chem. Res. 41, 452 (2008). 10.1021/ar700205f [DOI] [PubMed] [Google Scholar]
- Yarkony D. R., J. Phys. Chem. 100, 18612 (1996). 10.1021/jp962134y [DOI] [Google Scholar]
- Yarkony D. R., J. Phys. Chem. A 105, 6277 (2001). 10.1021/jp003731u [DOI] [Google Scholar]
- Ben Nun M. and Martinez T. J., Adv. Chem. Phys. 121, 439 (2002). 10.1002/0471264318.ch7 [DOI] [Google Scholar]
- Aquino A. J. A., Barbatti M., and Lischka H., Chem. Phys. Chem. 7, 2089 (2006). 10.1002/cphc.200600199 [DOI] [PubMed] [Google Scholar]
- Ruckenbauer M., Barbatti M., Muller T., and Lischka H., J. Phys. Chem. A 114, 6757 (2010). 10.1021/jp103101t [DOI] [PubMed] [Google Scholar]
- Celani P., Robb M. A., Garavelli M., Bernardi F., and Olivucci M., Chem. Phys. Lett. 243, 1 (1995). 10.1016/0009-2614(95)00821-K [DOI] [Google Scholar]
- Cui G. L., Ai Y. J., and Fang W. H., J. Phys. Chem. A 114, 730 (2010). 10.1021/jp908936u [DOI] [PubMed] [Google Scholar]
- Cui G. L., Ding L. N., Feng F., Liu Y. J., and Fang W. H., J. Chem. Phys. 132, 194308 (2010). 10.1063/1.3397067 [DOI] [PubMed] [Google Scholar]
- Fang W. H. and Phillips D. L., Chem. Phys. Chem. 3, 889 (2002). [Google Scholar]
- Fang Q., Han J., Jiang J. L., Chen X. B., and Fang W. H., J. Phys. Chem. A 114, 4601 (2010). 10.1021/jp911455r [DOI] [PubMed] [Google Scholar]
- Bearpark M. J., Robb M. A., and Schlegel H. B., Chem. Phys. Lett. 223, 269 (1994). 10.1016/0009-2614(94)00433-1 [DOI] [Google Scholar]
- Ben-Nun M., Quenneville J., and Martinez T. J., J. Phys. Chem. A 104, 5161 (2000). 10.1021/jp994174i [DOI] [Google Scholar]
- Bernardi F., Olivucci M., and Robb M. A., Chem. Soc. Rev. 25, 321 (1996). 10.1039/cs9962500321 [DOI] [Google Scholar]
- Lengsfield B. H. and Yarkony D. R., Adv. Chem. Phys. 82, 1 (1992). 10.1002/9780470141403.ch1 [DOI] [Google Scholar]
- Levine B. G., Coe J. D., and Martinez T. J., J. Phys. Chem. B 112, 405 (2008). 10.1021/jp0761618 [DOI] [PubMed] [Google Scholar]
- Perun S., Sobolewski A. L., and Domcke W., J. Phys. Chem. A 110, 13238 (2006). 10.1021/jp0633897 [DOI] [PubMed] [Google Scholar]
- Ragazos I. N., Robb M. A., Bernardi F., and Olivucci M., Chem. Phys. Lett. 197, 217 (1992). 10.1016/0009-2614(92)85758-3 [DOI] [Google Scholar]
- Toniolo A., Granucci G., and Martinez T. J., J. Phys. Chem. A 107, 3822 (2003). 10.1021/jp022468p [DOI] [Google Scholar]
- Schwalb N. K. and Temps F., Science 322, 243 (2008). 10.1126/science.1161651 [DOI] [PubMed] [Google Scholar]
- Middleton C. T., de La Harpe K., Su C., Law Y. K., Crespo-Hernandez C. E., and Kohler B., Annu. Rev. Phys. Chem. 60, 217 (2009). 10.1146/annurev.physchem.59.032607.093719 [DOI] [PubMed] [Google Scholar]
- Schreier W. J., Schrader T. E., Koller F. O., Gilch P., Crespo-Hernandez C. E., Swaminathan V. N., Carell T., Zinth W., and Kohler B., Science 315, 625 (2007). 10.1126/science.1135428 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti I., Altoe P., Stenta M., Garavelli M., and Orlandi G., Phys. Chem. Phys. Chem. 12, 5016 (2010). 10.1039/B926608A [DOI] [PubMed] [Google Scholar]
- Yarkony D. R., J. Phys. Chem. 97, 4407 (1993). 10.1021/j100119a026 [DOI] [Google Scholar]
- De Vico L. and Lindh R., J. Chem. Theory Comput. 5, 186 (2009). 10.1021/ct800348s [DOI] [PubMed] [Google Scholar]
- Schultz T., Samoylova E., Radloff W., Hertel I. V., Sobolewski A. L., and Domcke W., Science 306, 1765 (2004). 10.1126/science.1104038 [DOI] [PubMed] [Google Scholar]
- Lan Z., Dupays A., Vallet V., Mahapatra S., and Domcke W., J. Photochem. Photobiol. A 190, 177 (2007). 10.1016/j.jphotochem.2007.01.018 [DOI] [Google Scholar]
- Lan Z. G., Frutos L. M., Sobolewski A. L., and Domcke W., Proc. Natl. Acad. Sci. U.S.A. 105, 12707 (2008). 10.1073/pnas.0801062105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Galvez A., Hunt P., Robb M. A., Olivucci M., Vreven T., and Schlegel H. B., J. Am. Chem. Soc. 122, 2911 (2000). 10.1021/ja993985x [DOI] [Google Scholar]
- Toniolo A., Olsen S., Manohar L., and Martinez T. J., Faraday Discuss. 127, 149 (2004). 10.1039/b401167h [DOI] [PubMed] [Google Scholar]
- Thoss M., Miller W. H., and Stock G., J. Chem. Phys. 112, 10282 (2000). 10.1063/1.481668 [DOI] [Google Scholar]
- Sobolewski A. L., Domcke W., Dedonder-Lardeux C., and Jouvet C., Phys. Chem. Chem. Phys. 4, 1093 (2002). 10.1039/b110941n [DOI] [Google Scholar]
- Warshel A. and Levitt M., J. Mol. Biol. 103, 227 (1976). 10.1016/0022-2836(76)90311-9 [DOI] [PubMed] [Google Scholar]
- Warshel A., Annu. Rev. Biophys. Biomol. Struct. 32, 425 (2003). 10.1146/annurev.biophys.32.110601.141807 [DOI] [PubMed] [Google Scholar]
- Hu H. and Yang W. T., Annu. Rev. Phys. Chem. 59, 573 (2008). 10.1146/annurev.physchem.59.032607.093618 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y. K., Lee T. S., and Yang W. T., J. Chem. Phys. 110, 46 (1999). 10.1063/1.478083 [DOI] [Google Scholar]
- Zhang Y. K., Liu H. Y., and Yang W. T., J. Chem. Phys. 112, 3483 (2000). 10.1063/1.480503 [DOI] [Google Scholar]
- Senn H. M. and Thiel W., Curr. Opin. Chem. Biol. 11, 182 (2007). 10.1016/j.cbpa.2007.01.684 [DOI] [PubMed] [Google Scholar]
- Senn H. M. and Thiel W., Angew. Chem., Int. Ed. 48, 1198 (2009). 10.1002/anie.200802019 [DOI] [PubMed] [Google Scholar]
- Shaik S., Cohen S., Wang Y., Chen H., Kumar D., and Thiel W., Chem. Rev. 110, 949 (2010). 10.1021/cr900121s [DOI] [PubMed] [Google Scholar]
- Jorgensen W. L., Acc. Chem. Res. 22, 184 (1989). 10.1021/ar00161a004 [DOI] [Google Scholar]
- Acevedo O. and Jorgensen W. L., Acc. Chem. Res. 43, 142 (2010). 10.1021/ar900171c [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin H. and Truhlar D. G., Theor. Chem. Acc. 117, 185 (2007). 10.1007/s00214-006-0143-z [DOI] [Google Scholar]
- Pu J. Z., Gao J. L., and Truhlar D. G., J. Phys. Chem. A 108, 632 (2004). 10.1021/jp036755k [DOI] [Google Scholar]
- Pu J. Z., Gao J. L., and Truhlar D. G., Chem. Phys. Chem. 6, 1853 (2005).16086343 [Google Scholar]
- Eichinger M., Tavan P., Hutter J., and Parrinello M., J. Chem. Phys. 110, 10452 (1999). 10.1063/1.479049 [DOI] [Google Scholar]
- Laio A., VandeVondele J., and Rothlisberger U., J. Chem. Phys. 116, 6941 (2002). 10.1063/1.1462041 [DOI] [Google Scholar]
- Carloni P., Rothlisberger U., and Parrinello M., Acc. Chem. Res. 35, 455 (2002). 10.1021/ar010018u [DOI] [PubMed] [Google Scholar]
- Cui Q., Elstner M., Kaxiras E., Frauenheim T., and Karplus M., J. Phys. Chem. B 105, 569 (2001). 10.1021/jp0029109 [DOI] [Google Scholar]
- Xu D., Guo H., and Cui G., J. Am. Chem. Soc. 129, 10814 (2007). 10.1021/ja072532m [DOI] [PubMed] [Google Scholar]
- Virshup A. M., Punwong C., Pogorelov T. V., Lindquist B. A., Ko C., and Martinez T. J., J. Phys. Chem. B 113, 3280 (2009). 10.1021/jp8073464 [DOI] [PubMed] [Google Scholar]
- Dapprich S., Komaromi I., Byun K. S., Morokuma K., and Frisch M. J., J. Mol. Struct. 461, 1 (1999). [Google Scholar]
- Svensson M., Humbel S., Froese R. D. J., Matsubara T., Sieber S., and Morokuma K., J. Phys. Chem. 100, 19357 (1996). 10.1021/jp962071j [DOI] [Google Scholar]
- Ferre N., Assfeld X., and Rivail J. L., J. Comput. Chem. 23, 610 (2002). 10.1002/jcc.10058 [DOI] [PubMed] [Google Scholar]
- Hu H. and Yang W. T., J. Mol. Struct. 898, 17 (2009). [Google Scholar]
- Rosta E., Klahn M., and Warshel A., J. Phys. Chem. B 110, 2934 (2006). 10.1021/jp057109j [DOI] [PubMed] [Google Scholar]
- Cisneros G. A., Liu H. Y., Zhang Y. K., and Yang W. T., J. Am. Chem. Soc. 125, 10384 (2003). 10.1021/ja029672a [DOI] [PubMed] [Google Scholar]
- Parks J. M., Kondru R. K., Hu H., Beratan D. N., and Yang W. T., J. Phys. Chem. B 112, 3168 (2008). 10.1021/jp076885j [DOI] [PubMed] [Google Scholar]
- Hu H., Boone A., and Yang W. T., J. Am. Chem. Soc. 130, 14493 (2008). 10.1021/ja801202j [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao J. L., Acc. Chem. Res. 29, 298 (1996). 10.1021/ar950140r [DOI] [Google Scholar]
- Hu H., Lu Z. Y., Parks J. M., Burger S. K., and Yang W. T., J. Chem. Phys. 128, 034105 (2008). 10.1063/1.2816557 [DOI] [PubMed] [Google Scholar]
- Parks J. M., Hu H., Rudolph J., and Yang W. T., J. Phys. Chem. B 113, 5217 (2009). 10.1021/jp805137x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng X. C., Hu H., Hu X. Q., and Yang W. T., J. Chem. Phys. 130, 164111 (2009). 10.1063/1.3120605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H. Y., Zhang Y. K., and Yang W. T., J. Am. Chem. Soc. 122, 6560 (2000). 10.1021/ja9936619 [DOI] [Google Scholar]
- Hu H., Lu Z. Y., and Yang W. T., J. Chem. Theory Comput. 3, 390 (2007). 10.1021/ct600240y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeng X. C., Hu H., Hu X. Q., Cohen A. J., and Yang W. T., J. Chem. Phys. 128, 124510 (2008). 10.1063/1.2832946 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meech S. R., Chem. Soc. Rev. 38, 2922 (2009). 10.1039/b820168b [DOI] [PubMed] [Google Scholar]
- Cosa G., Lukeman M., and Scaiano J. C., Acc. Chem. Res. 42, 599 (2009). 10.1021/ar8001969 [DOI] [PubMed] [Google Scholar]
- Priyadarsini K. I., J. Photochem. Photobiol. C 10, 81 (2009). 10.1016/j.jphotochemrev.2009.05.001 [DOI] [Google Scholar]
- Lorente C. and Thomas A. H., Acc. Chem. Res. 39, 395 (2006). 10.1021/ar050151c [DOI] [PubMed] [Google Scholar]
- Toniolo A., Ben-Nun M., and Martinez T. J., J. Phys. Chem. A 106, 4679 (2002). 10.1021/jp014289y [DOI] [Google Scholar]
- Bearpark M. J., Larkin S. M., and Vreven T., J. Phys. Chem. A 112, 7286 (2008). 10.1021/jp802204w [DOI] [PubMed] [Google Scholar]
- Ferre N. and Olivucci M., J. Am. Chem. Soc. 125, 6868 (2003). 10.1021/ja035087d [DOI] [PubMed] [Google Scholar]
- Coto P. B., Strambi A., Ferre N., and Olivucci M., Proc. Natl. Acad. Sci. U.S.A. 103, 17154 (2006). 10.1073/pnas.0604048103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burghardt I., Cederbaum L. S., and Hynes J. T., Faraday Discuss. 127, 395 (2004). 10.1039/b315071b [DOI] [PubMed] [Google Scholar]
- Spezia R., Burghardt I., and Hynes J. T., Mol. Phys. 104, 903 (2006). 10.1080/00268970500417895 [DOI] [Google Scholar]
- Tenno S., Hirata F., and Kato S., J. Chem. Phys. 100, 7443 (1994). 10.1063/1.466888 [DOI] [Google Scholar]
- Yamazaki S. and Kato S., J. Chem. Phys. 123, 114510 (2005). 10.1063/1.2038867 [DOI] [PubMed] [Google Scholar]
- Yamazaki S. and Kato S., J. Am. Chem. Soc. 129, 2901 (2007). 10.1021/ja0669169 [DOI] [PubMed] [Google Scholar]
- Mori T., Nakano K., and Kato S., J. Chem. Phys. 133, 064107 (2010). 10.1063/1.3472033 [DOI] [PubMed] [Google Scholar]
- Aono S., Minezawa N., and Kato S., Chem. Phys. Lett. 492, 193 (2010). 10.1016/j.cplett.2010.04.045 [DOI] [Google Scholar]
- Galvan I. F., Sanchez M. L., Martin M. E., del Valle F. J.O., and Aguilar M. A., Comput. Phys. Commun. 155, 244 (2003). 10.1016/S0010-4655(03)00351-5 [DOI] [Google Scholar]
- Galvan I. F., Martin M. E., and Aguilar M. A., J. Comput. Chem. 25, 1227 (2004). 10.1002/jcc.20048 [DOI] [PubMed] [Google Scholar]
- Losa A. M., Martin M. E., Galvan I. F., and Aguilar M. A., Chem. Phys. Lett. 443, 76 (2007). 10.1016/j.cplett.2007.06.037 [DOI] [Google Scholar]
- Groenhof G., Schafer L. V., Boggio-Pasqua M., Grubmuller H., and Robb M. A., J. Am. Chem. Soc. 130, 3250 (2008). 10.1021/ja078024u [DOI] [PubMed] [Google Scholar]
- Wang M. L., Lu Z. Y., and Yang W. T., J. Chem. Phys. 121, 101 (2004). 10.1063/1.1757437 [DOI] [PubMed] [Google Scholar]
- Wang M. L., Lu Z. Y., and Yang W. T., J. Chem. Phys. 124, 124516 (2006). 10.1063/1.2181145 [DOI] [PubMed] [Google Scholar]
- Lu Z. and Yang W. T., J. Chem. Phys. 121, 89 (2004). 10.1063/1.1757436 [DOI] [PubMed] [Google Scholar]
- Gao J. L., Ma S. H., Major D. T., Nam K., Pu J. Z., and Truhlar D. G., Chem. Rev. 106, 3188 (2006). 10.1021/cr050293k [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keal T. W., Koslowski A., and Thiel W., Theor. Chem. Acc. 118, 837 (2007). 10.1007/s00214-007-0331-5 [DOI] [Google Scholar]
- Frisch M. J.Trucks G. W., Schlegel H. B.et al. , GAUSSIAN 03, Revision D.01, Gaussian, Inc., Wallingford, CT, 2004.
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Tuckerman M. E. and Berne B. J., J. Chem. Phys. 95, 8362 (1991). 10.1063/1.461263 [DOI] [Google Scholar]
- Schlick T., Skeel R. D., Brunger A. T., Kale L. V., Board J. A., Hermans J., and Schulten K., J. Comput. Phys. 151, 9 (1999). 10.1006/jcph.1998.6182 [DOI] [Google Scholar]
- Darden T. A., York D. M., and Pedersen L. G., J. Chem. Phys. 98, 10089 (1993). 10.1063/1.464397 [DOI] [Google Scholar]
- Berendsen H. J. C., Postma J. P. M., Vangunsteren W. F., Dinola A., and Haak J. R., J. Chem. Phys. 81, 3684 (1984). 10.1063/1.448118 [DOI] [Google Scholar]
- Chen S. L. and Fang W. H., J. Chem. Phys. 131, 054306 (2009). 10.1063/1.3196176 [DOI] [PubMed] [Google Scholar]
- Cui G. L. and Fang W. H., J. Phys. Chem. A 115, 1547 (2011). 10.1021/jp110632g [DOI] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1063/1.3593390 for additional tables.
- Martinez T. J., Acc. Chem. Res. 39, 119 (2006). 10.1021/ar040202q [DOI] [PubMed] [Google Scholar]