SUMMARY
The microtubule-based metaphase spindle is subjected to forces that act in diverse orientations and over a wide-range of timescales. Currently, we cannot explain how this dynamic structure generates and responds to forces while maintaining overall stability, as we have a poor understanding of its micromechanical properties. Here we combine the use of force-calibrated needles, high-resolution microscopy, and biochemical perturbations to analyze the vertebrate metaphase spindle's timescale- and orientation-dependent viscoelastic properties. We find that spindle viscosity depends on microtubule crosslinking and density. Spindle elasticity can be linked to kinetochore and non-kinetochore microtubule rigidity, and also to spindle pole organization by kinesin-5 and dynein. These data suggest a quantitative model for the micromechanics of this cytoskeletal architecture and provide insight into how structural and functional stability is maintained in the face of forces, such as those that control spindle size and position, and can result from deformations associated with chromosome movement.
INTRODUCTION
The accurate segregation of chromosomes during cell division depends on the microtubule-based bipolar metaphase spindle. For this micron-size structure to generate forces to move chromosomes, it must be robust to withstand forces of equal magnitude (Nicklas, 1983). Forces also act on a spindle to control its size, orientation and position during division (Cowan and Hyman, 2004; Inoue and Salmon, 1995). In addition, when chromosomes oscillate or congress from a spindle pole to the equator, the forces associated with these movements exert deformations in the spindle. In the last few decades, the force-generating functions of the metaphase spindle have been extensively studied and the list of proteins linked to these processes is now essentially complete (Neumann et al., 2010). However, our understanding of the mechanical architecture of this essential cellular structure remains rudimentary and we cannot explain how the spindle maintains its structural and functional stability in the face of different forces.
One strategy to gain insight into the micromechanical properties of the metaphase spindle is to analyze deformations that arise in the structure in response to applied forces. The response of the spindle should depend on two different mechanical properties: elasticity and viscosity. Elasticity determines the magnitude of deformation of the structure and acts to restore shape. Viscosity determines the rate of change of deformation and is associated with rearrangement in structural components that lead to changes in shape that persist. Due to the complex coupling between these mechanical properties in cytoskeletal networks, the magnitude and relative contributions of elasticity and viscosity to the structure's deformation depend on the timescales at which forces act (Fletcher and Mullins, 2010). However, the timescale-dependent viscoelastic properties of the metaphase spindle have not been examined. While studies of cytoskeletal networks reconstituted from purified components have provided insight into their mechanical properties (Gardel et al., 2008; Lin et al., 2007; Sato et al., 1988), linking these findings to the micromechanics of the metaphase spindle remains difficult, particularly as the in vitro networks analyzed in these studies consisted of non-dynamic polymers.
Another key difference between the metaphase spindle and many of the well characterized cytoskeletal networks is that the spindle is not isotropic. Microtubules, which are several microns in length, are anisotropically distributed, being predominantly aligned along the spindle's pole-to-pole axis. Further, the spindle microtubules are of at least two types. First, the kinetochore microtubules, which extend from the spindle pole and attach chromosomes to the spindle, are extensively crosslinked and turnover on the order of minutes (Zhai et al., 1995). Second, non-kinetochore microtubules, which comprise the majority of microtubules in mammalian spindles and are distributed across the structure (McIntosh et al., 1975), are known to turnover on the order of seconds (Salmon et al., 1984). Coincident with the stochastic polymerization dynamics of individual filaments, the kinetochore and non-kinetochore microtubules undergo poleward flux, a concerted movement of the microtubule lattice towards each pole (Sawin and Mitchison, 1991). In addition, while many microtubule-associated proteins (MAPs) required to organize these microtubules are distributed throughout the structure, specialized proteins, such as NuMA, accumulate exclusively at specific sites, such as spindle poles (Karki and Holzbaur, 1999). Therefore, the metaphase spindle's anisotropy is evident at two levels, the complex dynamics of its components and their distribution.
Consistent with this anisotropy, the spindle's deformation response has been found to depend on the orientation of the applied force (Dumont and Mitchison, 2009; Gatlin et al., 2010; Itabashi et al., 2009). However, as these analyses were carried out at only one timescale, or under conditions that did not allow control over the applied force, a quantitative understanding of how the spindle's mechanical responses are linked to underlying molecular processes is currently lacking. This is particularly important as the dynamics of several key spindle components, such as microtubule turnover (~5 min for kinetochore microtubules and ~10 s for non-kinetochore microtubules) and motor protein stepping (~10–100 ms), span over 4-decadess of timescales.
Here we have developed an assay system, in which the orientation- and timescale-dependent mechanical properties of the metaphase spindle can be quantitatively analyzed by using force-calibrated microneedles and high-resolution multi-mode microscopy. We have used this set-up to systematically characterize the viscoelastic properties of the metaphase spindle. Chemical and biochemical perturbations of key spindle components, combined with the analysis of spindle micromechanics, have helped elucidate the molecular basis of the spindle's elasticity and viscosity. Based on these data, we propose a quantitative model for how the spindle responds to forces and how it maintains structural stability while accommodating proportionately large deformations.
RESULTS
Forces acting along the spindle's pole-to-pole axis alter neither the spindle's length nor width
To examine the metaphase spindle's response to mechanical forces we designed a force-calibrated microneedle set-up in which needle position and spindle deformations can be tracked using high-resolution time-lapse microscopy (Fig. 1A–C). Our set-up incorporated two different types of microneedles. A stiff needle (stiffness >50 nN/μm), controlled by a piezo actuator, was used to displace the spindle. A flexible needle (typical stiffness, 0.2–0.5 nN/μm; diameter, 1–2 μm) was used to measure forces within the spindle. Both needles were passivated, so that they did not bind any cellular structure and would allow measurements of the native micromechanical properties of the network (Valentine et al., 2004). For these experiments we used metaphase spindles assembled in Xenopus egg extracts, a cell-free system that has been employed extensively to characterize the spindle's assembly mechanisms, regulation and architecture (Desai et al., 1999). In these cell-free extracts the two-needle set-up can directly capture a single metaphase spindle, which is essentially `floating' in cytoplasm, without having to penetrate a cell's membrane. This set-up was used to measure the spindle's response to mechanical forces applied at different timescales and in controlled orientations.
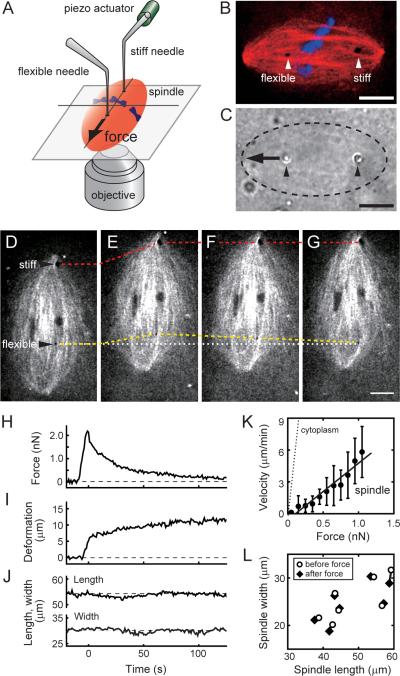
Figure 1. Mechanical force applied along the long axis of the metaphase spindle induces viscous deformation.
(A) Schematic shows the experimental set-up used to analyze the mechanical properties of the metaphase spindle. (B) Confocal image of a spindle, showing tubulin (red, X-rhodamine tubulin, 400 nM), DNA (blue, SYTOX dye, 10 nM), and the two needles (arrow heads). (C) Bright field image corresponding to (B). The spindle (dashed oval), tips of the needles (arrow heads), and the direction of applied force (arrow) are indicated. (D–L) Mechanical responses of the spindle along its long axis. (D–G) Confocal image of a spindle, labeled with fluorescent tubulin, 15 s before (D), 0 s (E), 11 s (F), and 75 s (G) after the stiff needle's displacement. Dashed lines indicate positions of the stiff (red) and flexible (yellow) needle tips. The original position of the flexible needle tip is also shown (white dotted line). (H–J) The changes in force, measured using the deflection of the flexible needle (H), deformation in the spindle, defined as the change in distance between the two needle tips from initial separation (I), and spindle length and width (J) are plotted against time. These measurements were used to determine the force-velocity relationship (solid circles, mean ± SD, n = 7) (K). A linear fit (black solid line) was used to estimate the effective viscosity. Similar analysis was performed for the metaphase cytoplasm (dotted line, n = 6, Fig. S1D). (L) Spindle length and width before force application (open circles) and after the applied force has decayed (solid diamonds) (n = 7). Scale bars, 10 μm. See Fig. S1 for additional supporting data.
In the first series of experiments, we examined the spindle's response to mechanical forces applied along its long axis (Fig. 1D–L and Movie S1). Needles were inserted into a metaphase spindle such that one needle was on either side of the metaphase plate (Fig. 1D). The flexible needle's base was held at a fixed position. The stiff needle was moved along the spindle's long axis towards its proximal spindle pole (Fig. 1D and E), causing the displacement of the entire spindle. This movement resulted in the development of a transient force in the flexible needle, as revealed by the displacement of its tip (Fig. 1H). After the motion of the stiff needle was stopped, the flexible needle's tip moved through the spindle and returned close to its original location (Fig. 1E–G). The time derivative of the deformation in the structure, defined as the change in distance between two needles (Fig. 1I), was used to obtain the force-velocity relationship (Fig. 1K), whose slope revealed the spindle's effective viscosity, η (~1.9×102 Pa·s). This value is >100 times greater than what we measured for the metaphase cytoplasm (η ~ 1.2 Pa·s) (Fig. 1K). Neither the spindle length nor width changed significantly before and after the application of force (Fig. 1J and L) (26.0 ± 4.4 μm to 25.4 ± 4.1 μm in width, 50.1 ± 7.4 μm to 49.8 ± 7.5 μm in length, mean ± SD, n = 7). These data suggest that viscosity dominates the spindle's response to the applied forces for at least two reasons. First, the applied force almost completely decayed to ~0 nN, indicating that spring-like elements to store strain energy are absent. Second, the overall shape of the spindle did not change during the experiment, implying that the strain is relaxed via local remodeling of the structure. This response is relevant for timescales over 10–100 s, a period during which the applied force decays.
To obtain data for shorter timescales in this experimental mode required even faster step-like motion, which resulted in highly variable responses, most likely due to irreversible changes in the structure. We therefore applied forces that varied sinusoidally over time, as this alternative experimental mode can reveal viscoelastic properties without applying larger forces (Janmey et al., 2007). However, over a range of timescales we examined (0.1–10 s) the stiff needle's motion resulted in local irreversible deformations in the structure, a behavior expected for viscous gels (Fig. S1A–C and Movie S2). Together, these data suggest that the spindle's response to forces, which act on timescales relevant to the dynamics of spindle components, is predominantly viscous when the forces are applied along the pole-to-pole axis. Forces acting in this orientation within the spindle do not alter the structure's overall size and shape.
Forces applied along the spindle's short axis change spindle length and width
We next examined the spindle's response to forces applied along its short axis (Fig. 2). In these experiments, the two needles were inserted into one half of the spindle near the chromosomes, without directly contacting them (Fig. 2A). The stiff needle was moved away from the flexible needle, and the motion was stopped. The positions of both needles were then tracked for >200 s (Fig. 2B–E and Movie S3). We found that, similar to the spindle's long axis response, force developed in the structure decayed over time (Fig. 2F). The distance between the two needles, which had increased at first, reached a new steady state greater than that at the start of the experiment (Fig. 2G). From the slope of the force-velocity relationship, the effective viscosity was found to be ~2.3×102 Pa·s (Fig. 2I), which was comparable to that measured along the spindle's long axis. However, unlike the response observed along the spindle's long axis, the applied force persisted for several minutes (residual force, Fr, 0.38 ± 0.19 nN, mean ± SD, n = 9) (Fig. 2F and I). Moreover, the spindle's responses to forces along its short axis were coupled to changes in its overall shape (Fig. 2H). The spindle's width increased by ~11% (23.9 ± 4.2 μm to 26.7 ± 6.2 μm) while its length decreased by ~9% (46.1 ± 6.0 μm to 42.4 ± 4.7 μm) (Fig. 2J). Interestingly, the residual force Fr is greater when the deformation increases (Fig. 2K), indicating that the spindle generates a restoring force that depends on the magnitude of deformation. These results suggest that the metaphase spindle, along with viscous mechanical elements, has elastic elements that act along its short axis.
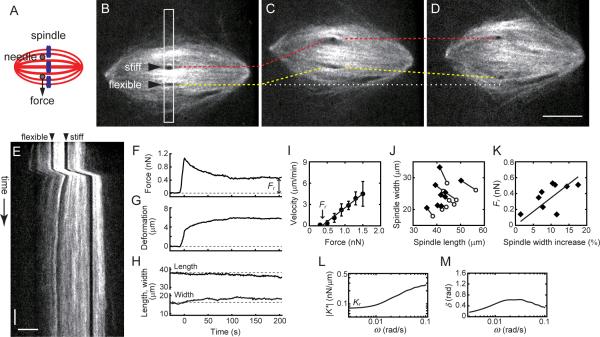
Figure 2. Mechanical force applied along the short axis of the metaphase spindle induces elastic deformation.
(A) Schematic of the experiment. (B–E) Step-like force was applied to a spindle, and the tips of the two needles (arrow heads) and spindle microtubule organization (X-rhodamine tubulin, 400 nM) were tracked for >200 s. Selected time lapse images acquired 15 s before (B), 0 s (C) and 100 s (D) after the stiff needle's displacement are shown. Dashed lines indicate the positions of stiff (red) and flexible (yellow) needle tips, respectively. The original position of the flexible needle tip is also shown (white dotted line). Scale bar, 10 μm. (E) The kymograph was generated using the highlighted region (white box) in (B). Scale bars, 20 s (vertical) and 5 μm (horizontal). (F–H) Force, measured using the deflection of the flexible needle (F), and deformation, defined as the change in distance between the two needle tips from their initial separation (G), are plotted against time. Changes in spindle length and width are also shown (H). The measured force and deformation were used to determine the force-velocity relationship (I) (solid circles, mean ± SD, n = 6). A linear fit (solid line) was used to estimate the effective viscosity. (J) Spindle length and width before force application (open circles) and after the applied force has decayed to a new steady state (solid diamonds) (n = 9). (K) Relationship between the change in spindle width (%) and the residual force, Fr. Solid line shows a liner fit. (L and M) Frequency-dependent profiles of dynamic stiffness (|K*|) (L) and phase shift (δ) (M) were obtained by processing the force and deformation records (see Methods). δ = 0 indicates a purely elastic response while δ = π/2 (~1.6) indicates an entirely viscous response.
Rigidity and viscoelasticity of the metaphase spindle depend on the timescale of force application
To further investigate the emergence of elasticity along the spindle's short axis, we examined the timescale-dependence of the spindle's deformation response. A Fourier transform-based analysis (Evans et al., 2009) revealed the contribution of viscous and elastic components to spindle mechanics on timescales ranging from 300 s to 10 s (or angular frequency, ω ≈ 0.003 to 0.1 rad/s)) (Fig. 2L and M). The spindle's response can be quantitatively described by two parameters: the dynamic stiffness (|K*|), which represents overall rigidity of the structure, and the phase shift (δ), which represents the proportion of viscous to elastic deformations in response to the applied force. |K*| reduces and reaches a plateau at low frequencies, yielding a residual stiffness, Kr (0.08 ± 0.03 nN/μm, mean ± SD, n = 9) (Fig. 2L), from which the elastic modulus can be estimated to be 2–10 Pa (see Supplemental Information). Interestingly, δ varied with frequency, indicating that the spindle's response to forces is dominated by elastic components at low frequencies and becomes more viscous at high frequencies (Fig. 2M).
To examine the spindle's response to forces at even shorter timescales (or higher frequencies), we applied forces that varied sinusoidally over time (Fig. 3A and B, Movie S4) (Janmey et al., 2007). As relatively low amplitude forces were used, the spindle responses were consistent and reversible (see Fig. S2 and Supplemental Information for details on the optimization of this method). The deflection of the flexible needle, and the distance between the needle tips (Fig. 3C and D), were used to derive the force-deformation relationship at each frequency (Fig. 3E). The tilt and area of each ellipsoidal trajectory yielded |K*| and δ, respectively. |K*| increased ~3-fold as the frequency increased from 0.06 to 3 rad/s, but increased no further, yielding a saturation stiffness, K0 (0.9 ± 0.4 nN/μm, mean ± SD, n = 9) (Fig. 3F), from which the elastic modulus can be estimated to be 20–100 Pa. In these experiments, δ approached zero as the frequency increased (Fig. 3G), indicating that as the dynamic stiffness |K*| approached K0, the mechanical response is once again dominated by elastic components in the spindle.
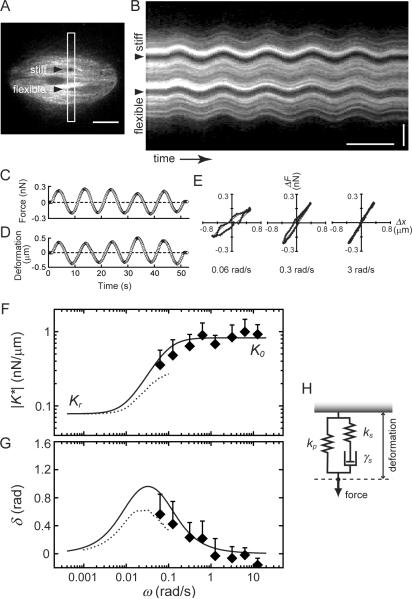
Figure 3. The metaphase spindle's viscoelastic response to forces applied along its short axis has a timescale dependence.
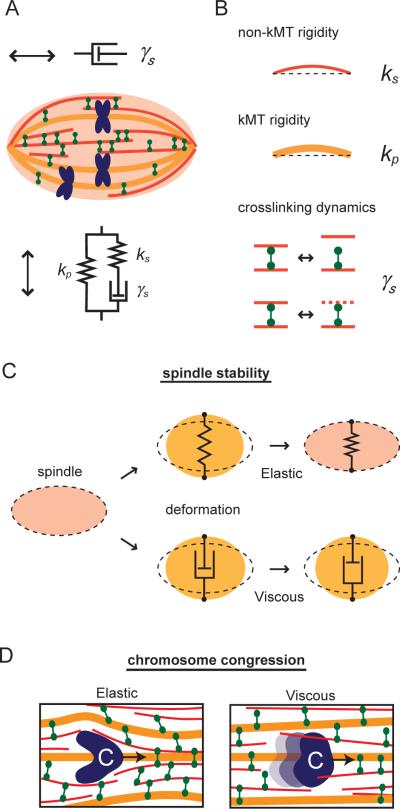
(A) Confocal fluorescence image of a spindle, labeled with X-rhodamine tubulin (400 nM), into which two needles have been inserted (arrow heads). The stiff needle tip was moved sinusoidally. Scale bar, 10 μm. (B) The kymograph was generated using the highlighted region (white box) in (A). Scale bars, 10 s (horizontal) and 5 μm (vertical). (C–E) Force, measured using the deflection of the flexible needle (C), and deformation, which is the change in distance between the two needle tips from initial separation (D), are plotted against time. These data were used to determine the force-deformation relationship (E) at different frequencies (rad/s, bottom in each panel). (F and G) The dynamic stiffness (|K*|) (F) and phase shift (δ) (G) of the spindle mechanics at different frequencies (solid diamonds, mean ± SD, n = 9), measured along the spindle's short axis. Data from Fig. 2L and M are also plotted (dotted lines) to show the viscoelastic properties of the metaphase spindle over 4-decades of timescales. (H) Schematic shows the arrangement of two springs (ks and kp) and a dashpot (γs) used to fit the timescale-dependent mechanical response of the spindle (solid lines in (F) and (G)). See Fig. S2 for additional supporting data.
The combined data, from both step-like and sinusoidal perturbations along the spindle's short axis, revealed how the spindle's deformation responses can vary between elastic and viscous on timescales from minutes to sub-seconds (Fig. 3F and G). The bell-shape profile of the phase shift (Fig. 3G) indicates that the spindle structure is predominantly elastic on two timescales, minutes (>100 s) and sub-seconds (<1–10 s), with the stiffness values Kr and K0, respectively. Viscous responses become more prominent at intermediate timescales (~30 s). A three-component mechanical model (Fig. 3H), which is comprised of an elastic spring (stiffness ks) and a viscous dashpot (γs) connected in series, and another spring (kp) connected in parallel, is the simplest arrangement of elastic and viscous elements that recapitulates the timescale dependence of metaphase spindle's response to forces applied perpendicular to the pole-to-pole axis. A material with such an arrangement of mechanical elements is referred to as Zener-type viscoelastic solid. For this type of material, the elasticity at long timescales (Kr) corresponds to kp and the elasticity at short timescales (K0) is equal to the sum of ks and kp (see below). By fitting the experimental data to this model (solid lines in Fig. 3F and G), we can determine the values of these three parameters for the metaphase spindle (ks = 0.78 nN/μm; kp = 0.08 nN/μm; γs = 7.5 nN·s/μm).
Dynamic crosslinking of microtubules contributes to spindle viscosity
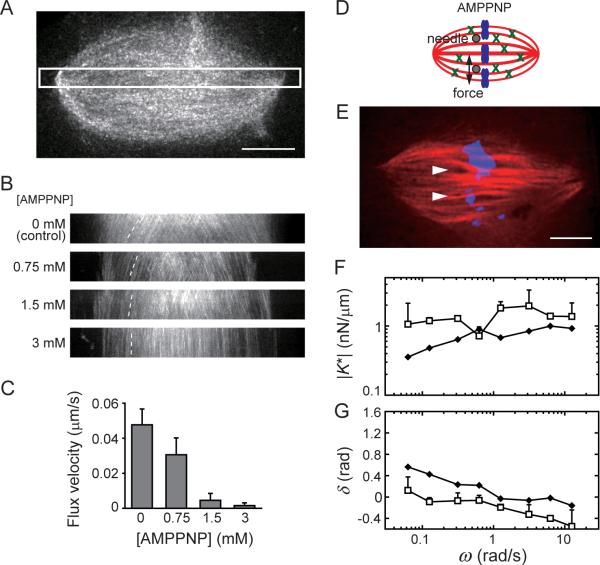
The microtubule arrays in the metaphase spindle are crosslinked by motor and non-motor proteins (Walczak and Heald, 2008). To examine the contributions of crosslinking dynamics to the spindle mechanics we used AMPPNP, a slowly hydrolyzing ATP analog that locks mitotic kinesins in a microtubule-bound state (called rigor) (Sawin and Mitchison, 1991), and could therefore lead to relatively stable inter-filament linkages mediated by proteins such as kinesin-5. Addition of AMPPNP to the spindle resulted in a dose-dependent reduction in the sliding of microtubules, as revealed by the reduced poleward flux of fluorescent tubulin incorporated into the spindle (Fig. 4A–C). Under these conditions the spindle size and shape remained unchanged over several minutes, as needed for our analysis (Fig. S3A and B). Using the two needle set-up and sinusoidal force application along the spindle's short axis (Fig. 4D and E), we found that in the presence of AMPPNP (1.5 mM) the spindle's short-timescale elastic stiffness, K0, which is the sum of the stiffness of two springs in our model (Fig. 3H), was not significantly altered (1.4 ± 0.6 nN/μm, mean ± SD, n = 7) compared to that measured for control spindles (Fig. 4F). Remarkably, we found that the viscous component of the spindle's response essentially disappeared (δ ≈ 0, Fig. 4G) in the presence of AMPPNP. The negative values of δ suggest an active response of the AMPPNP-treated spindles at short timescales, being likely related to the polymer dynamics that are not suppressed under these conditions. Together, these data suggest that the dynamics of crosslinking between spindle microtubules, which are suppressed in the presence of the slowly hydrolyzing ATP analog, are likely to be major contributors to spindle's viscous element (i.e., dashpot γs, Fig. 3H).
Figure 4. Inhibition of crosslinker dynamics suppresses the spindle's viscous response to applied force.
(A–C) Effect of AMPPNP on the dynamics of spindle microtubules. (A) An example of the metaphase spindle labeled with X-rhodamine tubulin (50 nM) used for fluorescent speckle microscopy. (B) Kymographs generated using a highlighted region similar to that in (A). Dotted lines highlight the motion of fluorescent speckles. (C) The average velocity of poleward motion of tubulin speckles (mean ± SD, n = 10). (D and E) Schematic (D) and an example of a spindle (E) in the presence of 1.5 mM AMPPNP (tubulin: red and DNA: blue). Needle positions are shown (arrow heads). Scale bars, 10 μm. (F and G) The dynamic stiffness (|K*|) and phase shift (δ) of the spindle's response to sinusoidal force at different frequencies were determined for AMPPNP-treated spindles (open squares, mean ± SD, n = 7). For comparison, data for control spindles (solid diamonds) (Fig. 3F, G) is also shown. See Fig. S3 for additional supporting data.
Non-kinetochore microtubules contribute to spindle viscosity and elasticity
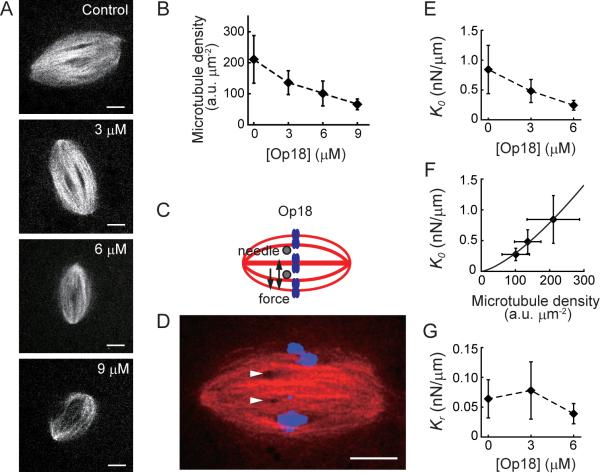
To examine how the spindle's viscosity is linked to microtubule density we used recombinant Op18/stathmin (hereafter Op18), a protein that directly suppresses microtubule assembly (Belmont and Mitchison, 1996). We have previously shown that addition of recombinant Op18 to assembled spindles preferentially depletes nonkinetochore microtubules (Houghtaling et al., 2009), which comprise ~90% of total microtubules in the meiotic metaphase spindle (Ohi et al., 2007). As expected, addition of Op18 to assembled spindles reduced their length (~85% of control at 3 μM Op18, and ~80% of control at 6 μM Op18), while the aspect ratio (width/length) of the structure remained unchanged (Fig. S4A and B) (Houghtaling et al., 2009). Consistent with the loss of non-kinetochore microtubules, we found that increasing Op18 concentrations led to a dose-dependent decrease in the overall microtubule density (Fig. 5A and B, Fig. S4C–E). Unlike other reagents that perturb microtubule dynamics, the overall spindle morphology and bipolar organization are maintained over several minutes under these conditions, as needed for our analysis.
Figure 5. Destabilization of non-kinetochore microtubules reduces spindle elasticity.
(A and B) Confocal image of spindles (X-Rhodamine tubulin, 100 nM) treated with different concentrations of recombinant Op18 (A). The microtubule density was determined by analyzing fluorescence intensity per unit area in the spindle (n ≥ 24 spindles for each condition, also see Fig. S4C–E) (B). (C–G) Responses of Op18-treated spindles to mechanical forces. (C and D) Schematic (C) and a representative example (D) of an Op18-treated spindle (6 μM). Tubulin (red), DNA (blue), and needle positions (arrow heads) are shown. (E) Short-timescale elastic stiffness (K0) of Op18-treated spindles (n ≥ 4 for each condition). (F) Relationship between K0 and the microtubule density in the spindle (dm). Solid line shows best fit by K0 ~ a·dmb (a = 4.3 ×10−4 and b = 1.42). (G) Long-timescale elastic stiffness (Kr) of Op18-treated spindles (n = 4–6 for each condition). Plots are mean ± SD. Scale bars, 10 μm. See Fig. S4 for additional supporting data.
We examined the micromechanics of Op18-treated spindles along the long and short axes by step-like application of force. We found that along the long axis the Op18-treated spindles (6 μM) behaved similar to control spindles and revealed a predominantly viscous response (Fig. S4F–J). However, the effective viscosity was significantly reduced compared to controls (η ~ 1.3×102 Pa·s, versus ~1.9×102 Pa·s). Along the short axis the effective viscosity was also reduced (η ~ 1.5×102 Pa·s, versus ~2.3×102 Pa·s in controls). Therefore, the spindle's viscosity, along both the long and short axes, depends on the density of non-kinetochore microtubules.
Forces applied along the spindle's short axis yielded an elastic response (Fig. 3). To examine how the non-kinetochore microtubules may contribute to this elasticity, we further analyzed the mechanical response of Op18-treated spindles along the short axis (Fig. 5C and D). We found that the short-timescale elastic stiffness (K0), which was analyzed by sinusoidal application of force, decreased in a dose-dependent manner as the Op18 concentration increased (Fig. 5E). Moreover, K0 shows a strong correlation with the density of spindle microtubules (dm) and could be fitted by K0 ~ a·dmb (solid line in Fig. 5F). The response of a Zener-type solid to forces that act on short timescales is dominated by the two elastic springs (i.e., ks + kp), as the dashpot γs behaves like a rigid rod when pulled or pushed quickly (Fig. 3H). As our analyses indicate that ks is much larger than kp, the measured stiffness K0 mainly depends on ks. Together, these data suggest that non-kinetochore microtubules contribute to the spring ks in our model. On the other hand, the long-timescale elastic stiffness (Kr), which was analyzed by step-like application of force, was less sensitive to Op18 treatments (Fig. 5G). On long timescales, the response of the Zener-type solid to forces is dominated by the parallel spring kp, as the dashpot γs readily relaxes the strain in the spring that is in series (ks). Therefore, kp is likely derived from spindle components other than the non-kinetochore microtubules. We suggest that this spring may depend on the kinetochore microtubules in the spindle, which remain in the presence of Op18 (Houghtaling et al., 2009).
The spindle pole organization by kinesin-5 and dynein contributes to spindle elasticity
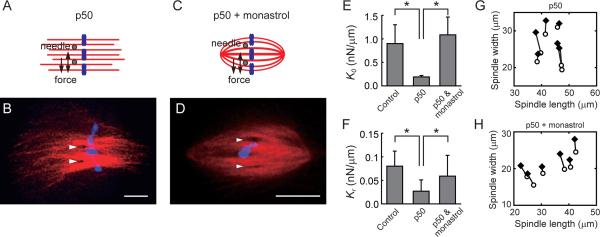
We next examined the contributions of key motor proteins to the spindle's elasticity along its short axis. We first focused on dynein-dynactin, a minus-end directed motor complex that is known to cluster minus-ends of microtubules and transport proteins to spindle poles (Karki and Holzbaur, 1999). To inhibit dynein-dynactin function we used p50/dynamitin (Wittmann and Hyman, 1999), which is a component of the dynactin complex. Addition of excess p50/dynamitin disrupts the dynactin complex and leads to spindle phenotypes that are similar to the loss of dynein function (Gaetz and Kapoor, 2004). As expected, addition of recombinant p50/dynamitin resulted in bipolar spindles with unfocused spindle poles (Fig. 6A and B). This spindle structure remained stable over minutes, allowing analysis of timescale-dependent spindle mechanics with the dual-needle set-up. The spindle's elastic stiffness was analyzed using sinusoidal (for K0) and step-like (for Kr) application of force. We find that both K0 and Kr were significantly reduced upon p50/dynamitin treatment (Fig. 6E and F). Unlike control spindles, the spindle length, measured using a thresholded fluorescence intensity of dye-labeled microtubules, was not significantly altered by forces acting along the spindle's short axis (Fig. 6G) (the ratio of spindle length to width changed, ΔL/ΔW, ~0.1, versus ~0.7 in control spindles). Therefore, inhibition of dynein-dynactin function resulted in spindles with reduced elasticity and diminished coupling between spindle length and width.
Figure 6. The spindle's elasticity depends on proper spindle pole organization.
(A–D) Schematic and representative examples of spindles in the presence of p50/dynamitin (20 μM) (A and B), or in the presence of both p50/dynamitin (20 μM) and monastrol (100 μM) (C and D). Tubulin (red), DNA (blue), and needle positions (arrow heads) are shown. Scale bars, 10 μm. (E and F) The short- and the long-timescale elastic stiffness, K0 and Kr, respectively, for spindles treated with p50/dynamitin alone or p50/dynamitin and monastrol. Data are mean ± SD (n ≥ 7 for each condition). For comparison, the stiffness values for control spindles (Fig. 3F) are also shown. Asterisks indicate t-test (P < 0.05). (G and H) The changes in the spindle length and width before force application (open circles) and after the applied force has decayed (solid diamonds) in spindles treated with p50/dynamitin alone (n = 6) (G) or p50/dynamitin and monastrol (n = 6) (H).
To analyze if the changes in spindle's micromechanics observed in the presence of p50/dynamitin were due to the loss of dynein-dynactin activity or the disruption of spindle pole organization, we inhibited kinesin-5 along with dynein-dynactin to recover the overall spindle organization (Mitchison et al., 2005). Consistent with previous reports, ~80% of the spindles that form under these conditions had microtubules that were observed to be focused at each pole (Fig. 6C and D). Analysis of the micromechanics of these spindles revealed that the coupling between spindle length and width was partially restored (ΔL/ΔW ~ 0.3) (Fig. 6H). Importantly, the elastic stiffness of these spindles (K0 and Kr) recovered to levels that were similar to those measured for control spindles (Fig. 6E and F). Currently, we do not understand how the spindle poles observed in the absence of dynein-dynactin and kinesin-5 function relate to those in untreated spindles. It is also unclear what the specific consequences are of dual inhibition of these motor proteins. Guided by models for how microtubules can be focused to form spindle poles (Chakravarty et al., 2004), we suggest that under dual inhibition conditions the balance in the different plus-end and minus-end directed motor proteins is set to a level that can restore overall spindle shape and pole microtubule organization. Together with these assumptions, our data suggest that the spindle pole may couple the mechanical elements along the spindle's long and short axes and could be an important determinant of its elasticity.
DISCUSSION
Our analysis reveals that micromechanics of the vertebrate metaphase spindle depend on the orientation and timescale of applied mechanical forces. Our findings shed new light on the metaphase spindle's material properties, its force-generating functions and how the dynamic structure accommodates deformations while maintaining stability.
Micromechanical properties of the metaphase spindle
The metaphase spindle is subjected to mechanical forces that can result from microtubule sliding, deformations associated with the movements of chromosomes as they align at the spindle equator, stretching of sister kinetochores, and activities that properly position the spindle in the dividing cell. These forces act in different directions and on timescales ranging from minutes to sub-seconds. Analysis of the viscoelastic properties of isotropic cytoskeletal networks reconstituted from stabilized, non-dynamic microtubules indicates that the responses of these structures to forces are predominantly elastic over 0.1–100 s (Lin et al., 2007; Sato et al., 1988). In contrast, our measurement reveals that the metaphase spindle is mechanically anisotropic and exhibits both elastic and viscous responses to forces acting on these timescales. The observed micromechanics along the spindle's long axis can be modeled by a viscous element, such as a dashpot (Fig. 7A). Force applied along this axis is dissipated and does not deform the overall structure. Along the spindle's short axis, the micromechanics are similar to those of a Zener-type viscoelastic solid, which is comprised of a spring (ks) and a dashpot (γs) in series that together are in parallel with another spring (kp) (Fig. 7A). In response to forces acting along its short axis, the spindle recoils elastically on short (<1–10 s) or long timescales (>100 s), but reveals viscous deformation at intermediate timescales (~10–100 s).
Figure 7. Molecular mechanisms underlying spindle micromechanics.
(A) Summary for the metaphase spindle micromechanics along its long and short axes. (B) Schematics show potential links between molecular components underlying the spindle's elastic and viscous responses. Non-kinetochore microtubules (non-kMT, red), kinetochore microtubules (kMT, orange), and green (crosslinkers) are shown. (C) Mechanical stability of the metaphase spindle depends on elasticity. Elastic deformation of the structure (upper panel) generates a restoring force that returns the spindle to the original shape while viscous deformation (lower panel) causes changes in shape that persist. Dotted line indicates original spindle shape. (D) Chromosome motion through the crosslinked microtubule array of the spindle at velocities at which the spindle's response is elastic (left panel) or viscous (right panel). Blue, chromosomes. Curvature in microtubules indicates elastic strain.
Metaphase spindle elasticity
The elasticity of a material provides a force that acts to restore its original shape. Our biochemical and chemical perturbations suggest that the two elastic elements in the spindle can be related to kinetochore (spring kp) and non-kinetochore microtubule (ks) mechanics (Fig. 7B). Based on the values of the spring constants ks and kp we determined, and using simple assumptions about the crosslinking of filaments and the number of microtubules in the spindle, we can estimate the bending stiffness of both kinetochore fibers and single non-kinetochore microtubules (~5 pN/μm and ~3×10−3 pN/μm, respectively) (see Supplemental Information). These values for stiffness are comparable to estimates based on the average length of kinetochore and nonkinetochore microtubules (Burbank et al., 2006; Yang et al., 2007) and the flexural rigidity of single microtubules measured in vitro (Gittes et al., 1993), supporting the overall validity of our model.
The spindle's elasticity is observed on two distinct timescales, seconds (and less) and minutes (and more). An example of a force that acts on the spindle on short timescales (~seconds) is the oscillatory force involved in spindle positioning during asymmetric cell division (Cowan and Hyman, 2004). In our model for the spindle mechanics, the elastic spring ks dominates the spindle's response to forces acting on this relatively rapid timescales. We therefore suggest that non-kinetochore microtubule mechanics would maintain structural stability in the face of these short-acting forces. An example of a force that acts on a relatively long timescale (~minutes) is the force associated with the stretching of sister kinetochores on chromosomes that are aligned at the metaphase plate (Waters et al., 1996). On these timescales the elastic spring kp dominates the spindle's response to forces. We propose that the mechanical properties of the kinetochore microtubules, which are relatively stable over minutes, can sustain forces applied on these long timescales to prevent the spindle from collapsing. Therefore, these elastic elements would maintain the spindle's overall organization in the face of different internal and external forces applied over a range of timescales (Fig. 7C).
We find that forces acting along the spindle's short axis and on long timescales result in changes in the structure's pole-to-pole length. Currently, the most widely discussed models for spindle size regulation focus on the balance of forces along the pole-to-pole axis of the spindle in only one dimension (reviewed in (Goshima and Scholey, 2010; Mogilner and Craig, 2010)). Our findings suggest that the interplay between mechanical elements that control spindle width and those that control spindle length plays an important role in determining the size and shape of this structure. We propose that the organization of the spindle pole plays a role in connecting the mechanical elements along these two orthogonal spindle axes. An important next step will be to directly apply controlled forces (e.g., via antibody-coated needles) to the spindle poles so that its role in spindle size control can be quantitatively analyzed.
Metaphase spindle viscosity
The viscosity of a material provides resistance to oppose motion, and is associated with remodeling of the structure. Two factors may contribute to the viscous response of the spindle. First, the viscosity of the fluid (e.g., cytoplasm) in which the spindle is assembled. Our measurements indicate that the effective viscosity of the metaphase spindle is >100 times higher than what we measure for the cytoplasm alone or what has been determined by examining the Brownian motion of cytoplasmic particles near spindles (~0.3 Pa·s) (Alexander and Rieder, 1991). Therefore, assuming that the fluid inside the spindle and the cytoplasm are likely to be the same, we suggest this fluid makes a relatively minor contribution to the spindle's viscous response on timescales ranging from minutes to sub-seconds. Second, viscous-like characteristics can result from frictional drag forces which arise due to proteins that crosslink microtubules (Tawada and Sekimoto, 1991). Forces driving the relative motion of two microtubules can stretch crosslinking proteins (e.g., motor and non-motor proteins). Detachment of these crosslinkers, which can be due to their intrinsic off-rates or microtubules undergoing repeated polymerization/depolymerization cycles (Mitchison and Kirschner, 1984), leads to filament slippage and dissipation of strain energy. The crosslinkers can then rebind the filaments and allow for structural remodeling (Fig. 7B). Cycles of such binding and unbinding events may contribute to the relatively high effective viscosity of the spindle. We propose that the dynamic crosslinking of non-kinetochore microtubules, which make up >90% of the microtubules in the Xenopus meiotic spindles (Ohi et al., 2007), is likely to be the major contributor to this spindle viscosity. Spindles from other cell types can have different microtubule densities and it is likely that the values describing their mechanical properties are going to vary accordingly. We anticipate that analyses of microtubule network architecture and density in these other spindles, and comparisons with our analysis of the Xenopus spindle micromechanics, may allow estimates of how these structures respond to different forces.
Estimating the force generated by poleward microtubule flux
In vertebrate spindles, the entire microtubule lattice continuously moves toward each spindle pole with an average velocity of 2–3 μm/min (Sawin and Mitchison, 1991). While numerous studies have analyzed these polymer dynamics and changes associated with the perturbation of key molecular players, the force generated during poleward flux has remained unknown (Kwok and Kapoor, 2007). Our data, revealing the effective viscosity of the interior of the metaphase spindle, can provide an estimate of this force. Consider the case in which a single microtubule moves at a constant velocity in the structure, with its filament axis parallel to the spindle's long axis. The frictional force arising due to this motion is proportional to viscosity and velocity, and can be calculated to be ~10 pN per micron per microtubule (see Supplemental Information). The active force that is needed to drive poleward flux must therefore be equal to this force and corresponds to a value 2–3 times greater than that generated by a single motor protein (Gennerich et al., 2007; Valentine et al., 2006) or by microtubule polymerization (Dogterom and Yurke, 1997). The substantial frictional load in the spindle meshwork could significantly alter motor and microtubule activities, and may thus be a major contributing factor to the differences in the dynamics and stability of microtubules observed in spindles and in cytoplasm (Leslie and Pickett-Heaps, 1984; Tirnauer et al., 2004).
Implications for the motion of cargo through dense microtubule networks
It is frequently observed that even after most chromosomes are aligned at the metaphase plate, a misaligned chromosome is transported through the spindle structure from one end of the spindle toward the equator (called congression) (Hughes et al., 2009; Kapoor et al., 2006; Nicklas, 1965). The motion of chromosomes, whose size is significantly larger than the average mesh size of the spindle microtubule array (McIntosh and Landis, 1971), will result in forces acting along both the long and short axes of the spindle. Our data show that the deformation along the spindle's long axis is almost entirely viscous. Along its short axis, the spindle exhibits maximum viscous deformation on the timescale of tens of seconds. Interestingly, this corresponds to the timescale for chromosome motion typically observed during congression (~60 s; as the period that a chromosome passes over its typical diameter of ~1 μm at the congression velocity of ~1 μm/min), suggesting that as the chromosome moves, microtubule filaments bend or buckle to accommodate this motion; however, the strain associated with these changes in the filaments is dissipated through their remodeling, possibly via motion or disassembly (Fig. 7D). This feature allows the spindle's dense microtubule array to accommodate local deformations with minimal effect on the overall spindle integrity, enabling the structure to maintain tension across the sister chromosomes that are already aligned at the metaphase plate.
The motion of cargo through dense microtubule networks occurs during a variety of other cellular processes, such as axonal transport in neurons (Hirokawa, 1998). It is likely that our findings have implications for these systems in which microtubules also form an anisotropic network whose filament density and crosslinking dynamics are precisely regulated in the cell. We propose that similar to the microtubule network in the spindle, these other cytoskeletal structures may also allow transport of different sized cargoes at specific velocity ranges, so that the strain due to deformations is readily dissipated and the integrity of the entire structure is not altered or destabilized. The viscoelasticity could be tuned by controlling filament geometry, either through biochemical regulation or external force. Examining the conserved mechanical features in different cytoskeletal networks should shed light on the design principles underlying their self-organization.
EXPERIMENTAL PROCEDURES
Spindle assembly in Xenopus egg extracts
Cytoplasmic extracts from the Xenopus laevis eggs, arrested in metaphase of meiosis II, were prepared as previously described (Desai et al., 1999). Meiotic spindles were assembled by addition of demembranated sperm nuclei to the extract, followed by cycling once through interphase back into metaphase, at 18 °C.
Micromanipulation of the spindle
The microneedle-based mechanical manipulation was performed in an inverted microscope (TE2000, Nikon) equipped with two micromanipulators (MHW-3, Narishige). The experimental chamber was consisted of a coverslip and an apertured rubber plate. The coverslip was coated by 0.1% agarose (Nedelec and Surrey, 2001) and the tips of microneedles were siliconized (SL2, Sigma-Aldrich) to minimize nonspecific binding. The extract containing metaphase spindles was spread onto the coverslip and overlaid with mineral oil (M8410, Sigma-Aldrich; viscosity ≤30 mPa·s at 25°C) to prevent sample desiccation. A bipolar spindle floating in the extract was found by imaging chromosomes. Then, a pair of glass microneedles, one stiff and the other flexible, was inserted into the spindle by steering micromanipulators. The tips of the needles were kept 2–3 μm above the coverslip surface, as estimated by the confocal image of spindle microtubules. Confocal imaging was also used to confirm that the needles were not contacting chromosomes. The motion of the stiff needle was controlled by a piezo actuator (P-841.10, Physik Instrumente) and a function generator (33120A, Hewlett-Packard) via a piezo driver in a closed-loop mode (E-665, Physik Instrumente). Measurements were performed at 20 ± 1 °C in a temperature-controlled room.
Microneedles
The microneedles were fabricated by pulling glass rods (G1000, Narishige) using a capillary puller (P-10, Narishige) and a microforge (MF200, World Precision Instruments). The tip length was typically 30–50 μm for stiff needles and 200–300 μm for flexible needles. The tip diameter of both needles was 1–2 μm. The stiffness of the flexible needles (0.25–0.46 nN/μm) was determined using a cross-calibration method (Kishino and Yanagida, 1988). The overall calibration error was <11%. The linearity of the needle stiffness was preserved for deflections over >20 μm.
Imaging
To track motion of the needle tips, bright field images were obtained with a cooled CCD camera (CoolSnap HQ, Photometrics), mounted on the microscope base-port. To visualize spindles, fluorescence images were acquired with an EM-CCD camera (512B, Photometrics) via a spinning-disk confocal unit (CSU-10, Yokogawa), which was mounted on the microscope side-port and equipped with 488 nm and 568 nm laser lines. A 100× objective (PlanApo, 1.4NA, Nikon) was used. Image acquisition was performed using Metamorph (Molecular Devices). X-rhodamine-labeled tubulin was prepared as described previously (Houghtaling et al., 2009) and added to extracts to image spindles. Chromosomes were labeled with SYTOX green.
Biochemical perturbations
Recombinant Op18 (Houghtaling et al., 2009) or AMPPNP (A2647, Sigma-Aldrich) were added to the extract after spindle assembly. Recombinant p50/dynamitin alone (Gaetz and Kapoor, 2004) or with monastrol (SC-2027, Santa Cruz Biotechnology) was added at the start of spindle assembly.
Data analysis
The motion of the needle tips were analyzed using centroid tracking in Image J and self-written Microsoft Excel macros. Deformation was determined by measuring the distance between the two needle tips, and force was estimated using the deflection of the flexible needle tip multiplied by its pre-calibrated stiffness.
The force-velocity relationship was obtained by processing the time-dependent force and deformation measurements. The frictional coefficient (γ) was determined by linear regression, according to F =γV + Fr, where F is the force, V is the velocity, and Fr is a residual force. The effective viscosity (η) was calculated by η = c·γ. Here, c (=(ln(L/d) + 0.84)/4πL) is the form factor for a cylinder (length, L, and diameter, d) (Howard, 2001). We used L = 20 μm as the average height of the metaphase spindle, which corresponds to the length of the needle tip embedded in the spindle, and d = 1 μm as the diameter of the tip. For cytoplasmic viscosity we used L = 200 μm, which is the average height of cytoplasmic layer in the experimental chamber. The force and deformation records were also processed to calculate the frequency-dependent viscoelastic parameters according to the previously described conversion method (Evans et al., 2009).
For the sinusoidal analysis, the force, f(t), and deformation, x(t), were fitted to f(t) = f0·sin(ωt + θ) + a1t + b1, and x(t) = x0·sin(ωt + θ + δ) + a2t + b2, respectively, and used to determine the dynamic stiffness, |K*| (= f0/x0), and the phase shift, δ. ai and bi are for drift and offset corrections, respectively (typically <5% of the amplitude). The fitting was performed in Origin 7.5.
The frequency profiles (Fig. 3F and G) were fitted by the constitutive equation for the Zener-type viscoelastic solid, comprised of two springs, ks and kp, and a dashpot, γs (Fig. 3H). The dynamic stiffness |K*| and the phase shift δ are, respectively, given by |K*(ω)| = |(kp + iβω)/(1 + iαω)| and δ(ω) = tan−1(γsω/(kp + ω2αβ)). Here, α = γs/ks and β = (kp + ks)·γs/ks.
Statistical tests were performed using the unpaired Student's t-test in Origin 7.5.
Supplementary Material
ACKNOWLEDGEMENTS
T.M.K. acknowledges support from the NIH/NIGMS (GM065933). We also thank the Uehara memorial foundation (Y.S.) and the Japan Society for the Promotion of Science (Y.S. and Y.T.M.).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
SUPPLEMENTAL INFORMATION Supplemental Information includes Supplemental Experimental Procedures, four figures, and four movies.
REFERENCES
- Alexander SP, Rieder CL. Chromosome motion during attachment to the vertebrate spindle: initial saltatory-like behavior of chromosomes and quantitative analysis of force production by nascent kinetochore fibers. J Cell Biol. 1991;113:805–815. doi: 10.1083/jcb.113.4.805. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Belmont LD, Mitchison TJ. Identification of a protein that interacts with tubulin dimers and increases the catastrophe rate of microtubules. Cell. 1996;84:623–631. doi: 10.1016/s0092-8674(00)81037-5. [DOI] [PubMed] [Google Scholar]
- Burbank KS, Groen AC, Perlman ZE, Fisher DS, Mitchison TJ. A new method reveals microtubule minus ends throughout the meiotic spindle. J Cell Biol. 2006;175:369–375. doi: 10.1083/jcb.200511112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakravarty A, Howard L, Compton DA. A mechanistic model for the organization of microtubule asters by motor and non-motor proteins in a mammalian mitotic extract. Mol Biol Cell. 2004;15:2116–2132. doi: 10.1091/mbc.E03-08-0579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowan CR, Hyman AA. Asymmetric cell division in C. elegans: cortical polarity and spindle positioning. Annu Rev Cell Dev Biol. 2004;20:427–453. doi: 10.1146/annurev.cellbio.19.111301.113823. [DOI] [PubMed] [Google Scholar]
- Desai A, Murray A, Mitchison TJ, Walczak CE. The use of Xenopus egg extracts to study mitotic spindle assembly and function in vitro. Methods Cell Biol. 1999;61:385–412. doi: 10.1016/s0091-679x(08)61991-3. [DOI] [PubMed] [Google Scholar]
- Dogterom M, Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278:856–860. doi: 10.1126/science.278.5339.856. [DOI] [PubMed] [Google Scholar]
- Dumont S, Mitchison TJ. Compression regulates mitotic spindle length by a mechanochemical switch at the poles. Curr Biol. 2009;19:1086–1095. doi: 10.1016/j.cub.2009.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans RM, Tassieri M, Auhl D, Waigh TA. Direct conversion of rheological compliance measurements into storage and loss moduli. Phys Rev E Stat Nonlin Soft Matter Phys. 2009;80:012501. doi: 10.1103/PhysRevE.80.012501. [DOI] [PubMed] [Google Scholar]
- Fletcher DA, Mullins RD. Cell mechanics and the cytoskeleton. Nature. 2010;463:485–492. doi: 10.1038/nature08908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gaetz J, Kapoor TM. Dynein/dynactin regulate metaphase spindle length by targeting depolymerizing activities to spindle poles. J Cell Biol. 2004;166:465–471. doi: 10.1083/jcb.200404015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardel ML, Kasza KE, Brangwynne CP, Liu J, Weitz DA. Mechanical response of cytoskeletal networks. Methods Cell Biol. 2008;89:487–519. doi: 10.1016/S0091-679X(08)00619-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatlin JC, Matov A, Danuser G, Mitchison TJ, Salmon ED. Directly probing the mechanical properties of the spindle and its matrix. J Cell Biol. 2010;188:481–489. doi: 10.1083/jcb.200907110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gennerich A, Carter AP, Reck-Peterson SL, Vale RD. Force-induced bidirectional stepping of cytoplasmic dynein. Cell. 2007;131:952–965. doi: 10.1016/j.cell.2007.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gittes F, Mickey B, Nettleton J, Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goshima G, Scholey JM. Control of Mitotic Spindle Length. Annu Rev Cell Dev Biol. 2010;26:21–57. doi: 10.1146/annurev-cellbio-100109-104006. [DOI] [PubMed] [Google Scholar]
- Hirokawa N. Kinesin and dynein superfamily proteins and the mechanism of organelle transport. Science. 1998;279:519–526. doi: 10.1126/science.279.5350.519. [DOI] [PubMed] [Google Scholar]
- Houghtaling BR, Yang G, Matov A, Danuser G, Kapoor TM. Op18 reveals the contribution of nonkinetochore microtubules to the dynamic organization of the vertebrate meiotic spindle. Proc Natl Acad Sci U S A. 2009;106:15338–15343. doi: 10.1073/pnas.0902317106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howard J. Mechanics of motor proteins and the cytoskeleton. Sinauer Associates; Massachusetts: 2001. [Google Scholar]
- Hughes SE, Gilliland WD, Cotitta JL, Takeo S, Collins KA, Hawley RS. Heterochromatic threads connect oscillating chromosomes during prometaphase I in Drosophila oocytes. PLoS Genet. 2009;5:e1000348. doi: 10.1371/journal.pgen.1000348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Inoue S, Salmon ED. Force generation by microtubule assembly/disassembly in mitosis and related movements. Mol Biol Cell. 1995;6:1619–1640. doi: 10.1091/mbc.6.12.1619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Itabashi T, Takagi J, Shimamoto Y, Onoe H, Kuwana K, Shimoyama I, Gaetz J, Kapoor TM, Ishiwata S. Probing the mechanical architecture of the vertebrate meiotic spindle. Nat Methods. 2009;6:167–172. doi: 10.1038/nmeth.1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Janmey PA, Georges PC, Hvidt S. Basic rheology for biologists. Methods Cell Biol. 2007;83:3–27. doi: 10.1016/S0091-679X(07)83001-9. [DOI] [PubMed] [Google Scholar]
- Kapoor TM, Lampson MA, Hergert P, Cameron L, Cimini D, Salmon ED, McEwen BF, Khodjakov A. Chromosomes can congress to the metaphase plate before biorientation. Science. 2006;311:388–391. doi: 10.1126/science.1122142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karki S, Holzbaur EL. Cytoplasmic dynein and dynactin in cell division and intracellular transport. Curr Opin Cell Biol. 1999;11:45–53. doi: 10.1016/s0955-0674(99)80006-4. [DOI] [PubMed] [Google Scholar]
- Kishino A, Yanagida T. Force measurements by micromanipulation of a single actin filament by glass needles. Nature. 1988;334:74–76. doi: 10.1038/334074a0. [DOI] [PubMed] [Google Scholar]
- Kwok BH, Kapoor TM. Microtubule flux: drivers wanted. Curr Opin Cell Biol. 2007;19:36–42. doi: 10.1016/j.ceb.2006.12.003. [DOI] [PubMed] [Google Scholar]
- Leslie RJ, Pickett-Heaps JD. Spindle microtubule dynamics following ultraviolet-microbeam irradiations of mitotic diatoms. Cell. 1984;36:717–727. doi: 10.1016/0092-8674(84)90352-0. [DOI] [PubMed] [Google Scholar]
- Lin Y, Koenderink GH, C. MF, Weitz DA. Viscoelastic properties of microtubule networks. Macromolecules. 2007;40:771407720. [Google Scholar]
- McIntosh JR, Cande WZ, Snyder JA. Structure and physiology of the mammalian mitotic spindle. Soc Gen Physiol Ser. 1975;30:31–76. [PubMed] [Google Scholar]
- McIntosh JR, Landis SC. The distribution of spindle microtubules during mitosis in cultured human cells. J Cell Biol. 1971;49:468–497. doi: 10.1083/jcb.49.2.468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitchison T, Kirschner M. Dynamic instability of microtubule growth. Nature. 1984;312:237–242. doi: 10.1038/312237a0. [DOI] [PubMed] [Google Scholar]
- Mitchison TJ, Maddox P, Gaetz J, Groen A, Shirasu M, Desai A, Salmon ED, Kapoor TM. Roles of polymerization dynamics, opposed motors, and a tensile element in governing the length of Xenopus extract meiotic spindles. Mol Biol Cell. 2005;16:3064–3076. doi: 10.1091/mbc.E05-02-0174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mogilner A, Craig E. Towards a quantitative understanding of mitotic spindle assembly and mechanics. J Cell Sci. 2010;123:3435–3445. doi: 10.1242/jcs.062208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nedelec F, Surrey T. Assaying spatial organization of microtubules by kinesin motors. Methods Mol Biol. 2001;164:213–222. doi: 10.1385/1-59259-069-1:213. [DOI] [PubMed] [Google Scholar]
- Neumann B, Walter T, Heriche JK, Bulkescher J, Erfle H, Conrad C, Rogers P, Poser I, Held M, Liebel U, et al. Phenotypic profiling of the human genome by time-lapse microscopy reveals cell division genes. Nature. 2010;464:721–727. doi: 10.1038/nature08869. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicklas RB. Chromosome velocity during mitosis as a function of chromosome size and position. J Cell Biol. 1965;25(SUPPL):119–135. doi: 10.1083/jcb.25.1.119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicklas RB. Measurements of the force produced by the mitotic spindle in anaphase. J Cell Biol. 1983;97:542–548. doi: 10.1083/jcb.97.2.542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ohi R, Burbank K, Liu Q, Mitchison TJ. Nonredundant functions of Kinesin-13s during meiotic spindle assembly. Curr Biol. 2007;17:953–959. doi: 10.1016/j.cub.2007.04.057. [DOI] [PubMed] [Google Scholar]
- Salmon ED, Leslie RJ, Saxton WM, Karow ML, McIntosh JR. Spindle microtubule dynamics in sea urchin embryos: analysis using a fluorescein-labeled tubulin and measurements of fluorescence redistribution after laser photobleaching. J Cell Biol. 1984;99:2165–2174. doi: 10.1083/jcb.99.6.2165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato M, Schwartz WH, Selden SC, Pollard TD. Mechanical properties of brain tubulin and microtubules. J Cell Biol. 1988;106:1205–1211. doi: 10.1083/jcb.106.4.1205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawin KE, Mitchison TJ. Poleward microtubule flux mitotic spindles assembled in vitro. J Cell Biol. 1991;112:941–954. doi: 10.1083/jcb.112.5.941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tawada K, Sekimoto K. Protein friction exerted by motor enzymes through a weak-binding interaction. J Theor Biol. 1991;150:193–200. doi: 10.1016/s0022-5193(05)80331-5. [DOI] [PubMed] [Google Scholar]
- Tirnauer JS, Salmon ED, Mitchison TJ. Microtubule plus-end dynamics in Xenopus egg extract spindles. Mol Biol Cell. 2004;15:1776–1784. doi: 10.1091/mbc.E03-11-0824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine MT, Fordyce PM, Krzysiak TC, Gilbert SP, Block SM. Individual dimers of the mitotic kinesin motor Eg5 step processively and support substantial loads in vitro. Nat Cell Biol. 2006;8:470–476. doi: 10.1038/ncb1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valentine MT, Perlman ZE, Gardel ML, Shin JH, Matsudaira P, Mitchison TJ, Weitz DA. Colloid surface chemistry critically affects multiple particle tracking measurements of biomaterials. Biophys J. 2004;86:4004–4014. doi: 10.1529/biophysj.103.037812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walczak CE, Heald R. Mechanisms of mitotic spindle assembly and function. Int Rev Cytol. 2008;265:111–158. doi: 10.1016/S0074-7696(07)65003-7. [DOI] [PubMed] [Google Scholar]
- Wittmann T, Hyman T. Recombinant p50/dynamitin as a tool to examine the role of dynactin in intracellular processes. Methods Cell Biol. 1999;61:137–143. doi: 10.1016/s0091-679x(08)61978-0. [DOI] [PubMed] [Google Scholar]
- Yang G, Houghtaling BR, Gaetz J, Liu JZ, Danuser G, Kapoor TM. Architectural dynamics of the meiotic spindle revealed by single-fluorophore imaging. Nat Cell Biol. 2007;9:1233–1242. doi: 10.1038/ncb1643. [DOI] [PubMed] [Google Scholar]
- Zhai Y, Kronebusch PJ, Borisy GG. Kinetochore microtubule dynamics and the metaphase-anaphase transition. J Cell Biol. 1995;131:721–734. doi: 10.1083/jcb.131.3.721. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.